| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527005 | |
| Published online | 04 December 2015 | |
Third-order development of shape, gravity, and moment of inertia for highly flattened celestial bodies. Application to Ceres
1 IMCCE, Observatoire de Paris – PSL Research University, Sorbonne Universités – UPMC Univ. Paris 06, Univ. Lille 1, CNRS, 77 Avenue Denfert-Rochereau, 75014 Paris, France
e-mail: Nicolas.Rambaux@obspm.fr
2 LGLTPE, CNRS UMR5276, ENS de Lyon, Site Monod, 15 parvis René Descartes, 69007 Lyon, France
3 Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA 91109, USA
Received: 20 July 2015
Accepted: 4 November 2015
Context. We investigate the hydrostatic shape and gravitational potential coefficients of self-gravitating and rotating bodies large enough to have undergone internal differentiation and chemical stratification. Quantifying these properties under the assumption of hydrostatic equilibrium forms the basis for interpreting shape and gravity data in terms of interior structure and infer deviations from hydrostaticity that can bring information on the thermal and chemical history of the objects.
Aims. The main purpose is to show the importance of developing the reference hydrostatic shape for relatively fast rotating bodies up to third order to reach an accuracy of a few tens of meters. This paper especially focuses on Ceres, for which high-resolution shape data are being obtained by the Dawn spacecraft, with a projected accuracy better than 200 m/pixel.
Methods. To improve the accuracy on the determination of geodetic parameters, we numerically integrated Clairaut’s equations of rotational equilibrium expanded up to third order in a small parameter m, the geodetic parameter.
Results. Previous studies of Ceres have been based on shape models developed to first order. However, we show that the first-order theory underestimates (a−c) (where a and c are the equatorial and polar radii) by 1.8 km, which leads to underestimating the extent of mass concentration and is insufficient to interpret the upcoming observations by Dawn space mission. Instead, by using the third-order theory, we obtain an accuracy of 25 meters that is better than the accuracy expected from Dawn. Then, we derive the following geodetical quantities: flattening and other shape parameters, gravitational potential coefficients, and moments of inertia, by using the Ceres models constrained by observations obtained with the Hubble Space Telescope and ground-based adaptive optics telescopes. The difference in equatorial and polar radii for a large parametric space of interior models is investigated, and the large (a−c) corresponds to a model with a low density contrast.
Conclusions. This type of modeling will also prove instrumental to infer non-hydrostatic contributions to Ceres’ shape that are to be measured by Dawn.
Key words: planets and satellites: fundamental parameters / planets and satellites: individual: Ceres / methods: numerical
© ESO, 2015
1. Introduction
We revisit the hydrostatic equilibrium modeling of the global shape, gravity field, and moment of inertia for rapidly rotating bodies. This study is motivated by the arrival of the Dawn spacecraft at Ceres (Raymond et al. 2011), which is the main application of the proposed modeling approach. The global shape properties contain information on the density profile, which is critical to understanding a body’s current internal structure and past evolution (e.g., McCord & Sotin 2005; Castillo-Rogez & McCord 2010; Castillo-Rogez 2011). In addition, knowledge of the theoretical hydrostatic shape, gravity coefficients, and moments of inertia are necessary to assess non-hydrostatic contributions to the shape, which contain information on a body’s thermal current state and evolution.
The theoretical approach to modeling the hydrostatic equilibrium of a planet or satellite typically are first-order developments that are sufficient for most known bodies because these rotate slowly (i.e., tens of hours to a few days) (e.g., Dermott 1979; Zharkov et al. 1985) or simply because available observations are not accurate enough to justify more complex forward modeling. Earth is one of several exceptions, requiring a second-order development, because its parameters are more accurately known. Ceres also needs a high-order shape expansion because of its fast rotation and low density. Computing the hydrostatic shape for a multi-layered solid body is not straightforward and involves theoretical and numerical techniques to reach high-order accuracy. Here, we follow the currently best technique for Earth studies, which is based on Kopal (1960), Lanzano (1974), and Chambat et al. (2010).
In the first part of this paper (Sect. 2), we introduce the shape-modeling framework inherited from Earth geodetic studies by Chambat et al. (2010) and extended to third order by using the formalism of Lanzano (1974). Then we introduce the density profiles we used to apply our modeling to Ceres. We highlight the importance of using density profiles that preserve chemical balance, which would otherwise lead to erroneous interpretations (Sect. 3). Finally, we apply our third-order approach to three representative interior models of Ceres and compare these results with previous shape models. In addition, we compute the difference in equatorial and polar radii, a signature of internal differentiation, for a large parametric space.
2. Hydrostatic equilibrium models
The dwarf planet Ceres rotates at a period of 9.074170 ± 0.000001 h (Chamberlain et al. 2007). Under the assumption of hydrostatic equilibrium, its shape is spheroidal in response to the centrifugal and the self-gravitational potentials. Hence the hydrostatic shape is defined by the angular spin velocity and the radial density profile.
2.1. Homogeneous MacLaurin ellipsoid
It has long been known that an ellipsoid can be a hydrostatic self-gravitating equilibrium figure of a rotating homogeneous planet. For this Maclaurin’s ellipsoid, the eccentricity e (e.g., Chandrasekhar 1969) is given after 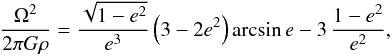 (1)where Ω is the angular spin velocity, G the gravitational constant, ρ the density, and e the eccentricity defined by
(1)where Ω is the angular spin velocity, G the gravitational constant, ρ the density, and e the eccentricity defined by 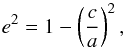 (2)with a and c the equatorial and polar radii, respectively.
(2)with a and c the equatorial and polar radii, respectively.
Equation (1) is either solved numerically or expanded in series of the small parameter 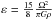 . In the latter case, the eccentricity is expressed as
. In the latter case, the eccentricity is expressed as 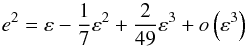 (3)up to the third order in ε. This yields the expansion of (a−c):
(3)up to the third order in ε. This yields the expansion of (a−c): 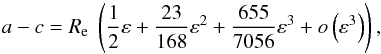 (4)where
(4)where ![\hbox{$R_{\rm e} = \sqrt[3]{a^2c}$}](/articles/aa/full_html/2015/12/aa27005-15/aa27005-15-eq16.png) is the equivolumetric radius of the ellipsoid. We use this expansion to quantify the uncertainties in the computation of the shape parameters at each order.
is the equivolumetric radius of the ellipsoid. We use this expansion to quantify the uncertainties in the computation of the shape parameters at each order.
2.2. Shape of a heterogeneous planet
The Maclaurin equation, Eq. (1), is valid for any eccentricity, but does not apply to stratified bodies. The shape modeling of radially heterogeneous planets originates in Clairaut’s work. It consists of solving the hydrostatic equilibrium equations to first order with respect to the height of equipotential surfaces, which is of first order with respect to the (small) geodetic parameter 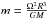 (M is the mass and R the external radius) (e.g., Kopal 1960; Moritz 1990; Murray & Dermott 1999). For the Earth, the method has been extended to the second order in m (Lanzano 1974; Chambat et al. 2010). For a fast rotator like Ceres, it is necessary to develop Clairaut’s approach up to third order to reach a hydrostatic shape estimate with an uncertainty of a few tens of meters consistently with the measurement accuracy expected from Dawn (Polanskey et al. 2014). We solve this problem following the equations provided in Lanzano (1974).
(M is the mass and R the external radius) (e.g., Kopal 1960; Moritz 1990; Murray & Dermott 1999). For the Earth, the method has been extended to the second order in m (Lanzano 1974; Chambat et al. 2010). For a fast rotator like Ceres, it is necessary to develop Clairaut’s approach up to third order to reach a hydrostatic shape estimate with an uncertainty of a few tens of meters consistently with the measurement accuracy expected from Dawn (Polanskey et al. 2014). We solve this problem following the equations provided in Lanzano (1974).
In this theory, the equipotential surfaces are described by their distance s to the center of the body for each co-latitude θ, and s is developed in the form of Legendre polynomials P2(cosθ),P4(cosθ),andP6(cosθ). Each surface is referenced by its mean spherical radius r in such a way that we write 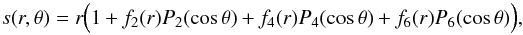 (5)where f2(r),f4(r),andf6(r) are functions to be determined. The condition that the surfaces must be equipotentials leads to differential relations that allow the numerical determination of these three functions for a given rotation velocity Ω and density profile ρ(r). We upgrade the free code provided by Chambat et al. (2010) with the third-order terms given by Lanzano (1974), Eqs. (26), (34), and (46). The shape parameters f2(r),f4(r),f6(r) are of magnitudes m, m2, and m3, respectively. Then the (a−c) radii difference is obtained by
(5)where f2(r),f4(r),andf6(r) are functions to be determined. The condition that the surfaces must be equipotentials leads to differential relations that allow the numerical determination of these three functions for a given rotation velocity Ω and density profile ρ(r). We upgrade the free code provided by Chambat et al. (2010) with the third-order terms given by Lanzano (1974), Eqs. (26), (34), and (46). The shape parameters f2(r),f4(r),f6(r) are of magnitudes m, m2, and m3, respectively. Then the (a−c) radii difference is obtained by 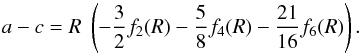 (6)
(6)
2.3. Gravity, mass, and moment of inertia
In the same way as for the shape, the external gravity potential can be expanded in the form of Legendre polynomials up to third order by 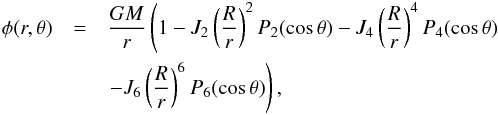 (7)where the gravitational coefficients J2n are non-dimensionalized using the length scale that we chose as the mean radius R. We here used the radius R to normalize all geodetical quantities since there is no reference value for a. When the Dawn measurements become available, these expressions can be normalized with the observed a, as is customary for Earth studies. Writing the condition that the external surface s(R,θ) is a gravity equipotential and expanding the quantities up to third order, we can express the gravitational coefficients as functions of the f2n and of m:
(7)where the gravitational coefficients J2n are non-dimensionalized using the length scale that we chose as the mean radius R. We here used the radius R to normalize all geodetical quantities since there is no reference value for a. When the Dawn measurements become available, these expressions can be normalized with the observed a, as is customary for Earth studies. Writing the condition that the external surface s(R,θ) is a gravity equipotential and expanding the quantities up to third order, we can express the gravitational coefficients as functions of the f2n and of m: ![\begin{eqnarray} J_2 & = & - \left[ f_2(\R) + \frac{m}{3} + \frac{11}{7} f_2^2(\R) + \frac{m}{7} f_2(\R) - \frac{223}{196} f_2^3(\R) \right. \nonumber \\[2mm] & & \left. - \frac{61}{196} m f^2_2(\R) - \frac{27}{28} f_4(\R) f_2(\R) - \frac{19}{84}m f_4(\R) \right] \left( \frac{a}{\RR} \right)^2 \nonumber \\[2mm] J_4 & = & - \left[ f_4(\R) + \frac{36}{35} f_2^2(\R) + \frac{6}{7} m f_2(\R) + \frac{594}{245} f_2^3(\R) \right. \nonumber \\[2mm] & & \left. + \frac{54}{245} m f_2^2(\R) \right] \left( \frac{a}{\RR} \right)^4 \nonumber \\[2mm] J_6 & = & - \left[ f_6(\R) +\frac{120}{77}m f_2^2(\R)+\frac{30}{11} f_4(\R) f_2(\R) \right. \nonumber \\[2mm] & & \left. +\frac{25}{33} m f_4(\R) + \frac{90}{77} f_2^3(\R) \right] \left( \frac{a}{\RR} \right)^6 \end{eqnarray}](/articles/aa/full_html/2015/12/aa27005-15/aa27005-15-eq37.png) (8)where the equatorial radius is given by
(8)where the equatorial radius is given by 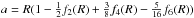 .
.
Other useful geodetic parameters are the mass and mean inertia (one third of the trace of the inertia tensor), which are defined as 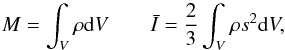 (9)where V is the volume of the body. We can write it with variables r,θ instead of s,θ using the Jacobian
(9)where V is the volume of the body. We can write it with variables r,θ instead of s,θ using the Jacobian 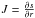 of the transformation. By defining the angular average of a function f over the unit sphere as
of the transformation. By defining the angular average of a function f over the unit sphere as 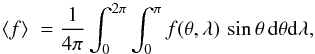 (10)we can express the mass and inertia for a stratified planet as
(10)we can express the mass and inertia for a stratified planet as 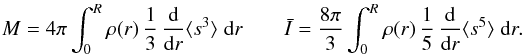 (11)Using Eq. (5) and after an expansion correct up to third order, we use the properties of Legendre polynomials (e.g., Lanzano 1974, Eqs. (12), (13)) to infer
(11)Using Eq. (5) and after an expansion correct up to third order, we use the properties of Legendre polynomials (e.g., Lanzano 1974, Eqs. (12), (13)) to infer
![\begin{eqnarray} && M = 4\pi \int_0^{\R} \rho(r) \left( 1 + \frac{3}{5} f_2^2 + \frac{2}{5} rf_2 \Ddroi{f_2}{r} + \frac{2}{35} f_2^3 \right. \nonumber \\ &&\qquad \left. + \frac{2}{35} rf_2^2 \Ddroi{f_2}{r} \right)r^2 {\rm d}r \\[2mm] && \bar{I} = \frac{8 \pi}{3} \int_0^{\R} \rho(r) \left( 1 + 2 f_2^2 + \frac{4}{5} rf_2 \Ddroi{f_2}{r} + \frac{4}{7} f_2^3 \right. \nonumber \\ &&\,\,\,\quad \left. + \frac{12}{35} rf_2^2 \Ddroi{f_2}{r} \right)r^4 {\rm d}r . \end{eqnarray}](/articles/aa/full_html/2015/12/aa27005-15/aa27005-15-eq47.png) This is different from the mass and inertia of the spherical reference model defined as
This is different from the mass and inertia of the spherical reference model defined as 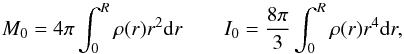 (14)and the differences between M and M0, as well as
(14)and the differences between M and M0, as well as 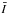 and I0, are of second order.
and I0, are of second order.
Notably, based on Eq. (5) and ⟨ Pn ⟩ = 0, the mean radius r is implicitly defined in this paper as r = ⟨ s ⟩ (Chambat et al. 2010). This is a practical definition for geophysics even if it does not conserve the mass. The equivolumetric radius preserves the mass but has a nonlinear definition: 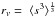 . Up to third order, the two are related after
. Up to third order, the two are related after 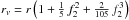 .
.
2.4. Radau-Darwin approximation
The Radau-Darwin approximation (RDA) establishes a relationship between the flattening, angular spin velocity, and the moment of inertia of a body. This approximation is valid only at first order because it is applied to solve Clairaut’s equations. It gives the following expression of the inertia (Chambat et al. 2010): 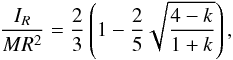 (15)where k is the degree-two Love number defined by
(15)where k is the degree-two Love number defined by 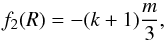 (16)which is computed from
(16)which is computed from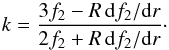 (17)We assess the inertia from the Radau-Darwin approximation to illustrate to which extend this first-order approximation is different from the third-order computation presented earlier.
(17)We assess the inertia from the Radau-Darwin approximation to illustrate to which extend this first-order approximation is different from the third-order computation presented earlier.
3. Ceres’ differentiation state
3.1. Chemical balance
Two types of interior models have been suggested for large ice-rock bodies like Ceres: (1) variable fractions of rock and ice distributed throughout the interior; (2) differentiation of a core of hydrated silicates and an ice-rich shell. Hydrated materials can store up to 10wt.% of water. A large proportion of hydrated materials are expected in Ceres by analogy with carbonaceous chondrite parent bodies (CM) and icy satellites (see Castillo-Rogez 2015, for a review). Ground-based observations also point to the direct detection of carbonates, and possibly brucite, two products of hydrothermal activity (Milliken & Rivkin 2009). Aqueous alteration is generally accompanied by the global scale redistribution of material as a consequence of the leaching of many elements under aqueous alteration. Some of these elements (especially alkali and earth alkaline) are soluble in water and eventually freeze in the form of hydrated salts (e.g., Kargel et al. 2000). Iron-rich compounds (e.g., iron sulfide) may sink and separate in a small seed, or at least lead to densification of the hydrated core with depth (e.g., Scott et al. 2002). Hence it is important that density profiles account for the chemical balance of hydrothermal systems so that the actual extent of differentiation of the interior is properly reflected.
However, previous models (e.g., Thomas et al. 2005; McCord & Sotin 2005) have assumed models of Ceres that were stratified with a core of density ~2700 kg/m3 and an icy shell at ~1000 kg/m3. These models did not properly account for the exchange of material from the rock to the icy shell as a consequence of leaching in hydrothermal conditions and also appear unrealistically devoid of metals. This problem was studied at length by Kargel et al. (2000), for example, who explored (in their Fig. 8) multiple chemical evolution pathways for Europa. This study showed that a model of Europa highly evolved from a geochemistry standpoint is characterized by a high moment of inertia as a result of the shell enrichment in a variety of salts and hydrates. Furthermore, Kirk & Stevenson (1987) pointed out that the oceanic layer of an icy body may be enriched in phyllosilicate particles that do not sink, but remain in suspension; these would eventually become trapped in Ceres’ frozen ocean layer at the interface between the shell and the rock-dominated core.
The average density of CM material (silicates mixed with salts metals Brearley 2006) taken as analog to Ceres’ core is about 2900 kg/m3 (e.g., McKinnon 1997). Following Scott et al. (2002), we have assumed that the metals separate from the silicates, a process that may not be warranted in the context of a low-gravity body like Ceres. The density of the shell is also difficult to estimate because it depends on the evolution of the salt mixture as the ice shell freezes and is a function of the temperature profile (Kargel 1991; Kargel et al. 2000). For this study we assumed an averaged salt and phyllosilicate density of between 1000 and 2000 kg/m3 based on Kargel et al. (2000) and Kirk & Stevenson (1987).
3.2. Test cases
Ceres dimensions.
Geophysical parameters of Ceres.
Preferred model of Ceres based on observations of Thomas et al. (2005) and Drummond et al. (2014) with a 5 km frozen ocean layer.
Several shape models are available for Ceres, derived from different observation techniques. Although the results are generally consistent with each other, the differences encompass a broad range of (a−c) values that overlap around 33–35 km, as shown in Table 1 (Millis et al. 1987; Thomas et al. 2005; Drummond & Christou 2008; Carry et al. 2008; Drummond et al. 2014). These studies are based on three different techniques: star occultation (Millis et al. 1987), visible imaging with the Hubble Space Telescope (HST; Thomas et al. 2005), and ground-based adaptive optics (AO) for the other references. Differences between the inferred shape models are in part due to the difference in the surface coverage enabled by the various techniques. As pointed out by Rivkin & Volquardsen (2008), longitudinal variations in the surface albedo are likely to induce a bias in the interpretation of optical images obtained over a short longitudinal range. Drummond et al. (2014) also noted the possible bias in limb fitting due to local darkening.
(a−c) radii difference for different interior models of Ceres assuming the mean radius derived from the Hubble Space Telescope observations by Thomas et al. (2005) (C1, C2, C3) and the mean radius derived from adaptive optics imaging Drummond et al. (2014) (C4).
We used the measurements of Thomas et al. (2005) and Drummond et al. (2014) because those of Thomas et al. (2005) are similar to the results of Drummond & Christou (2008) and the measurements of Drummond et al. (2014) are the most recent estimate of Ceres’ shape. The corresponding geophysical parameters are listed in Table 2. We used the same rotational periods as in these papers to facilitate the comparison of the computed shapes. The results are illustrated for four interior models. Three models use the Thomas et al. (2005) mass, radius and period: (C1) a homogeneous interior with a bulk density of 2077 kg m-3, (C2) a two-layer model with a core density of 2700 kg m-3 and an icy shell density of 1000 kg m-3, and (C3) a four-layer model whose stratification reflects a more realistic petrological model, with a core composed of Fe-FeS (5500 kg m-3), serpentine assemblage (2600 kg m-3), frozen ocean (1500 kg m-3), and ice layer (1000 kg m-3). The fourth model (C4) assumes the same structure as (C3) but using the Drummond et al. (2014) mass, radius and period. The parameters describing C3 and C4 are listed in Table 3.
4. Results
In this section we present the geodetic hydrostatic equilibrium computed for Ceres using the third-order approach described above for several petrological models. First, we assess the (a−c) radii using various methods. Then we present the gravity coefficients and moments of inertia for Ceres.
4.1. Shape models
Table 4 presents the (a−c) radii difference computed for several interior models and modeling methods. Column C1 shows the results for the homogeneous case. This case is used to provide a benchmark of the approximation intrinsic to the other approaches.
The first section of this table corresponds to the values numerically computed by the method described in Sect. 2.1. The results agree very well (below 0.001 m) with the Maclaurin solution displayed in the second section, which corresponds to the developments to first, second, and third order of the small parameter m. Moreoever, the last row of the Maclaurin section corresponds to the exact solution equal to 39.764 km. The departure of the first-order estimate from the exact value is significant (1.8 km). It is reduced to 200 meters and 25 meters at second and third order, respectively. Hence, development to third order is required for the forward modeling to be on the same level as Dawn’s observations. The numbers in parentheses correspond to the uncertainties computed at each order by using Eq. (4). These uncertainties are computed as the difference between the exact solution and the value obtained at each order. We assume that this uncertainty also applies to the heterogeneous models.
Column C1 also contains the analytical solution of the models of (c) Dermott (1979) and (d) Zharkov et al. (1985), which are developed to first order. The comparison of these values with the first order of this paper (a) agree well, as expected. Finally, the analytical method of (e) Thomas et al. (2005) agrees well with the exact value of the Maclaurin equation. The difference in (a−c) is about 150 meters, as quoted by Thomas et al. (2005).
 |
Fig. 1 Comparison of the solutions (a−c) for the models described in Table 3 with published observations. The blue boxes represent the values of (a−c) with uncertainties listed in Table 4 for the four models. For each model, the solutions are given with their uncertainties at first (left), second (center), and third order (right). Reported observations include Millis et al. (1987, Mi87), Thomas et al. (2005, Th05), Drummond & Christou (2008, Dr08), Carry et al. (2008, Ca08), and Drummond et al. (2014, Dr14). |
 |
Fig. 2 Differences between the equatorial and polar radii as a function of the thickness of the hydrated silicate layer for the broad parametric space described in Table 5 . Each dot corresponds to one model, and the dot separation shows the discretization used in the calculation. The blue dots correspond to models with a salt and phyllosilicate density below 1500 kg/m3, the green points to a density between 1500 kg/m3 and 2000 kg/m3, and red points to a density equal to 2000 kg/m3. |
The heterogeneous models described in Sect. 3.2 are reported in Cols. C2 through C4. The corresponding (a−c) values are lower than in the homogeneous case by 7 km at third order, including the uncertainties. This is a departure of 2 km from the first-order solution (accounting for uncertainties). However, it is outside the error bars of the HST shape model, which led Thomas et al. (2005) to conclude on the stratified nature of Ceres’ interior. The first-order computations with (c) and (d) agree very well, but the comparison with the determination of Thomas et al. (2005) shows a discrepancy of about 1 km for the C2 model.
Recently, Kong et al. (2010), Schubert et al. (2011), and Tricarico (2014) used an alternative approach to solve the hydrostatic shape of Ceres in terms of concentric ellipsoids. The problem with this approach is that the equilibrium shape cannot be described by heterogeneous ellipsoids as stated in Hamy’s theorem (Hamy 1889; Tassoul 1978; Moritz 1990). This equilibrium is possible only at first order in ellipticity (Clairaut’s equations); at higher orders, the equidensity surfaces can no longer be described by ellipsoids. This theorem is also called the “no go theorem” by Moritz (1990). On the other hand, the method developed by Hubbard (2012, 2013), which consists of a numerically computed closed equation, the interior equipotential surfaces, and gravitational coefficients, also yields an accurate solution of the shape, as demonstrated by this author for Jupiter.
Figure 1 illustrates that a 25-m shape measurement accuracy is required to separate the four selected interior models we highlighted here. In addition to these four examples, we built 16 343 interior models covering the range of parameters listed in Table 5. These models include an ice layer thickness of density 1000–1200 kg/m3 varying between 0 and 80 km (step 20 km); it overlies a mixture of ice, salts, and phyllosilicates ranging from 0 to 220 km. We fixed the density of this layer at 1000–2000 kg/m3, 50 kg/m3 steps to reduce the computer time. The deep interior consists of a hydrated silicate layer with a density varying between 2610 and 2990 kg/m3, which may overlie a metallic core with a density of 5500 kg/m3 of up to 80 km radius. We solved the equation of mass conservation and deduced the hydrated silicate layer thickness. Figure 2 shows the results of (a−c) to third order as a function of hydrated silicate layer thickness for core radius of 0 and 80 km, with color points as function of the densities chosen for the salt-phyllosilicates layer.
Gravity coefficients J2, J4, and J6, mean moments of inertia 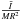 , moment of inertia of the spherical model
, moment of inertia of the spherical model 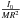 , moment of inertia computed with the RDA
, moment of inertia computed with the RDA 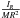 , M the mass of the flattened hydrostatic model, and M0 mass of the spherical model.
, M the mass of the flattened hydrostatic model, and M0 mass of the spherical model.
The first-order calculation would yield an offset of about −1.5 km for all models. Figure 2 shows that, as expected, the difference (a−c) is especially sensitive to the mass of material in the shell relative to the mass of the silicate mantle. Parameters of secondary influence are the thickness of an outer shell dominated by ice and the density of the hydrated silicate. On the other hand, (a−c) cannot distinguish the presence of a core. Upper limit models yield an (a−c) of about 35 km and cannot reproduce the mean 37.5 km radii difference reported by Drummond et al. (2014). They correspond to models without an ice layer on the top and density of phyllosilicates equal to 2000 kg/m3. Future observations of the shape combined with gravity field determinations will solve this uncertainty.
4.2. Gravity models
In addition to the equipotential shape, we computed and report in Table 6 the hydrostatic gravity coefficients of J2, J4, J6, the moments of inertia, and the masses for each interior models defined in Sect. 3.3. Table 6 shows that the difference in J2 amplitude between the homogeneous (C1) and the heterogeneous cases (C2, C3, C4) is about 30%. However, the variation of J2 across the set of heterogeneous cases (C2, C3, C4) is only ~3%. It is about 5% for J4 and less than 1% for J6. For the moment of inertia, whether 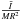 or
or 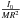 , the difference between the homogeneous (C1) and heterogeneous cases (C2, C3, C4) is about 11–13%, whereas the variation across the heterogeneous cases (C2, C3, C4) is below 3%. The values of the mean
, the difference between the homogeneous (C1) and heterogeneous cases (C2, C3, C4) is about 11–13%, whereas the variation across the heterogeneous cases (C2, C3, C4) is below 3%. The values of the mean 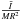 and mean spherical
and mean spherical 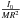 are similar, whereas the RDA overestimates that parameter by only 0.04%. This small offset agrees with Gao & Stevenson (2013), who found that the difference between the direct value of the moment of inertia and that computed via the RDA is small for fast-rotating bodies.
are similar, whereas the RDA overestimates that parameter by only 0.04%. This small offset agrees with Gao & Stevenson (2013), who found that the difference between the direct value of the moment of inertia and that computed via the RDA is small for fast-rotating bodies.
5. Discussion and conclusion
To infer the non-hydrostatic contributions to the shape and gravity, the hydrostatic shape needs to be accurately developed. We here investigated the hydrostatic shape and gravitational potential coefficients for Ceres. We expanded the Maclaurin solution to third order in small parameter m and compared test cases with the numerical integration of third-order Clairaut equations developed by Kopal (1960) and Lanzano (1974). We found that the third order is required to reach an accuracy below that expected for Dawn’s shape model (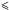 200 m/pixel) since the second order is inaccurate by about 200 meters. We also demonstrated that developments to first order underestimate the shape by up to 1.8 km. This in turn can lead to underestimating the extent of differentiation of Ceres’ interior. We also highlighted the importance of properly bookkeeping material redistribution for a body that is subject to early hydrothermal activity, as is believed to be the case for Ceres (Castillo-Rogez & McCord 2010; Castillo-Rogez 2015).
200 m/pixel) since the second order is inaccurate by about 200 meters. We also demonstrated that developments to first order underestimate the shape by up to 1.8 km. This in turn can lead to underestimating the extent of differentiation of Ceres’ interior. We also highlighted the importance of properly bookkeeping material redistribution for a body that is subject to early hydrothermal activity, as is believed to be the case for Ceres (Castillo-Rogez & McCord 2010; Castillo-Rogez 2015).
The Dawn spacecraft has been orbiting Ceres since March 2015 and will determine the shape, topography, and gravity field of Ceres with unprecedented accuracy (Raymond et al. 2011; Konopliv et al. 2011). Like for many other bodies, it is expected that the comparison of the measurements against the computed hydrostatic solution will reveal non-hydrostatic anomalies. The latter carry important information on past thermal evolution and large-scale events, such as large impact craters that may not have relaxed (e.g., Davison et al. 2015), fossil shape linked to a late stage of differentiation through silicate dehydration (Castillo-Rogez & McCord 2010), or large-scale material removal (Bowling et al. 2015). Supplementary information on the density profile can also be revealed by measuring the moment inertia by accurately measuring the precession-nutation motion from control point images and radio-science investigation as explained in Rambaux et al. (2011).
Acknowledgments
The authors are thankful to the anonymous referee for helpful comments. N. Rambaux is grateful to the CNU, Sect. 34, for supporting a six-month full-time research project through CRCT-2015 funding delivered by the MESR. Part of this work was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under contract to NASA.
References
- Bowling, T. J., Minton, D. A., Castillo-Rogez, J. C., Johnson, B. C., & Steckloff, J. K. 2015, in Proc. Astrobiol. Sci. Conf. 2015 [Google Scholar]
- Brearley, A. J. 2006, The Action of Water, eds. D. S. Lauretta, & H. Y. McSween, 584 [Google Scholar]
- Carry, B., Dumas, C., Fulchignoni, M., et al. 2008, A&A, 478, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castillo-Rogez, J. C. 2011, Icarus, 215, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Castillo-Rogez, J. C. 2015, Planetesimals, submitted [Google Scholar]
- Castillo-Rogez, J. C., & McCord, T. B. 2010, Icarus, 205, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Chambat, F., Ricard, Y., & Valette, B. 2010, Geophys. J. Int., 183, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Chamberlain, M. A., Sykes, M. V., & Esquerdo, G. A. 2007, Icarus, 188, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1969, Ellipsoidal figures of equilibrium, The Silliman Foundation Lectures (New Haven: Yale University Press) [Google Scholar]
- Davison, T. M., Collins, G. S., O’Brien, D. P., et al. 2015, in Lunar and Planetary Inst. Technical Rep., 46th, Lun. Planet. Sci. Conf., 2116 [Google Scholar]
- Dermott, S. F. 1979, Icarus, 37, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Drummond, J., & Christou, J. 2008, Icarus, 197, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Drummond, J. D., Carry, B., Merline, W. J., et al. 2014, Icarus, 236, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, P., & Stevenson, D. J. 2013, Icarus, 226, 1185 [NASA ADS] [CrossRef] [Google Scholar]
- Hamy, M. 1889, Annales de l’Observatoire de Paris, 19, F1 [Google Scholar]
- Hubbard, W. B. 2012, ApJ, 756, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Hubbard, W. B. 2013, ApJ, 768, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Kargel, J. S. 1991, Icarus, 94, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Kargel, J. S., Kaye, J. Z., Head, J. W., et al. 2000, Icarus, 148, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, R. L., & Stevenson, D. J. 1987, Icarus, 69, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, D., Zhang, K., & Schubert, G. 2010, J. Geophys. Res. (Planets), 115, 12003 [NASA ADS] [CrossRef] [Google Scholar]
- Konopliv, A. S., Asmar, S. W., Bills, B. G., et al. 2011, Space Sci. Rev., 163, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Kopal, S. 1960, Figures of Equilibrium of Celestial bodies (The University of Wisconsin Press) [Google Scholar]
- Kuchynka, P., & Folkner, W. M. 2013, Icarus, 222, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzano, P. 1974, Astrophys. Space Sci., 29, 161 [NASA ADS] [CrossRef] [Google Scholar]
- McCord, T. B., & Sotin, C. 2005, J. Geophys. Res. (Planets), 110, 5009 [Google Scholar]
- McKinnon, W. B. 1997, Icarus, 130, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Milliken, R. E., & Rivkin, A. S. 2009, Nature Geoscience, 2, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Millis, R. L., Wasserman, L. H., Franz, O. G., et al. 1987, Icarus, 72, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Moritz, H. 1990, The figure of the Earth: theoretical geodesy and the Earth’s interior (Karlsruhe: Wichmann) [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar system dynamics (Cambridge Univ. Press) [Google Scholar]
- Polanskey, C. A., Joy, S. P., Raymond, C. A., & Rayman, M. D. 2014, in 13th Int. Conf. on Space Operations 2014, Space Ops Conferences – AIAA 2014-1720, 2116 [Google Scholar]
- Rambaux, N., Castillo-Rogez, J., Dehant, V., & Kuchynka, P. 2011, A&A, 535, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raymond, C. A., Jaumann, R., Nathues, A., et al. 2011, Space Sci. Rev., 163, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Rivkin, A. S., & Volquardsen, E. L. 2008, in Lun. Planet. Sci. Conf., 39, 1920 [Google Scholar]
- Schubert, G., Anderson, J., Zhang, K., Kong, D., & Helled, R. 2011, Phys. Earth Planet. Interiors, 187, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, H. P., Williams, Q., & Ryerson, F. J. 2002, Earth Planet. Sci. Lett., 203, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, J.-L. 1978, Theory of rotating stars, Princeton Ser. Astrophys. (Princeton University Press) [Google Scholar]
- Thomas, P. C., Parker, J. W., McFadden, L. A., et al. 2005, Nature, 437, 224 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tricarico, P. 2014, ApJ, 782, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkov, V. N., Leontjev, V. V., & Kozenko, V. A. 1985, Icarus, 61, 92 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Preferred model of Ceres based on observations of Thomas et al. (2005) and Drummond et al. (2014) with a 5 km frozen ocean layer.
(a−c) radii difference for different interior models of Ceres assuming the mean radius derived from the Hubble Space Telescope observations by Thomas et al. (2005) (C1, C2, C3) and the mean radius derived from adaptive optics imaging Drummond et al. (2014) (C4).
Gravity coefficients J2, J4, and J6, mean moments of inertia 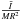 , moment of inertia of the spherical model
, moment of inertia of the spherical model 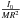 , moment of inertia computed with the RDA
, moment of inertia computed with the RDA 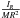 , M the mass of the flattened hydrostatic model, and M0 mass of the spherical model.
, M the mass of the flattened hydrostatic model, and M0 mass of the spherical model.
All Figures
 |
Fig. 1 Comparison of the solutions (a−c) for the models described in Table 3 with published observations. The blue boxes represent the values of (a−c) with uncertainties listed in Table 4 for the four models. For each model, the solutions are given with their uncertainties at first (left), second (center), and third order (right). Reported observations include Millis et al. (1987, Mi87), Thomas et al. (2005, Th05), Drummond & Christou (2008, Dr08), Carry et al. (2008, Ca08), and Drummond et al. (2014, Dr14). |
| In the text | |
 |
Fig. 2 Differences between the equatorial and polar radii as a function of the thickness of the hydrated silicate layer for the broad parametric space described in Table 5 . Each dot corresponds to one model, and the dot separation shows the discretization used in the calculation. The blue dots correspond to models with a salt and phyllosilicate density below 1500 kg/m3, the green points to a density between 1500 kg/m3 and 2000 kg/m3, and red points to a density equal to 2000 kg/m3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


