| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 8 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201526957 | |
| Published online | 18 November 2015 | |
The incidence of binaries in globular cluster stellar populations⋆,⋆⋆
1 INAF–Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
e-mail: sara.lucatello@oapd.inaf.it; raffaele.gratton@oapd.inaf.it; valentina.dorazi@oapd.inaf.it
2 Visiting scientist, European Southern Observatory, 85748 Garching, Germany
3 INAF–Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
e-mail: antonio.sollima@oabo.inaf.it; eugenio.carretta@oabo.inaf.it; angela.bragaglia@oabo.inaf.it
4 Department of Astronomy, Indiana University, Bloomington, IN 47401, USA
e-mail: evesperi@indiana.edu
5 Monash Centre for Astrophysics, School of Physics and Astronomy, Monash University, Clayton, VIC 3800, Australia
6 Department of Physics and Astronomy, Macquarie University, North Ryde, NSW 2109, Australia
Received: 13 July 2015
Accepted: 14 September 2015
Binary fraction and orbital characteristics provide indications on the conditions of star formation, as they shed light on the environment they were born in. Multiple systems are more common in low density environments than in higher density environments. In the current debate about the formation of globular clusters and their multiple populations, studying the binary incidence in the populations they host offers a crucial piece of information on the environment of their birth and their subsequent dynamical evolution. Through a multiyear observational campaign using FLAMES at VLT, we monitored the radial velocity of 968 red-giant-branch stars located around the half-light radii in a sample of ten Galactic globular clusters. We found a total of 21 radial velocity variables identified as bona fide binary stars, for a binary fraction of 2.2% ± 0.5%. When separating the sample into first generation and second generation stars, we find a binary fraction of 4.9% ± 1.3% and 1.2% ± 0.4%, respectively. Through simulations that take possible sources of bias into account in detecting radial velocity variations in the two populations, we show that the difference is significant and only marginally affected by these effects. This kind of different binary fraction strongly suggests different conditions in the environment of formation and evolution of first and second generations stars, with the latter being born in a much denser environment. Our result hence strongly supports the idea that the second generation forms in a dense subsystem at the center of the loosely distributed first generation, where (loose) binaries are efficiently destroyed.
Key words: binaries: general / binaries: spectroscopic / globular clusters: general
Based on data obtained with the Very Large Telescope at the European Southern Observatory, programs: 073.D-0100, 073.D-0211 and 083.D-0208.
Full Tables 1, 3, and table of the individual radial velocities are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/584/A52
© ESO, 2015
1. Introduction
Strong evidence has accumulated in the recent years supporting the concept that globular clusters (GCs) are composed of different stellar populations, characterized by differences in their chemical compositions (for reviews, see Gratton et al. 2004, 2012). In a typical globular cluster, about a third of the stars have element-to-element abundance ratios that are indistinguishable from those typically observed in field metal-poor stars with similar [Fe/H] values. However, the remaining (majority) stars show enhancements of some elements (N, Na, Al) and depletion of others (O, Mg), which can be attributed to high temperature H-burning, while, e.g., Fe-peak element abundances are very nearly the same in all stars. This abundance pattern is seen among all evolutionary phases (see Gratton et al. 2012, and references therein).
This has led most authors to think of a multiple generations scenario where the stars with peculiar composition (second generation, SG) formed from material lost at low velocity by a fraction of the stars with normal composition (first generation, FG; see, e.g., Ventura et al. 2001; Decressin et al. 2007). Recently, Bastian et al. (2013) proposed a scenario where the stars with peculiar composition actually formed together with those with normal composition, but accreted (quite a large) fraction of their mass from the ejecta of massive binaries. While this last scenario does not include two distinct stellar generations, it predicts the presence of stellar populations differing in chemical composition. For simplicity, throughout this paper we still use the terminology “first/second stellar generations” to distinguish between stars with primordial/altered chemical composition, respectively, although the real presence of different stellar generations is still under debate and one could refer to these two groups as pristine and enriched stars1.
FG and SG stars in globular clusters do not differ uniquely for their chemical composition. Several studies have demonstrated that at least in some clusters, the second generation stars are more centrally concentrated than the first generation stars (see, e.g., Sollima et al. 2007; Lardo et al. 2011; Milone et al. 2012; Kučinskas et al. 2014; but see also Larsen et al. 2015 for a study of M 15 showing that the primordial population fraction decreases from the outskirts to the half-mass radius and then increases again toward the very center). The correlation between chemical and dynamical properties may shed light onto the same mechanism of formation and evolution of the clusters (D’Ercole et al. 2008; Hénault-Brunet et al. 2015) in spite of the fact that they are very old objects.
The largest concentration of second generation stars suggest that they formed in higher density regions. On the other hand, two-body relaxation occurring in the long-term evolution of collisional systems like GCs tend to erase structural differences imprinted in the early stages of formation of these objects (Decressin et al. 2008; Vesperini et al. 2013).
Binary stars are the ideal tool to reveal the signature of primordial differences in the environment where FG and SG formed. Only a fraction of the primordial binaries are expected to survive the dynamical processes occurring during the evolution of a GC. The main process affecting the binary fraction is the ionization through collisions with single stars and other binaries whose efficiency depends on the environment density and velocity dispersion. So, the trace left by differences in the primordial environment, where FG/SG binaries formed on their fraction and period distribution, remain frozen and can still be visible today (Vesperini et al. 2011; Hong et al. 2015). In fact, while very wide binaries are destroyed even in environments with moderate density, and the closest binaries are expected to survive even at high densities, the destruction rate of those of intermediate separation, with binding energy comparable to the typical kinetic energy of cluster stars, is expected to strongly depend on the encounter rate and then on the density of their environment. We might then expect systematic differences in the fraction of this type of binaries among different generations. While there are several complicating factors, such as the segregation of binaries toward center of the clusters due to energy equipartition or the formation of new binaries in three-body encounters, it should still be possible to detect systematic differences in the frequency of binaries in stars of different stellar generations by comparing samples of stars of the different stellar generations observed at similar distances from the cluster center.
Studies of the fraction of binaries in clusters have been presented by several authors, based on both variation of radial velocities (RVs; see e.g., Yan & Mateo 1994; Yan & Cohen 1996; Yan & Reid 1996; Albrow et al. 2001; Sommariva et al. 2009), mainly in giants, and from photometry, mainly for main-sequence stars (see, e.g., Sollima et al. 2007; Rubenstein & Bailyn 1997; Ji & Bregman 2013; Dalessandro et al. 2011). Milone et al. (2012) presented a very extensive photometric study, based on the HST ACS survey, showing that the binary fraction is generally very low in globular clusters and is a function of the cluster absolute magnitude and, likely, of the cluster mass. Massive clusters have very few binaries, while the binary fraction in smaller clusters is much closer to the value observed in field stars and open clusters. While this result is of high interest, we are however not yet able to tag the stars observed by Milone et al. as members of different stellar generations, though this will perhaps be possible in the future through the analysis of the extensive photometric data gathered with the HST (see, e.g., Piotto et al. 2015).
To date, the largest homogeneous sample of GC stars with high resolution spectroscopy is that collected within the FLAMES Globular Cluster Na-O survey by Carretta et al. 2015, and references therein). Fe, O, and Na abundances have been measured for these objects, allowing them to be classified into first and second generation stars. The spectra also provide first epoch RVs. In the last few years, we gathered additional second epoch RVs for a significant fraction of these stars, which allowed us to measure RV variations and possibly indicating their membership in binary systems.
D’Orazi et al. (2010) studied the incidence of Ba stars in GC populations, finding that they are much more common among the so-called primordial population (essentially equivalent to the FG) than in the intermediate and extreme components, which make up the SG. This finding provided evidence of a different binary fraction in the GC populations. In fact, the abundance pattern characteristic of Ba stars originates from mass transfer in a binary from a companion of ~1.5 M⊙ during its asymptotic giant branch phase. Hence, while the incidence of Ba-stars does not measure the binary fraction of the parent population itself, it does trace it indirectly. In the same paper D’Orazi et al. also presented an RV based study of the binaries in NGC 6121, obtained a relatively large frequency of binaries for first generation stars, and only a low upper limit for the second generation stars, indicating a large difference between the two populations.
2. Observations and data analysis
We consider a combination of archival and proprietary data collected with the ESO Very Large Telescope at Cerro Paranal, using GIRAFFE-FLAMES (Pasquini et al. 2004). Proprietary observations were obtained within ESO programs 072.D-0507, 073.D-0211, 083.D-0208, 085.D-205, and 088.D-403. Programs 072.D-0507, 073.D-0211, and 083.D-0208 targeted 19 GCs with the aim of characterizing the Na-O anticorrelation in a large sample of GCs (see Carretta et al. 2009). Observations were collected using the HR11 and HR13 setups, which yield spectra in the range 5600–5840 Å with R ≃ 24 200, which are appropriate for the measurement of Na abundance, and 6120–6405 Å with R ≃ 22 500, for O abundances, respectively. Because of the choice of maximizing the number of targets observed with the UVES fibers, different exposures have slightly different fiber positionings, however, most stars are observed 1 for details) with each of the setups. For further details about the observations and the adopted target selection criteria, see Carretta et al. (2009).
Program 085.D-205 collected spectra with the HR21 setup (8757–9001 Å and R ~ 16 200) to derive Al abundances (using the same positionings) in four of the clusters (NGC 104, NGC 1904, NGC 6121, NGC 6752) involved in the Na-O survey. For one of the clusters, NGC 7078, we collected archival data (ESO program 080.B-0784) taken using the same fiber positionings as in our programs, using the HR14 setup, (6300–6690 Å, R ≃ 17 700). Finally, we collected data for six of the clusters (NGC 104, NGC 288, NGC 1851, NGC 3201, NGC 5904, NGC 7099) using the HR9 setup (5143–5356 Å, R ~ 25 900; program 088.B-403), centered on the Mg i b triplet. With the exception of the last one, the primary scientific aim of the different projects were abundance analysis, hence, the temporal baseline and spacing of the observations is far from ideal for a systematic search of RV variables.
The combination of this data set provides multiepoch observations with a baseline of at least 3 yr for ten GCs, namely: NGC 104 (47Tuc), NGC 1851, NGC 1904, NGC 288, NGC 3201, NGC 5904, NGC 61212 , NGC 6752, NGC 7078, and NGC 7099. Atmospheric parameters, Fe, Na, and O abundances are measured for all of the stars in the present sample (see Carretta et al. 2009, 2011, and references therein). Table 1 shows the details of the observations.
Observational log.
We reduced data with the standard ESO FLAMES GIRAFFE pipeline. We used different versions (2.5.1 and 2.5.3), however, this does not make any difference for the purposes of the present analysis, given that possible systematic shifts in RV introduced by differences in adopted wavelength calibrations are accounted for; see what follows in this section. Continuum fitting, sky, and telluric spectra subtractions were performed in IRAF3.
Number of stars considered.
For each cluster and setup, we selected the highest signal-to-noise ratio (S/N) spectrum and estimated the spectrum’s RV by identifying several dozens of spectral lines and measuring their shifts. These spectra were then brought to rest frame and then used as templates in the subsequent cross-correlation (performed with the IRAF task fxcor) with which we measured the RVs for the rest of the stars in the clusters. Appropriate barycentric corrections for the different spectra were applied to derive heliocentric RVs. Those derived from spectra taken within a 24 h period were averaged and considered as a single RV point. Before accomplishing this, we checked for RV shifts between the exposures taken within this period and found them to be negligible for all cluster members stars in all cases.
In the case of very metal poor clusters, such as NGC 7078 and NGC 1904, even combining exposures taken less than one day apart, errors on a single RV determination (which also takes into account the error introduced when shifting to a common RV system, see what follows in this section) for a star are quite large, ranging from ~0.5 to over 2 km s-1, while for more metal rich clusters, whose stars have spectra characterized by a large number of features, the error is typically much smaller, ~0.3 km s-1.
To check for systematic offsets between RVs measured from spectra collected with different setups and/or at different times and reduced with different version of the pipeline, we determined a 3 σ-clipped mean (after discarding outliers flagged from chemical composition as in Carretta et al. 2009) for the RV in each exposure. We then compared those mean values from each exposure in each setup and for each cluster. The derived offsets are quite small, ~0.2 km s-1, between spectra taken with the same setups at different times, while they are typically larger between different setups, as much as ~3 km s-1. This suggests the presence of systematic offsets, which might hamper the derivation of the correct RV and detection of RV variables. This offset between different setups has been noted by others, see, e.g., the cases discussed by the Gaia-ESO Survey (Lardo et al. 2015).
To address this problem, we proceeded as follows. For each cluster, we chose as reference frames the RV determined from spectra obtained with the HR11 setup. If multiple HR11 exposures existed, we selected that with the highest S/N. The reason behind the choice of this setup is that HR11, with HR13, is the only setup available for all clusters and the RV measured from the HR11 spectra typically have smaller errors than those from the HR13, especially for metal poor clusters. This could be because the spectral region covered with this setup has more detectable lines and less contamination from telluric lines, whose subtraction residuals can lead to larger uncertainties in the RV determinations via cross-correlation. For each frame a correction was calculated (accounting for the differences in the mean RV in that frame with respect to that of the reference frame) and applied to the individual RVs. This procedure brings all the RVs to a common system and minimizes the effects of instrumental/data reduction offsets in RV variable searches. The adopted RV errors on the individual stars account for the errors due to the application of these shifts, which are typically larger in clusters with fewer stars observed.
Because of the already discussed change of fiber positioning between different exposures, not all stars were observed in every single exposure. Moreover, because of the wide variety of extension and concentration of the clusters in our sample, due to FLAMES fiber collision limitations, the number of stars observed at more than one epoch for each clusters varies from 44 (NGC 7099) to 150 (NGC 6752; see Table 2 for details). Table 2 also lists the derived average RVs, which are in excellent agreement with those published in the Harris (1996) catalog. The derived velocity dispersions are generally smaller, which is what is expected given that Harris lists the central velocity dispersion, while our observations target stars around half-light radius.
Preston & Sneden (2001) found that velocity errors derived from multiple observations of constant RV metal-poor giant stars are larger than the error in RV from individual spectra by a factor of ~2–3. It is known that some metal-poor red giants exhibit velocity jitter to the level of ~1.5–2 km s-1 (Carney et al. 2003). This phenomenon seems to affect the intrinsically brightest stars only, within ~0.5–1 mag from the red giant branch tip and is unfortunately indistinguishable from RV variations as a result of its binarity. In five out of the ten clusters in our sample there are stars that meet this criterion (1 mag from the red giant tip), for a total of 17 objects. To ensure that our results are not influenced by the RV jitter, we have excluded those stars from our sample.
To determine the probability of RV variations, we follow the procedure described in Lucatello et al. (2005). We calculated for each star the χ2 value for the RV distribution and then evaluated the probability Q(χ2|f) that the RV values derived for each star are not compatible with different measurements of the same quantity, i.e., the probability that the observed scatter is due to an intrinsic change in the measured quantity rather than to experimental errors.
We consider a value of Q> 0.995, i.e., a probability that the observed RV variations arise from observational scatter P = 1−Q< 0.005, a positive RV variable identification. Our criterion is very restrictive and it is likely to fail to detect a non-negligible fraction of binaries in our sample. However, since our aim is to assess binarity ratio in a strictly differential way between the two populations (see next section), we prefer to minimize the number of false detections, which scale with P, rather than reaching higher completeness. Results are reported in Table 3.
Probability result for each star in the sample.
3. Discussion
While the clusters in our sample have in fact very different characteristics in terms of concentration and extension, our observations are typically concentrated around the half-light radius, i.e., the distance typical of the bulk of the stellar mass in a cluster. In Fig. 1, the distribution of distances from the cluster center (in units of half-mass radii; from the Harris catalog) of our observed sample is compared with that predicted for the entire cluster population. To compute this last quantity, we calculated the mass profiles of clusters in our sample from their best-fit King (1966) model, normalized to the number of targets and summed together. The two distributions are similar, with ours being slightly shifted toward more central stars, indicating that our sample is a fair representation of the entire cluster population. Therefore, conclusions derived for the stars in our sample apply to the bulk of the stars in the clusters.
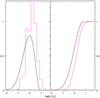 |
Fig. 1 Left panels: distribution of mass as a function of radius (expressed in half-light radius units) for our sample clusters (black) and distribution of stars observed in this study (magenta). Right panels: cumulative distribution for the mass of our sample GCs (black) and of the stars observed in this study (magenta). |
The sample of GCs observed in the present study is quite heterogeneous in terms of metallicity, mass, and horizontal-branch morphology, and it would be of great interest to study the binary fraction as a function of these characteristics. However, small number statistics hampers our capability of deriving a reliable binary fraction in each of the clusters and investigating any correlations of these characteristics with binarity. This exercise is thus not be attempted and the discussion is limited to the combined sample, which yields robust results.
Out of a grand total of 968 objects, 21 show evidence of RV variation at the 0.995 confidence level, for an overall binary fraction of 2.2% ± 0.5%. This fraction cannot be simply compared to the values found with other methods and/or other evolutionary stages (see, e.g., Milone et al. 2012; Ji & Bregman 2013, 2015; Moni Bidin et al. 2011), as it is established purely from RV variations measured in RGB stars with our particular observing pattern and RV precision, which is typically effective in detecting binaries with periods shorter than ~10 yr (see Sect. 4).
Moreover, it is limited to a very partial area within each cluster (because of the FLAMES field size) typically around the half-light radius, where the binary fraction is likely different from the cluster center.
Figure 2 shows the cumulative distributions of a few characteristics of the bona fide binaries and single stars, which also shows the p-value for a two-sided Kolmogorov-Smirnov test for each of the distributions. We see no significant difference in effective temperatures and luminosity distributions. There is no strong indication of a difference in distribution as a function of distance from cluster center (scaled with respect to the half-light radii of the respective cluster). The lack of such a finding does not exclude the presence of this kind of an effect, given the limited range in radius spanned by our study. On the other hand, the distributions of the Na enhancement (defined for each star as the difference between its [Na/Fe] and [Na/Fe]min for its host cluster, as listed in Carretta et al. 2009 and 2010), are very different for bona fide single and binary stars, with the latter having a typically lower Na content, in line with that typically found among FG stars.
In fact, when considering the binary fraction in the two populations, we emphasize that they are quite different. Our sample includes 288 FG and 604 SG stars, with 14 and 7 binaries, respectively. The number of stars in the combined sample is larger than the sum of FG and SG because, for 76 objects, Na abundances could not be measured, as the appropriate spectral range was not observed. So, since Na abundances are required to label a star as belonging to one of the populations, the stars without Na measurements are not labelled. The binary incidence in the two population is hence 4.9% ± 1.3% among FG stars and 1.2% ± 0.4% among SG stars.
This difference is quite striking. While we stress again that these values are by no means an accurate estimate of the overall binary fraction among these population, the ratios of the two fractions is a much more robust quantity. In fact, observations, reduction and analysis were performed identically, regardless of which population the object belonged to.
It is interesting to compare these results to the findings of D’Orazi et al. (2010). They reported an overall Ba fraction of ~0.4%, and an incidence among FG stars of ~2%, to be compared to our finding an overall binary fraction of 2.2% ± 0.5% and 4.9% ± 1.3%, respectively. The reported numbers are consistent with Ba stars being a special case among binaries, even if it should be kept in mind that small number statistics do play a role (out of 1205 stars they find just five Ba stars, four of which are FG).
When considering the binary fraction in NGC 6121, they reported an overall fraction of ~5%, ~1% for SG and ~12% for FG, which is a larger difference than we find in the overall sample. It should, however, be kept in mind that the present analysis adopts a procedure that minimizes the systematic effects on RV measurements due to using different setups and adopts a much more restrictive criterion to identify a star as a binary, making the results more robust.
There are, however, a number of biases that might in principle affect our findings. Figure 3 shows the same distributions as Fig. 2, but for FG and SG objects. Once again, there is no evidence of difference in radial distribution, which has however little significance, as discussed in the case of single vs. binary stars. Beside the obvious difference in the Na enhancement distributions, both effective temperature and luminosity distributions show marked differences in the two populations. This is not surprising: SG stars are expected to have an enhanced He content with respect to FG stars, and hence a slightly brighter magnitude; and higher luminosity (⟨ Δlog (L/L⊙) ⟩ = 0.11 ± 0.03, see Bragaglia et al. 2010). Given that the method followed to determine Teff in the present sample is based on the derivation of a temperature-magnitude relation, the difference in the temperature (⟨ ΔT ⟩ = 63 ± 15 K) distribution follows.
 |
Fig. 2 Cumulative distribution of distance from the center (scaled with respect to half-light radii), luminosity, effective temperature and Na enhancement (see text for definition) for bona fide binary (green) and single (black) stars, 21 and 931 objects respectively. The p-value for two-sided Kolmogorov-Smirnov test is also reported. |
This difference in luminosity should result in spectra of typically higher S/Ns for SG stars than for FG stars, which translate into smaller errors on the derived RVs. However, because of the nonuniformly accurate fiber positioning, the S/N is not related just to magnitude, but also depends on position on the field. Other factors that can play a (smaller) role are the abundance enhancement and depletion. In fact, spectra of SG stars have stronger Na lines than FG stars of similar atmospheric parameters, which produce stronger signatures in the cross-correlation and lower errors in RVs derived from HR11 spectra. On the other hand, SG stars have often depleted Mg abundances, yielding higher errors in the RV measured from HR9, which contains the Mg b triplet. A simple direct assessment of these biases is hard to quantify, however, simulations can provide an estimate of the completeness of the binary detections in the two populations.
4. Simulations and completeness
To estimate the completness of both samples of FG and SG stars, we simulated a synthetic population of binaries and applied the same technique, described in Sect. 2, to detect their velocity changes. For this purpose, for each observed target, we simulated a sample of 103 synthetic binaries by assuming a mass of the primary component of m1 = 0.8 M⊙ (typical of a GC RGB star) and randomly extracting a secondary component (m2) from a flat distribution (Milone et al. 2012) between 0.1 and 0.8 M⊙. We assigned periods (P) and orbital eccentricities (e), following the prescriptions of Duquennoy & Mayor (1991) and calculated the corresponding semimajor axes (a) using the third Kepler law. From this library of binaries we removed all those objects whose pericenter were smaller than a minimum separation linked to the volume averaged Roche lobe size (see Lee & Nelson 1988). We then calculated the projected velocity of the primary components via the following relation: 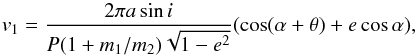 where α is the longitude of the periastron, i is the inclination angle, and θ is the phase from periastron. The distribution of the angles at the first epoch was chosen according to their corresponding probability distributions (Prob(i) = Prob(α) = const.; Prob
where α is the longitude of the periastron, i is the inclination angle, and θ is the phase from periastron. The distribution of the angles at the first epoch was chosen according to their corresponding probability distributions (Prob(i) = Prob(α) = const.; Prob ). Then, we calculated the sequence of phase angles according to the observational pattern of the associated target and derived the corresponding velocities. A velocity shift extracted from a Gaussian function with a standard deviation equal to the target uncertainty has been added to mimic the observational error. Finally, we applied the detection procedure described in Sect. 2 to the sample of synthetic binaries, and estimated the completeness as the fraction of recovered binaries. For comparison, we applied the same procedure to the sample of field metal-poor RGB stars of Carney et al. (2003).
). Then, we calculated the sequence of phase angles according to the observational pattern of the associated target and derived the corresponding velocities. A velocity shift extracted from a Gaussian function with a standard deviation equal to the target uncertainty has been added to mimic the observational error. Finally, we applied the detection procedure described in Sect. 2 to the sample of synthetic binaries, and estimated the completeness as the fraction of recovered binaries. For comparison, we applied the same procedure to the sample of field metal-poor RGB stars of Carney et al. (2003).
 |
Fig. 4 Binary detection completeness for the Carney et al. sample (in black), FG (blue), and SG (red) as a function of orbital period. |
The completeness as a function of the orbital period is shown in Fig. 4. As expected, the completeness of all samples decrease for increasing periods because of the smaller portion of the sampled velocity curve. The maximum completeness at short periods (<30 d) reaches ~70–80% dropping to 50% at P ~ 100 d, while at P> 104 d no binaries are expected to be detectable. It is apparent that the sample of FG binaries presents a slightly larger (by ~3.4%) completeness with respect to SG. This kind of difference, while significant, cannot explain the observed excess of FG/SG binaries reported in Sect. 3 unless the period distribution of FG and SG binaries were strikingly different. This last occurrence is however very unlikely. Indeed, to reproduce the detected ratio of FG/SG binaries one should assume that the majority of SG binaries have periods >104 d and corresponding semiaxes >10 AU. These wide binaries cannot survive in the dense environment of GCs since they are immediately ionized by collisions with other cluster stars.
From the completeness derived above, it is possible to check whether the fraction of binaries in the FG is compatible with that observed in the Galactic field. To accomplish this, we simulated a synthetic population made by a mixture of binaries and single stars. In this case, the period distribution of binaries has been truncated at 6000 d (the longest time lapse in the Carney et al. sample), corresponding to a maximum semiaxis of 7.7 AU.
We calculated the projected velocity of binaries as described above, while for singles we only added the shift due to the velocity uncertainty to a constant velocity. The fraction of binaries of the synthetic population has been tuned to reproduce the same ratio in the observed sample. In this way, we account for both the completeness and the false detections and we can estimate the global fraction of binaries for the different sample of GC and field stars. With this approach, we implicitly assume that FG, SG, and field binaries share the same period, eccentricity, and mass-ratio distribution. This assumption is clearly false, since only the hardest binaries (with short periods and smaller semiaxes) are expected to survive in GCs at odds with what happens in the Galactic field where collisions are almost absent.
On the other hand, this exercise provides a rough comparison between these different samples. The resulting binary fractions turns out to be 15.3%, 2.8%, and 45.6% for the FG, SG, and field samples, respectively. The above fractions appear in good agreement with the fractions estimated by Duquennoy & Mayor (1991) for field stars and Sollima et al. (2007) and Milone et al. (2012) for GCs. The above fractions depend on the adopted period upper limit: by assuming a period distribution truncated at P< 1000 d (corresponding to a maximum semiaxis a< 2.3 AU), they reduce to 11.6%, 2.8%, and 18.8% for the FG, SG, and field sample, respectively.
In any case, we conclude that the field contains a significantly larger fraction of binaries with respect to both FG and SG. Assuming a period distribution for GCs stars shifted to shorter periods would result in an even smaller fraction of binaries (the detection completeness of our observations is bigger in case of shorter periods), thus reinforcing this conclusion.
5. Conclusions
In this study we have presented the results of the RV monitoring of the largest sample to date of GC stars with measured composition. We detected 21 stars, which met our criteria to be identified as bona fide binary stars, 14 of which belong to the FG (which includes 288 stars) and 7 to the SG (604 stars), for resulting binary fractions of 4.9% ± 1.3% and 1.2% ± 0.4%, respectively.
Simulations have shown that we cannot account for this difference neither in terms of observational biases, which affect the binary detection completeness almost identically for FG and SG objects, nor in terms of different period distribution, as it would require SG to have such long periods (104 d) and corresponding semiaxes (>10 AU), which would imply immediate destruction at the typical cluster density.
Our findings are hence robust and provide strong evidence of an intrinsic different binary fraction in the parent populations of FG and SG stars. The observed difference is consistent with the results of theoretical studies on the dynamical evolution of binaries in multiple-population clusters (Vesperini et al. 2010; Hong et al. 2015) in which the SG forms in a dense subsystem at the center of the loose FG early cluster, as first suggested by D’Ercole et al. (2008). The denser environment in which SG stars form and evolve until SG and FG stars are completely mixed leads to an enhancement in the SG binary disruption and evolution. While initial differences in the FG and SG structural properties can be gradually erased during the cluster dynamical evolution, the fingerprints of these differences can still be visible in the different FG and SG binary fraction4.
While this is the most likely explanation, in principle, there are additional possibilities. The SG stars might have formed with a lower birth binary fraction because of their different composition. Variations of binary fraction as a function of metallicity and/or composition is a very poorly studied property of stellar population, however, to date no such effect has been reported in the literature. Differences in the FG and SG kinematical properties (like, e.g., anisotropy, rotation, etc.) in combination with differences in the spatial structure might affect the survival rate for FG and SG binaries. Finally, the fact that the SG stars are, at a given time, expected to have on average slightly smaller masses (because of the slightly shorter lifetime of He enriched stars), the SG binaries have on a average a smaller binding energy (which scales with m2), resulting on a smaller binary fraction. This effect is expected to be very small and could not explain the present results.
Finally in the context of the link between globular clusters and halo field stars and the possible contribution of globular clusters to the assembly of the Galactic halo, it is interesting to point out our results concerning the comparison between the binary fraction in clusters and in the field. In particular for P< 1000 d, we find that the FG binary fraction is 11.6% (the SG is 2.8%), while that of the field population is about 18.8%. The FG binary population, according to the scenario outlined above, is less affected by dynamical processes than the SG and its binary fraction is indeed much more similar to that of the field population. Considering that FG binaries evolved for one Hubble time in a cluster environment (though less concentrated than SG binaries) and that the estimated fraction includes long-period binaries, the difference found between FG and field binary fraction might be due to dynamical effects.
The FG cluster stars share similar chemical properties with halo stars (Gratton et al. 2012). Multiple-population cluster formation models based on self-enrichment predict that the FG population was initially significantly more massive, was released in the halo during the cluster early evolution (see, e.g., D’Ercole et al. 2008), and possibly contributed significantly to halo field population.
Some theoretical and observational efforts to constrain the possible contribution of clusters to the halo have already been made (see, e.g., Carretta et al. 2009; Martell et al. 2011; Lind et al. 2015; Vesperini et al. 2010; Schaerer & Charbonnel 2011), however, the wealth of data that will soon be available through several upcoming or ongoing surveys (APOGEE, Gaia-ESO, GALAH, WEAVE etc.) will allow us to address this issue more thoroughly.
Even more recently however Bastian et al. (2015) have argued that no self-enrichment scenario can explain the full variety of phenomena observed in GCs.
The present findings are compatible also with the early disk accretion hypothesis put forward by Bastian et al. (2013). In fact, in this kind of scenario, the circumstellar disks on which accretion of polluting material takes place have radii of ~100 AU. On the other hand, our technique is effective in detecting binaries that have typically a smaller semiaxis, on the order of 10 AU, and the presence of this kind of closeby companion would hamper the formation and stability of the circumstellar disk, preventing the accretion of polluting material and thus the imprinting of chemical signatures typical of the SG on binary stars.
Acknowledgments
This research was partially supported by the Munich Institute for Astro- and Particle Physics (MIAPP) of the DFG cluster of excellence “Origin and Structure of the Universe”. S.L., A.S., E.C., A.B. acknowledge partial support from PRIN-MIUR 2010-2011 PI Francesca Matteucci Evoluzione chimica e dinamica della nostra galassia e delle galassie del gruppo locale. E.V. acknowledges support by grants NASA-NNX13AF45G and HST-12830.01-A.
References
- Albrow, M. D., Gilliland, R. L., Brown, T. M., et al. 2001, ApJ, 559, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Lamers, H. J. G. L. M., de Mink, S. E., et al. 2013, MNRAS, 436, 2398 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bastian, N., Cabrera-Ziri, I., & Salaris, M. 2015, MNRAS, 449, 3333 [NASA ADS] [CrossRef] [Google Scholar]
- Bragaglia, A., Carretta, E., Gratton, R., et al. 2010, A&A, 519, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carney, B. W., Latham, D. W., Stefanik, R. P., Laird, J. B., & Morse, J. A. 2003, AJ, 125, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2009, A&A, 505, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Lucatello, S., Gratton, R. G., Bragaglia, A., & D’Orazi, V. 2011, A&A, 533, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carretta, E., Bragaglia, A., Gratton, R. G., et al. 2015, A&A, 578, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalessandro, E., Lanzoni, B., Beccari, G., et al. 2011, ApJ, 743, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Decressin, T., Charbonnel, C., & Meynet, G. 2007, A&A, 475, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decressin, T., Baumgardt, H., & Kroupa, P. 2008, A&A, 492, 101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
- D’Orazi, V., Gratton, R., Lucatello, S., et al. 2010, ApJ, 719, L213 [NASA ADS] [CrossRef] [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Hénault-Brunet, V., Gieles, M., Agertz, O., & Read, J. I. 2015, MNRAS, 450, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, J., Vesperini, E., Sollima, A., et al. 2015, MNRAS, 449, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, J., & Bregman, J. N. 2013, ApJ, 768, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Ji, J., & Bregman, J. N. 2015, ApJ, 807, 32 [NASA ADS] [CrossRef] [Google Scholar]
- King, I. R. 1966, AJ, 71, 64 [Google Scholar]
- Kučinskas, A., Dobrovolskas, V., & Bonifacio, P. 2014, A&A, 568, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lardo, C., Bellazzini, M., Pancino, E., et al. 2011, A&A, 525, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lardo, C., Pancino, E., Bellazzini, M., et al. 2015, A&A, 573, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsen, S. S., Baumgardt, H., Bastian, N., et al. 2015, ApJ, 804, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H. M., & Nelson, L. A. 1988, ApJ, 334, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K., Koposov, S. E., Battistini, C., et al. 2015, A&A, 575, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lucatello, S., Tsangarides, S., Beers, T. C., et al. 2005, ApJ, 625, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Martell, S. L., Smolinski, J. P., Beers, T. C., & Grebel, E. K. 2011, A&A, 534, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012, A&A, 540, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moni Bidin, C., Villanova, S., Piotto, G., & Momany, Y. 2011, A&A, 528, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pasquini, L., Castillo, R., Dekker, H., et al. 2004, Proc. SPIE, 5492, 136 [Google Scholar]
- Piotto, G., Milone, A. P., Bedin, L. R., et al. 2015, AJ, 149, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Preston, G. W., & Sneden, C. 2001, AJ, 122, 1545 [NASA ADS] [CrossRef] [Google Scholar]
- Rubenstein, E. P., & Bailyn, C. D. 1997, ApJ, 474, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., & Charbonnel, C. 2011, MNRAS, 413, 2297 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Sollima, A., Beccari, G., Ferraro, F. R., Fusi Pecci, F., & Sarajedini, A. 2007, MNRAS, 380, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Sommariva, V., Piotto, G., Rejkuba, M., et al. 2009, A&A, 493, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., D’Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Vesperini, E., McMillan, S. L. W., D’Antona, F., & D’Ercole, A. 2010, ApJ, 718, L112 [NASA ADS] [CrossRef] [Google Scholar]
- Vesperini, E., McMillan, S. L. W., D’Antona, F., & D’Ercole, A. 2011, MNRAS, 416, 355 [NASA ADS] [Google Scholar]
- Vesperini, E., McMillan, S. L. W., D’Antona, F., & D’Ercole, A. 2013, MNRAS, 429, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., & Cohen, J. G. 1996, AJ, 112, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., & Mateo, M. 1994, AJ, 108, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., & Reid, I. N. 1996, MNRAS, 279, 751 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Left panels: distribution of mass as a function of radius (expressed in half-light radius units) for our sample clusters (black) and distribution of stars observed in this study (magenta). Right panels: cumulative distribution for the mass of our sample GCs (black) and of the stars observed in this study (magenta). |
| In the text | |
 |
Fig. 2 Cumulative distribution of distance from the center (scaled with respect to half-light radii), luminosity, effective temperature and Na enhancement (see text for definition) for bona fide binary (green) and single (black) stars, 21 and 931 objects respectively. The p-value for two-sided Kolmogorov-Smirnov test is also reported. |
| In the text | |
 |
Fig. 3 Same as Fig. 3 for FG (red) and SG (blue) objects. |
| In the text | |
 |
Fig. 4 Binary detection completeness for the Carney et al. sample (in black), FG (blue), and SG (red) as a function of orbital period. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


