| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 8 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201526661 | |
| Published online | 20 November 2015 | |
Unified numerical model of collisional depolarization and broadening rates that are due to hydrogen atom collisions
1 Astronomy Deptment, Faculty of Science, King Abdulaziz University, 21589 Jeddah, Saudi Arabia
e-mail: derouichmoncef@gmail.com
2 Sousse University, ESSTHS, Lamine Abbassi street, 4011 H. Sousse, Tunisia
3 Ain Shams University, Faculty of Science, Department of Physics, Abbassia, 11 566 Cairo, Egypt
4 The British University in Egypt (BUE), 11 837 Cairo, Egypt
5 Theoretical Astrophysics, Department of Astronomy and Space Physics, Uppsala University, Box 515, S 751 20 Uppsala, Sweden
Received: 3 June 2015
Accepted: 26 August 2015
Context. Accounting for partial or complete frequency redistribution when interpreting solar polarization spectra requires data on various collisional processes. Data for depolarization and polarization transfer are needed, but are often lacking, while data for collisional broadening are usually more readily available. Recently it was concluded that despite underlying similarities in the physics of collisional broadening and depolarization processes, the relations between them cannot be derived purely analytically.
Aims. We aim to derive accurate numerical relations between the collisional broadening rates and the collisional depolarization and polarization transfer rates that are due to hydrogen atom collisions. These relations would enable accurate and efficient estimates of collisional data for solar applications.
Methods. Using earlier results for broadening and depolarization processes based on general (i.e., not specific to a given atom), semi-classical calculations that employ interaction potentials from perturbation theory, we used genetic programming (GP) to fit the available data and generate analytical functions describing the relations between them. The predicted relations from the GP-based model were compared with the original data to estimate the accuracy of the method.
Results. We obtain strongly nonlinear relations between the collisional broadening rates and the depolarization and polarization transfer rates. They are shown to reproduce the original data with an accuracy of about 5%. Our results allow determining the depolarization and polarization transfer rates for hyperfine or fine-structure levels of simple and complex atoms.
Conclusions. We show that by using a sophisticated numerical approach and a general collision theory, useful relations with sufficient accuracy for applications are possible.
Key words: scattering / line: formation / atomic processes / polarization / Sun: atmosphere / line: profiles
© ESO, 2015
1. Introduction
Accounting for partial or complete frequency redistribution when interpreting solar polarization spectra (the so-called second solar spectrum) requires understanding the collisional processes that occur in the solar atmosphere. In particular, data for depolarization and polarization transfer by collisions with the most abundant perturber, hydrogen atoms, are needed, but they are often lacking and therefore are neglected in modelling. On the other hand, data for collisional broadening that is due to hydrogen collisions are usually more readily available. It would be helpful to understand the possible relations between these processes to enable accurate and efficient estimates of depolarization data, which would further our understanding of the formation of the second solar spectrum.
During the 1990s, Anstee, Barklem and O’Mara (ABO) developed a semi-classical theory for collisional line broadening by neutral hydrogen (Anstee 1992; Anstee & O’Mara 1991, 1995; Anstee et al. 1997; Barklem 1998; Barklem & O’Mara 1997; Barklem et al. 1998). This theory was later extended by Derouich, Sahal-Bréchot & Barklem (DSB) to the depolarization and polarization transfer by collisions with neutral hydrogen (see for example Derouich et al. 2003a,b, 2004 and Derouich 2004). The same potentials, based on the Rayleigh-Schrödinger perturbation theory in the Unsöld approximation, the so-called RSU potentials, were used in both cases. In addition, the same time-dependent Schrödinger equation was solved to obtain the scattering S-matrix; an essential ingredient in the determination of the collisional depolarization and broadening rates.
A great advantage of the ABO and DSB methods is that they are general, that is, not specific to a given perturbed atom or ion, and therefore adaptable to any neutral or singly ionised atom. The general, semi-classical methods of ABO and DSB give results that agree well with accurate but time-consuming quantum chemistry calculations to better than 20% for solar temperatures (T ~ 5000 K). For instance, at T = 5000 K, the difference between results for depolarization rates from the general semi-classical theory (Derouich et al. 2003a) and quantal results is 11% for Mg i 3p 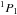 , 8% for Ca i 4p
, 8% for Ca i 4p 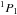 , and 13% for Na I 3p
, and 13% for Na I 3p 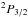 . In addition, Derouich et al. (2006) showed in their Fig. 6 that the error bar on their collisional rate determination is located well within the expected error bar on the value of the solar magnetic field. They showed that the error bar for the magnetic field determination that is due to the typical uncertainty in DSB collisional depolarization rates is similar to the error bar for the magnetic field value that is due to a polarimetric uncertainty of ~10-4, which corresponds to the uncertainty attainable with polarimeters such as the Zurich IMaging POLarimeter (ZIMPOL) and the Heliographic Telescope for the Study of the Magnetism and Instabilities on the Sun (THEMIS).
. In addition, Derouich et al. (2006) showed in their Fig. 6 that the error bar on their collisional rate determination is located well within the expected error bar on the value of the solar magnetic field. They showed that the error bar for the magnetic field determination that is due to the typical uncertainty in DSB collisional depolarization rates is similar to the error bar for the magnetic field value that is due to a polarimetric uncertainty of ~10-4, which corresponds to the uncertainty attainable with polarimeters such as the Zurich IMaging POLarimeter (ZIMPOL) and the Heliographic Telescope for the Study of the Magnetism and Instabilities on the Sun (THEMIS).
The underlying similarity between collisional depolarization and broadening processes as calculated by DSB and ABO suggests the possibility of establishing relations between them. The possibility of obtaining such relations was examined from a theoretical viewpoint by Sahal-Bréchot & Bommier (2014). However, they concluded that there is no possible purely analytical relation between the collisional depolarization rate and the collisional broadening coefficient, even if the same basic methods and computer codes can be used to obtain the interaction potentials and collisional scattering matrix. In this work we aim to provide these relations between the results of the ABO and DSB methods through a numerical approach.
The paper is organized as follows. In Sect. 2 we briefly review the basic definitions and notations and describe the collisional data employed in the context of this work. Section 3 explains the optimization approach used to obtain the unified numerical model. The results for simple atoms without hyperfine structure, simple atoms with hyperfine structure, and complex atoms are presented in Sect. 4. We conclude in Sect. 5.
2. Background and theory
The theory of partial or complete redistribution of polarized radiation in a magnetized plasma, which permits determining the Stokes parameters, must account for the effects of collisions (e.g. Stenflo 1994; Bommier 1997a,b; Landi Degl’Innocenti et al., 1997, Casini et al. 2014). The resulting effect of the collisional depolarization and the collisional broadening by neutral hydrogen is accompanied by a variety of interesting spectropolarimetry effects. Collisions mainly produce three distinct but correlated effects: depolarization and polarization transfer, line broadening, and frequency redistribution in scattering events (partial destruction of the correlation between incident and scattered frequencies). The theory of collisions and their relation to the theory of polarization in spectral lines is expounded in detail elsewhere (e.g. Stenflo 1994; Landi Degl’Innocenti & Landolfi 2004). Here we recall the important relations for our work and define our notations.
We consider the broadening of the line profile between the initial electronic state | nl1 ⟩ and the final state | nl2 ⟩, where n is the principal quantum number and l1 and l2 are the orbital angular momentum quantum numbers of the states | nl1 ⟩ and | nl2 ⟩, respectively. We denote by ml1 and ml2 the projections of the orbital angular momentums l1 and l2 onto the interatomic axis, which is taken as the axis of quantization (see ABO papers for more details). Figure 1 shows examples of the collisions that result in the broadening of the line profile for the transition between the initial electronic state | nl1 ⟩ and the final state | nl2 ⟩. The ABO theory neglects the effects of the spin, which means that fine structure is ignored. As in the ABO theory, we consider two electronic states | nl1 ⟩ and | nl2 ⟩ connected by a radiative transition. The collisional broadening of the line pofile between the levels | nl1 ⟩ and | nl2 ⟩ is a linear combination of all the collisional rates between the Zeeman sublevels inside the state | nl1 ⟩ and the collisional rates between the Zeeman sublevels inside the state | nl2 ⟩.
 |
Fig. 1 Examples of the collisions that result in the broadening of the line profile for the transition between the initial electronic state | nl1 ⟩ and the final state | nl2 ⟩. Level spacings are not to scale. |
To calculate the depolarization rates of the fine structure level | nlJ ⟩, DSB used the basis of irreducible tensorial operators, and the atomic states are described by the density matrix elements 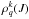 where the tensorial order 0 ≤ k ≤ 2J and the coherence −k ≤ q ≤ k. More details about the physical meaning of the tensorial order k and the coherence q can be found, for instance, in Omont (1977), Sahal-Bréchot (1977), and Landi Degl’Innocenti & Landolfi (2004). We denote by Dk(J) the depolarization rates and by
where the tensorial order 0 ≤ k ≤ 2J and the coherence −k ≤ q ≤ k. More details about the physical meaning of the tensorial order k and the coherence q can be found, for instance, in Omont (1977), Sahal-Bréchot (1977), and Landi Degl’Innocenti & Landolfi (2004). We denote by Dk(J) the depolarization rates and by 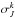 the depolarization cross sections. The depolarization rate of the fine structure level | nlJ ⟩ is a linear combination of the purely elastic collisions that occur between Zeeman sublevels | nlJMJ ⟩ (see Fig. 2). MJ is the projection of the total angular momentum J on the interatomic axis, which is taken as the axis of quantization (see DSB papers for more details).
the depolarization cross sections. The depolarization rate of the fine structure level | nlJ ⟩ is a linear combination of the purely elastic collisions that occur between Zeeman sublevels | nlJMJ ⟩ (see Fig. 2). MJ is the projection of the total angular momentum J on the interatomic axis, which is taken as the axis of quantization (see DSB papers for more details).
 |
Fig. 2 Examples of the collisions that result in depolarization of the state | nlJ ⟩. Level spacings are not to scale. |
The polarization transfer rates from the | nlJ1 ⟩ to the level | nlJ2 ⟩ are denoted by Ck(J1 → J2); 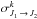 are the polarization transfer cross sections. Figure 3 shows that the transfer of polarization between the levels | nlJ1 ⟩ and | nlJ2 ⟩ is a linear combination of the inelastic collisional rates between the Zeeman sublevels of the level | nlJ1 ⟩ and the Zeeman sublevels of the level | nlJ1 ⟩. The inealstic collisions that contribute to the polarization transfer rates occur inside one electronic state.
are the polarization transfer cross sections. Figure 3 shows that the transfer of polarization between the levels | nlJ1 ⟩ and | nlJ2 ⟩ is a linear combination of the inelastic collisional rates between the Zeeman sublevels of the level | nlJ1 ⟩ and the Zeeman sublevels of the level | nlJ1 ⟩. The inealstic collisions that contribute to the polarization transfer rates occur inside one electronic state.
 |
Fig. 3 Schematic representation of the collisional transfer of polarization between different fine structure levels. Level spacings are not to scale. |
The depolarization rates and the polarization transfer rates are 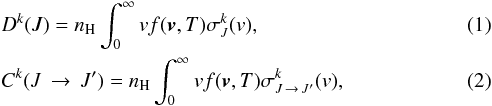 where DSB found a similar power-law relation with velocity:
where DSB found a similar power-law relation with velocity: 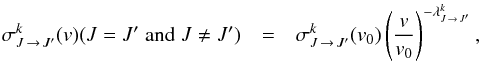 (3)with
(3)with 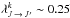 . The DSB cross sections, as the ABO cross sections, are tabulated for a reference velocity of v0 = 104 m s-1.
. The DSB cross sections, as the ABO cross sections, are tabulated for a reference velocity of v0 = 104 m s-1.
The probability that a collision does not destroy the polarization associated with a 2k-multipole during a scattering event is (e.g. Eq. (10.19) of Stenflo 1994) 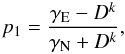 (4)where γE is the elastic collision rate, γN the radiative broadening rate, and Dk is the rate of depolarizing collisions. The probability that the tensorial order k is collisionally destroyed during the scattering process is (Eq. (10.21) of Stenflo 1994)
(4)where γE is the elastic collision rate, γN the radiative broadening rate, and Dk is the rate of depolarizing collisions. The probability that the tensorial order k is collisionally destroyed during the scattering process is (Eq. (10.21) of Stenflo 1994) 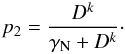 (5)The ratio of these probabilities is
(5)The ratio of these probabilities is 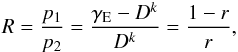 (6)where r = Dk/γE. r should not be greater than unity since the rate of elastic collisions leading to depolarization may not exceed the total elastic collision rate.
(6)where r = Dk/γE. r should not be greater than unity since the rate of elastic collisions leading to depolarization may not exceed the total elastic collision rate.
For an isolated spectral line in which inelastic collisions are assumed negligible and if lower state interactions are ignored, the full width at half maximum (FWHM) of the collisionally broadened line, γC, in the impact approximation is equal to the total elastic collision rate γE; see, for instance, Baranger (1962). In line broadening calculations, including the ABO theory, the broadening cross section is commonly defined such that it gives the half width (HWHM), here denoted w (see below). In this case therefore r = Dk/γE ≈ Dk/γC = Dk/ (2w), and so in this work we find it convenient to define 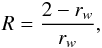 (7)where
(7)where 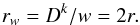 (8)The collisional line width is defined in terms of the broadening cross section σw, by
(8)The collisional line width is defined in terms of the broadening cross section σw, by 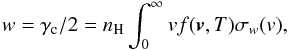 (9)where f(v,T) is the Maxwellian velocity distribution for a local temperature T and nH the perturber density. ABO found that the cross sections have approximately a power-law behaviour with velocity, such that they define
(9)where f(v,T) is the Maxwellian velocity distribution for a local temperature T and nH the perturber density. ABO found that the cross sections have approximately a power-law behaviour with velocity, such that they define 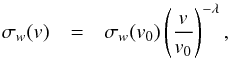 (10)where v0 = 104 m s-1 is the reference velocity for which cross sections are tabulated and λ is the so-called velocity exponent. ABO found that λ has a limited variation range of about 0.25 and, as a result, that w typically results in a temperature dependence of T0.38.
(10)where v0 = 104 m s-1 is the reference velocity for which cross sections are tabulated and λ is the so-called velocity exponent. ABO found that λ has a limited variation range of about 0.25 and, as a result, that w typically results in a temperature dependence of T0.38.
We note that several works have attempted to make simple estimates of the relation between broadening and depolarization. Smitha et al. (2014) calculated the case where the interaction between particles can be described by a single tensor operator of given rank, using the equations given by Landi Degl’Innocenti & Landolfi (2004). They calculated for their specific case a Sc ii line with an upper state of J = 2 for rank 1 and 2 operators and found that r = D2/γE = 0.1 and 0.243 (or rw = 0.2 and 0.486), respectively. Interactions of rank 1 correspond to the dipolar interaction, and those of rank 2 correspond to dipole-dipole interactions; neither is strictly applicable to atom-atom or atom-ion interactions. Faurobert et al. (1995) found r = D2/γC = 0.5 (or rw = 1) for the Sr i resonance line.
The ABO and DSB calculations consider a simple neutral atom with only one optical electron with orbital angular momentum 0 ≤ l ≤ 3, that is, s-, p-, d- and f-states. We note that while the theories can be used for singly ionised atoms, this requires calculating the parameter Ep for each state. For neutrals, this parameter can be approximated by a constant value in all cases, Ep = −4/9 atomic units (see, e.g., Anstee 1992; Barklem & O’Mara 1998). For this reason, the current work is restricted to neutral atoms. In the ABO broadening theory, spin is ignored. However, calculating the depolarisation requires that spin be accounted for, and thus we must consider specific groups of the periodic table. We treat the alkaline earth group where the total angular momentum J = l. In addition, we study the alkali metals where the spin s = 1/2 and J = l + s. This means that we here consider p-states where J = l = 1, J = 1/2 or 3/2, d-states where J = l = 2, J = 3/2 or 5/2, and f-states where J = l = 3, J = 5/2 or 7/2. We study complex atoms and atoms with hyperfine structure, and the treatment is easily derived from the results derived for simple atoms. This is explained in Sects. 4.4 and 4.5.
Our goal is to retrieve the numerical relation between the collisional depolarization rates and the collisional broadening line widths; that is, Dk(J) /w and Ck(J → J′) /w. If the velocity exponents are assumed to be the same in the case of both broadening and depolarization, that is, 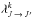 = λ, which is approximately the case, this reads
= λ, which is approximately the case, this reads 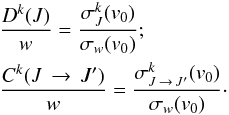 (11)In the next sections we use the tabulated cross sections by ABO and DSB for a wide range of cases and effective quantum numbers n∗ to establish relations between σw(v0),
(11)In the next sections we use the tabulated cross sections by ABO and DSB for a wide range of cases and effective quantum numbers n∗ to establish relations between σw(v0), 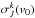 and
and 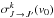 .
.
3. Optimization approach
To obtain these relations, multipart data analysis and artificial intelligence (AI) techniques are needed. AI techniques are becoming very useful as alternate approaches to conventional ones (Whiteson & Whiteson 2009). Within AI, genetic programming (GP) is a global optimization algorithm and an automatic programming technique that has been applied in physics and astrophysics (Cohen et al. 2003; El-Bakry & Radi 2007; Teodorescu & Sherwood 2008; El-dahshan 2009; Schmidt & Lipson 2009; Indranil et al. 2013). GP is a powerful tool that can be used to solve complex fitting problems. It is a rather recently developed evolutionary computation method for deriving analytical functions and data analysis. GP is based on Darwin’s theory of evolution and uses population of individuals, selects them according to an accuracy criterion, and produces genetic variation using one or more genetic operators (Koza 1992).
GP stores the individuals that are then presented as an expression tree for evaluation (Oakley 1994). GP provides the possible solutions to a given optimization problem, using the Darwinian principle of survival of the fittest. It uses biologically inspired operations such as replication, recombination, and mutation. In GP, the chromosome or genome composed of a linear, symbolic string of fixed length, each consists of one or more genes. Each gene can be represented by an algebraic expression and is composed of a head and a tail. The head contains symbols that represent functions F (with F = sqr, + ,−,/, ∗, or other operators) and terminals T (with T = x,y,z, or other random constants), while the tail only contains terminals.
As an example, the algebraic expression: ((x ∗ (x ∗ y)) + (x ∗ y)) can be represented as a tree (Fig. 4). We note that { + ,−, ∗ } represents the head and { x,y,x,z } represents the tail. This is the straightforward reading of the tree from left to right and from top to bottom. The set of functions and set of terminals must satisfy the closure and sufficiency properties. The sufficiency property requires that the set of functions and the set of terminals be able to express the solution of a problem. The function set may contain standard arithmetic operators, mathematical functions, logical operators, and domain-specific functions. The terminal set usually consists of feature variables and constants.
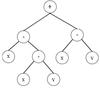 |
Fig. 4 Tree representation of the equation + (∗ (x,y), ∗ (x, ∗ (x,y))), i.e., ((x ∗ (x ∗ y)) + (x ∗ y)). |
To measure the error between the actual data found by ABO (denoted by Z) and the data predicted by the numerical model (denoted by zmodel), we calculated the root of square mean error (RSME), 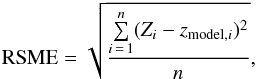 (12)where n is the number of the values of the data. The best solution, which is adopted to obtain the results of this paper, corresponds to the minimum value of RSME (Medhat et al. 2002).
(12)where n is the number of the values of the data. The best solution, which is adopted to obtain the results of this paper, corresponds to the minimum value of RSME (Medhat et al. 2002).
4. Results and discussion
ABO presented the broadening cross sections in tabular form for general s−p, p−d, d−f and f−d transitions. Each cross section was obtained for given effective principal quantum numbers associated with the upper and lower levels of the transition. For instance, for p−d transitions, broadening cross sections σw are tabulated, for a relative velocity of 104 m s-1, with effective principal quantum numbers 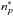 and
and 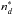 . This table can be fit to obtain an analytic function of two variables σw(
. This table can be fit to obtain an analytic function of two variables σw(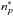 ,
, 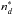 ).
).
DSB tabulated the variation of the depolarization cross section σk associated with the p, d, and f-states for a relative velocity of 104 m s-1 with effective principal quantum numbers 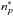 ,
, 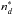 , and
, and 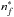 . For instance, for the d-state, it is possible to obtain an analytic function of one variable σk(
. For instance, for the d-state, it is possible to obtain an analytic function of one variable σk(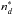 ).
).
The ABO and DSB results were combined to obtain analytic functions of two variables: σw(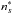 , σk(
, σk(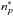 )), σw(
)), σw(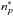 , σk(
, σk(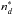 )) and σw(
)) and σw(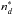 , σk(
, σk(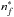 )), for the p, d and f states, respectively. For a transition between a lower level (with effective quantum number
)), for the p, d and f states, respectively. For a transition between a lower level (with effective quantum number 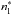 ) and an upper level (with effective quantum number
) and an upper level (with effective quantum number 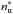 ), our choice in this paper was to consider σw as a function of
), our choice in this paper was to consider σw as a function of 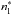 and
and 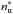 and possible depolarization and polarization transfer cross sections σk associated with
and possible depolarization and polarization transfer cross sections σk associated with 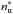 . It is also possible to consider σk associated with
. It is also possible to consider σk associated with 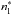 , instead of to
, instead of to 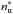 . However, in models typically the broadening associated with (
. However, in models typically the broadening associated with (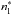 ,
, 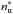 ) and the depolarization associated with the upper level
) and the depolarization associated with the upper level 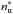 is of greatest interest.
is of greatest interest.
In the following we use GP to treat each possible case and give the corresponding analytic functions. We note that the most common situation in astrophysical modelling is that the collisional broadening rate can be obtained and estimated, but an estimate for depolarization and polarization transfer rates is still required.
4.1. s-p and p-s transitions
For transtions between s-states (l = 0) and p-states (l = 1), the cross sections σw are given in Table 1 of Anstee & O’Mara (1991) as functions of the effective quantum number 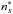 (corresponding to the s-state) and of the effective quantum number
(corresponding to the s-state) and of the effective quantum number 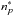 (corresponding to the p-state). For l = 1, the non-zero depolarization and polarization transfer cross sections are
(corresponding to the p-state). For l = 1, the non-zero depolarization and polarization transfer cross sections are 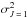 ,
, 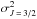 and
and 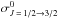 . These cross sections are given as functions of
. These cross sections are given as functions of 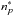 in Table 6.1 of Derouich (2004). We here only considered the tensorial orders k = 0 and k = 2 that are relevant to the second solar spectrum studies (i.e. the scattering linear polarization spectrum). We wish to establish the relations between the function σw(
in Table 6.1 of Derouich (2004). We here only considered the tensorial orders k = 0 and k = 2 that are relevant to the second solar spectrum studies (i.e. the scattering linear polarization spectrum). We wish to establish the relations between the function σw(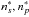 ) and the functions
) and the functions 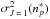 ,
, 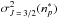 and
and 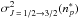 . Since
. Since 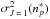 ,
, 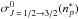 and
and 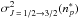 depend on
depend on 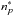 , the problem becomes determining the general functions σw(
, the problem becomes determining the general functions σw(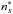 ,
,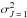 ), σw(
), σw(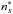 ,
, 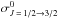 ), and σw(
), and σw(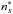 ,
, 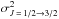 ).
).
4.1.1. Depolarization rate: J = J′ = 1 and k = 2 (s = 0)
For a depolarization rate with a total angular momentum J = l = 1, the relation obtained from our GP modelling is 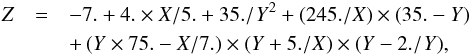 (13)where Z, Y, and X are introduced for the sake of clarity where,
(13)where Z, Y, and X are introduced for the sake of clarity where, 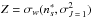 ,
, 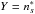 , and
, and 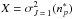 .
.
To test the performance of our fitting method, we employed “hare and hound” approaches consisting of comparing the exact solution (called input) and the solution provided by Eq. (13) (called output). Figure 5 shows with a solid line the perfect correspondence (output = input) and the result of the fit is shown with squares. The averaged relative error is ~5%, which is sufficiently precise for applications.
 |
Fig. 5 The solid line shows the perfect solution and the result of the fit is shown with squares. |
As an example, we applied Eq. (13) to determine the relation between the collisional depolarization and the collisional broadening rates associated with the photospheric Sr i 4607 Å line. The 4607 Å line is the resonance line of Sr i, namely 5s2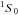 →5s5p
→5s5p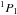 , and for this line,
, and for this line, 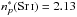 and
and 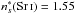 . According to the DSB method (see Derouich 2004 and references therein),
. According to the DSB method (see Derouich 2004 and references therein), 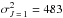 a.u. (atomic units). By applying Eq. (13), we find that σw(Sr i) = 430, implying that
a.u. (atomic units). By applying Eq. (13), we find that σw(Sr i) = 430, implying that 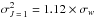 (rw = 1.12). We note that this value is rather similar to the one adopted by Faurobert et al. (1995), who assumed that
(rw = 1.12). We note that this value is rather similar to the one adopted by Faurobert et al. (1995), who assumed that 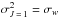 (rw = 1) for the Sr i 4607 Å line.
(rw = 1) for the Sr i 4607 Å line.
As mentioned, the more common case is that w or σw are known and D2 or 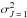 are to be derived. An equation giving X (
are to be derived. An equation giving X (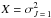 ) as a function of Z (Z = σw) and Y (
) as a function of Z (Z = σw) and Y (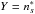 ) was therefore determined using our GP model and the tables of collisional data given by ABO and DSB:
) was therefore determined using our GP model and the tables of collisional data given by ABO and DSB: 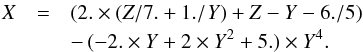 (14)For the Sr i line discussed above, we find σw(Sr i) = 405 a.u. by interpolation in the tables of Anstee & O’Mara (1995). Since Z = 405 a.u. and Y = 1.55, using the general Eq. (14) we recover
(14)For the Sr i line discussed above, we find σw(Sr i) = 405 a.u. by interpolation in the tables of Anstee & O’Mara (1995). Since Z = 405 a.u. and Y = 1.55, using the general Eq. (14) we recover 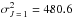 a.u., a value about 0.5% lower than the value calculated directly by DSB (see Derouich 2004), 483 a.u. Thus the depolarization and polarization transfer rates can be obtained by determining the broadening rates. We note that by determining the depolarization and polarization transfer rates of simple atoms such as Sr i, the rates associated to complex atoms and atoms with hyperfine structure can be easily obtained (see Sects. 4.4 and 4.5).
a.u., a value about 0.5% lower than the value calculated directly by DSB (see Derouich 2004), 483 a.u. Thus the depolarization and polarization transfer rates can be obtained by determining the broadening rates. We note that by determining the depolarization and polarization transfer rates of simple atoms such as Sr i, the rates associated to complex atoms and atoms with hyperfine structure can be easily obtained (see Sects. 4.4 and 4.5).
In the same homologous group, our results can be applied to the corresponding transitions in the Mg i and Ca i atoms. For Mg i 3s2 and 3p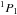 levels,
levels, 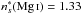 and
and 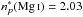 . Then, using Derouich (2004),
. Then, using Derouich (2004), 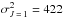 a.u. at
a.u. at 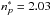 . The application of Eq. (10) permits us to determine σw(Mg i) = 361 a.u. and thus
. The application of Eq. (10) permits us to determine σw(Mg i) = 361 a.u. and thus 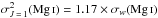 (rw = 1.17). Similarly, for the case of Ca i where
(rw = 1.17). Similarly, for the case of Ca i where 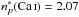 and
and 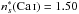 ,
, 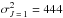 a.u., and thus Eq. (13) gives σw = 394 a.u. Therefore,
a.u., and thus Eq. (13) gives σw = 394 a.u. Therefore, 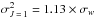 (rw = 1.13). The results obtained for the resonance lines of Sr i , Ca i and Mg i, are summarized in Table 1.
(rw = 1.13). The results obtained for the resonance lines of Sr i , Ca i and Mg i, are summarized in Table 1.
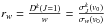 for the resonance lines of Sr i , Ca i , and Mg i.
for the resonance lines of Sr i , Ca i , and Mg i.
4.1.2. Depolarization rate: J = J′ = 3/2, k = 2 (s = 1/2)
We adopted the same strategy as for J = J′ = 1 to determine the ratio 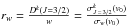 . We obtain the following relation:
. We obtain the following relation: 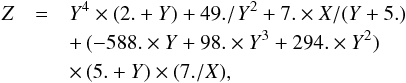 (15)where
(15)where 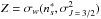 ,
, 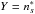 , and
, and 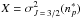 . For the Na I 3s
. For the Na I 3s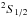 and 3p
and 3p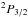 levels,
levels, 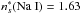 and
and 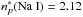 . According to Derouich (2004),
. According to Derouich (2004), 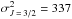 a.u. Thus, by applying Eq. (15), σw = 433 a.u. Consequently,
a.u. Thus, by applying Eq. (15), σw = 433 a.u. Consequently, 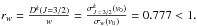 In addition, according to our GP method, the equation giving
In addition, according to our GP method, the equation giving 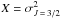 as a function of Z = σw and
as a function of Z = σw and 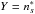 is
is 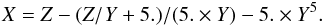 (16)
(16)
4.1.3. Transfer of population rate, J = 1/2, J′ = 3/2, k = 0
The transfer rate of a population is denoted by Ck(J → J′) and the cross section of the transfer of a population is 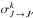 . The relation between σw and
. The relation between σw and 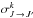 is given by
is given by 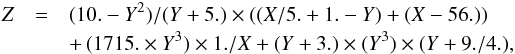 (17)where Z = σw,
(17)where Z = σw, 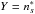 , and
, and 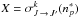 . For example, for the Na I 3s
. For example, for the Na I 3s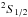 and 3p
and 3p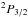 levels,
levels, 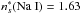 and
and 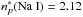 , and from Derouich (2004),
, and from Derouich (2004), 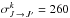 a.u. The application of Eq. (17) gives σw = 433, thus
a.u. The application of Eq. (17) gives σw = 433, thus 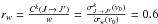 . Furthermore, by applying our GP method, the equation giving
. Furthermore, by applying our GP method, the equation giving 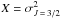 as a function of Z = σw and
as a function of Z = σw and 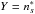 is
is 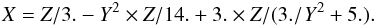 (18)
(18)
4.2. p-d and d-p transitions
4.2.1. Depolarization rate: J = J′ = 2, k = 2 (s = 0)
The depolarization rate for the d-states (l = 2) has been calculated by Derouich (2004) and references therein. In addition, the collisional broadening by neutral hydrogen was obtained by Barklem & O’Mara (1997). After using our optimization method, we obtain 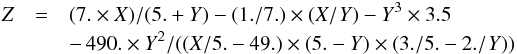 (19)and
(19)and 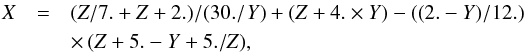 (20)where Z = σw,
(20)where Z = σw, 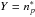 , and
, and 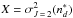 . As an example, we consider
. As an example, we consider 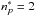 and
and 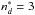 . For
. For 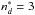 , Derouich (2004) found that
, Derouich (2004) found that 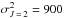 a.u. Equation (19) gives σw = 820 a.u. The value given in Table 1 of Barklem & O’Mara (1997) is σw = 834 a.u., the relative error is 1.65%. Figure 6 shows the comparison between the exact solution (the input from Barklem & O’Mara 1997) as a solid line, and the solution provided by Eq. (19) (called output) is presented as squares.
a.u. Equation (19) gives σw = 820 a.u. The value given in Table 1 of Barklem & O’Mara (1997) is σw = 834 a.u., the relative error is 1.65%. Figure 6 shows the comparison between the exact solution (the input from Barklem & O’Mara 1997) as a solid line, and the solution provided by Eq. (19) (called output) is presented as squares.
 |
Fig. 6 The solid line shows the perfect solution (i.e. the one-to-one relation) and the result of the fit is shown with squares. |
The precision of Eqs. (19) and (20) is practically the same since the same optimization method and the same data were used to establish these two equations. This remark is true for all equations of this paper giving Z and X. For this reason, we usually checked the accuracy of the equation giving Z. It can easily be verified that the accuracy of the equation giving X is practically the same as the accuracy of the equation giving Z.
4.2.2. Depolarization rate: J = J′ = 3/2, k = 2
The relation between σw and 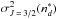 is
is 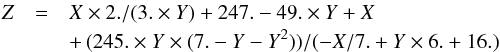 (21)and
(21)and 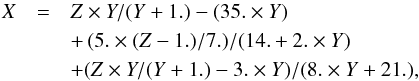 (22)where Z = σw,
(22)where Z = σw, 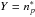 , and
, and 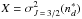 . Taking again the case of
. Taking again the case of 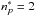 and
and 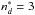 , we have
, we have 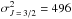 a.u., which gives σw = 799 a.u. The relative error in the calculation of the σw from the relation of Eq. (21) is 4.2%.
a.u., which gives σw = 799 a.u. The relative error in the calculation of the σw from the relation of Eq. (21) is 4.2%.
4.2.3. Depolarization rate: J = J′ = 5/2, k = 2
Using the optimization method, we find that the relation between σw and 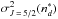 is
is 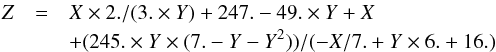 (23)and
(23)and 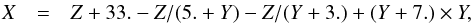 (24)where Z = σw,
(24)where Z = σw, 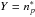 , and
, and 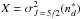 . At
. At 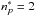 and
and 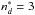 , we have from Derouich (2004)
, we have from Derouich (2004) 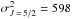 a.u., which gives σw = 827 a.u. The relative error in the calculation of the σw from the relation of Eq. (23) is 0.89% and
a.u., which gives σw = 827 a.u. The relative error in the calculation of the σw from the relation of Eq. (23) is 0.89% and 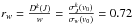 .
.
4.2.4. Transfer of population rate: J = 3/2, J′ = 5/2, k = 0
We find the function giving the relation between σw and 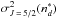 :
: ![\begin{eqnarray} \label{eq_D_transferk0J32J52} Z&=&X/(7. \times Y)+(1.-Y) \times 49.+ X-56.- (Y-7.) \times (X/7.) \nonumber \\ && +\, (5. \times Y^3+Y^5 \times 5.)/[X/(10. \times Y)-8.)] \end{eqnarray}](/articles/aa/full_html/2015/12/aa26661-15/aa26661-15-eq220.png) (25)and
(25)and 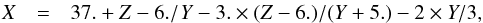 (26)where Z = σw,
(26)where Z = σw, 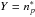 , and
, and 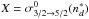 . At
. At 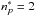 and
and 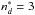 , we have from Derouich (2004)
, we have from Derouich (2004) 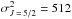 a.u., which gives σw = 821 a.u. The relative error in the calculation of the σw from the relation of Eq. (25) is 1.6%.
a.u., which gives σw = 821 a.u. The relative error in the calculation of the σw from the relation of Eq. (25) is 1.6%.
4.2.5. Transfer of alignment rate: J = 3/2, J′ = 5/2, k = 2
Using our numerical method we obtain: 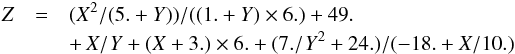 (27)and
(27)and 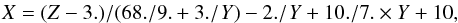 (28)where, Z = σw,
(28)where, Z = σw, 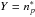 , and
, and 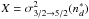 . At
. At 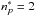 and
and 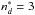 , according to Derouich (2004),
, according to Derouich (2004), 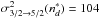 a.u., which gives σw = 826 a.u. The relative error in the calculation of the σw from the relation of Eq. (27) is 1.0%. The ratio
a.u., which gives σw = 826 a.u. The relative error in the calculation of the σw from the relation of Eq. (27) is 1.0%. The ratio 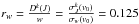 .
.
4.3. d-f and f-d transitions
4.3.1. Depolarization rate: J = J′ = 3, k = 2 (s = 0)
The depolarization rate for the f-states (l = 3) has been calculated by Derouich (2004) and references therein. The collisional broadening by neutral hydrogen was obtained by Barklem & O’Mara (1998). The analytical relation between σw and 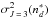 is
is 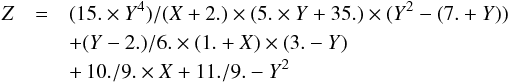 (29)and
(29)and 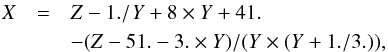 (30)where, Z = σw,
(30)where, Z = σw, 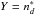 , and
, and 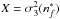 . This equation gives the relation between σw and
. This equation gives the relation between σw and 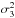 for any line, that is, for all typical values of
for any line, that is, for all typical values of 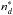 and
and 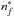 . We consider the values of the effective quantum number,
. We consider the values of the effective quantum number, 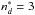 and
and 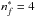 . The σw given by Barklem & O’Mara (1998) is 1419 a.u. For the case
. The σw given by Barklem & O’Mara (1998) is 1419 a.u. For the case 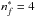 , Derouich (2004) found that
, Derouich (2004) found that 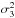 (
(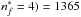 a.u. According to Eq. (29), it can easily be shown that σw = 1464 a.u. The relative error in calculating the cross section with Eq. (29) is −3.1%. Figure 7 shows the comparison between the exact solution (the input from Barklem & O’Mara 1998) as a solid line and the solution provided by Eq. (29) (called output) as squares.
a.u. According to Eq. (29), it can easily be shown that σw = 1464 a.u. The relative error in calculating the cross section with Eq. (29) is −3.1%. Figure 7 shows the comparison between the exact solution (the input from Barklem & O’Mara 1998) as a solid line and the solution provided by Eq. (29) (called output) as squares.
 |
Fig. 7 The solid line shows the perfect solution (output = input) and the result of the fit is shown with squares. |
It is worth commenting on the noticeable difference in scatter in Figs. 5–7, and the somewhat surprising result that the smallest scatter is seen in Fig. 6 for p-d and d-p transitions, and not, for example, for the scatter correlating with orbital angular momentum quantum number. The scatter is largely traceable to non-smooth behaviour in the input data, especially the tabulated broadening cross sections. Figures 5–7 correspond to the cases of s-p (and p-s), s-p (and p-s), and d-f (and f-d) transitions, respectively, and the behaviour of the cross sections with n∗ is displayed graphically in the relevant ABO papers. There we see that non-smooth behaviour is especially seen at the extremities (i.e. large n∗) of the tabulated data. This occurs as a result of the stronger effect of oscillations on the electronic wave-functions on the calculations. That is, the wave functions have approximately n∗−l−1 nodes, and so at around n∗>l + 2 these effects start to be seen in the broadening cross sections. We note that for the s-p and p-s transitions, the results are tabulated for s-states up to n∗ = 3 = l + 3. However, in all other cases of the ABO data, the tabulations stop at n∗ = l + 2. Thus, the rather unexpected behaviour of the scatter is attributed to the wider range of n∗ calculated for s-p and p-s . If we were to restrict the s-p and p-s case to s-states with n∗ = 2, we could reasonably expect significantly reduced scatter in Fig. 5; see Fig. 1, upper panel, of Anstee & O’Mara (1995), which shows that the behaviour is very smooth in this regime.
4.3.2. Depolarization rate: J = J′ = 5/2, k = 2 (l = 3)
The relation between σw and 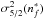 is
is 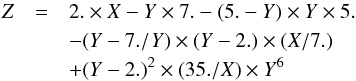 (31)and
(31)and 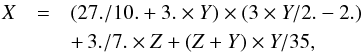 (32)where Z = σw,
(32)where Z = σw, 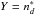 , and
, and 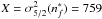 a.u. For
a.u. For 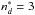 and
and 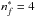 , we find that σw = 1428 a.u. and that the error in calculating the cross section with Eq. (31) is −0.65%.
, we find that σw = 1428 a.u. and that the error in calculating the cross section with Eq. (31) is −0.65%.
4.3.3. Depolarization rate: J = J′ = 7/2, k = 2 (l = 3)
The relation between σw and 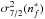 is
is 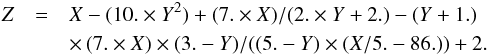 (33)For
(33)For 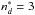 and
and 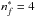 , the σw inferred from Eq. (33) is 1457 a.u., implying that the percentage of the relative error is −2.7%. Since
, the σw inferred from Eq. (33) is 1457 a.u., implying that the percentage of the relative error is −2.7%. Since 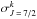 (
(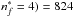 a.u., the ratio
a.u., the ratio 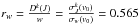 . In addition, we find that
. In addition, we find that 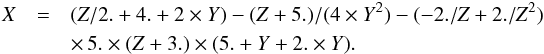 (34)
(34)
4.3.4. Transfer of population rate: J = 5/2, J′ = 7/2, k = 0 (l = 3)
We find that 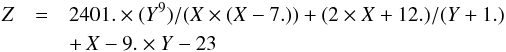 (35)and
(35)and 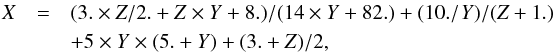 (36)where Z = σw,
(36)where Z = σw, 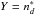 , and
, and 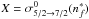 . For
. For 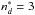 and
and 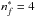 , the σw inferred from Eq. (35) is 1447 a.u. Therefore, by compring this value to the actual value calculated by Barklem & O’Mara (1998), we determine the percentage of the relative error to be −2%. We note that according to DSB,
, the σw inferred from Eq. (35) is 1447 a.u. Therefore, by compring this value to the actual value calculated by Barklem & O’Mara (1998), we determine the percentage of the relative error to be −2%. We note that according to DSB, 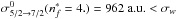 .
.
4.3.5. Transfer of alignment rate: J = 5/2, J′ = 7/2, k = 2 (l = 3)
Our final relation is 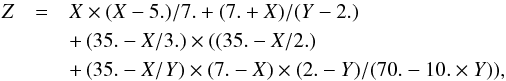 (37)where Z = σw,
(37)where Z = σw, 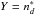 , and
, and 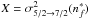 . For
. For 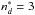 and
and 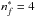 , the σw inferred from Eq. (37) is 1476.6 a.u., implying that the percentage of the relative error is −4%.
, the σw inferred from Eq. (37) is 1476.6 a.u., implying that the percentage of the relative error is −4%. 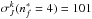 . <σw. In addition, we obtain
. <σw. In addition, we obtain 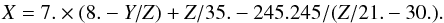 (38)
(38)
4.4. Atoms with hyperfine structure
The numerical results presented in the previous subsections are concerned with simple neutral atoms for which the electronic configurations have only one valence electron and no hyperfine structure. The problem of atoms with hyperfine structures can be easily dealt with by using the fact that in the framework of the frozen nuclear spin approximation, the hyperfine depolarization and polarization transfer rates are given as a linear combination of the fine rates Dk(J) and Ck(J → J′) (e.g. Nienhuis 1976 & Omont 1977). We note that in typical solar conditions, the frozen nuclear spin approximation is well satisfied. The hyperfine splitting is usually much lower than the inverse of the typical time duration of a collision, and therefore the nuclear spin can be assumed to be conserved (frozen) during the collision.
4.5. Complex atoms
The electronic configuration of a complex atom (Fe, Ti, etc.) often has one valence electron outside an open subshell with non-zero angular momentum. We assumed that only the valence electron is affected by collisions with hydrogen atoms (the frozen core approximation). For more details about our approach concerning complex atoms we refer to Sect. 2 of Derouich et al. (2005a). In this and following papers (Derouich et al. 2005b; Derouich & Barklem 2007; Sahal-Bréchot et al. 2007), it has been shown that the expression for the depolarization rate of a complex atom can be written as a linear combination of the depolarization rates of a simple atom. Thus, the relations obtained and illustrated in this work are applicable to complex atoms provided that one takes into account the formulae giving the depolarization rates of complex atoms as a function of the depolarization rates of simple atoms.
5. Conclusion
A coherent scattering theory that accounts for partial or complete frequency redistribution in the presence of isotropic collisions is a challenging problem. Consequently, models of scattering are usually developed in a collisionless regime (e.g. Casini et al. 2014, and references therein). Stenflo (1994) proposed an approximate model that includes redistribution effects and self-consistently accounts for collisions. Stenflo (1994) confronted the problem of properly including the collisional depolarization rates and the collisional broadening coefficients.
Using GP techniques, we here obtained accurate relations for the collisional broadening as functions of the depolarization and polarization transfer rates, typically accurate to about 5%. Since the more common case is that collisional broadening is known and the depolarization and polarization tranfer rates
are required, we determined accurate relations giving the depolarization and polarization tranfer cross-sections as functions of the broadening line width. As such, these relations should be useful to the solar polarization community.
Interestingly, from the values of broadening coefficients and our relations, it is possible to find the depolarization and polarization transfer rates for any hyperfine or fine-structure level of simple and complex atoms.
Acknowledgments
This work was supported by the Royal Swedish Academy of Sciences, the Wenner-Gren Foundation, Göran Gustafssons Stiftelse, and the Swedish Research Council. P.S.B. is a Royal Swedish Academy of Sciences Research Fellow supported by a grant from the Knut and Alice Wallenberg Foundation. P.S.B. was also supported by the project grant “The New Milky Way” from the Knut and Alice Wallenberg foundation.
References
- Anstee, S. D. 1992, Ph.D. Thesis, University Queensland [Google Scholar]
- Anstee, S. D., & O’Mara, B. J. 1991, MNRAS, 253, 549 [Google Scholar]
- Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Anstee, S. D., O’Mara, B. J., & Ross, J. E. 1997, MNRAS, 284, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Baranger, M. 1962, in Atomic and Molecular Processes, ed. D. R. Bates (Academic Press), 550 [Google Scholar]
- Barklem, P. S. 1998, Ph.D. Thesis, University Queensland [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1997, MNRAS, 290, 102 [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1998, MNRAS, 300, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., Anstee, S. D., & O’Mara, B. J. 1998, PASA, 15, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Bommier, V. 1997a, A&A, 328, 706 [NASA ADS] [Google Scholar]
- Bommier, V. 1997b, A&A, 328, 726 [NASA ADS] [Google Scholar]
- Casini, R., Landi Degl’Innocenti, M., Manso Sainz, R., Landi Degl’Innocenti, E., & Landolfi, M. 2014, ApJ, 791, 17 [CrossRef] [Google Scholar]
- Cohen, J., Cohen, P., West, S., & Aiken, L. 2003, Applied multiple regression/correlation analysis for the behavioral sciences (Mahwah, NJ: Erlbaum) [Google Scholar]
- Derouich, M. 2004, Ph.D. Thesis, Paris VII-Denis Diderot University, France [Google Scholar]
- Derouich, M., & Barklem, P. S. 2007, A&A, 462, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Sahal-Bréchot, S., Barklem, P. S., & O’Mara, B. J. 2003a, A&A, 404, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Sahal-Bréchot, S., & Barklem, P. S. 2003b, A&A, 409, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Sahal-Bréchot, S., & Barklem, P. S. 2004, A&A, 414, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Sahal-Bréchot, S., & Barklem, P. S. 2005a, A&A, 434, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Barklem, P. S., & Sahal-Bréchot, S. 2005b, A&A, 441, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Derouich, M., Bommier, V., Malherbe, J.M., & Landi Degl’Innocenti, E. 2006, A&A, 457, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- El-Bakry, S. 2007, Radi A., Int. J. Mod. Phys. C, 18, 351 [NASA ADS] [CrossRef] [Google Scholar]
- El-dahshan, E., Radi, A., & El-Bakry, M.Y. 2009, Int. J. Mod. Phys. C, 20, 1817 [NASA ADS] [CrossRef] [Google Scholar]
- Faurobert-Scholl, M., Feautrier, N., Machefert, F., Petrovay, K., & Spielfiedel, A. 1995, A&A, 298, 289 [NASA ADS] [Google Scholar]
- Indranil, Pan, Daya Shankar, Pandey, & Saptarshi, Das 2013, J. Renewable and Sustainable Energy, 5, 063129 [CrossRef] [Google Scholar]
- Koza, J.R. 1992, Genetic Programming: On the Programming of Computers by means of Natural Selection (Cambridge, MA: The MIT Press) [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer) [Google Scholar]
- Medhat, M., El-zaiat, S., Abdou, S. M., Radi, A., & Omar, M. 2002, J. Opt. A: Pure Appl. Opt., 4, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Nienhuis, G. 1976, J. Phys. B: Atom. Molec. Phys., 9, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Omont, A. 1977, Prog. Quantum Electronics, 5, 69 [Google Scholar]
- Oakley E. H. N. 1994, In Advances in Genetic Programming, ed. K. E. Kinnear Jr. (Cambridge, MA: The MIT Press), 369 [Google Scholar]
- Sahal-Bréchot, S. 1977, ApJ, 213, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Sahal-Bréchot, S., & Bommier, V. 2014, Adv. Space Res., 54, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- Sahal-Bréchot, S., Derouich, M., Bommier, V., Barklem, P. S. 2007, A&A, 465, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, M., Lipson, H. 2009, Science, 324, 81 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Smitha, H. N., Nagendra, K. N., Stenflo, J. O., Bianda, M., & Ramelli, R. 2014, ApJ, 794, 9 [Google Scholar]
- Stenflo, J. O., 1994, Solar Magnetic Fields (Dordrecht: Kluwer Academic Publishers), Astrophys. Space Sci. Libr., 189 [Google Scholar]
- Teodorescu, L., Sherwood, D. 2008, Comput. Phys. Commun., 178, 409 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Examples of the collisions that result in the broadening of the line profile for the transition between the initial electronic state | nl1 ⟩ and the final state | nl2 ⟩. Level spacings are not to scale. |
| In the text | |
 |
Fig. 2 Examples of the collisions that result in depolarization of the state | nlJ ⟩. Level spacings are not to scale. |
| In the text | |
 |
Fig. 3 Schematic representation of the collisional transfer of polarization between different fine structure levels. Level spacings are not to scale. |
| In the text | |
 |
Fig. 4 Tree representation of the equation + (∗ (x,y), ∗ (x, ∗ (x,y))), i.e., ((x ∗ (x ∗ y)) + (x ∗ y)). |
| In the text | |
 |
Fig. 5 The solid line shows the perfect solution and the result of the fit is shown with squares. |
| In the text | |
 |
Fig. 6 The solid line shows the perfect solution (i.e. the one-to-one relation) and the result of the fit is shown with squares. |
| In the text | |
 |
Fig. 7 The solid line shows the perfect solution (output = input) and the result of the fit is shown with squares. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


