| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 6 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526569 | |
| Published online | 17 November 2015 | |
Super-Eddington wind scenario for the progenitors of type Ia supernovae: Accreting He-rich matter onto white dwarfs
1 Yunnan Observatories, Chinese Academy of Sciences, 650216 Kunming, PR China
e-mail: wangbo@ynao.ac.cn
2 Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, 650216 Kunming, PR China
Received: 21 May 2015
Accepted: 27 September 2015
Context. Supernovae of type Ia (SNe Ia) are believed to be thermonuclear explosions of carbon-oxygen white dwarfs (CO WDs). However, the mass accretion process onto CO WDs is still not completely understood.
Aims. In this paper, we study the accretion of He-rich matter onto CO WDs and explore a scenario in which a strong wind forms on the surface of the WD if the total luminosity exceeds the Eddington limit.
Methods. Using a stellar evolution code called modules for experiments in stellar astrophysics (MESA), we simulated the He accretion process onto CO WDs for WDs with masses of 0.6−1.35 M⊙ and various accretion rates of 10-8−10-5 M⊙ yr-1.
Results. If the contribution of the total luminosity is included when determining the Eddington accretion rate, then a super-Eddington wind could be triggered at relatively lower accretion rates than those of previous studies based on steady-state models. The super-Eddington wind can prevent the WDs with high accretion rates from evolving into red-giant-like He stars. We found that the contributions from thermal energy of the WD are non-negligible, judging by our simulations, even though the nuclear burning energy is the dominating source of luminosity. We also provide the limits of the steady He-burning regime in which the WDs do not lose any accreted matter and increase their mass steadily, and calculated the mass retention efficiency during He layer flashes for various WD masses and accretion rates. These obtained results can be used in future binary population synthesis computations.
Key words: stars: evolution / binaries: close / supernovae: general / white dwarfs
© ESO, 2015
1. Introduction
Supernovae of type Ia (SNe Ia) are of great importance in astrophysics, especially in Cosmology and the chemical evolution of galaxies (e.g., Howell 2011; Matteucci & Greggio 1986). They are also accelerators of cosmic rays (see Fang & Zhang 2012). These supernovae are thought to originate from thermonuclear explosions of carbon-oxygen white dwarfs (CO WDs) in binaries, although the mass donor is still under debate (see Podsiadlowski et al. 2008). The mass donor could be a non-degenerate star in the single degenerate model (e.g., Whelan & Iben 1973; Nomoto et al. 1984; Hachisu et al. 1996; Li & van den Heuvel 1997; Han & Podsiadlowski 2004, 2006; Wang et al. 2010; Meng & Podsiadlowski 2013, 2014) or another WD in the double degenerate model (e.g., Iben & Tutukov 1984; Webbink 1984; Chen et al. 2012). To date, two explosion models of SNe Ia have been discussed frequently, the Chandrasekhar mass model and the sub-Chandrasekhar mass model. Recent reviews of the theoretical models of SNe Ia and the observational constraints include Wang & Han (2012), Hoeflich et al. (2013), Hillebrandt et al. (2013), Wang et al. (2013a) and Maoz et al. (2014).
The He accretion process onto WDs plays a critical role in understanding the progenitor models of SNe Ia. First, in the classical Chandrasekhar mass model, a WD could directly accrete matter from a non-degenerate or degenerate He-rich companion. The accreted He-rich matter is burned into carbon and oxygen, leading to the mass increase of the WD. The WD may explode as an SN Ia when it grows in mass to the Chandrasekhar limit (e.g., Yoon & Langer 2003; Wang et al. 2009a; Piersanti et al. 2014). Second, in the sub-Chandrasekhar mass model, the explosion of a CO WD may be triggered by the detonation of a substantial surface layer of accreted He, where the mass donor could be a non-degenerate He star or a He WD. This model is also known as the He double-detonation model (see, e.g., Woosley et al. 1986; Livne 1990; Fink et al. 2007; Wang et al. 2013b; Piersanti et al. 2014).
The He accretion process onto WDs is also related to the formation of some peculiar objects, such as He novae (e.g., Kato et al. 2000; Ashok & Banerjee 2003) and AM CVn systems (e.g., Nelemans et al. 2001; Shen & Bildsten 2009; Brooks et al. 2015; Piersanti et al. 2015). Meanwhile, single He layer detonation at the surface of accreting WDs may produce some faint and fast transients like the hypothetical. Ia SNe (see, e.g., Bildsten et al. 2007; Shen et al. 2010; Woosley & Kasen 2011; Sim et al. 2012; Kasliwal et al. 2012; Brooks et al. 2015). In addition, Wang et al. (2013b) recently argued that some type Iax SNe (a kind of sub-luminous SNe Ia) may be explained by the specific class of He-ignited WD explosions. Furthermore, many recent binary population synthesis studies also involved the He accretion onto the surface of WDs (see, e.g., Wang et al. 2009b, 2013b; Ruiter et al. 2009, 2013, 2014; Toonen et al. 2014; Claeys et al. 2014).
In the observations, there are many massive WD+He star binaries, e.g., CD−30° 11223, KPD 1930+2752, V445 Puppis, and HD 49798 with its WD companion. It has been suggested that they are all progenitor candidates of SNe Ia (e.g., Geier et al. 2007, 2013; Kato et al. 2008; Woudt et al. 2009; Mereghetti et al. 2009; Wang & Han 2010). In addition, the companion of SN 2012Z was probably a He star (e.g., McCully et al. 2014; Wang et al. 2014a; Liu et al. 2015), and the mass donor of SN 2014J may also be a He star (see Diehl et al. 2014). Additionally, US 708 (a hypervelocity He star) is likely to be the ejected donor remnant of an SN Ia that originated from a WD binary where the mass donor is a He star (e.g., Geier et al. 2015; see also Wang & Han 2009; Justham et al. 2009).
However, the He accretion process onto CO WDs is still not clearly understood. If the accretion rate is too low, a He layer flash happens on the surface of the WD (e.g., Kato & Hachisu 2004). If the accretion rate of the WD is too high, it will become a red-giant-like He star owing to the accumulation of the accreted matter on its surface (e.g., Nomoto 1982). Therefore, the steady He layer burning only occurs in a narrow regime, in which the accreted He can be completely burned into carbon and oxygen. Wang et al. (2009a) recently investigated the WD+He star channel of SN Ia progenitors on the basis of an optically thick wind assumption (e.g., Hachisu et al. 1996). In this assumption, the red-giant-like regime was replaced by the optically thick wind regime; the He-rich matter can be transformed into carbon and oxygen at a critical rate in this regime, whereas the unprocessed matter is blown away via the optically thick wind. However, this assumption is still under debate (e.g., Langer et al. 2000), and the metallicity threshold predicted by this model has not been observed (e.g., Badenes et al. 2009).
At low accretion rates, the accreting WDs will undergo multicycle He layer flashes like nova outbursts, but previous studies mainly involved one cycle when simulating He layer flashes (e.g., Kato & Hachisu 2004). In this paper, we also investigate a multicycle evolution of the He layer flash with various WD masses and obtain the mass retention efficiency during He layer flashes.
The purpose of this paper is to study the He layer burning on the surface of WDs. These WDs have masses from 0.6 to 1.35 M⊙ with various accretion rates. In Sect. 2, the basic assumptions and methods for numerical calculations are described. Our numerical calculation results are given in Sect. 3. Finally, we present the discussion and summary in Sect. 4.
2. Numerical code and methods
Employing the stellar evolution code called modules for experiments in stellar astrophysics (MESA, version 3661; see Paxton et al. 2011, 2013), we simulated the accretion process of He-rich matter onto CO WDs. The MESA default OPAL opacity is adopted in our simulations (see Fig. 2 in Paxton et al. 2011). Twenty-one isotopes are included in the nuclear network, which are coupled by 50 nuclear reactions. We selected two MESA suite cases for our numerical calculations: make_co_wd and wd2.
We used the MESA suite case make_co_wd to construct CO WD models. In order to get the initial CO WD models, we chose zero age main-sequence stars with intermediate masses and evolved them to the cooling sequence. We obtained a series of CO WD models with masses from 0.6 to 1.0 M⊙ based on this method. To obtain CO WDs with masses >1.0 M⊙, we added the mass to our 1.0 M⊙ WD model by accreting matter with its surface composition. Finally, we constructed ten hot WD models as our initial models with masses in the range of 0.6–1.35 M⊙. We note that we came across some numerical problems when simulating the evolution of cold WDs during mass accretion, possibly owing to the high degeneracy of matters in their outer layers1. Thus, we selected hot WD models at the top of the WD cooling track as our initial models in the simulations of mass accretion. The ten WD models have masses (central temperatures) of 0.6 M⊙ (7.1 × 107 K), 0.7 M⊙ (7.0 × 107 K), 0.8 M⊙ (6.9 × 107 K), 0.9 M⊙ (7.7 × 107 K), 1.0 M⊙ (10.0 × 107 K), 1.1 M⊙ (10.4 × 107 K), 1.2 M⊙ (12.2 × 107 K), 1.25 M⊙ (13.7 × 107 K), 1.3 M⊙ (16.0 × 107 K), and 1.35 M⊙ (20.7 × 107 K)2. The metallicity of these WDs is set to be 0.02.
We used the MESA suite case wd2 to calculate the He accretion onto the surface of CO WDs. The suite case wd2 controls mass accretion and includes an acceleration term in the equation of hydrostatic equilibrium so that we can calculate the mass ejection processes during nova outbursts. The accreted matter is composed of He mass fraction Y = 0.98, and metallicity Z = 0.02. We carried out a series of calculations for all of our WD models with various accretion rate of 10-8−10-5 M⊙ yr-1. In each simulation, we calculated for a long time to get detailed information about accretion.
The luminosity L of the accreting WD may exceed the Eddington limit once the accretion rate is too high. In this case, a super-Eddington wind can be triggered. The Eddington luminosity can be expressed as 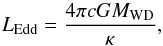 (1)in which MWD, c, G, and κ are the WD mass, vacuum speed of light, the gravitational constant, and the opacity, respectively.
(1)in which MWD, c, G, and κ are the WD mass, vacuum speed of light, the gravitational constant, and the opacity, respectively.
The luminosity L of accreting WDs usually has three contributors: nuclear burning energy, thermal energy, and the accretion energy released by the accreted matter. Among these three contributors, the nuclear burning luminosity accounts for most of the total luminosity of the WD. The values of the nuclear burning luminosity are always much higher than the other two contributors. The nuclear burning luminosity Lnuc can be expressed as 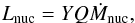 (2)in which Ṁnuc, Q, and Y are the nuclear burning rate of the accreted He, the nuclear energy released by per unit mass of He, and the He mass fraction in the accreted matter, respectively. The accretion luminosity Lacc due to the gravitational energy released is
(2)in which Ṁnuc, Q, and Y are the nuclear burning rate of the accreted He, the nuclear energy released by per unit mass of He, and the He mass fraction in the accreted matter, respectively. The accretion luminosity Lacc due to the gravitational energy released is 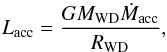 (3)in which Ṁacc and RWD are the accretion rate and the WD radius, respectively. The accretion energy deposited at or near the photosphere of the WD does not get absorbed by the WD, as heat always escapes much more quickly than the speed at which the fluid moves inward (e.g., Townsley & Bildsten 2004). Because the accretion energy can be radiated away from the WD surface rapidly, here we define the luminosity Lprime as (L−Lacc) (see also Ma et al. 2013).
(3)in which Ṁacc and RWD are the accretion rate and the WD radius, respectively. The accretion energy deposited at or near the photosphere of the WD does not get absorbed by the WD, as heat always escapes much more quickly than the speed at which the fluid moves inward (e.g., Townsley & Bildsten 2004). Because the accretion energy can be radiated away from the WD surface rapidly, here we define the luminosity Lprime as (L−Lacc) (see also Ma et al. 2013).
By setting Lacc = LEdd, the Eddington accretion rate can be expressed as 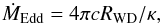 (4)which was adopted in Nomoto (1982). In this paper, we first set Lacc = LEdd as the wind triggering criteria to reproduce the results of the steady-state models of Nomoto (1982), which can be used to test the reliability of our code. Then we set Lprime = LEdd as the wind triggering criteria to investigate the long-term evolution of WDs during He accretion. In the steady He burning regime, we note that L and Lprime are not so different from each other because Lnuc is far greater than Lacc. Thus, the distinction between using L or Lprime as the wind triggering criterion is relatively small. Additionally, if Lnuc = LEdd is assumed and the accreted matter is burned completely (i.e., Ṁacc = Ṁnuc), then the Eddington accretion rate can be expressed as ṀEdd = 4πcGMWD/ (YQκ) (see also Shen & Bildsten 2007).
(4)which was adopted in Nomoto (1982). In this paper, we first set Lacc = LEdd as the wind triggering criteria to reproduce the results of the steady-state models of Nomoto (1982), which can be used to test the reliability of our code. Then we set Lprime = LEdd as the wind triggering criteria to investigate the long-term evolution of WDs during He accretion. In the steady He burning regime, we note that L and Lprime are not so different from each other because Lnuc is far greater than Lacc. Thus, the distinction between using L or Lprime as the wind triggering criterion is relatively small. Additionally, if Lnuc = LEdd is assumed and the accreted matter is burned completely (i.e., Ṁacc = Ṁnuc), then the Eddington accretion rate can be expressed as ṀEdd = 4πcGMWD/ (YQκ) (see also Shen & Bildsten 2007).
3. Numerical results
3.1. Reproducing previous results
 |
Fig. 1 Evolution of the luminosity, radius, and mass of an accreting WD with 1 M⊙ in the steady He layer burning regime (Ṁacc = 2 × 10-6 M⊙ yr-1; panel a), and in the red-giant-like He star regime (Ṁacc = 4 × 10-6 M⊙ yr-1; panel b). |
In order to compare our results with those of the steady-state models of Nomoto (1982), we studied the evolution of CO WDs during He accretion by setting Lacc = LEdd. Two representative examples of our calculations are shown in Fig. 1. In panel (a), the He layer burning is steady on the surface of the WD at an accretion rate of 2 × 10-6 M⊙ yr-1. In this case, the WD can increase its mass to the condition of the explosive carbon ignition, resulting in an SN Ia explosion as a consequence. The WD explosion mass can exceed the Chandrasekhar limit if rotation is taken into account (e.g., Yoon & Langer 2004; Chen & Li 2009; Justham 2011; Hachisu et al. 2012; Wang et al. 2014b). In panel (b), the WD will evolve into a red-giant-like He star because of a high accretion rate of 4 × 10-6 M⊙ yr-1 that is higher than the critical value of ṀRG presented in Fig. 2. In such a case, the WD will not form an SN Ia but will evolve into a red-giant-like He star.
 |
Fig. 2 Properties of the He layer burning on the surface of WD in the plane of WD mass and accretion rate, in which we set Lacc = LEdd. The red solid lines are the results of our simulations, whereas the blue dotted line and the black dashed line are taken from Nomoto (1982) and Piersanti et al. (2014), respectively. The Eddington accretion rate ṀEdd in this case is much higher than the values of ṀRG. We note that Piersanti et al. (2014) did not present the Eddington accretion rate in their paper. |
In Fig. 2, we show the stable He burning regime by setting Lacc = LEdd, in which the WD can increase its mass steadily in this regime. The critical values of ṀRG and the minimum accretion rate Ṁst for stable He layer burning here are approximated by the algebraic form ![\begin{eqnarray} && \dot{M}_{\rm RG}=2.156\times10^{-6}\left({M}_{\rm WD}^2+0.820{M}_{\rm WD}-0.379\right),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \\[2mm] && \dot{M}_{\rm st}\!=\!1.132 \! \times \! 10^{-5}\left(-{M}_{\rm WD}^3 \! + \! 2.562{M}_{\rm WD}^2 \! - \!\! 1.845{M}_{\rm WD} \! + \! 0.435\right),\, \end{eqnarray}](/articles/aa/full_html/2015/12/aa26569-15/aa26569-15-eq58.png) where MWD is in units of M⊙, and ṀRG and Ṁst are in units of M⊙ yr-1. These two critical values strongly depend on the WD mass and were determined through the bisection method for each WD mass. Here, we adopt the Thomson opacity for comparison with previous studies. In this figure, we also show the Eddington accretion rate, which is very close to that of Nomoto (1982).
where MWD is in units of M⊙, and ṀRG and Ṁst are in units of M⊙ yr-1. These two critical values strongly depend on the WD mass and were determined through the bisection method for each WD mass. Here, we adopt the Thomson opacity for comparison with previous studies. In this figure, we also show the Eddington accretion rate, which is very close to that of Nomoto (1982).
The WD will evolve into a red-giant-like He star if the accretion rate is larger than ṀRG, above which the envelope of the WD expands to red-giant dimensions and outflow may occur. In Fig. 2, we also compared the values of ṀRG between this work and those of the steady-state models of Nomoto (1982) and Piersanti et al. (2014). It seems that our results are close to those of Piersanti et al. (2014). However, there are still some small differences with the results of Nomoto (1982) when MWD< 1 M⊙, which likely results from the different methods adopted. Nomoto (1982) studied the stability of the steady-state models via a linear stability analysis, whereas we performed a series of stellar evolution simulations by adopting a detailed He accretion process.
3.2. Super-Eddington wind scenario
We calculated the Eddington accretion rate ṀEdd for various WD masses using Lprime = LEdd as a criterion for triggering the super-Eddington wind. The final results are presented in Fig. 3. Here, we used the opacity of the photosphere when calculating the Eddington luminosity as was done in Denissenkov et al. (2013; see also Ma et al. 2013). The values of the Eddington critical accretion rate ṀEdd are approximated by the following algebraic form: 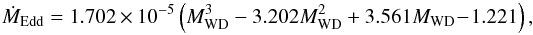 (7)where MWD is in units of M⊙, and ṀEdd is in units of M⊙ yr-1.
(7)where MWD is in units of M⊙, and ṀEdd is in units of M⊙ yr-1.
 |
Fig. 3 Properties of the He layer burning on the surface of WD in the plane of WD mass and accretion rate, in which the super-Eddington wind is triggered when Lprime = LEdd. The red solid line shows the Eddington accretion rate ṀEdd, whereas the green solid line presents the minimum accretion rate Ṁst for stable He layer burning. For comparison, we also present the boundaries of |
The values of ṀEdd obtained here are much lower than those in Nomoto (1982) since Lprime is far greater than the accretion luminosity. We note that the values of ṀEdd are even lower than ṀRG, which is caused by a high value of opacity. For the case of 1 M⊙ WD with an accretion rate of 2.14 × 10-6 M⊙ yr-1, Lprime can reach the Eddington critical limit. The temperature at the photosphere for this accreting WD is 9.15 × 105 K, and the density is 4.07 × 10-4 g/cm3. The opacity in this case is 0.427 cm2/ g, which is higher than that for electron scattering in fully ionized He (κ ~ 0.2 cm2/ g). In addition to the contribution of electron scattering, the free-free transition of electrons also contributes to the opacity of the photosphere for the accreting WD.
For comparison, we also give the Eddington critical accretion rate 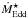 by setting Lnuc = LEdd as the wind triggering criteria (see the black dashed line in Fig. 3). The contributions from thermal energy are non-negligible in our simulations even though Lnuc dominates the luminosity. For hot massive WDs, the thermal energy can account for up to 20% of Lprime. The values of
by setting Lnuc = LEdd as the wind triggering criteria (see the black dashed line in Fig. 3). The contributions from thermal energy are non-negligible in our simulations even though Lnuc dominates the luminosity. For hot massive WDs, the thermal energy can account for up to 20% of Lprime. The values of 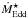 are approximated by the algebraic form
are approximated by the algebraic form 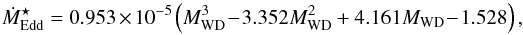 (8)where MWD is in units of M⊙, and
(8)where MWD is in units of M⊙, and 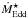 is in units of M⊙ yr-1.
is in units of M⊙ yr-1.
The red-giant regime is now replaced by a super-Eddington wind regime. In this regime, the super-Eddington wind can be formed, which can blow away the surface matter of the WD and prevent the He-rich envelope from expanding. In this case, the WD will never become a red-giant-like He star. The He layer burning in this regime is steady on the surface of the WD, in which the accreted He-rich matter is burned into carbon and oxygen at a rate of ṀEdd; the unprocessed matter can be blown away by the super-Eddington wind with a mass-loss rate of (Ṁacc−ṀEdd). Therefore, the super-Eddington wind provides an alternative way to the optically thick wind, in the sense that it can prevent an accreting WD from expanding to a red-giant-like He star. In comparison to the optically thick wind, the super-Eddington wind is not dependent on the metallicity (see Fig. 4 of Ma et al. 2013). We note that the accretion rate Ṁacc might have an upper limit (e.g., 3 ṀEdd) above which all the unprocessed matter cannot be blown away by the super-Eddington wind, resulting in the formation of a common envelope (e.g., Langer et al. 2000; Tauris et al. 2013).
3.3. Mass retention efficiency in He layer flashes
 |
Fig. 4 Representative example of He layer flashes on the surface of a 1 M⊙ WD, in which we set Ṁacc = 6 × 10-7 M⊙ yr-1. |
When the accretion rate is smaller than Ṁst, a He layer flash occurs on the surface of the WD to develop a nova outburst. The mass loss via the wind carries away a part of the envelope matter if the He layer flashes happen, which reduces the mass-growth rate of the WD. According to the stellar evolution code MESA, multi-cycle nova evolutionary sequences with CO WD cores were recently constructed by Denissenkov et al. (2013), in which Lprime = LEdd was employed as the triggering criteria for the super-Eddington wind. As was done in the works of Denissenkov et al. (2013), we also assume that the rate at which the mass-loss kinetic energy changes is determined by the excess of nova luminosity over the Eddington luminosity.
We obtained the mass retention efficiency of He layer flashes for various WD masses. In Fig. 4, we show a representative example of He layer flashes on the surface of a 1 M⊙ WD with a constant accretion rate Ṁacc = 6 × 10-7 M⊙ yr-1. The He layer in this case periodically experiences He layer flashes. The WD quickly enters into a recurring condition of flashes in which mass is accreted after the first He layer flash. During a He layer flash some of the envelope matter is lost via the super-Eddington wind (see also Denissenkov et al. 2013). The positive slope for the mass growth of the WD shows that the WD grows in mass at a rate of 6.571 × 10-8 M⊙ yr-1 for a constant accretion rate of 6 × 10-7 M⊙ yr-1. This represents a mass retention efficiency per cycle of ≈11%.
 |
Fig. 5 Mass retention efficiency of He layer flashes, ηHe, is plotted against accretion rate for various initial WD masses. |
In Fig. 5, we present the mass retention efficiency of He layer flashes for a wide range of initial WD masses with various accretion rates. The mass retention efficiency ηHe is a function of the accretion rate and the WD mass. From this figure, we can see that ηHe increases with the WD mass for a given accretion rate. This is because the nuclear burning rates are much higher than the wind mass-loss rates for more massive WDs due to the strong gravity. Consequently, most of the layer mass accumulates on the surface of these more massive WDs. The mass retention efficiency in He layer flashes plays an important role in binary evolution, which has an important influence on the birthrates of SNe Ia. Note that ηHe may be increased if rotation is considered (e.g., Yoon et al. 2004). The data points in Fig. 5 can be used in the studies of binary population synthesis computations. These data points and the corresponding interpolation FORTRAN code can be provided by contacting the author.
4. Discussion and conclusions
When calculating the Eddington accretion rate, we did not consider the contribution of Lacc to the total luminosity of the WD (see also Ma et al. 2013) because the accretion energy can be radiated away from the WD surface rapidly (e.g., Townsley & Bildsten 2004). If we include Lacc in the total luminosity of the WD, the super-Eddington wind will be formed more easily as the accretion energy will also contribute to expelling the accreted matter. Ma et al. (2013) recently investigated the evolution of CO WDs accreting H-rich matter, and examined the effect of Lacc on the accretion process of WDs. They found that the accretion luminosity has no significant influence on the Eddington accretion rate (see Fig. 3 of Ma et al. 2013). The difference between using L or Lprime as a criterion for driving wind is fairly small, since the nuclear burning luminosity is far greater than the accretion energy.
The super-Eddington He wind may be formed when the luminosity exceeds the Eddington limit, which can be expected in the observed WD+He star systems. For WD+He star systems with long orbital periods, the He star will fill its Roche lobe when it evolves to the subgiant stage (it now contains a CO core). In this case, the super-Eddington wind would be encountered owing to a high mass-transfer rate resulting from the rapid expansion of the He star during the subgiant stage (e.g., Wang et al. 2009a). HD 49798 (a hydrogen depleted He star) with its massive WD companion may be a progenitor candidate of SNe Ia. After about 4 × 104 yr, HD 49798 will fill its Roche lobe due to the rapid expansion of its envelope (see Wang & Han 2010). In this binary system, a super-Eddington wind may be triggered on the surface of the massive WD owing to a high mass-transfer rate soon after the onset of Roche-lobe overflow (see Fig. 2 in Wang & Han 2010).
It has been suggested that cataclysmic variables are progenitor candidates of SNe Ia (e.g., Parthasarathy et al. 2007; Wang & Han 2012). In Fig. 5, we can see that the WD can still undergo mass growth during nova outbursts. This suggests that some observational cataclysmic variables may be candidates of SN Ia progenitors. In the observations, such a He layer flash could be observed as a He nova outburst. V445 Puppis was discovered at its outburst stage in late 2000, which is the first He nova that has been detected so far (e.g., Kato et al. 2000; Ashok & Banerjee 2003). Kato et al. (2008) recently fitted the light curve of V445 Puppis, and argued that the WD mass is above 1.35 M⊙ and half of the accreted matter is still on the surface of the WD. Therefore, V445 Puppis is a strong candidate of SN Ia progenitors (see also Woudt et al. 2009). However, it is still unclear whether WDs lose more matter during nova outbursts than during the accretion (e.g., Bours et al. 2013; Idan et al. 2013; Newsham et al. 2014; Hillman et al. 2015).
At low accretion rates (e.g., <Ṁst), the accreting WD would develop He layer flashes. For a given mass of the CO WD core, the strength of He layer flashes increases with decreasing Ṁacc. If the accretion rate of the WD is too low (e.g., <4 × 10-8 M⊙ yr-1), a thick He layer is believed to grow on its surface. In this case, a sub-Chandrasekhar double-detonation may happen once a He layer with a critical mass accumulates on the WD (e.g., Woosley et al. 1986; Piersanti et al. 2014). CD−30° 11223 has been identified as a WD+He star system with a ~1.2 h orbital period (e.g., Vennes et al. 2012; Geier et al. 2013). The masses of the He star and the WD are constrained to be ~0.51 M⊙ and ~0.76 M⊙, respectively (see Geier et al. 2013). Wang et al. (2013b) recently suggested that CD−30° 11223 might produce an SN Ia through the double-detonation scenario in its future evolution (see also Geier et al. 2013).
Employing the stellar evolution code MESA, we have investigated the long-term evolution of He accreting WDs. In order to reproduce the results of the steady-state models, we first set Lacc = LEdd as the wind triggering criteria, and found that the properties of He burning in our simulations are almost similar to those of the steady-state models. If the total luminosity is considered when determining the Eddington accretion rate, a super-Eddington wind could be formed at relatively lower accretion rates than those of previous studies of the steady-state models. The super-Eddington wind can prevent CO WDs with high accretion rates from becoming red-giant-like He stars. We also presented the steady He-burning regime in which the He-rich matter can be burned into carbon and oxygen completely on the surface of the WD. Additionally, we performed a multi-cycle evolution of He layer flashes in the simulations of nova outbursts, and obtained the mass retention efficiency of He layer flashes for various WD masses, which will be useful in future binary population synthesis studies. Note also that we used the opacity of the photosphere when we calculate the Eddington luminosity as was done in Denissenkov et al. (2013). However, the opacity in the wind may change compared to the values at the photosphere, which should be further studied.
At the beginning of the He layer burning, the evolution of cold WDs may be somewhat different to that of the hot ones during mass accretion. However, the difference is not significant once an equilibrium condition is reached. Iben (1982) also used hot WD models when simulating the evolution of accreting WDs (see also Iben & Tutukov 1989).
Acknowledgments
We acknowledge the anonymous referee for the valuable comments that helped us to improve the paper. We thank Philipp Podsiadlowski, Pavel A. Denissenkov, Xuefei Chen and Xiangcun Meng for their helpful discussions. We also thank Yan Gao for his kind help to improve the language of this paper, and thank the computing time granted by the Supercomputing Platform of Yunnan Observatories. This work is supported by the National Basic Research Program of China (973 programme, 2014CB845700), the National Natural Science Foundation of China (Nos 11390374, 11521303, 11322327 and U1331117), the Chinese Academy of Sciences (Nos KJZD-EW-M06-01 and XDB09010202), and the Natural Science Foundation of Yunnan Province (Nos 2013HB097 and 2013FB083).
References
- Ashok, N. M., & Banerjee, D. P. K. 2003, A&A, 409, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Badenes, C., Harris, J., Zaritsky, D., & Prieto, J. L. 2009, ApJ, 700, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., Shen, K. J., Weinberg, N. N., & Nelemans, G. 2007, ApJ, 662, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Bours, M. C. P., Toonen, S., & Nelemans, G. 2013, A&A, 552, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brooks, J., Bildsten, L., Marchant, P., & Paxton, B. 2015, ApJ, 807, 74 [Google Scholar]
- Chen, W.-C., & Li, X.-D. 2009, ApJ, 702, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Jeffery, C. S., Zhang, X., & Han, Z. 2012, ApJ, 755, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Claeys, J. S. W., Pols, O. R., Izzard, R. G., Vink, J., & Verbunt, F. W. M. 2014, A&A, 563, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Denissenkov, P. A., Herwig, F., Bildsten, L., & Paxton, B. 2013, ApJ, 762, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, R., Siegert, T., Hillebrandt, W., et al. 2014, Science, 345, 1162 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, J., & Zhang, L. 2012, MNRAS, 424, 2811 [NASA ADS] [CrossRef] [Google Scholar]
- Fink, M., Hillebrandt, W., & Röpke, F. K. 2007, A&A, 476, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geier, S., Nesslinger, S., Heber, U., et al. 2007, A&A, 464, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geier, S., Marsh, T. R., Wang, B., et al. 2013, A&A, 554, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geier, S., Fürst, F., Ziegerer, E., et al. 2015, Science, 347, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, Ph. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, Ph. 2006, MNRAS, 368, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., Saio, H., & Nomoto, K. 2012, ApJ, 744, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Hillebrandt, W., Kromer, M., Röpke, F. K., & Ruiter, A. J. 2013, Frontiers Phys., 8, 116 [Google Scholar]
- Hillman, Y., Prialnik, D., Kovetz, A., & Shara, M. M. 2015, ApJ, submitted [arXiv:1508.03141] [Google Scholar]
- Hoeflich, P., Dragulin, P., Mitchell, J., et al. 2013, Frontiers of Physics, 8, 144 [Google Scholar]
- Howell, D. A. 2011, Nat. Comm., 2, 350 [Google Scholar]
- Iben, I. 1982, ApJ, 259, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., & Tutukov, A. V. 1989, ApJ, 342, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Idan, I., Shaviv, N. J., & Shaviv, G. 2013, MNRAS, 433, 2884 [NASA ADS] [CrossRef] [Google Scholar]
- Justham, S. 2011, ApJ, 730, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Justham, S., Wolf, C., Podsiadlowski, P., & Han, Z. 2009, A&A, 493, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasliwal, M. M., Kulkarni, S. R., Gal-Yam, A., et al. 2012, ApJ, 755, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 2004, ApJ, 613, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, T., Kanatsu, K., Takamizawa, K., Takao, A., & Stubbings, R. 2000, IAU Circ., 7552, 1 [NASA ADS] [Google Scholar]
- Kato, M., Hachisu, I., Kiyota, S., & Saio, H. 2008, ApJ, 684, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, ApJ, 362, 1046 [Google Scholar]
- Li, X.-D., & van den Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS] [Google Scholar]
- Liu, Z.-W., Stancliffe, R. J., Abate, C., & Wang, B. 2015, ApJ, 808, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Livne, E. 1990, ApJ, 354, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, X., Chen, X., Chen, H., Denissenkov, P. A., & Han, Z. 2013, ApJ, 778, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Greggio, L. 1986, A&A, 154, 279 [NASA ADS] [Google Scholar]
- McCully, C., Jha, S. W., Foley, R. J., et al. 2014, Nature, 512, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., & Podsiadlowski, Ph. 2013, ApJ, 778, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., & Podsiadlowski, Ph. 2014, ApJ, 789, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S., Tiengo, A., Esposito, P., et al. 2009, Science, 325, 1222 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nelemans, G., Portegies Zwart, S. F., Verbunt, F., & Yungelson, L. R. 2001, A&A, 368, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newsham, G., Starrfield, S., & Timmes, F. 2014, ASP Conf. Ser., 490, 287 [NASA ADS] [Google Scholar]
- Nomoto, K. 1982, ApJ, 253, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Thielemann, F., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Parthasarathy, M., Branch, D., Jeffery, D. J., & Baron, E. 2007, New Astron. Rev., 51, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, Ph., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Tornambé, A., & Yungelson, L. R. 2014, MNRAS, 445, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Tornambé, A., & Yungelson, L. R. 2015, MNRAS, 452, 2897 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, P., Mazzali, P., Lesaffre, P., Han, Z., & Förster, F. 2008, New Astro. Rev., 52, 381 [Google Scholar]
- Ruiter, A. J., Belczynski, K., & Fryer, C. 2009, ApJ, 699, 2026 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Sim, S. A., Pakmor, R., et al. 2013, MNRAS, 429, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Belczynski, K., Sim, S. A., Seitenzahl, I. R., Kwiatkowski, D., 2014, MNRAS, 440, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., & Bildsten, L. 2007, ApJ, 660, 1444 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., & Bildsten, L. 2009, ApJ, 699, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Kasen, D., Weinberg, N. N., Bildsten, L., & Scannapieco, E. 2010, ApJ, 715, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Sim, S. A., Fink, M., Kromer, M., et al. 2012, MNRAS, 420, 3003 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., Sanyal, D., Yoon, S.-C., & Langer, N. 2013, A&A, 558, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toonen, S., Claeys, J. S. W., Mennekens, N., & Ruiter, A. J. 2014, A&A, 562, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Townsley, D. M., & Bildsten, L. 2004, ApJ, 600, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Vennes, S., Kawka, A., O’Toole, S. J., Németh, P, & Burton, D. 2012, ApJ, 759, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., & Han, Z. 2009, A&A, 508, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, B., & Han, Z. 2010, Res. Astron. Astrophys., 10, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., & Han, Z. 2012, New Astron. Rev., 56, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Meng, X., Chen, X., & Han, Z. 2009a, MNRAS, 395, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Chen, X., Meng, X., & Han, Z. 2009b, ApJ, 701, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Li, X.-D., & Han, Z. 2010, MNRAS, 401, 2729 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X.-F., Wang, L., Filippenko, A. V., Zhang, T., & Zhao, X. 2013a, Science, 340, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Justham, S., & Han, Z. 2013b, A&A, 559, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, B., Meng, X., Liu, D., Liu, Z., & Han, Z. 2014a, ApJ, 794, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Justham, S., Liu, Z., Zhang, J., Liu, D., & Han, Z. 2014b, MNRAS, 445, 2340 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Kasen, D. 2011, ApJ, 734, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Taam, R. E., & Weaver, T. A. 1986, ApJ, 301, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Woudt, P. A., Steeghs, D., Karovska, M., et al. 2009, ApJ, 706, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2003, A&A, 412, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2004, A&A, 419, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Langer, N., & Scheithauer, S. 2004, A&A, 425, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Evolution of the luminosity, radius, and mass of an accreting WD with 1 M⊙ in the steady He layer burning regime (Ṁacc = 2 × 10-6 M⊙ yr-1; panel a), and in the red-giant-like He star regime (Ṁacc = 4 × 10-6 M⊙ yr-1; panel b). |
| In the text | |
 |
Fig. 2 Properties of the He layer burning on the surface of WD in the plane of WD mass and accretion rate, in which we set Lacc = LEdd. The red solid lines are the results of our simulations, whereas the blue dotted line and the black dashed line are taken from Nomoto (1982) and Piersanti et al. (2014), respectively. The Eddington accretion rate ṀEdd in this case is much higher than the values of ṀRG. We note that Piersanti et al. (2014) did not present the Eddington accretion rate in their paper. |
| In the text | |
 |
Fig. 3 Properties of the He layer burning on the surface of WD in the plane of WD mass and accretion rate, in which the super-Eddington wind is triggered when Lprime = LEdd. The red solid line shows the Eddington accretion rate ṀEdd, whereas the green solid line presents the minimum accretion rate Ṁst for stable He layer burning. For comparison, we also present the boundaries of |
| In the text | |
 |
Fig. 4 Representative example of He layer flashes on the surface of a 1 M⊙ WD, in which we set Ṁacc = 6 × 10-7 M⊙ yr-1. |
| In the text | |
 |
Fig. 5 Mass retention efficiency of He layer flashes, ηHe, is plotted against accretion rate for various initial WD masses. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


