| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 11 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201526498 | |
| Published online | 27 November 2015 | |
Orbit determination of trans-Neptunian objects and Centaurs for the prediction of stellar occultations⋆,⋆⋆
1
Observatório Nacional/MCTI, Rua Gal. José Cristino 77, CEP, 20921-400
Rio de Janeiro,
Brazil
2
Institut de Mécanique Céleste et de Calcul des Éphémérides –
Observatoire de Paris, UMR 8028 CNRS, 77 avenue Denfert-Rochereau, 75014
Paris,
France
e-mail: desmars@imcce.fr
3
Laboratório Interinstitucional de e-Astronomia –
LIneA, Rua Gal. José Cristino
77, CEP
20921-400, Rio de
Janeiro, Brazil
4
Federal University of Technology – Paraná (UTFPR /
DAFIS), Rua Sete de Setembro,
3165, CEP
80230-901, Curitiba, PR,
Brazil
5
Observatório do Valongo/UFRJ, Ladeira do Pedro Antônio 43, CEP 20080-090, Rio de Janeiro,
Brazil
6
Instituto de Astrofísica de Andalucía,
CSIC, Apartado 3004,
18080
Granada,
Spain
7
LESIA, Observatoire de Paris, CNRS UMR 8109, Université Pierre et
Marie Curie, Université Paris-Diderot, 5 place Jules Janssen, 92195
Meudon Cedex,
France
Received:
8
May
2015
Accepted:
7
September
2015
Context. The prediction of stellar occultations by trans-Neptunian objects (TNOs) and Centaurs is a difficult challenge that requires accuracy both in the occulted star position and in the object ephemeris. Until now, the most used method of prediction, involving dozens of TNOs/Centaurs, has been to consider a constant offset for the right ascension and for the declination with respect to a reference ephemeris, usually the latest public version. This offset is determined as the difference between the most recent observations of the TNO/Centaur and the reference ephemeris. This method can be successfully applied when the offset remains constant with time, i.e. when the orbit is stable enough. In this case, the prediction even holds for occultations that occur several days after the last observations.
Aims. This paper presents an alternative method of prediction, based on a new accurate orbit determination procedure, which uses all the available positions of the TNO from the Minor Planet Center database, as well as sets of new astrometric positions from unpublished observations.
Methods. Orbits were determined through a numerical integration procedure called NIMA, in which we developed a specific weighting scheme that considers the individual precision of the observation, the number of observations performed during one night by the same observatory, and the presence of systematic errors in the positions.
Results. The NIMA method was applied to 51 selected TNOs and Centaurs. For this purpose, we performed about 2900 new observations in several observatories (European South Observatory, Observatório Pico dos Dias, Pic du Midi, etc.) during the 2007–2014 period. Using NIMA, we succeed in predicting the stellar occultations of 10 TNOs and 3 Centaurs between July 2013 and February 2015. By comparing the NIMA and Jet Propulsion Laboratory (JPL) ephemerides, we highlight the variation in the offset between them with time, by showing that, generally, the constant offset hypothesis is not valid, even for short time scales of a few weeks. Giving examples, we show that the constant offset method cannot accurately predict 6 out of the 13 observed positive occultations that have been successfully predicted by NIMA. The results indicate that NIMA is capable of efficiently refining the orbits of these bodies. Finally, we show that the astrometric positions given by positive occultations can help to refine the orbit of the TNO and, consequently, the future predictions. We also provide unpublished observations of the 51 selected TNOs and their ephemeris in a usable format by the SPICE library.
Key words: astrometry / celestial mechanics / occultations / Kuiper belt: general / methods: numerical
We provide ephemerides of TNO/Centaurs usable with SPICE library and available at http://www.imcce.fr/~desmars/research/tno/
The offset observations of the selected TNOs are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/584/A96
© ESO, 2015
1. Introduction
When a trans-Neptunian object (TNO) or a Centaur occults a star, their sizes and shapes can be determined with kilometric accuracy (Elliot et al. 2010; Sicardy et al. 2011; Ortiz et al. 2012; Braga-Ribas et al. 2013) from the resulting light curves of ground-based observers located inside the shadow path or just outside it. This level of accuracy in dimensions can only be rivaled by space missions. Also, ring systems (Braga-Ribas et al. 2014a) and atmospheres that are as tenuous as a few nanobars (Widemann et al. 2009; Sicardy et al. 2011; Braga-Ribas et al. 2013) can be detected when present. These parameters are important when studying TNOs1, and as a consequence, when retrieving the history and evolution of the outer solar system. However, the prediction of an occultation (where and when the event can be detected on Earth) is essential before any observation.
Predicting stellar occultations requires the accurate position of both the occulted star and the TNO ephemeris. The uncertainty of star position and ephemeris must be smaller than the apparent angular size of the body radius to observe the occultation at the predicted location on Earth. The position of the star is initially taken from an astrometric catalogue that takes its proper motion into account, if available. Since the proper motion and astrometry may be inaccurate, the star is observed before the occultation to refine its position. Depending on the number and quality of observations, the accuracy of the final position is about is about 10 mas to 20 mas, which is similar to the apparent angular size of the objects.
The ephemeris is obtained using an orbit determination process. This consists of determining orbital elements that minimise the difference between the observed and the computed positions, i.e. the O–C. The ephemeris remains precise during the observational period but starts to diverge after the last observations.
Previous studies about predictions of occultations tried to overcome the problem of ephemeris divergence by using more recent observations. Assafin et al. (2012) and Camargo et al. (2014) used a constant offset to the ephemeris to refine the predictions. The offset was determined by using a set of observations performed a few weeks to a few months before the predicted occultation. In practice, the offset was computed as the difference between the observed position and a reference ephemeris at the date of the offset observations. This method assumes that the offset remains constant or varies by less than the body radius until the occultation date, which only happens when the occultation occurs a few days after the offset observations or when the orbit is determined relatively well.
Fraser et al. (2013) highlight that the offset is not constant and could lead to unreliable predictions. They propose refining the orbit using the offset observations and adopt a maximum-likelihood approach to correct the orbital elements. They use only their own observations and not the past observations from the Minor Planet Center (MPC) database. As a consequence, their new orbits strongly depend on their new observations. As such, their ephemeris is likely to diverge during a time span that is shorter than desired. Finally, the MIT group (Bosh et al., in prep.) also provides predictions of stellar occultations based on a drift and a periodic term for the offset2.
In this paper, we present a new numerical procedure called NIMA (Sect. 2) that computes the orbits of TNOs. NIMA consists of a complete process of orbit determination that benefits from all available observations of the TNO/Centaur (e.g. past observations from MPC, offset observations, and unpublished observations, see Sect. 3) and from a specific weighting scheme for observations (see Sect. 2.3). In Sect. 4, we present the results of using NIMA on a set of 51 TNOs and Centaurs selected for their physical, observable, and dynamical characteristics. We conclude (Sect. 5) that NIMA is capable of providing significantly improved ephemeris for TNOs and Centaurs, allowing for the prediction of more accurate stellar occultations within a more extended time span – more than for any other methods used to date.
2. NIMA ephemeris
The NIMA3 ephemeris was originally developed to determine the orbit of near Earth asteroids (NEAs) in the context of detecting the Yarkovsky effect (Desmars 2015). It can be used to determine the orbit of any asteroid, TNO, or Centaur, given their similar dynamical conditions, (see Sect. 2.1).
The NIMA code enables the determination and propagation of an orbit thanks to a numerical integration of the equations of motion. Compared with either the version applied to NEAs or with other codes for orbit determination, e.g. OrbFit4, the main difference is in the weighting scheme that is adapted to get accurate short-term orbits, specifically for predicting occultations.
The following sections describe the dynamical model, the fitting process, and the weighting scheme.
2.1. Numerical integration
The dynamical model of a TNO’s motion includes the gravitational perturbations of the Sun and the eight planets. All planets are considered as point masses, and the Earth-Moon system is considered as a point mass located at the Earth-Moon barycentre. No other perturbations are required since TNOs are distant objects. For example, after adding the three biggest asteroids (Ceres, Vesta, and Pallas) or by adding Pluto into the dynamical model, we noticed only insignificant changes when determining orbits. The masses of the eight planets and their positions are given by JPL ephemeris DE431 (Folkner et al. 2014).
The equations of motion, given by the dynamical model, are numerically integrated through a Gauss Radau integrator (Everhart 1985). The equations of variation, as described in Lainey et al. (2004), are also integrated to determine the partial derivatives of the position and the velocity components related to the components of state vector (cj) that encompasses the position and the velocity vectors at a specific epoch.
2.2. Fitting process
The fitting process consists in determining six parameters C = (cj) (the state vector) that minimise the residuals ΔY (the difference between observed and computed positions). This determination uses a Levenberg-Marquardt algorithm to make iterative corrections to each component in the state vector 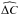 . For each iteration, the corrections are determined using the partial derivatives (represented by matrix A), a weighting matrix Vobs, and the least square method (LSM; for more information, see for example, Desmars et al. 2009):
. For each iteration, the corrections are determined using the partial derivatives (represented by matrix A), a weighting matrix Vobs, and the least square method (LSM; for more information, see for example, Desmars et al. 2009): 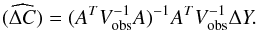 (1)In the LSM, a weighting matrix Vobs is required, and we specifically discuss the weighting scheme in the next section.
(1)In the LSM, a weighting matrix Vobs is required, and we specifically discuss the weighting scheme in the next section.
The normal matrix N and covariance matrix Λ0 are defined as 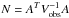 and Λ0 = N-1.
and Λ0 = N-1.
The standard deviation of each parameter (cj) is given by the root square of the diagonal elements of Λ0. Moreover, the covariance matrix can be linearly propagated at any date t using the equation 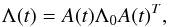 (2)where A(t) is the matrix of partial derivatives at date t. This linear relation can thus provide the estimated precision of the position in the celestial sphere (right ascension and declination) at any date.
(2)where A(t) is the matrix of partial derivatives at date t. This linear relation can thus provide the estimated precision of the position in the celestial sphere (right ascension and declination) at any date.
2.3. Weighting scheme
Observed positions have various accuracies and can be correlated. In this context, we have to consider the covariance matrix of the observed position Vobs that is supposed to be known in the LSM. In practice, we neglect correlations so that the covariance matrix of the observed position Vobs is considered as a diagonal matrix where the diagonal components are 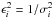 , and where
, and where 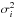 is the estimated variance of the observed position i (Desmars et al. 2009).
is the estimated variance of the observed position i (Desmars et al. 2009).
When determining the orbit, the main difficulty is to give an appropriate weight to each position. Positions contain not only a random error but also many systematic errors from several different sources, such as the telescope used for observation, the stellar catalogue used for the reduction.
Carpino et al. (2003) and Chesley et al. (2010) discuss weighting schemes and show the improvement in determining orbits by weighting positions in relation to the observatory and the stellar catalogue that was used for the reduction.
However, a problem can occur when using this weighting scheme if several dozens of observations are performed on the same night in the same observatory. If individual observed positions have a weight ϵi, the mean weight for the set of positions is 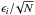 , where N is the number of positions per night. The mean weight can become low whereas the positions can become biased. In which case, determining the orbit will be degraded by this set of positions. This problem mainly concerns our offset observations (see Sect. 3.2), with an average of 13.1 observations per night, whereas in MPC observations (see Sect. 3.1), 2.8 observations of the studied objects occurred per night.
, where N is the number of positions per night. The mean weight can become low whereas the positions can become biased. In which case, determining the orbit will be degraded by this set of positions. This problem mainly concerns our offset observations (see Sect. 3.2), with an average of 13.1 observations per night, whereas in MPC observations (see Sect. 3.1), 2.8 observations of the studied objects occurred per night.
To overcome this problem, we adopt a specific weighting scheme, by taking the estimated precision of each position into account, depending on which observatory and stellar catalogue are used, as well as any possible bias due to the observatory.
The estimated variance ωi of each position i is given by 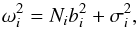 (3)where Ni is the number of observations performed during the same night and in the same observatory, while position i, bi corresponds to the possible bias that depends on the stellar catalogue and observatory, and σi is the estimated precision of individual position i provided by Chesley et al. (2010) or by Table 2 for some specific cases.
(3)where Ni is the number of observations performed during the same night and in the same observatory, while position i, bi corresponds to the possible bias that depends on the stellar catalogue and observatory, and σi is the estimated precision of individual position i provided by Chesley et al. (2010) or by Table 2 for some specific cases.
This weighting scheme avoids assigning an artificially strong weight for a night with several dozen observations. In this case, the mean variance tends to 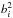 and not 0. Another interpretation is that the mean variance cannot be smaller than
and not 0. Another interpretation is that the mean variance cannot be smaller than 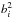 for a single night. Estimated bias bi and precision σi depend on the type of position we deal with. For example, positions from MPC are considered average positions, since the process of reduction for each position is not completely known. In contrast, the positions we used to determine the offset are precise positions, since we know exactly how they were reduced and the quality of the stellar catalogue that was used for their reduction.
for a single night. Estimated bias bi and precision σi depend on the type of position we deal with. For example, positions from MPC are considered average positions, since the process of reduction for each position is not completely known. In contrast, the positions we used to determine the offset are precise positions, since we know exactly how they were reduced and the quality of the stellar catalogue that was used for their reduction.
We performed many tests to determine appropriate bias and precision for the different types of positions (see Sect. 3). Finally, we empirically adopt the values given in Table 1 for the bias bi and the values given in Table 2 for the individual precision of each position σi. For positions from MPC, we adopt bi = 300 mas, while σi depends on the stellar catalogue and observatory and is given by Chesley et al. (2010).
Estimated bias for offset observations in both right ascension and declination for different stellar catalogues and observatories.
Estimated precision for offset observations in both right ascension and declination for different observatories.
As a comparison, Fraser et al. (2013) use an uncertainty of 40 and 80 mas for their positions, whereas the average value for a position from MPC in AstDys database is about 0.5 arcsec. Consequently, the positions from Fraser et al. (2013) have a weight that is 100 times greater than an average position, which does not seem appropriate.
In our study, the maximum precision for a series of several positions in one single night is given by the bias. Based on this, our best positions, which come from ESO and which were reduced with the WFI catalogue (described below), will have a weight that is about 50 times stronger than an average position from MPC. Positions from ESO and reduced with UCAC4 will have a weight that is ten times stronger than average positions.
3. Astrometric observations
Most positions of TNOs and Centaurs come from the MPC database. But since about 2007 we have also started to observe these objects to check occultation predictions. Obviously, the first computed information to evaluate the orbit’s status was the average offset between the observed positions and the object ephemeris. For this reason, these kinds of observations are called offset observations here and throughout the paper. Lastly, we also used astrometric positions that were deduced from previous positive occultations.
3.1. MPC observations
Minor Planet Center5 (MPC) is in charge of receiving and distributing the positional measurements of minor planets, comets, and outer, irregular natural satellites. For one specific object, the MPC gives the file of observations, the orbital elements, the ephemeris, and many other data. Observations are provided by many different observers and observatories (from professional to amateur telescopes), and positions are derived from a variety of reference catalogues and position reduction procedures. Consequently, the quality of the observations is heterogeneous, and that is why the use of a weighting scheme in orbit determination is important, when taking the quality of positions into account.
Owing to their average level of quality and precision, most of the positions on the MPC database are supplied with five decimal digits in time, which correspond to less than one second of uncertainty. This is enough for TNO/Centaurs with two decimal digits in right ascension, which corresponds to 150 mas of uncertainty, and with one decimal digit in declination, which corresponds to 100 mas of uncertainty. Clearly, if this uncertainty is adequate for resolving the problems of identification and ephemeris of positions it is not so in the context of stellar occultations that require a precision of at least 50 mas. However, recent observations are sometimes provided with one extra decimal digit in time, right ascension, and declination.
3.2. Offset observations
A useful step in the process of predicting stellar occultations for a large number of TNOs, over a span of a few years, is to determine a set of initial predictions properly. This set of initial predictions must be complete, that is, must contain all possible events of a given TNO that involves stars up to a given magnitude, and must be accurate enough to allow for selecting of those for which observational efforts to refine the initial prediction are worth employing.
All initial predictions of stellar occultations to the objects presented in Table 4, with the exception of (2060) Chiron and (60558) Echeclus, are detailed in Assafin et al. (2012) and Camargo et al. (2014) and are based on observations made at La Silla (Chile) with the ESO 2.2 m telescope that is equipped with the Wide Field Imager (WFI).
The observational runs have two different purposes: to cover the future sky path of a given TNO and then to observe the TNO itself. The aim of the first set of observations was to identify candidate stars that will be occulted by the TNO. As a by-product of the respective observations, catalogues with positions and proper motions were created to serve as an accurate and – most importantly – dense reference catalogue for astrometry. These are called WFI catalogues. The second set of observations was used to obtain positions of the TNOs and to determine the respective corrections to their ephemerides. The WFI catalogues were used as reference for the astrometry of these images. The planets (2060) Chiron and (60558) Echeclus were later included in our list of objects. Candidate stars that would be occulted by them were selected from the UCAC4 (Zacharias et al. 2013) and USNO-B1 (Monet et al. 2003) catalogues, and subsequent observations were carried out to refine the position of the candidate stars and to correct their ephemerides at the Pico dos Dias observatory.
For the initial predictions given by both Assafin et al. (2012) and Camargo et al. (2014), corrections to ephemerides were done by considering an average offset, which was determined by the position differences in the sense “observation minus ephemeris”. As mentioned earlier in the text, this kind of correction (offset) was assumed to be constant until a new one is determined on the basis of newer observations.
Although good results have been obtained using this method, because of the efforts of many observers, the use of offsets is not ideal (see, for instance, Fig. 3). This method does not allow for predictions with an accuracy greater than 30 mas, for the position of the TNO, with an advance greater than six months. Redetermining the orbit is a more straightforward solution, and the offset observations are still useful for refining the orbit.
3.3. Astrometry from occultations
Once a stellar occultation is detected, we can determine its position in the sky relative to the occulted star, as well as the physical properties of the object. From a multi-site observation, the limb fit of the object to the observed occultation light curves (chords) has the centre of the body as a by-product. This position is relative to a given position, usually the occulted star position, so the position of the object’s centre, at the middle of the event, can be directly calculated with kilometric accuracy.
The absolute position of the object is then dependent on (and limited to) the accuracy of the star position, which is usually many times greater than the lib-fit errors. We performed observations of the occulted stars at Pico dos Dias Observatory to reduce this source of uncertainty. The observations were made near the epoch of the occultation, which are usually used to update predictions, so proper motion errors were avoided. Astrometric reductions were made using the WFI catalogue when available, otherwise the UCAC4 catalogue was used as reference. Accuracies obtained on the star positions range from 10 mas to 20 mas, which is about the apparent angular size of the TNOs on our list.
Accurate TNO positions from stellar occultation can be obtained even for single-chord detections. In this case, it is not possible to derive the size of the object, but we can use its estimated size6 to derive its centre. The observed chord is fitted to a presumed circular object, and the centre is calculated with respect to the star position. This leads to a calculation of its centre with an error of a few hundred kilometres (about the precision of the object size), even when taking a north or south solution into consideration. The error on the absolute object centre is still dominated by the absolute star position.
This is a very straightforward way to obtain precise TNO positions and was applied to all the stellar occultations by TNOs (Braga-Ribas et al. 2014b) we detetected. This will be specially interesting when the GAIA catalogue is available because the position of the objects will no longer be limited by the accuracy of the star position.
4. Results
4.1. Comparison between ephemerides
Ephemerides for TNOs can be found on several databases. To make comparisons with the NIMA ephemeris, we considered the main databases: JPL Horizons7, VO-Miriade8, and AstDys9 (AstDys makes use of the Orbfit package). MPC also provides ephemeris, but we did not consider it because its coordinate values are truncated to 0.1 s in right ascension and 1 arcsec in declination, which is clearly not enough for predicting occultations.
Assuming that these databases were produced using the same set of positions available on the MPC, we can say that they fitted their orbits with the same set of positions as we used with NIMA. We compared the ephemeris for two specific objects: (50 000) Quaoar, which has a long observational period (1954–2014) and 2008OG19 with a short observational period (2008–2012). Figures 1 and 2 present the difference between the various ephemerides in right ascension10, declination, and geocentric distance during the 2010 to 2020 period. We also used a version of NIMA (nima v0) without changing the weight of positions, i.e. using the weights of Chesley et al. (2010) as in Orbfit. Moreover for Quaoar, we added the ephemeris from Fraser et al. (2013) for information purposes only because the ephemeris cannot be fully compared with the others since it makes use of additional observations published in the same paper.
 |
Fig. 1 Difference in right ascension, weighted by cosδ, declination, and geocentric distance between NIMA and each ephemeris for (50 000) Quaoar. |
 |
Fig. 2 Difference in right ascension, weighted by cosδ, declination, and geocentric distance between NIMA and each ephemeris for 2008OG19. |
For objects with a long period of observations, as for Quaoar, the differences between the ephemerides are small (less than 0.1 arcsec) in the 2010 to 2020 period. Even with Fraser ephemeris, the difference is small, despite using additional observations. Because they used OrbFit package for orbit determination, the difference without these additional observations would probably be close to AstDys ephemeris. The small differences between ephemerides for Quaoar indicate the good quality of the orbit because of the long period of observations available. For objects with a short period of observations, such as 2008OG19, the differences between ephemerides are larger (several arcseconds), which indicates the low quality of the orbit.
The difference between ephemerides consists of a secular drift and a 1 yr period term. This periodic term corresponds to the parallax that results from the Earth’s revolution and the difference in distance between the ephemerides. By using the classical weighting scheme, with the weights given by Chesley et al. (2010), we have a very similar orbit between NIMA and OrbFit (corresponding to AstDys ephemeris). Compared to other ephemerides, the advantages of the NIMA ephemeris allow us to use more observations, not just MPC observations, and to control the weighting process.
4.2. Offset variation
By comparing the differences between the NIMA ephemeris, which has been fitted to all positions (MPC + Offset observations), and the JPL ephemeris, which has only been calculated with MPC positions, we have an estimation of the offset variation. Figure 3 represents the differences between NIMA and JPL ephemerides for 2004NT33. For this object, we have two additional sets of offset observations made at ESO in November 2012 and May 2013. Obviously, NIMA ephemeris fits to ESO observations whereas JPL ephemeris does not. As mentioned in the previous section, the offset variation consists of a secular drift and a one-year periodic term that corresponds to a difference in the heliocentric distance between the two orbits. As expected, the offset is not constant with time. We note that the extrema of the oscillations correspond to the quadrature of the object (when elongation is 90 deg). The grey area in the figure represents the estimated uncertainty (1σ) of the NIMA ephemeris, and we note that this uncertainty increases with time.
 |
Fig. 3 Difference between NIMA and JPL ephemerides for 2004NT33 in right ascension (weighted by cosδ) and declination during 2012–2017. The grey area represents the uncertainty of NIMA ephemeris. The sets of observations correspond to one single night of offset observations where several observations were performed. The blue dots represent the average positions of each set and the error bar represents the standard deviation (1σ). |
4.3. Predictions of occultations
By design, the NIMA ephemeris is most suited to predicting occultations because its higher accuracy allows for more confident predictions further in advance. We compare two predictions for the occultation by (28978) Ixion on 24 June 2014 with the offset method and with the NIMA ephemeris. Figure 4 shows the different predictions. The path of the shadow crosses over the north of Australia for the offset method and the centre of Australia for the NIMA ephemeris. Actually, the occultation was successfully observed in the centre of Australia (indicated by the green point), indicating that the prediction with NIMA ephemeris was more accurate. In fact, since July 2013 when NIMA ephemeris was applied to the occultation predictions up to February 2015, ten TNOs and three Centaur events were detected, whereas 13 occultations by TNOs were detected between 2009 and 2012.
 |
Fig. 4 Prediction map of the occultation by Ixion on 24 June 2014 with the offset method (top) and with the NIMA ephemeris (bottom). The occultation was detected in the place indicated by the green point. |
4.4. Precise positions from occultations
As explained in Sect. 3.3, precise astrometric positions of TNOs can be deduced from previous positive occultations. We have reduced 14 astrometric positions for eight different objects so far. Table 3 presents the residuals in right ascension, weighted by cosδ (RA*) and in declination of these positions. Most of the positions have a precision of less than 50 mas.
Residuals of 14 astrometric positions deduced from previous occultations.
 |
Fig. 5 Difference between NIMA and JPL ephemerides for (50 000) Quaoar in right ascension weighted by cosδ (top) and declination (bottom) during 2011–2016, by using only the positions until October 2012 (left) and by using the positions until October 2012, and the two positions from the two previous occultations in May 2011 and February 2012 (right). The grey area represents the uncertainty of NIMA ephemeris and the blue bullets and their error bars represent the positions from the offset observations used for NIMA ephemeris. |
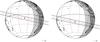 |
Fig. 6 Prediction map of the occultation by Quaoar on 15 October 2012, using only observations (left) and using observations and 2 previous occultations (right). |
These positions can be used to refine the orbit and to improve the prediction of stellar occultations. For example, three positive occultations by (50 000) Quaoar were observed in 2011 and 2012 (Braga-Ribas et al. 2013). To show that the positions provided by these occultations help to improve the orbit quality, we present the prediction of a third observed event on 15 October 2012 with two different sets of positions: the first, using all the available observations up to this date (including offset observations); and the second using the same observations plus the two previous positions that were deduced from the previous detected occultations on May 2011 and February 2012. We have created the prediction maps for the two cases, see Fig. 6. Figure 5 shows the difference between NIMA and JPL ephemerides in right ascension (weighted by cosδ) and declination for these two cases. The difference between the two orbits is about 50 mas in declination at the date of the occultation. To configure this event, an uncertainty in right ascension mainly corresponds to to an uncertainty in time of occultation, whereas an uncertainty in declination corresponds to an uncertainty in the location of the path, which is greater for observation purposes. The two orbits correspond to two different paths of the shadow for the occultation on 15 October 2012 (Fig. 6). Using only the observations, the first predicts an occultation by Quaoar in the south of Peru, whereas the second orbit, using observations and positions of occultations, predicts an occultation over Chile. Finally, the occultation was positively detected at Cerro Tololo by the PROMPT telescopes in the centre of Chile (green point on the figure), which shows that the prediction was improved because of the position given by previous occultations.
4.5. Discussion
Since the position deduced from occultations is only affected by the error on the position of the occulted star, the derived position is more accurate than classical observations. In particular, these positions can highlight systematic errors in observations. Figure 5 reveals systematic errors in the positions from the last two sets of observations performed in May and July 2012. Even if the positions of previous occultations are taken into account, the orbit cannot match these observed positions accurately. The reason comes from the quality of all the positions used to make the orbit. The change of 80 mas in right ascension and 90 mas in declination between May and July 2012 can only be explained by systematic errors. These may come from zonal errors in the stellar catalogue, the telescope, the sky conditions, etc.
As a comparison, the positions from the offset observations in Fig. 3 may also be affected by systematic errors, but since there are fewer observations for 2004NT33, the two additional positions fit the NIMA orbit (black line) well. In that case, systematic errors are hard to detect so we can only trust the observations. The main difference of this study is that the orbit determination, as well as the uncertainty of the ephemeris, now take possible systematic errors in the positions through the adopted weighting scheme into account.
Systematic errors in the positions are currently the main limiting factor when calculating accurate orbits. Some systematic errors are linked to observation, such as the zonal error in the catalogue or the differential chromatic refraction, and they may be partially corrected with the help of the Gaia catalogue. Other systematic errors are linked to dynamics, such as the difference between the positions of the photocentre and the barycentre for binary systems, and may only be corrected with a careful modelling of the mutual orbit of the two bodies.
The theory of orbit determination enables us to deal with positions with different precisions by using a weighting scheme but without systematic errors. Until systematic errors in positions from CCD images are reduced to a minimum using the astrometry from Gaia, the weighting scheme used in this study allows us to partially deal with these errors.
4.6. TNO’s ephemerides and observations
As an output of this study, we will make the ephemeris of the 51 selected TNOs during the period 2010–2020 available. To make predictions of stellar occultations, these ephemerides are available in bsp file for use with the SPICE library (Acton 1996) at the address11. These ephemerides will be regularly updated once new observations become available.
The predictions of forthcoming stellar occultations are available at http://devel2.linea.gov.br/~braga.ribas/campaigns/ or http://www.lesia.obspm.fr/perso/bruno-sicardy/. For comparisons, predictions for past occultations are available at http://devel2.linea.gov.br/~braga.ribas/campaigns/old.html.
The offset observations of the selected TNOs are available at the CDS. The statistics of the residuals, the number, and the time span of MPC observations and offset observations are given in Table 4. The offset observations have a better quality than MPC positions, and generally, they help to extend the period of positions.
Statistics of post-fit residuals for the 51 selected TNO for MPC positions (first line) and for the positions from the offset observations (second line) used to determine orbits.
continued.
5. Conclusion
The prediction of stellar occultations by TNOs is and will, for a long time, be thoroughly dependent on observations. Although the astrometry from the GAIA space mission will provide star positions with an accuracy from a few microarcseconds to hundreds of microarcseconds, observations that aim to determine the positions of TNOs are still necessary for precise orbit calculation purposes. In this context, a large contribution is expected from deep-sky surveys, such as Pan-STARRS12 or the LSST13. This survey will repeatedly observe the southern sky up to δ = + 10 deg in six bands, and provide multiple observations for tens of thousands of TNOs. NIMA is a suitable tool to ingest these data and to provide improved ephemerides for these objects.
In addition, the astrometry and photometry from GAIA will greatly improve the astrometric reduction of CCD and photographic images, as well as renew the importance of old epoch images. In fact, old plates with solar system objects may be reduced with reference star positions having sub-mas accuracies at the plates’ epoch. These old epoch positions are of utmost importance for the accuracy of ephemerides for objects with long (hundreds of years) periods. In this context, it should be noted that our team has an image database of solar system objects, acquired at the Pico dos Dias Observatory, that spans about 20 yr. Those with TNOs from Pico dos Dias and La Silla span half this time. All of them will be re-reduced using the GAIA astrometric catalogue.
Another source of ephemeris improvement could also be obtained from observational strategy. Errors in the TNO’s distance may amount to thousands of kilometres and reflect the oscillations in plots that show position differences between various ephemerides of the same object as a one-year period. Here, it should be noted that observations are preferably made close to opposition, a configuration that is less sensitive to parallax effects in position when compared to quadrature. Therefore, more frequent observations of TNOs in quadrature would improve the accuracy of their ephemerides.
The package OrbFit is available on http://adams.dm.unipi.it/~orbmaint/orbfit/
Sizes of objects are from http://www.johnstonsarchive.net/astro/tnodiam.html.
Panoramic Survey Telescope and Rapid Response System: http://pan-starrs.ifa.hawaii.edu
Large Synoptic Survey Telescope: http://www.lsst.org/lsst/
Acknowledgments
J.D. was supported by CNPq grant 161605/2012-5, J.C. acknowledges CNPq for a PQ2 fellowship (process No. 308489/2013-6), F.B.R. acknowledges PAPDRJ-FAPERJ/CAPES E-43/2013 No. 144997, E-26/101.375/2014, and R.V.M. is grateful for grants CNPq-306885/2013, Capes/Cofecub-2506/2015, Faperj/PAPDRJ-45/2013. M.A. acknowledges CNPq grants 473002/2013-2, 482080/2009-4, and 308721/2011-0, and FAPERJ grant 111.488/2013. A.R.G.J. is grateful for the financial support of CAPES. J.L.O. acknowledges support from Proyecto de Excelencia de la Junta de Andalucía, J.A. 2012-FQM1776, and FEDER funds
References
- Acton, C. H. 1996, Planet. Space Sci., 44, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Assafin, M., Camargo, J. I. B., Vieira Martins, R., et al. 2012, A&A, 541, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Braga-Ribas, F., Sicardy, B., Ortiz, J. L., et al. 2013, ApJ, 773, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Braga-Ribas, F., Sicardy, B., Ortiz, J. L., et al. 2014a, Nature, 508, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Braga-Ribas, F., Vieira-Martins, R., Assafin, M., et al. 2014b, in Rev. Mex. Astron. Astrofis., 44, 3 [Google Scholar]
- Camargo, J. I. B., Vieira-Martins, R., Assafin, M., et al. 2014, A&A, 561, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carpino, M., Milani, A., & Chesley, S. R. 2003, Icarus, 166, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Chesley, S. R., Baer, J., & Monet, D. G. 2010, Icarus, 210, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Desmars, J. 2015, A&A, 575, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmars, J., Arlot, S., Arlot, J.-E., Lainey, V., & Vienne, A. 2009, A&A, 499, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elliot, J. L., Person, M. J., Zuluaga, C. A., et al. 2010, Nature, 465, 897 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proceedings of IAU Colloq. 83, held in Rome, Italy, June 11–15, 1984, eds. A. Carusi, & G. B. Valsecchi (Dordrecht: Reidel), Astrophys. Space Sci. Libr., 115, 185 [Google Scholar]
- Folkner, W., Williams, J., Boggs, D., Park, R., & Kuchynka, P. 2014, JPL IPN Progress Reports, 42-196, http://ipnpr.jpl.nasa.gov/progress_report/42-196/196C.pdf [Google Scholar]
- Fraser, W. C., Gwyn, S., Trujillo, C., et al. 2013, PASP, 125, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Duriez, L., & Vienne, A. 2004, A&A, 420, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, J. L., Sicardy, B., Braga-Ribas, F., et al. 2012, Nature, 491, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Sicardy, B., Ortiz, J. L., Assafin, M., et al. 2011, Nature, 478, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Widemann, T., Sicardy, B., Dusser, R., et al. 2009, Icarus, 199, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Estimated bias for offset observations in both right ascension and declination for different stellar catalogues and observatories.
Estimated precision for offset observations in both right ascension and declination for different observatories.
Statistics of post-fit residuals for the 51 selected TNO for MPC positions (first line) and for the positions from the offset observations (second line) used to determine orbits.
All Figures
 |
Fig. 1 Difference in right ascension, weighted by cosδ, declination, and geocentric distance between NIMA and each ephemeris for (50 000) Quaoar. |
| In the text | |
 |
Fig. 2 Difference in right ascension, weighted by cosδ, declination, and geocentric distance between NIMA and each ephemeris for 2008OG19. |
| In the text | |
 |
Fig. 3 Difference between NIMA and JPL ephemerides for 2004NT33 in right ascension (weighted by cosδ) and declination during 2012–2017. The grey area represents the uncertainty of NIMA ephemeris. The sets of observations correspond to one single night of offset observations where several observations were performed. The blue dots represent the average positions of each set and the error bar represents the standard deviation (1σ). |
| In the text | |
 |
Fig. 4 Prediction map of the occultation by Ixion on 24 June 2014 with the offset method (top) and with the NIMA ephemeris (bottom). The occultation was detected in the place indicated by the green point. |
| In the text | |
 |
Fig. 5 Difference between NIMA and JPL ephemerides for (50 000) Quaoar in right ascension weighted by cosδ (top) and declination (bottom) during 2011–2016, by using only the positions until October 2012 (left) and by using the positions until October 2012, and the two positions from the two previous occultations in May 2011 and February 2012 (right). The grey area represents the uncertainty of NIMA ephemeris and the blue bullets and their error bars represent the positions from the offset observations used for NIMA ephemeris. |
| In the text | |
 |
Fig. 6 Prediction map of the occultation by Quaoar on 15 October 2012, using only observations (left) and using observations and 2 previous occultations (right). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


