| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526456 | |
| Published online | 13 November 2015 | |
Disk-integrated brightness of a Lommel-Seeliger scattering ellipsoidal asteroid
1 Department of Physics, University of Helsinki, Gustaf Hällströmin katu 2a, PO Box 64, 00014 U. Helsinki, Finland
e-mail: Karri.Muinonen@helsinki.fi
2 Finnish Geospatial Research Institute FGI, Geodeetinrinne 2, 02430 Masala, Finland
Received: 3 May 2015
Accepted: 8 September 2015
Context. The scattering of light by an asteroid’s surface depends on the properties of its particles, volume density, and roughness. It is described by the reflection coefficient which, upon integration over the illuminated and observed part of the surface, yields the disk-integrated photometric brightness of the asteroid. The Lommel-Seeliger reflection coefficient is applicable to dark, low-albedo C-class asteroids, with prospects for moderate-albedo S-class and M-class asteroids.
Aims. We calculate the disk-integrated brightness for an ellipsoidal asteroid with a Lommel-Seeliger reflection coefficient (LS ellipsoid). Furthermore, we calculate the photocenter for the LS ellipsoid, that is, the distance of the center of light from the barycenter.
Methods. Because of their analytical nature, the closed-form expressions can be readily utilized in numerical simulations.
Results. We show lightcurves and photocenter variations for realistic examples of ellipsoidal shapes for a number of pole orientations. The results highlight the reciprocity principle of the radiative-transfer theory and suggest a nontrivial dependence of the photocenter on the pole orientation and viewing geometry.
Conclusions. Finally, we outline a number of applications and future prospects.
Key words: minor planets, asteroids: general / radiative transfer / scattering / methods: analytical / techniques: photometric / comets: general
© ESO, 2015
1. Introduction
The ellipsoidal figure is justified for a small solar system object on both physical and mathematical grounds. For a rotating fluid object, a reasonable model for a small body composed of particles of varying size, the figure of hydrostatic equilibrium tends toward an ellipsoidal shape. When parameterizing a nonspherical shape, the ellipsoid provides a mathematical model with only two parameters, i.e., the axial ratios.
Indeed, the ellipsoidal shape model is popular in studies of asteroids. Magnusson et al. (1989) applied the ellipsoid in retrieving asteroid pole orientations from the photometric lightcurves. Drummond et al. (2010) gave the ellipsoid axial ratios for (21) Lutetia, one of the asteroid fly-by targets of the Rosetta mission. Torppa et al. (2008) characterized large numbers of irregular asteroids by the axial ratios of the best-fit ellipsoids. Cellino et al. (2009) introduced the ellipsoid as the asteroid shape model to be utilized in the interpretation of the sparse photometric data by the Gaia mission.
We calculate analytically the disk-integrated brightness and photocenter of a triaxial ellipsoidal asteroid with a Lommel-Seeliger surface reflection coefficient (LS reflection coefficient). The LS coefficient originates from the radiative-transfer equation (Chandrasekhar 1960; Lumme & Bowell 1981). For a small single-scattering albedo and a semi-infinite, plane-parallel medium of particles, diffuse reflection of incident unidirectional radiation can be described by the first-order multiple-scattering approximation, that is, the Lommel-Seeliger approximation. Strictly, the LS reflection coefficient is valid for media of sparsely distributed particles in each other’s far-field scattering regimes. However, close-packed particulate media that are weakly multiply scattering, such as the surfaces of C-class asteroids and many other solar system objects, scatter light in accordance with the Lommel-Seeliger approximation. There are indications that the applicability can further extend toward brighter asteroids, such as the S-class and M-class asteroids. The LS reflection coefficient can be analytically integrated over a spherical asteroid (LS sphere) and the photocenter of the LS sphere is also readily available in a closed form (see Kaasalainen & Tanga 2004 and below).
The Lommel-Seeliger ellipsoid (LS ellipsoid) is an appealing model for dark, nonspherical asteroids. In conventional lightcurve inversion for asteroid rotation periods, pole orientations, and scattering properties, the ellipsoidal shape offers a tool for the initial scanning of the rotation period (cf. Kaasalainen et al. 2001). In the inversion of sparse photometry, as is the case for the Gaia mission, the ellipsoid has been selected as the primary shape model (cf. Cellino et al. 2009; Carbognani et al. 2012). The present work facilitates an efficient initial scanning of rotation periods and pole orientations. It allows for a full-scale initial statistical inversion of sparse photometry for the rotation, shape, and scattering parameters.
In Sect. 2, we describe the Lommel-Seeliger reflection coefficient and give the analytical disk-integrated brightness and photocenter offset for the LS ellipsoid. In Sect. 3, we utilize the disk-integrated brightness and photocenter in the computation of example lightcurves and photocenter variations in differing illumination and observation geometries. In Sect. 4, we close the article with conclusions and future prospects.
2. Photometry
2.1. Reflection coefficient
The reflection coefficient R of a surface element on a solar system object relates the incident flux density πF0 and the emergent intensity I as 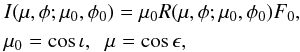 (1)where ι and ϵ are the angles of incidence and emergence as measured from the outward normal vector of the surface element, and φ0 and φ are the azimuthal angles. It is customary to measure the azimuth angle φ so that the backscattering (or light source) direction is at φ = 0°. For the common assumption of an isotropic surface, φ0 is unnecessary and presently omitted. The reflection coefficient obeys the reciprocity relation
(1)where ι and ϵ are the angles of incidence and emergence as measured from the outward normal vector of the surface element, and φ0 and φ are the azimuthal angles. It is customary to measure the azimuth angle φ so that the backscattering (or light source) direction is at φ = 0°. For the common assumption of an isotropic surface, φ0 is unnecessary and presently omitted. The reflection coefficient obeys the reciprocity relation 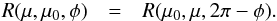 (2)The Lommel-Seeliger reflection coefficient (subscript LS) is
(2)The Lommel-Seeliger reflection coefficient (subscript LS) is 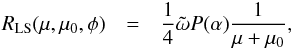 (3)where
(3)where 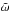 is the single-scattering albedo, P is the single-scattering phase function, and α is the phase angle, the Sun-object-observer angle.
is the single-scattering albedo, P is the single-scattering phase function, and α is the phase angle, the Sun-object-observer angle.
The Lommel-Seeliger reflection coefficient, which is the first-order, multiple-scattering approximation from the radiative transfer theory (Chandrasekhar 1960; Lumme & Bowell 1981), is applicable to dark, weakly scattering media of particles; the intensity terms ![\hbox{$[\tilde{\omega}^k]$}](/articles/aa/full_html/2015/12/aa26456-15/aa26456-15-eq15.png) , k ≥ 2 are assumed negligible. The single-scattering albedo
, k ≥ 2 are assumed negligible. The single-scattering albedo 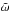 is the fraction of the incident flux scattered by the single scatterer in the random particulate medium exhibited by the asteroid surfaces. The single scatterers can be single particles or volume elements within the medium. In scalar radiative transfer omitting polarization, the scattering phase function P provides the angular distribution of scattered light in an individual interaction. It is normalized so that
is the fraction of the incident flux scattered by the single scatterer in the random particulate medium exhibited by the asteroid surfaces. The single scatterers can be single particles or volume elements within the medium. In scalar radiative transfer omitting polarization, the scattering phase function P provides the angular distribution of scattered light in an individual interaction. It is normalized so that 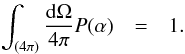 (4)It is well known that although the radiative-transfer theory is, in principle, only applicable to sparse media of particles in their far-field scattering regimes, the theory can satisfactorily describe the diffuse reflection from close-packed, particulate media, such as the surfaces of atmosphereless solar system objects.
(4)It is well known that although the radiative-transfer theory is, in principle, only applicable to sparse media of particles in their far-field scattering regimes, the theory can satisfactorily describe the diffuse reflection from close-packed, particulate media, such as the surfaces of atmosphereless solar system objects.
2.2. Disk-integrated brightness
The disk-integrated brightness L equals the surface integral 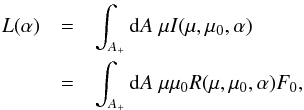 (5)where A+ stands for the part of the surface that is both illuminated by the light source and visible to the observer. For a nonspherical asteroid, L can depend strongly on the orientation of the asteroid with respect to the scattering plane, where L is measured.
(5)where A+ stands for the part of the surface that is both illuminated by the light source and visible to the observer. For a nonspherical asteroid, L can depend strongly on the orientation of the asteroid with respect to the scattering plane, where L is measured.
For a spherical asteroid (subscript “s” ) with diameter D, 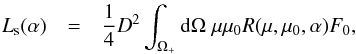 (6)where Ω+ stands for the part of the unit sphere both illuminated and observable. The computation of Ls can be carried out in a coordinate system, where, for example, the Sun is in the direction of the x-axis and the observer is on the xy-plane. For the Lommel-Seeliger surface reflection coefficient, we obtain
(6)where Ω+ stands for the part of the unit sphere both illuminated and observable. The computation of Ls can be carried out in a coordinate system, where, for example, the Sun is in the direction of the x-axis and the observer is on the xy-plane. For the Lommel-Seeliger surface reflection coefficient, we obtain ![\begin{eqnarray} L_{\rm s}(\alpha) &=& \frac{1}{32} \pi F_0 D^2 \tilde{\omega} P(\alpha) \nonumber\\ &&\times \left[1-\sin\frac{1}{2}\alpha\; \tan\frac{1}{2}\alpha \; \ln\left(\cot\frac{1}{4}\alpha\right)\right]. \label{eqlss} \end{eqnarray}](/articles/aa/full_html/2015/12/aa26456-15/aa26456-15-eq27.png) (7)We consider next an ellipsoidal asteroid with the semiaxes a, b, and c, and denote
(7)We consider next an ellipsoidal asteroid with the semiaxes a, b, and c, and denote 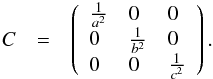 (8)Let e⊙ and e⊕ be the unit vectors in the directions of the Sun and the observer, respectively, in the principal axes reference frame of the ellipsoid.
(8)Let e⊙ and e⊕ be the unit vectors in the directions of the Sun and the observer, respectively, in the principal axes reference frame of the ellipsoid.
The disk-integrated brightness of an LS ellipsoid (subscript “e” ) can be computed with the help of the coordinate system 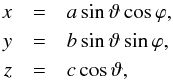 (9)and is given by
(9)and is given by ![\begin{eqnarray} L_{\rm e}(\alpha) &=& \frac{1}{8} \; \pi F_0 \tilde{\omega} P(\alpha) \; a b c \frac{S_{\odot} S_{\oplus}}{S} \nonumber\\ && \times \left\{ \cos(\lambda'-\alpha') + \cos \lambda' + \sin\lambda' \sin(\lambda'-\alpha') \phantom{\left[\cot \frac{1}{2} \lambda' \cot \frac{1}{2} (\alpha'-\lambda') \right]} \right. \nonumber\\ && \left. \times \ln \left[\cot \frac{1}{2} \lambda' \cot \frac{1}{2} (\alpha'-\lambda') \right] \right\}, \label{eq:bright} \end{eqnarray}](/articles/aa/full_html/2015/12/aa26456-15/aa26456-15-eq35.png) (10)where we utilize a number of auxiliary quantities. First, the solar phase angle α follows from the directions of the light source e⊙ and observer e⊕,
(10)where we utilize a number of auxiliary quantities. First, the solar phase angle α follows from the directions of the light source e⊙ and observer e⊕, 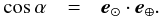 (11)Second, the scalars S⊙ and S⊕ are
(11)Second, the scalars S⊙ and S⊕ are 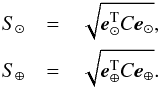 (12)For their relation to the projected area of the ellipsoid, see Eq. (16) below. Third, the angle α′ is defined by
(12)For their relation to the projected area of the ellipsoid, see Eq. (16) below. Third, the angle α′ is defined by 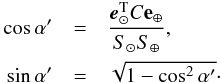 (13)Finally, the amplitude S and angle λ′ are given by
(13)Finally, the amplitude S and angle λ′ are given by 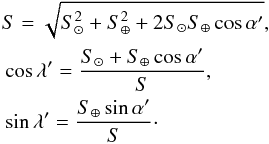 (14)We can verify that, in the limit of a = b = c, the disk-integrated brightness of the triaxial ellipsoid reduces to that of the sphere. For the sphere, the auxiliary quantities above are
(14)We can verify that, in the limit of a = b = c, the disk-integrated brightness of the triaxial ellipsoid reduces to that of the sphere. For the sphere, the auxiliary quantities above are 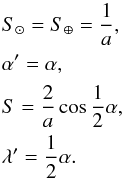 (15)Inserting these auxiliary quantities into Eq. (10) gives the expression in Eq. (7). Furthermore, for the illumination and observation geometry e⊙ = e⊕ corresponding to the astronomical opposition, that is, α = 0°, the disk-integrated brightness becomes proportional to the projected area A⊥ of the ellipsoid,
(15)Inserting these auxiliary quantities into Eq. (10) gives the expression in Eq. (7). Furthermore, for the illumination and observation geometry e⊙ = e⊕ corresponding to the astronomical opposition, that is, α = 0°, the disk-integrated brightness becomes proportional to the projected area A⊥ of the ellipsoid, 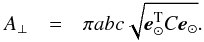 (16)
(16)
 |
Fig. 1 Lightcurves (Eq. (10)) computed for two Lommel-Seeliger ellipsoids (left and right) illuminated and observed in the ecliptic plane with a phase angle of α = 0° (bottom), 45° (middle), and 90° (top). The ellipsoid axial ratios are b/a = 0.86, c/a = 0.82 (left) and b/a = 0.88, c/a = 0.63 (right). The pole longitudes and latitudes are (λ,β) = (0°,90°) (solid line), (0°,30°) (dashed line), and (45°,30°) (dotted line). |
 |
Fig. 2 Photocenter variations (Eq. (25)) computed for two Lommel-Seeliger ellipsoids illuminated and observed in the ecliptic plane with a phase angle of α = 45° (bottom three curves) and 90° (top three curves), with the constant photocenter offsets for the Lommel-Seeliger sphere (dash-dotted lines). The ellipsoid axial ratios are b/a = 0.86, c/a = 0.82 (left) and b/a = 0.88, c/a = 0.63 (right). The pole longitudes and latitudes are (λ,β) = (0°,90°) (solid line), (0°,30°) (dashed line), and (45°,30°) (dotted line). |
2.3. Photocenter
The photocenter offset d is the brightness-weighted measure of the distance between an asteroid’s apparent photometric center and barycenter, 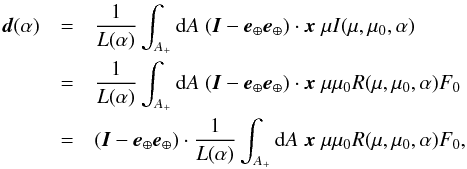 (17)where I is a unit dyadic, I−e⊕e⊕ is a projection dyadic, and · denotes scalar product.
(17)where I is a unit dyadic, I−e⊕e⊕ is a projection dyadic, and · denotes scalar product.
The photocenter of the LS ellipsoid is, in the ecliptic coordinate system, ![\begin{eqnarray} {\vec d}(\alpha) &=& \frac{1}{L(\alpha)} \; \frac{1}{3} F_0 \tilde{\omega} P(\alpha) \; a b c \frac{S_{\odot} S_{\oplus} }{S} \; \sqrt{C^{-1}} R_{\rm E}^{\rm T} \left[ \begin{array}{l} I_1 \\ I_2 \\ 0 \\ \end{array} \right], \end{eqnarray}](/articles/aa/full_html/2015/12/aa26456-15/aa26456-15-eq66.png) (18)where RE is the Euler rotation matrix and
(18)where RE is the Euler rotation matrix and ![\begin{eqnarray} I_1 &=& \frac{1}{2} (\pi -\alpha') \left[ \cos(\lambda-\alpha') + \sin 2\lambda \sin(\lambda-\alpha' )\right] \nonumber\\ &&+ \frac{1}{2} \cos \lambda \sin \alpha' - \ln \left[\frac{-\sin (\lambda-\alpha') }{\sin\lambda}\right] \sin^2 \lambda \sin (\lambda-\alpha'), \nonumber\\ I_2 &=& \frac{1}{2} (\pi -\alpha') \left[ -\cos 2\lambda \sin(\lambda-\alpha') \right] \\ &&+ \frac{1}{2} \sin \lambda \sin \alpha' + \ln \left[\frac{-\sin (\lambda-\alpha') }{\sin\lambda}\right] \cos \lambda \sin \lambda \sin (\lambda-\alpha'). \nonumber \end{eqnarray}](/articles/aa/full_html/2015/12/aa26456-15/aa26456-15-eq68.png) (19)For a disappearing argument in the logarithm, asymptotic analytical expressions are readily available.
(19)For a disappearing argument in the logarithm, asymptotic analytical expressions are readily available.
The rotation matrix RE is constructed using the angles γE, βE, and αE in a standard manner, 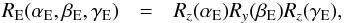 (20)where Rz and Ry denote rotations about the third and second coordinate axes, respectively. Let K be the principal-axes coordinate system of the ellipsoid and let us define the K′′ coordinate system as
(20)where Rz and Ry denote rotations about the third and second coordinate axes, respectively. Let K be the principal-axes coordinate system of the ellipsoid and let us define the K′′ coordinate system as 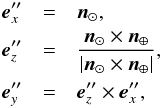 (21)where n⊙ and n⊕ denote the unit outward normal vectors on the surface in the directions of e⊙ and e⊕, respectively. In detail,
(21)where n⊙ and n⊕ denote the unit outward normal vectors on the surface in the directions of e⊙ and e⊕, respectively. In detail, 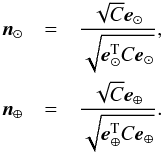 (22)Then, we obtain βE and γE from
(22)Then, we obtain βE and γE from 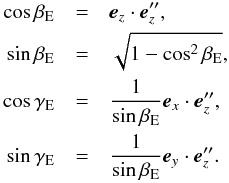 (23)Here, the case of βE = 0° implies a pole in the direction of the ecliptic pole and alternative expressions are available. Finally, αE follows with the help of the intermediate coordinate system K′ as
(23)Here, the case of βE = 0° implies a pole in the direction of the ecliptic pole and alternative expressions are available. Finally, αE follows with the help of the intermediate coordinate system K′ as 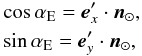 where
where 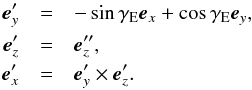 (24)In what follows, we utilize the norm of d(α), that is,
(24)In what follows, we utilize the norm of d(α), that is, 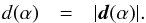 (25)For a spherical asteroid, Eq. (25) reduces to
(25)For a spherical asteroid, Eq. (25) reduces to 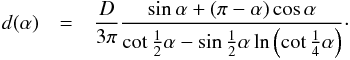 (26)
(26)
3. Results and discussion
We illustrate the disk-integrated brightness and photocenter of the LS ellipsoid with a number of examples (Figs. 1 and 2). We utilize two example sets of axial ratios from Torppa et al. (2008): first, b/a = 0.86 and c/a = 0.82, mimicking the C-class asteroid (19) Fortuna; and, second, b/a = 0.88 and c/a = 0.63, mimicking the C-class asteroid (1580) Betulia. The direction of the Sun is given by the ecliptic longitude and latitude (λ⊙,β⊙) = (0°,0°) in all examples, and the directions of the observer are (λ⊕,β⊕) = (0°,0°), (45°,0°), and (90°,0°). Accordingly, the solar phase angle is α = 0°, 45°, or 90°. Three different pole orientations are assumed for the asteroid with ecliptic longitudes and latitudes of (λ,β) = (0°,90°), (0°,30°), and (45°,30°). Lightcurves and photocenter variations are computed over a full rotation of the asteroid about the shortest axis, that is, the axis of maximum inertia assuming a homogeneous asteroid.
The lightcurves in Fig. 1 exhibit the typical double-maximum and double-minimum characteristics of ellipsoids in the principal-axis rotation state. In all cases, the lightcurve amplitude reaches its maximum for the pole that coincides with the ecliptic pole, that is, (λ,β) = (0°,90°). This is a natural consequence of illumination and observation in the ecliptic plane, producing a maximum aspect angle, the angle between the pole and observer directions. For α = 0°, the two lightcurves corresponding to the pole orientations with λ = 0° are seen to be in phase with each other. The remaining lightcurve with pole longitude λ = 45° stands out with a clear phase shift. For the phase angles α = 45° and 90°, the lightcurves pertaining to the different poles become differently phased. There is an exchange of order for the lightcurve amplitudes: for α = 0°, the amplitude for (λ,β) = (45°,30°) exceeds that of (0°,30°), whereas the opposite is true for α = 90°. This is in agreement with the variation of the aspect angle from one case to another. Overall, the lightcurves are more pronounced for the ellipsoid with b/a = 0.86 and c/a = 0.82.
For the pole orientations (λ,β) = (0°,30°) and (45°,30°) and the phase angle α = 45°, Fig. 1 (graphs in the middle, dotted and dashed lines) illustrates how the reciprocity relation in Eq. (2) gives rise to lightcurves that are identical except for a constant phase shift. In these specific geometries, exchanging the light source and observer directions results in mirror configurations and similar lightcurves.
As to the photocenter variations in Fig. 2, first of all, since there is no photocenter offset for the opposition geometry, the cases of α = 0° have been omitted and the variations for α = 45° and 90° have been combined into single graphs. Overall, the photocenter offset becomes more pronounced for increasing α, reaching the peak amplitude for the pole orientation (λ,β) = (0°,90°). There are, however, exceptions to that rule at certain rotational phases. The same mutual phase is seen for the photocenter variations at α = 45° for the two poles with λ = 0°, and the photocenter variations reach their maxima nearly in phase with the corresponding lightcurve minima in Fig. 1. As for the lightcurve phasing, the photocenter variation for the pole (λ,β) = (45°,30°) stands out with a clear phase shift. Overall, the range of the photocenter variation from one case to another is more pronounced for the ellipsoid with b/a = 0.88 and c/a = 0.63. In particular, this is evident for the phase angle of α = 90°.
For both example ellipsoids and α = 90°, except for a phase shift, Fig. 2 shows a peculiar similarity between the photocenter variations for the poles (λ,β) = (0°,30°) and (45°,30°). A closer inspection of the numerical values indicates, however, a modest difference in the variations. For β = 30° and λ approaching 90°, the photocenter variations enhance rapidly. Finally, for comparison, we also show the constant photocenter offsets for the LS sphere in Fig. 2. It is noteworthy that the LS sphere offsets are only exceeded by the LS ellipsoid offsets near the lightcurve minima.
4. Conclusions
We have derived analytical expressions for the disk-integrated photometric brightness and the photocenter offset of a dark ellipsoidal asteroid with a Lommel-Seeliger surface-reflection coefficient. The expressions allow for rapid computation of lightcurves and photocenter variations in arbitrary illumination and observation geometries. Typical regular lightcurves and photocenter variations with two maxima and two minima follow for principal-axis rotation over a single rotation period, with increasing amplitude for increasing solar phase angle.
There are natural extensions to the ellipsoid shape model and how it can be utilized in studies of asteroids. Michalowski (1996) succeeded in explaining irregular lightcurve features with the ellipsoid model, assuming a rotation axis misaligned from the ellipsoid principal axes. Cellino et al. (1989) combined together octants from different ellipsoids and provided the so-called Cellinoid shape model. Whereas the present results can be readily utilized in the case of differing axis of rotation and shape, it remains to be seen if analytical work can be carried out for the Cellinoid shape model.
There are a number of topical applications for the LS ellipsoid. First, the sparse photometry of asteroids to be provided by the Gaia mission will be initially analyzed using the LS ellipsoid. Second, the LS ellipsoid allows for efficient lightcurve computation for binary asteroids outside their mutual eclipse, thus giving potential for efficient lightcurve inversion methods for binaries. Third, the LS ellipsoid enables rapid identification of binary asteroid candidates from astrometric observations via the photocenter offset. Fourth, asteroid phase-curve dependence on the illumination and observation geometries in a specific apparition can be assessed, giving estimates for intrinsic variations
in the phase curves. Finally, in addition to asteroids, the LS ellipsoid has future prospects in the photometric studies of cometary nuclei, transneptunian objects, and planetary satellites.
Acknowledgments
Prof. emer. Kari Lumme passed away unexpectedly in Nov. 23, 2013 before the completion of the present article. A thoughtful review by Paolo Tanga helped improve the article. Karri Muinonen is grateful to Alberto Cellino, Xiaobin Wang, Johanna Torppa, Antti Penttilä, and Olli Wilkman for valuable comments. Research supported, in part, by the Academy of Finland Grant No. 1257966 entitled Electromagnetic Wave Scattering in Complex Media.
References
- Carbognani, A., Tanga, P., Cellino, A., et al. 2012, Planet. Space Sci., 73, 80 [Google Scholar]
- Cellino, A., Zappalá, V., & Farinella, P. 1989, Icarus, 78, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Cellino, A., Hestroffer, D., Tanga, P., Mottola, S., & Dell’Oro, A. 2009, A&A, 506, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1960, Radiative Transfer (New York: Dover) [Google Scholar]
- Drummond, J. D., Conrad, A., Merline, W. J., et al. 2010, A&A, 523, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaasalainen, M., & Tanga, P. 2004, A&A, 416, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Lumme, K., & Bowell, E. 1981, AJ, 86, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Magnusson, P., Barucci, M. A., Drummond, J., et al. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson: The University of Arizona Press), 66 [Google Scholar]
- Michalowski, T. 1996, A&A, 309, 970 [NASA ADS] [Google Scholar]
- Torppa, J., Hentunen, V-P., Pääkkönen, P., Kehusmaa, P., & Muinonen, K. 2008, Icarus, 198, 91 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Lightcurves (Eq. (10)) computed for two Lommel-Seeliger ellipsoids (left and right) illuminated and observed in the ecliptic plane with a phase angle of α = 0° (bottom), 45° (middle), and 90° (top). The ellipsoid axial ratios are b/a = 0.86, c/a = 0.82 (left) and b/a = 0.88, c/a = 0.63 (right). The pole longitudes and latitudes are (λ,β) = (0°,90°) (solid line), (0°,30°) (dashed line), and (45°,30°) (dotted line). |
| In the text | |
 |
Fig. 2 Photocenter variations (Eq. (25)) computed for two Lommel-Seeliger ellipsoids illuminated and observed in the ecliptic plane with a phase angle of α = 45° (bottom three curves) and 90° (top three curves), with the constant photocenter offsets for the Lommel-Seeliger sphere (dash-dotted lines). The ellipsoid axial ratios are b/a = 0.86, c/a = 0.82 (left) and b/a = 0.88, c/a = 0.63 (right). The pole longitudes and latitudes are (λ,β) = (0°,90°) (solid line), (0°,30°) (dashed line), and (45°,30°) (dotted line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


