| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201526436 | |
| Published online | 03 November 2015 | |
New XMM-Newton observation of the thermally emitting isolated neutron star 2XMM J104608.7-594306⋆
1
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam, Germany
e-mail: apires@aip.de
2
Observatoire Astronomique de Strasbourg, Université de Strasbourg,
CNRS, UMR 7550, 11 rue de
l’Université, 67000
Strasbourg,
France
3
Universitá di Padova, Dipartimento di Fisica e
Astronomia, via Marzolo
8, 35131
Padova,
Italy
4
Mullard Space Science Laboratory, University College
London, Holmbury St. Mary,
Dorking, Surrey,
RH5 6NT,
UK
5
Sternberg Astronomical Institute, Lomonosov Moscow State
University, Universitetskii pr.
13, 119991
Moscow,
Russia
6
Universitá dell’Insubria, Dipartimento di Fisica e
Matematica, via Valleggio
11, 22100
Como,
Italy
Received: 29 April 2015
Accepted: 20 August 2015
Context. The isolated neutron star (INS) 2XMM J104608.7-594306 is one of the only two to be discovered through their thermal emission since the ROSAT era. Possibly a remnant of a former generation of massive stars in the Carina nebula, the exact nature of the source is unclear, and it might be unique amongst the several classes of Galactic INSs.
Aims. In a first dedicated XMM-Newton observation of the source, we found intriguing evidence of a very fast spin period of P ~ 18.6 ms at the 4σ confidence level. Moreover, spectral features in absorption have also been identified. We re-observed 2XMM J104608.7-594306 with XMM-Newton to better characterise the spectral energy distribution of the source, confirm the candidate spin period, and possibly constrain the pulsar spin-down.
Methods. We used the two XMM-Newton observations of 2XMM J104608.7-594306 to perform detailed timing and spectral X-ray analysis. Both the spin-down rate and the energy of the spectral features provide estimates on the neutron star magnetic field, which are crucial for investigating the evolutionary state of the neutron star.
Results. Statistically acceptable spectral fits and meaningful physical parameters for the source are only obtained when the residuals at energies 0.55 keV and 1.35 keV are taken into account by the spectral modelling. While the former can result from the inhomogeneous temperature distribution on the surface of the neutron star or can be related to a local overabundance of oxygen in the Carina nebula, the one at 1.35 keV is only satisfactorily accounted for by invoking a line in absorption. In this case, the best-fit neutron star atmosphere models constrain the hydrogen column density, the effective temperature, and the luminosity of the source within NH = (2.5−3.3) × 1021 cm-2, Teff = (6−10) × 105 K, and LX = (1.1−7.4) × 1032 erg s-1. The implied distance is consistent with a location in (or in front of) the Carina nebula, and radiation radii are compatible with emission originating on most of the surface. Non-thermal X-ray emission is ruled out at levels above 0.5% (3σ) of the source luminosity. Unfortunately, the second XMM-Newton observation proved inconclusive in terms of confirming (discarding) the fast candidate spin, providing an upper limit on the pulsed fraction of the source that is very close to the limiting sensitivity for detecting the modulation found previously.
Conclusions. In the absence of an unambiguous period determination and an estimate of the magnetic field, the nature of the source remains open to interpretation. Its likely association with the Carina cluster and its overall spectral properties (only shared by a handful of other peculiar INSs) disfavour a standard evolutionary path or one in which the source was previously recycled by accretion in a binary system. The star 2XMM J104608.7-594306 may be similar to Calvera (1RXS J141256.0+792204), a neutron star for which the scenario of an evolved anti-magnetar has been discussed. A better age estimate and deeper radio and γ-ray limits are required to further constrain the evolutionary state of the neutron star.
Key words: stars: neutron / pulsars: general / X-rays: individuals: 2XMM J104608.7-594306
Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA (Target 2XMM J104608.7-594306, obsids 0650840101, 0691970101).
© ESO, 2015
1. Introduction
In the standard scenario of pulsar evolution, a neutron star is born rotating fast. As a consequence of rotational energy losses, it is expected to evolve towards longer periods until electron-positron pairs can no longer be produced; the radio emission ceases and the pulsar crosses the so-called death line. The radio emission is, however, energetically unimportant relative to the power emitted at high energies. While young, these objects are strong sources of X-ray and γ-ray emission with radiative processes that include non-thermal emission from charged particles that were accelerated in the pulsar magnetosphere and thermal emission from the hot surface. However, after a maximum of ~107 yr, pulsars have probably exhausted their internal source of particle creation and acceleration and cooled down to temperatures undetectable in X-rays.
This relatively simple picture has been challenged by the discovery of peculiar groups of isolated neutron stars (INSs) that are radio quiet or transient. Their (mostly unpredicted) properties significantly differ from those displayed by standard pulsars (see Kaspi 2010; Harding 2013, for an overview and references). Among them are magnetars (anomalous X-ray pulsars (AXPs) and soft gamma repeaters (SGRs)), the central compact objects in supernova remnants (CCOs), the rotating radio transients (RRATs), and the ROSAT-discovered thermally-emitting INSs, also known as the Magnificent Seven (M7).
In particular, the M7 constitute a nearby (d ≲ 1 kpc) group of middle-aged (0.1−1 Myr) neutron stars, observable through their bright and purely thermal X-ray emission (see, for example, Haberl 2007; Kaplan 2008; Turolla 2009, for reviews). Amounting to about half of all young INSs known in the solar neighbourhood (Popov et al. 2003), they could be as numerous as radio pulsars, with consequences for the total number of neutron stars populating the Milky Way (see Keane & Kramer 2008). Timing studies in X-rays (see Kaplan & van Kerkwijk 2011, and references therein) have shown that the M7 rotate more slowly (P ~ 3−11 s) and have higher magnetic field intensities, Bdip ~ (1−3) × 1013 G, than the bulk of the (rotation-powered) radio pulsar population. Also at variance with pulsars detected at high energies, the X-ray luminosity of the M7 is in excess of the spin-down power. To a certain extent, such properties resemble those of the young and energetic magnetars (see, for example, Mereghetti 2008, for a review). On the other hand, the M7 experience less dramatic spin-down and do not show the complex phenomenology usually observed in magnetars (e.g. emission of flares, bursts, quasi-periodic oscillations, spectral variability, timing noise, etc.).
Another group consisting of radio-quiet, thermally emitting INSs, is that of CCOs (see, for example, de Luca 2008; Gotthelf & Halpern 2010; Halpern & Gotthelf 2010, for reviews). CCOs were first observed as point-like, radio-quiet X-ray sources, located near the geometrical centre of supernova remnants. Of the dozen objects known at present, including other candidates, at least three fit in the anti-magnetar scenario, in which these sources are young (aged 103 yr to 104 yr) and weakly magnetised (Bdip = 1010−1011 G) neutron stars that are experiencing very low spin-down (Gotthelf et al. 2013a, and references therein).
If the weak dipolar field of anti-magnetars remains constant, they are confined to a region of the P − Ṗ diagram of INSs that is devoid of other pulsars, between those occupied by the normal and millisecond (recycled) part of the population. The fact that no old (orphaned, or without a supernova remnant) CCO is recognised in this region of the P − Ṗ diagram in either radio or X-ray surveys (Halpern & Gotthelf 2010; Gotthelf et al. 2013b; Luo et al. 2015; see also Bogdanov et al. 2014, who searched for CCO descendants among supposedly old radio pulsars in supernova remnants) may favour the alternative scenario of field burial by hypercritical accretion (e.g. Chevalier 1989; Geppert et al. 1999; Viganò et al. 2012). In this scenario, the original neutron star magnetic field is submerged by fallback accretion of supernova ejecta, remaining hidden for several ~103 yr to 105 yr. As a result, the neutron star shows, in its early evolution, the typical anti-magnetar behaviour. As the field re-emerges, the pulsar quickly joins the rest of the population, moving upwards in the P − Ṗ diagram; its subsequent evolution would then follow according to the original field intensity. Residual thermal luminosity in the first ~104 yr, as well as enhanced cooling after ~105 yr, compared to its peers of similar characteristic ages, are expected to result from the accreted light-element envelope (e.g. Yakovlev & Pethick 2004).
For several years, considerable efforts have been made to discover new thermally emitting INSs (e.g. Chieregato et al. 2005; Turner et al. 2010; Agüeros et al. 2011). The INS 2XMM J104608.7-594306 (hereafter J1046), is one of only two to be discovered through their thermal emission and lack of obvious counterparts since the ROSAT era (Pires et al. 2009a). Possibly a remnant of a former generation of massive stars in the Carina nebula (Townsley et al. 2011), its exact nature is not clear, and it may be unique. The other source, 1RXS J141256.0+792204, also known as Calvera (Rutledge et al. 2008), is a relatively bright ROSAT source with a short spin period of P ~ 59 ms (Zane et al. 2011). Calvera is the only INS to date to be recognised as an evolved anti-magnetar, with a magnetic field of Bdip = 4.4 × 1011 G that is, possibly, regaining its original strength (Halpern et al. 2013).
Thanks to its proximity (angular distance of 8.5′) to the well-studied Eta Carinae system, J1046 was serendipitously detected on many occasions by the XMM-Newton Observatory (Jansen et al. 2001). The analysis of the serendipitous data shows no significant long-term variability in either the X-ray flux or in the overall spectral properties of the source (Pires et al. 2009b). Follow-up observations in the optical with the European Southern Observatory Very Large Telescope (ESO-VLT) set a deep limit on the brightness of the optical counterpart, mV> 27 (2σ), and a very high X-ray-to-optical flux ratio of log (FX/FV) > 3.8. At present, no radio or γ-ray counterparts are known.
As revealed by a first dedicated XMM-Newton observation, performed on 2010 December 6 (AO9, as reference for the text), the spectral energy distribution of J1046 is soft and purely thermal with significant deviations from a blackbody continuum of kT ~ 135 eV (Pires et al. 2012). While these properties are reminiscent of those of the middle-aged M7, the XMM-Newton observation also revealed intriguing evidence of a very fast rotation, at P ~ 18.6 ms. Such a rapid spin is difficult to reconcile with the spectral properties of the source.
Instrumental configuration and duration of the EPIC scientific exposures of the XMM-Newton AO11 observation of 2XMM J104608.7-594306.
We re-observed J1046 with XMM-Newton two years later to further improve the characterisation of the source’s spectral energy distribution, confirm the candidate spin period, and eventually constrain the pulsar spin-down. We report here the results of this observation in detail. We also reanalysed the AO9 dataset to consistently compare our findings in a joined timing and spectral X-ray analysis. The paper’s outline is as follows: in Sect. 2 we describe the new XMM-Newton observation and the data reduction. Analysis and results are presented in detail in Sect. 3. We examine the evolutionary state and possible nature of the neutron star in light of the observed properties of the known galactic INS population in Sect. 4. The main conclusions and results are summarised in Sect. 5.
2. XMM-Newton observation and data reduction
For details on the instrumentation set-up and execution of the AO9 observation, we refer to Pires et al. (2012). The new XMM-Newton observation of J1046 (AO11) was carried out on 2012 December 20 for a total exposure time of 87.714 ks. Table 1 contains information on the scientific exposures and instrumentation set-up of the EPIC pn (Strüder et al. 2001) and MOS (Turner et al. 2001) detectors. We adopted the thin filter for all EPIC instruments, given its better response at soft X-ray energies and the very low (<1%) expected level of spectral pile-up at aimpoint. The pn camera was operated in small window (SW) mode, providing high time resolution (6 ms) at the expense of a reduced exposure (deadtime of ~29%). Although the MOS cameras operating in timing uncompressed mode could provide sufficient resolution (1.75 ms) for investigating the periodicity at P ~ 18.6 ms, calibration uncertainties between the EPIC detectors (e.g. Zane et al. 2011) and the impossibility of using the data for spectral analysis or for astrometrical corrections motivated us to choose the full-frame (FF) imaging mode instead. Standard data reduction was performed with SAS 13 (xmmsas_20131209_1901-13.5.0), using the latest calibration files. We processed the MOS and pn raw event files using the EPIC meta tasks emchain and epchain, respectively, applying default corrections. We ensured that the pn event file was clean of unrecognised time jumps (i.e. those uncorrected by standard SAS processing) by checking the output files of the epproc routine. Additionally, we reprocessed and reduced the AO9 observation consistent with the new dataset.
Parameters of 2XMM J104608.7-594306, as extracted from the AO11 (and AO9) XMM-Newton EPIC images.
A few minor background flares were registered during the observation, effectively reducing the exposures in the MOS1 and MOS2 cameras to 79 ks and 84 ks, respectively. In the pn camera, the background level for the duration of the observation was below what is recommended by standard filtering of “good-time intervals”. Therefore, the effective observing time (60 ks) was only reduced by the camera livetime in SW mode.
For the analysis, we filtered the event lists to exclude bad CCD pixels and columns, as well as to retain the predefined photon patterns with the highest quality energy calibration. Unless otherwise noted, single and double events were selected for pn (pattern ≤4) and single, double, triple, and quadruple for MOS (pattern ≤12). We defined the source centroid for each EPIC camera with the task eregionanalyse, which results at optimal radii of ~20′′ (0.3−2 keV). Background circular regions of size 60′′ to 100′′ (depending on the camera) were defined off-source on the same CCD as the target whenever possible.
The detected source count rates, hardness ratios, and other parameters based on a maximum likelihood PSF fitting are listed in Table 2. These are determined with the SAS task emldetect on images created for each camera and in each of the five predefined XMM-Newton energy bands. For comparison, we also list the source parameters as determined from the EPIC detection in the AO9 observation. The errors are nominal 1σ statistical uncertainties. There is no sign of variability in the source’s overall properties; typically, J1046 displays a very soft energy distribution, with no counts above 2 keV, and count rates and hardness ratios are consistent within errors between the two XMM-Newton observations (see also Sect. 3.1).
We used the task eposcorr to refine the astrometry, by cross-correlating the list of EPIC X-ray source positions with those of near-infrared (2MASS, Skrutskie et al. 2006) objects lying within 15′ from J1046. Based on a number of 60 X-ray/infrared matches, we found a slight offset in right ascension, not significant within the astrometric errors, and an offset of 1.6′′ ± 0.5′′ in declination. We double-checked the offsets with eposcorr using other catalogues, in particular the Chandra Carina Cluster Project catalogue of X-ray sources (CCCP; Broos et al. 2011), the Guide Star Catalog (GSC 2.3.2; Lasker et al. 2008), and the Naval Observatory Merged Astrometric Dataset (NOMAD; Zacharias et al. 2004). The EPIC source position (Table 2), updated accordingly, was found to be consistent within errors with previous determinations. For consistency, we revised the source position in the AO9 observation also by cross-correlating the EPIC source list with the 2MASS catalogue. We found offsets of −2.6′′±0.4′′ in right ascension and 1.6′′±0.5′′ in declination (46 matches). The updated source coordinates in the AO9 epoch are also listed in Table 2.
 |
Fig. 1 Best-fit column density NH as a function of blackbody temperature kT, for each individual (pn/MOS1/MOS2) spectrum used in the analysis (see legend). Also shown are the results by fitting all data simultaneously, as well as results of the stacked (combined) spectrum. AO11 datasets are highlighted in red. Error bars are 1σ confidence levels. |
Best-fit spectral parameters and count rates of 2XMM J104608.7-594306 per XMM-Newton observation and EPIC camera.
The statistics for the EPIC lightcurves (corrected for bad pixels, deadtime, exposure, as well as background counts, and binned into 875 s intervals) show the 3σ upper limits for the rms fractional variation of 0.12, 0.11 and 0.24 for pn, MOS1, and MOS2, respectively. On the basis of the same lightcurves, the reduced chi-square, assuming a constant flux, is 1.02 (pn, 99 d.o.f.), 0.97, and 0.71 (MOS1 and MOS2; 98 d.o.f.).
3. Analysis and results
3.1. Spectral analysis
The analysis of the EPIC data is based on source and background spectra extracted from regions as described in Sect. 2, together with the respective response matrices and ancillary files created for each of the EPIC cameras. Owing to the frequent readout of pn in SW mode, detector noise dominates the low-energy count distribution. We therefore restricted the analysis of the pn camera to photons with energies above 0.35 keV. The energy band of the MOS cameras is restricted above 0.3 keV, which is in accordance with the guidelines and calibration status of the instrument. Including the AO9 observation, the available data amount to a total of six spectra and ~1.7 × 104 counts (0.3−12 keV), of which 10% can be ascribed to background. For each spectrum, energy channels within 0.3/0.35 keV and 2 keV were rebinned according to a minimum number of 25 counts per spectral bin. We also took care not to oversample the instrument energy resolution at a given bin by more than a factor of three, which is especially important at low energies; this is done by fixing the parameter oversample = 3 in the SAS task specgroup.
To fit the spectra we used XSPEC 12.8.2 (Arnaud 1996). Unless otherwise noted, the fit parameters were allowed to vary freely and within reasonable ranges. The photoelectric absorption model and elemental abundances of Wilms et al. (2000, tbabs were adopted to account for the interstellar absorption. Owing to the intrinsically soft energy distribution of J1046 and its location in the galactic plane (b =−0.6°), as well as to uncertainties resulting from the choice of abundance table in XSPEC, we estimate that the amount of intervening material derived from the spectral fits is uncertain by 15%.
Results of spectral fitting of blackbody models.
First, we fitted each of the six spectra individually, using a simple absorbed blackbody model. The resulting best-fit parameters (Table 3 and Fig. 1) argue against any significant variability between the two XMM-Newton observations. However, the NH and kT derived from the MOS spectra, even though statistically consistent, are systematically higher and softer, by 30% and 5% respectively, than those derived from pn. We then proceeded with the analysis using two different approaches, both relying on the assumption that the spectral parameters of J1046 are constant between the XMM-Newton observations: (i) we performed simultaneous fits of all spectra, where we allowed for a renormalisation factor to account for cross-calibration uncertainties between the detectors; and (ii) using the task epicspeccombine, we merged all six spectra and corresponding background and response files into one single, stacked dataset. While both approaches give a similarly well-constrained parameter space, the exercise shows that the best-fit NH and kT, derived from the second approach, are biased and inconsistent with those from individual fits. On the other hand, the results from the first approach, while naturally dominated by the better statistics of the two pn spectra, are consistent with most measurements. We henceforth adopted for the spectral analysis simultaneous fits, including all EPIC data from the two XMM-Newton observations accordingly.
We summarise the results of the analysis in Tables 4−6. Table 4 contains the results of spectral fits where we assumed a (single- or double-temperature) blackbody continuum, and tested for different element abundances and for the presence of absorption lines. The fitted models are labelled (A) to (F), as reference for the text (see caption). To test for overabundance of elements with transitions in the range of 0.3 keV to 2 keV (C, N, O, Ne, Mg, etc.), we adopted the variable photoelectric absorption model vphabs and restricted abundance values in the range 1 <Z< 5 in solar units.
The best-fit parameters of (more physically-motivated) neutron star atmosphere models are
in Tables 5 and 6, where they are labelled (a) to (e). We tested magnetised and non-magnetised
model atmospheres, consisting of fully- and partially-ionized hydrogen, as well as of
carbon and other mid-Z elements (the models nsa, nsmaxg, and carbatm in
XSPEC; see Zavlin et al. 1996; Pavlov et al. 1995; Ho
et al. 2008; Mori & Ho 2007; Suleimanov et al. 2014). Wherever appropriate, the
magnetic field was held fixed at values B = 0,1012,1013 G (nsa, Table
5); for nsmaxg, we tested 19 models with
B = (0.01−30) ×
1012 G (only the results with
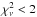 are listed in Table 6). We first assumed canonical values for the neutron star mass and
radius, Mns =
1.4 M⊙ and Rns = 10 km;
these parameters were also allowed to vary to check for an improved fit. The size of the
emission region, with respect to the neutron star physical radius, can also be
parametrised for nsmaxg models; we restricted values to have Rem ≤
Rns. Finally, we also added a second
thermal component, varied the elemental abundances, and added lines to the continuum to
obtain statistically acceptable fits and derive plausible physical solutions for the
neutron star. For double-temperature nsa and nsmaxg models, we fixed the mass of the
neutron star at 1.4 M⊙, let the radii (Rns or
Rem) of the two components vary
independently of each other, and limited the distance to the source to within 10 pc and
50 kpc. The mass, magnetic field, and distance normalisation of the second thermal
component were set equal to those of the first.
are listed in Table 6). We first assumed canonical values for the neutron star mass and
radius, Mns =
1.4 M⊙ and Rns = 10 km;
these parameters were also allowed to vary to check for an improved fit. The size of the
emission region, with respect to the neutron star physical radius, can also be
parametrised for nsmaxg models; we restricted values to have Rem ≤
Rns. Finally, we also added a second
thermal component, varied the elemental abundances, and added lines to the continuum to
obtain statistically acceptable fits and derive plausible physical solutions for the
neutron star. For double-temperature nsa and nsmaxg models, we fixed the mass of the
neutron star at 1.4 M⊙, let the radii (Rns or
Rem) of the two components vary
independently of each other, and limited the distance to the source to within 10 pc and
50 kpc. The mass, magnetic field, and distance normalisation of the second thermal
component were set equal to those of the first.
Results of spectral fitting of neutron star atmosphere models (nsa).
Results of spectral fitting of neutron star atmosphere models (nsmaxg).
 |
Fig. 2 Results of spectral fitting of source 2XMM J104608.7-594306. We show the two pn spectra and folded best-fit models, with residuals. Top: simple absorbed blackbody. Bottom: best-fit neutron star atmosphere at d ~ 2 kpc (B = 1012 G, Teff ~ 106 K, NH = 2.6 × 1021 cm-2). Two Gaussian lines in absorption are added to the model (with energies around 0.55 keV and 1.35 keV). |
The analysis confirms the results of Pires et al. (2012), with much improved count statistics. Overall, the spectrum of the source is soft and purely thermal. However, significant deviations from a Planckian shape are identified around energies 0.55 keV and 1.35 keV (see top plot of Fig. 2). The residuals are present independently of the choice of the thermal continuum, abundance table, source or background extraction regions, as well as regardless of the EPIC instrument and XMM-Newton observation.
The best-fit absorbed blackbody (A) has kT = (133.1 ± 1.9) eV and NH = (3.20 ± 0.15) ×
1021 cm-2, with 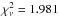 for 169 degrees of freedom (d.o.f.) (Table
4). The column density is consistent with the one
towards Eta Carina, NH ~ 3 ×
1021 cm-2 (Leutenegger et al.
2003). Assuming the neutron star is at a comparable distance, dCar = 2.3 kpc
(Smith 2006), the redshifted radiation radius
derived from the blackbody fit is
for 169 degrees of freedom (d.o.f.) (Table
4). The column density is consistent with the one
towards Eta Carina, NH ~ 3 ×
1021 cm-2 (Leutenegger et al.
2003). Assuming the neutron star is at a comparable distance, dCar = 2.3 kpc
(Smith 2006), the redshifted radiation radius
derived from the blackbody fit is 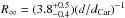 km. We note that the redshifted radiation
radii of the M7, as derived from X-ray blackbody fits and distance estimates, are in the
range of roughly 2 km to 7 km (see, for example, Kaplan
2008). The residuals mentioned above mostly contribute to the high value of
chi-square.
km. We note that the redshifted radiation
radii of the M7, as derived from X-ray blackbody fits and distance estimates, are in the
range of roughly 2 km to 7 km (see, for example, Kaplan
2008). The residuals mentioned above mostly contribute to the high value of
chi-square.
Similarly, if the residuals are not taken into account by adding more spectral
complexity, atmosphere models do not provide good fits or plausible physical parameters
for J1046. This is illustrated by fits (a) in Table 5 and 6, which consist of simply absorbed
nsa and nsmaxg models respectively, with fixed element abundances (no carbatm model
provided a fit with 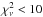 ). The fits lead to inconsistent column
densities, sizes of the emission region, and distances; the quality is poor
(
). The fits lead to inconsistent column
densities, sizes of the emission region, and distances; the quality is poor
(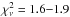 , for 166 to 169 d.o.f.) and several
parameters are unconstrained. The effective temperature of magnetised nsa models is
usually above 106 K
as they consist of fully-ionized hydrogen atmospheres. The only nsmaxg models with
, for 166 to 169 d.o.f.) and several
parameters are unconstrained. The effective temperature of magnetised nsa models is
usually above 106 K
as they consist of fully-ionized hydrogen atmospheres. The only nsmaxg models with
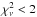 consist of cold, Teff ~ (4−5) ×
105 K, partially-ionized hydrogen atmospheres, under
moderately strong magnetic fields of B ~ (2−3) × 1013 G. The large
column density, NH
~ (5−7) × 1021 cm-2, is inconsistent with a
best-fit distance of only ~60 pc. We verified that other element atmospheres (C, O, and Ne) in
nsmaxg do not improve the spectral fitting.
consist of cold, Teff ~ (4−5) ×
105 K, partially-ionized hydrogen atmospheres, under
moderately strong magnetic fields of B ~ (2−3) × 1013 G. The large
column density, NH
~ (5−7) × 1021 cm-2, is inconsistent with a
best-fit distance of only ~60 pc. We verified that other element atmospheres (C, O, and Ne) in
nsmaxg do not improve the spectral fitting.
To test a multi-temperature spectral distribution, we next tried adding one extra thermal
component to the absorbed blackbody and atmosphere models. With respect to (A), we obtain
an improved fit quality (by 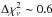 ), and blackbody temperatures of
), and blackbody temperatures of
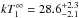 eV and
eV and
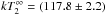 eV (B). However, the large column density
of NH = (5.3 ± 0.3)
× 1021 cm-2 requires the model normalisation of the soft component
to be large (the unabsorbed flux is nearly three orders of magnitude higher than that of a
single-temperature blackbody). At 2.3 kpc, the radiation radius of the soft component,
eV (B). However, the large column density
of NH = (5.3 ± 0.3)
× 1021 cm-2 requires the model normalisation of the soft component
to be large (the unabsorbed flux is nearly three orders of magnitude higher than that of a
single-temperature blackbody). At 2.3 kpc, the radiation radius of the soft component,
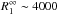 km, is inconsistent with that of a compact
object. Even if the neutron star is in the foreground of the Carina complex, it should be
at a maximum distance of 10 pc from the Sun to constrain
km, is inconsistent with that of a compact
object. Even if the neutron star is in the foreground of the Carina complex, it should be
at a maximum distance of 10 pc from the Sun to constrain
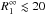 km. Considering the large NH of the model,
the low galactic latitude of the source, and a chance alignment with the Carina nebula,
the solution is unlikely.
km. Considering the large NH of the model,
the low galactic latitude of the source, and a chance alignment with the Carina nebula,
the solution is unlikely.
A second thermal component in the atmosphere models worsens the chi-square (b).
Nonetheless, in spite of a rather poor fit (χ2 ~ 1.7 for 166 d.o.f.), one
solution is more physical, the nsa model for B = 1012 G, with
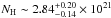 cm-2,
cm-2,
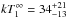 eV and
eV and
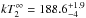 eV, at a best-fit distance of
~3.9 kpc. The best-fit
radiation radii are, however, pegged at their boundary values of
eV, at a best-fit distance of
~3.9 kpc. The best-fit
radiation radii are, however, pegged at their boundary values of
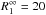 km and
km and
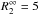 km. All other (b) models in Tables 5 and 6 show
large
km. All other (b) models in Tables 5 and 6 show
large 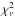 , high NH, and
distances below 500 pc.
, high NH, and
distances below 500 pc.
In (C)/(c), we found that the agreement between model and data is improved below
0.7 keV (typically by
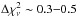 ), by allowing oxygen to be extrasolar,
with ZO ~ 1.2−1.6 in solar units, depending on the choice of continuum. In general,
there is no significant change in the best-fit parameters (the exception is for the nsa
model with for B =
1013 G). Despite the improvement, all nsmaxg models (c)
still show large NH and distances contradictorily below
100 pc, regardless of the magnetic field strength. The abundance of oxygen was the only
one tightly constrained by the vphabs fits, which were found to be either insensitive to
other elements (e.g. C, Ne, Si, or Fe), or to produce large overabundances (e.g. N, Mg,
and Ca). In particular, elements with lines around 1.35 keV were verified to be arbitrarily
overabundant in the model. A variable absorption model, combined with a double-temperature
blackbody, has no effect on the elemental abundances, which are insensitive to the fit.
This is likely due to the fact that the two blackbody components cross around an energy of
0.5 keV, where the vphabs
model tries to accomodate for the extrasolar amount of oxygen.
), by allowing oxygen to be extrasolar,
with ZO ~ 1.2−1.6 in solar units, depending on the choice of continuum. In general,
there is no significant change in the best-fit parameters (the exception is for the nsa
model with for B =
1013 G). Despite the improvement, all nsmaxg models (c)
still show large NH and distances contradictorily below
100 pc, regardless of the magnetic field strength. The abundance of oxygen was the only
one tightly constrained by the vphabs fits, which were found to be either insensitive to
other elements (e.g. C, Ne, Si, or Fe), or to produce large overabundances (e.g. N, Mg,
and Ca). In particular, elements with lines around 1.35 keV were verified to be arbitrarily
overabundant in the model. A variable absorption model, combined with a double-temperature
blackbody, has no effect on the elemental abundances, which are insensitive to the fit.
This is likely due to the fact that the two blackbody components cross around an energy of
0.5 keV, where the vphabs
model tries to accomodate for the extrasolar amount of oxygen.
Independently of the continuum – single or double-temperature, blackbody or atmosphere,
with fixed or overabundant elements – we verified that the introduction of a Gaussian line
in absorption around an energy of 1.35 keV significantly improves the quality of the spectral fitting.
With respect to (C), the presence of the line improves the fit by
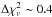 , resulting in a less absorbed model, with
, resulting in a less absorbed model, with
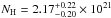 cm-2 and kT = (157 ± 5) eV (D). The
oxygen abundance is similar, ZO = (1.64 ± 0.12), and a best-fit line
energy is centred at
cm-2 and kT = (157 ± 5) eV (D). The
oxygen abundance is similar, ZO = (1.64 ± 0.12), and a best-fit line
energy is centred at 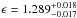 keV, with equivalent width EW ~ 220 eV. Similar
parameters and chi-square values are obtained when, alternatively, the abundances are
fixed, and two lines in absorption are added to the blackbody continuum (E). In this case,
the best-fit line energies are centred at
keV, with equivalent width EW ~ 220 eV. Similar
parameters and chi-square values are obtained when, alternatively, the abundances are
fixed, and two lines in absorption are added to the blackbody continuum (E). In this case,
the best-fit line energies are centred at 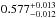 keV, and
keV, and
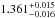 keV and have equivalent widths of 90 eV
and 120 eV. (To better constrain the model parameters, the Gaussian σ of the two components
were held fixed to 0.1 keV and 0.2 keV, respectively.)
keV and have equivalent widths of 90 eV
and 120 eV. (To better constrain the model parameters, the Gaussian σ of the two components
were held fixed to 0.1 keV and 0.2 keV, respectively.)
As for (B), the presence of a line at 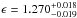 keV results in a lower flux normalisation
and a column density consistent with that towards Carina,
keV results in a lower flux normalisation
and a column density consistent with that towards Carina,
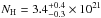 cm-2 (F); the fit quality is
improved by
cm-2 (F); the fit quality is
improved by 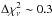 and the temperature of the two components
are higher (
and the temperature of the two components
are higher (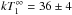 eV and
eV and
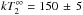 eV). Still, the neutron star should be at
a maximum distance of 150 pc to constrain
eV). Still, the neutron star should be at
a maximum distance of 150 pc to constrain 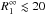 km. Regarding the double-temperature
atmosphere models, the presence of the absorption line at ~1.35 keV also results in solutions
with more consistent physical parameters (d). In particular for nsa with B = 0 G and B = 1013 G, the
column density is NH = (2.6−2.8) ×
1021 cm-2 and the distance is within d ~ 1.9 kpc to
3.3 kpc, i.e. consistent
with a neutron star in Carina. The best-fit solutions have
km. Regarding the double-temperature
atmosphere models, the presence of the absorption line at ~1.35 keV also results in solutions
with more consistent physical parameters (d). In particular for nsa with B = 0 G and B = 1013 G, the
column density is NH = (2.6−2.8) ×
1021 cm-2 and the distance is within d ~ 1.9 kpc to
3.3 kpc, i.e. consistent
with a neutron star in Carina. The best-fit solutions have
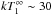 eV and
eV and
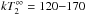 eV, with
eV, with
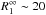 km and
km and
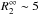 km.
km.
Finally, we tested a combination similar to that in (E), i.e. a single-temperature model with two lines, for the nsa and nsmaxg models. These are models (e) in Table 5 and 6, respectively, which are also the ones with the lowest-χ2 values in the analysis. Interestingly, all relevant parameters show best-fit values in a much narrower range. The energy of the lines are centred at ϵ1 ~ 0.55 keV and ϵ2 ~ 1.31 − 1.37 keV, and the equivalent widths are EW1 ~ 72 − 81 eV and EW2 ~ 200 − 300 eV. As for (E), the Gaussian σ of the two components was fixed. Canonical Mns and Rns values typically provided the least chi-square fits. The size of the redshifted emitting region is within 8.5 km and 13 km – overall consistent with the emission originating from most of the surface. The magnetic field intensity is not constrained by the atmosphere models, as the least-χ2 fits have B = (0−3) × 1013 G. In the lower plot of Fig. 2, we show the two pn spectra folded with the best-fit nsa model (e), for B = 1012 G.
Best-fit parameters per observation and EPIC camera.
In Table 7 we summarise the best-fit parameters of this same model for the six individual EPIC spectra. The results are consistent overall. The most deviant parameters result from fitting the MOS2 spectrum of the AO9 observation. Indeed, this spectrum was not considered in the analysis of Pires et al. (2012).
The inclusion of power-law tails extending towards higher energies has no effect on the parameters of the least-χ2 models. Considering again the best-fit nsa model (e), we found that non-thermal power-law components with typical photon indices of Γ = 1.7−2.1 (see, for example, De Luca et al. 2005) contribute at most 0.5 % (3σ confidence level) to the luminosity of the source.
3.2. Timing analysis
To reassess the significance of the periodic signal detected at P ~ 18.6 ms, we restricted the timing analysis to the pn data and completely reanalysed the AO9 dataset consistent with the new XMM-Newton observation. We considered events with photon patterns 12 or lower and tested different energy bands and radii of the source extraction region; the purpose was to unveil potential pulsations from the neutron star by minimising the background contribution. The spatial and energy selection cuts provide roughly Nph ~ (4−6) × 103 pn events in each observation.
Each pn time series was Fourier-analysed in frequency domain to search for the presence
of periodic signals. The 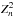 (Rayleigh) statistic (Buccheri et al. 1983) was computed directly on the
photon times-of-arrival; these were converted from the local satellite to the solar system
barycentric frame using the SAS task barycen and the source coordinates in each pn
observation (Table 2). We adopted a step in
frequency of 2 μHz (or an oversampling factor of the expected width
of the
(Rayleigh) statistic (Buccheri et al. 1983) was computed directly on the
photon times-of-arrival; these were converted from the local satellite to the solar system
barycentric frame using the SAS task barycen and the source coordinates in each pn
observation (Table 2). We adopted a step in
frequency of 2 μHz (or an oversampling factor of the expected width
of the 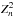 peaks of nearly 10), warranting that a periodic signal is
not missed in our searches. The number of statistically independent trials in each
Z2 test is estimated as
peaks of nearly 10), warranting that a periodic signal is
not missed in our searches. The number of statistically independent trials in each
Z2 test is estimated as
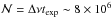 , with Δν ~ 87.7 Hz and
texp ~
87 ks to 90 ks. In the absence of a periodic component, the mean and standard
deviation of the
, with Δν ~ 87.7 Hz and
texp ~
87 ks to 90 ks. In the absence of a periodic component, the mean and standard
deviation of the 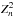 values, with n = 1, are equal to 2, as
the
values, with n = 1, are equal to 2, as
the 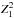 statistic is distributed as a
χ2 with two degrees of freedom. Therefore,
the probability of obtaining a noise peak of a given power Z2 in
statistic is distributed as a
χ2 with two degrees of freedom. Therefore,
the probability of obtaining a noise peak of a given power Z2 in
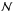 independent trials is given by
independent trials is given by 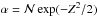 ;
the confidence level of a detection can then be established as C = (1 − α) ×
100%.
;
the confidence level of a detection can then be established as C = (1 − α) ×
100%.
 |
Fig. 3 Results of |
The analysis of the AO9 dataset yields only one statistically significant periodic
signal, at ν∗ =
53.645804(3) Hz (P∗ = 18.6407869(12) ms; see top plot of
Fig. 3). The power of the
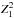 statistic at ν∗ is energy and
signal-to-noise (S/N) dependent, being measured at best (or most significantly) when
photons with energy below ~0.35 keV (where the noise of the pn camera in SW mode dominates) are
excluded from the analysis, or when the source extraction region is around an optimal
value between 17′′ and
22′′. These reflect the
intervals where the S/N ratio is optimal, indicating an origin on the neutron star itself.
statistic at ν∗ is energy and
signal-to-noise (S/N) dependent, being measured at best (or most significantly) when
photons with energy below ~0.35 keV (where the noise of the pn camera in SW mode dominates) are
excluded from the analysis, or when the source extraction region is around an optimal
value between 17′′ and
22′′. These reflect the
intervals where the S/N ratio is optimal, indicating an origin on the neutron star itself.
The measured fluctuation of the power of the 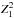 statistic at ν∗,
statistic at ν∗,
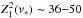 , is consistent with that expected from a
sinusoidal modulation of amplitude pf = (12.5 ± 1.9)% (see, for example,
Pavlov et al. 1999). Indeed, this is the
amplitude derived from a sinusoidal fit of the light curve of the pn camera, folded at
P =
P∗ (Fig. 4); the pulsed fraction is also consistent with the non-parametric determination
of the signal strength, pf = (13.1 ± 1.6)%, computed directly
from the sample phases according to the bootstrap method proposed by Swanepoel et al. (1996).
, is consistent with that expected from a
sinusoidal modulation of amplitude pf = (12.5 ± 1.9)% (see, for example,
Pavlov et al. 1999). Indeed, this is the
amplitude derived from a sinusoidal fit of the light curve of the pn camera, folded at
P =
P∗ (Fig. 4); the pulsed fraction is also consistent with the non-parametric determination
of the signal strength, pf = (13.1 ± 1.6)%, computed directly
from the sample phases according to the bootstrap method proposed by Swanepoel et al. (1996).
 |
Fig. 4 AO9 pn light curve, folded at P ~ 18.6 ms (the epoch of phase zero is defined at T0 = MJD 5536.00884 days). The energy band is 0.36−2.25 keV and the size of the extraction region is 18.6′′. Two cycles are shown for clarity. The best-fit sinusoidal function is also shown (dashed line). |
The inclusion of higher harmonics n ≥ 2 in the
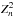 test was found to be statistically
insignificant. Extensive searches showed no other significant signal (above the
1σ
confidence level, or with
test was found to be statistically
insignificant. Extensive searches showed no other significant signal (above the
1σ
confidence level, or with 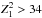 ) across the frequency range of the
analysis, and safety checks did not suggest an unknown instrumental or background origin
for the periodic signal at ν∗ (see Pires et al. 2012, for details). We also verified that the periodic signal is
always present at the same frequency, independently of the details on the processing of
the raw event file (e.g. included calibration files, SAS version, randomisation in energy
within a PI channel, event filtering, or randomisation in time within the sampling
detector time).
) across the frequency range of the
analysis, and safety checks did not suggest an unknown instrumental or background origin
for the periodic signal at ν∗ (see Pires et al. 2012, for details). We also verified that the periodic signal is
always present at the same frequency, independently of the details on the processing of
the raw event file (e.g. included calibration files, SAS version, randomisation in energy
within a PI channel, event filtering, or randomisation in time within the sampling
detector time).
In the AO11 dataset, however, no obviously significant candidate frequency results from
our 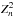 tests. Extensive tests positively exclude
modulations with pf> 14%
(
tests. Extensive tests positively exclude
modulations with pf> 14%
(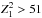 , 4σ) in the ν = (0.01−87.73) Hz
frequency range of the search. However, at the brightness level of J1046, a modulation
with pf =
11% to 13%
may be missed in searches with too large a number of trials. As the background level in
the second observation is higher and the exposure time slightly shorter, the pulsed signal
at P∗ may have been more severely affected
(or smeared out) by noise. Alternatively, the AO9 signal is spurious and/or unrelated with
the spin period of the neutron star (see discussion in Sect. 4.1).
, 4σ) in the ν = (0.01−87.73) Hz
frequency range of the search. However, at the brightness level of J1046, a modulation
with pf =
11% to 13%
may be missed in searches with too large a number of trials. As the background level in
the second observation is higher and the exposure time slightly shorter, the pulsed signal
at P∗ may have been more severely affected
(or smeared out) by noise. Alternatively, the AO9 signal is spurious and/or unrelated with
the spin period of the neutron star (see discussion in Sect. 4.1).
By considering Δν =
87.7 Hz, the only signal that shows a
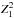 power above the 1σ confidence level –
regardless of the energy band of the search – is at νAO11 =
30.252122(22) Hz (see lower plot of Fig. 3). The measured fluctuation in our tests is
power above the 1σ confidence level –
regardless of the energy band of the search – is at νAO11 =
30.252122(22) Hz (see lower plot of Fig. 3). The measured fluctuation in our tests is
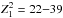 , consistent with a pulsed fraction of
pf =
11.5(9)%. The overall signficance of the signal is low: on average, the
probability of obtaining such a peak by chance is ~23%. Furthermore, the shift in frequency
with respect to the first XMM-Newton observation is too large
(ν∗ −
νAO11 ~ 23.4 Hz) for the two signals
to be associated. The implied spin-down rate would produce, within the usual
magneto-rotational dipole-braking scenario in a vacuum, a magnetic field of
Bdip = 6.6 ×
1013 G. In particular, a field with B> 5 × 1012 G
would spin down the pulsar at a rate >0.1 Hz yr-1, making the detection of a very short period of
~20 ms unlikely in the
first place.
, consistent with a pulsed fraction of
pf =
11.5(9)%. The overall signficance of the signal is low: on average, the
probability of obtaining such a peak by chance is ~23%. Furthermore, the shift in frequency
with respect to the first XMM-Newton observation is too large
(ν∗ −
νAO11 ~ 23.4 Hz) for the two signals
to be associated. The implied spin-down rate would produce, within the usual
magneto-rotational dipole-braking scenario in a vacuum, a magnetic field of
Bdip = 6.6 ×
1013 G. In particular, a field with B> 5 × 1012 G
would spin down the pulsar at a rate >0.1 Hz yr-1, making the detection of a very short period of
~20 ms unlikely in the
first place.
Regardless of the absence of an obvious candidate periodicity, the new
XMM-Newton observation can still be used in combination with the AO9
data in a coherent two-dimensional 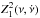 search, i.e. allowing the
search, i.e. allowing the
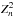 test to account for the neutron star
spin-down. In this case, the ephemeris parameters
test to account for the neutron star
spin-down. In this case, the ephemeris parameters 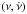 that determine the phase φj of each photon
time-of-arrival,
that determine the phase φj of each photon
time-of-arrival, 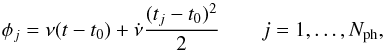 are estimated as the values that give the
highest power of the
are estimated as the values that give the
highest power of the 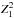 statistic. Here, t0 is the event
time-of-arrival counted from an epoch of phase zero and Nph = 10 355 is
the total number of photons in the search, when joining the two datasets for the optimal
choices of energy band and extraction region.
statistic. Here, t0 is the event
time-of-arrival counted from an epoch of phase zero and Nph = 10 355 is
the total number of photons in the search, when joining the two datasets for the optimal
choices of energy band and extraction region.
We searched for significant 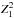 peaks in an interval of ± 5σ around ν∗, in steps of
5 × 10-9 Hz, and
explored frequency derivatives from −1 ×
10-18 Hz s-1 up to a maximum of
peaks in an interval of ± 5σ around ν∗, in steps of
5 × 10-9 Hz, and
explored frequency derivatives from −1 ×
10-18 Hz s-1 up to a maximum of
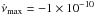 Hz s-1, in steps of −2 × 10-16 Hz s-1. The choice of the maximum
frequency derivative is reasonable, as only three isolated pulsars – the Crab and the energetic pulsars PSR J0537-6910 and PSR
J0540-6919 in the Large Magellanic Cloud, out of about 2400 known objects – are known to slow down
at a rate faster than
Hz s-1, in steps of −2 × 10-16 Hz s-1. The choice of the maximum
frequency derivative is reasonable, as only three isolated pulsars – the Crab and the energetic pulsars PSR J0537-6910 and PSR
J0540-6919 in the Large Magellanic Cloud, out of about 2400 known objects – are known to slow down
at a rate faster than 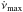 .
The number of independent trials is given by
.
The number of independent trials is given by 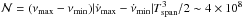 , where Tspan = 6.4 ×
107 s is the time span between the AO9 and AO11
observations.
, where Tspan = 6.4 ×
107 s is the time span between the AO9 and AO11
observations.
We found that the power of the 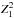 statistic increases significantly when
folding the two datasets, even though the number of trials is boosted by a factor of
100. The highest peak
resulting from our search, with
statistic increases significantly when
folding the two datasets, even though the number of trials is boosted by a factor of
100. The highest peak
resulting from our search, with  , occurs at ν = 53.645805460(5) Hz and
, occurs at ν = 53.645805460(5) Hz and
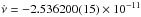 Hz s-1 (T0 = MJD
55 536.008840 days is the epoch of phase zero); the chance probability of the solution
considering all number of independent trials is 0.01% (confidence level of 3.885σ). A total of 17 solutions, out of
~6 × 109, were found at or above
the 3σ level
(with
Hz s-1 (T0 = MJD
55 536.008840 days is the epoch of phase zero); the chance probability of the solution
considering all number of independent trials is 0.01% (confidence level of 3.885σ). A total of 17 solutions, out of
~6 × 109, were found at or above
the 3σ level
(with 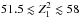 ); none was above the 4σ level. All
high-
); none was above the 4σ level. All
high-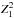 solutions have frequency derivatives
within
solutions have frequency derivatives
within 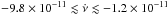 Hz s-1. Within the scenario of
magnetic braking in vacuum, the spin-down values imply a dipolar field of Bdip = (3−8) ×
1011 G for the source.
Hz s-1. Within the scenario of
magnetic braking in vacuum, the spin-down values imply a dipolar field of Bdip = (3−8) ×
1011 G for the source.
To test the result beyond its formal significance, we reproduced (in full resolution and
over the same parameter space) the two-dimensional 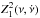 search, but folded AO11 events extracted
from a background region over the original AO9 time series of the source. The background
region was scaled to have roughly the same number of counts as collected for J1046, and
two different energy bands were tested: the 0.36−2.2 keV of the original search, where the S/N ratio is optimal,
and the 3−10 keV energy
band, which aims at excluding contamination from the neutron star. The goal is to verify
empirically the power of the
search, but folded AO11 events extracted
from a background region over the original AO9 time series of the source. The background
region was scaled to have roughly the same number of counts as collected for J1046, and
two different energy bands were tested: the 0.36−2.2 keV of the original search, where the S/N ratio is optimal,
and the 3−10 keV energy
band, which aims at excluding contamination from the neutron star. The goal is to verify
empirically the power of the 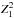 statistic on a search with similar
sensitivity, total duration, and time span of the original one, but conducted over the
times of arrival of noise events that should not relate with the periodic signal at
ν∗.
statistic on a search with similar
sensitivity, total duration, and time span of the original one, but conducted over the
times of arrival of noise events that should not relate with the periodic signal at
ν∗.
We found that 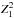 peaks of similar power are obtained on
these tests for intervals of frequency derivative that are roughly of the same order as
those of the original search. In the 0.36 −
2.2 keV energy band, we found 14 solutions above the 3σ level (again out of
~6 × 109 grid points), with
peaks of similar power are obtained on
these tests for intervals of frequency derivative that are roughly of the same order as
those of the original search. In the 0.36 −
2.2 keV energy band, we found 14 solutions above the 3σ level (again out of
~6 × 109 grid points), with
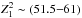 and
and
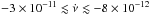 Hz s-1. The highest
Hz s-1. The highest
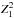 power occurs at
power occurs at
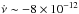 Hz s-1 and implies Bdip ~ 2.3 ×
1011 G. For the 3−10 keV energy band, 28 solutions with frequency derivatives in the
range
Hz s-1 and implies Bdip ~ 2.3 ×
1011 G. For the 3−10 keV energy band, 28 solutions with frequency derivatives in the
range 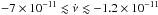 Hz s-1 were found with
Hz s-1 were found with
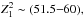 and the highest power is for
and the highest power is for
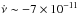 Hz s-1, which implies Bdip ~ 7 ×
1011 G. The tests show that the high
Hz s-1, which implies Bdip ~ 7 ×
1011 G. The tests show that the high
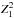 power is likely to be caused by
statistical fluctuations in a search with a large number of trials and that the best
power is likely to be caused by
statistical fluctuations in a search with a large number of trials and that the best
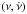 solution derived for J1046 is not significant.
solution derived for J1046 is not significant.
4. Discussion
4.1. Summary of results
At present, we cannot rule out the possibility that the periodic signal at P∗ ~ 18.6 ms, which was only significantly detected in the AO9 observation (pf = 12.5(1.9)%, c.l. 3σ to 4σ, depending on the S/N ratio of the search; see Sect. 3.2) is unrelated to the true spin period of the neutron star. The second XMM-Newton observation proved inconclusive at confirming the fast candidate spin, providing an upper limit that is close to the limiting sensitivity for detecting the AO9 modulation (pf< 14% at 4σ, for P = 0.0114 − 100 s and 0.35 − 2 keV). No other periodic signal was found to be statistically significant in extensive searches performed over the individual datasets (in a wide frequency range and for different tested energy bands). In particular, pulsations with P> 0.6 s (a range relevant for AXPs, the M7 INSs, and RRATs1) are constrained down to pf ~ 10% (3σ, 0.35−2 keV: Pires et al. 2012). Such smooth X-ray pulsations are usually more frequently observed in the M7 and CCOs, as AXPs typically show pf ≳ 15−30%.
The coherent combination of the two EPIC-pn time series, in a joint periodicity search around the candidate spin and accounting for a wide range of possible pulsar spin-down values, provides a (P,Ṗ) solution with a probability of 1 in 10 000 of it being spurious. Across the searched parameter space, the solutions above 3σ imply a dipolar magnetic field of Bdip = (3−8) × 1011 G, under the assumption of magnetic braking in vacuum. However, additional tests suggest that the timing solutions are likely to be below their formal statistical significance.
In the absence of a clear period determination and good estimate of the magnetic field, the evolutionary state and nature of this neutron star remain as yet to be constrained. Unfortunately, at the flux level of the source and with current X-ray facilities, pulsations are difficult to detect below the limits provided by present data.
We were nonetheless able to study the spectral properties of J1046 with unprecedented
detail and statistics (Sect. 3.1). Interestingly, we
found that good fits and meaningful physical parameters are only derived when the
residuals at energies 0.55 keV and 1.35 keV are taken into account by the spectral
modelling. Independently of the exact choice of the thermal continuum, we found that the
former residuals may result either from a local overabundance of oxygen in the Carina
nebula (with ZO =
1.2−1.7, relative to solar) or from the inhomogenous temperature
distribution on the surface of the neutron star (the best-fit double-temperature models
have 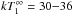 eV and
eV and
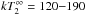 eV). Phenomenologically, the residuals at
0.55 keV can also be
described by a Gaussian absorption line with EW ~ 70−90 eV. On the other hand, of all
models tested in Sect. 3.1, the residuals at
1.35 keV are only
satisfactorily accounted for by invoking a line in absorption, with EW ~ 120−400 eV
(depending on the choice of the continuum). In this case, the fits lead to overall
physically consistent (as well as much more tightly constrained) spectral parameters:
NH = (2.5−3.3)
× 1021 cm-2, T∞ = (5−8) × 105 K,
eV). Phenomenologically, the residuals at
0.55 keV can also be
described by a Gaussian absorption line with EW ~ 70−90 eV. On the other hand, of all
models tested in Sect. 3.1, the residuals at
1.35 keV are only
satisfactorily accounted for by invoking a line in absorption, with EW ~ 120−400 eV
(depending on the choice of the continuum). In this case, the fits lead to overall
physically consistent (as well as much more tightly constrained) spectral parameters:
NH = (2.5−3.3)
× 1021 cm-2, T∞ = (5−8) × 105 K,
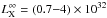 erg s-1, and d ~ 1−3 kpc
(considering the solutions with
erg s-1, and d ~ 1−3 kpc
(considering the solutions with 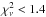 ).
).
4.2. Comparison with other pulsars
Of all the INSs that clearly show thermal X-ray emission (see, for example, the compilation of Viganò et al. 2013), J1046 displays spectral properties that are quite close to those of the M7 and CCOs – namely, the soft energy distribution, constant X-ray properties on a long timescale (≳15 yr), absence of significant magnetospheric emission, and evidence of absorption features. Deeper radio and γ-ray limits are, however, needed to exclude a middle-aged rotation-powered pulsar (RPP) or a mildly-recycled neutron star (e.g. Belczynski et al. 2010).
The likely presence of J1046 in the Carina open cluster excludes a neutron star much older than ~106 yr (see discussion in Pires et al. 2012). In millisecond pulsars (MSPs), as well as in middle-aged and old RPPs, a considerable fraction of the X-ray emission arises from polar caps, which are heated by back-flowing charges accelerated in the pulsar magnetosphere. The spectral analysis shows that the X-ray emitting region in J1046 is consistent with the surface of a canonical neutron star when realistic atmosphere models are adopted. This is in contrast to the ~0.1 km blackbody radii typically derived for MSPs (e.g. Bogdanov et al. 2006, 2011).
Middle-aged RPPs (e.g. the Three Musketeers, with ages of a few ~105 yr and spin-down power of a
few ~1034 erg s-1) are dominated by thermal
emission and show much lower residual magnetospheric activity (at levels within
0.3% and 1.7% of the source luminosity; De Luca et al. 2005). In J1046, no such weak hard tail
(above 0.5% of the source
luminosity) is present, and we found no compelling evidence for a second (hotter) thermal
component, as that typically arising from heated polar caps (see discussion in Sect. 4.3). For most RPPs, the efficiency at converting
rotational energy into X-rays is generally above η = 10-5 (Kargaltsev et al. 2012). By considering the
3σ upper
limit on the source non-thermal X-ray luminosity, 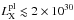 erg s-1 (Sect. 3.1, for the best-fit nsa model (e) and B = 1012 G), and
assuming a maximum age of 106 yr for the neutron star, we can derive a lower limit on
the spin-down luminosity of the source, Ė> 2.1 × 1036 erg s-1, if the neutron star is indeed
a fast rotator. This implies an exceptionally low efficiency ratio of η ≲ 10-6 for
J1046, if the neutron star is a typical RPP. Alternatively, if the signal at
P∗ is not related with the INS spin
period, the possibility remains that J1046 is a fainter and more distant M7-like INS.
erg s-1 (Sect. 3.1, for the best-fit nsa model (e) and B = 1012 G), and
assuming a maximum age of 106 yr for the neutron star, we can derive a lower limit on
the spin-down luminosity of the source, Ė> 2.1 × 1036 erg s-1, if the neutron star is indeed
a fast rotator. This implies an exceptionally low efficiency ratio of η ≲ 10-6 for
J1046, if the neutron star is a typical RPP. Alternatively, if the signal at
P∗ is not related with the INS spin
period, the possibility remains that J1046 is a fainter and more distant M7-like INS.
4.3. Origin of absorption lines
The detection of spectral features in absorption in several (non-accreting) thermally emitting neutron stars – including the M7, CCOs, magnetars, and Calvera – have been widely reported (e.g. Sanwal et al. 2002; Mori et al. 2005; Haberl 2007; McLaughlin et al. 2007; Zane et al. 2011; Tiengo et al. 2013). The physical interpretation is not unique. The features can be due to atomic transitions in the magnetised atmosphere or condensed surface of the neutron star, or be cyclotron lines generated in a hot ionized layer near the surface. Importantly, the central energies of the features have been used to give estimates on the state of magnetisation of the neutron star. Recently, Viganò et al. (2014) showed that, in some cases (as for the M7 RX J0806.4-4123; Haberl et al. 2004), rather than an actual transition between energy levels, the spectral deviation may be induced simply by the inhomogeneous temperature distribution on the surface.
In J1046, we verified that a double-temperature spectral model is only a plausible (physical) solution when we introduce an absorption feature at 1.35 keV. Even in this case, the reduced chi-square values are still high (with respect to single-temperature models) and the radiation radii are uncertain. Possibly, the poor fit reflects the inadequate description of the anisotropic temperature distribution on the surface of a neutron star by the simple superposition of two atmosphere models.
If we assume that the feature at energy ϵ ~ 1.35 keV is the fundamental electron cyclotron absorption, similar to the case of the CCO 1E 1207.4-5209 (Bignami et al. 2003), we can derive an estimate of the magnetic field on the surface for J1046. According to the relation ϵcyc = 1.16(B/ 1011 G)(1 + zg)-1, we obtain Bcyc ~ 1.5 × 1011 G for the gravitational redshift of a canonical neutron star, zg ~ 0.3.
4.4. Association with a runaway star in Carina
A runaway massive star in the Carina nebula, MJ 218 (listed in the UCAC4 catalogue as 153-055048) was recently proposed to have been associated with the progenitor of J1046 in a binary system, which was then disrupted by the supernova explosion that created the neutron star (Ngoumou et al. 2013). At a distance of 2.3 kpc, the 18′ angular separation of the two objects on the sky implies a physical distance of ~12 pc. The total proper motion of the runaway star corresponds to a transverse speed of vt = 95 ± 52 km s-1 (Zacharias et al. 2004). Assuming typical masses of 1.4 M⊙ and 9.6 M⊙ (spectral type B1.5 V; Pecaut & Mamajek 2013), respectively, for the neutron and runaway stars, the estimated flight time is of tkin ~ (1.1−3) × 104 yr, which is roughly consistent with the absence of a supernova remnant. Although uncertain, the implied velocity of J1046, vt ~ 650 ± 360 km s-1, if previously associated with MJ 218, is also consistent with the distribution of transverse speeds observed in non-recycled radio pulsars (Hobbs et al. 2005).
4.5. Thermal evolution
Based on our best-fit spectral solutions, we can investigate the thermal state of the neutron star amidst the several INS populations for the first time. Figure 5 shows a representative sample of INSs, in a cooling-age diagram. The temperature T∞ is the apparent effective surface temperature, as derived from either atmosphere or blackbody models. Whenever possible, age estimates and intervals are derived from proper motion measurements (flight time) or associations with supernova remnants; otherwise the pulsar spin-down age, uncertain by a factor of two, is adopted. The data on RPPs (14 objects including the Crab and Vela pulsars, as well as the Three Musketeers and the old pulsar PSR J2043+2740) are collected from Yakovlev et al. (2008). The five CCOs in the diagram are the neutron stars in the Cas A, Puppis A, G296.5, Kes 79, and HESS J1731-347 supernova remnants (Bogdanov 2014; Klochkov et al. 2015, and references therein); in particular, their emission can be interpreted as radiation from the entire surface, using either hydrogen or carbon atmosphere models. The locus of magnetars (SGRs and AXPs) is represented by the seven objects investigated by Kaminker et al. (2009, and references therein). Data points for the M7 are according to the compilations of Kaplan et al. (2011) and Viganò et al. (2013). For these sources, characteristic ages are shown as upper limits on true ages in the absence of a kinematic estimate.
Following our previous discussion, we adopt J1046’s flight time as a lower limit for its age estimate; a conservative value of 106 yr is taken as an upper limit, based on an association with the Carina nebula. The temperature range is as reported in Sect. 4.3. For Calvera, we adopt the temperature of the best-fit atmosphere (nsa) model (Zane et al. 2011) and the INS characteristic age (again uncertain by a factor of two, Halpern et al. 2013).
 |
Fig. 5 Cooling-age diagram for different groups of isolated neutron stars (data points: see legend). Theoretical cooling curves for a canonical neutron star are shown as lines (see text). No effects of magnetic field decay are considered. |
The set of theoretical cooling curves in Fig. 5 correspond to four representative families, which are described in, for example, Weisskopf et al. (2011), Yakovlev et al. (2011), Klochkov et al. (2015)2. In a nutshell, the so-called standard neutrino candle, represented in Fig. 5 by a solid line, shows the thermal evolution of a canonical neutron star (of mass M = 1.5 M⊙ and radius R = 12 km, with a nucleon core), where cooling is governed by the modified Urca process, and an iron envelope is assumed (no enhanced cooling in the first 100 yr). The dotted line shows the same star affected by strong proton superfluidity in the core, which highly suppresses the Urca reactions and results in a hotter neutron star at t ≳ 100 yr. The dashed and dot-dashed lines are the corresponding (non-superfluid and superfluid) models for a star with a full amount of accreted light elements (in particular, ΔM ~ 10-8 M⊙ of carbon) in the blanketing envelope. The presence of light elements in the envelope of the neutron star increases the thermal conductivity (Potekhin et al. 1997); as a result, the light-element envelope regulates and slows down the cooling in the first ~104−105 yr, depending on the amount and composition of the accreted material. The effect of the magnetic field on cooling is not taken into account, which is a valid approximation for B ≲ 1012 G.
The strong thermal emission (high temperature at a given age) observed in magnetars and the M7, with respect to the standard cooling theory and other INS groups, cannot be explained without taking into account the effects of magnetic field decay as an additional source of heating of the neutron star crust. Magneto-thermal evolutionary models (Viganò et al. 2013) show that, for strongly magnetised INSs, field dissipation keeps the stellar crust hot for a longer time than expected from standard cooling (see, Aguilera et al. 2008, and references therein); moreover, strong fields at birth (B> 1014 G) can significantly brake the neutron star spin to an asymptotic value in a relatively short timescale (~105 yr). Interestingly, whereas for the bulk of the neutron star population such effects are negligible, the model implies an evolutionary link between the M7 and magnetars.
On the other hand, consistent with the standard theory, CCOs are young neutron stars that show the slow cooling in the neutrino-cooling era typical of sources with light-element accreted envelopes. For these neutron stars, the turning point towards the steep drop in temperature of the photon-cooling stage takes place earlier than for neutron stars with an iron envelope. As a result, old CCOs may be invisible to X-ray observations after ~1 Myr, where luminosities may have dropped below ~1031 erg s-1, and surface temperatures are colder than ~20 eV to 30 eV. Nuclear burning in the envelope, and hence a change of composition, might nonetheless slow down the cooling in the last stages of the thermal life of the neutron star (Page et al. 2011).
Overall, the cooling status of Calvera appears consistent with a scenario where this neutron star evolved from a CCO (see Sect. 1). However, Calvera’s real surface temperature may be considerably softer than the adopted value in Fig. 5, kT ~ 98 eV, as the source shows a clear indication of a double-temperature energy distribution (Zane et al. 2011). In particular, the fit with a double thermal (blackbody or nsa) model constrains the apparent temperature of the cooler component within T∞ ~ (6−9) × 105 K, which is very similar to the interval estimated for J1046. Given its resemblance to Calvera, and if the fast spin and indication of a low magnetic field in J1046 are to be confirmed, the INS in Carina may be another potential candidate for the elusive class of evolved anti-magnetars.
5. Summary and conclusions
Following the intriguing detection of a short periodic signal in the neutron star 2XMM J104608.7-594306 (Pires et al. 2012), we targeted the source again with XMM-Newton, aiming at better characterising its spectral energy distribution and timing properties. The new XMM-Newton dataset unfortunately proved inconclusive in confirming the fast spin of the neutron star. The derived 4σ upper limit on the pulsed fraction, pf< 14%, shows that the observation is just at the limiting sensitivity to detect the modulation found previously.
Without a clear determination of the spin period and a robust estimate of the magnetic field of the neutron star, its exact nature remains open to interpretation. The INS 2XMM J104608.7-594306 may be similar to Calvera, a neutron star for which the scenario of an evolved anti-magnetar, within the framework of the magnetic field burial by fallback of supernova debris, has been discussed. The overall spectral properties of 2XMM J104608.7-594306 and its likely presence in the Carina open cluster disfavour a recycled object or a standard evolutionary path, typical of that of a rotation-powered pulsar. However, better age estimates (e.g. through kinematic studies), as well as deeper radio and γ-ray limits, are required to further constrain the evolutionary status of this neutron star. In particular, studies in the optical and near-infrared may offer the opportunity to assess properties which, for J1046, are not assessible by other means.
The prospect of finding more thermally emitting isolated neutron stars with the upcoming all-sky survey X-ray mission, eROSITA (Predehl et al. 2014; Merloni et al. 2012), is of course of much interest. eROSITA will scan the X-ray sky at unprecedented flux levels, making it possible to recognise orphaned CCOs and M7-like neutron stars through their residual thermal emission, either among the known radio pulsar population or even if these elusive objects are intrinsically radio silent.
As of 2015, over 1000 sources in the ATNF pulsar catalogue (of which 30 are X-ray pulsars and 58 are RRATs) are known to spin at periods longer than 0.6 s (Manchester et al. 2005).
As noted by Klochkov et al. (2015), these curves are mostly aimed at explaining the residual heating observed in CCOs. Colder neutron stars, like some RPPs in Fig. 5, may be regarded as sufficiently massive stars with higher neutrino luminosity owing to the onset of the direct Urca process in the core.
Acknowledgments
We thank the anonymous referee for useful comments and suggestions that helped to improve the paper. The work of A.M.P. is supported by the Deutsche Forschungsgemeinschaft (PI 983/1-1). R.T. is partially funded through an INAF PRIN grant. S.B.P. was supported by the Russian Science Foundation, project 14-12-00146. The authors acknowledge the use of the ATNF Pulsar Catalogue (Manchester et al. 2005, http://www.atnf.csiro.au/research/pulsar/psrcat), the McGill Online Magnetar Catalog (Olausen & Kaspi 2014, http://www.physics.mcgill.ca/~{}pulsar/magnetar/main.html), the RRATalog of discovered rotating radio transients (http://astro.phys.wvu.edu/rratalog), as well as the online catalogue of isolated neutron stars with significant thermal emission, described in Viganò et al. (2013, http://www.neutronstarcooling.info.
References
- Agüeros, M. A., Posselt, B., Anderson, S. F., et al. 2011, AJ, 141, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilera, D. N., Pons, J. A., & Miralles, J. A. 2008, ApJ, 673, L167 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Belczynski, K., Lorimer, D. R., Ridley, J. P., & Curran, S. J. 2010, MNRAS, 407, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Bignami, G. F., Caraveo, P. A., De Luca, A., & Mereghetti, S. 2003, Nature, 423, 725 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bogdanov, S. 2014, ApJ, 790, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanov, S., Grindlay, J. E., Heinke, C. O., et al. 2006, ApJ, 646, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdanov, S., van den Berg, M., Servillat, M., et al. 2011, ApJ, 730, 81 [Google Scholar]
- Bogdanov, S., Ng, C.-Y., & Kaspi, V. M. 2014, ApJ, 792, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Broos, P. S., Townsley, L. K., Feigelson, E. D., et al. 2011, ApJS, 194, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Buccheri, R., Bennett, K., Bignami, G. F., et al. 1983, A&A, 128, 245 [NASA ADS] [Google Scholar]
- Chevalier, R. A. 1989, ApJ, 346, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Chieregato, M., Campana, S., Treves, A., et al. 2005, A&A, 444, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Luca, A. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 311 [Google Scholar]
- De Luca, A., Caraveo, P. A., Mereghetti, S., Negroni, M., & Bignami, G. F. 2005, ApJ, 623, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Geppert, U., Page, D., & Zannias, T. 1999, A&A, 345, 847 [NASA ADS] [Google Scholar]
- Gotthelf, E. V., & Halpern, J. P. 2010, in BAAS, 42, 694 [Google Scholar]
- Gotthelf, E. V., Halpern, J. P., & Alford, J. 2013a, ApJ, 765, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Gotthelf, E. V., Halpern, J. P., Allen, B., & Knispel, B. 2013b, ApJ, 773, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Haberl, F. 2007, Ap&SS, 308, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Haberl, F., Motch, C., Zavlin, V. E., et al. 2004, A&A, 424, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Halpern, J. P., & Gotthelf, E. V. 2010, ApJ, 709, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Halpern, J. P., Bogdanov, S., & Gotthelf, E. V. 2013, ApJ, 778, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Harding, A. K. 2013, Frontiers of Physics, 8, 679 [Google Scholar]
- Ho, W. C. G., Potekhin, A. Y., & Chabrier, G. 2008, ApJS, 178, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaminker, A. D., Potekhin, A. Y., Yakovlev, D. G., & Chabrier, G. 2009, MNRAS, 395, 2257 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, D. L. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, ed. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 331 [Google Scholar]
- Kaplan, D. L., & van Kerkwijk, M. H. 2011, ApJ, 740, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplan, D. L., Kamble, A., van Kerkwijk, M. H., & Ho, W. C. G. 2011, ApJ, 736, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kargaltsev, O., Durant, M., Pavlov, G. G., & Garmire, G. 2012, ApJS, 201, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M. 2010, Proc. National Academy of Science, 107, 7147 [Google Scholar]
- Keane, E. F., & Kramer, M. 2008, MNRAS, 391, 2009 [NASA ADS] [CrossRef] [Google Scholar]
- Klochkov, D., Suleimanov, V., Pühlhofer, G., et al. 2015, A&A, 573, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lasker, B. M., Lattanzi, M. G., McLean, B. J., et al. 2008, AJ, 136, 735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Leutenegger, M. A., Kahn, S. M., & Ramsay, G. 2003, ApJ, 585, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, J., Ng, C.-Y., Ho, W. C. G., et al. 2015, ApJ, 808, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, M. A., Rea, N., Gaensler, B. M., et al. 2007, ApJ, 670, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S. 2008, A&ARv, 15, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012, ArXiv e-prints [arXiv:1209.3114] [Google Scholar]
- Mori, K., & Ho, W. C. G. 2007, MNRAS, 377, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, K., Chonko, J. C., & Hailey, C. J. 2005, ApJ, 631, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Ngoumou, J., Preibisch, T., Ratzka, T., & Burkert, A. 2013, ApJ, 769, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Olausen, S. A., & Kaspi, V. M. 2014, ApJS, 212, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., Prakash, M., Lattimer, J. M., & Steiner, A. W. 2011, Phys. Rev. Lett., 106, 081101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Pavlov, G. G., Shibanov, Y. A., Zavlin, V. E., & Meyer, R. D. 1995, in The Lives of the Neutron Stars, eds. M. A. Alpar, U. Kiziloglu, & J. van Paradijs, 71 [Google Scholar]
- Pavlov, G. G., Zavlin, V. E., & Trümper, J. 1999, ApJ, 511, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Pires, A. M., Motch, C., & Janot-Pacheco, E. 2009a, A&A, 504, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pires, A. M., Motch, C., Turolla, R., Treves, A., & Popov, S. B. 2009b, A&A, 498, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pires, A. M., Motch, C., Turolla, R., et al. 2012, A&A, 544, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popov, S. B., Colpi, M., Prokhorov, M. E., Treves, A., & Turolla, R. 2003, A&A, 406, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., Chabrier, G., & Yakovlev, D. G. 1997, A&A, 323, 415 [NASA ADS] [Google Scholar]
- Predehl, P., Andritschke, R., Becker, W., et al. 2014, in SPIE Conf. Ser., 9144, 1 [Google Scholar]
- Rutledge, R. E., Fox, D. B., & Shevchuk, A. H. 2008, ApJ, 672, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Sanwal, D., Pavlov, G. G., Zavlin, V. E., & Teter, M. A. 2002, ApJ, 574, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N. 2006, ApJ, 644, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suleimanov, V. F., Klochkov, D., Pavlov, G. G., & Werner, K. 2014, ApJS, 210, 13 [Google Scholar]
- Swanepoel, J. W. H., de Beer, C. F., & Loots, H. 1996, ApJ, 467, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Tiengo, A., Esposito, P., Mereghetti, S., et al. 2013, Nature, 500, 312 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Townsley, L. K., Broos, P. S., Chu, Y.-H., et al. 2011, ApJS, 194, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, M. L., Rutledge, R. E., Letcavage, R., Shevchuk, A. S. H., & Fox, D. B. 2010, ApJ, 714, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Turolla, R. 2009, in Astrophys. Space Sci. Lib. 357, ed. W. Becker, 141 [Google Scholar]
- Viganò, D., Pons, J. A., & Miralles, J. A. 2012, Comput. Phys. Comm., 183, 2042 [NASA ADS] [CrossRef] [Google Scholar]
- Viganò, D., Rea, N., Pons, J. A., et al. 2013, MNRAS, 434, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Viganò, D., Perna, R., Rea, N., & Pons, J. A. 2014, MNRAS, 443, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Tennant, A. F., Yakovlev, D. G., et al. 2011, ApJ, 743, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., & Pethick, C. J. 2004, ARA&A, 42, 169 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Yakovlev, D. G., Gnedin, O. Y., Kaminker, A. D., & Potekhin, A. Y. 2008, in 40 Years of Pulsars: Millisecond Pulsars, Magnetars and More, eds. C. Bassa, Z. Wang, A. Cumming, & V. M. Kaspi, AIP Conf. Ser., 983, 379 [Google Scholar]
- Yakovlev, D. G., Ho, W. C. G., Shternin, P. S., Heinke, C. O., & Potekhin, A. Y. 2011, MNRAS, 411, 1977 [Google Scholar]
- Zacharias, N., Monet, D. G., Levine, S. E., et al. 2004, in BAAS, 36, 1418 [Google Scholar]
- Zane, S., Haberl, F., Israel, G. L., et al. 2011, MNRAS, 410, 2428 [NASA ADS] [CrossRef] [Google Scholar]
- Zavlin, V. E., Pavlov, G. G., & Shibanov, Y. A. 1996, A&A, 315, 141 [NASA ADS] [Google Scholar]
All Tables
Instrumental configuration and duration of the EPIC scientific exposures of the XMM-Newton AO11 observation of 2XMM J104608.7-594306.
Parameters of 2XMM J104608.7-594306, as extracted from the AO11 (and AO9) XMM-Newton EPIC images.
Best-fit spectral parameters and count rates of 2XMM J104608.7-594306 per XMM-Newton observation and EPIC camera.
All Figures
 |
Fig. 1 Best-fit column density NH as a function of blackbody temperature kT, for each individual (pn/MOS1/MOS2) spectrum used in the analysis (see legend). Also shown are the results by fitting all data simultaneously, as well as results of the stacked (combined) spectrum. AO11 datasets are highlighted in red. Error bars are 1σ confidence levels. |
| In the text | |
 |
Fig. 2 Results of spectral fitting of source 2XMM J104608.7-594306. We show the two pn spectra and folded best-fit models, with residuals. Top: simple absorbed blackbody. Bottom: best-fit neutron star atmosphere at d ~ 2 kpc (B = 1012 G, Teff ~ 106 K, NH = 2.6 × 1021 cm-2). Two Gaussian lines in absorption are added to the model (with energies around 0.55 keV and 1.35 keV). |
| In the text | |
 |
Fig. 3 Results of |
| In the text | |
 |
Fig. 4 AO9 pn light curve, folded at P ~ 18.6 ms (the epoch of phase zero is defined at T0 = MJD 5536.00884 days). The energy band is 0.36−2.25 keV and the size of the extraction region is 18.6′′. Two cycles are shown for clarity. The best-fit sinusoidal function is also shown (dashed line). |
| In the text | |
 |
Fig. 5 Cooling-age diagram for different groups of isolated neutron stars (data points: see legend). Theoretical cooling curves for a canonical neutron star are shown as lines (see text). No effects of magnetic field decay are considered. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


