| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526249 | |
| Published online | 02 November 2015 | |
Physical properties of the extreme Centaur and super-comet candidate 2013 AZ60
1
Konkoly Observatory, MTA Research Centre for Astronomy and Earth Sciences,
Konkoly-Thege Miklós út 15–17, 1121
Budapest,
Hungary
e-mail:
apal@szofi.net
2
Department of Astronomy, Loránd Eötvös University,
Pázmány Péter sétány 1/A,
1117
Budapest,
Hungary
3
Computational Engineering and Science Research Centre, University
of Southern Queensland, Toowoomba, 4350
Queensland,
Australia
4
Australian Centre for Astrobiology, UNSW Australia,
Sydney, 2052
New South Wales,
Australia
5
Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312, Giessenbachstr.,
85741
Garching,
Germany
6
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg 3,
37077
Göttingen,
Germany
7
Instituto de Astrofísica de Canarias, 38205, La Laguna, Tenerife, Spain
8
Departamento de Astrosfísica, Universidad de La
Laguna, 38206, La
Laguna, Tenerife,
Spain
9
Gothard Astrophysical Observatory, Loránd Eötvös
University, 9700
Szombathely,
Hungary
10
Lowell Observatory, 1400 W Mars Hill Rd, Arizona, AZ
86001,
USA
11
Centre for Astrophysics Research, University of
Hertfordshire, College
Lane, Hatfield
AL10 9AB,
UK
12
Instituto de Astrofísica de Andalucía – CSIC,
Apt 3004, 18008
Granada,
Spain
Received: 2 April 2015
Accepted: 7 July 2015
We present estimates of the basic physical properties including size and albedo of the extreme Centaur 2013 AZ60. These properties have been derived from optical and thermal infrared measurements. Our optical measurements revealed a probable full period of ≈9.4 h with a shallow amplitude of 4.5%. By combining optical brightness information and thermal emission data, we are able to derive a diameter of 62.3 ± 5.3 km and a geometric albedo of 2.9%, which corresponds to an extremely dark surface. Additionally, our finding of ≳50 Jm-2 K-1 s− 1/2 for the thermal inertia is also remarkable for objects in such a distance. The results of dynamical simulations yield an unstable orbit, with a 50% probability that the target will be ejected from the solar system within 700 000 yr. The current orbit of this object and its instability could imply a pristine cometary surface. This possibility agrees with the observed low geometric albedo and red photometric colour indices for the object, which match the surface of a dormant comet well, as would be expected for a long-period cometary body approaching perihelion. Although it was approaching ever closer to the Sun, however, the object exhibited star-like profiles in each of our observations, lacking any sign of cometary activity. According to the albedo, 2013 AZ60 is a candidate for the darkest body among the known trans-Neptunian objects.
Key words: Kuiper belt objects: individual: 2013 AZ60 / radiation mechanisms: thermal / techniques: photometric
© ESO, 2015
Summary of Herschel observations of 2013 AZ60, obtained in the DDT program DDT_ckiss_3.
1. Introduction
The object 2013 AZ60 is a recently discovered extreme Centaur, moving on an eccentric orbit with e ≈ 0.992 and a perihelion distance of q ≈ 7.9 AU. As a result, 2013 AZ60 is among the trans-Neptunian objects (TNOs) with the largest known aphelion distance at ≈1950 AU. 2013 AZ60 may be classified as a Centaur based on its perihelion distance (Horner et al. 2003) but due to its large semimajor axis, it could equally be considered to be a scattered-disk object (Gladman et al. 2008). Its Tisserand parameter (Duncan et al. 2004) w.r.t. Jupiter is TJ = 3.47, which is typical for Centaurs (Horner et al. 2004a,b) and differs from that of Jupiter-family comets (2 <TJ< 3) and especially for from that of Damocolids and Halley-type comets (TJ< 2, see Jewitt 2005), which exhibit cometary dynamics.
To recover the basic physical and surface characteristics of this object, we need measurements both in the visual and in the thermal infrared range. Optical data can yield information about the intrinsic colours, the absolute brightness, rotational period, shape, and surface homogeneity of the object, while thermal observations aid us in deciding whether we see a “large but dim” or a “small but bright” surface. For this latter purpose, the Herschel Space Observatory (Pilbratt et al. 2010) is an ideal instrument since the expected peak of the thermal emission is close to the shortest wavelengths of its PACS detector (Poglitsch et al. 2010).
In our current analysis, we follow the same methodology as presented in our previous study of the Centaur 2012 DR30 (Kiss et al. 2013), another object moving on a similar orbit to 2013 AZ60. The structure of this paper is as follows. In Sect. 2 we describe our observations, including the detection of thermal emission by Herschel/PACS, optical photometry by the IAC-80 telescope (Teide Observatory, Tenerife, Spain), optical reflectance by the Gran Telescopio Canarias (GTC, Roque de los Muchachos Observatory, La Palma, Spain), and near-infrared photometry by the William Herschel Telescope (WHT, Roque de los Muchachos Observatory, La Palma, Spain). In Sect. 3 we derive the basic physical properties of the object by applying well-understood thermophysical models. The dynamics of 2013 AZ60 are then discussed in Sect. 4. Finally, our results are summarized in Sect. 5.
2. Observations and data reduction
2.1. Thermal observations and flux estimations
Thermal infrared images have been acquired with the Photoconductor Array Camera and Spectrometer (PACS Poglitsch et al. 2010) of the Herschel Space Observatory (Pilbratt et al. 2010) in two series, each of 1.3 h duration. As we summarize in Table. 1, these two measurement cycles were separated by more than four hours, allowing the target object 2013 AZ60 to move, but still be in the same field of view. This type of data collection has almost exclusively been employed in the “TNOs are Cool!” open time key programme of Herschel (Müller et al. 2009, 2010; Vilenius et al. 2012). For both series of measurements, we used both the blue/red (70/160 μm) and green/red (100/160 μm) channel combinations. This scheme allowed us to use the second series of images as a background for the first series of images (and vice versa) to eliminate the systematic effects of the strong thermal background. This type of data acquisition and the respective reduction scheme were described in our previous works related to both the “TNOs are Cool!” project (see e.g. Vilenius et al. 2012; Pál et al. 2012) and subsequent measurements (see e.g. Kiss et al. 2013).
Unfortunately, the astrometric uncertainties of 2013 AZ60 were relatively large at the time of Herschel observations as a result of its rather recent discovery. Thus, the apparent position of the object was slightly (≈29′′) off from the image center, which also implied that the double-differential photometric method (Kiss et al. 2014) yielded larger photometric uncertainties. In addition, shortly before the Herschel observations, on February 16, 2013 (at OD-13751), one half of the red (160 μm) channel pixel array became faulty. Hence, only the images from the first visit were sufficient to obtain fluxes at 160 μm, and it was not possible to create double-differential maps in this channel.
 |
Fig. 1 Image stamps showing the Herschel/PACS maps of 2013 AZ60 in the 70 μm (blue), 100 μm (green), and 160 μm (red) channels. Each stamp covers an area of 64′′×64′′, while the tick marks on the axes show the relative positions in pixels. The effective beam size (i.e. the circle with a diameter corresponding to the full width at half maximum) is also displayed in the lower left corners of the stamps. The upper panels show the stamps directly combined from the individual frames where the lower stamps are obtained using the double-differential method. Because of the failure of the red channel half and the astrometric uncertainties, the second visit is nearly unusable in red, hence double-differential maps cannot be created. |
Raw Herschel/PACS data have been processed in the HIPE environment (Ott 2010) with custom scripts described in Kiss et al. (2014). The double-differential maps were created and analysed using the FITSH package (Pál 2012). The resulting images are displayed in Fig. 1. Photometry on the individual as well as on the combined double-differential images were performed by using aperture photometry where the fluxes were corrected by the respective growth curve functions. Photometric uncertainties were estimated by involving artificial source implantation in a Monte Carlo fashion (Santos-Sanz et al. 2012; Mommert et al. 2012; Kiss et al. 2014). This method works both for the double-differential images (blue and green channels) and on the individual maps (here, the red channel).
Based on the individual images, we obtained thermal fluxes of 36.6 ± 2.9, 25.2 ± 3.7, and 15.9 ± 4.5 mJy in the blue, green, and red wavelengths, respectively. By involving the double-differential maps, we derived 32.5 ± 2.2 and 23.0 ± 2.8 mJy in the blue and green regimes. Because of the lower level of confusion noise (see Fig. 1), the accuracy of the latter series of fluxes is better. Therefore, for further modelling we adopted the double-differential fluxes for blue and green. Thermal fluxes should undergo colour correction according to the temperatures of the bodies (see Poglitsch et al. 2010, for the respective coefficients). Since the subsolar temperature of 2013 AZ60 is around 110 K, the colour correction is negligible (less than a percent) in blue and green, while it is +4% in red. Our reported fluxes consider the respective colour correction factors. In addition, in the error estimation of these fluxes, we included the 5% systematic error for the absolute flux calibration (Balog et al. 2014). The summary of these thermal fluxes is reported in Table 2.
Thermal fluxes of 2013 AZ60 derived from our Herschel measurements.
2.2. Optical photometry
Since 2013 AZ60 has been discovered only recently, one of our goals was to obtain precise photometric time series for this object to estimate both the absolute magnitudes (in various passbands) and the rotational period based on light-curve variability. For these purposes, we used the IAC-80 telescope located at the Teide Observatory, Tenerife. During our observing runs, we used the CAMELOT camera, equipped with a CCD-E2V detector of 2k × 2k, with a pixel scale of ≈0.3′′ providing a field of view of roughly 10′ × 10′. Time series were gathered for several hours on the nights of 2013 November 4–9 using Sloan g′, r′ and i′ filter sets. Since 2013 AZ60 can currently be found at the edge of the spring Sloan field, several dozen stars with accurate reference magnitudes were available on each image. The night conditions were photometric on 2013 November 5, 7, and 9 where the individual photometric uncertainties were nearly constant and varied between 0.04 and 0.05 mags in Sloan r′ band. The conditions were worse on the other three nights (November 4, 6 and 8) when the formal uncertainties scattered in the range of 0.04−0.08, indicating the variable transparency of the sky (which was also notable during the observations). The poorest conditions were on the first night, where some of the measurements had a formal uncertainty of 0.09.
 |
Fig. 2 Folded optical light curves of 2013 AZ60 using photometric data taken on six subsequent nights of 2013 November 4–9. Note that the folding frequency is related to the preferred double-peaked solution, n = (5.11/2) d-1. See text for further details. |
The scientific images were analysed with the standard calibration, source extraction, astrometry, cross matching, and photometry tasks of the FITSH package (Pál 2012). As a hint, we used the MPC predictions for the target coordinates and then performed individual centroid fits on each image and smoothed with polynomial regression for a better (much more precise and accurate) input for aperture photometry. Instrumental magnitudes were then extracted for both the reference stars and the target itself. After applying the standard photometric transformations, we then obtained the intrinsic g′, r′ and i′ magnitudes.
We searched for possible light-curve variations using the most frequently sampled Sloan r′-band data (every second image was taken in Sloan r′, while every fourth image was in g′ and i′). To search for periodic variations in our data set, we fitted a function in the form of f(t) = a + b·sin(2πnt) + c·cos(2πnt) to the Sloan r′ photometric series, where t indicates the independent value (the time in this case). If the value of n is scanned in the appropriate domain (n = 0.01...15) with a proper step size (n = 0.01, that is, abouteight times smaller than the step size implied by the Nyquist criterion), then the parameters a, b, and c can be obtained via a simple weighted linear least-squares fit procedure. The unbiased χ2 values can then be compared with the reference value of  . This reference value is obtained when n is set to 0 and the error bars are scaled by a factor of 1.51 to yield a
. This reference value is obtained when n is set to 0 and the error bars are scaled by a factor of 1.51 to yield a  equivalent to the degrees of freedom. The difference between the
equivalent to the degrees of freedom. The difference between the  and the χ2 related to the adopted period tells the significance of the detection, while various additional possible periods can also be checked and/or ruled out according to the difference between the respective χ2 values. We found a significant variation (
and the χ2 related to the adopted period tells the significance of the detection, while various additional possible periods can also be checked and/or ruled out according to the difference between the respective χ2 values. We found a significant variation (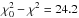 ) with a corresponding amplitude of Δr′ = 0.045 ± 0.007 that has a frequency of n = 5.11 ± 0.12 d-1. The folded light curves are displayed in Fig. 2. The mean magnitudes of these observations were
) with a corresponding amplitude of Δr′ = 0.045 ± 0.007 that has a frequency of n = 5.11 ± 0.12 d-1. The folded light curves are displayed in Fig. 2. The mean magnitudes of these observations were 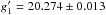 ,
, 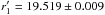 and
and 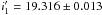 .
.
We have to note here that due to the daily aliases, the peaks around n ± 1 d-1 are also remarkable and there is a non-negligible chance that one of these frequencies belong to the intrinsic rotation of the object. The peak at n = 6.11 has a χ2 value that is only higher than that of the main peak by 3.5.
In general, minor bodies in the solar system feature double-peaked light curves. Hence, the rotational frequency of 2013 AZ60 is more likely to be nrot = n/ 2 d-1, equivalent to a period of Prot = 9.39 ± 0.22 h. To test the significance of a double-peaked light-curve solution, we coadded a sinusoidal component with half of the frequency to the primary variations. The amplitude of this component is found to be 0.013 ± 0.008 mag. This is only a 1.7σ detection, however, a good argument for confirming the assumption for an intrinsic rotation period of Prot ≈ 9.4 h.
In addition, we repeated the photometric observations for 2013 AZ60 in 2014 January 28 in g′ and r′ bands. The results of these photometric measurements yielded the Sloan magnitudes of 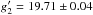 and
and  . During the first series of measurements (in 2013 November), the geocentric and heliocentric distance of 2013 AZ60 were Δ1 = 8.176 AU and r1 = 8.244 AU, while in 2014 January 28, these distances were Δ2 = 7.148 AU and r2 = 8.114 AU. Based on these distances, the expected change in the apparent brightness was 5 [log 10(r2Δ2)−log 10(r1Δ1)] = −0.326, but the actual brightness changes were Δg′ = −0.56 ± 0.04 and Δr′ = −0.53 ± 0.03, whose mean is Δm = −0.54 ± 0.03. Since the phase angle of 2013 AZ60 was α1 = 6.9° in 2013 November 5 and α2 = 1.5° in 2014 January 28, these values imply a phase correction factor of β = [(0.54 ± 0.03)−0.326] /(6.9−1.5) = 0.039 ± 0.006 mag/deg. This agrees very well with MPC observations. Based on the MPC observation database, the best-fit phase correction parameter can also be derived, but with a larger uncertainty: βMPC = 0.040 ± 0.025 mag/deg.
. During the first series of measurements (in 2013 November), the geocentric and heliocentric distance of 2013 AZ60 were Δ1 = 8.176 AU and r1 = 8.244 AU, while in 2014 January 28, these distances were Δ2 = 7.148 AU and r2 = 8.114 AU. Based on these distances, the expected change in the apparent brightness was 5 [log 10(r2Δ2)−log 10(r1Δ1)] = −0.326, but the actual brightness changes were Δg′ = −0.56 ± 0.04 and Δr′ = −0.53 ± 0.03, whose mean is Δm = −0.54 ± 0.03. Since the phase angle of 2013 AZ60 was α1 = 6.9° in 2013 November 5 and α2 = 1.5° in 2014 January 28, these values imply a phase correction factor of β = [(0.54 ± 0.03)−0.326] /(6.9−1.5) = 0.039 ± 0.006 mag/deg. This agrees very well with MPC observations. Based on the MPC observation database, the best-fit phase correction parameter can also be derived, but with a larger uncertainty: βMPC = 0.040 ± 0.025 mag/deg.
These parameters allowed us to derive the absolute brightness of the object 2013 AZ60 in a manner described below. First, we employed a simple Monte Carlo run whose input were the observed Sloan brightnesses, the derived phase correction factor, and the parameters and the respective uncertainties of the corresponding Sloan-UBVRI transformation equation (for converting g′ and r′ brightnesses to V, see Jester et al. 2005). This Monte Carlo run yielded a value of HV = 10.42 ± 0.07. Next, we checked the available photometric data series presented in the MPC database, which yielded slightly fainter values, namely HV,MPC = 10.60 ± 0.15. To reflect MPC photometry in our derived absolute brightness value, we adopted the weighted mean value of these two values, namely HV = 10.45 with a conservative uncertainty of ± 0.10 in the subsequent modelling.
2.3. Reflectance spectrum
To accurately compare the surface colour characteristics of 2013 AZ60 with other TNOs (see Lacerda et al. 2014), we obtained a low-resolution spectrum using the Optical System for Imaging and Low Resolution Integrated Spectroscopy (OSIRIS) camera spectrograph (Cepa et al. 2000; Cepa 2010) at the 10.4 m Gran Telescopio Canarias (GTC), located at the El Roque de los Muchachos Observatory (ORM) in La Palma, Canary Islands, Spain. The OSIRIS instrument consists of a mosaic of two Marconi CCD detectors, each with 2048 × 4096 pixels and a total unvignetted field of view of 7.8′ × 7.8′, giving a plate scale of 0.127′′/ pixel. However, to increase the signal-to-noise ratio for our observations, we selected the 2 × 2 binning mode with a readout speed of 200 kHz (that has a gain of 0.95 e−/ ADU and a readout noise of 4.5 e−), which corresponds with the standard operation mode of the instrument. A 300 s exposure time spectrum was obtained on January 28.17 (UTC), 2014 at an airmass of X = 1.14 using the OSIRIS R300R grism that produces a dispersion of 7.74 Å/pixel, covering the 4800−9000 Å spectral range. A 1.5′′ slit width was used oriented at the parallactic angle.
 |
Fig. 3 Reflectance spectrum of 2013 AZ60, taken with the OSIRIS spectrometer on the GTC in January, 2014. This spectrum is normalised to unity at λ = 5500 Å. |
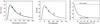 |
Fig. 4 Spectral energy distribution of 2013 AZ60 in the far-infrared region, based on Herschel/PACS measurements. Left panel: far-infrared measurements superimposed are the best-fit NEATM curves with their respective uncertainty. Middle panel: TPM model curve for thermal inertia of 100 Jm-2 K-1 s− 1/2, rotation period of 9.39 h and equator-on geometry. Right panel: the value of χ2 as the function of thermal inertia for pole-on and equator-on geometries. See text for further details. |
Spectroscopic reduction was made using the standard IRAF tasks. Images were initially bias and flat-field corrected, using lamp flats from the GTC Instrument Calibration Module. The two-dimensional spectra were then wavelength calibrated using Xe+Ne+HgAr lamps. After the wavelength calibration, sky background was subtracted and a one-dimensional spectrum was extracted. To correct for telluric absorption and to obtain the relative reflectance, the G2V star Land102_1081 (Landolt 1992) was observed using the same spectral configuration and at a similar airmass immediately after the Centaur observation. The spectrum of the 2013 AZ60 was then divided by that of Land102_1081, and then normalised to unity at 0.55 μm.
The derived spectrum is displayed in Fig. 3. Based on this spectrum, the slope parameter of this object is found to be S′ = 13.4 ± 3.0 % (1000 Å)-1 by a linear fit across the interval 5000−9000 Å.
The measured photometric colours (g′−r′ = 0.755 ± 0.018 and 0.72 ± 0.05 on 2013.11.04 and 2014.01.28, respectively) completely agree with the derived spectral slope. The spectrum was normalised at 5500 Å, just between the g′ and r′ bands. We can therefore write S′ to Eq. (2) of Jewitt (2002), if we write SDSS colours instead of Bessel ones, and set Δλ = 1480 Å. This results in a synthetic colour index from spectral slope (g − r)synth = 0.76 ± 0.04, in a perfect agreement with our photometry within the errors.
2.4. Near-infrared photometry
CCD observations of 2013 AZ60 were obtained on 2013 September 24 with the 4.2 m William Herschel Telescope at La Palma Observatory, equipped with the LIRIS instrument. LIRIS is a near-IR imager/spectrograph that uses a 1k × 1k HAWAII detector with a field of view of 4.27′ × 4.27′. The number of exposures taken in different filters are 5 × 30 s in Y and J, 15 × 20 s in H, 15 × 13 s in CH4, and 180 × 20 s exposures in Ks. Local comparison stars were selected from the 2MASS catalogue, and magnitude transformations were applied following Hodgkin et al. (2009).
The result of the photometry is Y = 18.66 ± 0.08, J = 18.34 ± 0.05, H = 18.00 ± 0.06 and Ks = 17.72 ± 0.10, where Y refers to the UKIDDS system, while JHKs are 2MASS magnitudes. Thus, 2013 AZ60 exhibits almost exactly solar colour indices, with a slightly redder slope than solar, Y − J = 0.32, J − H = 0.34 ± 0.07, and H − Ks = 0.28 ± 0.11, while according to Casagrande et al. (2012) and estimating solar Y − J according to Hodgkin et al. (2009), the respective solar colours are (Y − J)⊙ = 0.235 ± 0.018,(J − H)⊙ = 0.286 ± 0.018, and (H − Ks)⊙ = 0.076 ± 0.018. We note here that LIRIS is equipped with the Mauna Kea Observatories (MKO) system of J, H and K filters. According to Hodgkin et al. (2009)2, the expected systematic differences between 2MASS and LIRIS/MKO colours of 2013 AZ60 are in the range of −0.010··· + 0.015, which is clearly smaller than the photometric uncertainties. This observation indicates a flat and featureless spectrum of 2013 AZ60: the slope is equivalent in the infrared and in the optical, being quite similar to dormant cometary nuclei.
During the observation the heliocentric and geocentric distance of 2013 AZ60 were 8.87 and 8.32 AU, respectively, indicating an absolute mid-IR brightness of J = 9.00 ± 0.06 without correcting for the solar phase angle.
Orbital and optical data for 2013 AZ60 at the time of the Herschel observations.
3. Thermal emission modelling
3.1. Near-Earth asteroid thermal model
The basic physical properties such as albedo and diameter can be obtained by combining optical brightness data with thermal emission. Assuming an absolute optical brightness for a certain object, the higher the thermal emission, the smaller the actual albedo and hence the larger the diameter. As a result of the observing strategies constrained by the spatial attitude of the Herschel, objects close to the ecliptic are best observable by Herschel during quadratures. Nevertheless, in quadratures these minor objects exhibit a large phase angle, hence the standard thermal model (STM Lebofsky et al. 1986) might not be as accurate as desired. 2013 AZ60 had a phase angle of α = 6.6° at the time of our Herschel/PACS observations. To gain accurate estimates for larger phase angles, we employed the near-Earth asteroid thermal model (NEATM Harris 1998): this model integrates the thermal emission for arbitrary viewing angles. Throughout the modelling we used the heliocentric and geocentric distances at the instance of the Herschel/PACS measurements, namely rhelio = 8.702 AU and rgeo = 8.560 AU.
The diameter and albedo can then be derived in a similar manner like as in our earlier works (see e.g. Kiss et al. 2013; Pál et al. 2012). As an input for the fit procedures, we used the previously obtained thermal fluxes (see Table 2) and the absolute brightness HV = 10.45 ± 0.10 (derived earlier, see above).
The absolute physical parameters (diameter, albedo, and beaming parameter) were obtained in a Monte Carlo fashion. In each step, a Gaussian value was drawn for the four input values (three thermal fluxes and the absolute brightness HV) and the model parameters were adjusted through a nonlinear Levenberg-Marquardt fit. A sufficiently long series of such steps yields the best-fit values and respective uncertainties and correlations. This procedure was performed in two iterations. First, we let the value for the beaming parameter η free to vary. This run yielded relatively high correlations between the parameters and a highly long-tailed distribution for η: we found that the mode for η was 0.8 while the median is 2.6, and the uncertainties yielded by the lower and upper quartiles are 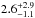 . This skewed distribution arises because beaming parameters cannot really be constrained if thermal fluxes are not known for shorter wavelengths (i.e. shorter than the peak of the spectral energy distribution). Hence, in the next run we used η as an input (instead of an adjusted variable), while its value was drawn uniformly between 0.8 and 2.6. This domain also agrees with the possible physical domain of the beaming parameter (see also Fig. 4 of Lellouch et al. 2013). The results of this second run were d = 62.3 ± 5.3 km, pV = 0.029 ± 0.006, while the beaming parameter can be written as η = 1.7 ± 0.9. The resulting albedo refers to a remarkably dark surface. The fluxes along with the best-fit NEATM model curve are shown in the left panel of Fig. 4.
. This skewed distribution arises because beaming parameters cannot really be constrained if thermal fluxes are not known for shorter wavelengths (i.e. shorter than the peak of the spectral energy distribution). Hence, in the next run we used η as an input (instead of an adjusted variable), while its value was drawn uniformly between 0.8 and 2.6. This domain also agrees with the possible physical domain of the beaming parameter (see also Fig. 4 of Lellouch et al. 2013). The results of this second run were d = 62.3 ± 5.3 km, pV = 0.029 ± 0.006, while the beaming parameter can be written as η = 1.7 ± 0.9. The resulting albedo refers to a remarkably dark surface. The fluxes along with the best-fit NEATM model curve are shown in the left panel of Fig. 4.
3.2. Thermophysical model
In addition to the derivation of the NEATM parameters, we conducted an analysis of thermal emission based on the asteroid thermophysical model (TPM, see Müller & Lagerros 1998, 2002). The observational constraints employed by this model were the thermal fluxes (see Table 2), the absolute magnitude of HV = 10.45 ± 0.10 (see earlier), the rotational period of 9.39 h, and the actual geometry at the time of Herschel observations (see the values for phase angle and heliocentric and geocentric distances above).
Our procedures showed that the best-fit model occurs at high thermal inertia values. Assuming an equator-on geometry, a value for reduced χ2 ≲ 1 corresponds to Γ ≳ 10 Jm-2 K-1 s− 1/2 (see also the right panel of Fig. 4), but the gradually decreasing form of the function χ2(Γ) implies a lower limit of Γ ≳ 50 Jm-2 K-1 s− 1/2. The corresponding values at Γ = 50 Jm-2 K-1 s− 1/2 for geometric albedo and diameter are pV = 0.028 and d = 64.9 km. These values are also compatible within uncertainties with those derived from the NEATM analysis (see above). The spectral energy distribution provided by these TPM values are shown in the middle panel of Fig. 4. This value for the thermal inertia is close to the values of 30−300 Jm-2 K-1 s− 1/2 reported for comets (see e.g. Julian et al. 2000; Campins & Fernández 2000; Davidsson et al. 2013) and the value of 10−50 Jm-2 K-1 s− 1/2 for 67P/Churyumov-Gerasimenko (Gulkis et al. 2015). We note here that models either with thermal inertia values lower than 50 Jm-2 K-1 s− 1/2 or with an assumption for pole-on view underestimate the observed flux at 160 μm.
Our findings for high preferred values of the beaming parameter η and for the thermal inertia Γ (even Γ ≳ 10 Jm-2 K-1 s− 1/2) can be compared with the statistical expectations of Lellouch et al. (2013). By considering the small heliocentric distance of this object, both of these values are expected to be lower (see Figs. 6 and 11 in Lellouch et al. 2013).
4. Dynamics of 2013 AZ60
2013 AZ60 moves on a highly eccentric orbit, with perihelion between the orbits of Jupiter and Saturn. The best-fit solution for the epoch of 2015 March 15 is shown in Table 4.
Best-fit orbital solution (semimajor axis a, perihelion distance q, eccentricity e, inclination i, longitude of ascending node Ω, argument of perihelion ω, mean anomaly M, and perihelion date Tperi), and associated uncertainties, for 2013 AZ60, taken3 from the Minor Planet Center on 2015 March 15.
To assess the dynamical history and potential future behaviour of 2013 AZ60, we followed a well-established route (see e.g. Horner et al. 2004a,b, 2010, 2012; Kiss et al. 2013) and used the hybrid integrator within the n-body dynamics package MERCURY (Chambers 1999) to follow the evolution of a swarm of test particles centred on the best-fit orbit for the object to obtain a statistical overview of the object’s behaviour. A total of 91 125 test particles were created, distributed uniformly across the region of orbital element phase space within ± 3σ of the best-fit perihelion distance, q, eccentricity, e, and inclination, i. In this manner, we created a grid of 45 × 45 × 45 test particles distributed in even steps across the ± 3σ error ranges about the nominal best-fit orbit in each of the three orbital elements studied. Each of these test particles was then followed in our integrations, with its orbit evolving under the gravitational influence of the giant planets Jupiter, Saturn, Uranus, and Neptune for a period of four billion years. Test particles were considered to have been ejected from the solar system (and were therefore removed from the integrations) if they reached a barycentric distance of 10 000 AU. Similarly, any test particles that collided with one of the giant planets or with the Sun were removed from the simulations. Each time a test particle was removed in either of these manners, the time at which the removal occurred was recorded, allowing us to track the number of surviving test particles as a function of time. The results of our simulations are shown below in Figs. 5 and 6.
 |
Fig. 5 Decay of our population of 91 125 clones of 2013 AZ60 as a function of the time elapsed in our integrations. The plots on the right show the same data as those on the left, but are plotted on a log/log scale. The upper panels show the decay of the population over the first billion years of the four billion year integrations, whilst the lower panels show the decay over the first million years. |
It is immediately apparent that the population of clones of 2013 AZ60 is highly dynamically unstable, with 63.9% of the particles (58 191 of 91 125) being removed from the simulations within the first million years of the integrations, as a result of either ejection or collision with one of the giant planets or the Sun. Half of the test particles are ejected within the first 682 kyr of the integrations, revealing that the orbit of 2013 AZ60 is more than two orders of magnitude more unstable than that of the similar object 2012 DR30 (Kiss et al. 2013).
 |
Fig. 6 Mean (upper) and median (lower) lifetimes of 2013 AZ60 as a function of the initial perihelion distance, q, and eccentricity, e, of the orbit tested. The location of the best-fit orbital solution for 2013 AZ60, as detailed in Table 4, is shown by the hollow square at the centre of the figure, with the ±1σ uncertainties on the perihelion distance and eccentricity denoted by the solid black lines that radiate from that box. Each coloured square in the figures shows the mean (or median) lifetime of the 45 individual runs carried out at that particular a−e location. Each of those 45 runs tested a different orbital inclination for 2013 AZ60, evenly distributed across the ± 3σ uncertainty range on the best-fit orbital solution. As was the case with the high-eccentricity Centaur 2012 DR30 (Kiss et al. 2013), the stability of the orbit of 2013 AZ60 does not vary significantly across the range of perihelion distance and eccentricities tested in this work – a reflection of the relatively high precision with which the object’s orbit is known. |
The orbit of 2013 AZ60 proves to be highly dynamically unstable on timescales of just a few hundred thousand years. Fully half of the test particles in our simulations were removed from the simulations within just 682 kyr, and almost two-thirds were removed within the first million years. This extreme level of instability is not that surprising, however: 2013 AZ60 passes through the descending node of its orbit4 at essentially the same time as it passes through perihelion, maximising the likelihood that it will be perturbed by either Jupiter or Saturn. This extreme level of instability is typical of objects moving on Centaur-like orbits (e.g. Horner et al. 2004a,b) and suggests that 2013 AZ60 may have been captured only recently to its current orbit. This argument is supported by the fact that, averaged over our entire population of 91 125 test particles, the mean lifetime of 2013 AZ60 is just 1.56 Myr.
Given that 2013 AZ60 exhibits such an extreme instability and may well be a relatively pristine object, it is interesting to consider whether it will have experienced significant solar heating and cometary activity over its past history. As a result of our large dynamical dataset on the evolution of 2013 AZ60, it is possible to determine the fraction of the population of clones that may one day evolve onto Earth-crossing orbits, and the fraction of the population that approach the Sun to within a given heliocentric distance at some point in their lifetime. Since dynamical evolution under the influence of gravity alone is a time-reversible process, we can use these values to estimate the probability that 2013 AZ60 has moved on orbits that bring it within those heliocentric distances at some point in the past, before being ejected to its current orbit. Because of the extreme instability exhibited by 2013 AZ60, we found that a relatively small number of the total population of clones were captured to Earth-crossing orbits through their lifetimes. Indeed, just 3805 of the 91 125 test particles we studied (just 4.2% of the population) became Earth-crossing at any point in our integrations, and the total fraction of the object’s lifetime spent as an Earth-crossing object (averaged across all 91 125 test particles) was 0.12%. Our results for a variety of other perihelion distances are displayed in Table 5, together with estimates of the mean amount of time for which clones of 2013 AZ60 exhibited perihelion distances smaller than the specified value.
Number of the 91 125 clones of 2013 AZ60 simulated in this work that evolved to orbits with perihelion distances smaller than 2, 4, and 6 AU, and the number that evolved onto Earth-crossing orbits (following Horner et al. 2003).
5. Discussion
Since the orbit of 2013 AZ60 is highly eccentric and takes the object out to approximately 1950 AU, it is clear that it spends the vast majority of its orbit at a large heliocentric distance. It is quite plausible that 2013 AZ60 is a relatively recent entrant to the inner solar system. Hence, it is interesting to consider how much time, cumulative over its entire history since it was first emplaced on a planet crossing orbit, it has spent at a heliocentric distance of less than 1, 10 or 100 AU. Again, we can take advantage of the large dynamical dataset available to us from our integrations to gauge the amount of time the object will have spent within these distances. Clearly, this is only an estimate (and implicitly assumes that, before its injection to a planet-crossing orbit, the object was well beyond the 100 AU boundary – i.e. that it was injected from the inner or outer Oort cloud, rather than the trans-Neptunian region). Given this implicit assumption, we find that, on average, clones of 2013 AZ60 spend just 6.68 yr within 1 AU of the Sun, 4620 yr within 10 AU of the Sun, and 273 000 yr within 100 AU of the Sun. The time spent within 10 and 100 AU is strongly biased by a few particularly long-lived clones, especially those that are captured onto Centaur-like orbits. We note that more than two-thirds of the clones (64 904 objects) spent less than a thousand years within 100 AU of the Sun, and 37493 (41.1%) spent less than one hundred years within 100 AU. Taken into considerations, our dynamical results suggest that 2013 AZ60 has only recently been captured to its current planet-crossing orbit, and that it is quite likely that it is a relatively pristine object. Indeed, it seems highly probable that the surface of 2013 AZ60 has experienced only minimal outgassing and loss of volatiles since being captured to a planet crossing orbit, and so it represents a particularly interesting object to target with further observations as it pulls away from the Sun following its recent perihelion passage.
Outer solar system objects can also be characterised in a way recently put forward by Lacerda et al. (2014), using their visual range colours and albedos. In this frame, Centaurs and TNOs typically form two clusters, a dark-neutral and a bright-red one (see Fig. 2 in Lacerda et al. 2014). In this scheme, 2013 AZ60 is located at the dark (very low albedo) edge of the dark-neutral cluster, see Fig. 7. 2013 AZ60 is even darker than the object 2002 GZ32, the object with the lowest albedo in the sample of Duffard et al. (2014). Objects with characteristics similar to our target belong rather to “dead comets” or Jupiter-family comets, which are the end states of Centaurs and Oort cloud comets (Fig. 4 in Lacerda et al. 2014); in this sense, 2013 AZ60 is more similar to objects in the inner solar system than to those in the trans-Neptunian population. We also checked the distribution of the slope parameters of various Centaurs based on Fornasier et al. (2009). Although in that work, a correlation between the slope parameters and orbital eccentricity was suspected (the higher the eccentricity, the redder the object), the high eccentricity of 2013 AZ60 does not fit in this model since it has a clearly lower slope parameter than the mean of that sample of Centaurs.
 |
Fig. 7 Slope parameter vs. albedo relations for 111 TNOs, including 2013 AZ60 and 2012 DR30. Data (except for these two latter objects) have been taken from Lacerda et al. (2014). The blue and red dots indicate the two major groups identified by Lacerda et al. (2014), black points represent ambiguous objects (due to their large respective uncertainties), while green and yellow dots show the large bodies and Haumea-type surfaces, respectively. The isolated purple square shows the place of 2013 AZ60 at the very left side of the diagram. The other purple square indicates 2012 DR30, just in between of the dark neutral (blue) and bright red (red) object groups. |
While the dynamical analysis indicates that 2013 AZ60 has recently been pulled from the Oort cloud, there is a much higher likelihood for this object that it has spent a considerable time in the inner solar system than 2012 DR30, for instance, which might just be in a transitional phase between the two main albedo-colour clusters (Kiss et al. 2013).
As can be seen in the elegant Java visualisation of the object’s orbit at http://ssd.jpl.nasa.gov/sbdb.cgi? sstr=2013%20AZ60;orb=1;cov=0;log=0;cad=0#orb
Acknowledgments
We thank for the comments and the thoughtful review of the anonymous referee. The work of A.P., Cs.K. and R.Sz. has been supported by the grant LP2012-31 of the Hungarian Academy of Sciences as well as the ESA PECS grant No. 4000109997/13/NL/KML of the Hungarian Space Office and the European Space Agency, and the K-104607 and K-109276 grants of the Hungarian Research Fund (OTKA). The work of Gy.M.Sz. has also been supported by the Bolyai Research Fellowship of the Hungarian Academy of Sciences. Additionally, Gy.M.Sz. and K.S. has been supported by ESA PECS No. 4000110889/14/NL/NDe and the City of Szombathely under agreements No. S-11-1027 and 61.360-22/2013. K. S. has also been supported by the “Lendület” 2009 program of the Hungarian Academy of Sciences. J.L. acknowledge support from the project AYA2012-39115-C03-03 (MINECO, Spanish Ministry of Economy and Competitiveness). Part of this work was supported by the German DLR project number 50 OR 1108. Based on observations made with the Gran Telescopio Canarias (GTC), instaled in the Spanish Observatorio del Roque de los Muchachos (ORM) of the Instituto de Astrofísica de Canarias (IAC), in the island of La Palma, the William Herschel telescopes (WHT) operated in the ORM by the Isaac Newton Group and on observations made with the IAC-80 telescope operated on the island of Tenerife by the IAC in the Spanish Observatorio del Teide. WHT/LIRIS observations were carried out under the proposal SW2013a15.
References
- Balog, Z., Müller, T., Nielbock, M., et al. 2014, Exp. Astron., 37, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campins, H., & Fernández, Y. 2000, Earth, Moon, Planets, 89, 117 [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., & Asplund, M. 2012, ApJ, 761, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Cepa, J. 2010, Highlights of Spanish Astrophysics V., Astrophys. Space Sci. Proc., 15 [Google Scholar]
- Cepa, J., Aguiar, M., Escalera, V. G., et al. 2000, Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, Proc. SPIE, 4008, 623 [Google Scholar]
- Chambers, J. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Davidsson, B. J. R., Gutiérrez, P. J., Groussin, O., et al. 2013, Icarus, 224, 154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duffard, R., Pinilla-Alonso, N., Santos-Sanz, P., et al. 2014, A&A, 564, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, M., Levison, H., & Dones, L., 2004, Dynamical evolution of ecliptic comets in Comets II, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press) [Google Scholar]
- Fornasier, S., Barucci, M. A., de Bergh, C., et al. 2009, A&A, 508, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gladman, B., Marsden, B. G., & Vanlaerhoven, C. 2008, The Solar System Beyond Neptune, 43 [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, 0709 [Google Scholar]
- Harris, A. W. 1998, Icarus, 131, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hodgkin, S. T., Irwin, M. J., Hewett, P. C., & Warren, S. J. 2009, MNRAS, 394, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, J., & Lykawka, P. S. 2010, MNRAS, 405, 49 [NASA ADS] [Google Scholar]
- Horner, J., Evans, N. W., Bailey, M. E., & Asher, D. J. 2003, MNRAS, 343, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, J., Evans, N. W., & Bailey, M. E. 2004a, MNRAS, 354, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, J., Evans, N. W., & Bailey, M. E. 2004b, MNRAS, 355, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, J., Lykawka, P. S., Bannister, M. T., & Francis, P. 2012, MNRAS, 422, 2145 [NASA ADS] [CrossRef] [Google Scholar]
- Jester, S., Schneider, D. P., Richards, G. T., et al. 2005, AJ, 130, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C. 2002, AJ, 123, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C. 2005, AJ, 129, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Julian, W. H., Samarasinha, N. H., & Belton, M. J. S. 2000, Icarus, 144, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Kiss, Cs., Szabó, G., Horner, J., et al. 2013, A&A, 555, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiss, Cs., Müller, T. G., Vilenius, E., et al. 2014, Exp. Astron., 37, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P., Fornasier, S., Lellouch, E., et al. 2014, ApJ, 793, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Lebofsky, L. A., Sykes, M. V., Tedesco, E. F., et al. 1986, Icarus, 68, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Lellouch, E., Santos-Sanz, P., Lacerda, P., et al. 2013, A&A, 557, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mommert, M., Harris, A. W., Kiss, C., et al. 2012, A&A, 541, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., & Lagerros, J. S. V. 1998, A&A, 338, 340 [NASA ADS] [Google Scholar]
- Müller, T. G., & Lagerros, J. S. V. 2002, A&A, 381, 324 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., Lellouch, E., Böhnhardt, H., et al. 2009, Earth, Moon, Planets, 105, 209 [Google Scholar]
- Müller, T. G., Lellouch, E., Stansberry, J., et al. 2010, A&A, 518, A146 [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Pál, A. 2012, MNRAS, 421, 1825 [NASA ADS] [CrossRef] [Google Scholar]
- Pál, A., Kiss, C., Müller, T. G., et al. 2012, A&A, 541, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, A2 [Google Scholar]
- Ramírez, I., Michel, R., Sefako, R., et al. 2012, ApJ, 752, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Santos-Sanz, P., Lellouch, E., Fornasier, S., et al. 2012, A&A, 541, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sparke, L. S., & Gallagher, J. S. 2007, Galaxies in the Universe (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Vilenius, E., Kiss, C., Mommert, M., et al. 2012, A&A, 541, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Summary of Herschel observations of 2013 AZ60, obtained in the DDT program DDT_ckiss_3.
Best-fit orbital solution (semimajor axis a, perihelion distance q, eccentricity e, inclination i, longitude of ascending node Ω, argument of perihelion ω, mean anomaly M, and perihelion date Tperi), and associated uncertainties, for 2013 AZ60, taken3 from the Minor Planet Center on 2015 March 15.
Number of the 91 125 clones of 2013 AZ60 simulated in this work that evolved to orbits with perihelion distances smaller than 2, 4, and 6 AU, and the number that evolved onto Earth-crossing orbits (following Horner et al. 2003).
All Figures
 |
Fig. 1 Image stamps showing the Herschel/PACS maps of 2013 AZ60 in the 70 μm (blue), 100 μm (green), and 160 μm (red) channels. Each stamp covers an area of 64′′×64′′, while the tick marks on the axes show the relative positions in pixels. The effective beam size (i.e. the circle with a diameter corresponding to the full width at half maximum) is also displayed in the lower left corners of the stamps. The upper panels show the stamps directly combined from the individual frames where the lower stamps are obtained using the double-differential method. Because of the failure of the red channel half and the astrometric uncertainties, the second visit is nearly unusable in red, hence double-differential maps cannot be created. |
| In the text | |
 |
Fig. 2 Folded optical light curves of 2013 AZ60 using photometric data taken on six subsequent nights of 2013 November 4–9. Note that the folding frequency is related to the preferred double-peaked solution, n = (5.11/2) d-1. See text for further details. |
| In the text | |
 |
Fig. 3 Reflectance spectrum of 2013 AZ60, taken with the OSIRIS spectrometer on the GTC in January, 2014. This spectrum is normalised to unity at λ = 5500 Å. |
| In the text | |
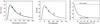 |
Fig. 4 Spectral energy distribution of 2013 AZ60 in the far-infrared region, based on Herschel/PACS measurements. Left panel: far-infrared measurements superimposed are the best-fit NEATM curves with their respective uncertainty. Middle panel: TPM model curve for thermal inertia of 100 Jm-2 K-1 s− 1/2, rotation period of 9.39 h and equator-on geometry. Right panel: the value of χ2 as the function of thermal inertia for pole-on and equator-on geometries. See text for further details. |
| In the text | |
 |
Fig. 5 Decay of our population of 91 125 clones of 2013 AZ60 as a function of the time elapsed in our integrations. The plots on the right show the same data as those on the left, but are plotted on a log/log scale. The upper panels show the decay of the population over the first billion years of the four billion year integrations, whilst the lower panels show the decay over the first million years. |
| In the text | |
 |
Fig. 6 Mean (upper) and median (lower) lifetimes of 2013 AZ60 as a function of the initial perihelion distance, q, and eccentricity, e, of the orbit tested. The location of the best-fit orbital solution for 2013 AZ60, as detailed in Table 4, is shown by the hollow square at the centre of the figure, with the ±1σ uncertainties on the perihelion distance and eccentricity denoted by the solid black lines that radiate from that box. Each coloured square in the figures shows the mean (or median) lifetime of the 45 individual runs carried out at that particular a−e location. Each of those 45 runs tested a different orbital inclination for 2013 AZ60, evenly distributed across the ± 3σ uncertainty range on the best-fit orbital solution. As was the case with the high-eccentricity Centaur 2012 DR30 (Kiss et al. 2013), the stability of the orbit of 2013 AZ60 does not vary significantly across the range of perihelion distance and eccentricities tested in this work – a reflection of the relatively high precision with which the object’s orbit is known. |
| In the text | |
 |
Fig. 7 Slope parameter vs. albedo relations for 111 TNOs, including 2013 AZ60 and 2012 DR30. Data (except for these two latter objects) have been taken from Lacerda et al. (2014). The blue and red dots indicate the two major groups identified by Lacerda et al. (2014), black points represent ambiguous objects (due to their large respective uncertainties), while green and yellow dots show the large bodies and Haumea-type surfaces, respectively. The isolated purple square shows the place of 2013 AZ60 at the very left side of the diagram. The other purple square indicates 2012 DR30, just in between of the dark neutral (blue) and bright red (red) object groups. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


