| Issue |
A&A
Volume 583, November 2015
Rosetta mission results pre-perihelion
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526099 | |
| Published online | 30 October 2015 | |
Permittivity measurements of porous matter in support of investigations of the surface and interior of 67P/Churyumov-Gerasimenko
1 University of Bern, Physics Institute, Sidlerstrasse 5, 3012 Bern, Switzerland
e-mail: yann.brouet@space.unibe.ch
2 UPMC (Sorbonne Univ.); UVSQ (UPSay); CNRS/INSU; LATMOS-IPSL, BC 102, 4 place Jussieu, 75005 Paris, France
3 Aix–Marseille Université, CNRS, Centrale Marseille, Institut Fresnel, UMR 7249, Campus universitaire de Saint-Jérôme, avenue Escadrille-Normandie-Niemen, 13013 Marseille, France
4 Observatoire de Paris, LERMA, 61 avenue de l’Observatoire, 75014 Paris, France
5 University of Southern California, Viterbi School of Engineering, 1042 Downey Way, Los Angeles, CA 90089-1112, USA
6 UJF-Grenoble 1/CNRS-INSU, IPAG, UMR 5274, 38041 Grenoble, France
Received: 15 March 2015
Accepted: 15 July 2015
Aims. Permittivity measurements on porous samples of volcanic origin have been performed in the 0.05–190 GHz range under laboratory conditions in support of the Rosetta mission to comet 67P/Churyumov–Gerasimenko, specifically with the MIRO radiometric experiment and CONSERT radar experiment.
Methods. The samples were split into several subsamples with different size ranges covering a few μm to 500 μm. Bulk densities of the subsamples were estimated to be in the 800 to 1500 kg/m3 range. The porosities were in the range of 48% to 65%. From 50 MHz to 6 GHz and at 190 GHz, permittivity has been determined with a coaxial cell and with a quasi-optical bench, respectively.
Results. Without taking into account the volume-scattering effect at 190 GHz, the real part of the permittivity, normalized by the bulk density, is in the range of 2.1 to 2.6. The results suggest that the real part of the permittivity of an ice-free dust mantle covering the nucleus is in the 1.5−2.2 range at 190 GHz. From these values, a lower limit for the absorption length for the millimeter receiver of MIRO has been estimated to be between 0.6 and 2 cm, in agreement with results obtained from MIRO in September 2014. At frequencies of interest for CONSERT experiment, the real part of the permittivity of a suspected ice-free dust mantle should be below 2.2. It may be in the range of 1.2 to 1.7 for the nucleus, in agreement with first CONSERT results, taking into account a mean temperature of 110 K and different values for the dust-to-ice volumetric ratio. Estimations of contributions of the different parameters to the permittivity variation may indicate that the porosity is the main parameter.
Key words: comets: individual: 67P/Churyumov-Gerasimenko / techniques: radar astronomy / methods: laboratory: solid state / comets: general / methods: data analysis
© ESO, 2015
1. Introduction
The European Space Agency’s Rosetta spacecraft has been orbiting the nucleus of comet 67P/Churyumov-Gerasimenko (hereafter 67P) since August 2014 and dropped the Philae lander onto its surface in November 2014, allowing it to collect data for about 63 h. Some of the numerous instruments carried by Rosetta and Philae make use of remote-sensing radar techniques in the millimeter to meter domain to constrain the properties of the subsurface and interior of 67P. The Microwave Instrument for the Rosetta Orbiter (MIRO), described by Gulkis et al. (2007), is a dual-band radiometer composed of a millimeter receiver with a center-band frequency equal to 190 GHz (i.e., wavelength, λ, equal to 1.6 mm in the vacuum) and a submillimeter receiver with a center-band frequency equal to 560 GHz (i.e., λ = 0.5 mm in the vacuum). It is dedicated to measurements of the near-surface brightness temperatures and temperature gradients in the uppermost layers of 67P. Brightness temperatures measured by a radiometer are related to the thermal and physical properties of the material via its dielectric properties, which are included in inverse models used to interpret the data (Gulkis et al. 2010, 2012, 2015). The COmet Nucleus Sounding Experiment by Radiowave Transmission (CONSERT), described by Kofman et al. (1998, 2007), is a bistatic penetrating radar for tomography of the nucleus, operating at 90 MHz (i.e., λ = 3.3 m). The optimization of the investigations depends on the three-dimensional distribution of dielectric properties, which define, first, the interaction of the radar wave with the surface and second, its propagation vector inside the nucleus (Heggy et al. 2012).
The dielectric properties of a material are represented by the complex relative permittivity ϵ (hereafter permittivity) and the loss tangent, tanδ. The real part of the permittivity ϵ′ is related to the ability of a material to store and re-radiate energy, while the imaginary part ϵ′′ describes losses in the material, so that the signal attenuation is proportional to ϵ′′. The loss tangent is defined as the ratio of the imaginary part to the real part of the permittivity and is needed in the calculation of the absorption coefficient of a radio-wave that propagates in a lossy medium. These properties vary with frequency, temperature conditions, and material properties, specifically total porosity (hereafter porosity, i.e., the percentage of the bulk volume occupied by empty space) and composition (e.g., Heggy et al. 2012; Ulaby & Long 2014).
The composition of comets has been estimated from a few flyby missions and from numerous spectroscopic and polarimetric remote observations of their comae. Nuclei are built up of ices and refractory species, the dominant volatile species being H2O and the refractory species seeming to be mostly composed of silicates, organics, and amorphous carbon (see, e.g., Cochran et al. 2015, for a review). Early results from experiments operating onboard Rosetta provide evidence for carbon-bearing compounds on the nucleus surface, most likely opaque minerals associated with non-volatile organic macromolecular materials (Capaccioni et al. 2015).
The bulk density of cometary nuclei, initially indirectly estimated by modeling the non-gravitational forces induced by the sublimation of ices, had suggested low values, in the 100 to 1000 kg/m3 (e.g., Davidsson & Gutiérrez 2005). Comparisons between such values for specific comets and values derived from other indirect methods (e.g., for 9P/Tempel 1, Thomas et al. 2007) confirmed these estimations and strongly suggested that cometary nuclei have a low density and thus a high porosity (e.g., Levasseur-Regourd et al. 2009). The value derived from non-gravitational force modeling for 67P of about 370 kg/m3 (Lamy et al. 2007) agrees fairly well with the value of 470 ± 45 kg/m3 derived from Rosetta data by Sierks et al. (2015). These values imply a porosity in the 70 to 80% range. In addition, dust particles in cometary comae have also been suggested to be porous and to consist of easily fragmenting aggregates (Levasseur-Regourd et al. 2007). From local observations by the Giotto spacecraft at 1P/Halley, the dust bulk density was estimated to be about 100 kg/m3 (Fulle et al. 2000). Polarimetric studies of light scattered by dust in the comae of 1P/Halley and C/1995 O1 Hale-Bopp, combined with numerical simulations, suggest that a significant proportion of dust particles consists of fluffy aggregates (e.g., Lasue et al. 2009). Early results from experiments onboard Rosetta provide evidence for fluffy and fragile particles in the inner coma of 67P (Schulz et al. 2015); the presence of large grains and clumps has also been reported (Rotundi et al. 2015).
Together with the suspected presence of an ice-free dust mantle in many areas of the nucleus (Thomas et al. 2015), the porosity is a key parameter for the interpretation of MIRO and CONSERT data onboard the Rosetta spacecraft. We have developed a program of permittivity measurements on porous granular samples of volcanic origin over a novel frequency range of more than three orders of magnitude (between 50 MHz and 190 GHz) under ambient laboratory conditions. The natural porosity of samples of volcanic origin has been considered as a first approximation for the high porosity of cometary material, making them suitable, from the point of view of porosity, as cometary dust analogs.
Previous measurements on Etna volcanic ash and on JSC Mars-1 Martian soil simulant have been reported in Brouet et al. (2014). These samples were split into four and three subsamples, respectively, whose grain size was in the range of a few μm to 500 μm. Different bulk densities, ranging from 800 kg/m3 to 1300 kg/m3, have been obtained during the measurements. Permittivity measurements were performed at 50, 100 and 500 MHz with an open-coaxial probe, at 2.45, 5.6, 8, and 12 GHz with resonant cavities and at 190 GHz with a quasi-optical bench mounted in transmission. In the current paper we describe in the next section the properties of a newly studied sample: the JSC-1A Lunar regolith simulant. New measurements, from 50 MHz to 6 GHz, have been obtained on this sample, with different grain size ranges and bulk densities, and also on the Etna subsamples. We present the coaxial cell used to perform these measurements. We also briefly summarize the method with which new measurements at 190 GHz have been obtained on the JSC-1A simulant (see also Brouet et al. 2014). Finally, the results are analyzed and discussed not only in terms of frequency dependence of the permittivity, but also in terms of bulk density and porosity dependence of the permittivity at frequencies relevant to the MIRO and CONSERT experiments.
2. Sample characteristics and preparation
Our previous permittivity measurements have been performed on four subsamples of Etna volcanic ash, numbered from 1 to 4, and three subsamples of JSC Mars-1 Martian soil simulant, numbered from 5 to 7 (Brouet et al. 2014). We have also had access to five hundred grams of the NASA JSC-1A Lunar regolith simulant, the chemical composition of which simulates the low-titanium mare lunar regolith. This sample also corresponds to volcanic ashes of basaltic composition (Hill et al. 2007), collected on the Merriam Crater’s south flank in Arizona (USA). A main interest of JSC-1A is that it has already been extensively documented through a variety of approaches. It mostly consists of dark and basaltic porous grains and tiny crystallized grains. It is mostly composed of crystalline silicate phases of plagioclase, pyroxene, and olivine. Its iron oxide content is estimated to be about 11%.
For the purpose of this analysis, six more subsamples were prepared after sieving the new sample, with sizes below 50 μm (#8), between 50 and 125 μm (#9), between 125 and 160 μm (#10), between 160 and 250 μm (#11), between 250 and 355 μm (#12) and finally between 355 and 500 μm (#13), as illustrated in Fig. 1. The figure also shows the very irregular shape of the tiny crystals present in the lowest sized subsample and the high intrinsic porosity of the larger grains, containing vesicles formed during the outgassing and cooling of the initial magma. The packing effect, which depends on grain shape, and the intrinsic porosity of the grains may vary between the different subsamples, resulting in a change of the bulk density (linked to the porosity). The mean bulk density of each subsample was determined during the permittivity measurements to be between 50 MHz and 6 GHz (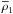 ), and at 190 GHz (
), and at 190 GHz (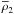 ), as presented in Sects. 3.1 and 3.2.
), as presented in Sects. 3.1 and 3.2.
 |
Fig. 1 Scanning electron microscope images of Etna subsamples (#1, #2, #3, and #4) and JSC-1A Lunar regolith simulant subsamples (#8, #9, #10, #11, #12, and #13), with sizes of about a few to 500 μm. Different scales are used to show as best possible both the grain size distribution and the high intrinsic porosity of individual grains. The white line in the bottom right corner of each image provides the scale, equal to 100 μm (#8), 300 μm (#1, #2, #9, and #10), and 1 mm (#3, #4, #11, #12, and #13). |
To study the dependence of the permittivity on grain size, a dimensional analysis by optical microscopy was performed on a given number of grains N (about 100) to determine a mean grain size for each subsample (Brouet 2013). The characteristics of the subsamples whose new measurements are presented here are summarized in Table 1. These are the four subsamples from Etna and the six subsamples of JSC-1A simulant. The mean bulk densities are higher for the measurements between 50 MHz and 6 GHz than for the measurements at 190 GHz, most likely because of a stronger compaction of the porous grains in the sample holders dedicated to permittivity measurements between 50 MHz and 6 GHz, as presented in Sect. 3.1. However, it is of interest to point out that the variation of the bulk density from one subsample to the next one obtained for the measurements between 50 and 6 GHz agrees with the one obtained for the measurements at 190 GHz, meaning that the change in bulk density measured might be also consistent with a change of the porosity from one sample to the next one of the order of a few percent. Alshibli & Hasan (2009) have estimated the mean particle density of the JSC-1A simulant to be equal to 2920 kg/m3. Knowing the relation between the bulk density 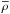 , the mean particle density
, the mean particle density 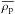 , and the porosity Φ (with
, and the porosity Φ (with 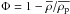 ), porosities of all JSC-1A subsamples are estimated to be in the range of 48 to 58% during the measurements between 50 MHz and 6 GHz and in the range of 52 to 62% during the measurements at 190 GHz. Assuming that the mean particle density of the JSC-1A simulant is also relevant for the Etna volcanic ash, which is also composed of basaltic porous grains, porosities of all Etna subsamples were estimated to be in the range of 52 to 59% during the measurements between 50 MHz and 6 GHz and in the range of 58 to 63% during the measurements at 190 GHz. The values of mean bulk densities are higher and the porosities of the current samples are lower than those expected for the nucleus of the comet 67P, but they are, at least, representative of a material built up of porous solid particles.
), porosities of all JSC-1A subsamples are estimated to be in the range of 48 to 58% during the measurements between 50 MHz and 6 GHz and in the range of 52 to 62% during the measurements at 190 GHz. Assuming that the mean particle density of the JSC-1A simulant is also relevant for the Etna volcanic ash, which is also composed of basaltic porous grains, porosities of all Etna subsamples were estimated to be in the range of 52 to 59% during the measurements between 50 MHz and 6 GHz and in the range of 58 to 63% during the measurements at 190 GHz. The values of mean bulk densities are higher and the porosities of the current samples are lower than those expected for the nucleus of the comet 67P, but they are, at least, representative of a material built up of porous solid particles.
Main characteristics of the four subsamples from Etna and of the six subsamples from JSC-1A simulant.
Microwave interacts with water molecules, leading to an increase of the permittivity of the sample with the increasing moisture (e.g., Sabouroux & Ba 2011). To remove some possible adsorbed moisture, a moisture analyzer was used to dry all the samples and to estimate their volumetric moisture content (found to be in the range of 0.1% to 0.6%) before any measurements between 50 MHz and 6 GHz. The subsamples were also dried in an oven for 24h at 373 K before any measurements at 190 GHz.
3. Instrumentation
Measurements of the real part of the permittivity between 50 MHz and 6 GHz on Etna and JSC-1A subsamples were performed in 2014 at Institut Fresnel (Marseille, France). Measurements of ϵ′′ for low-loss materials (i.e., tanδ much lower than 1), such as the samples presented in the current paper, are challenging between 50 MHz and 6 GHz because of technical reasons (Heggy et al. 2012). Therefore, even though the imaginary part of the permittivity was determined over this frequency band for all subsamples, it is not presented in this paper because specific improvements of the setup, currently in progress, are needed to make the values more accurate. There are no consequences for the purpose of the current paper (see Sect. 4.3.5). Permittivity measurements at 190 GHz on JSC-1A subsamples has been performed in 2013 (Brouet 2013) at the LERMA laboratory (Observatoire de Paris, France). All the measurements were performed under ambient laboratory conditions, with a temperature in the 293–300 K range and a relative humidity in the 37–48% range during measurements at 190 GHz and in the 50–60% range during measurements at lower frequencies. Temperature and relative humidity variations (i.e., air moisture) are not expected to alter the measurements, given the very little variation of the real part of the permittivity of the air inside the experiments (about 10-6 to 5 × 10-5, following Fawley & Ferrie 2012).
3.1. Measurements with a conical coaxial cell between 50 MHz and 6 GHz
Between 50 MHz and 6 GHz, values of ϵ′ were determined with a coaxial cell connected to a vector network analyzer (VNA) and equipped with a sample holder that can contain any kind of non-gaseous material: solids, semi-solids (powdered materials), and liquids. The cell is segmented into three parts (cf. Fig. 2): the central containment area of material sample, the transition lines, and the connectors (precision connectors of 7 mm outer diameter, i.e., PC7). The outer diameter of the containment area is equal to 13 mm, allowing a larger volume of material for the measurements than the work area of a standard straight coaxial line. The containment area is delimited by two dielectric walls in PolyTetraFluoroEthylene (PTFE). The conical geometry of the transition lines was designed to link the work area to the PC7. With this original design, handling, containment, and positioning of the sample are improved compared to the straight coaxial line, and thus uncertainties related to the material sample are reduced. For all measurements, the mass of the holder filled with the sample was determined to estimate the bulk density of the sample, knowing the filled volume (cf. Table 1). Two sample holders, with a useful volume equal to about 0.6 cm3 and 0.3 cm3, were used (the second one was only dedicated to the measurements on Etna subsample #1 because of the small available mass).
The complex scattering parameters S11 and S21 of the cell filled with the sample were measured with a calibrated VNA. A first step of de-embedding allows determining the sample scattering parameters, which takes into account the electrical distances, d1 and d2, the thickness of the sample L (see Fig. 2), the attenuation coefficient of the coaxial line, and the wavenumber in vacuum (Georget et al. 2014). Then the Nicolson-Ross procedure (see Nicolson & Ross 1970; De Paula & Barroso 2010) was applied to the sample S-matrix to determine ϵ′. The scattering parameters were measured (again, from 50 MHz to 6 GHz) over a sweeping of more than 200 frequencies.
More details on the experimental setups and procedure of measurements are presented in Georget et al. (2014).
 |
Fig. 2 Image a) and schematic b) of the conical coaxial cell used to perform the permittivity measurements between 50 MHz and 6 GHz. |
Permittivity measurements at 190 GHz (and at 180 GHz for JSC-1A subsample #13).
 |
Fig. 3 Real part of the permittivity normalized by the bulk density versus frequency for subsamples #1 a), 2 b), 3 c), and 4 d) from Etna. The measurements made between 50 MHz and 6 GHz are shown by filled circles, and those at 190 GHz are shown by filled triangles. |
 |
Fig. 4 Real part of the permittivity normalized by the bulk density versus frequency for subsamples #8 a), 9 b), 10 c), 11 d), 12 e), and 13 f) from JSC-1A Lunar regolith simulant. The measurements made between 50 MHz and 6 GHz are shown by filled circles, and those at 190 GHz are shown by filled triangles. |
3.2. Measurements with a quasi-optical bench at 190 GHz
At 190 GHz, permittivity measurements on JSC-1A subsamples were performed with a quasi-optical bench mounted in transmission, with two corrugated horns as emitting and receiving antennas, connected to a VNA working in the millimeter domain. These measurements were performed with the same setup and procedure used to perform permittivity measurements at 190 GHz on the three subsamples of JSC Mars-1 simulant and the four subsamples of Etna volcanic ash (Brouet et al. 2014). The transmission coefficient of the millimeter signal generated by the VNA was measured in phase and amplitude. By placing the sample at a Gaussian beam waist within the system, phase rotation and amplitude damping of the signal within a narrow frequency range allow one to determine ϵ′ and ϵ′′, respectively. Bulk densities of all JSC-1A subsamples were determined during the measurements (cf. Table 1).
3.3. Error bar estimation
The data obtained in the frequency band from 50 MHz to 6 GHz presented in Sect. 3.1 correspond to the mean of three, four, or five individual measurements for which the sample holder was filled without any handling or mechanical compaction. The absolute errors on each measurement on a given subsample were estimated to be the sum of standard deviation and experimental errors. The standard deviation of a measurement on a given sample was estimated to be below 10% for ϵ′. Experimental error originates from the measurement of magnitude and phase of the scattering parameters, line losses, connector mismatching, irregular sample surface, air gaps between the sample and the coaxial line, eventually by determining distances between the reference planes and the sample, and was estimated to be about or less than 10% (Georget et al. 2014).
The data obtained at 190 GHz presented in Sect. 3.2 correspond to the mean of five individual measurements for which the sample holder was filled without any handling or mechanical compaction. The absolute errors on each measurement on a given subsample, taking into account the standard deviation (cf. Table 2) and the experimental errors, were estimated to be below 10% for ϵ′ and below 2% for ϵ′′. Experimental errors on the determination of ϵ′ and ϵ′′ are expected to be below 1% using the method of error propagation and taking into account the errors on the thickness measurements of samples, the signal phase measurements by the VNA, and the attenuation measurement.
4. Results and discussion
Figures 3a−d show the real part of the permittivity, normalized by the bulk density, of the Etna subsamples #1, 2, 3, and 4 as a function of the measurement frequency on a logarithmic scale between 50 MHz and 190 GHz. Figures 4a−f show the real part of the permittivity, normalized by the bulk density, of the JSC-1A subsamples #8, 9, 10, 11, 12, and 13 in the same format. Measurements of the real and imaginary parts of the permittivity performed on JSC-1A subsamples with the quasi-optical bench at 180 and 190 GHz are summarized in Table 2.
The results at 190 GHz can also be expressed in terms of the absorption length La (cf. Table 2), that is, the distance over which a collimated power flux decreases by a factor e. This parameter characterizes how deep an electromagnetic wave can penetrate a lossy medium. For low-loss materials, La/λ can be approximated as (Campbell & Ulrichs 1969) 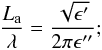 (1)showing that the smaller the dielectric losses, the greater the absorption length.
(1)showing that the smaller the dielectric losses, the greater the absorption length.
4.1. Frequency dependence of permittivity
For all Etna subsamples, the normalized real part of the permittivity over the frequency range remains within the 2.1−2.6 range, except for subsamples #3 and 4, for which the values are equal to about 2.7 and 3.3, respectively, at 190 GHz. The normalized imaginary part measured at 190 GHz remains below 0.10, except for subsamples #3 and 4, for which the values are equal to about 0.12 and 0.25. These discrepancies for results regarding subsamples #3 and 4 are discussed in Sect. 4.2.
The normalized real part of the permittivity of JSC-1A subsamples over the frequency range is in the range of 2.1 to 2.5 except for subsamples #12 and 13 at 190 GHz, while the normalized imaginary part measured at 190 GHz remains below 0.06 for all subsamples, except for subsamples #11, 12, and 13. These discrepancies for results regarding the subsamples #11, 12 and 13 are discussed in Sect. 4.2.
To summarize, the results appear to be consistent over a frequency range of more than three orders of magnitude although two different instruments were used. Not taking into account the highest sized subsamples affected by volume scattering (only at 190 GHz, see Sect. 4.2), slight variations of the real part normalized by the bulk density of the permittivity are observed over the frequency range for all subsamples. This behavior of ϵ′ is expected for this frequency range (e.g., Campbell & Ulrichs 1969; Ulaby & Long 2014).
4.2. Volume-scattering effect at 190 GHz
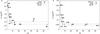 |
Fig. 5 Real part a) and imaginary part b) of the permittivity ϵ normalized by the bulk density (g/cm3) as a function of the ratio of the wavelength (corresponding to the frequency of 190 GHz) to the mean grain φ size for Etna and JSC-1A subsamples. The solid lines represent the exponential regressions of the measured points, expressed as g(λ/φ) = a × e(λ/φ) × b + c. Panel a): a equal to 4.13 ± 1.72 and 3.75 ± 0.61; b equal to −0.51 ± 0.13 and −0.48 ± 0.05; c equal to 2.40 ± 0.05 and 2.28 ± 0.02, for the Etna and the JSC-1A subsamples, respectively. Panel b): a equal to 0.80 ± 0.34 and 0.59 ± 0.14; b equal to −0.45 ± 0.13 and −0.59 ± 0.08; c equal to 0.06 ± 0.01 and 0.050 ± 0.003, respectively. |
At 190 GHz the results present a systematic increase of the permittivity when the mean grain size becomes greater than 200 μm (cf. Table 2). When the grain size becomes comparable to the wavelength, volume scattering may become significant enough to control the measurement of permittivity values of JSC-1A subsamples #11, #12, and #13. Volume-scattering effects on permittivity measurements at 190 GHz have previously been observed for the Etna subsamples during measurements with the same instrument and procedure. Figure 5 shows the variation of the real and imaginary parts of the permittivity normalized by the bulk density (ϵ′/ρ and ϵ′′/ρ) as a function of the ratio of the wavelength to the mean grain size (λ/φ) for Etna and JSC-1A subsamples. The variation of ϵ′/ρ and ϵ′′/ρ ratios with the decreasing λ/φ ratio suggests an exponential increase when λ/φ becomes smaller than about 8. No such effect is obtained for the measurements at lower frequencies for which the wavelength is much longer than the grain size for any subsamples.
4.3. Discussion
4.3.1. Comparison with other measurements
Although our samples are subdivided into subsamples with different grain size distributions, the results may be compared to previous measurements on volcanic ashes and on powdered samples from crushed rocks.
For comparisons with samples formed with similar processes, it is interesting to mention results of permittivity measurements between 4 and 19 GHz obtained by Adams et al. (1996) on volcanic ashes of basaltic composition: the real part of the permittivity is in the range of 3.45 to 3.70. Knowing that these results have been obtained with samples with a lower porosity of about 40%, they are consistent with our measurements obtained between 1 and 6 GHz for ϵ′ for all subsamples. Moreover, our measurements at frequencies between 1 and 6 GHz of the subsamples from JSC-1A simulant agree with those performed at 31 GHz by Calla & Rathore (2012) on the initial JSC-1A simulant. They obtained a real part of the permittivity equal to 3.61 ± 0.05 and an imaginary part equal to 0.11 ± 0.01, at 300 K for a bulk density equal to 1500 kg/m3, resulting in a normalized real part equal to about 2.40 and a normalized imaginary part equal to about 0.07. In our previous work, permittivity measurements on the same Etna subsamples were made with an open coaxial cell at 50, 100, and 500 MHz and resonant cavities at 2.45, 5.6, 8, and 12 GHz. Values of the real part of the permittivity over the frequency range are also consistent with the current work for Etna subsamples #1, 2, and 3.
Campbell & Ulrichs (1969) have measured dielectric properties of powdered basalts with a grain size equal to about 37 μm at 450 MHz and 35 GHz on samples obtained from crushed rocks. Their results have been obtained at 450 MHz for ϵ′ and with a porosity of 40%. These results are consistent with the current measurements for ϵ′, which do not show a significant dependence on the frequency and particle size distribution either, as noted by Campbell & Ulrichs (1969). In addition, Heggy et al. (2012) measured the dielectric properties of three ordinary chondrites and of a mesosiderite reduced in fine powder. For compacted samples with a porosity of about 30%, they obtained values of the real part of the permittivity greater than 4.5 between 5 and 100 MHz at room temperature. These values are consistent with the current results on Etna and JSC-1A subsamples for which measurements have been obtained with non-compacted subsamples, resulting in lower values of ϵ′.
4.3.2. Bulk density dependence of the permittivity
The denser the medium, the greater the energy storage and the dielectric losses, and hence the greater the real and imaginary parts of the permittivity (see, e.g., Ulaby & Long 2014). Figure 6 shows the real part of the permittivity obtained from measurements on the Etna subsamples and on the JSC-1A subsamples at 80 MHz, 110 MHz, and 190 GHz as a function of the bulk density, without taking into account the results affected by the volume scattering. The results suggest, as a first approximation, that ϵ′ decreases quasi-linearly with the decreasing bulk density. This result agrees with the bulk density dependence derived from mixing formulae, which predict a quasi-linear increase of the permittivity with the increasing bulk density for this range of bulk densities (Campbell & Ulrichs 1969).
 |
Fig. 6 Real part of the permittivity ϵ′ versus bulk density ρ (kg/m3). Results obtained for the Etna and JSC-1A subsamples are presented at 80 MHz, 110 MHz, and 190 GHz. The solid line and the two dotted lines represent the linear regressions (written as A × ρ + 1) of the measured points at 80 MHz, 110 MHz, and 190 GHz, respectively. At 80 MHz and 110 MHz, the slopes are equal to (1.59 ± 0.02) × 10-3 (kg/m3)-1 and (1.60 ± 0.02) × 10-3 (kg/m3)-1, respectively. At 190 GHz, the slope is equal to (1.53 ± 0.02) × 10-3 (kg/m3)-1. |
4.3.3. Temperature dependence of the permittivity
Our measurements were made at room temperature between 293 K and 300 K. Surface and subsurface temperatures of 67P, as obtained from Rosetta during the second half of 2014, were lower. From the VIRTIS instrument, Capaccioni et al. (2015) determined surface temperatures of the nucleus to be in the range of 180 to 230 K during daytime. From MIRO, Gulkis et al. (2015) provided values for subsurface temperatures in the range from 40 to 190 K, in good agreement with theoretical near-surface temperatures predicted before the Rosetta rendezvous (e.g., Prialnik et al. 2004; De Sanctis et al. 2005). These temperature variations would lead to a variation of the permittivity.
A linear temperature dependence of the real and imaginary parts of the permittivity is suggested by the measurements of Calla & Rathore (2012) on the initial JSC-1A simulant performed at 1.7, 2.6, 6.6, and 31.6 GHz with a weaker linear temperature dependence at higher frequencies. For the real part, the slope varies from (2.6 ± 0.2) × 10-3 K-1 at 1.7 GHz to (4.7 ± 0.7) × 10-4 K-1 at 31.6 GHz for ϵ′. Measurements also show a small linear temperature dependence for the imaginary part with a slope equal to (8 ± 2) × 10-5 K-1 at 31.6 GHz. From 300 K, the decrease ϵ′′ with the decreasing temperature is assumed to be of approximately 10, 20, and 40% at 230, 180, and 40 K, respectively.
For the lower frequencies, Heggy et al. (2001) measured the temperature dependence of the permittivity of a powdered basalt at 2 MHz and found a decrease of about 6% from 300 K to 230 K for the real part of the permittivity and no significant change for the imaginary part. At 90 MHz, Heggy et al. (2012) measured the temperature dependence of the permittivity of a powdered LL5 chondrite from 233 K to 113 K and found a linear temperature dependence with a slope equal to about 9.7 × 10-3 K-1. The temperature dependence of the permittivity seems to be greater at lower frequencies, in agreement with the results obtained by Calla & Rathore (2012). More measurements are still needed to better estimate the temperature dependence of the imaginary part of the permittivity and also to estimate the temperature dependence of the permittivity at temperatures lower than 110 K. Both powdered basalt and LL5 chondrite are likely to be less porous than our samples, which consist of porous grains.
4.3.4. Significance for MIRO observations of the nucleus of 67P
MIRO, the passive microwave experiment onboard Rosetta, needs estimates of the permittivity of the surface and subsurface of the nucleus of comet 67P to interpret the data. The current measurements on what one might regard as appropriate analogs for the refractory component of a cometary nucleus, may provide relevant measurements for this experiment by estimating the bulk density dependence and porosity dependence of the permittivity measured at one of its frequencies of interest. Taking into account the expected mean bulk density, mean porosity, and composition of the nucleus, these results may give insights that allow us to estimate the permittivity of the first centimeters of regions that are composed of an ice-free dust mantle.
Measurements at 190 GHz on JSC-1A subsamples, without taking into account those affected by volume scattering, are consistent with results obtained from previous permittivity measurements (Brouet et al. 2014) for which a quasi-linear relation between the real part of the permittivity and the bulk density was suggested. Figure 7 shows that the porosity dependence of the permittivity, derived from the current measurements (as discussed in Sect. 2), provides a real part of the permittivity within the 1.90−2.35 range for the expected mean porosity of the nucleus ranging from 70 to 80%. Assuming that the range of the bulk density determined for the whole nucleus (i.e., 420−520 kg/m3, Sierks et al. 2015) is also representative of the bulk density of non-icy regions at the surface and that the mean particle density of an ice-free dust mantle is within the range from 2500 kg/m3 (CI chondrites, e.g., Consolmagno & Britt 1998) to 3500 kg/m3 (typical silicates), the porosity for an ice-free dust mantle is within the 75–88% range. With these values, an ice-free dust mantle with a temperature of about 300 K may have a real part of the permittivity in the range of 1.54 to 2.12. A temperature of about 300 K may be reached by the surface and the subsurface when the comet approaches perihelion in August 2015 (De Sanctis et al. 2005). These values may be also relevant for the lower temperatures, assuming that the results obtained by Calla & Rathore (2012) at 31.6 GHz are relevant at 190 GHz (see Sect. 4.3.3), with a maximum variation of 10% from 300 to 40 K, as presented in Table 3.
 |
Fig. 7 Real part of the permittivity ϵ′ versus porosity Φ (%). Results obtained for the Etna and JSC-1A subsamples are presented at 80 MHz, 110 MHz, and 190 GHz. The solid line and the two dotted lines represent the linear regressions (written as B × (Φ−100) + 1, with B being a constant) of the measured points at 80 MHz, 110 MHz, and 190 GHz, respectively. At 80 MHz and 110 MHz, the slopes are equal to (− 4.65 ± 0.04) × 10-2 per percent and (− 4.68 ± 0.06) × 10-2 per percent. At 190 GHz, the slope is equal to (− 4.49 ± 0.05) × 10-2 per percent. |
The imaginary part of the permittivity is expected to decrease quasi-linearly with decreasing bulk density (Campbell & Ulrichs 1969). The current measurements provide an upper limit equal to 0.05 at 190 GHz. Assuming that the temperature dependence of ϵ′′ at 190 GHz is similar to what is obtained at 31.6 GHz by Calla & Rathore (2012) (see Sect. 4.3.3), the upper limit of ϵ′′ is estimated to be approximately equal to 0.03 at 40 K.
The increasing iron oxide content causes ϵ′ and ϵ′′ to increase (Heggy et al. 2001, 2012). The iron oxide content of the current samples may be higher than the oxide iron content expected for cometary dust (e.g., Lisse et al. 2006; Harker et al. 2007). In this particular case, dielectric properties expected for an ice-free mantle composed of cometary dust would be, as derived from our measurements, slightly overestimated.
The lower limit of the absorption length of the millimeter signal received by MIRO, which would propagate through an ice-free dust mantle of the nucleus, may be estimated from the estimations of the real and imaginary parts mentioned above, as presented in Table 3. As the temperature dependence of the imaginary part of the permittivity is greater than the temperature dependence of ϵ′, as presented in Sect. 4.3.3, the absorption length, which is inversely proportional to ϵ′′, increases with the decreasing temperature. The lower limit of the absorption length for an ice-free dust mantle with a porosity of about 88% may be at a depth of about 0.6 cm below the surface at a temperature of about 300 K and at a depth of about 1 cm at a temperature of about 40 K. The lower limit for an ice-free dust mantle with a porosity of about 75% may be at a depth of about 0.7 cm at a temperature of about 300 K and at a depth of about 1.2 cm at a temperature of about 40 K.
These results are consistent with the interpretation of MIRO data obtained mostly from the Imhotep region (Gulkis et al. 2015), identified by Thomas et al. (2015) as a terrain dominated by a smooth surface. Indeed, the signal measured by the millimeter receiver of MIRO may have a diurnal component, which suggests a sensitivity to diurnal temperature variation, where the thermal penetration depth is of about 1−2 cm (Gulkis et al. 2015). Given that the imaginary part is over-estimated with respect to the porosity estimated for the whole nucleus, the absorption length of the millimeter signal may also propagate through more than the first centimeters of the dust mantle. This may be consistent with the seasonal component of the millimeter signal measured by MIRO below the diurnal layer.
Real part of the permittivity ϵ′, upper limit of the imaginary part ϵ′′, and lower limit of the absorption length La estimated at 190 GHz for regions of the nucleus coated by an ice-free dust mantle, as a function of the temperature from 300 to 40 K and for different porosities equal to 50, 60, 70, 80, and 90%.
4.3.5. Significance for CONSERT observations of 67P nucleus
CONSERT, the bistatic radar dedicated to the probing of nucleus at 90 MHz, needs estimates of the surface permittivity to determine the reflecting and transmitting conditions of the radar waves at the surface interface. Moreover, permittivity estimates of the interior are required to produce inversion models dedicated to the interpretation of the data (Herique et al. 1999). After the Philae landing, CONSERT data have been obtained through the first hundreds of meter of the subsurface and through the small lobe of the nucleus (Ciarletti et al. 2015; Kofman et al. 2015). Variations in ϵ′ are expected to arise from (unknown) variations in density or porosity, in composition, and in temperature.
Figure 7 shows the estimation of the porosity dependence of the real part of the permittivity determined at 80 and 110 MHz. Values of ϵ′ can be assessed at 90 MHz for an ice-free dust mantle surrounding the nucleus, as a function of the temperature from 300 to 40 K and for porosities equal to 50, 60, 70, 80, and 90%, as presented in Table 4.
Real part of the permittivity ϵ′ estimated at 90 MHz for an ice-free dust mantle surrounding the nucleus, as a function of the temperature from 300 to 40 K and for different porosities equal to 50, 60, 70, 80, and 90%.
Temperatures in the deep interior of the nucleus are expected to be of about 110 K and possibly lower (Prialnik et al. 2004; De Sanctis et al. 2005). At the frequency of interest for CONSERT, Heggy et al. (2012) measured the permittivity of mixtures composed of water ice and dust with different dust mass fractions and a porosity of about 50%. Results show, for different temperatures within the 113–233 K range, a quasi-linear increase of ϵ′ with the increasing dust mass fraction with slopes in the range of 2 × 10-3 to 6 × 10-3 per percent. From these complementary results and those presented in Fig. 7, ϵ′ in the nucleus may be assessed for low temperatures and different dust-to-ice volumetric ratios and porosities. The values of ϵ′, assuming a mean temperature of about 110 K, a dust-to-ice volumetric ratio ([D/I] V) within the 0.1−1.5 range and a porosity (Φ) range of 80 to 50% are indicated in Table 5.
Real part of the permittivity ϵ′ suggested for the nucleus of 67P, assuming a mean temperature of about 110 K, as a function of the dust-to-ice volumetric ratio ([D/I] V) within the 0.1–1.5 range and a porosity (Φ) range of 80 to 50%.
For a porosity in the range of 70 to 80% for the bulk nucleus, the real part of the permittivity is obtained to be in the range of 1.2 to 1.7. These results are consistent with the interpretation of CONSERT data obtained during the First Science Sequence of the Philae lander (Kofman et al. 2015).
The question of the internal structure and the homogeneity of the nucleus have been the subject of speculation in the past. For instance, to estimate the radar properties in preparation of the interpretation of the data expected from CONSERT experiment, Heggy et al. (2012) considered a linear decrease of the porosity profile inward from the nucleus surface, whereas Kamoun et al. (2014), who have estimated a bulk density range of approximately 600 to 1000 kg/m3 for the first meters of the subsurface of the nucleus from analysis of past ground-based radar observations of comet 67P, did not exclude the possibility that the bulk density decreases inward from the nucleus surface, which would mean an increasing porosity. The composition and the porosity of the nucleus are likely to be refined by the first determination of the bulk permittivity of the small lobe of the nucleus by CONSERT (Kofman et al. 2015). Moreover, analysis of CONSERT data at grazing angles by Ciarletti et al. (2015) suggests a possible near-surface decrease of the real part of the permittivity below the area of the Philae’s final landing site, which could be interpreted as an increase of the porosity with depth or by a drop of the dust-to-ice volumetric ratio. The data presented in Tables 4 and 5 are directly relevant to these analyses, which are based essentially on the behavior of the real part of the permittivity along the electrical path of the radar wave.
5. Conclusions
We reported new broadband measurements, under ambient laboratory conditions, of the real part of the permittivity of the JSC-1A Lunar regolith simulant and Etna volcanic ash, from 50 MHz to 6 GHz, and at 190 GHz, at which the imaginary part was also determined. The high natural porosity of these samples, composed mostly of silicate phases, makes them suitable to investigate the permittivity of very porous materials, such as the nucleus of 67P and an ice-free dust mantle that is suspected to exist in many areas of the nucleus. Without taking into account the measurements affected by the volume scattering at 190 GHz and by normalizing the results of the real part of the permittivity with the bulk density from 50 MHz to 190 GHz, the results are consistent over the entire frequency range considered, although two different instruments were used. For all subsamples, the normalized real part remains in the 2.1–2.6 range. Expressed as a function of the porosity, the results show that for a porosity range within 60 and 90%, the real part of the permittivity probably is in the range of about 1.5 to 2.9 at a temperature of 300 K at frequencies of the MIRO and CONSERT experiments onboard Rosetta.
From morphological studies of the surface of the nucleus 67P, smooth surfaces were identified and may be interpreted as an ice-free dust mantle. In particular, the Imhotep region located on the large lobe of the nucleus that was measured by MIRO shows near-surface temperatures and diurnal variations, which suggest the presence of an insulating material with very low thermal inertia. The measurements we reported show that ϵ′ probably is in the 1.5–2.2 range for these regions at a temperature of 300 K. This temperature may be reached by the surface and the subsurface when the comet approaches perihelion in August 2015. These values may also be applicable at lower temperatures, with a reduction of at most 10% from 300 to 40 K. In addition, the lower limit of the absorption length of the millimeter signal measured by MIRO was estimated for different values for the temperature and porosity, resulting in a range of values between 0.6 and 2 cm. These estimations are, to first order, consistent with the interpretation of the MIRO data (e.g., Gulkis et al. 2015; Schloerb et al. 2015).
Even though early results from Rosetta indicate a generally dehydrated nature for the surface of the nucleus and a porous dust mantle is strongly suspected, ice-rich materials may be expected just below the surface. Internal structures of the nucleus may have different components, such as pure ice (mostly water ice), ice-dust mixture, dust, and voids. At 90 MHz, the results suggest that the real part of the permittivity for a dust mantle probably is in the 1.1–2.2 range with a porosity of about 75% and below 1.5 with a porosity of about 90%, taking into account a temperature range between 300 and 40 K. For an icy nucleus with a porosity in the range of 70 to 80% at a mean temperature of 110 K, ϵ′ probably is in the 1.2–1.7 range with a dust-to-ice volumetric ratio between 0.1 and 1.5. By comparing the slopes of the porosity dependence of the permittivity (this study) with those of the temperature and the dust mass fraction dependencies (available literature), one can conclude that a permittivity variation in the whole nucleus would be mostly sensitive to the porosity.
Permittivity measurements at microwave frequencies reported in this article may have applications for other microwave observations of solar system objects in the near-future, such as the ExoMars WISDOM penetrating radar and the JUICE SWI submillimeter radiometer and spectrometer and RIME penetrating radar.
Acknowledgments
Support from the Swiss National Science Foundation is acknowledged. Partial support from CNES is acknowledged. We warmly acknowledge Pierre-Yves Meslin from IRAP laboratory (Toulouse, France) and V. Ciarletti from the LATMOS laboratory (Paris, France), who allowed us to make measurements on the JSC-1A Lunar regolith simulant and on the Etna volcanic ash, respectively. We also acknowledge Luisa Neves and Nicolas Cochinaire from the Fresnel Institute (Marseille, France) for their support with the measurements.
References
- Adams, R. J., Perger, W. F., Rose, W. I., & Kostinski, A. 1996, J. Geophys. Res., 101, 8175 [NASA ADS] [CrossRef] [Google Scholar]
- Alshibli, K. A., & Hasan, A. 2009, J. Geotechnical and Geoenvironmental Engineering, 135, 673 [CrossRef] [Google Scholar]
- Brouet, Y. 2013, Ph.D. Thesis, Université Pierre et Marie Curie (Sorbonne Universités), Paris, France [Google Scholar]
- Brouet, Y., Levasseur-Regourd, A. C., Encrenaz, P., & Gulkis, S. 2014, Planet. Space Sci., 103, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Calla, O. P. N., & Rathore, I. S. 2012, Adv. Space Res., 50, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell, M. J., & Ulrichs, J. 1969, J. Geophys. Res., 74, 5867 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioni, F., C. A., Filacchione, G., Erard, S., et al. 2015, Science, 347, aaa0628 [Google Scholar]
- Ciarletti, V., Levasseur-Regourd, A. C., Lasue, J., et al. 2015, A&A, 583, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cochran, A. L., Levasseur-Regourd, A. C., Cordiner, M., et al. 2015, Space Sci. Rev., in press [Google Scholar]
- Consolmagno, G. J., & Britt, D. T. 1998, Meteorit. Planet. Sci., 33, 1231 [Google Scholar]
- Davidsson, B. J. R., & Gutiérrez, P. J. 2005, Icarus, 176, 453 [NASA ADS] [CrossRef] [Google Scholar]
- De Paula, A. L., & Barroso, J. J. 2010, J. Electromagnetic Waves and Applications, 24, 1563 [CrossRef] [Google Scholar]
- De Sanctis, M. C., Capria, M. T., & Coradini, A. 2005, A&A, 444, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fawley, R., & Ferrie, P. 2012, 3rd Annual Seminar on Passive RF and Microwave components, IEEE Abstracts, 79 [Google Scholar]
- Fulle, M., Levasseur-Regourd, A. C., McBride, N., & Hadamcik, E. 2000, AJ, 119, 1968 [Google Scholar]
- Georget, E., Abdeddaim, R., & Sabouroux, P. 2014, Comptes Rendus Physique, 15, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Frerking, M., Crovisier, J., et al. 2007, Space Sci. Rev., 128, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Keihm, S., Kamp, L., et al. 2010, Planet. Space Sci., 58, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Keihm, S., Kamp, L., et al. 2012, Planet. Space Sci., 66, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Gulkis, S., Allen, M., von Allmen, P., et al. 2015, Science, 347, 0709 [Google Scholar]
- Harker, D. E., Woodward, C. E., Wooden, D. H., Fisher, R. S., & Trujillo, C. A. 2007, Icarus, 190, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Heggy, E., Paillou, P., Ruffie, G., et al. 2001, Icarus, 154, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Heggy, E., Palmer, E. M., Kofman, W., et al. 2012, Icarus, 221, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Herique, A., Kofman, W., Hagfors, T., Caudal, G., & Ayanides, J.-P. 1999, Planet. Space Sci., 47, 885 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, E., Mellin, M. J., Deane, B., Liu, Y., & Taylor, L. A. 2007, J. Geophys. Res., 112, 2006 [CrossRef] [Google Scholar]
- Kamoun, P., Lamy, P. L., Toth, I., & Herique, A. 2014, A&A, 568, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kofman, W., Barbin, Y., Klinger, J., et al. 1998, Adv. Space Res., 21, 1589 [NASA ADS] [CrossRef] [Google Scholar]
- Kofman, W., Herique, A., Goutail, J.-P., et al. 2007, Space Sci. Rev., 128, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Kofman, W., Hérique, A., Barbin, Y., et al. 2015, Science, DOI: 10.1126/science.aab0639 [Google Scholar]
- Lamy, P. L., Toth, I., Davidsson, B. J. R., et al. 2007, Space Sci. Rev., 128, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Lasue, J., Levasseur-Regourd, A. C., Hadamcik, E., & Alcouffe, G. 2009, Icarus, 199, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Levasseur-Regourd, A. C., Mukai, T., Lasue, J., & Okada, Y. 2007, Planet. Space Sci., 55, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Levasseur-Regourd, A. C., Hadamcik, E., Desvoivres, E., & Lasue, J. 2009, Planet. Space Sci., 57, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Lisse, C. M., VanCleve, J., Adams, A. C., et al. 2006, Science, 313, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Nicolson, A. M., & Ross, G. F. 1970, IEEE Trans. Instr. Measurement, 19, 377 [Google Scholar]
- Prialnik, D., Benkhoff, J., & Podolak, M. 2004, in Modeling the structure and activity of comet nuclei, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (University of Arizona Press), 359 [Google Scholar]
- Rotundi, A., Sierks, H., Della Corte, V., et al. 2015, Science, 347, 3905 [Google Scholar]
- Sabouroux, P., & Ba, D. 2011, Progress Electromagn. Res., 29, 191 [CrossRef] [Google Scholar]
- Schloerb, F. P., Keihm, S., von Allmen, P., et al. 2015, A&A, 583, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schulz, R., Hilchenbach, M., Langevin, Y., et al. 2015, Nature, 518, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Sierks, H., Barbieri, C., Lamy, P. L., et al. 2015, Science, 347, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, P. C., Veverka, J., Belton, M. J. S., et al. 2007, Icarus, 187, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, N., Sierks, H., Barbieri, C., et al. 2015, Science, 347, 440 [Google Scholar]
- Ulaby, F. T., & Long, D. G. 2014, Microwave radar and radiometric remote sensing (The University Michigan Press) [Google Scholar]
All Tables
Main characteristics of the four subsamples from Etna and of the six subsamples from JSC-1A simulant.
Real part of the permittivity ϵ′, upper limit of the imaginary part ϵ′′, and lower limit of the absorption length La estimated at 190 GHz for regions of the nucleus coated by an ice-free dust mantle, as a function of the temperature from 300 to 40 K and for different porosities equal to 50, 60, 70, 80, and 90%.
Real part of the permittivity ϵ′ estimated at 90 MHz for an ice-free dust mantle surrounding the nucleus, as a function of the temperature from 300 to 40 K and for different porosities equal to 50, 60, 70, 80, and 90%.
Real part of the permittivity ϵ′ suggested for the nucleus of 67P, assuming a mean temperature of about 110 K, as a function of the dust-to-ice volumetric ratio ([D/I] V) within the 0.1–1.5 range and a porosity (Φ) range of 80 to 50%.
All Figures
 |
Fig. 1 Scanning electron microscope images of Etna subsamples (#1, #2, #3, and #4) and JSC-1A Lunar regolith simulant subsamples (#8, #9, #10, #11, #12, and #13), with sizes of about a few to 500 μm. Different scales are used to show as best possible both the grain size distribution and the high intrinsic porosity of individual grains. The white line in the bottom right corner of each image provides the scale, equal to 100 μm (#8), 300 μm (#1, #2, #9, and #10), and 1 mm (#3, #4, #11, #12, and #13). |
| In the text | |
 |
Fig. 2 Image a) and schematic b) of the conical coaxial cell used to perform the permittivity measurements between 50 MHz and 6 GHz. |
| In the text | |
 |
Fig. 3 Real part of the permittivity normalized by the bulk density versus frequency for subsamples #1 a), 2 b), 3 c), and 4 d) from Etna. The measurements made between 50 MHz and 6 GHz are shown by filled circles, and those at 190 GHz are shown by filled triangles. |
| In the text | |
 |
Fig. 4 Real part of the permittivity normalized by the bulk density versus frequency for subsamples #8 a), 9 b), 10 c), 11 d), 12 e), and 13 f) from JSC-1A Lunar regolith simulant. The measurements made between 50 MHz and 6 GHz are shown by filled circles, and those at 190 GHz are shown by filled triangles. |
| In the text | |
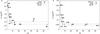 |
Fig. 5 Real part a) and imaginary part b) of the permittivity ϵ normalized by the bulk density (g/cm3) as a function of the ratio of the wavelength (corresponding to the frequency of 190 GHz) to the mean grain φ size for Etna and JSC-1A subsamples. The solid lines represent the exponential regressions of the measured points, expressed as g(λ/φ) = a × e(λ/φ) × b + c. Panel a): a equal to 4.13 ± 1.72 and 3.75 ± 0.61; b equal to −0.51 ± 0.13 and −0.48 ± 0.05; c equal to 2.40 ± 0.05 and 2.28 ± 0.02, for the Etna and the JSC-1A subsamples, respectively. Panel b): a equal to 0.80 ± 0.34 and 0.59 ± 0.14; b equal to −0.45 ± 0.13 and −0.59 ± 0.08; c equal to 0.06 ± 0.01 and 0.050 ± 0.003, respectively. |
| In the text | |
 |
Fig. 6 Real part of the permittivity ϵ′ versus bulk density ρ (kg/m3). Results obtained for the Etna and JSC-1A subsamples are presented at 80 MHz, 110 MHz, and 190 GHz. The solid line and the two dotted lines represent the linear regressions (written as A × ρ + 1) of the measured points at 80 MHz, 110 MHz, and 190 GHz, respectively. At 80 MHz and 110 MHz, the slopes are equal to (1.59 ± 0.02) × 10-3 (kg/m3)-1 and (1.60 ± 0.02) × 10-3 (kg/m3)-1, respectively. At 190 GHz, the slope is equal to (1.53 ± 0.02) × 10-3 (kg/m3)-1. |
| In the text | |
 |
Fig. 7 Real part of the permittivity ϵ′ versus porosity Φ (%). Results obtained for the Etna and JSC-1A subsamples are presented at 80 MHz, 110 MHz, and 190 GHz. The solid line and the two dotted lines represent the linear regressions (written as B × (Φ−100) + 1, with B being a constant) of the measured points at 80 MHz, 110 MHz, and 190 GHz, respectively. At 80 MHz and 110 MHz, the slopes are equal to (− 4.65 ± 0.04) × 10-2 per percent and (− 4.68 ± 0.06) × 10-2 per percent. At 190 GHz, the slope is equal to (− 4.49 ± 0.05) × 10-2 per percent. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


