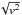| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A90 | |
| Number of page(s) | 18 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201525763 | |
| Published online | 30 October 2015 | |
Relativistic Bondi-Hoyle-Lyttleton accretion: A parametric study⋆
Laboratory for Scientific Computing, Department of Physics, Cavendish Laboratory, J J Thomson Avenue, Cambridge, CB3 0HE, UK
e-mail: pmb39@cam.ac.uk; nn10005@cam.ac.uk
Received: 29 January 2015
Accepted: 31 August 2015
Aims. We investigate Bondi-Hoyle-Lyttleton accretion onto a black hole for ultra-relativistic flows, and how flow features are affected by density perturbations, upstream fluid velocity, and black hole spin.
Methods. We use high-resolution shock-capturing (HRSC) schemes solved on curvilinear overlapping grids as demonstrated in a previous publication.
Results. We demonstrate the quantitative dependence of the shock-angle and mass accretion rate on black hole spin, upstream fluid velocity, and density perturbations. We also demonstrate the qualitative dependence of the accretion region and flow features on the same parameters.
Conclusions. We find that the mass accretion rate does not depend strongly on these parameters, and most of the difference in flow is seen in the shock angle and general flow patterns close to the black-hole, as previously predicted by lower-dimensional simulations. Moreover, we demonstrate independence of initial conditions in that a steady flow around a non-spinning black-hole which suddenly starts to spin will converge to the same flow pattern as if the black-hole had been spinning initially.
Key words: methods: numerical / accretion, accretion disks / hydrodynamics / shock waves / black hole physics
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Bondi-Hoyle-Lyttleton (hereafter BHL) accretion is the accretion of a uniform fluid onto a compact object. It is used as a model for studying the accretion of interstellar gas onto astrophysical objects. The relativistic extension of this is the accretion of fluid onto a black hole.
Work has previously been done in the relativistic case by Font et al. (1999) for an ideal gas accreting onto a black hole. However, due to computational constraints, their work concentrated on two-dimensional cases: those of axisymmetric accretion onto a Schwarzschild black hole, and of the thin-disc approximation of accretion onto a Kerr black hole. As expected from the Newtonian case, they found that supersonic flow produced a shock-cone, which was often, but not necessarily, attached to the horizon of the black hole. Subsonic flow, on the other hand, produced a smooth flow. They further found that the accretion pattern in the case of a Kerr black hole is fairly similar to that of a non-spinning black hole at large distances from the horizon. However, near the horizon, the shock cone (if present) wrapped itself around the black hole in the direction of spin. This effect decreased at large distances from the horizon.
Work on BHL accretion in the Newtonian case was also performed by Ruffert. In a series of papers (Ruffert 1994, 1995, 1997, 1999), he explored the dependence of the flow properties on the accretion radius, the adiabatic index of the ideal gas, and perturbations of the density and velocity upstream of the accretor.
More recently, Farris et al. (2010) have performed an in-depth parametric study of a binary black hole system accreting gas from a surrounding gas cloud, using a high-resolution shock-capturing (HRSC) scheme for the fluid evolution, and 4th order Runge-Kutta time-stepping for the metric evolution, on a Cartesian mesh with AMR. Also, Penner (2011) has performed a parametric study of general relativistic magneto-hydrodynamic (GRMHD) BHL, again using HRSC methods on a Cartesian mesh. Dönmez et al. (2011) have also investigated instabilities within Bondi-Hoyle flows, but in the thin-disc approximation.
In this work, we have combined the investigations of Font, Ibáñez, and Papodopoulos, and Ruffert, as cited above, into a more general parametric study. We took our inspiration for appropriate parameters from all the papers cited above. We have performed a parametric study incorporating the combined effects of black hole spin, the angle of the wind to the spin-axis, and perturbations of the fluid density. We investigated the effects of these on the flow structure, the mass accretion rate, and the angle which the shock-cone (if any) made to the incident wind direction.
In Sect. 2, we summarise the numerical methods we used to generate these results. In Sect. 3 we describe the grids and initial conditions used for the study and we give details of the models we study, the parameters we have chosen to vary, and our reasons for choosing particular models. In order to make quantitative deductions from our simulations, we need to perform some post-processing, of which we give details in Sect. 4.
As a precursor to the main study, we give in Sect. 5 some results giving a general overview of the fluid morphologies that can be expected from BHL accretion, covering a small selection of fluid velocities and adiabatic indices. Then, in Sect. 6, we present our results from our full parametric study, focusing on one model from those presented in the preceding section. Results of the study are given in Sect. 7, in graphical form, with a qualitative description of the flow features. Then, in Sect. 8, we give some quantitative results from our study. In Sect. 9 we include two simulations demonstrating the effect of instantaneously changing the upstream conditions on the final solution. Finally, we show in Sect. 10 conclusions we have drawn from our work, and suggestions of future work in this area.
Throughout this paper, we use units where the speed of light, c = 1, and the Newtonian constant, G = 1. Greek indices run over space and time: μ,ν,... = 0,1,2,3, and Roman indices run over space only: i,j,... = 1,2,3.
2. Numerical methods
A detailed exposition of the system of equations we solve and our numerical approach is given in our previous papers, Blakely et al. (2015a,b). We summarise the approach in the following paragraphs.
We note that the equations of general relativistic hydrodynamics (GRHD) form a conservation law with source terms. We can therefore use a finite-volume approach to solving the hyperbolic part of the system. Since we expect shocks to be produced in the accretion in the supersonic case, we should use high-resolution shock-capturing schemes. However, approximate or exact Riemann solvers may be prohibitively expensive for this, both in terms of time taken to implement and test and in terms of computational expense. We have therefore discussed this in more detail and validated in Blakely et al. (2015a) the GFORCE scheme of Toro & Titarev (2006), which can be applied to any system of equations in flux-conservation form with little effort and relatively low computational expense, but with higher accuracy than previous similar schemes. We use GFORCE with piecewise linear slope-limited reconstruction of the solution (SLIC), so that we obtain a second-order scheme overall, in regions of smooth flow, and first-order at shocks in the flow.
In order to advance the source-terms which are introduced by the non-flat metric, we use the second-order Runge-Kutta algorithm, which is combined with the finite-volume update using Strang splitting, which maintains second-order accuracy of the overall scheme.
In order to solve the system of equations on a set of curvilinear grids, we calculate the fluxes in the coordinate system of the grid, and transform them to Cartesian coordinates. The reason that we keep all solution variables in Cartesian coordinates is that this avoids any need to transform the solution variables between grid frames in order to interpolate between grids.
We note that we have included the free-stream preservation correction referred to in Blakely et al. (2015a), which ensures that a constant fluid state can be maintained up to round-off error on even the most distorted of curvilinear grids.
In the conservation-law form of the equations for GRHD, the metric enters the system through the fluxes. Our preceding approaches therefore require no adaptation to evolve a fluid on a non-flat metric. However, we have found it necessary to make some alterations to the flux calculations in order to maintain accuracy. These were detailed in Blakely et al. (2015b), and ensured that the metric and variables were evaluated at the correct locations. This was of particular importance when using the slope-limited reconstruction, which reconstructs solution variables at cell-faces, whereas metric values are only known at cell-centres. We therefore had to transform the fluid variables to ensure that they were expressed with the correct metric. We note that the approach of Rossmanith et al. (2004) is the rigorous way to deal with this, but that it would seem to be prohibitively computationally expensive.
Our approach for the complex problem of dealing with interpolation between overlapping grids is to use the Overture package of Henshaw et al. (2015). Overture is a library of routines that deal with general curvilinear overlapping grids, and provide sufficient geometric information for developers to implement their own numerical methods on those grids. It also handles interpolation between the various grids, and reading/writing of an HDF file for saving information. It is parallelised and has its own visualisation package, which we have used to generate the plots herein.
3. Simulation set-up
In order to generate a spherical grid with no singularities, we took two spherical grids and restricted their latitudinal coordinates to lie in [0.18π,0.82π]. One of the grids was then rotated through π/ 2 and the two grids were then overlapped so that each grid filled in the region where the other’s pole had been removed. An image of the grid is shown in Fig. 1. In Table 1 we show the resolutions of the grids that we used.
 |
Fig. 1 Overlapping grid structure forming a hollow sphere without any polar singularities. |
Grid cell statistics for the resolutions used.
It was suggested by Papadopoulos & Font (1998) that the metric written in Eddington-Finkelstein coordinates (for spin a = 0) or Kerr-Schild coordinates (a> 0) was most suited to simulations of the type we present here. These allow the coordinate system to extend smoothly inside the horizon, as opposed to other systems such as Boyer-Lindquist, which have a singularity at the horizon.
Therefore, for all of the simulations presented in this paper, we use the Kerr-Schild metric, expressed in Cartesian coordinates. However, since Font & Ibáñez (1998a) used Boyer-Lindquist coordinates, we have, in the post-processing stages, transformed into this coordinate system. This is also preferable when generating streamline plots as the velocity then approaches c = 1 at the horizon, as it would appear to for a distant observer. The forms of the metrics and the transformation between them are given explicitly in Blakely et al. (2015b). The inner excision boundary is always placed between the outer horizon at r+ and the inner horizon at r−, although its precise location varies depending on the spin parameter. The outer boundary always lies at 50M.
At the inner excision boundary, we use zeroth-order extrapolation of the conserved variables to fill the two ghost-cells, scaling them by the appropriate ratio due to the metric determinants. Physically, these boundary conditions cannot have any effect as they are inside the event horizon and, numerically, we have not found that any significant effects propagate into the main flow. At the upwind outer boundary at 50M, we use Dirichlet boundary conditions, defined by the initial data as discussed below. At the outer boundary where the fluid is outgoing, we simply extrapolate to zeroth order in conserved variables as for the inner boundary, except that we now do not adjust for the metric, since the space-time is essentially flat at 50M. Full details are given in Blakely et al. (2015b).
Test model parameters, as taken from Font & Ibáñez (1998b).
In order to cover the range of flow patterns covered by Bondi-Hoyle-Lyttleton accretion, we make use of some configurations suggested by Font & Ibáñez (1998b). We give the parameters for these in Table 2. Note that, for consistency, we use the same naming convention as Font and Ibáñez throughout for the models. As initial data for our fluid we use constant density, constant pressure, and constant velocity (in Kerr-Schild coordinates) over the whole domain. The density and pressure are defined so as to give a constant sound speed of c∞ if required (it is not, for example, required for a stiff fluid where the sound speed is always c = 1). The velocity is normalised as follows: given a wind direction vector, ni, and a velocity at spatial infinity, v∞, the wind velocity at a point is defined as 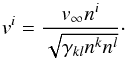 (1)We also allow for the fluid to have a spatially non-uniform density upstream of the black hole, following Ruffert (1999), who defines the density to be
(1)We also allow for the fluid to have a spatially non-uniform density upstream of the black hole, following Ruffert (1999), who defines the density to be ![\begin{equation} \begin{gathered} \rho_\infty=\rho_0\left(1-\frac{1}{2}\tanh\left[2\epsilon_\rho\frac{y}{R_A}\right]\right), \end{gathered} \label{eqn:DensityPert} \end{equation}](/articles/aa/full_html/2015/11/aa25763-15/aa25763-15-eq21.png) (2)where ρ∞ is the fluid density at spatial infinity, ϵρ is a density perturbation parameter, and the accretion radius is defined to be
(2)where ρ∞ is the fluid density at spatial infinity, ϵρ is a density perturbation parameter, and the accretion radius is defined to be 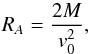 (3)although Font & Ibáñez use a different definition:
(3)although Font & Ibáñez use a different definition: 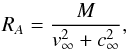 (4)where c∞ is the sound-speed at spatial infinity.
(4)where c∞ is the sound-speed at spatial infinity.
One would ordinarily use a linear modulation for the density perturbations but, for sufficiently large ϵρ, this leads to negative density at large distances from the black hole. Ruffert therefore uses the tanh variation as it is approximately linear near the origin but tends to ± 1 as r → ∞, and so avoids this problem while maintaining approximately the same problem set-up. In our set-up, the pressure is defined such that the sound speed is given by a constant value c∞ upstream.
Following (2), therefore, we generalise to the case of a non-flat metric, and our initial density is given by ![\begin{equation} \begin{gathered} \rho(\vect{x}) = \rho_\infty\left(1 - \frac{1}{2}\tanh\left[2 \epsilon_\rho\frac{\vect{x}\cdot\vect{p}}{R_A}\right]\right), \end{gathered} \label{eqn:WAPert} \end{equation}](/articles/aa/full_html/2015/11/aa25763-15/aa25763-15-eq29.png) (5)where p is orthogonal to the wind direction n, and specifies the direction in which the perturbation occurs. The vectors n and p are unit vectors defined at spatial infinity, so that the notions of orthogonality and normalisation are defined in terms of the flat-space Euclidean metric
(5)where p is orthogonal to the wind direction n, and specifies the direction in which the perturbation occurs. The vectors n and p are unit vectors defined at spatial infinity, so that the notions of orthogonality and normalisation are defined in terms of the flat-space Euclidean metric 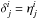 .
.
4. Analysis of results
After running the simulations, we must process them in order to extract useful conclusions from them and to compare different models in a quantitative way.
In order to calculate the mass accretion rate Ṁ from our numerical output, we note that (Petrich et al. 1989): 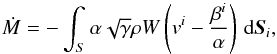 (6)where α is the lapse function, βi the shift vector, W the Lorentz factor, and
(6)where α is the lapse function, βi the shift vector, W the Lorentz factor, and 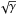 the determinant of the spatial metric. In order to evaluate this numerically, we interpolate the integrand at evenly spaced points in the θ and φ coordinates on a sphere with some radius r and sum them weighted by the infinitesimal area dSi = γijnjdA at those points. We use 150 points in the θ (latitudinal) direction and 300 points in the φ (longitudinal) direction. We showed this to be sufficient in Blakely et al. (2015b). We carry out the calculation in Kerr-Schild coordinates, as opposed to Font & Ibáñez (1998b), who calculated in Boyer-Lindquist coordinates. However, since the result is a scalar, it should be the same in both coordinate systems.
the determinant of the spatial metric. In order to evaluate this numerically, we interpolate the integrand at evenly spaced points in the θ and φ coordinates on a sphere with some radius r and sum them weighted by the infinitesimal area dSi = γijnjdA at those points. We use 150 points in the θ (latitudinal) direction and 300 points in the φ (longitudinal) direction. We showed this to be sufficient in Blakely et al. (2015b). We carry out the calculation in Kerr-Schild coordinates, as opposed to Font & Ibáñez (1998b), who calculated in Boyer-Lindquist coordinates. However, since the result is a scalar, it should be the same in both coordinate systems.
For a more direct comparison with Font & Ibáñez (1998b), we have scaled the mass accretion rate in the same way, by a factor 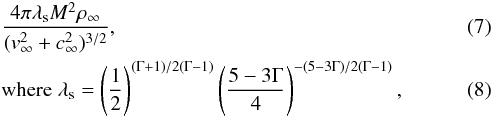 and Γ is the adiabatic index of the fluid. In order to provide a suitable comparison with previous work, we transform the velocities we obtain into those in Boyer-Lindquist coordinates. This is only possible outside the horizon of the black hole, and so results derived from these cannot extend inside the black hole. We can calculate the total velocity
and Γ is the adiabatic index of the fluid. In order to provide a suitable comparison with previous work, we transform the velocities we obtain into those in Boyer-Lindquist coordinates. This is only possible outside the horizon of the black hole, and so results derived from these cannot extend inside the black hole. We can calculate the total velocity 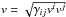 and, in some cases, locate the stagnation point of the flow, which lies downstream of the black hole.
and, in some cases, locate the stagnation point of the flow, which lies downstream of the black hole.
We can also extract some more information about the flow structure by calculating streamlines, generated by starting a set of tracers on a circle at a distance of 40M upstream of the black hole, and with radius 8M, and evolving them forwards in time. This is done on the final steady state of the velocity at t = 300M, using velocity vectors in the Boyer-Lindquist coordinate basis as described in Sect. 4. The streamline algorithm has also been used to determine the size and shape of the accretion region, being the region inside of which fluid will fall into the black hole, by starting a set of streamlines covering a circle at a distance of 40M upstream of the black hole and checking which tracers fall into the hole. From this we can determine a low-resolution approximation to the accretion region.
In Sect. 5 we shall see that under some circumstances a shock-cone forms (for example, Fig. 8). Far from the black hole, the sides of the cone become straight, and we use this part of the flow to calculate the opening angle of the cone.
In order to find the shock location, we plot the velocity 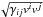 in Boyer-Lindquist coordinates around circles centred on the origin, at various radii. We can then take the centre of the jump in velocity as the shock location, since conserved schemes preserve the shock location. The circles are in the plane containing the wind direction and the y-axis (or the perturbation direction, if different). We show one of these plots in Fig. 2, where we see that, although the shock is spread over about 0.2 radians, the centre of the shock is fairly easy to find. In particular, we note that the centre of the shock in the angular direction corresponds to the centre of the shock in the velocity component, as we would expect from the conservation property of finite-volume methods. The data points are interpolated; however, we interpolate to the same number of points as there are grid cells, so there is a close correspondence between the data points and the actual values computed.
in Boyer-Lindquist coordinates around circles centred on the origin, at various radii. We can then take the centre of the jump in velocity as the shock location, since conserved schemes preserve the shock location. The circles are in the plane containing the wind direction and the y-axis (or the perturbation direction, if different). We show one of these plots in Fig. 2, where we see that, although the shock is spread over about 0.2 radians, the centre of the shock is fairly easy to find. In particular, we note that the centre of the shock in the angular direction corresponds to the centre of the shock in the velocity component, as we would expect from the conservation property of finite-volume methods. The data points are interpolated; however, we interpolate to the same number of points as there are grid cells, so there is a close correspondence between the data points and the actual values computed.
 |
Fig. 2 Velocity against equatorial angle measured at radius r = 30M for model UB1. This shows how we calculate the shock angle. The upper and lower horizontal lines on the left of the plot mark the upper and lower bounds of the shock, the central horizontal line is midway between these, and the shock location is taken to be where this crosses the numerical solution, at θ ≈ π/ 4 in this case. |
However, since the shock-cone is not centred at the origin, we calculate the actual angle of the shock with the wind direction as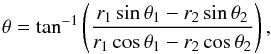 (9)where (r1,θ1) and (r2,θ2) are two points on the shock. The radii used here should be sufficiently large that the shock has become straight. In practice, we use r1 = 20M and r2 = 30M. We calculate the angle of the shock-cone both above and below the axis.
(9)where (r1,θ1) and (r2,θ2) are two points on the shock. The radii used here should be sufficiently large that the shock has become straight. In practice, we use r1 = 20M and r2 = 30M. We calculate the angle of the shock-cone both above and below the axis.
5. Fluid morphology
We examine the effect of varying the adiabatic index, Γ, and the flow velocity, using some models suggested by Font & Ibáñez, as given in Table 2. Qualitatively, our results are the same as those of Font and Ibáñez, although there are some differences in the numerical values that we find.
In order to have our code converge to steady state in a reasonable time, we have chosen all our models to be ultra-relativistic, meaning that the sound speed in the fluid upstream of the black hole is close to its theoretical maximum of 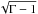 . The effect of the black hole can therefore propagate throughout the computational domain in a fairly short period of time, of the order of a few hundred M. We use the medium resolution grid whose parameters are given in Table 1.
. The effect of the black hole can therefore propagate throughout the computational domain in a fairly short period of time, of the order of a few hundred M. We use the medium resolution grid whose parameters are given in Table 1.
As well as testing these base models, we also test variations on these models with a spinning black hole and a density perturbation. We use a spin of a = 0.9, with the spin-axis along the z-axis, and a density perturbation of ϵρ = 0.2, perturbing along the y-axis (i.e. p = ey in (5)). The upstream fluid flow direction is along the x-axis in all cases.
We note that the flow regime we are considering should result in steady flows, following the work of Foglizzo & Ruffert (1999), as none of the flow fields approach the conditions identified therein as potentially leading to unstable flows.
5.1. Features common to all models
Far upstream of the black hole, the fluid motion is mostly undisturbed by the presence of the hole. Since fluid with a small enough impact parameter will always fall into the black-hole, there will be a stagnation point on the downstream side of the hole. Extending the idea of the stagnation point, we can also identify a region at a large distance upstream of the hole, inside which fluid will eventually fall onto the hole, and outside which it will not do so. In the case of symmetrical Bondi-Hoyle-Lyttleton accretion, this region always has a circular cross-section, and is therefore referred to as the accretion cylinder. We shall see that our choices of parameters cause it to deviate from the cylindrical, and so we refer to it instead as the accretion region.
When considering fluid velocities, we always use Boyer-Lindquist coordinates, which have a coordinate singularity at the horizon. In these coordinates, therefore, the fluid velocity approaches the speed of light at the horizon, although this is not the case in Kerr-Schild coordinates.
We now split our discussion into two cases, those of subsonic and supersonic flow.
5.2. Subsonic models
The subsonic models that we have tested are UC0 and UB0 (see Table 2), with a Mach number of ℳ = 0.6. These models differ primarily in their adiabatic indices, although the fluid velocity has to be changed to allow for the maximum velocity permitted by 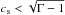 . We run the simulations to time t = 400M, and the results are shown in Figs. 3 and 4.
. We run the simulations to time t = 400M, and the results are shown in Figs. 3 and 4.
 |
Fig. 3 Contour plots of density and velocity for a uniform subsonic flow past a non-spinning black hole with flow parameters given by model UB0. The plots are evaluated at time t = 400M. a) Equally spaced contours of log ρ. b) Velocity contours evaluated in Boyer-Lindquist coordinates. The stagnation point is marked. |
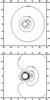 |
Fig. 4 Contour plots of density and velocity for a uniform subsonic flow past a non-spinning black hole with flow parameters given by model UC0. The plots are evaluated at time t = 400M, and the axes are in units of M. a) Equally spaced contours of log ρ. b) Velocity contours evaluated in Boyer-Lindquist coordinates. The stagnation point is marked. |
For both models the density contours near the hole are nearly circular, but offset slightly in the downstream direction relative to the centre of the hole so that the density at the horizon is higher on the downstream side. Model UC0, with the higher adiabatic index, gives a lower fluid density close to the horizon than does model UB0, since the fluid is less compressible for higher adiabatic index. The velocity at a given distance upstream of the singularity is higher for model UC0, and the velocity at a given distance downstream of the hole is higher for model UB0, the stagnation point for which lies further downstream than for model UC0.
 |
Fig. 5 Contour plots of density and velocity for a subsonic flow with density perturbed by ϵρ = 0.2 past a black hole with spin a = 0.9 and flow parameters given by model UB0. The plots are evaluated at time t = 400M, and the axes are in units of M. a) Equally spaced contours of log ρ. b) Velocity contours evaluated in Boyer-Lindquist coordinates. |
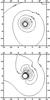 |
Fig. 6 Contour plots of density and velocity for a subsonic flow with density perturbed by ϵρ = 0.2 past a black hole with spin a = 0.9 and flow parameters given by model UC0. The plots are evaluated at time t = 400M, and the axes are in units of M. a) Equally spaced contours of log ρ. b) Velocity contours evaluated in Boyer-Lindquist coordinates. |
 |
Fig. 7 Accretion regions for all four subsonic models. The solid line shows the accretion region for a = 0, ϵρ = 0, and the dashed line shows the accretion region for a = 0.9, ϵρ = 0.2. a) Model UB0. b) Model UC0. |
In Figs. 5 and 6 we show the effect on these models of including spin a = 0.9 and density perturbation ϵρ = 0.2. The flow is still in the equatorial plane of the black hole, however. In both cases the flow is wrapped around the horizon significantly, in the direction of the spin.
The velocity contours show the development of two regions of lower velocity flow. From the form of the ellipse-shaped contours around the black hole and extending into the south-west of the plots, we see that the main flow morphology has been twisted around the horizon by about 45°, although there are now no stagnation points, due to the added effect of the fluid rotating around the hole before falling in. Examining iso-surfaces of the velocity shows that neither are there any stagnation points away from the z = 0 plane.
The cross-sections of the accretion regions upstream of the black hole are shown in Fig. 7. As expected by symmetry, the accretion regions for the unperturbed, non-spinning cases are circular. The combined effect of the spin and density perturbation is to deflect fluid from the upper half of the domain away from the black hole so that it does not accrete onto the black hole. We also see that the accretion regions for the higher adiabatic index in model UC0 are somewhat smaller than those for model UB0.
We note that the tilted form of the flow and the development of a line of lower density are features that also appear in the simulations of Ruffert (1999) involving a density perturbed fluid onto a compact object. This suggests that the major changes to the flow features are the result of the density perturbation, rather than the spin of the black hole, as such an effect was not included in Ruffert’s simulations, not being relevant in the Newtonian regime. In both cases we see from Table 3 that the joint effect of the spinning black hole and the density perturbation is to lower the rate at which mass is accreted onto the black hole. This is as suggested by the reduction in the size of the accretion regions in Fig. 7. The reasons for this will be discussed in the full parametric study in Sect. 6.
Note that the mass accretion rates for the two models cannot be compared directly, as they have already been scaled by the factor given in Eq. (8).
5.3. Supersonic models
The supersonic models we have tested are UA1 and UB1, at Mach number ℳ = 1.5. Results for model UB1 are shown in the main text, while those for UA1 are shown in Appendix A. The results for velocity are shown in Figs. 8 and A.1. The main feature of these plots is the shock-cone that has formed downstream of the black hole, in a manner similar to that of a solid body immersed in an Eulerian flow in flat space-time. Analogously to that case, the opening angle of the shock-cone at a large distance from the hole should be sin-1(1/ℳ), with higher Mach numbers corresponding to a narrower shock-cone (see Appendix B in Petrich et al. 1989, and references therein for more details).
In both models UA1 and UB1, the density of the fluid increases sharply across the shock-cone, and also increases as the horizon is approached, both from the downstream direction and from the upstream direction. We now have a considerably larger ratio between the density on the upstream and downstream sides of the horizon than for the subsonic models, with a high density inside the shock-cone as fluid is focused through it onto the horizon. The UA1 model, with the lower adiabatic index, exhibits a higher density inside the shock-cone and, in particular, at the horizon, than the UB1 model. As in the subsonic case, this is due to the fact that the fluid with the higher adiabatic index is less compressible.
The flow for model UB1 has its stagnation point closer to the black hole than that for model UA1, but upstream, outside the shock-cone, the flow velocity is lower for model UB1. Since both models have the same Mach number, ℳ = 1.5, both shock-cones have approximately the same opening-angles.
 |
Fig. 8 Contour plot of velocity contours evaluated in Boyer-Lindquist coordinates for a uniform supersonic flow past a non-spinning black hole with flow parameters given by model UB1, evaluated at time t = 300M. The stagnation point is marked. |
 |
Fig. 9 Contour plot of velocity for a supersonic flow with density perturbed by ϵρ = 0.2 past a black hole with spin a = 0.9 and flow parameters given by model UB1, evaluated at time t = 300M, and the axes are in units of M. |
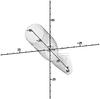 |
Fig. 10 Streamlines for a perturbed flow with ϵρ = 0.2, model UB1, parallel to the equatorial plane, onto a Kerr black hole with spin a = 0.9. |
 |
Fig. 11 Streamlines for a perturbed flow with ϵρ = 0.2, model UA1, parallel to the equatorial plane, onto a Kerr black hole with spin a = 0.9. |
In Figs. 9 and A.2 we show the effect on these models of including a spin of a = 0.9 and a density perturbation of ϵρ = 0.2. The flow is still in the equatorial plane of the black hole, however. We see that the shock-cone is pulled round the hole in the positive (anti-clockwise) direction. The velocity contour plots in Figs. 9 and A.2 show similar twisting and distortion to the subsonic case. The velocity drops significantly across the shock-cone, and there are then two regions of low velocity. It is not clear from the numerical solution whether either of these contain stagnation points.
It is more instructive, however, to examine the streamlines shown in Fig. 10 for model UB1. The flow is compressed in from the sides, and the tracers that escape the domain downstream of the black hole form a tear-drop shape. For model UA1, where the streamlines are shown in Fig. 11 we note that the tracers were started on a larger radius circle, but we still see a qualitatively fairly similar flow. However, at the top of the tear-drop, we see that two vortices have developed in the flow. These correspond to the two low density regions mentioned above.
 |
Fig. 12 Accretion regions for two supersonic models based on UB1. The solid line shows the accretion region for a = 0, ϵρ = 0, and the dashed line shows the accretion region for a = 0.9, ϵρ = 0.2. |
The cross-sections of the accretion regions upstream of the black hole are shown in Figs. 12 and A.3. Again the accretion regions corresponding to the unperturbed, non-spinning cases are circular. The combined effect of the spin and perturbation is to move the accretion region towards the top of the domain, and to cause it to decrease in size. The accretion regions for the higher adiabatic index (model UB1) are somewhat smaller than those for model UA1.
Again, the gross flow features are borne out by an examination of simulations in Ruffert (1999) for a density perturbed flow. We also note that the angle by which the shock-cone is tilted is approximately the same in both models. From Table 3 we see the accretion rates for the supersonic models. As in the subsonic case, the effect of spinning the black hole and introducing a density perturbation is to lower the mass accretion rate, as suggested by the decrease in area of the accretion regions.
Comparison of mass accretion rates found using our code (Ṁ) with those of Font & Ibáñez (1998b) (ṀFI).
5.4. Comparison with previous results
We show the limiting values for the mass accretion rates in Table 3, with results from Font & Ibáñez (1998b) for comparison. Although our results are similar in magnitude to those previously found, our rates are persistently higher. The reasons for this are not clear but, as suggested in Blakely et al. (2015b), it may result from different far-field boundary conditions between the simulations, due to the use of different metrics.
Comparison of stagnation point locations found using our code (xstag) with those of Font & Ibáñez (1998b) (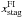 ), which have been scaled to be in units of M rather than of RA.
), which have been scaled to be in units of M rather than of RA.
In Table 4 we show the location of the stagnation points for the four non-spinning unperturbed models we have presented above. An examination of the velocity plots in Font & Ibáñez (1998b) suggests that the stagnation point locations are written in units of the accretion radius ra. The location of the stagnation points found using our code is similar to, but consistently further out than, those found by Font & Ibáñez.
In this section we have shown some of the flow morphologies that can arise from accretion onto a black hole. We have, to a large extent, confirmed the results of Font and Ibáñez, although there is disagreement in the mass accretion rates and locations of the stagnation points.
We have also demonstrated the combined effects of allowing a spinning black hole and a fluid whose density is perturbed upstream. These show significant alterations in the flow properties, some of which were demonstrated by Ruffert in the Newtonian regime. In particular, including spin and a density perturbation cause the flow to twist around the spin-axis of the black hole. The flow also develops complex features; all the models show the development of a line of lower density in the z = 0 plane, and one model develops vortices.
The overall effect of spin and density perturbation for all the models is to lower the mass accretion rate, and to change the area and location of the accretion region. However, in order to understand these effects more fully, we shall perform a parametric study, examining the separate and combined effects of spin, density perturbation, and wind direction.
6. Parametric study
As previously mentioned, we are basing our work on a combination of the studies carried out by Font et al. (1999) and Ruffert (1999). Font et al. varied the adiabatic index of the fluid, the spin of the black hole, and the asymptotic upstream fluid velocity. Ruffert used the idea of a non-uniform fluid density upstream to start an investigation of stability issues.
We have used all these possible variations and, since we are performing our simulations in three space dimensions, also allowed for varying the wind direction relative to the spin axis, whereas Font et al. only considered the case where the upstream fluid velocity was perpendicular to the spin axis.
Within the framework of Bondi-Hoyle-Lyttleton flow, we therefore have the following parameters that can be varied entirely independently of each other:
| M | black hole mass; | |
| a | black hole spin (0 ≤ a< 1); | |
| ℳ | asymptotic Mach number of the flow; | |
| v∞ | asymptotic velocity of the flow; | |
| (the sound speed is c∞ = v∞/ ℳ); | ||
| Γ | adiabatic index of ideal fluid; | |
| ni | incident wind direction; | |
| pi | perturbation direction; | |
| ϵρ | strength of density perturbation (ϵρ ≪ 1). |
Since it is just a scaling parameter, we can fix the black hole to have mass M = 1. The spin axis is fixed to be the z-axis, and we vary the incident wind direction n in the y = 0 plane, at angles of θw = 0,π/ 6,π/ 3,π/ 2 to the x-axis. This corresponds to n·ey = 0 and n·ez = cosθw.
The perturbation will have most effect if it occurs perpendicular to the wind direction. Due to the asymmetry induced by any spin that might be present, this still leaves us with one degree of freedom, and we fix the perturbation direction to be parallel to the y-axis (i.e. p = ey in (5)). The various vectors can be seen in Fig. 13.
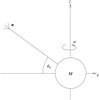 |
Fig. 13 Geometric set-up of wind accretion parametric study. The black hole spin is always in a positive direction around the z-axis, the wind direction is in the x-z plane at an angle θw to the x-axis, and any fluid perturbations are in the y-direction (positive y goes into the page). |
Since low spins do not seem to affect the flow by a large amount, according to the results of Font & Ibáñez, we use three spin parameters: a = 0,0.5, and 0.9.
Ruffert et al. have used ϵρ = 0,0.03,0.2. Since we have specified the spin always to be positive, we have to allow for this handedness and allow ϵρ< 0 where appropriate.
We apply perturbations to one of the models suggested by Font & Ibáñez: UB1. This is an ultra-relativistic flow of a medium stiffness fluid at a moderate Mach number. Note that the sound speed cs = 0.57 is close to the maximum permitted value of 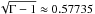 . This model has the advantage that it converges fairly quickly to steady state. All of the simulations were run until T = 300M, which was sufficient to reach this steady-state in all cases.
. This model has the advantage that it converges fairly quickly to steady state. All of the simulations were run until T = 300M, which was sufficient to reach this steady-state in all cases.
To summarise: we allow for the following perturbations to the base solution: 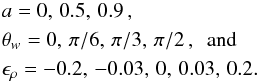 (10)These are applied in all possible combinations, although some combinations are not necessary as they duplicate others. For example, θw is irrelevant when a = 0, by symmetry, and as shown in the next section.
(10)These are applied in all possible combinations, although some combinations are not necessary as they duplicate others. For example, θw is irrelevant when a = 0, by symmetry, and as shown in the next section.
We now give details as to how the plots in the following sections were generated.
The streamlines show up some slight issues with the low resolution used, such as the fact that, for the base model with no spin and uniform flow, we found the cross-section of the streamlines at the end to be not quite circular. The higher resolution simulations described in Sect. 5 do not have this problem, but otherwise display the same flow features. We are therefore justified in drawing conclusions from the lower-resolution plots.
All the plots in the following sections are standardised for easy comparison. We plot velocity with equally spaced contours at 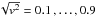 where the velocity is evaluated in Boyer-Lindquist coordinates. The outer horizon of the black hole is shown with a dashed line at r = r+ (and is non-circular when the spin-axis is not perpendicular to the plot plane), and the plot ranges are ± 15M. The plane in which we plot the contours contains the y-axis and the incoming wind direction. That is, for θw = 0, the black hole spin axis is normal to the plot, and for θw = π/ 2, the spin axis lies in the plot plane, from left to right. The wind direction is always from the left of the plot.
where the velocity is evaluated in Boyer-Lindquist coordinates. The outer horizon of the black hole is shown with a dashed line at r = r+ (and is non-circular when the spin-axis is not perpendicular to the plot plane), and the plot ranges are ± 15M. The plane in which we plot the contours contains the y-axis and the incoming wind direction. That is, for θw = 0, the black hole spin axis is normal to the plot, and for θw = π/ 2, the spin axis lies in the plot plane, from left to right. The wind direction is always from the left of the plot.
7. Parametric study results
In this section we present plots from our parametric study, demonstrating how the flow morphology depends on the independent and combined variation of the various parameters. This only represents a sample of the main results found. We have made the full results available on the University of Cambridge’s DSpace site (Blakely 2010).
As performing a parametric study is very CPU-intensive, we calculated these results on the low resolution grid whose parameters are given in Table 1. However, from our validation results, we believe that the effects of the low resolution on our results are not significant.
 |
Fig. 14 Effect of increasing black hole spin on uniform wind accretion parallel to the equatorial plane of a Kerr black hole. The black hole spin is in the positive direction. We plot the velocity in Boyer-Lindquist coordinates. a) a = 0.5, |
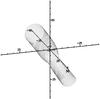 |
Fig. 15 Streamlines for a uniform flow parallel to the equatorial plane onto a Kerr black hole with spin a = 0.9. |
In Fig. 14, we see the effect of varying the spin of the black hole for a uniform flow. The flow is parallel to the equatorial plane of the hole, and we expect our results to be close to those of Font et al. (1999), although their results were for the thin-disc approximation, not the fully three-dimensional results we have here.
As we increase the spin of the black hole, the points where the shock cone meets the horizon move around in the direction of spin. Although the flow is altered near the horizon, the effect further out is far less, and is nearly indistinguishable from that of the non-spinning case. This is particularly evident from the results when measuring the shock angles, as we shall see in Sect. 8.
Examining the streamlines for the a = 0.9 case (Fig. 15) shows that fluid on the co-rotating side of the hole can escape to infinity when it starts from a smaller radius as compared to fluid on the counter-rotating side, and the minimum impact parameter for which fluid can escape is smaller for higher spin. This is evident in the accretion region which for spin a = 0.9 is entirely in the upper half of the domain.
 |
Fig. 16 Effect of density perturbation on accretion in the equatorial plane of a non-spinning Kerr black hole, with density increasing down the page. We plot the velocity in Boyer-Lindquist coordinates. a) ϵρ = 0.03, |
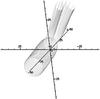 |
Fig. 17 Streamlines for flow with density perturbation ϵρ = 0.2 onto a non-spinning Kerr black hole. |
Perturbing the density of the flow onto a non-spinning black hole gives results as in Fig. 16. The density upstream of the black hole increases down the page.
The shock-cone is visibly skewed round in the anti-clockwise direction in both cases, although more so for ϵρ = 0.2, and this effect persists far away from the hole, unlike the effect of the spin. There is also a line of higher velocity in the upper part of the shock-cone, so that there are almost two separate cones, although this is only really visible for ϵρ = 0.2. These features are similar to those for highly perturbed Newtonian flow seen in Ruffert (1999). The streamlines in Fig. 17 also show the fluid forming a pair of vortices as it moves downstream.
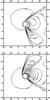 |
Fig. 18 Effect of density perturbation on accretion in the equatorial plane of a Kerr black hole with spin a = 0.9. The black hole spin is in the positive direction. We plot the velocity in Boyer-Lindquist coordinates. a) ϵρ = −0.2, |
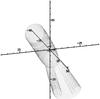 |
Fig. 19 Streamlines for a perturbed flow with ϵρ = −0.2 onto a Kerr black hole with spin a = 0.9. |
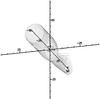 |
Fig. 20 Streamlines for a perturbed flow with ϵρ = 0.2 onto a Kerr black hole with spin a = 0.9. |
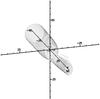 |
Fig. 21 Streamlines for a perturbed flow with ϵρ = 0.03 onto a Kerr black hole with spin a = 0.5. |
If we add spin to the most perturbed case, we obtain the results shown in Fig. 18. Now we expect to see a combination of the effects explored earlier.
For ϵρ = 0.2, the perturbation takes the point where the shock-cone attaches to the horizon round to the upstream region of the flow. A large distance downstream of the black hole, this effect is still present as we would expect from the non-spinning case above, and at the horizon, the shock-cone has wrapped further around in the anti-clockwise direction due to the added effect of the spin.
For ϵρ = −0.2, the effect of the perturbation a long way downstream of the black hole is the reverse of that for the non-spinning positive perturbation. At the horizon, we expect the spin to take the point where the shock-cone attaches round in the anti-clockwise direction, and the negative perturbation to take it in the clockwise direction. We see that the effect of the spin is dominant, in that the point of attachment has overall moved in an anti-clockwise direction.
For both cases, the divided shock-cone is still visible. For the ϵρ = 0.2 case, the effect has increased, so that the contour lines extend further towards the horizon, demonstrating a deepening of the division. For ϵρ = −0.2, the effect has reduced, showing a shallower division in the cone.
For the perturbation ϵρ = −0.2, the flow streamlines in Fig. 19 appear similar to that for the non-spinning case, although the two vortices have now been moved apart from each other to some extent. For ϵρ = 0.2, shown in Fig. 20, we now see a qualitatively different flow, in that no vortices are visible, but the ends of the streamlines form a tear-drop shape downstream of the black hole. From an examination of the streamlines for spin a = 0.5 and perturbation ϵρ = 0.03 in Fig. 21, it appears that the effect of the positive spin is to elongate the two vortices in the vertical direction, at the same time moving them closer together, so that the tear-drop is composed of the inner sides of the original vortices.
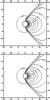 |
Fig. 22 Effect of increasing black hole spin on uniform wind accretion along the spin axis of a spinning Kerr black hole. The axis of spin is the horizontal axis, and the spin direction goes into the page in the upper half of the plot. We plot the velocity in Boyer-Lindquist coordinates. a) a = 0.5, |
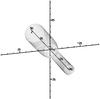 |
Fig. 23 Streamlines for a uniform flow along the spin-axis of a Kerr black hole with spin a = 0.9. |
We now orient the flow so that it comes in along the spin-axis of the black hole. The result of increasing the spin in this case is shown in Fig. 22. In this case we hardly see any change to the qualitative features of the flow. There is no apparent change in the streamlines (shown in Fig. 23) from the non-spinning case.
The relative lack of change is due to the fact that the direction of spin is perpendicular to the streamlines. There is some evidence that the flow has been pulled round by the black hole but, again, the effect is only very slight, due to the high velocity of the flow.
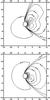 |
Fig. 24 Effect of density perturbation ϵρ = 0.2 on wind accretion along the spin axis of a Kerr black hole with spin a = 0.9. The axis of spin is the horizontal axis, and the spin direction goes into the page in the upper half of the plots. We plot velocity in Boyer-Lindquist coordinates. a) x = 0 plane, |
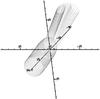 |
Fig. 25 Streamlines for a perturbed flow with ϵρ = 0.2 along the spin-axis of a Kerr black hole with spin a = 0.9. |
The effect of perturbing the upstream density of flow by ϵρ = 0.2 along the spin axis of a black hole with spin a = 0.9 is shown in Fig. 24. The shock-cone is still tilted away from the symmetric position, but the perturbation makes little difference to the overall flow. The contours in the x = 0 plane do not demonstrate any splitting of the shock cone as we saw in, for example, Figure 16. The splitting is still just evident in the y = 0 plane.
The streamlines (Fig. 25) show that there is still a pair of vortices emerging along the shock-cone, but that they have been distorted by the spin, starting to merge into each other.
8. Analysis
We now proceed to show the processed results, with the effect of the density perturbation and black hole spin on the overall flow characteristics.
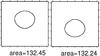 |
Fig. 26 Overall effect of changing the density perturbation on the accretion volume for a non-spinning black hole, for two extreme values of ϵρ = ± 0.2. The axis tick-marks are at −15M, −10M,..., 10M, 15M. a) θw = 0 and ϵρ = −0.2; b) θw = π/ 2 and ϵρ = + 0.2. |
 |
Fig. 27 Overall effect on the accretion region for a black hole with spin a = 0.5. Even between the extremes of the values for θw and ϵρ there is little change in the accretion region and volume. The axis tick marks are at −15M, −10M,..., 10M, 15M. a) θw = 0 and ϵρ = −0.2; b) θw = π/ 2 and ϵρ = + 0.2. |
 |
Fig. 28 Overall effect on the accretion region for a black hole with spin a = 0.9. Even between the extremes of the values for θw and ϵρ there is little change in the accretion region and volume. The axis tick marks are at −15M, −10M,..., 10M, 15M. a) θw = 0 and ϵρ = −0.2; b) θw = π/ 2 and ϵρ = + 0.2. |
The accretion region plots are shown in Figs. 26−28. The effect of each change is only very slight, so we show the overall effect via the plots for θw = 0 and θw = π/ 2 or ϵρ = −0.2 and ϵρ = 0.2.
The effect of increasing θw is only very slight, but the trend is that the accretion region decreases in area, and shifts in the negative y-direction. As ϵρ increases, the accretion region moves appreciably in the negative y direction.
We have included the graphical results for the following in Appendix B.
In Figs. B.1 and B.2 we show the effect of varying the density perturbation parameter on the mass accretion rate for spins of a = 0, 0.5, 0.9. The overall effect on the mass accretion rate is fairly small, at less than 10%.
When the wind direction is along the spin axis (θw = π/ 2), the direction of the perturbation does not affect the mass accretion rate, as we would expect from symmetry considerations. The greatest effect on the mass accretion rate occurs when the wind is parallel to the equatorial plane of the black hole.
From Fig. B.2, we see that for flow parallel to the equatorial plane, the mass accretion rate is reduced more strongly by increased perturbation than for flow along the spin axis, since the area of the accretion region has a wider variation for θw = 0 than for θw = π/ 2. The effect of the change with perturbation is once again the result of two combined effects: change in location and size of the accretion region and change in available material in that region due to density perturbation.
In Figs. B.3 and B.4 we show the effect of spin and density perturbation on the asymptotic angle of the shock cone. As a specific example, we note that the shock-cone opening angle for zero spin and no perturbation is found to be 38°, which is less than the analytical value from sin-1(1/ℳ) = 41.8°, but greater than θ = 35° as found by Font & Ibáñez (1998b) (Table 2).
We have seen earlier that both the spin and the perturbation affect the innermost regions of the flow very strongly, but that the only major effect on the shock cone a long way from the black hole is the density perturbation. This is confirmed by Fig. B.3.
Further, we now see from Fig. B.4 that varying the angle between the equatorial plane and the wind direction has no effect on the angle between the shock-cone edges and the wind direction, within numerical and shock location errors. The spin of the black hole does not appear to have any effect on the shock-cone angle either. However, the effect of the perturbation is very noticeable, varying the direction of the shock-cone by nearly 30° overall. The total opening angle of the shock-cone is unaffected by the perturbation.
9. Independence of initial conditions
Although we have consistently found steady final states of the flows that we have simulated, all of these have derived from the same initial conditions. In order to confirm the universality of our results, we should test whether changing the set-up of the model part way through a simulation affects its final state.
9.1. Perturbed flow reverting to a uniform flow
The first scenario we test is that of a perturbed flow that has settled down to steady-state having its upwind inflow conditions reverted to uniform flow. We use as initial conditions for our test the steady-state solution given by a black hole with spin parameter a = 0.9 and density perturbation ϵρ = 0.2, with θw = 0, but change the inflow boundary condition to be that for an unperturbed flow, ϵρ = 0. We then evolve the set-up until it again reaches steady state.
It turns out that the final state of the simulation is identical to the state that resulted from specifying ϵρ = 0 initially. The way the flow pattern changes in time is also unremarkable, in that the shock-cone smoothly changes to its final position, and the two parts of the divided shock-cone merge smoothly to form a single one.
 |
Fig. 29 Mass accretion rate plot for an initially perturbed model with ϵρ = 0.2, but reverting to ϵρ = 0 upstream at time t = 300M. The black hole has spin a = 0.9 and the wind is in the equatorial plane. The solid line shows the final mass accretion rate from the equivalent flow with ϵρ = 0 throughout. |
In Fig. 29 we show the rate of mass accretion resulting from this simulation. Up to time t = 300M the density is perturbed by ϵρ = 0.2, and after that it reverts to ϵρ = 0. The solid line shows the final mass accretion rate from the simulation where the density was not initially perturbed. The kink in the rate at t ≈ 350M corresponds to the time when the effect of the changed upstream conditions reaches the black hole (recall that the outer boundary is at r = 50M). Following that, the accretion rate then climbs monotonically to its final value.
9.2. Spinning-up a black hole
In our second test, we note that in the close encounter of two black holes, it is possible that they will interact so as to result in a black hole with a spin somewhat larger than before the interaction. As a simple model of this we examine what happens to the steady-state accretion flow when the spin of the black hole is instantaneously increased.
The specific set-up we use is that of the case where a greatly perturbed fluid with ϵρ = 0.2 is accreting onto a non-spinning black hole, and the flow is in steady state. We then change the black hole to have spin a = 0.9 and allow the simulation to reach a steady state again. At the change-over point, the fluid variables were converted to their primitive form in the original metric, and then converted to conserved form in the new metric with spin.
 |
Fig. 30 Mass accretion rate plot for a perturbed density flow onto a non-spinning black hole which recieves a kick at time t = 300M, increasing its spin to a = 0.9. The solid line shows the final mass accretion rate from the equivalent flow with a = 0.9 throughout. |
As with the previous example, the final state of the simulation is identical to that resulting from the simulation that maintained a = 0.9 throughout, as seen in Fig. 18. We show the results for the mass accretion rate in Fig. 30. We see a discontinuity in the mass accretion rate at the time when the black hole is “kicked” (t = 300M). The accretion rate falls slightly below its final value, then rises above it and oscillates slightly before quickly reaching a steady state.
10. Conclusions
In this paper, we have studied the effects of introducing spin and a density perturbation into relativistic Bondi-Hoyle-Lyttleton accretion simulations. We have investigated the effect of these on both subsonic and supersonic flows, before applying an extensive parametric study to one supersonic base model.
We have seen that the qualitative effects of adding spin and having a perturbed density upstream of the black hole are independent of the velocity, Mach number, and adiabatic index of the fluid. In all cases presented in Sect. 5 we saw that the flow was wrapped around the black hole in the spin direction and that the fluid developed regions of lower density, as well as being deflected by the black hole. The extent to which these effects were seen was, however, dependent on the flow properties. In particular, only the subsonic models demonstrated any large change in the flow upstream of the black hole, as we would expect.
Investigating the supersonic model UB1 more extensively, we discovered how the separate effects of spin and density perturbation affected the flow structure. In particular, there is little dependence of the accretion rate on black-hole spin, upstream fluid speed and direction, and density perturbations for the ultra-relativistic regime. The most obvious flow differences are found very close to the black-hole in the shock-angle and flow patterns. This is as predicted by lower-dimensional simulations. Further, it appears that ultra-relativistic flows are independent of their initial conditions, in that a steady flow around a non-spinning black-hole which suddenly starts to spin will converge to the same flow pattern as if the black-hole had been spinning initially.
Specifically, we found that:
-
For a uniform flow, the effect of the spin on the flow structure ismostly restricted to the region close to the black hole, where thepoints at which the shock-cone meets the horizon are pulled roundin the spin direction. The mass accretion rate reduces slightly asthe spin rate increases, but not to any great extent.
-
Moving the flow direction from being in the equatorial plane to being along the spin axis removes any deflection of the flow by the black hole, and also slightly reduces the mass accretion rate.
-
Perturbing the density changes the flow most dramatically. The flow is appreciably deflected from its original direction, and this effect persists to large distances downstream of the black hole. Vortices develop in the flow, on either side of the plane containing the wind and perturbation directions. The mass accretion rate changes by up to 10%, although the sign of the change and its magnitude depends strongly on the spin of the black hole, and the angle of the incoming wind to the spin axis.
-
The angle of the shock-cone to the wind-direction, at large distances downstream of the black hole, is independent of the spin of the black hole and the angle of the wind direction to the spin-axis. However, it is strongly dependent on the extent to which the density is perturbed, varying by about 30° over the range of ϵρ that we use.
-
The final flow structures are apparently independent of any past history of the flow. This was demonstrated by changing firstly the perturbation and secondly the spin of a flow after it had settled into its steady state, and seeing that the flow rapidly became identical to the flow that would have developed had the parameters not begun with separate values.
We have made some progress towards implementing the evolution of the metric in our code, but we have not yet applied it to complex three-dimensional problems such as binary black-hole coalescence. However, we see no essential difficulty in adapting the latest developments in the solution of such problems to be used in our code.
In particular, we note that Overture is capable of interpolating an existing numerical solution to a new set of grids. This leads to the possibility of changing the grid structure, including the location of the excision region(s) as the flow evolves.
Online material
Appendix A: Results from model UA1
In this section we show results from model UA1. These can be compared to those results for UB1 as found in the main text.
 |
Fig. A.1 Contour plot of velocity contours evaluated in Boyer-Lindquist coordinates for a uniform supersonic flow past a non-spinning black hole with flow parameters given by model UA1, evaluated at time t = 300M. The stagnation point is marked. |
 |
Fig. A.2 Contour plot of velocity for a supersonic flow with density perturbed by ϵρ = 0.2 past a black hole with spin a = 0.9 and flow parameters given by model UA1, evaluated at time t = 400M, with the axes in units of M. |
 |
Fig. A.3 Accretion regions for two supersonic models based on UA1. The solid line shows the accretion region for a = 0, ϵρ = 0, and the dashed line shows the accretion region for a = 0.9, ϵρ = 0.2. |
Appendix B: Mass accretion and shock-angle dependence
In this section we show details of how the mass accretion rates and shock-angles depend on the size of the density perturbation.
 |
Fig. B.1 Mass accretion rate against density perturbation for different spins. The wind direction is parallel to the equatorial plane of the black hole in all cases. |
 |
Fig. B.2 Mass accretion rates against density perturbation. The labels refer to the angle between the equatorial plane and the wind direction. a) Spin a = 0.5; b) Spin a = 0.9. |
 |
Fig. B.3 Shock angles against density perturbation, varying the spin of the black hole. The wind direction is in the equatorial plane of the black hole in all cases. |
 |
Fig. B.4 Shock-cone angles against density perturbation. The angles are all taken in the plane containing the wind direction and the y-axis. The data points above and below the axis correspond to the shock-angles above and below the wind-direction axis. The labels correspond to the angle between the equatorial plane of the black hole and the wind direction. a) Spin a = 0.5; b) Spin a = 0.9. |
Acknowledgments
This work was funded by an EPSRC Doctoral Training Grant, and use was also made of the Darwin Supercomputer of the University of Cambridge High Performance Computing Service (http://www.hpc.cam.ac.uk/), provided by Dell Inc. using Strategic Research Infrastructure Funding from the Higher Education Funding Council for England. Following the EPSRC policy on research data, source-code required to produce results found in this paper is available from Blakely (2015). The authors would like to thank the reviewer for comments and suggestions on this paper.
References
- Blakely, P. M. 2010, Numerical Solutions of the General Relativistic Equations for Black Hole Fluid Dynamics, http://www.dspace.cam.ac.uk/handle/1810/226117 [Google Scholar]
- Blakely, P. M. 2015, Source code for Bondi-Hoyle-Lyttleton Accretion, http://www.repository.cam.ac.uk/handle/1810/250362 [Google Scholar]
- Blakely, P. M., Nikiforakis, N., & Henshaw, W. D. 2015a, A&A, 575, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blakely, P. M., Nikiforakis, N., & Henshaw, W. D. 2015b, A&A, 575, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dönmez, O., Zanotti, O., & Rezzolla, L. 2011, MNRAS, 412, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Farris, B., Liu, Y., & Shapiro, S. 2010, Phys. Rev. D, 81, 084008 [NASA ADS] [CrossRef] [Google Scholar]
- Foglizzo, T., & Ruffert, M. 1999, A&A, 347, 901 [NASA ADS] [Google Scholar]
- Font, J. A., & Ibáñez, J. M. 1998a, MNRAS, 298, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Font, J. A., & Ibáñez, J. M. 1998b, ApJ, 494, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Font, J. A., Ibáñez, J. M., & Papadopoulos, P. 1999, MNRAS, 305, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Henshaw, W., Chand, K., Fast, P., & Quinlan, D. 2015, Overture – Object-oriented Tools for solving PDEs in Complex Geometries, www.overtureframework.org, accessed 12th January 2015 [Google Scholar]
- Papadopoulos, P., & Font, J. A. 1998, Phys. Rev. D, 58, 024005 [NASA ADS] [CrossRef] [Google Scholar]
- Penner, A. J. 2011, MNRAS, 414, 1467 [NASA ADS] [CrossRef] [Google Scholar]
- Petrich, L. I., Shapiro, S. L., Stark, R. F., & Teukolsky, S. A. 1989, ApJ, 336, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Rossmanith, J. A., Bale, D. S., & LeVeque, R. J. 2004, J. Comput. Phys., 199, 631 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ruffert, M. 1994, ApJ, 427, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffert, M. 1995, A&AS, 113, 133 [NASA ADS] [Google Scholar]
- Ruffert, M. 1997, A&A, 317, 793 [NASA ADS] [Google Scholar]
- Ruffert, M. 1999, A&A, 346, 861 [NASA ADS] [Google Scholar]
- Toro, E., & Titarev, V. 2006, J. Comput. Phys., 216, 403 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison of mass accretion rates found using our code (Ṁ) with those of Font & Ibáñez (1998b) (ṀFI).
Comparison of stagnation point locations found using our code (xstag) with those of Font & Ibáñez (1998b) (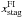 ), which have been scaled to be in units of M rather than of RA.
), which have been scaled to be in units of M rather than of RA.
All Figures
 |
Fig. 1 Overlapping grid structure forming a hollow sphere without any polar singularities. |
| In the text | |
 |
Fig. 2 Velocity against equatorial angle measured at radius r = 30M for model UB1. This shows how we calculate the shock angle. The upper and lower horizontal lines on the left of the plot mark the upper and lower bounds of the shock, the central horizontal line is midway between these, and the shock location is taken to be where this crosses the numerical solution, at θ ≈ π/ 4 in this case. |
| In the text | |
 |
Fig. 3 Contour plots of density and velocity for a uniform subsonic flow past a non-spinning black hole with flow parameters given by model UB0. The plots are evaluated at time t = 400M. a) Equally spaced contours of log ρ. b) Velocity contours evaluated in Boyer-Lindquist coordinates. The stagnation point is marked. |
| In the text | |
 |
Fig. 4 Contour plots of density and velocity for a uniform subsonic flow past a non-spinning black hole with flow parameters given by model UC0. The plots are evaluated at time t = 400M, and the axes are in units of M. a) Equally spaced contours of log ρ. b) Velocity contours evaluated in Boyer-Lindquist coordinates. The stagnation point is marked. |
| In the text | |
 |
Fig. 5 Contour plots of density and velocity for a subsonic flow with density perturbed by ϵρ = 0.2 past a black hole with spin a = 0.9 and flow parameters given by model UB0. The plots are evaluated at time t = 400M, and the axes are in units of M. a) Equally spaced contours of log ρ. b) Velocity contours evaluated in Boyer-Lindquist coordinates. |
| In the text | |
 |
Fig. 6 Contour plots of density and velocity for a subsonic flow with density perturbed by ϵρ = 0.2 past a black hole with spin a = 0.9 and flow parameters given by model UC0. The plots are evaluated at time t = 400M, and the axes are in units of M. a) Equally spaced contours of log ρ. b) Velocity contours evaluated in Boyer-Lindquist coordinates. |
| In the text | |
 |
Fig. 7 Accretion regions for all four subsonic models. The solid line shows the accretion region for a = 0, ϵρ = 0, and the dashed line shows the accretion region for a = 0.9, ϵρ = 0.2. a) Model UB0. b) Model UC0. |
| In the text | |
 |
Fig. 8 Contour plot of velocity contours evaluated in Boyer-Lindquist coordinates for a uniform supersonic flow past a non-spinning black hole with flow parameters given by model UB1, evaluated at time t = 300M. The stagnation point is marked. |
| In the text | |
 |
Fig. 9 Contour plot of velocity for a supersonic flow with density perturbed by ϵρ = 0.2 past a black hole with spin a = 0.9 and flow parameters given by model UB1, evaluated at time t = 300M, and the axes are in units of M. |
| In the text | |
 |
Fig. 10 Streamlines for a perturbed flow with ϵρ = 0.2, model UB1, parallel to the equatorial plane, onto a Kerr black hole with spin a = 0.9. |
| In the text | |
 |
Fig. 11 Streamlines for a perturbed flow with ϵρ = 0.2, model UA1, parallel to the equatorial plane, onto a Kerr black hole with spin a = 0.9. |
| In the text | |
 |
Fig. 12 Accretion regions for two supersonic models based on UB1. The solid line shows the accretion region for a = 0, ϵρ = 0, and the dashed line shows the accretion region for a = 0.9, ϵρ = 0.2. |
| In the text | |
 |
Fig. 13 Geometric set-up of wind accretion parametric study. The black hole spin is always in a positive direction around the z-axis, the wind direction is in the x-z plane at an angle θw to the x-axis, and any fluid perturbations are in the y-direction (positive y goes into the page). |
| In the text | |
 |
Fig. 14 Effect of increasing black hole spin on uniform wind accretion parallel to the equatorial plane of a Kerr black hole. The black hole spin is in the positive direction. We plot the velocity in Boyer-Lindquist coordinates. a) a = 0.5, |
| In the text | |
 |
Fig. 15 Streamlines for a uniform flow parallel to the equatorial plane onto a Kerr black hole with spin a = 0.9. |
| In the text | |
 |
Fig. 16 Effect of density perturbation on accretion in the equatorial plane of a non-spinning Kerr black hole, with density increasing down the page. We plot the velocity in Boyer-Lindquist coordinates. a) ϵρ = 0.03, |
| In the text | |
 |
Fig. 17 Streamlines for flow with density perturbation ϵρ = 0.2 onto a non-spinning Kerr black hole. |
| In the text | |
 |
Fig. 18 Effect of density perturbation on accretion in the equatorial plane of a Kerr black hole with spin a = 0.9. The black hole spin is in the positive direction. We plot the velocity in Boyer-Lindquist coordinates. a) ϵρ = −0.2, |
| In the text | |
 |
Fig. 19 Streamlines for a perturbed flow with ϵρ = −0.2 onto a Kerr black hole with spin a = 0.9. |
| In the text | |
 |
Fig. 20 Streamlines for a perturbed flow with ϵρ = 0.2 onto a Kerr black hole with spin a = 0.9. |
| In the text | |
 |
Fig. 21 Streamlines for a perturbed flow with ϵρ = 0.03 onto a Kerr black hole with spin a = 0.5. |
| In the text | |
 |
Fig. 22 Effect of increasing black hole spin on uniform wind accretion along the spin axis of a spinning Kerr black hole. The axis of spin is the horizontal axis, and the spin direction goes into the page in the upper half of the plot. We plot the velocity in Boyer-Lindquist coordinates. a) a = 0.5, |
| In the text | |
 |
Fig. 23 Streamlines for a uniform flow along the spin-axis of a Kerr black hole with spin a = 0.9. |
| In the text | |
 |
Fig. 24 Effect of density perturbation ϵρ = 0.2 on wind accretion along the spin axis of a Kerr black hole with spin a = 0.9. The axis of spin is the horizontal axis, and the spin direction goes into the page in the upper half of the plots. We plot velocity in Boyer-Lindquist coordinates. a) x = 0 plane, |
| In the text | |
 |
Fig. 25 Streamlines for a perturbed flow with ϵρ = 0.2 along the spin-axis of a Kerr black hole with spin a = 0.9. |
| In the text | |
 |
Fig. 26 Overall effect of changing the density perturbation on the accretion volume for a non-spinning black hole, for two extreme values of ϵρ = ± 0.2. The axis tick-marks are at −15M, −10M,..., 10M, 15M. a) θw = 0 and ϵρ = −0.2; b) θw = π/ 2 and ϵρ = + 0.2. |
| In the text | |
 |
Fig. 27 Overall effect on the accretion region for a black hole with spin a = 0.5. Even between the extremes of the values for θw and ϵρ there is little change in the accretion region and volume. The axis tick marks are at −15M, −10M,..., 10M, 15M. a) θw = 0 and ϵρ = −0.2; b) θw = π/ 2 and ϵρ = + 0.2. |
| In the text | |
 |
Fig. 28 Overall effect on the accretion region for a black hole with spin a = 0.9. Even between the extremes of the values for θw and ϵρ there is little change in the accretion region and volume. The axis tick marks are at −15M, −10M,..., 10M, 15M. a) θw = 0 and ϵρ = −0.2; b) θw = π/ 2 and ϵρ = + 0.2. |
| In the text | |
 |
Fig. 29 Mass accretion rate plot for an initially perturbed model with ϵρ = 0.2, but reverting to ϵρ = 0 upstream at time t = 300M. The black hole has spin a = 0.9 and the wind is in the equatorial plane. The solid line shows the final mass accretion rate from the equivalent flow with ϵρ = 0 throughout. |
| In the text | |
 |
Fig. 30 Mass accretion rate plot for a perturbed density flow onto a non-spinning black hole which recieves a kick at time t = 300M, increasing its spin to a = 0.9. The solid line shows the final mass accretion rate from the equivalent flow with a = 0.9 throughout. |
| In the text | |
 |
Fig. A.1 Contour plot of velocity contours evaluated in Boyer-Lindquist coordinates for a uniform supersonic flow past a non-spinning black hole with flow parameters given by model UA1, evaluated at time t = 300M. The stagnation point is marked. |
| In the text | |
 |
Fig. A.2 Contour plot of velocity for a supersonic flow with density perturbed by ϵρ = 0.2 past a black hole with spin a = 0.9 and flow parameters given by model UA1, evaluated at time t = 400M, with the axes in units of M. |
| In the text | |
 |
Fig. A.3 Accretion regions for two supersonic models based on UA1. The solid line shows the accretion region for a = 0, ϵρ = 0, and the dashed line shows the accretion region for a = 0.9, ϵρ = 0.2. |
| In the text | |
 |
Fig. B.1 Mass accretion rate against density perturbation for different spins. The wind direction is parallel to the equatorial plane of the black hole in all cases. |
| In the text | |
 |
Fig. B.2 Mass accretion rates against density perturbation. The labels refer to the angle between the equatorial plane and the wind direction. a) Spin a = 0.5; b) Spin a = 0.9. |
| In the text | |
 |
Fig. B.3 Shock angles against density perturbation, varying the spin of the black hole. The wind direction is in the equatorial plane of the black hole in all cases. |
| In the text | |
 |
Fig. B.4 Shock-cone angles against density perturbation. The angles are all taken in the plane containing the wind direction and the y-axis. The data points above and below the axis correspond to the shock-angles above and below the wind-direction axis. The labels correspond to the angle between the equatorial plane of the black hole and the wind direction. a) Spin a = 0.5; b) Spin a = 0.9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.