| Issue |
A&A
Volume 583, November 2015
Rosetta mission results pre-perihelion
|
|
|---|---|---|
| Article Number | A10 | |
| Number of page(s) | 6 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201525703 | |
| Published online | 30 October 2015 | |
Research Note
Optical observations of comet 67P/Churyumov-Gerasimenko with the Nordic Optical Telescope
Comet activity before the solar conjunction
1 Tuorla Observatory, Department of Physics and Astronomy, University of Turku, Väisäläntie 20, 21500 Piikkiö, Finland
e-mail: bozapr@utu.fi
2 Finnish Centre for Astronomy with ESO (FINCA), Väisäläntie 20, 21500 Piikkiö, Finland
3 Nordic Optical Telescope, Apartado 474, 38700 Santa Cruz de La Palma, Spain
4 Planetary and Space Sciences, Department of Physical Sciences, The Open University, Milton Keynes, MK7 6AA, UK
5 ESA/ESTEC, Research and Scientific Support Department, PO Box 299, 2200 AG Noordwijk, The Netherlands
Received: 21 January 2015
Accepted: 31 July 2015
Context. 67P/Churyumov-Gerasimenko (67P) is a short-period Jupiter-family comet that was chosen as a target for the Rosetta mission by the European Space Agency (ESA). Monitoring of 67P with the Nordic Optical Telescope (NOT; La Palma, Spain) intends to aid this mission by providing ground-based reference information about the overall activity of the target and its astrometric position before the rendezvous. One motivation for our observations was to monitor sudden major increases in activity because they might have affected the Rosetta mission planning. None were observed. Ground-based photometric observations register the global activity of the comet, while the Rosetta spacecraft mostly measures local events. These data combined can lead to new insights into the comet behavior.
Aims. The aim of this work is to perform the photometric and the astrometric monitoring of comet 67P with the NOT and to compare the results with the latest predictions for its position and activity. A new method of fitting extended-source components to the target surface brightness distribution was developed and applied to the data to estimate the size and contribution of the coma to the total brightness of the target.
Methods. Comet 67P was monitored by the NOT in service mode during the period between 12.5.2013 and 11.11.2014. The very first observations were performed in the V band alone, but in the latest observations, the R band was used as well to estimate the color and nature of activity of the target. We applied a new method for estimating the coma size by deconvolving the point spread function profile from the image, which used Markov chain Monte Carlo and Bayesian statistics. This method will also be used for coma size estimations in further observations after the solar conjunction of 67P.
Results. Photometric magnitudes in two colors were monitored during the period of observations. At the end of April 2014, the beginning of activity was observed. In late September 2014, a minor dip in cometary activity was measured. Otherwise, the activity of the comet was close to the expected values. For some of the observations, we were able to determine limits for the physical size and brightness of the coma by studying the surface brightness distribution of the target. The astrometric calibration results we obtained were consistent with the predictions of the ephemerides of the Minor Planet Center, but at the moment these results are superseded with the more precise astrometric data from the Rosetta spacecraft.
Key words: comets: individual: 67P/Churyumov-Gerasimenko / techniques: photometric / astrometry
© ESO, 2015
1. Introduction
One of the most important space missions of the European Space Agency’s HORIZON 2000 program, Rosetta is targeting the short-period Jupiter-family comet 67P/Churyumov-Gerasimenko (67P), which has been studied closely from various ground-based facilities since 2003 (Schulz et al. 2004). Rosetta is a unique mission and essentially different from any previous cometary space missions. The spacecraft does not pass over the comet, as did the Stardust mission by NASA, or impact it with high velocity, as the Deep Impact mission by NASA, but it orbits the target throughout its perihelion passage and has deployed the Philae lander unit on the surface of the comet. Rosetta will not return any samples to the Earth, but it is examining cometary material in situ. This prevents contamination or transmutation of samples during the flight.
The Rosetta spacecraft consists of two modules: a lander and an orbiter. The lander has been deployed on the surface of the comet on 12 November 2014, while the orbiter measures dust grains, plasma, gases, and magnetic fields in close proximity to the cometary nucleus. Rosetta carries 21 scientific instruments on board: UV, optical and thermal IR spectrographs, optical and IR cameras, microwave and radio devices, and a variety of mass-spectrometry and dust detection devices. Rosetta has already provided much and will provide more precious information about cometary material, its chemical and physical properties as well as isotopic compositions.
The Rosetta spacecraft was launched successfully in March 2004 and has approached the target in August 2014. At the end of April 2014, first signs of activity were detected by the Osiris camera onboard Rosetta (Tubiana et al. 2015). We can also see this in our data. As Rosetta approached the target, the coma became unobservable as a whole by on-board detectors, as it is impossible to see the size of the cloud from inside of a cloud. The overall activity of the comet is monitored with ground-based facilities, such as the ESO Very Large Telescope (VLT) on the Southern Hemisphere and Nordic Optical Telescope (NOT) on the Northern Hemisphere. Photometry data are used to monitor any kind of unexpected activity of 67P that might affect the mission. Global activity observed by ground-based facilities can also be used as a counterpart to local observations of the Rosetta instruments.
The NOT observations will become especially important around the comet perihelion when other professional telescopes cannot observe it because of the low altitude. NOT is able to observe at very low altitudes (down to 8 degrees above the horizon) and was one of the first professional ground-based devices to see comet 67P after its January 2015 conjunction. Around perihelion, increased activity is most probable because the solar radiation is at its peak. Thus, optical monitoring plays a very important role in keeping the mission safe. We have developed automated data analysis programs and established the routines and procedures, hence future monitoring can be made with a short-term response, and information can directly be transmitted to the Rosetta team through well-established communication channels.
2. Observations
Comet 67P was observed with the NOT located on the island of La Palma, Spain. Observations were performed in service mode during the period between 12 May 2013 and 11 November 2014, before the solar conjunction, using the ALFOSC or the StanCam camera with standard V- and R-band filters. ALFOSC is a CCD camera with a field of view of 6.4 × 6.4 arcmin and an angular resolution of 0.189 arcsec. The backup instrument StanCam is an optical imaging instrument with a field of view of 3 × 3 arcmin and an angular resolution of 0.179 arcseconds. Exposure times were chosen to be 15 s for calibration images and chart comparison and 200 s for the main exposures of the target. Starting from March 2014, long exposures (200 s) were also taken without tracking the comet before and after the main target observations. Images were reduced and calibrated using the standard procedures of bias level subtraction and flat-field correction with IRAF (Tody 1986). The dark current is negligibly small in ALFOSC and StanCam.
Comet 67P was hardly visible during our early observations due to the large distance and inactivity. The target was identified by comparing (blinking) two or more images and finding a moving object near the expected coordinates. A sky motion of the target during exposure time is clearly noticeable. In some observations, the field in the object’s proximity was very crowded, which precluded correct photometry. In case of low signal-to-noise ratio (S/N), only the upper limit for the 3σ detection was defined.
 |
Fig. 1 Images of comet 67P taken with the NOT. On the left side: observations from the summer 2013. Images are smoothed with the Gaussian kernel with σ = 3 pixels. On the right side: observations from the late spring 2014. The comet is clearly visible and the good S/N allows precise brightness measurements and even the study of the surface brightness profile. |
3. Analysis
3.1. Photometry
Aperture photometry was performed on the obtained images. The size of the aperture was mostly ten pixels, but was increased to twelve pixels when the seeing of a current night was poor. This is always a concern when measuring an extended source, like a comet. Still, as we discuss in Sect. 3.2, the non-stellar component of the target PSF, if detected, was always smaller than the aperture.
A good photometric calibration catalog is essential for photometry. We used UCAC-4 catalog, which includes APASS photometry entries to the B, V, r and i filter magnitudes (Zacharias et al. 2013). Photometric magnitudes for SDSS r- and i- band filters were used to estimate the value of the Landolt R magnitude through the equation given by Lupton (2005)1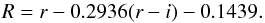 (1)For some of the observed fields, APASS photometry was not available. In this case, we used the Hubble Guide Star catalog 2.3 (Lasker et al. 2008) and the conversion formula given by Pursimo et al. (2013)
(1)For some of the observed fields, APASS photometry was not available. In this case, we used the Hubble Guide Star catalog 2.3 (Lasker et al. 2008) and the conversion formula given by Pursimo et al. (2013)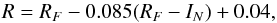 (2)where RF and IN are the respective filtered magnitudes in the Hubble Guide Star catalog.
(2)where RF and IN are the respective filtered magnitudes in the Hubble Guide Star catalog.
A group of 5 to 40 catalog stars were selected for photometry in each image, excluding any multiple stars or stars with a bad background. The aperture photometry was performed with IRAF. To make a color correction, Vmeas−VUCAC values were plotted against the catalog V−R color of the star (see Fig. 2). Because catalog values are more accurate, we used a least-squares fitting method with the linear model. Standard errors for the linear fit were also determined and used later to estimate the magnitude uncertainty. The instrument-specific color correction constant for the ALFOSC is 0.09 for the R/V−R fit and 0.04 for the V/B−V fit. This defines the slope of the fitted line. For the StanCam corresponding values are 0.11 and for the R/V−R fit and 0.06 for the V/B−V fit.
 |
Fig. 2 Close to linear dependence on a magnitude correction Vmeasured−V on the color of the star for observations on 11 March 2014. Some points clearly deviate from general statistics, which is an indicator for a bad photometric measurement such as the saturation of the CCD or background objects in the aperture. These points are excluded from the calculations. |
This method was used to calculate V and R magnitudes for comet 67P. Snodgrass et al. (2013) found the V−R colour of the coma of 67P to be 0.45 ± 0.05, based on VLT observations when the comet was at 3.4 AU from the Sun in 2008. The S/N in aperture photometry was estimated using Eq. (3) (Howell 1989): 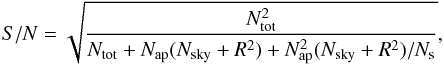 (3)where Ntot is the electron number, Nsky is the brightness of the sky, Nap is the amount of pixels inside the aperture, and Ns is the number of pixels used in the background level (Nsky) estimation. Instrument-dependent parameters are gain G = 0.327e−/ADU (ALFOSC) or 1.68e−/ADU (StanCam) and the readout noise R = 4.2e−/pixel (ALFOSC) or 6.8e−/pixel (StanCam). The overall error of magnitude estimation was obtained by adding a zero-point correction error to the photometry measurement error according to the error propagation law.
(3)where Ntot is the electron number, Nsky is the brightness of the sky, Nap is the amount of pixels inside the aperture, and Ns is the number of pixels used in the background level (Nsky) estimation. Instrument-dependent parameters are gain G = 0.327e−/ADU (ALFOSC) or 1.68e−/ADU (StanCam) and the readout noise R = 4.2e−/pixel (ALFOSC) or 6.8e−/pixel (StanCam). The overall error of magnitude estimation was obtained by adding a zero-point correction error to the photometry measurement error according to the error propagation law.
Photometry results.
During the first observations, the telescope followed the comet and not the sky. Therefore, star profiles were stretched in the images. This would result in a systematic error in the aperture photometry because different amounts of the elongated objects’ flux would fit inside a round aperture compared with the flux of the round object. This effect was compensated for by introducing an additional correction term, derived by fitting elongated star profiles (modeled as a sum of multiple symmetric Moffat profiles) to the images and comparing them to the round profile of the tracked object via numerical simulations. For most of the images, this effect was negligible. Still, in a few observations with a sharp seeing and fast motion of an object, the correction term indicated a loss of flux of up to 11%. Fluxes were corrected for this effect where needed, and the final results are presented in Table 1. The light curve is presented in Fig. 3.
 |
Fig. 3 Light curve of 67P. Blue points represent V-band observations and red snowflakes R-band observations. Error bars represent 1σ error limits for magnitude estimates. Prediction of the visual magnitude by the MPC ephemerides shifted down by 2 is shown as a solid green line. In case of no-detection, 3σ upper limits for low S/N observations are presented by the down pointing triangles. |
Resolved 68% confidence limits (1σ limits) of the coma fitting.
3.2. Coma analysis
At the end of April 2014, when the comet distance to the Sun was around 4.11 AU, activity had started and the signs of coma formation were observed by us and other instruments, including the OSIRIS camera onboard the Rosetta spacecraft (Tubiana et al. 2015) and the VLT (Snodgrass 2015).
In our observations, start of cometary activity was seen around 4.11 AU as a jump in the overall brightness of the target (see Fig. 3) and the alteration of its radial profile. In its inactive phase, the surface brightness profile of the target was similar to a star profile of the image, as the cometary nucleus can be assumed to be a point source from the Earth. When the activity had started, the coma contributed to the overall brightness of the target. The coma is not a point source, and it alters the PSF profile of the target in a way that depends on its shape, extension, and the brightness.
To model the size and flux contribution of the coma, a few approximations were made. Considering a low spatial resolution and S/N, a simple circularly symmetrical exponential profile should suffice. The model for the image of the coma is then the convolution of this exponential radial profile and the PSF-function of point-like source, approximated by a Moffat-profile fitted to the sky-following observations immediately after the image of the comet were obtained. The Moffat profiles of 20 to 200 stars were fitted to each reference image. As optical distortion may occur in the telescope, PSF parameters were studied as a function of image coordinates and interpolated to the target position.
The model now has three free parameters: the flux contribution of the nucleus, the flux contribution of the coma, and the size of the coma: 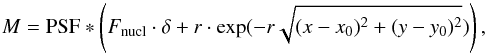 (4)where x0 and y0 are the pixel coordinates of the cometary nucleus (and also the center of the coma), PSF is the point spread function measured from the reference image, Fnucl is the photon flux from the nucleus, and δ is a Dirac delta-function. The exact physical position of the object on the image was defined with the separate routine. For further observations when asymmetry of the coma or the tail are expected, the method requires a more complicated coma profile with a few additional parameters.
(4)where x0 and y0 are the pixel coordinates of the cometary nucleus (and also the center of the coma), PSF is the point spread function measured from the reference image, Fnucl is the photon flux from the nucleus, and δ is a Dirac delta-function. The exact physical position of the object on the image was defined with the separate routine. For further observations when asymmetry of the coma or the tail are expected, the method requires a more complicated coma profile with a few additional parameters.
Because of the nonlinearity of the problem and complex error propagation, the Bayesian framework was chosen to be the tool. A smaller image of the comet was extracted from the observations and compared with the model pixel by pixel using Bayesian inference as a fit quality indicator. For every point of parameter space, a Bayesian probability of the model versus observations PModel was calculated by taking the product of all the individual pixel probabilities multiplied by a non-informative prior distribution Π: 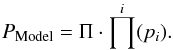 (5)The pixel probability pi is derived from the PDF of the error distributions of the current observation, with the dominating error of a photon noise following the Poisson distribution combined with the constant readout noise of the instrument.
(5)The pixel probability pi is derived from the PDF of the error distributions of the current observation, with the dominating error of a photon noise following the Poisson distribution combined with the constant readout noise of the instrument.
To explore the posterior distribution of the model, the Metropolis-Hastings algorithm was used. This relatively simple iterative algorithm explores the posterior distribution by making random jumps from point to point in a parameter space and accepts or declines the move. It finally converges toward the area of the best fit, with the density of the accepted iterations reflecting the posterior distribution. By plotting contour lines of the density of accepted iterations, we can study the shape of the posterior distribution, the maximum likelihood parameter set, or the 68% confidence area. This is analogous to the 1σ error limit in normally distributed statistics. An example of the posterior distribution is presented in Fig. 4.
 |
Fig. 4 Posterior distribution of the exponential model fitting the coma on 21 August 2014 R-band observations. The red area indicates the 68% confidence limits, and the yellow square in the center is a maximum likelihood point corresponding to a coma contribution of 85% to the overall brightness and the FWHM of the coma profile at about the 240 km distance. The result is in some sense degenerated: the brighter coma implies more compact distribution, while the fainter coma is connected with its larger spatial size. |
The method benefits from a stable PSF profile during the observations. Thus, only observations made in stable seeing conditions were accepted to this procedure. The detailed study of the comet surface brightness profile during the observations revealed many limitations of the method. A poor model for the reference PSF would result in a systematic error. A good seeing is also critical. In most of the data presented here, seeing is large in comparison with the coma we wish to resolve. For these reasons, we present only the 68% confidence limits for the size and the flux contribution of the coma. The results presented in Table 2 seem to agree reasonably well with the observations of the coma from the Rosetta spacecraft (Tubiana et al.2015).
In our observations, the estimated confidence area is large, which produces a large uncertainty in the result. On the other hand, the whole modeling was performed as a proof of concept and as a basis for future observations, where we will be able to use working algorithms on new data with a better S/N and spatial resolution to reliably estimate size, brightness, and even the color of the coma.
4. Conclusions
We performed aperture photometry of comet 67P using the UCAC4 or GSC2.3 catalogs as a reference. Until the solar conjunction, measured photometric magnitudes and activity development agreed well with the values predicted by Snodgrass et al. (2013). The observable activity had started at the end of April 2014. At the end of September 2014 (after 3.51 AU) the level of activity had slightly decreased, which was not expected. Observations in October indicated that comet had regained its normal activity. Along with the photometry, the astrometrical calibrations of each image were performed. The results are not presented here because they were completely superseded by the Rosetta measurements.
A new method for deconvolving the coma profile was developed and applied to the data. The method uses direct modeling
of coma features and Bayesian statistics to determine confidence intervals for the used parameters such as size and brightness of the coma. The results obtained with this method agree with the early Rosetta observations (Tubiana et al. 2015), but the large uncertainty of the results presented here is mainly due to the small apparent size and the faintness of the comet coma.
Although the S/N of some observations are relatively low, the results show that optical monitoring of 67P with the NOT is feasible and can provide the information needed to aid the Rosetta mission. Starting from late Spring 2014, the brightness of 67P has increased significantly, and the S/N has improved. This allows us to obtain more precise photometry and to closely follow the comet activity during the Rosetta mission. The enhanced S/N after the conjunction will make it possible to estimate size, color, and brightness of the coma using the automatic algorithms presented above. It is also planned to correlate observed magnitudes with the area of illuminated surface, gas density, or other in situ measurements made by the Rosetta spacecraft. Automated background-subtraction methods such as the one presented by Snodgrass et al. (2013) can also be applied to the observations in the near future to improve photometry in crowded fields.
SDSS data release 4, http://classic.sdss.org/dr4/algorithms/sdssUBVRITransform.html
Acknowledgments
This work was supported by the Academy of Finland grant number 277375 (H.L., B.Z.). This research is based on observations made with the Nordic Optical Telescope, operated by the Nordic Optical Telescope Scientific Association at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. The data presented here were obtained with ALFOSC, which is provided by the Instituto de Astrofisica de Andalucia (IAA) under a joint agreement with the University of Copenhagen and NOTSA.
References
- Howell, S. B. 1989, PASP, 101, 616 [NASA ADS] [CrossRef] [Google Scholar]
- Lasker, B. M., Lattanzi, M. G., McLean, B. J., et al. 2008, AJ, 136, 735 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pursimo, T., Ojha, R., Jauncey, D. L., et al. 2013, ApJ, 767, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, R., Stüwe, J. A., & Boehnhardt, H. 2004, A&A, 422, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Snodgrass, C., Tubiana, C., Bramich, D. M., et al. 2013, A&A, 557, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tody, D. 1986, in Instrumentation in Astronomy VI, ed. D. L. Crawford, SPIE Conf. Ser., 627, 733 [Google Scholar]
- Tubiana, C., Snodgrass, C., Bertini, I., et al. 2015, A&A, 573, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zacharias, N., Finch, C. T., Girard, T. M., et al. 2013, AJ, 145, 44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Images of comet 67P taken with the NOT. On the left side: observations from the summer 2013. Images are smoothed with the Gaussian kernel with σ = 3 pixels. On the right side: observations from the late spring 2014. The comet is clearly visible and the good S/N allows precise brightness measurements and even the study of the surface brightness profile. |
| In the text | |
 |
Fig. 2 Close to linear dependence on a magnitude correction Vmeasured−V on the color of the star for observations on 11 March 2014. Some points clearly deviate from general statistics, which is an indicator for a bad photometric measurement such as the saturation of the CCD or background objects in the aperture. These points are excluded from the calculations. |
| In the text | |
 |
Fig. 3 Light curve of 67P. Blue points represent V-band observations and red snowflakes R-band observations. Error bars represent 1σ error limits for magnitude estimates. Prediction of the visual magnitude by the MPC ephemerides shifted down by 2 is shown as a solid green line. In case of no-detection, 3σ upper limits for low S/N observations are presented by the down pointing triangles. |
| In the text | |
 |
Fig. 4 Posterior distribution of the exponential model fitting the coma on 21 August 2014 R-band observations. The red area indicates the 68% confidence limits, and the yellow square in the center is a maximum likelihood point corresponding to a coma contribution of 85% to the overall brightness and the FWHM of the coma profile at about the 240 km distance. The result is in some sense degenerated: the brighter coma implies more compact distribution, while the fainter coma is connected with its larger spatial size. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


