EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 582 (October 2015) A&A, 582 (2015) L13 Full HTML
Free Access
Issue
A&A
Volume 582, October 2015
Article Number L13
Number of page(s) 4
Section Letters
DOI https://doi.org/10.1051/0004-6361/201526874
Published online 21 October 2015

© ESO, 2015

1. Introduction

It is largely accepted that Galactic cosmic rays, which pervade the interstellar medium, are likely produced in shock waves in supernova remnants (Drury 1983). Cosmic rays activate the rich chemistry that is observed in a molecular cloud (Duley & Williams 1984), and also regulate its collapse timescale (Balbus & Hawley 1991; Padovani et al. 2014), determining the efficiency of star and planet formation. However, cosmic rays cannot penetrate the densest parts of a molecular cloud, where the formation of stars is expected, as a result of energy losses and magnetic field deflections (Padovani et al. 2009, 2013; Padovani & Galli 2011; 2013; Cleeves et al. 2013). Recently, observations towards young protostellar systems show a surprisingly high value of the ionisation rate (Ceccarelli et al. 2014; Podio et al. 2014), the main indicator of the presence of cosmic rays in molecular clouds. Synchrotron emission, the typical feature of relativistic electrons, was also detected towards the bow shock of a T Tauri star (Ainsworth et al. 2014). Nevertheless, the origin of these signatures unique to energetic particles is still puzzling. Here we show that particle acceleration can be driven by shock waves occurring within protostars.

2. Particle acceleration in shocks

This works focuses on shock acceleration by means of the diffusive shock acceleration (DSA) mechanism. Also known as first-order Fermi acceleration, DSA is a process where charged particles systematically gain energy while crossing a shock front. Multiple shock crossings allow the particle energy to rapidly increase, reaching the relativistic domain. The motion of particles back and forth from upstream to downstream requires the presence of magnetic fluctuations that produce a scattering of the pitch angle, namely the angle between the particle’s velocity and the mean magnetic field (Drury 1983; Kirk 1994). We argue below that the accelerated particles themselves can produce the necessary fluctuations to maintain DSA around shocks, as discussed e.g. in Bell (1978).

In the following subsections, we describe all the conditions that have to be satisfied to effectively accelerate protons and electrons through DSA. The acceleration of helium and heavier nuclei will be presented in a subsequent paper. All the constraints limiting the maximum energy of the accelerated particles are written as functions of the upstream flow velocity in the shock reference frame, Ush = vfl − vsh, vfl and vsh are the flow and the shock velocities in the observer reference frame, respectively. Our aim is to compute the maximum energy, Emax, reached by a particle in the regime where ions and neutrals are coupled. As explained in Sect. 2.3, in this case the damping of the Alfvén waves, which determines the confinement of particles, is weak and particle acceleration is more effective.

2.1. Condition on shock velocity

In order to have efficient particle acceleration, the flow has to be supersonic and super-Alfvénic. These two conditions are combined into the following relation Ush,2>max{9×10-2[γadT4(1+x)]0.5,2×10-4n6-0.5B-5},\begin{equation} \label{Uhighercsva} U_{\rm sh,2}>\max\left\{9\times10^{-2}\left[\gamma_{\rm ad} T_{4}(1+x)\right]^{0.5},2\times10^{-4}n_{6}^{-0.5}B_{-5}\right\}, \end{equation}(1)where Ush,2 has units of 102 km s-1, γad is the adiabatic index, T4 the upstream temperature in 104 K, n6 the total number density of hydrogen in 106 cm-3, x the ionisation fraction, and B-5 the magnetic field strength in 10-5 G. The two terms in square brackets on the right-hand side of Eq. (1) are the ambient (or upstream) sound speed and the Alfvén speed of the total gas in 102 km s-1, respectively.

2.2. Condition on low-energy particle acceleration: collisional losses

We are interested in the acceleration of low-energy particles (≲100 MeV−1 GeV) because they are responsible for the bulk of the ionisation. We have to verify that the shock acceleration rate is larger than the collisional loss rate (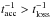tacc-1>tloss-1\hbox{$t^{-1}_{\rm acc}>t^{-1}_{\rm loss}$}). Following Drury et al. (1996), the acceleration rate is given by 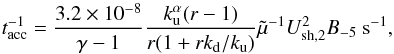tacc-1=3.2×10-8γ−1kuα(r−1)r(1+rkd/ku)μ-1˜Ush,22B-5s-1,\begin{equation} \label{nuacc} t^{-1}_{\rm acc}=\frac{3.2\times10^{-8}}{\gamma-1}\frac{k_{\rm u}^{\alpha}(r-1)}{r(1+rk_{\rm d}/k_{\rm u})} \tilde\mu^{-1} U_{\rm sh,2}^{2}B_{-5}~\mathrm{s^{-1}}, \end{equation}(2)where 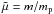˜μ=m/mp\hbox{$\tilde\mu=m/m_{\rm p}$} is the particle mass normalised to the proton mass, ku and kd are the diffusion coefficients in the upstream and downstream media, respectively, normalised to the Bohm value for protons, ku,d−α=κu,dκB=3eBγβ2mpc3κu,d,\begin{equation} k_{\rm u,d}^{-\alpha}=\frac{\kappa_{\rm u,d}}{\kappa_{\rm B}}=\frac{3eB}{\gamma\beta^{2}m_{\rm p}c^{3}}\kappa_{\rm u,d}, \end{equation}(3)where γ is the Lorentz factor, β=γ-1γ2−1\hbox{$\beta=\gamma^{-1}\sqrt{\gamma^{2}-1}$}, and r is the shock compression ratio. For a parallel shock, α = −1 and κu = κd, while for a perpendicular shock, α = 1 and κu = rκd1. The energy loss rate is given by tloss-1=3.2×10-9βγ−1μ-1˜n6L-25s-1,\begin{equation} \label{nuloss} t^{-1}_{\rm loss}=3.2\times10^{-9}\frac{\beta}{\gamma-1} \tilde\mu^{-1}n_{6}L_{-25}~\mathrm{s^{-1}}, \end{equation}(4)where L-25 is the energy loss function (Padovani et al. 2009) in units of 10-25 GeV cm2 which was extended to lower energies including Coulomb losses (for protons, Mannheim & Schlickeiser 1994; and electrons, Swartz et al. 1971) and synchrotron losses (Schlickeiser 2002). The maximum energy of accelerated particles set by energy losses, Eloss, is found when 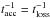tacc-1=tloss-1\hbox{$t^{-1}_{\rm acc}=t^{-1}_{\rm loss}$}, specifically 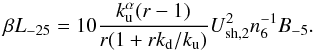βL-25=10kuα(r−1)r(1+rkd/ku)Ush,22n6-1B-5.\begin{equation} \label{FEloss} \beta L_{-25} = 10\frac{k_{\rm u}^{\alpha}(r-1)}{r(1+rk_{\rm d}/k_{\rm u})} U_{\rm sh,2}^{2}n_{6}^{-1}B_{-5}. \end{equation}(5)

2.3. Condition on particle acceleration: ion-neutral friction

The main limit on the possibility of particle acceleration is given by the presence of an incomplete ionised medium. In fact, the collision rate between ions and neutrals can be as high as to decrease the effectiveness of the DSA, damping the particle’s self-generated Alfvén waves responsible for the particle scattering the shock back and forth. Ions and neutrals are effectively decoupled if the wave frequency is larger than the ion-neutral collision frequency. Following Drury et al. (1996) and accounting for the fact that particles are not fully relativistic, we find that the critical energy separating these two regimes, Ecoup, is derived by solving the following relation 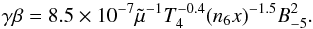γβ=8.5×10-7μ-1˜T4-0.4(n6x)-1.5B-52.\begin{equation} \label{Edamp} \gamma\beta=8.5\times10^{-7}\tilde\mu^{-1}T_{4}^{-0.4}(n_{6}x)^{-1.5}B_{-5}^{2}. \end{equation}(6)If the particle energy is larger than Ecoup, ions and neutrals are coupled.

The upper cut-off energy due to wave damping, Edamp, is set by requiring that the flux of accelerated particles advected downstream by the flow is equal to the flux of particles lost upstream because of the lack of waves (due to wave damping) to confine the particles. Following Drury et al. (1996), using their exact equation for the wave damping rate, accounting for departures from fully relativistic behaviour, and assuming Ush to be much larger than the Alfvén speed, Edamp follows from 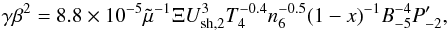γβ2=8.8×10-5μ-1˜ΞUsh,23T4-0.4n6-0.5(1−x)-1B-5-4P-2′,\begin{equation} \label{Ecut} \gamma\beta^{2}=8.8\times10^{-5}\tilde\mu^{-1}\Xi U_{\rm sh,2}^{3}T_{4}^{-0.4}n_{6}^{-0.5}(1-x)^{-1}B_{-5}^{-4}P^{\prime}_{-2}, \end{equation}(7)where 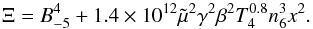Ξ=B-54+1.4×1012μ2˜γ2β2T40.8n63x2.\begin{equation} \label{XI} \Xi=B_{-5}^{4}+1.4\times10^{12}\tilde\mu^{2}\gamma^{2}\beta^{2} T_{4}^{0.8}n_{6}^{3}x^{2}. \end{equation}(8)Both Eqs. (6) and (7) are valid for T ∈ [ 102,105 ] K. 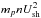The parameter P-2′\hbox{$P^{\prime}_{-2}$} is the fraction of the shock energy (mpnUsh2\hbox{$m_{p}nU_{\rm sh}^{2}$}) going into particle acceleration in 10-2, which is proportional to the shock efficiency η ∈ [ 10-6,10-3 ] (Bykov 2004) and represents the fraction of particles extracted from the thermal plasma that is injected into the acceleration process by a shock. We predict both non-relativistic and mildly relativistic accelerated particles and we checked a posteriori that there is no strong back reaction. This means that the upstream medium is not warned by these particles that a shock is coming and we can safely assume that the shock and DSA process are unmodified. In other words, calculations are carried out in the test-particle limit.

If Edamp>Ecoup, then Edamp is in the coupled regime, namely neutrals coherently move with ions and ion-generated waves are weakly damped. The last inequality can be written by combining Eqs. (6) and (7) as 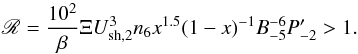R=102βΞUsh,23n6x1.5(1−x)-1B-5-6P-2′>1.\begin{equation} \label{Rratio} {\mathscr R} =\frac{10^{2}}{\beta} \Xi U_{\rm sh,2}^{3} n_{6}x^{1.5}(1-x)^{-1} B_{-5}^{-6}P^{\prime}_{-2} >1. \end{equation}(9)We consider shocks in three types of environments: in jets as well as in accretion flows in the collapsing envelopes and on the surfaces of protostars. Using the range of parameters of Table 1, we find that R≪ 1 in protostellar envelopes (Sect. 3). This is to say that the following two conditions on shock age and geometry (Sect. 2.4) are only discussed with reference to shocks in jets and on protostellar surfaces.

2.4. Conditions due to shock age and geometry

The maximum energy set by the age of the shock, Eage, is found when the acceleration time, given by the inverse of Eq. (2), is equal to the age of the shock. The latter can be assumed of the order of the dynamical time of the jet (≳103 yr, de Gouveia Dal Pino 1995) or equal to the accretion time in the case of a surface shock (~105 yr, Masunaga & Inutsuka 2000). Then, Eage is computed from γ−1=103kuα(r−1)r(1+rkd/ku)μ-1˜Ush,22B-5tage,3,\begin{equation} \label{Eage} \gamma-1=10^{3}\frac{k_{\rm u}^{\alpha}(r-1)}{r(1+rk_{\rm d}/k_{\rm u})} \tilde\mu^{-1} U_{\rm sh,2}^{2}B_{-5}t_{\rm age,3}, \end{equation}(10)with tage,3 in units of 103 yr.

A further constraint is given by the geometry of the shock. In particular, the upstream diffusion length, λu = κu/Ush, has to be at most a given fraction ϵ< 1 of the shock radius, Rsh; besides, in the jet configuration particles may also escape in the transverse direction. The shock can be assumed to be planar as long as the particle’s mean free path around the shock is smaller than the transverse size of the jet, R⊥. The maximum energy due to upstream escape losses, Eesc,u, follows from 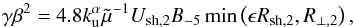γβ2=4.8kuαμ-1˜Ush,2B-5min(ϵRsh,2,R⊥,2),\begin{equation} \label{FEescu} \gamma\beta^{2}=4.8 k_{\rm u}^{\alpha} \tilde\mu^{-1} U_{\rm sh,2}B_{-5}\min\left(\epsilon R_{\rm sh,2},R_{\perp,2}\right), \end{equation}(11)where both Rsh,2 and R⊥ ,2 are in units of 102 AU. In the following we assume ϵ = 0.1 (Berezhko et al. 1996). Since jet shocks have a small transverse dimension, there is a further condition for the escape of particles downstream: the maximum energy due to downstream escape losses, Eesc,d, is found when the acceleration time, inverse of Eq. (2), is equal to the downstream diffusion time, 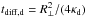tdiff,d=R⊥2/(4κd)\hbox{$t_{\rm diff,d}=R_{\perp}^{2}/(4\kappa_{\rm d})$} 2, namely 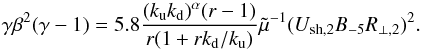γβ2(γ−1)=5.8(kukd)α(r−1)r(1+rkd/ku)μ-1˜(Ush,2B-5R⊥,2)2.\begin{equation} \label{FEescd} \gamma\beta^{2}(\gamma-1)=5.8\frac{(k_{\rm u}k_{\rm d})^{\alpha}(r-1)}{r(1+rk_{\rm d}/k_{\rm u})} \tilde\mu^{-1} (U_{\rm sh,2}B_{-5}R_{\perp,2})^{2}. \end{equation}(12)Finally, if the shock is supersonic and super-Alfvénic (Eq. (1)) and if R> 1 (Eq. (9)), the maximum energy reached by a particle is Emax = min [ Eloss,Edamp,Eage,Eesc,u,Eesc,d ].

3. Potential particle acceleration sites

In this section, we identify and characterise possible sites of particle acceleration in protostars. In particular, we consider accretion flows in the collapsing envelopes and on protostellar surfaces as well as jets. The required parameters needed to prove the effectiveness of shock acceleration are shown in Table 1.

It is straightforward to verify that Eq. (9) is not fulfilled in envelopes (R≪ 1). The ionisation fraction and the shock velocity are too small, quenching the particle acceleration. The magnetic field strength is also large enough to produce a sub-Alfvénic shock. This rules out envelopes as a possible shock acceleration sites. From now on we focus on shocks in jets and on protostellar surfaces.

Table 1

Values of the parameters described in the text.

3.1. Jets

Jets are observed at all stages during the evolution of a protostar (e.g. McCaughrean et al. 2002; Reipurth et al. 1997; Watson & Stapelfeldt 2004). Jet speeds, vfl, are similar for different classes (60−300 km s-1) with shock velocities, vsh, of the order of 20−140 km s-1 (Raga et al. 2002; 2011; Hartigan & Morse 2007; Agra-Amboage et al. 2011), then Ush = 40−160 km s-1. The neutral density is between 104 and 107 cm-3 (Lefloch et al. 2012; Gómez-Ruiz et al. 2012) with temperatures of the order of 104 K up to about 106 K (Frank et al. 2014). There is only one theoretical estimate for the magnetic field strength (B ~ 300−500 μG) for Class II sources (Teşileanu et al. 2009; 2012). The transverse radius of a jet is about 5 AU, 10 AU, and 50 AU at 15 AU, 100 AU, and 1000 AU from the source, respectively (Cabrit et al. 2007; Hartigan et al. 2004). The ionisation fraction in Class I and II are similar, x ~ 0.05−0.9 (Nisini et al. 2005; Maurri et al. 2014), while Class 0 jets are mainly molecular (Dionatos et al. 2010).

3.2. Accretion flows on protostellar surfaces

We use the computational results of the protostellar collapse of an initially homogeneous cloud core described in Masunaga & Inutsuka (2000). Their simulation describes the phase of main accretion, when the protostar mass grows because of the steady accretion from the infalling envelope. They give the temporal evolution of temperature, density, and flow velocity which, assuming a stationary shock, is equal to the shock velocity. The radius of the protostar is set to 2 × 10-2 AU and we find that only the last time step of the simulation, corresponding to the end of the main accretion phase, leads to a strong proton acceleration. Parameters are listed in the third row of Table 1.

4. Maximum energy of the accelerated particles

For jet shocks we perform a parametric study using the values in the second row of Table 1, assuming a parallel shock, η = 10-5, and T = 104 K. We also consider κu = κB, which is the most favourable circumstance for accelerating particles (Drury et al. 1983) and we compute Emax for Rsh = 100 AU and R⊥ = 10 AU. The upper panel of Fig. 1 shows the maximum energy that a shock-accelerated proton can reach. By increasing both Ush and B, Emax attains higher values up to about 13 GeV for protons. Once the combination of parameters satisfies the condition R> 1, Emax rapidly reaches a constant value, encompassed by the cyan contours in each subplot. In fact, the maximum energy is controlled by Eesc,d that is independent of both n and x. Supposing the magnetic field to have a strong toroidal component, we repeat the calculation for the case of a perpendicular shock finding that Emax decreases by a factor of about 1.3, since Eesc,d⊥/Eesc,d∥∝(r+1)/(2r)\hbox{$E_{\rm esc,d}^{\perp}/E_{\rm esc,d}^{\parallel}\propto (r+1)/(2r)$} 3.

For shocks on protostellar surfaces, we use values in the third row of Table 1, varying x and B. Assuming η = 10-5, ku=1, and a parallel shock, we find values of Emax for protons up to about 26 GeV for B ~ 3−10 G (see lower panel of Fig. 1), which are comparable with magnetic field intensities computed by e.g. Garcia et al. (2001). As a result of high temperatures, Coulomb losses are dominant and Emax is constrained by Eloss. Thus, for a perpendicular shock, Emax is a factor of about 1.3 larger, since 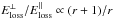Eloss⊥/Eloss∥∝(r+1)/r\hbox{$E_{\rm loss}^{\perp}/E_{\rm loss}^{\parallel}\propto (r+1)/r$}. Hatched areas in both panels of Fig. 1 show regions where acceleration is not possible because of strong wave damping.

Electrons can be accelerated as well, but generally Emax for electrons is much smaller than Emax for protons because of wave damping and stronger energy losses. For instance, for Ush = 160 km s-1 and B = 1 mG, Emax ~ 300 MeV for a narrow range of density and ionisation fraction (n ≳ 3 × 106 cm-3, x ≳ 0.6). For lower values of B and Ush, Emax ≲ 50 MeV. We also find that electron acceleration is not triggered by protostellar surface shocks.

thumbnail Fig. 1

Upper panel: case of a parallel shock in jets: ionisation fraction, x, versus density of neutrals, n, for Ush = 40 and 160 km s-1, B = 50 μG and 1 mG, and T = 104 K. Lower panel: case of parallel (left) and perpendicular (right) shocks on protostellar surfaces: ionisation fraction, x, versus magnetic field strength, B, for Ush = 260 km s-1, T = 9.4 × 105 K, and n = 1.9 × 1012 cm-3. Colour maps show values of Emax for protons and cyan contours delimit the regions where Emax reaches its maximum constant value shown in GeV in each subplot. Vertically hatched regions refer to combinations of parameters corresponding to strong wave damping (R< 1).

5. Discussion and conclusions

We investigated the possibility of accelerating particles within a protostellar source by means of shock processes through the diffusive shock acceleration mechanism. We focused our attention on the effectiveness of shocks in envelopes, on protostellar surfaces, and in jets. We concluded that:

  • (i)

    In envelopes, x and Ush are too small, preventing any particle acceleration. Besides, B is as large as to yield sub-Alfvénic shocks.

  • (ii)

    Jet shocks are possible accelerators of particles that can be easily boosted up to relativistic energies. The acceleration is more efficient for protons which can reach up to about 13 or 10 GeV (for parallel or perpendicular shocks, respectively), while electrons attain at most about 300 MeV because of wave damping and energy losses.

  • (iii)

    Protostellar surface shocks can accelerate protons up to about 26 or 37 GeV (for parallel or perpendicular shocks, respectively). Electrons cannot be accelerated mainly because of large magnetic field strengths leading to synchrotron losses.

The set of conditions that has to be fulfilled is highly non-linear: small variations in one or more parameters (B, x, n, T, Ush, η, ku, kd) can make the acceleration process inefficient. As a consequence, since young protostars are highly dynamic systems, particle acceleration can be a very intermittent process. In a subsequent paper, we will discuss in detail other possible acceleration mechanisms as well as the effect of variations in the parameter set and the distance of the jet shocks from the protostar, including departures from Bohm-type diffusion with the aim of studying the propagation of high-energy particles in the protostellar environment to explain the available observations.

1

A parallel/perpendicular shock is when the shock normal is parallel/perpendicular to the ambient magnetic field, respectively.

2

The factor 4 in the denominator comes from the fact that the diffusion process in the perpendicular direction is in two dimensions.

3

Superscripts ⊥ and ∥ refer to perpendicular and parallel shocks, respectively.

Acknowledgments

We thank Elena Amato, Francesca Bacciotti, Sylvie Cabrit, Claudio Codella, Daniele Galli, and Linda Podio for valuable discussions about jets in protostars and shock properties. We also thank the anonymous referee for a careful reading and thoughtful comments. We acknowledge the financial support of the Agence National pour la Recherche (ANR) through the COSMIS project. This work has been carried out thanks to the support of the OCEVU Labex (ANR-11-LABX-0060) and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French government programme managed by the ANR. M.P. and A.M. also acknowledge the support of the CNRS-INAF PICS project “Pulsar wind nebulae, supernova remnants and the origin of cosmic rays”.

References

  1. Agra-Amboage, V., Dougados, C., Cabrit, S., & Reunanen, J. 2011, A&A, 532, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Ainsworth, R. E., Scaife, A. M. M., Ray, T. P., et al. 2014, ApJ, 792, 18 [NASA ADS] [CrossRef] [Google Scholar]
  3. Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bell, A. R. 1978, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
  5. Berezhko, E. G. 1996, Astropart. Phys., 5, 367 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bykov, A. M. 2004, Adv. Space Rev., 33, 366 [Google Scholar]
  7. Cabrit, S., Codella, C., Gueth, F., et al. 2007, A&A, 468, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Ceccarelli, C., Dominik, C., López-Sepulcre, A., et al. 2014, ApJ, 790, L1 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cleeves, L. I., Adams, F. C., & Bergin, E. A. 2013, ApJ, 772, 5 [NASA ADS] [CrossRef] [Google Scholar]
  10. de Gouveia Dal Pino, E. M. 1995, AIP Conf. Ser., 345, 427 [Google Scholar]
  11. Dionatos, O., Nisini, B., Cabrit, S., Kristensen, L., & Pineau Des Forêts, G. 2010, A&A, 521, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Drury, L. O’C. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
  13. Drury, L. O’C., Duffy, P., & Kirk, J. G. 1996, A&A, 309, 1002 [NASA ADS] [Google Scholar]
  14. Duley, W. W., & Williams, D. A. 1984, Interstellar Chemistry (Academic Press) [Google Scholar]
  15. Frank, A., Ray, T. P., Cabrit, S., et al. 2014, Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & Th. Henning (Tucson: University of Arizona Press), 451 [Google Scholar]
  16. Garcia, P. J. V., Ferreira, J., Cabrit, S., & Binette, L. 2001, A&A, 377, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Gómez-Ruiz, A. I., Gusdorf, A., Leurini, S., et al. 2012, A&A, 542, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Hartigan, P., & Morse, J. 2007, ApJ, 660, 426 [NASA ADS] [CrossRef] [Google Scholar]
  19. Hartigan, P., Edwards, S., & Pierson, R. 2004, ApJ, 609, 261 [NASA ADS] [CrossRef] [Google Scholar]
  20. Kirk, J. G. 1994, in Plasma Astrophysics, eds. A. O. Benz, & T., J.-L. Courvoisier (Berlin: Springer Verlag), 225 [Google Scholar]
  21. Lefloch, B., Cabrit, S., Busquet, G., et al. 2012, ApJ, 757, 25 [Google Scholar]
  22. Mannheim, K., & Schlickeiser, R. 1994, A&A, 286, 983 [NASA ADS] [Google Scholar]
  23. Masunaga, H., & Inutsuka, S. 2000, ApJ, 531, 350 [NASA ADS] [CrossRef] [Google Scholar]
  24. Maurri, L., Bacciotti, F., Podio, L., et al. 2014, A&A, 565, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. McCaughrean, M., Zinnecker, H., Andersen, M., Meeus, G., & Lodieu, N. 2002, The Messenger, 109, 28 [NASA ADS] [Google Scholar]
  26. Nisini, B., Bacciotti, F., Giannini, T., et al. 2005, A&A, 441, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Padovani, M., & Galli, D. 2011, A&A, 530, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Padovani, M., & Galli, D. 2013, in Cosmic Rays in Star-Forming Environments, eds. D. F. Torres, & O. Reimer, ASSP, 34, 61 [Google Scholar]
  29. Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Padovani, M., Hennebelle, P., & Galli, D. 2013, A&A, 560, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Padovani, M., Galli, D., Hennebelle, P., Commerçon, B., & Joos, M. 2014, A&A, 571, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Podio, L., Lefloch, B., Ceccarelli, C., Codella, C., & Bachiller, R. 2014, A&A, 565, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Raga, A. C., Velázquez, P. F., Cantó, J., & Masciadri, E. 2002, A&A, 395, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Raga, A. C., Noriega-Crespo, A., Lora, V., Stapelfeldt, K. R., & Carey, S. J. 2011, ApJ, 730, 17 [Google Scholar]
  35. Reipurth, B., Hartigan, P., Heathcote, S., Morse, J. A., & Bally, J. 1997, AJ, 114, 757 [NASA ADS] [CrossRef] [Google Scholar]
  36. Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
  37. Swartz, W. E., Nisbet, J. S., & Green, A. E. S. 1971, J. Geophys. Res., 76, 8425 [NASA ADS] [CrossRef] [Google Scholar]
  38. Teşileanu, O., Massaglia, S., Mignone, A., Bodo, G., & Bacciotti, F. 2009, A&A, 507, 581 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Teşileanu, O., Mignone, A., Massaglia, S., & Bacciotti, F. 2012, ApJ, 746, 96 [NASA ADS] [CrossRef] [Google Scholar]
  40. Watson, A. M., & Stapelfeldt, K. R. 2004, ApJ, 602, 860 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Values of the parameters described in the text.

In the text

All Figures

thumbnail Fig. 1

Upper panel: case of a parallel shock in jets: ionisation fraction, x, versus density of neutrals, n, for Ush = 40 and 160 km s-1, B = 50 μG and 1 mG, and T = 104 K. Lower panel: case of parallel (left) and perpendicular (right) shocks on protostellar surfaces: ionisation fraction, x, versus magnetic field strength, B, for Ush = 260 km s-1, T = 9.4 × 105 K, and n = 1.9 × 1012 cm-3. Colour maps show values of Emax for protons and cyan contours delimit the regions where Emax reaches its maximum constant value shown in GeV in each subplot. Vertically hatched regions refer to combinations of parameters corresponding to strong wave damping (R< 1).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.