| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526536 | |
| Published online | 20 October 2015 | |
Optical and radio variability of BL Lacertae⋆
1 Key Laboratory for Research in Galaxies and Cosmology, Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, PR China
e-mail: haritma@shao.ac.cn
2 Aryabhatta Research Institute of Observational Sciences (ARIES), Manora Peak, 263002 Nainital, India
3 Institute of Astronomy and National Astronomical Observatory, Bulgarian Academy of Sciences, 72 Tsarigradsko Shosse Blvd., 1784 Sofia, Bulgaria
4 Department of Physics, The College of New Jersey, PO Box 7718, Ewing, NJ 08628-0718, USA
5 Radio Astronomy Laboratory of Crimean Astrophysical Observatory, Crimea
6 Taras Shevchenko National University of Kyiv, 01601 Kiev, Ukraine
7 Instituto de Astrofísica de Andalucía (CSIC), Apartado 3004, 18080 Granada, Spain
8 Department of Astronomy, University of Michigan, 1085 South University Avenue, Ann Arbor, MI 48109, USA
9 Abastumani Observatory, Mt. Kanobili, 0301 Abastumani, Georgia
10 ZAH, Landessternwarte Heidelberg, Königsthul 12, 69117 Heidelberg, Germany
11 Engelhardt Astronomical Observatory, Kazan Federal University, 420 000 Tatarstan, Russia
12 Aalto University Metsähovi Radio Observatory, 00076 Aalto, Finland
13 Aalto University Department of Radio Science and Engineering, 00076 Aalto, Finland
Received: 15 May 2015
Accepted: 3 August 2015
Context. We extensively observed the prototype blazar, BL Lacertae, in optical and radio bands during an active phase in the period 2010–2013 when the source showed several prominent outbursts. We searched for possible correlations and time lags between the optical and radio band flux variations using multi-frequency data to learn about the mechanisms producing variability.
Aims. During an active phase of BL Lacertae, we searched for possible correlations and time lags between multi-frequency light curves of several optical and radio bands. We tried to estimate any possible variability timescales and inter-band lags in these bands.
Methods. We performed optical observations in B, V, R, and I-bands from seven telescopes in Bulgaria, Georgia, Greece, and India and obtained radio data at 36.8, 22.2, 14.5, 8, and 4.8 GHz frequencies from three telescopes in Crimea, Finland, and USA.
Results. Significant cross-correlations between optical and radio bands are found in our observations with a delay of cm-fluxes with respect to optical bands of ~250 days. The optical and radio light curves do not show any significant timescales of variability. BL Lacertae showed many optical “mini-flares” on short timescales. Variations on longer term timescales are mildly chromatic with the superposition of many strong optical outbursts. In radio bands, the amplitude of variability is frequency dependent. Flux variations at higher radio frequencies lead the lower frequencies by days or weeks.
Conclusions. The optical variations are consistent with being dominated by a geometric scenario where a region of emitting plasma moves along a helical path in a relativistic jet. The frequency dependence of the variability amplitude supports an origin of the observed variations intrinsic to the source.
Key words: galaxies: active / BL Lacertae objects: general / BL Lacertae objects: individual: BL Lacertae / galaxies: jets / quasars: general
Tables of the light curves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/582/A103
© ESO, 2015
1. Introduction
BL Lacertae is the prototype of the BL Lac class of active galactic nuclei and has long been observed in optical bands. It is highly variable in all wavelengths, ranging from radio to γ-ray bands (Raiteri et al. 2013, and references therein). This source is a favourite target of multi-wavelength campaigns of the Whole Earth Blazar Telescope/GLAST-Agile Support program (WEBT/GASP) and is well known for its intense optical variability in all accessible timescales (Villata et al. 2009; Raiteri et al. 2009; 2010; 2011; 2013, and references therein).
Raiteri et al. (2009) presented the multi-wavelength data (from radio to X-rays) of BL Lacertae of their 2007–2008 WEBT campaign and fitted the SEDs with an inhomogeneous, rotating helical jet model (Villata & Raiteri 1999; Ostorero et al. 2004; Raiteri et al. 2003), which includes synchrotron plus self-Compton emission from a helical jet plus a thermal component from the accretion disc. Larionov et al. (2010) studied the behaviour of BL Lacertae optical flux and colour variability and suggested the variability to be mostly caused by changes of the Doppler factor. Raiteri et al. (2010) studied the broadband emission and variability properties of the BL Lacertae during the period 2008–2009 and argued for a jet geometry in which changes in our viewing angle to the emitting regions plays an important role in the source’s multi-wavelength behaviour. Within the optical bands, a chromatic trend that is bluer when brighter was detected in BL Lacertae in previous studies (e.g. Villata et al. 2002; Gaur et al. 2012a; Agarwal & Gupta 2015).
Connection of optical and radio light curves has shown significant correlations, with a radio time delay of about 100 days, which can be explained by the geometric effects in a rotating helical path in a curved jet (Villata et al. 2009). This source is known to vary on different timescales, with the usual abbreviations of intra-day variations (IDV, within one night) to short-term variations (STV, on timescales of days to weeks) to long-term variations (LTV, on timescales of months and years; Gupta et al. 2004). BL Lacertae has been claimed to exhibit periodicities in its radio flux variations with a long-term component of P ~ 8 yr (Hagen-Thorn et al. 1997; Villata et al. 2004, 2009). Raiteri et al. (2013) collected exceptional optical sampling by the GLAST-AGILE Support Program of the WEBT during the outburst period of the BL Lacertae (2008–2012) and performed cross-correlations between the optical, γ-ray, X-ray and mm-wavelengths and suggest that the region producing the mm and X-ray radiation is located downstream from the optical and γ-ray emitting zone in the jet. They found a significant cross-correlation between the optical and mm flux densities with a time lag of 120−150 days. Recently, Guo et al. (2015) analysed the historical light curves of optical and radio bands from 1968–2014 to find possible periods of ~1.26 and ~7.50 yr, respectively.
The search for correlations between different bands provides crucial information for the emission mechanism and since the radio and optical bands are both attibuted to the synchrotron emission from the relativistic electrons in the jets of blazars, they are of particular importance. A key motivation of this study is to investigate the correlated optical and radio variability (at cm wavelengths) of BL Lacertae during its active state in 2010−2013 when the source showed multiple outbursts in both of these bands. Also, we studied the nature of STV and LTV in optical bands as well as variability behaviour in radio bands and their possible variability timescales. Over the course of three years, we performed quasi-simultaneous optical multi-band photometric data from seven telescopes in Bulgaria, Greece, Georgia, and India on 192 nights. The radio data were observed from Cremia, Finland, and USA at five frequencies: 36.8, 22.2, 14.5, 8, and 4.8 GHz on 302 nights.
The paper is presented as follows: in Sect. 2, we briefly describe the observations and data reductions. We present our results in Sect. 3, and Sect. 4 includes a discussion and our conclusions.
2. Observations and data reduction
2.1. Optical data
Observations of BL Lacertae started on June 2010 and ran through July 2013 and the entire timeline of the observational period, along with the long-term light curves, are shown in Fig. 1. The observations were carried out at seven telescopes in Bulgaria, Greece, Georgia, and India. The telescopes and cameras that were involved in these observations are described in detail in Gaur et al. (2012b).
Most of the observations were made at the 50/70 cm Schmidt and the 2 m Ritchey–Chretien telescopes at the Rozhen National Astronomical Observatory, Bulgaria, the 60 cm Cassegrain Telescope at the Astronomical Observatory in Belogradchik, Bulgaria, and the 1.3 m Skinakas Observatory in Crete, Greece during the period June 2010 and July 2013. Instrumental magnitudes and the comparison stars were extracted using the MIDAS package DAOPHOT with an aperture radii of 4 arcsec. We used data of 50 days of observations from Rozhen 50/70 cm telescope, 35 from 2 m Rozhen, 72 from Belogradchik, and 25 from Skinakas Observatory.
The calibration of the source magnitude was performed with respect to the comparison stars B, C, and H (Fiorucci & Tosti 1996). The host galaxy of BL Lacertae is relatively bright. Hence, to remove its contribution from the observed magnitudes, we dereddened the data first, using the Galactic extinction coefficients of Schlegel et al. (1998), and then subtracted the host galaxy contribution from the observed magnitudes corresponding to that aperture radii (using Nilsson et al. 2007) to avoid its contamination in the extraction of colour indicies.
Observations of BL Lacertae on 10, 11, 12 and 14 June 2010 were carried out using the 1.04 m Sampurnanand telescope located at Nainital, India. Preprocessing of the raw data, which includes bias subtraction, flat-fielding, and cosmic ray removal was performed using standard data reduction procedures in IRAF. Reduction of the image frames was done using DAOPHOT II. Aperture photometry was carried out using four concentric aperture radii, i.e. ~1 × FWHM, 2 × FWHM, 3 × FWHM, and 4 × FWHM. We found that aperture radii of 2 × FWHM always provides the best S/N, so we adopted that aperture for our final results.
The observations at the Abastumani Observatory were conducted on 9, 11, 12, 14, 15, and 16 December 2010 at the 70-cm meniscus telescope (f/3). These measurements were made with an Apogee CCD camera Ap6E (1 K × 1 K, 24 micron square pixels) through a Cousins R filter with exposures of 60−120 s. Preprocessing of the raw data is done by IRAF. Reduction of the image frames were done using DAOPHOT II. An aperture radius of 5 arcsec was used for data analysis.
Finally, we also include the published R-band data from WEBT/GASP observations (Raiteri et al. 2013) during the period 2010−2013 where magnitudes are extracted for the BL Lacertae and the standard stars using an aperture radius of 8 arcsec. Hence, we dereddened the data using the Galactic extinction coefficient of Schlegel et al. (1998) and then removed the host galaxy contribution as described above. All the optical data are presented in the upper panel of Fig. 1.
2.2. Radio data
The observations were carried out with the 22-m radio telescope (RT-22) at the Crimean Astronomical Observatory (CrAO). For our measurements, we used two similar Dicke switched radiometers of 22.2 and 36.8 GHz. The antenna temperatures from sources were measured with the standard on–on method. Before measuring the intensity, we determined the source position with scanning. The radio telescope was then pointed at the source alternately by the principal and reference (arbitrary) beam lobes formed during beam modulation and having mutually orthogonal polarizations. The antenna temperature from a source was defined as the difference between the radiometer responses averaged over 30 s at two different antenna positions. Depending on the intensity of the emission from sources, we made a series of 6−20 measurements and then calculated the mean signal intensity and estimated the rms error of the mean.
 |
Fig. 1 Entire timeline of the observations in optical B, V, R, and I-bands (upper panel), the radio bands at 230 and 86 GHz (middle panel) and at 36.8 (and 37.0), 22.2, 14.5, 8.0, and 4.8 GHz frequencies (lower panel). The individual light curves and their offsets are labelled. |
The gain of the receiver was monitored using a noise generator every two to three hours. The orthogonal polarization of the lobes allowed us to measure the total intensity of the emission from sources, irrespective of the polarization of this emission. We took absorption in the Earth’s atmosphere into account using atmospheric scans made every three to four hours. The errors of the calculated optical depths are believed to be less than 10%. The errors of the measured flux densities include the uncertainties of: (1) the detected mean value of the antenna temperature of the sources; (2) the calibration source measurements; (3) the noise generator level measurement; and (4) the atmosphere attenuation corrections. The main contributions to the quoted errors come from the first two terms. The flux density scale of observations was calibrated using DR 21, 3C 274, Jupiter, and Saturn.
 |
Fig. 2 Short-term variability data for BL Lacertae in the R-band (in upper panel portions) for each labelled date and the respective average colour indices (B−R) for those nights (lower portions). |
Observations at 37.0 GHz were made with the 14 m radio telescope of Aalto University’s Metsähovi Radio Observatory in Finland. Data obtained at Metsähovi and RT-22 were combined in a single array to supplement each other. The flux density scale is set by observations of DR 21. Sources NGC 7027, 3C 274, and 3C 84 are used as secondary calibrators. A detailed description of the data reduction and analysis of Metsähovi data is given in Teraesranta et al. (1998). The error estimate in the flux density includes the contribution from the measurement rms and the uncertainty of the absolute calibration.
The lower frequency flux density observations were obtained with the University of Michigan 26-m equatorially-mounted, prime focus paraboloid (UMRAO) as part of the University of Michigan extragalactic variable source-monitoring program (Aller et al. 1985). Both total flux density and linear polarization observations were obtained as part of the programs measurements. Each daily-averaged observation of the target consisted of a series of 8 to 16 individual measurements obtained over 25 to 40 min. At 14.5 GHz the polarimeter consisted of dual, rotating feed horns that are linearly polarized, which were placed symmetrically about the paraboloids prime focus; these fed a broadband, uncooled HEMPT amplifier with a bandwidth of 1.68 GHz. At 8.0 GHz an uncooled, dual feed-horn beam-switching polarimeter and an on–on observing technique were employed; the bandwidth was 0.79 GHz. At 4.8 GHz a single feed-horn system with a central operating frequency of 4.80 GHz and a bandwidth of 0.68 GHz was used. The adopted flux density scale is based on Barrs et al. (1977) and uses Cassiopeia A (3C 461) as the primary standard. In addition to the observations of this primary standard, observations of nearby secondary flux density calibrators selected from a grid were interleaved with the observations of the target source every 1.5 to 3 h to verify the stability of the antenna gain and to verify the accuracy of the telescope pointing. For observations of BL Lacertae, Cygnus A (3C 405), DR 21 and NGC 7027 were used as calibrators.
We also included the published radio data at 230 and 86 GHz of Raiteri et al. (2013) from the IRAM 30 m Telescope. The calibration procedure for the IRAM 30 m Telescope’s data was described in detail in Agudo et al. (2010; 2014). The entirity of the radio band data are presented in the middle and lower panels of Fig. 1.
3. Results
3.1. Optical flux and colour variations
Short-term variablity timescales. We first discuss the variations that occured on timescales of days and weeks. These variations are seen by combining the continuous observations and the observations completed within one week. The light curves showing the short-term variability are shown in the upper portions of each panel in Fig. 2. It is obvious from the figures that during our observations BL Lacertae was very active and showed significant flux variations on short-term timescales. Typical rates of brightness change were 0.2−0.3 mag/day.
We have examined the nature of colour variations along with the flux variations on short-term timescales (shown in the lower portions of Fig. 2 panels) and we notice that colour variations generally follow flux variations, in the sense that the source is bluer when brighter.
 |
Fig. 3 Upper and lower panels respectively show the (B−R) and (V−R) behaviour with respect to R-band magnitude. |
Long-term variability timescales. We now discuss the variations that occured on months-long timescales. The long-term variability light curves are shown in Fig. 1 (upper panel). We found significant flux variations in the B, V, R, and I-bands and the variability in all the bands appears to be well correlated. During the first full multicolour observing season (segment 1), a roughly constant baseline flux is observed with small flares superimposed on it. In the next observing season (segment 2), BL Lacertae showed a ~2.5 mag decay leading to a decrease of the variability amplitude.
Variability analysis parameters at radio wavelengths.
We calculated (B−R) and (V−R) colour indices to examine the colour variability, and the resulting colour–magnitude diagrams are shown in Fig. 3. A linear fit is drawn in each plot and a slope of 0.039 ± 0.013 is found for (B−R) vs. R, with a linear Pearson correlation coefficient, r = 0.224, and its probability value, p = 0.003. The corresponding values for (V−R) vs. R are 0.042 ± 0.005 with r = 0.512 and p = 3.4 × 10-13. Together, these suggest a significant positive correlation between the colour index and brightness, in the sense that BL Lacertae is bluer when brighter.
On short-term timescales, the significant flux and colour variations can be explained by pure intrinsic phenomena, such as shocks accelerating electrons in the turbulent plasma jets, which then cool by synchrotron emission (e.g. Marscher 2014; Calafut & Wiita 2015) or the evolution of the electron density distribution of the relativistic particles leading to variable synchrotron emission (e.g. Bachev et al. 2011). The faster variations are mostly associated with the spectral changes and are related to very rapid electron injection and cooling processes.
Longer term variations are generally explained with a mixture of intrinsic and extrinsic mechanisms. The former are often thought to involve a plasma blob moving through the helical structures of the magnetic field in the jets (e.g. Marscher et al. 2008), which leads to variable compression and polarization (Marscher et al. 2008; Raiteri et al. 2013; Gaur et al. 2014) or shocks in the helical jets (e.g. Larionov et al. 2013). The latter include the geometrical effects when our viewing angle to a moving, discrete emitting region changes, thus causes variable Doppler boosting of the emitting radiation (e.g. Villata et al. 2009; Larionov et al. 2010; Raiteri et al. 2013). Hence, the long-term behaviour in blazar light curves is likely due to the superposition of both mechanisms (e.g. Pollack et al. 2015). The long-term trend, which is only mildly chromatic and may be quasi-periodic (e.g. Ghisellini et al. 1997; Raiteri et al. 2001; 2003; Villata et al. 2002; 2009) determines the base level flux oscillations (Villata et al. 2004), while the medium-term can come from turbulence (Pollack et al. 2015). Long-term variations of BL Lacertae were found to be mildly chromatic with slopes of ~0.1 by Villata et al. (2004). We found a significant positive correlation between (V−R) against R magnitude with a slope of 0.042, which can be explained by a Doppler factor variation on a spectrum slightly deviating from a power-law shape and is convex for a bluer-when-brighter trend (Villata et al. 2004). Also, for the LTV, spectrum shape changes over time are plausible; because of those changes, the chromatism can also vary and the resulting superposition of different slopes could yield an overall flattening of the spectrum (Bonning et al. 2012).
3.2. Radio data
The radio flux density (in Jy) light curves at 36.8, 22.2, 14.5, 8, and 4.8 GHz are presented in the lower panel of Fig. 1. Data at 230 and 86 GHz are taken from Raiteri et al. (2013) and are shown in the middle panel. The most frequently sampled data were at 36.8 GHz; they show moderate activity until JD 2 455 750. After that one strong radio outburst occured at around JD 2 455 890 and a more moderate one is seen at JD 2 455 960. The figure shows that the light curves at all the radio frequencies exhibit similar behaviours and appear to be well correlated with each other during the first flare; this is the case at 36.8 and 14.5 GHz during the second, briefer flare as well. However, at the radio frequency 22.2 GHz, there was a gap in the observations around JD 2 455 960 that is not clearly seen in the light curve, as presented in Fig. 1, so that flare was not detected.
The variability parameters are characterized as in Fuhrmann et al. (2008). The mean flux ⟨ S ⟩, variability index m, variability index of the calibrators m0, noise bias corrected variability amplitude Y and a reduced χ2 for a fit (where the BL Lacertae is considered to be variable if the χ2 gives a probability of ≤0.001 for the assumption of a constant flux) are presented in Table 1.
We find that BL Lacertae varies at all cm frequencies, on timescales of days with a variability index m of about 1.6−3.6 per cent. There is a systematic increase in the calibration-bias corrected variability index Y, from 5.73 at 4.8 GHz to 10.91 at 36.8 GHz. This type of variability amplitude increase with frequency was also observed in earlier studies (e.g. Aller et al. 1985; Raiteri et al. 2003; Fuhrmann et al. 2008). However, the opposite trend, i.e. variability amplitude decreasing with increase in frequency, has also been observed (Beckert et al. 2002; Gupta et al. 2012). These can be interpreted in terms of a variable source size arising from interstellar scintillation (ISS). The type of change of variation strength with observed frequency thus can be used to find the relative dominance of ISS over source intrinsic variability (e.g. Beckert et al. 2002; Krichbaum et al. 2002; Gupta et al. 2012). The observed frequency dependence of the variability amplitude and the correlated variability across all bands in our observations argue in favour of a source instrinsic origin of these observed variations. These are usually explained in the blazars by synchrotron cooling and adiabatic expansion of a flaring component or a shock (e.g. Marscher & Gear 1985).
To consider the behaviour of the radio spectra, we first calculate the 36.8−14.5 GHz spectral index α, defined as Sν ∝ να, for different brightnesses. The behaviour of the spectral index is plotted with respect to the flux density at 14.5 GHz and is shown in Fig. 4. There is a significant negative correlation with r = −0.378 and p = 0.0062. Hence, we see that the spectrum is becoming harder when the flux increases and we conclude that the strongly variable component then dominates the radio spectrum.
 |
Fig. 4 Radio spectral index between 36.8 and 14.5 GHz against flux density at 14.5 GHz. |
3.3. Auto and cross-correlations
We computed discrete correlation functions (DCF) following Edelson & Krolik (1988) to search for possible variability timescales and the time lags between multi-frequency light curves, respectively. The first step is to calculate the unbinned correlation (UDCF) using the given time series by  (1)Here, ai and bj are the individual points in two time series a and b, respectively,
(1)Here, ai and bj are the individual points in two time series a and b, respectively,  and
and  are the means of the time series, and
are the means of the time series, and 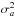 and
and  are their variances. The correlation function is binned after calculation of the UDCF. The DCF can be calculated by averaging the UDCF values for each time delay Δtij = (tbj−tai) lying in the range
are their variances. The correlation function is binned after calculation of the UDCF. The DCF can be calculated by averaging the UDCF values for each time delay Δtij = (tbj−tai) lying in the range 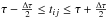 via
via  (2)The DCF analysis is used for finding the correlation and possible lags between the optical and radio frequencies. When the same data train is used, i.e. a = b, it is called the auto correlation function (ACF) and has always has a peak at zero lag, indicating that there is no time lag between the two, but any other strong peaks give indications of variability timescales. The normalization of the DCF depends on the selection of the means
(2)The DCF analysis is used for finding the correlation and possible lags between the optical and radio frequencies. When the same data train is used, i.e. a = b, it is called the auto correlation function (ACF) and has always has a peak at zero lag, indicating that there is no time lag between the two, but any other strong peaks give indications of variability timescales. The normalization of the DCF depends on the selection of the means 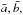 and variances
and variances 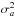 ,
,  , of each of the time series ai and bj, respectively (White & Peterson 1994). Hence, the most accurate determination of the peak of the DCF depends on using the best estimates of the means and the variances of both series in Eq. (1), which are generally taken to be the values determined from the entire time series. However, as these light curves are non-stationary statistical processes, their means and variances change with time. Hence, following White & Peterson (1994), we computed the mean and variance for both series ai and bj, only using the points that fall within a given time-lag bin to contribute to the calculation of the DCFs at each τ.
, of each of the time series ai and bj, respectively (White & Peterson 1994). Hence, the most accurate determination of the peak of the DCF depends on using the best estimates of the means and the variances of both series in Eq. (1), which are generally taken to be the values determined from the entire time series. However, as these light curves are non-stationary statistical processes, their means and variances change with time. Hence, following White & Peterson (1994), we computed the mean and variance for both series ai and bj, only using the points that fall within a given time-lag bin to contribute to the calculation of the DCFs at each τ.
 |
Fig. 5 ACF (R−R) of the optical data. |
3.3.1. Optical correlations
We performed auto-correlations in various optical bands to find the variability timescales in the optical bands. Figure 5 shows the ACF of the R-band. The ACF of R-band shows a peak at zero lag and then it decorrelates very fast with another peak at around 300 days. Since this peak is of low significance, we do not claim any variability timescale in the R-band. Similar behaviours are shown in the ACFs of the light curves in the B, V, and I-bands, hence, we do not show them in the figure. We conclude that we did not find any characteristic variability timescales in these optical measurements of BL Lacertae.
We performed a DCF between the B and R-bands, which is shown in Fig. 6, to examine any time delays between various optical bands. In the basic shock-in-jet model, time delays are expected between higher and lower frequencies as the high energy electrons emit synchrotron radiation first and then cool, emitting at lower frequencies. The DCF between the light curves shows a peak of around 0.8, indicating close correlation between the optical bands. In order to search for time delays, we fitted the peaks of the DCFs with Gaussian functions, but the time delay was consistent with zero lag. Similar behaviour was found with V versus R and I versus R DCFs. Hence, we conclude that we did not find any optical inter-band time lags on long-term trends. This could be because of the small differences in frequency between the various optical bands.
 |
Fig. 6 DCF (B vs. R) of the optical data. |
 |
Fig. 7 ACFs of the radio data at 36.8 GHz (upper panel) and 14.5 GHz (lower panel). |
 |
Fig. 8 DCFs of the radio data. Frequencies compared are written in each panel. |
3.3.2. Radio correlations
Similarly, we performed auto-correlations for various radio frequencies to search for any characteristic timescales. In Fig. 7, we show the ACF of the 36.8 (upper panel) and 14.5 GHz (lower panel) frequency light curves to search for variability timescales in radio bands. The ACFs of 36.8 and 14.5 GHz both show a strong peak (of >0.5) at ~500 days time lag but this timescale is just half of the duration of the overall coverage of the radio data, hence, we do not regard this timescale to be significant.
It is clear from Fig. 1 that all the radio frequencies exhibit similar behaviours and that the flux variations are decreasing when going from the higher to lower frequencies. To confirm this, we performed DCFs between the radio frequencies (36.8 vs. 22.2 GHz, 36.8 vs. 14.5 GHz, 36.8 vs. 8.0 GHz, and 36.8 vs. 4.8 GHz, shown in upper to lower panels in Fig. 8, respectively) and found that they are well correlated with each other in the sense that higher frequencies lead the lower frequencies. The DCF between 36.8 and 22.2 GHz frequencies (shown in the upper panel of Fig. 8) is very broad, but does not appear to be centered at zero lag; we fit it with a Gaussian function of the form ![\begin{equation} {\rm DCF} (\tau)=a \times {\rm exp}\left[\frac{-(\tau - m)^{2}}{2 \sigma^{2}}\right] \cdot \end{equation}](/articles/aa/full_html/2015/10/aa26536-15/aa26536-15-eq55.png) (3)Here, a is the peak value of the DCF; m is the time lag at which DCF peaks, and σ is the width of the Gaussian function. The error in the location of the peak of the DCF is clearly much smaller than the width of the Gaussian function (e.g. Peterson et al. 1988). We found that the variations at higher frequencies are very well correlated with a lag of 2.11 ± 1.19 days, with 36.8 leading the 22.2 GHz. Via visual inspection, it is clear that lower frequencies also lag behind the higher frequencies in the other panels. The Gaussian function fits to the DCFs yield time lags of ~ 2.90 ± 0.66 days between 36.8 GHz and 14.5 GHz (second panel), ~ 8.86 ± 2.71 days between 36.8 and 8 GHz (third panel), and ~ 25.76 ± 7.25 days between 36.8 and 4.8 GHz (lower panel), respectively. Hence, the flux variations at the higher frequencies are leading with respect to the lower frequencies, as is very common in blazars (e.g. Marscher & Gear 1985; Aller et al. 1999; Raiteri et al. 2001; 2003; Gupta et al. 2012).
(3)Here, a is the peak value of the DCF; m is the time lag at which DCF peaks, and σ is the width of the Gaussian function. The error in the location of the peak of the DCF is clearly much smaller than the width of the Gaussian function (e.g. Peterson et al. 1988). We found that the variations at higher frequencies are very well correlated with a lag of 2.11 ± 1.19 days, with 36.8 leading the 22.2 GHz. Via visual inspection, it is clear that lower frequencies also lag behind the higher frequencies in the other panels. The Gaussian function fits to the DCFs yield time lags of ~ 2.90 ± 0.66 days between 36.8 GHz and 14.5 GHz (second panel), ~ 8.86 ± 2.71 days between 36.8 and 8 GHz (third panel), and ~ 25.76 ± 7.25 days between 36.8 and 4.8 GHz (lower panel), respectively. Hence, the flux variations at the higher frequencies are leading with respect to the lower frequencies, as is very common in blazars (e.g. Marscher & Gear 1985; Aller et al. 1999; Raiteri et al. 2001; 2003; Gupta et al. 2012).
Flux variations where shorter wavelengths lead the longer wavelengths are commonly interpreted as a source intrinsic opacity effect due to synchrotron self-absorption (e.g. Kudryavtseva et al. 2011), which is further related to the source activity and shape of the radio spectrum. Similar evidence was found by Gupta et al. (2012), where they detected a significant time lag between 2.8 cm and the longer wavelengths, again with shorter leading the longer wavelengths.
3.3.3. Optical versus radio correlations
The optical and radio light curves of our observations are presented in Fig. 1. BL Lacertae exhibited multiple flares at optical frequencies in all bands. We have included the published WEBT data of optical R-band of Raiteri et al. (2013) to improve the data sampling even more. To investigate the possible correlations between optical and radio frequencies, we performed DCF analysis for the almost three year-long simultaneous data trains. There are two prominent flares in radio frequencies, one at JD 2 455 890 and the other at JD 2 455 960, and we first performed cross-correlations of the optical R-band with respect to the radio frequency at 36.8 GHz; this is the best sampled radio band, given that, as noted above, the second flare was missed at 22.2 GHz. The light curves reveal that the behaviour of the radio frequencies are quite different from those in the optical and there is no immediate correspondence between the flares in optical bands and those in the radio.
 |
Fig. 9 DCF between optical R-band versus radio frequency at 36.8 GHz. |
The DCF between R and 36.8 GHz band for the whole observing season is shown in Fig. 9 and produces a peak at around 250.28 ± 10.21 days. We fit the peak with Gaussian functions of the form described above and found significant correlations between them where positive lags indicate that the R-band is leading the radio frequency. The peak in the DCF presumably arises predominantly from connecting the optical outburst at around JD 2 455 700 with the radio outburst around JD 2 455 960. In the DCF, there is no significant correlation between the R-band and radio flux at zero time lag, which rules out the possibility of simultaneous optical and radio flares. We also performed cross-correlations between optical R-band and the lower radio frequencies in order to investigate the delays between them; we fit their DCFs with Gaussians and found peaks between 235 and 260 days.
The lags of around 235−260 days of the cm-frequencies with respect to the optical frequencies are in reasonable accordance with the results of Villata et al. (2009) for BL Lacertae during the period 1994−2003 where they found fair optical–radio correlations with different time delays of optical with respect to the radio events, varying from about 100 days to 300 days. The variable radio delay could be explained by the jet changing its orientation with respect to the line of sight, in that relativistic effects produce a variation in the observed timescales; if the jet region emitting the optical-to-radio radiation makes a smaller viewing angle, it yields a shorter delay of radio events with respect to the optical events (e.g. Villata et al. 2009).
4. Discussion and conclusions
We performed observations of the well-known blazar BL Lacertae in optical and radio bands during the period 2010−2013 and searched for possible correlations among them. Our optical observations were obtained from seven ground-based telescopes and taken on almost 200 nights. The source was very active and showed repeated “mini-flares” of 0.2−0.5 mag in amplitude on short timescales. Colour analysis of the long-term light curve reveals a significant correlation between the colour index and source brightness, with a bluer-when-brighter trend. But the slope of this trend is only 0.042, which is mildly chromatic according to Villata et al. (2004). Hence it can be explained by the superposition of different slopes during the flaring states, leading to an overall flattening of the spectrum.
Radio light curves at different frequencies are well correlated, with the flux amplitude becoming smaller with a decrease in radio frequency. The radio spectral index decreases with source brightness, which is very commonly observed in blazars. We cross correlated the different radio frequencies and found that flux variations at lower frequencies lag those at higher frequency with time delays ranging from days to weeks. This can be interpreted as the higher frequencies being emitted from the inner and denser parts of the jets, with the lower frequencies being emitted from comparatively more distant and less dense parts. Alternatively, Villata & Raiteri (1999) explained this type of behaviour by a rotating helical jet model, which causes time lags since the different frequency emitting portions of the jet acquire the same viewing angle at different times.
Many authors studied the correlations between optical and radio bands in the literature but the results of different sources do not show a common behaviour. On IDV timescales, radio and optical bands have been found to be correlated for the blazar S5 0716+714, which strongly favours an intrinsic origin for the former instead of the ISS effect (e.g. Quirrenbach et al. 1991; Wagner et al. 1996; Fuhrmann et al. 2008, and references therein). However, Gupta et al. (2012) did not find any significant correlation between these bands for the same source, and attributed the lack of correlation at that time to different physical causes: ISS at long radio wavelengths, but intrinsic origin in the optical.
On longer timescales, Villata et al. (2009) found significant delays among variations in optical and radio bands by about 100 days in the WEBT campaign of BL Lacertae and explained them in terms of an emitting plasma flowing along a rotating helical path in a curved jet. On other occasions, very weak correlations are found for BL Lacertae between optical and radio bands (i.e. Böttcher et al. 2003; Raiteri et al. 2003; Guo et al. 2015, and references therein).
In searching for possible correlations and time lags in the optical and radio bands for the observing seasons 2010–2013, where BL Lacertae has shown outbursts in both the bands, we included the published data of the optical R-band from Raiteri et al. (2013) to obtain better data sampling. Major optical outbursts, such as the strong flare at JD 2 455 700, do not produce simultaneous radio flux enhancements, but strong radio flares at JD 2 455 890 and 2 455 970 appear to be associated with the optical flares with time delays. In order to investigate the correlations, we performed DCFs between the R-band and various radio frequencies and found significant correlations between them with optical leading the radio frequencies. The typical time lag of ~ 250 days between the optical and the various radio frequencies appears to be due to the connection of the strong optical outburst at JD 2 455 700 with the strong radio outburst at JD 2 455 960. Raiteri et al. (2013) performed the correlation between their R-band and at mm-flux densities (at 230 and 86 GHz) and found strong correlation at a lag of 120−150 days. Hence, our results are consistent with those of Raiteri et al. (2013) since higher radio frequencies usually show shorter delays with respect to the optical emission. The delayed cm radio lags with respect to the R-band are in accordance with the inhomogeneous jet model, where synchrotron photons at lower frequencies are emitted from progressively more external regions as compared to the higher frequency photons.
In previous studies of BL Lacerate, it has been argued that the long-term variability arises because of the intrinsic as well as geometrical effects, and the relativistic effects produce a variation in the observed timescales due to a change of the jet orientation with respect to our line of sight (Villata et al. 2009; Raiteri et al. 2013, and references therein). During this period of 2010−2013, the behaviour of BL Lacerate can be explained by taking these scenarios where the higher radio frequencies lag behind the optical by about 120−150 days into account, and then the mechanism producing the flux enhancements propagates downstream where it produces the lower frequencies that lag behind the optical by ~250 days. Much longer and better sampled light curves are required to better understand the correlation and time lags between these bands.
Acknowledgments
We thank the referee for useful and constructive comments. We thank Dr. C. M. Raiteri for providing us with the WEBT R-band data. This work is partly based on data taken and assembled by the WEBT collaboration and stored in the WEBT archive at the Osservatorio Astrofisico di Torino – INAF (http://www.oato.inaf.it/blazars/webt/). This research was partially supported by Scientific Research Fund of the Bulgarian Ministry of Education and Sciences under grant DO 02-137 (BIn 13/09). The Skinakas Observatory is a collaborative project of the University of Crete, the Foundation for Research and Technology – Hellas, and the Max-Planck-Institut für Extraterrestrische Physik. H.G. is sponsored by the Chinese Academy of Sciences Visiting Fellowship for Researchers from Developing Countries (grant No. 2014FFJB0005) and supported by the NSFC Research Fund for International Young Scientists (grant No. 11450110398). A.C.G. is partially supported by the Chinese Academy of Sciences Visiting Fellowship for Researchers from Developing Countries (grant No. 2014FFJA0004). M. F. Gu acknowledges support from the National Science Foundation of China (grant No. 11473054) and the Science and Technology Commission of Shanghai Municipality (14ZR1447100). The Abastumani team acknowledges financial support of the project FR/639/6-320/12 by the Shota Rustaveli National Science Foundation under contract 31/76. The work at UMRAO was supported in part by a series of grants from the NSF and from the NASA Fermi Guest Investigator Program. The work is partially supported by India-Ukraine inter-governmental project Multiwavelength Observations of Blazars, No. INT/UKR/2012/P-02. The Metsähovi team acknowledges the support from the Academy of Finland to our observing projects (numbers 212656, 210338, 121148, and others). This paper is partly based on observations carried out at the IRAM 30-m Telescope, which is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain).
References
- Agudo, I., Thum, C., Wiesemeyer, H., & Krichbaum, T. P. 2010, ApJS, 189, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Agudo, I., Thum, C., Gómez, J. L., & Wiesemeyer, H. 2014, A&A, 566, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aller, H. D., Aller, M. F., Latimer, G. E., & Hodge, P. E. 1985, ApJS, 59, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Aller, M. F., Aller, H. D., Hughes, P. A., & Latimer, G. E. 1999, ApJ, 512, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Agarwal, A., & Gupta, A. C. 2015, MNRAS, 450, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Bachev, R., Semkov, E., Strigachev, A., et al. 2011, A&A, 528, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 61, 99 [NASA ADS] [Google Scholar]
- Beckert, T., Fuhrmann, L., Cimò, G., et al. 2002, Proc. 6th EVN Symp., 79 [Google Scholar]
- Bonning, E., Urry, C. M., Bailyn, C., et al. 2012, ApJ, 756, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M., Marscher, A. P., Ravasio, M., et al. 2003, ApJ, 596, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Calafut, V., & Wiita, P. J. 2015, JApA, 25 [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Fiorucci, M., & Tosti, G. 1996, A&AS, 116, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, L., Krichbaum, T. P., Witzel, A., et al. 2008, A&A, 490, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaur, H., Gupta, A. C., Strigachev, A., et al. 2012a, MNRAS, 420, 3147 [NASA ADS] [CrossRef] [Google Scholar]
- Gaur, H., Gupta, A. C., Strigachev, A., et al. 2012b, MNRAS, 425, 3002 [NASA ADS] [CrossRef] [Google Scholar]
- Gaur, H., Gupta, A. C., Wiita, P. J., et al. 2014, ApJ, 781, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Villata, M., Raiteri, C. M., et al. 1997, A&A, 327, 61 [NASA ADS] [Google Scholar]
- Guo, Y. C., Hu, S. M., Xu, C., et al. 2015, New A, 36, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A. C., Banerjee, D. P. K., Ashok, N. M., & Joshi, U. C. 2004, A&A, 422, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, A. C., Krichbaum, T. P., Wiita, P. J., et al. 2012, MNRAS, 425, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Hagen-Thorn, V. A., Marchenko, S. G., Mikolaichuk, O. V., & Yakovleva, V. A. 1997, Astron. Rep., 41, 154 [NASA ADS] [Google Scholar]
- Kudryavtseva, N. A., Gabuzda, D. C., Aller, M. F., & Aller, H. D. 2011, MNRAS, 415, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Krichbaum, T. P., Kraus, A., Fuhrmann, L., Cimò, G., & Witzel, A. 2002, PASA, 19, 14 [Google Scholar]
- Larionov, V. M., Villata, M., & Raiteri, C. M. 2010, A&A, 510, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larionov, V. M., Jorstad, S. G., Marscher, A. P., et al. 2013, ApJ, 768, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. 2014, ApJ, 780, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., D’Arcangelo, F. D., et al. 2008, Nature, 452, 966 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nilsson, K., Pasanen, M., Takalo, L. O., et al. 2007, A&A, 475, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ostorero, L., Villata, M., & Raiteri, C. M. 2004, A&A, 419, 913 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, B. M., Wanders, I., Horne, K., et al. 1998, PASP, 110, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, M., Pauls, D., & Wiita, P. J. 2015, ApJ, submitted [Google Scholar]
- Quirrenbach, A., Witzel, A., Wagner, S., et al. 1991, ApJ, 372, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Aller, H. D., et al. 2001, A&A, 377, 396 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raiteri, C. M., Villata, M., Tosti, G., et al. 2003, A&A, 402, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raiteri, C. M., Villata, M., Capetti, A., et al. 2009, A&A, 507, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raiteri, C. M., Villata, M., Bruschini, L., et al. 2010, A&A, 524, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raiteri, C. M., Villata, M., Aller, M. F., et al. 2011, A&A, 534, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raiteri, C. M., Villata, M., D’Ammando, F., et al. 2013, MNRAS, 436, 1530 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Teraesranta, H., Tornikoski, M., Mujunen, A., et al. 1998, A&AS, 132, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., & Raiteri, C. M. 1999, A&A, 347, 30 [NASA ADS] [Google Scholar]
- Villata, M., Raiteri, C. M., Kurtanidze, O. M., et al. 2002, A&A, 390, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., Raiteri, C. M., Kurtanidze, O. M., et al. 2004, A&A, 421, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villata, M., Raiteri, C. M., Larionov, V. M., et al. 2009, A&A, 501, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagner, S. J., Witzel, A., Heidt, J., et al. 1996, AJ, 111, 2187 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. J., & Peterson, B. M. 1994, PASP, 106, 879 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Entire timeline of the observations in optical B, V, R, and I-bands (upper panel), the radio bands at 230 and 86 GHz (middle panel) and at 36.8 (and 37.0), 22.2, 14.5, 8.0, and 4.8 GHz frequencies (lower panel). The individual light curves and their offsets are labelled. |
| In the text | |
 |
Fig. 2 Short-term variability data for BL Lacertae in the R-band (in upper panel portions) for each labelled date and the respective average colour indices (B−R) for those nights (lower portions). |
| In the text | |
 |
Fig. 3 Upper and lower panels respectively show the (B−R) and (V−R) behaviour with respect to R-band magnitude. |
| In the text | |
 |
Fig. 4 Radio spectral index between 36.8 and 14.5 GHz against flux density at 14.5 GHz. |
| In the text | |
 |
Fig. 5 ACF (R−R) of the optical data. |
| In the text | |
 |
Fig. 6 DCF (B vs. R) of the optical data. |
| In the text | |
 |
Fig. 7 ACFs of the radio data at 36.8 GHz (upper panel) and 14.5 GHz (lower panel). |
| In the text | |
 |
Fig. 8 DCFs of the radio data. Frequencies compared are written in each panel. |
| In the text | |
 |
Fig. 9 DCF between optical R-band versus radio frequency at 36.8 GHz. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


