| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 10 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201526442 | |
| Published online | 29 September 2015 | |
FTIR laboratory measurement of Ne i Rydberg states in 1.43−14.3 μm spectral range
1
J. Heyrovský Institute of Physical Chemistry, Academy of Sciences
of the Czech Republic, Dolejškova
3, 18223
Prague 8, Czech
Republic
e-mail:
svatopluk.civis@jh-inst.cas.cz
2
Institute of Physics, Academy of Sciences of the Czech
Republic, Na Slovance
2, 18221
Prague 8, Czech
Republic
3
Voronezh State University, 394693
Voronezh,
Russia
Received: 30 April 2015
Accepted: 26 July 2015
Context. The Ne i spectrum in the 800−1800 cm-1 (5.55−14.3 μm) domain has not been previously investigated.
Aims. To address this spectral gap, we performed high-resolution laboratory measurements of the Ne i emission spectrum over the 800−7000 cm-1 (1.43−14.3 μm) range.
Methods. The Ne i laboratory spectra were obtained from a pulsed discharge plasma and recorded using time-resolved Fourier transform spectroscopy. The identification of the spectral lines was performed according to the transition probability values calculated using the quantum defect method.
Results. Based on these measurements, we report the wavenumbers of 151 Ne i lines and energy values for 14 Ne i levels that are not listed in the available databases.
Key words: atomic data / line: identification / methods: laboratory: atomic / techniques: spectroscopic
© ESO, 2015
1. Introduction
Neon is one of the most abundant elements in space and has been detected in various interstellar objects in various spectral regions (Helton et al. 2012; Pandey & Lambert 2011; Takeda et al. 2010; Smith et al. 2009; Gehrz et al. 2008; Baldovin-Saavedra et al. 2011, 2012). An estimation of this α-element’s abundance in stars and star-forming regions provides useful information on the metallicity and rates of formation of these objects (Ho & Keto 2007). Moreover, neon is an inert gas and does not undergo chemical reactions with itself or other species. This makes neon a useful tool for studying the chemical evolution of star-forming regions because it is not affected by depletion factors associated with dust grains (Dors et al. 2013).
The abundance of neon (and other light elements) in stars also significantly affects the opacity of the stellar plasma. This in turn influences the overall conditions in the stellar body. Recently, a number of studies have been published concerning the abundances of the light elements such as C, N, O, and Ne (Drake 2011; Pandey & Lambert 2011; Takeda et al. 2010; Laming 2009; Drake & Ercolano 2007; Drake & Testa 2005; Cunha et al. 2006). These elements attract attention because they have played a crucial role in the development of solar models over the last several decades (Serenelli 2013). The so-called solar model problem, which arose from disagreements in the predictions of theoretical solar models as well as helioseismological measurements and simulations (Antia & Basu 2006; Morel & Butler 2008; Robrade et al. 2008), appeared after the solar abundances of light elements were lowered by 25−35% (Grevesse et al. 2007). Although a number of additional measurements and analyses have been reported (Cunha et al. 2006; Bochsler 2007; Morel & Butler 2008), the precise values of Ne abundances in stars are still being discussed.
The detection of neon in stars and other astronomical objects is based mainly on the measurement of the spectra of neon ions (Ne ii−Ne ix) over various spectral regions. Important and well-established tools for the estimation of neon abundance include X-ray spectrometry (Drake et al. 1994; Choi & Dotani 1998; Stelzer & Schmitt 2004; Liefke & Schmitt 2006; Balman 2005) and spectrometry in the UV/VIS spectral region (Curdt et al. 2001, 1997; Werner et al. 2004; Crockett et al. 2006; Baldovin-Saavedra et al. 2012).
A number of works have also been published in which Ne ion emission lines were detected in infrared (IR) spectra (Helton et al. 2012; Inami et al. 2013; Verma et al. 2003; Gehrz et al. 2008; Martín-Hernández et al. 2006; Sturm et al. 2002; Floc’h et al. 2001). In fact, the emission lines of Ne ions (Ne ii, Ne iii) are among the most prominent features in the mid-IR spectra of star-forming regions (Ho & Keto 2007).
However, the detection of Ne i is quite difficult. Neon atoms (and other noble gases) have very high excitation energies. For this reason, the Ne i upper excited states are not populated and the spectral lines do not appear in the solar spectrum (Magazzu et al. 1983). Still, the Ne i spectrum has been observed in other stellar objects. Takeda et al. (2010) detected two spectral lines ascribed to Ne i (6163.594 Å and 6143.063 Å) in the VIS spectra of a number of B-type stars.
This observation suggests the possibility that the Ne i spectra can also be detected in the IR region. The detection of Ne i in the spectra of certain types of stars could provide additional information that would be useful for determining neon abundance and for other applications (such as the estimation of ionization correction factors). Moreover, mid-IR spectra are considered to be an excellent tool for studying the nature of IR bright galaxies, such as galaxies containing active galactic nuclei (AGNs), as they contain a great deal of information on the present atomic, ionic, and molecular species, as well as data on various solid-state particles and dust (Sturm et al. 2002). However, the analysis of the spectra measured using astronomical spectrometric instruments requires high-quality spectral data obtained under laboratory conditions. This work builds on our earlier studies (Civiš et al. 2012a,c,e, 2013a) regarding the IR spectra of atoms and reports new precise laboratory measurements for a Ne spectrum in the IR region, including the 4.8−14 μm domain, which has not been previously investigated.
The neutral neon Ne i is a closed shell atom with a ground electron configuration of 1s2 2s2 2p6. The excited energy levels (2PJ1)nl [K] J are classified in the J1K coupling scheme with a total angular momentum of 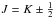 with K = l ± J1. These levels are subdivided into two groups depending on the angular momentum
with K = l ± J1. These levels are subdivided into two groups depending on the angular momentum 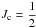 or
or 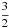 of the 2p5 core. In this work we use the primed orbital momentum l of the valence electron to denote the
of the 2p5 core. In this work we use the primed orbital momentum l of the valence electron to denote the 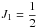 core states, nl′ [K] J, and the unprimed orbital momentum for the
core states, nl′ [K] J, and the unprimed orbital momentum for the 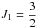 core states, nl [K] J.
core states, nl [K] J.
Neon spectra have been studied since the very beginning of the field of spectroscopy (Paschen 1919). Probably the most complete review of the Ne i energy transitions and levels was compiled by Saloman & Sansonetti (2004). They prepared a comprehensive critically evaluated study containing data from 19 sources spanning the region from 256 Å to 54931 Å. These data have been adopted for use in the NIST Atomic Spectra Database (Kramida et al. 2015).
The IR part of the line list covered by Saloman & Sansonetti (2004) is based on the authors’ previous studis of Ne, Kr, and Xe spectra using microwave-excited electrodeless discharge lamps (Sansonetti et al. 2002, 2004). These spectra were recorded with a 2 m Fourier transform spectrometer and covered the regions from 6929−47589 Å, with a resolution of 0.007−0.01 cm-1. Other Fourier transform spectra among the 19 sources compiled by Saloman & Sansonetti (2004) include a hollow cathode spectra from the archives of the Fourier transform spectrometer from the National Solar Observatory at the Kitt Peak National Observatory Chang et al. (1994; over the 1800−9000 cm-1 or 1.1−5.6 μm range with a resolved power up to 500 000) and the 1.25 m BOMEM Fourier transform spectrometer measurements by Mishra et al. (2000; 4000−8000 cm-1 or 1.25−2.5 μm range, with a resolution of 0.1 cm-1), as well as old grid spectrometer measurements performed by Morillon (1972; 4.5−5.5 μm range with a resolution of 0.06 cm-1).
To the authors’ knowledge, experimental data on the Ne i spectrum below 1800 cm-1 (corresponding to wavelengths longer than 5.6 μm) have not been reported yet. According to our earlier work (Civiš et al. 2012a,b,c,e; 2013a, 2014), the most prominent lines in this domain are due to transitions between the g-, h-, or i- Rydberg states, which are neither reported on in the literature nor listed in the atomic databases. Our aim is to present new knowledge on these high-l Ne i states. In this work, we present the results of an extensive laboratory study of the Ne i energy transitions in the IR spectral region from 1.43 to 14.0 μm. A significant portion of the transitions measured have not been observed experimentally before. From the recorded spectra, we extracted the energies for the 6h, 7h, and 7i levels that were not previously reported.
2. Experimental setup
The Ne i excited energy states were produced using a pulsed discharge plasma. A 20 cm long discharge tube with water-cooled stainless steel electrodes was filled with a slow, constant flow of pure neon. The neon pressure was set to 2.1 torr. The voltage drop across the discharge was 0.9 kV, with a pulse width of 22 μs and a peak-to-peak current of 50 mA.
The IR spectra of Ne i were recorded using the time-resolved Fourier transform spectrometric method developed in our laboratory. The instrumental details of this method have been described elsewhere (Kawaguchi et al. 2005; Ferus et al. 2011; Civiš et al. 2012b). This approach enables the measurement of IR spectra with a high spectral resolution (up to 0.0075 cm-1) and a 1 μs time resolution over a wide spectral region. In the current experiment, the time resolution was applied to increase the signal-to-noise ratio in the low-intensity spectral lines by selecting the best time period after the discharge pulse when the intensities of the weak spectral lines are at their maxima (Civiš et al. 2014). To cover the spectral range from 700−7000 cm-1, we used several band pass interference filters (procured from Northumbria Optical Coatings Limited, UK), two different beam splitters (KBr and CaF2), and two detectors (MCT, InSb). These filters, detectors, and splitters are listed in Table 1 for all the spectral ranges covered in this work.
Spectral ranges covered by the present measurement.
3. Methods
In this study, seven measurements in different spectral regions between 700 and 7000 cm-1 were selected for further analysis (see Table 1). Every measurement provides 30 time-shifted spectra with time steps of 2 μs. To increase the signal-to-noise ratio, time-resolved spectra with intense atomic spectral lines were selected and summed up over the time periods where the intensity was maximized (typically from 4 to 12 μs). The line features listed in Table 3 were obtained by fitting the measured data using Voigt profile function.
 |
Fig. 1 Measured spectra with the 6l–7(l + 1) transitions of Ne i. |
The wavelength calibration was conducted using several H2O and CO lines found in the discharge spectra and was performed by linearly fitting the measured wavenumbers to high-precision values taken from the HITRAN database (Rothman et al. 2009). The resulting wavenumbers ν were recalculated from the non-calibrated values ν′ using the equation ν = (1 + α)ν′, where α is a linear fit parameter. The α values were obtained for each spectral range with typical values of α ≃ 1.5 × 10-6 ± 3 × 10-7 (with a relative uncertainty Δα/α of approximately 15−25%).
The statistical uncertainties for the line wavenumbers were calculated according to Brault (1987), 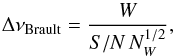 (1)where S/N is the signal-to-noise ratio, W is the FWHM, NW is the number of statistically independent data points per W, and NW = W/ 0.0075 cm-1. We assume that the statistical uncertainty is equal to the maximum value, Δνstat = max { ΔνBrault,Δνfit }, where Δνfit is the uncertainty of the Voigt profile fitting procedure. The uncertainties (at one standard deviation) presented in Table 3 are calculated by adding the statistical and calibration uncertainties in quadrature:
(1)where S/N is the signal-to-noise ratio, W is the FWHM, NW is the number of statistically independent data points per W, and NW = W/ 0.0075 cm-1. We assume that the statistical uncertainty is equal to the maximum value, Δνstat = max { ΔνBrault,Δνfit }, where Δνfit is the uncertainty of the Voigt profile fitting procedure. The uncertainties (at one standard deviation) presented in Table 3 are calculated by adding the statistical and calibration uncertainties in quadrature: ![\begin{equation} \Delta\wavenumber=\left[\Delta\wavenumber_\mathrm{stat}^2+\Delta\wavenumber_\mathrm{calibr}^2\right]^{1/2} . \end{equation}](/articles/aa/full_html/2015/10/aa26442-15/aa26442-15-eq37.png) (2)The calibration uncertainties, Δνcalibr, are primarily determined by the statistical uncertainties of the calibration factor found from the linear fit of the measured versus the reference wavenumber dependence. For the wavenumbers ν = 1000..4000, there are uncertainties defined as Δνcalibr ≃ Δαν ~ 0.0005..0.001 cm-1, which are much greater than the uncertainties from the HITRAN reference wavenumbers used for the calibration. Thus, we do not take the uncertainty of the reference values into account when determining the calibration uncertainties.
(2)The calibration uncertainties, Δνcalibr, are primarily determined by the statistical uncertainties of the calibration factor found from the linear fit of the measured versus the reference wavenumber dependence. For the wavenumbers ν = 1000..4000, there are uncertainties defined as Δνcalibr ≃ Δαν ~ 0.0005..0.001 cm-1, which are much greater than the uncertainties from the HITRAN reference wavenumbers used for the calibration. Thus, we do not take the uncertainty of the reference values into account when determining the calibration uncertainties.
 |
Fig. 2 Measured spectra with the 5l–6(l + 1) transitions of Ne i. |
To assign the observed spectral lines listed in Table 3, we use the latest Ne i energy level list available (Kramida et al. 2015; Saloman & Sansonetti 2004). In the case of the lines corresponding to the transitions that involved high-l = 5,6 (h- or i-) states, the assignment was made using two steps. First, we used approximate energy values for the h- or i-levels calculated by the Rydberg formula with small quantum defects μ ~ 0.001. This gave only approximate expected positions for the lines corresponding to the h- and i-levels. Then, we classified the observed lines according to their expected intensities, which are calculated using the quantum defect theory (QDT) approximation (Chernov et al. 2000, 2005; Civiš et al. 2012b). After the line classification (see Table 3), the energies of the previously unknown h- and i-levels are extracted (see Table 2). The procedure for refining the energy levels is described in our earlier work (Civiš et al. 2012d).
Energies of the high-l levels of Ne i found in the present work.
4. Results and discussion
Some examples of the recorded spectra are given in Figs. 1 and 2. These two wavenumber regions are very important for observing the transitions from the i-, h-, and g- levels and have not been studied before. Only with the help of the QDT calculations to estimate the expected intensities were we able to classify the observed lines.
The list of the measured line features (wavenumber νki, intensity Iki, full width at half maximum (FWHM), and identification) is presented in Table 3. The measurements are performed over the seven spectral ranges specified in Table 1. The scale of the arbitrary units of Iki only applies within the same spectral range. These values are obtained by fitting to a Voigt line shape or by the sum of a set of component curves. Their uncertainties are reported in the parentheses immediately following the values and should be interpreted using the rightmost significant digits in the main numbers, e.g., 123.4(56) represents 123.4 ± 5.6.
It is apparent from Table 3 that the variations in FWHM are large between lines in the spectral regions where the MCT detector was used (see Table 1). In fact, owing to the higher noise level associated with this detector, we co-added several time-resolved components (several IR spectra recorded using different time delays, e.g., 10−20 μs) to obtain a better signal-to-noise ratio. This procedure not only resulted in better accuracy when determining the peak position, but also lead to the widening of some lines. There is another reason for such widening, which is clearly observed for the lines involving the states with l ≥ 3 and n ≥ 5. Indeed, the fine splitting of such lines is very small (see Figs. 1 and 2). Thus, the fine structural components corresponding to different J states are not resolved and merge into single widened lines. These lines are observed instead of the fine structured multiplets. In some cases (e.g., for the transitions between the 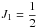 core states denoted by the primed l values, such as 5g′, 6h′), even the components with the different K values are not resolved.
core states denoted by the primed l values, such as 5g′, 6h′), even the components with the different K values are not resolved.
List of the measured line features (wavenumbers νki, intensities Iki, full widths at half maxima (FWHM) and identification).
Most of the measured transition wavenumbers agree with the values listed in the NIST compilation by Saloman & Sansonetti (2004) within the uncertainties. In the case of the multiplet 5p−5d, we can only compare our values with some components from a multiplet measured in 1972 by Morillon (1972). Given a resolution of 0.06 cm-1 for the measurements performed by Morillon (1972), we can say the wavenumbers in the 1820−2060 cm-1 range agree with our results. The line at 1930.315 cm-1 can be multiply assigned. Within the given uncertainties, this line may be classified as both a 5s′ [1/2] 1−5p′ [1/2] 0 transition and a 5p′ [1/2] 1−5d′ [3/2] 2 transition, the former being slightly more probable according to our QDT calculations of the dipole transition moments.
We note that we have resolved two components of the fine splitting structure of the 3d [3/2] 1 − 4f [3/2] 1,2 transition for which Saloman & Sansonetti (2004) reported a single value of 5416.0382 cm-1.
In the case of the transition from high-l (g-, h-, and i-) levels and 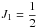 (6g′-7i′, 6g′-7h′, 5g′-6h′, 5f′-6g′), we observe only one line instead of multiple lines. However, in other cases when
(6g′-7i′, 6g′-7h′, 5g′-6h′, 5f′-6g′), we observe only one line instead of multiple lines. However, in other cases when 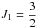 , we can always discriminate four or even more components in the multiplet.
, we can always discriminate four or even more components in the multiplet.
The energies of the high-l (h- and i-) levels are listed in Table 2. The fine splitting structure (i.e., the individual J components) are not resolved in our spectra. Indeed, even for the 6g configuration, the fine splitting between the different J components (with the same K value) is 0.007−0.019 cm-1 (Saloman & Sansonetti 2004). Such splitting should be less for the h- and i-states.
In this work, we only report new energy levels for Ne I that have never been measured before in the laboratory. From our measured spectra we can determine that there are a significant number of energy levels that coincide (within the uncertainty range) with the corresponding values reported by Saloman & Sansonetti (2004) and Chang et al. (1994). However, publishing these results would lead to excessively long tables.
5. Conclusion
To maximize the use of infrared astronomical instruments, a large amount of atomic data (such as the line wavenumbers and excited-level energy values) is needed. These data are absent for Ne i levels with high orbital momentum, such as l> 4 (e.g., h- or i-states). The transitions involving these states appear near 800 cm-1 (12.5 μm) and 1350 cm-1 (7.5 μm), correspondingly, but no laboratory-measured spectra for Ne i have been reported for wavelengths longer than 5.55 μm. Using the time-resolved Fourier transform spectroscopy technique, we recorded a high-resolution Ne i emission spectrum over the 800−7000 cm-1 (1.43−14.3 μm) range in a pulsed discharge plasma. The identification of the lines was performed according to the transition probability values calculated from the quantum defect method. Based on these measurements, we report wavenumbers for 151 Ne i lines and energy values for 14 Ne i levels that are not listed in the available databases.
Acknowledgments
This work was financially supported by the Ministry of Education, Youth, and Sports of the Czech Republic (grant No. LG13029 and COST Action CM1104, grant No. LD14115). V. E. Chernov acknowledges the support by the Ministry of Education and Science of the Russian Federation, state order No. 1122.
References
- Antia, H. M., & Basu, S. 2006, ApJ, 644, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Baldovin-Saavedra, C., Audard, M., Güdel, M., et al. 2011, A&A, 528, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldovin-Saavedra, C., Audard, M., Carmona, A., et al. 2012, A&A, 543, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balman, S. 2005, ApJ, 627, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Bochsler, P. 2007, A&A, 471, 315 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brault, J. W. 1987, Microchim. Acta, 93, 215 [Google Scholar]
- Chang, E. S., Schoenfeld, W. G., Biémont, E., Quinet, P., & Palmeri, P. 1994, Phys. Scr., 49, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Chernov, V., Manakov, N., & Starace, A. 2000, Eur. Phys. J. D, 8, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chernov, V. E., Dorofeev, D. L., Kretinin, I. Y., & Zon, B. A. 2005, Phys. Rev. A, 71, 022505 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, C. S., & Dotani, T. 1998, ApJ, 492, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Civiš, S., Ferus, M., Kubelík, P., Jelinek, P., & Chernov, V. E. 2012a, A&A, 541, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Civiš, S., Ferus, M., Kubelík, P., et al. 2012b, J. Opt. Soc. Am. B, 29, 1112 [Google Scholar]
- Civiš, S., Ferus, M., Kubelík, P., et al. 2012c, A&A, 542, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Civiš, S., Ferus, M., Kubelík, P., Chernov, V. E., & Zanozina, E. M. 2012d, J. Phys. B, 45, 175002 [Google Scholar]
- Civiš, S., Ferus, M., Kubelík, P., Chernov, V. E., & Zanozina, E. M. 2012e, A&A, 545, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Civiš, S., Ferus, M., Chernov, V. E., & Zanozina, E. M. 2013a, A&A, 554, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Civiš, S., Ferus, M., Chernov, V. E., Zanozina, E. M., & Juha, L. 2013b, J. Quant. Spectrosc. Radiat. Transf., 129, 324 [Google Scholar]
- Civiš, S., Kubelík, P., Ferus, M., et al. 2014, J. Anal. At. Spectrom., 29, 2275 [CrossRef] [Google Scholar]
- Crockett, N. R., Garnett, D. R., Massey, P., & Jacoby, G. 2006, ApJ, 637, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., Hubeny, I., & Lanz, T. 2006, ApJ, 647, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Curdt, W., Feldman, U., Laming, J. M., et al. 1997, A&AS, 126, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dors, Jr., O. L., Hägele, G. F., Cardaci, M. V., et al. 2013, MNRAS, 432, 2512 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J. 2011, ApJ, 743, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., & Ercolano, B. 2007, ApJ, 665, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., & Testa, P. 2005, Nature, 436, 525 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Drake, S. A., Singh, K. P., White, N. E., & Simon, T. 1994, ApJ, 436, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Ferus, M., Kubelík, P., Kawaguchi, K., et al. 2011, J. Phys. Chem. A, 115, 1885 [CrossRef] [Google Scholar]
- Floc’h, E. L.,Mirabel, I. F., Laurent, O., et al. 2001, A&A, 367, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrz, R. D., Woodward, C. E., Helton, L. A., et al. 2008, ApJ, 672, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., Asplund, M., & Sauval, A. J. 2007, in The Composition of Matter (Springer Science + Business Media), 105 [Google Scholar]
- Helton, L. A., Gehrz, R. D., Woodward, C. E., et al. 2012, AJ, 755, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., & Keto, E. 2007, ApJ, 658, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Inami, H., Armus, L., Charmandaris, V., et al. 2013, ApJ, 777, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaguchi, K., Hama, Y., & Nishida, S. 2005, J. Mol. Spectrosc., 232, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team. 2015, NIST Atomic Spectra Database (version 5.2) [Google Scholar]
- Laming, J. M. 2009, ApJ, 695, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Liefke, C., & Schmitt, J. H. M. M. 2006, A&A, 458, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magazzu, A., Pirronello, V., & Strazzulla, G. 1983, A&A, 120, 139 [NASA ADS] [Google Scholar]
- Martín-Hernández, N. L., Schaerer, D., Peeters, E., Tielens, A. G. G. M., & Sauvage, M. 2006, A&A, 455, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mishra, A. P., Kshirsagar, R. J., Bellary, V. P., & Balasubramanian, T. K. 2000, J. Quant. Spectr. Radiat. Transf., 67, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, T., & Butler, K. 2008, A&A, 487, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morillon, C. 1972, Spectrochim. Acta, Part B, 27, 527 [CrossRef] [Google Scholar]
- Pandey, G., & Lambert, D. L. 2011, ApJ, 727, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Paschen, F. 1919, Ann. Phys. (Leipzig), 365, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Robrade, J., Schmitt, J. H. M. M., & Favata, F. 2008, A&A, 486, 995 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothman, L., Gordon, I., Barbe, A., et al. 2009, J. Quant. Spectr. Radiat. Transf., 110, 533 [Google Scholar]
- Saloman, E. B., & Sansonetti, C. J. 2004, J. Phys. Chem. Ref. Data, 33, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Sansonetti, C. J., Blackwell, M. M., & Saloman, E. B. 2002, Phys. Scr., T100, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Sansonetti, C. J., Blackwell, M. M., & Saloman, E. B. 2004, J. Res. Natl. Inst. Stand. Technol., 109, 371 [CrossRef] [Google Scholar]
- Serenelli, A. 2013, in the XXV Int. Conf. on Neutrino Physics and Astrophysics, Nucl. Phys. B – Proc. Suppl., 235−236, 41 [Google Scholar]
- Smith, J. D. T., Rudnick, L., Delaney, T., et al. 2009, ApJ, 693, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Stelzer, B., & Schmitt, J. H. M. M. 2004, A&A, 418, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sturm, E., Lutz, D., Verma, A., et al. 2002, A&A, 393, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, Y., Kambe, E., Sadakane, K., & Masuda, S. 2010, PASJ, 62, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Verma, A., Lutz, D., Sturm, E., et al. 2003, A&A, 403, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, K., Rauch, T., Reiff, E., Kruk, J. W., & Napiwotzki, R. 2004, A&A, 427, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
List of the measured line features (wavenumbers νki, intensities Iki, full widths at half maxima (FWHM) and identification).
All Figures
 |
Fig. 1 Measured spectra with the 6l–7(l + 1) transitions of Ne i. |
| In the text | |
 |
Fig. 2 Measured spectra with the 5l–6(l + 1) transitions of Ne i. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


