EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 581 (September 2015) A&A, 581 (2015) A35 Full HTML
Free Access
Issue
A&A
Volume 581, September 2015
Article Number A35
Number of page(s) 12
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201525867
Published online 28 August 2015

© ESO, 2015

1. Introduction

High-frequency quasi-periodic oscillations (HF QPOs) have been observed in several microquasars and low-mass X-ray binaries (LMXBs). Their frequencies are roughly comparable to frequencies of the orbital motion of test particles in the vicinity of the central compact object. The black hole HF QPOs occur at frequencies that are characteristic of a particular source and that seem to be constant in time. Strictly speaking, the current observational data only enables HF QPOs to be distinguished for fairly specific spectral states (Belloni et al. 2012). However, provided that HF QPOs with lower amplitudes and different frequencies exist in the remaining time, their detection goes beyond our present technological capabilities.

Two kinds of sharp HF QPO peaks can be distinguished, so-called lower and upper HF QPOs (see van der Klis 2004; Remillard & McClintock 2006, for a review). If both HF QPO peaks are observed simultaneously (twin-peak HF QPOs), the ratio of frequencies of upper and lower HF QPO peaks is often close to 3:2, indicating the possible presence of unspecified resonant phenomena (Abramowicz & Kluźniak 2001; Török et al. 2005)1. At present, there is no consensus about the QPO nature. However, the inverse mass scaling of the QPOs frequencies (Abramowicz & Kluźniak 2001) provides a strong argument for interpreting the observed QPO peaks by the frequencies of perturbed orbital motion in the strong gravitational field or oscillation of some accretion structures. Such interpreting naturally promises an attractive possibility of measuring the mass and spin of the black hole (e.g. Abramowicz & Kluźniak 2001; Abramowicz & Fragile 2013; Ingram & Motta 2014; Motta et al. 2014; Török 2005; Török et al. 2012). Many QPO models have been proposed (Alpar & Shaham 1985; Lamb et al. 1985; Miller et al. 1998; Psaltis et al. 1999; Stella & Vietri 1999; Abramowicz & Kluźniak 2001, 2004; Kato 2001, 2007; Titarchuk & Wood 2002; Rezzolla et al. 2003; Schnittman & Bertschinger 2004; Pétri 2005; Zhang 2005; Tagger & Varnière 2006; Stuchlík et al. 2008; Mukhopadhyay 2009; Čadež et al. 2008; Kostić et al. 2009; Germanà et al. 2009; Germanà 2013; Lai et al. 2013; Pecháček et al. 2008, 2013); however, each model still faces several difficulties. Moreover, the capabilities of the present X-ray observatories (e.g. Rossi X-ray Timing Explorer – RTXE) are insufficient for adequately analysing the harmonic content of the power spectra of observed lightcurves, which can be crucial for distinguishing between particular QPO models (Bakala et al. 2014; Karas et al. 2014). Hopefully, the proposed future instruments represented by the Large Observatory for X-ray Timing (LOFT) project (Feroci et al. 2014), for instance, which is targeted to explore strong gravity environment, will advance QPOs observational possibilities.

A specific class of QPO models assumes oscillations excited in accretion tori. The first QPO model involving numerically modelled thick accretion tori was developed by Rezzolla et al. (2003), and related lightcurves and power spectra were analysed by Schnittman & Rezzolla (2006). Lightcurves and power spectra of radially and vertically oscillating slender torus with a circular cross-section were investigated in the background of the Schwarzschild geometry by Bursa et al. (2004). Numerical simulations of epicyclic modes of tori oscillations were compared to the analytical results by Šrámková (2005). Later on, several studies devoted to more realistic analytic treatment of oscillating slender tori appeared (e.g. Abramowicz et al. 2006; Blaes et al. 2006). These studies were extended to the case of non-slender tori by Šrámková et al. (2007) and Straub & Šrámková (2009).

In this paper, we examine the timing properties of the numerically simulated flux emitted from a slender, polytropic, perfect fluid, non-self-gravitating accretion torus with constant specific angular momentum, which oscillates simultaneously in radial and vertical directions2. The article is a follow-up of the studies of Mazur et al. (2013) and Vincent et al. (2014), who investigated the observable signatures of simple time-periodic slender torus deformations, as well as the slender torus motion described by the set of oscillation modes derived by Blaes et al. (2006). Using their results, we took the next step towards a fully realistic model of HF QPO based on oscillations of accretion tori. To model detected twin-peak HF QPOs pairs, we defined a new dual oscillation mode as a linear combination of the two lowest slender torus oscillation modes: radial and vertical ones. We assumed that the observed twin peaks HF QPOs can be identified with the pairs of the most prominent peaks in the modelled power spectra. We examined two different setups of the dual oscillation regime corresponding to the twin peaks HF QPOs frequency relation of epicyclic resonance HF QPOs model (Abramowicz & Kluźniak 2001) and slightly modified analogous relations of relativistic precession QPOs model (Stella & Vietri 1999; Török et al. 2012). Those two competing QPOs models are probably the most discussed ones at present (Feroci et al. 2014).

Our simulations were performed in the background of the Kerr geometry that corresponds to the case of microquasars with the black hole binary component. It was shown that the spacetime around slowly rotating high-mass neutron stars can be approximated fairly well by the Kerr metric (Török et al. 2010, 2012; Urbanec et al. 2013). Therefore, such a finding sets conditions and constraints for the applicability of our results for the case of LMXBs with neutron star.

The commonly accepted model of X-ray energy spectrum of microquasars and LMXBs assumes that the illumination of the cold accretion disk or torus by the primary component of X-ray spectrum, interpreted as the inverse Compton scattering of thermal photons in a hot corona, produces spectral lines by fluorescence. The strongest observed line is the Kα iron line located at 6.4 keV in the rest frame. Observed broad profiles of the spectral lines are substantially influenced by the spacetime metric, the geometry of the emitting region and the distant observer inclination (Fabian et al. 1989; Čadež & Calvani 2005; Bambi 2013). To develop an additional tool for distinguishing various configurations of radiating slender torus, we computed related Kα iron line profiles.

The article consits of the following parts. Section 2 is devoted to the theory that describes the slender torus model and its dual oscillation regime. Section 3 provides more details of the investigated particular setup of the model of slender torus. Section 4 describes our numerical implementation of relativistic ray-tracing and the following construction of lightcurves, power spectra, and iron Kα line profiles. Section 5 is devoted to the methodology of simulations performance and results analysis. Section 6 shows the obtained results, and Sect. 7 gives conclusions and future research perspectives.

2. Slender torus

2.1. Equilibrium torus configuration

We consider an axisymmetric, non self-gravitating, perfect fluid, constant specific angular momentum, circularly orbiting accretion torus in the background of the Kerr geometry. Using the (−+++) signature and geometrical units (c = G = M = 1), the line element of the Kerr spacetime in Boyer-Lindquist coordinates parameterized by specific angular momentum (spin) a reads ds2=−(1−2rΣ) dt2−4raΣsin2θ dt dϕ+ΣΔ dr2\begin{eqnarray} \mathrm{d}s^2 &=& -\left(1-\frac{2 r}{\Sigma}\right) \,\mathrm{d}t^2 - \frac{4 r a }{\Sigma} \sin^2\theta\,\mathrm{d}t\, \mathrm{d}\varphi + \frac{\Sigma}{\Delta}\, \mathrm{d}r^2 \nonumber \\ &&+ \,\Sigma \,\mathrm{d}\theta^2 + \left(r^2 + a^2 +\frac{2 r a^2 \sin^2\theta}{\Sigma}\right)\sin^2\theta\, \mathrm{d}\varphi^2, \label{kerr_metric} \end{eqnarray}(1)where Σ ≡ r2 + a2cos2θ and Δ ≡ r2−2r + a2. Moreover, we assume that the radial extent of the torus cross-section is smaller than its central radius. The perfect fluid that forms the torus is described by the polytropic equation of state (with a polytropic constant K and polytropic index n). In this case, the energy density e is a function of pressure p and mass density ρ. The pressure is a function of mass density alone. The torus surface is given by the zero pressure, while the pressure gradient is equal to zero in the torus centre. Using the conservation law, one can get (see Abramowicz et al. 2006; Blaes et al. 2006) pρ=p0ρ0f(r,θ),\begin{equation} \frac{p}{\rho} = \frac{p_{0}}{\rho_{0}}f(r,\theta), \end{equation}(2)where the surface function f is constant at isobaric and isodensity surfaces. Naturally, the surface function vanishes at the torus surface. Here and below, values of the quantities denoted with a subscript 0 are taken in the centre of the torus in the equilibrium state.

Following Abramowicz et al. (2006), we use the new radial and vertical coordinates x̅=(grr)0(r−r0βr0),y̅=(gθθ)0(π/2−θβr0)\begin{equation} \bar{x} = \left(\!\!\sqrt{g_{\rm rr}} \right)_0 \left( \frac{r - r_0}{ \beta r_0}\right),~~ \bar{y} = \left(\!\!\sqrt{g_{\theta\theta}} \right)_0 \left( \frac{\pi/2 - \theta}{\beta r_0}\right) \end{equation}(3)with zero in the torus centre. Parameter β determines the torus thickness and is given by formula β2=2ncs02r02(u0t)2Ω02,\begin{equation} \beta^2 = \frac{2n c^2_{{\rm s}0}}{r^2_0 (u^{\rm t}_{0})^2 \Omega^2_0}, \label{eq:beta} \end{equation}(4)where u0t\hbox{$u^{\rm t}_{0}$} denotes the four-velocity of the fluid and square of the sound speed cs02≪1\hbox{$c_{\rm s0}^{2} \ll 1$} can be expressed in the form cs02=(∂p∂ρ)0=n+1np0ρ0·\begin{equation} c_{\rm s0}^2 = \left(\frac{\partial p}{\partial \rho}\right)_{0} = \frac{n + 1}{n} \frac{p_{0}}{\rho_{0}}\cdot \end{equation}(5)Keplerian angular velocity ΩK0 in the Kerr spacetime reads asΩK0=1/(r03/2+a).\begin{equation} \Omega_{{\rm K}0} = 1/(r_{0}^{3/2} + a). \label{OMEGA} \end{equation}(6)In the case of slender torus, the parameter β must fulfil the condition β≪1.\begin{equation} \beta \ll 1. \label{slendercondition} \end{equation}(7)In such a coordinate frame, the surface function f(r,θ) can be rewritten as f(x̅,y̅)=1−ω̅2rx̅2−ω̅2θy̅2,\begin{equation} f(\bar{x},\bar{y}) = 1 - \bar{\omega}_{r}^{2}\bar{x}^{2} - \bar{\omega}_{\theta}^{2}\bar{y}^{2}, \end{equation}(8)where ω̅r=ω̅θ=\begin{eqnarray} \bar{\omega}_{r} &=& \sqrt{1 - \frac{6}{r_{0}} + \frac{8a}{r_{0}^{3/2}} - \frac{3a^{2}}{r_{0}^{2}}}, \label{omegar} \\ \bar{\omega}_{\theta} &=& \sqrt{1 - \frac{4a}{r^{3/2}_{0}} + \frac{3a^{2}}{r_{0}^{2}}}, \label{omegatheta} \end{eqnarray}are radial and vertical epicyclic frequencies of free test particles in the centre of the torus scaled to ΩK0 (see e.g. Aliev & Galtsov 1981; Abramowicz & Kluźniak 2005; Aliev 2008). We can easily see that the slender torus cross-section (given by \hbox{$f(\bar{x},\bar{y}) = 0$}) has elliptical shape in the \hbox{$\bar{x}$}-\hbox{$\bar{y}$} plane.

2.2. Oscillating slender torus

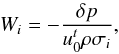We assume small pressure perturbation in the form δp∝ei(mϕ−Ωt),\begin{equation} \delta p \propto {\rm e}^{{\rm i}(m\varphi - \Omega t)}, \end{equation}(11)where m is azimuthal wave number (m ∈ N), and Ω is oscillation angular frequency. It is useful to introduce a new variable – eigenfunction Wi, which is the function of perturbation in pressure in the form Wi=−δpu0tρσi,\begin{equation} W_{i} = -\frac{\delta p}{u^{t}_{0}\rho\sigma_{i}}, \end{equation}(12)where related eigenfrequency σi reads σi=Ωi−miΩK0.\begin{equation} \sigma_{i}=\Omega_{i}-m_{i}\Omega_{{\rm K}0}. \end{equation}(13)The perturbative surface equation ˜f(r,θ)\hbox{$\tilde{f}(r,\theta)$} and torus four-velocity can be expressed in the form (Vincent et al. 2014) uμ=u0μ+Re{iρ0p0+e0(∂Wi∂xμ)}·\begin{eqnarray} && \tilde{f}(r,\theta) = f(r,\theta) - \frac{1}{n + 1}\frac{\rho_{0}}{p_{0}}u^{\rm t}_{0}{\rm Re}\left\{W_{i}\right\} \sigma_{i}, \label{surfaceeq}\\ && u^{\mu} = u^{\mu}_{0} + {\rm Re}\left\{\frac{{\rm i}\rho_{0}}{p_{0} + e_{0}}\left(\frac{\partial W_{i}}{\partial x^{\mu}}\right)\right\}\cdot \end{eqnarray}A discrete set of eigefunctions Wi and related eigenfrequencies σi describing different oscillation modes was found by Blaes et al. (2006) solving Papaloizou-Pringle equation for slender torus case corresponding to the condition β → 0 (Abramowicz et al. 2006; Papaloizou & Pringle 1984). Here we use only the two simplest solutions: radial oscillation mode and vertical oscillation mode. In the case of radial oscillation mode, the eigenfunction and related eigenfrequency are given as Wr=arx̅ei(mrϕ−Ωrt), σr=ω̅rΩK0,\begin{equation} W_{\rm r} = a_{\rm r} \bar{x}{\rm e}^{{\rm i}(m_r\varphi - \Omega_r t)},\qquad \sigma_{\rm r} = \bar{\omega}_{r}\Omega_{{\rm K}0}, \end{equation}(16)where ar is a free parameter related to the amplitude of oscillations. Then the surface Eq. (14) takes the form 1−ω̅2rx̅2−ω̅2θy̅2−Arx̅cos(mrϕ−Ωrt)=0,\begin{equation} 1 - \bar{\omega}_{\rm r}^{2}\bar{x}^{2} - \bar{\omega}_{\theta}^{2}\bar{y}^{2} - A_{r}\bar{x} \cos(m_{\rm r}\varphi - \Omega_{\rm r}t) = 0, \label{rsurfaceeq} \end{equation}(17)where amplitude Ar is given by the formula Ar=1n+1ρ0p0u0tσrar,\begin{equation} A_{r} = \frac{1}{n+1}\frac{\rho_{0}}{p_{0}}u^{t}_{0}\sigma_{r} a_{r}, \end{equation}(18)and the mode oscillation angular frequency reads asΩr=σr+ΩK0mr.\begin{equation} \Omega_{r}=\sigma_{r} + \Omega_{{\rm K}0} m_{\rm r}. \label{rad.os.f} \end{equation}(19)To rewrite the surface Eq. (17) to the form 1−ω̅2r(x̅+δx̅)2−ω̅2θy̅2=0,\begin{equation} 1 - \bar{\omega}_{r}^{2}\left(\bar{x} + \delta \bar{x}\right)^{2} - \bar{\omega}_{\theta}^{2}\bar{y}^{2}= 0, \label{rad.os} \end{equation}(20)the term (Ar2ω̅rcos(mrϕ−Ωrt))2\begin{equation} \left(\frac{A_{r}}{2\bar{\omega}_{r}} \cos(m_{r}\varphi - \Omega_{\rm r}t)\right)^{2} \end{equation}(21)must be added. Then the displacement \hbox{$\delta \bar{x}$} can be expressed by the formula δx̅=Ar2ω̅2rcos(mrϕ−Ωrt).\begin{equation} \delta \bar{x} = \frac{A_{r}}{2\bar{\omega}_{r}^{2}} \cos\left(m_{r}\varphi - \Omega_{\rm r}t\right). \label{rad.disp} \end{equation}(22)In this approximation, the added term should be small enough, which corresponds to the condition for radial amplitudes Ar24ω̅2r≪1.\begin{equation} \frac{A_{r}^{2}}{4\bar{\omega}_{r}^{2}} \ll 1. \label{r_small_ampl} \end{equation}(23)The radial component of the surface four-velocity is simply given by a derivative of the displacement \hbox{$\delta \bar{x}$} with respect to proper time τ as usurr=drdτ=dx̅dτβr0(grr)0=d(−δx̅)dτβr0(grr)0,\begin{equation} u^{r}_{sur} =\frac{{\rm d}r}{{\rm d}\tau} = \frac{{\rm d}\bar{x}}{{\rm d}\tau} \frac{\beta r_{0}}{\left(\!\! \sqrt{g_{\rm rr}} \right)_0} = \frac{{\rm d}(-\delta \bar{x})}{{\rm d}\tau} \frac{\beta r_{0}}{\left(\!\!\sqrt{g_{\rm rr}} \right)_0}, \end{equation}(24)and it takes the covariant form ursur=−βr0(grr)0Ar2ω̅rΩK0u0tsin(mrϕ−Ωrt).\begin{equation} u_{r}^{\rm sur} = - \beta r_{0}\left(\!\! \sqrt{g_{\rm rr}} \right)_0\frac{A_{r}}{2\bar{\omega}_{\rm r}}\Omega_{{\rm K}0}u^{t}_{0}\sin(m_{r}\varphi - \Omega_{\rm r}t). \label{rad.os.u} \end{equation}(25)Analogously, in the case of the vertical oscillation mode, the eigenfunction and related eigenfrequency are given as Wθ=aθy̅ei(mθϕ−Ωθt), σθ=ω̅θΩK0.\begin{equation} W_{\theta} = a_{\theta} \bar{y}{\rm e}^{{\rm i}(m_{\theta}\varphi - \Omega_{\theta} t)},\qquad \sigma_{\theta} = \bar{\omega}_{\theta}\Omega_{{\rm K}0}. \end{equation}(26)Using the condition for vertical amplitudes Aθ24ω̅2θ≪1\hbox{$\frac{A_{\theta}^{2}}{4\bar{\omega}_{\theta}^{2}} \ll 1$}, the surface equation, displacement \hbox{$\delta \bar{y}$} and surface four-velocity component uθsur\hbox{$u_{\theta}^{\rm sur}$} for the vertical mode can be expressed as

\begin{eqnarray} &&1 - \bar{\omega}_{\rm r}^{2}\bar{x}^{2} - \bar{\omega}_{\theta}^{2}\left(\bar{y} + \delta \bar{y}\right)^{2}= 0, \label{ver.os} \\ &&\delta \bar{y} = \frac{A_{\theta}}{2\bar{\omega}_{\theta}^{2}} \cos\left(m_{\theta}\varphi - \Omega_{\theta}t\right), \label{ver.disp}\\ &&u_{\theta}^{\rm sur} = \beta r_{0}\left(\!\!\sqrt{g_{\theta \theta }}\right)_0 \frac{A_{\theta}}{2\bar{\omega}_{\theta}}\Omega_{{\rm K}0}u^{t}_{0}\sin(m_{\theta}\varphi - \Omega_{\theta}t), \label{ver.os.u} \end{eqnarray}where amplitude Aθ given by formula Aθ=1n+1ρ0p0u0tσθaθ,\begin{equation} A_{\theta} = \frac{1}{n+1}\frac{\rho_{0}}{p_{0}}u^{t}_{0}\sigma_{\theta}a_{\theta}, \end{equation}(30)and mode oscillation angular frequency reads Ωθ=σθ+ΩK0mθ.\begin{equation} \Omega_{\theta}=\sigma_{\theta} + \Omega_{{\rm K}0} m_{\theta}. \label{ver.os.f}\\ \end{equation}(31)

2.3. Dual oscillation mode

In such an approximation, radial and vertical oscillations are independent, and we can easily combine them into a new surface equation 1−ω̅2r(x̅+δx̅)2−ω̅2θ(y̅+δy̅)2=0.\begin{equation} 1 - \bar{\omega}_{r}^{2}\left(\bar{x} + \delta \bar{x}\right)^{2} - \bar{\omega}_{\theta}^{2}\left(\bar{y} + \delta \bar{y}\right)^{2}= 0. \label{dualsurface} \end{equation}(32)The equation above defines the dual oscillation mode with four parameters: amplitudes Ar, Aθ and azimuthal wave numbers mr, mθ.

3. Investigated model of oscillating slender torus

3.1. Location, thickness, and frequencies identification

Radial and vertical angular frequencies Ωr,Ωθ of the dual oscillation mode are given as a linear combination of eigenfrequencies σr,σθ, and Keplerian angular velocity ΩK0. Therefore the location of the torus centre in equilibrium r0, value of the spin of the central Kerr black hole and wave number pair mr, mθ fully determine the ratio of oscillation angular frequencies Ωθ/ Ωr. Considering the properties of epicyclic and orbital frequencies in the Kerr spacetime (Török & Stuchlík 2005), our model identifies the lower and upper kHz QPOs frequencies with νl = |Ωr/ 2π| and νu = |Ωθ/ 2π|, respectively. As the aim of the article is to model twin peak HF QPOs with peaks frequency ratio close to 3:2, we choose r0 in such a way that the ratio Ωθ/ Ωr is just equal to 3:2 for a given wave number pair3. In each of these positions of the torus centre, we set the radial extent of the torus cross-section to r0/10. Corresponding values of the parameter β are in accordance with a slender torus condition (7). Arbitrary amplitudes of oscillations are fixed by setting \hbox{$A_{r,\theta}=\bar{\omega}_{r,\theta}$}.

3.2. Optical properties of the torus

The torus described above is assumed to be optically thick. Moreover, we use two other very simple assumptions. The torus surface emits radiation isotropically in its comoving local frame and the local flux integrated over the surface area of a thin vertical slice of the torus is conserved. Such a surface area is proportional to rc(tem,φ) × C(tem,φ), where C(tem,φ) is the torus cross-section circumference, tem the time of emission, and rc(tem,φ) the radial coordinate of the centre of the torus cross-section. In the case of the approximation we used, the investigated dual oscillation mode describes pure radial and vertical displacements, and the torus cross-section circumference remains constant. Therefore, using normalization to 1 for the equilibrium state, the local emitted intensity simply reads as Iem(tem,φ)=r0/rc(tem,φ).\begin{equation} I_{\rm em}(t_{\rm em},\phi)=r_0/r_{\rm c}(t_{\rm em},\phi). \label{local_intensity} \end{equation}(33)

3.3. Epicyclic resonance axisymmetric setup

The first investigated torus setup combines pure epicyclic axisymmetric vertical and radial oscillation, where radial and vertical oscillation frequencies are identical with radial νr=ω̅ΩK0r/2π\hbox{$\nu_r=\bar{\omega}_{r}\Omega_{{\rm K}0}/2\pi$} and vertical νθ=ω̅ΩK0θ/2π\hbox{$\nu_{\theta}=\bar{\omega}_{\theta}\Omega_{{\rm K}0}/2\pi$} epicyclic frequencies, respectively. This setup corresponds to the often quoted epicyclic resonance (ER) HF QPOs model (Abramowicz & Kluźniak 2001) based on the presence of non-linear resonant phenomena between epicyclic disc oscillation modes (Kluźniak & Abramowicz 2001; Abramowicz et al. 2003a,b; Horák 2008). The dual oscillation mode with such behaviour is related to wave number pair mr = 0, mθ = 0. Therefore the frequency relation determining the radial coordinate of the torus centre r0 reads asνuνlmr = 0mθ = 0=νθνr=32·\begin{equation} \frac{\nu_{\rm u}}{\nu_{\rm l}}\Bigg\arrowvert_{m_{r}\,=\,0}^{m_{\theta}\,=\,0}=\frac{\nu_{\theta}}{\nu_{r}}=\frac{3}{2}\cdot \label{model1rel} \end{equation}(34)

3.4. Relativistic precession-like non-axisymmetric setup

The dual oscillation mode related to wave number pair mr = −1, mθ = −2 yields the frequency relation in the form νuνlmr = −1mθ = −2=2νK−νθνK−νr=32,\begin{equation} \frac{\nu_{\rm u}}{\nu_{\rm l}}\Bigg\arrowvert_{m_{r}\,=\,-1}^{m_{\theta}\,=\,-2}=\frac{2\nu_{\rm K}-\nu_{\theta}}{\nu_{\rm K}-\nu_{r}}=\frac{3}{2}, \label{model2rel} \end{equation}(35)where νK = ΩK0/ 2π is the Keplerian orbital frequency at r0. As the denominator matches the periastron precession frequency, in the Schwarzschild case the relation corresponds exactly to the relation of the relativistic precession (RP) QPOs model νuνlRP=νKνK−νr·\begin{equation} \frac{\nu_{\rm u}}{\nu_{\rm l}}\Bigg\arrowvert_{\rm RP}=\frac{\nu_{\rm K}}{\nu_{\rm K}-\nu_{r}}\cdot \label{RPrel} \end{equation}(36)The RP model was proposed in a series of papers by Stella & Vietri (1998, 1999, 2002), Morsink & Stella (1999) and explains the QPOs as a direct manifestation of relativistic epicyclic motion of radiating blobs (Stella & Vietri 1999). In the case of slow rotation, the frequency relation (35) still almost coincides with the ratio of twin peaks HP QPOs frequencies predicted by the relation (36) (Török et al. 2012). Such an approach can be understood as a redefinition of the modulation mechanism of RP model, but it preserves the predictive power of the model.

4. Numerical modelling of radiation emission, propagation, and detection

4.1. Ray-tracing in the Kerr spacetime

thumbnail Fig. 1

Schematic ray-tracing geometry for the cases of a general observer and distant observer (robs → ∞).

Relativistic ray-tracing is a key ingredient of proper models of relativistic imaging, lightcurves of accretion structures, related power spectra, as well as relativistic spectral line profiles. Different ray-tracing techniques were developed using direct numerical integration, transfer functions, and elliptic integrals (see e.g. Cunningham & Bardeen 1972; Karas et al. 1992; Viergutz 1993; Schnittman 2006; Rauch & Blandford 1994; Beckwith & Done 2005; Broderick & Loeb 2005; Bakala et al. 2007; Dexter & Agol 2009; Vincent et al. 2011; Schee & Stuchlík 2013; Chan et al. 2013; Yang & Wang 2014). Our parallel code LSDplus uses reverse ray-tracing implemented by a direct numerical integration of the null geodesics.

Components of the four-momentum of a photon in the Kerr spacetime are given by pr=ṙ=srΣ-2Rλ,q(r),pθ=θ̇=sθΣ-2Θλ,q(θ),pφ=φ̇=Σ-2Δ-1[2ar+λ(Σ2−2r)cosec2θ],pt=ṫ=Σ-2Δ-1(Σ2−2arλ),\begin{eqnarray} \label{CarterEQs} && p^{r} = \dot{r} = s_r\Sigma^{-2} \sqrt{R_{\lambda,q}(r)}, \nonumber\\ &&p^{\theta} = \dot{\theta} = s_{\theta}\Sigma^{-2} \sqrt{\Theta_{\lambda,q}(\theta)},\\ && p^{\phi} = \dot{\phi} = \Sigma^{-2} \Delta^{-1} \left[2ar + \lambda \left( \Sigma^{2} - 2r \right) \mathrm{cosec}^{2} \theta \right], \nonumber\\ &&p^{t} = \dot{t} = \Sigma^{-2} \Delta^{-1} \left( \Sigma^{2} - 2ar \lambda \right), \nonumber \end{eqnarray}(37)where the dotted quantities denote differentiation with respect to some affine parameter, and the sign pair sr,sθ describes orientation of radial and latitudinal evolution, respectively (see e.g. Carter 1968; Misner et al. 1973; Chandrasekhar 1983). Radial and latitudial effective potentials read as Rλ,q(r)=[(r2+a2)−aλ]2−Δ[q−(λ−a)2],Θλ,q(θ)=q+a2cos2θ−λ2cot2θ.\begin{eqnarray} \label{eqn:2.1.3} &&R_{\lambda,q} \left( r \right) = \left[\left( r^{2} + a^{2} \right) - a \lambda \right] ^{2} - \Delta \left[q - \left( \lambda - a \right) ^{2} \right],\nonumber \\ &&\Theta_{\lambda,q} \left( \theta \right) = q + a^{2} \cos^{2} \theta -\lambda^{2} \mathrm{cot}^{2} \theta. \end{eqnarray}(38)Here, λ and q are constants of motion related to the photons covariant angular and linear momenta. The LSDplus code performs a time-reverse integration of the package of null geodesics falling on a virtual detector of a distant observer with the screen resolution 1000 × 1000 pixels located at (θobs, r = 1000 M, ϕ = 0) and traces the intersection of the geodesics with the disk surface corresponding to the emission events.

The code LSDplus enables modelling relativistic optical effects in the sky of the observer located anywhere above the event horizon of a Kerr black hole. In the local reference frame related to such an observer, the components of the four-momentum of photons with energy normalized to one, falling on the pixel with coordinates x, y, can be written as follows (see the right side of Fig. 1): kt=−1,   kr=1−x2−y2,   kθ=−y,   kϕ=−x.\begin{equation} \label{for.mom} k_{t} = -1, \,\,\, k_{r} = \sqrt{1 - x^{2} - y^{2}}, \,\,\, k_{\theta} = - y, \,\,\, k_{\varphi} = - x. \end{equation}(39)Then one can obtain the coordinate covariant components of the four-momentum by transforming the local components (39), using appropriate frame tetrads of one-form by relation pμ=eμ⟨α⟩k⟨α⟩.\begin{equation} \label{st.for.mom} p_{\mu} = e_{\mu}^{\langle\alpha\rangle}k_{\langle\alpha\rangle}. \end{equation}(40)The frame tetrad of one-form related to static observer in the Kerr spacetime is given as e(t)=⎧⎪⎪⎨⎪⎪⎩1−2rΣ,0,0,2arsin2θΣ2−2rΣ)⎫⎪⎪⎬⎪⎪⎭,e(ϕ)=⎧⎪⎪⎨⎪⎪⎩0,0,0,ΔΣΣ−2rsinθ⎫⎪⎪⎬⎪⎪⎭.\begin{eqnarray} & & {e}^{({t})}=\left\{\!\!\sqrt{1-\frac{2r}{\Sigma}},0,0,\frac{2ar\sin^2\theta}{\sqrt{\Sigma^2-2r\Sigma)}} \right\},\\ & & {e}^{({r})}=\left\{0,\sqrt{\Sigma/\Delta},0,0 \right\},\label{LC9} \nonumber \\ && {e}^{(\theta)}=\left\{0,0,\sqrt{\Sigma},0 \right\}.\label{LC10} \nonumber \\ & & {e}^{(\varphi)}=\left\{ 0,0,0,\sqrt{\frac{\Delta\Sigma}{\Sigma-2r}}\sin\theta \right\}. \nonumber \end{eqnarray}(41)The constants of motion λ(x,y) and q(x,y) can be easily obtained by straightforward calculation from the components of the four-momentum (40), using the relations (see e.g. Chandrasekhar 1983) λ=−pφpt, q2=(pθpt)2+(λtan(π2−θ))2−a2cos2θ.\begin{eqnarray} &&\lambda = -\frac{p_{\phi}}{p_{t}}, \,\\ &&q^{2} = \left(\frac{p_{\theta}}{p_{t}}\right)^{2} + \left(\lambda\tan\left(\frac{\pi}{2} - \theta\right)\right)^{2} - a^{2}\cos^{2}\theta. \nonumber \end{eqnarray}(42)However, in the investigated case of a distant static observer (robs → ∞), when the rays reaching the observer position are almost parallel (see Fig. 1), the relations between coordinates on the detector screen and constants of motion can be simply written as (e.g. Cunningham & Bardeen 1973) x=−λsin θobs, y=Θλ,q(θobs).\begin{equation} x=-\frac{\lambda}{\sin\,\theta_{\rm obs}}, \qquad y=\Theta_{\lambda,q} \left( \theta_{\rm obs} \right). \end{equation}(43)In the event of detection, the constants λ(x,y) and q(x,y), together with the initial conditions (coordinates of observer and sign pair sr, sθ), fully determine the reverse temporal evolution of the zero geodesics of photons falling on a pixel of the detector screen with the coordinates x, y. The Runge Kutta method of the eighth order (Dorman-Prince method) (Press et al. 2002) used here, integrates the null geodesics and reaches the relative accuracy of 10-15, which, in the case of a central black hole with stellar mass M = 5 M⊙, corresponds to an order of accuracy of 10-11 m on a radial coordinate. To determine the proper orientation of the radial and latitudinal component of the four-momentum (37), the code also analyses the positions of the radial and vertical turning point and sets the corresponding signs sr and sθ. The integration of Eq. (37) by the Runge Kutta method of the eighth order proceeds naturally with an adaptive step. However, the resulting null geodesic is then finally interpolated by the polynomials of the third order for the chosen equidistant time step ΔT, in the case of central black hole mass M = 5 M⊙, corresponding to 10-5 s.

4.2. Radiating surfaces and lightcurves

The surfaces of the tori are modelled by the grid with a resolution of 15 nodes in the radial direction and 75 nodes in the azimuthal one. The grid contains the time-dependent information about coordinates, local intensity, and the four-velocity in the nodes. The time resolution of the surface of the tori necessarily corresponds to the time resolution of the interpolation steps of the geodesics package ΔT. The code LSDplus traces the intersections of the geodesics and linearly interpolated surface of a torus between triads of the nodes of the grid. Assuming the normalized energy in the local observer’s frame, the frequency ratio of the emitted and observed radiation from the torus can be expressed using projection of the four-momentum of a photon pμ to the four-velocity of the surface of the torus uμsur\hbox{$u_{\mu}^{\rm sur}$} in the event of the emission as follows: g=1pμuμsur·\begin{equation} g = \frac{1}{p^{\mu}u_{\mu}^{\rm sur}}\cdot \end{equation}(44)Radial and vertical components of the surface four-velocity are given by equations (25) and (29). The remaining components uϕsur\hbox{$u_{\varphi}^{\rm sur}$}, utsur\hbox{$u_{\rm t}^{\rm sur}$} can easily be obtained using the normalisation condition uμuμ = −1, together with the assumption of constant specific angular momentum (Vincent et al. 2014). Then the instantaneous bolometric intensity detected by each pixel of the screen of a small virtual detector is calculated as Iobs(tobs)=Iem(tobs−tdelay)g4,\begin{equation} I_{\rm obs}(t_{\rm obs}) = I_{\rm em}(t_{\rm obs} - t_{\rm delay})g^{4}, \label{bol_int} \end{equation}(45)where tdelay corresponds to the time delay (the change of a time coordinate) along the appropriate photon trajectory connecting the event of detection of a photon on a pixel with the event of emission on the surface of the torus. Here, Iem is local intensity on the surface in the comoving frame given by the Eq. (33). The total instantaneous detected bolometric flux F(tobs) is a sum of intensities (45) detected by individual pixels multiplied by the solid angle ΔΠ subtended by the pixel in the observer sky F(tobs)=∑i = 11000∑j = 11000Iij(tobs) ΔΠ,\begin{equation} \label{totalflux} F(t_{\rm obs}) = \sum^{1000}_{i \,= \,1}\sum^{1000}_{j\, =\, 1}I_{ij}(t_{\rm obs})\,\Delta \Pi, \end{equation}(46)where i is the index of a pixel column and where j is the index of a pixel row4. Since we are using relative units, we can simply set ΔΠ = 1. The resulting lightcurves are generated in the time resolution ΔT that corresponds to 20 time samples per characteristic vertical oscillation period of the analysed dual oscillation mode.

4.3. Power spectra

To calculate power spectral densities (PSD), the resulting lightcurves are processed by fast Fourier transform (FFT). The PSD at frequency fk = k/ (NΔt) is given as the square of the modulus of the FFT of the signal as PSD(fk)=|1N∑j = 0N−1F(tj)exp(2πijk/N)|2,\begin{equation} \textrm{PSD}(f_k)= \left| \frac{1}{N}\sum_{j\,=\,0}^{N-1}F(t_j) \mathrm{exp}(2\pi ijk/N)\right|^{2}, \label{PSD} \end{equation}(47)where F(tj) is the observed flux (46) at observation time tj = jΔt, and N is the total number of time samples in the lightcurve.

4.4. Iron Kα line profiles

The fluorescent iron Kα line consists of two components with FWHM ≈ 3.5 eV and separation ≈13 eV (see Basko 1978, for details). Considering the energy resolution ΔE = 10 eV of the simulation code, we approximated the rest iron Kα line profile by Lorentzian peak with the scale factor γ = 20 eV located at E0 = 6.4 keV. The instantaneous observed flux per pixel in the energy bin with the central energy Ec is given as Φ(tobs,Ec)=Iem(tobs−tdelay)g3f(Ec/g,γ,E0) ΔΠ,\begin{equation} \label{ebin_flux} \Phi(t_{\rm obs},E_{\rm c}) = I_{\rm em}(t_{\rm obs} - t_{delay})g^{3}f(E_{\rm c}/g,\gamma,E_0)\,\Delta \Pi, \end{equation}(48)where Lorentzian function f reads asf(x,γ,x0)=1πγ[1+(x−x0γ)2]·\begin{equation} f(x,\gamma,x_0)=\frac{1}{\pi\gamma\left[1+\left(\frac{x-x_0}{\gamma}\right)^2\right]}\cdot \end{equation}(49)Then the observed instantaneous iron Kα line profile is constructed by summing energy bin fluxes per pixels (48) over all pixels of the virtual detector in the given time sample. The final integrated line profile is obtained by summing instantaneous line profiles over all time samples.

5. Methods

Applying ray-tracing methods described in the previous section, we performed simulations of lightcurves of the model discussed above of a slender accretion torus oscillating in the dual-mode regime. To obtain closed trajectories of the torus surface and corresponding closed lightcurves, we simulated the behaviour of emitted radiation during three periods of vertical oscillation considering the fixed ratio of oscillation frequencies νu/νl = 3:2. Then we calculated power spectra of obtained lightcurves by relation (47). We studied the impact of the central black hole spin using its three representative values a ∈ (0, 0.5, 0.96). The upper limit of the investigated spin value is almost the highest one, for which the location of equilibrium torus centre r0 can be found by the RP-like frequency relation (35). The impact of the observer inclination (polar angle) i is analysed using the following set of inclination values: i∈(0.01, π12, π6, π4, π3, 512π, 5.512π, 5.7512π, π2)·\begin{eqnarray*} i \in \left(0.01,\,\frac{\pi}{12},\, \frac{\pi}{6},\,\frac{\pi}{4},\,\frac{\pi}{3},\,\frac{5}{12}\pi,\,\frac{5.5}{12}\pi,\,\frac{5.75}{12}\pi,\,\frac{\pi}{2}\right)\cdot \nonumber \end{eqnarray*}We analyse the magnitude relations of five prominent PSD peaks corresponding to two main dual-mode oscillation frequencies, their higher harmonics, and their sum or difference, particularly summarised in the Table 1.

Table 1

Most prominent peaks observed in power density spectra of simulated lightcurves.

Power spectra are calculated for all combinations of investigated values for the spin and the inclination. We plot the magnitudes of these peaks as linearly interpolated functions of the inclination for all the investigated values of the spin and for both investigated torus setups separately (see left panels of Figs. 3 and 4).

Moreover, the integrated iron Kα line profiles emitted from the torus surface are modelled for inclination values i∈(π12, π6, π4, π3, π2)\hbox{$i \in \left(\frac{\pi}{12},\, \frac{\pi}{6},\,\frac{\pi}{4},\,\frac{\pi}{3},\,\frac{\pi}{2}\right)$}. The geometry of the torus’s optical projection is illustrated in Fig. 2 by the frequency shift maps on the virtual detector screen drawn in false colours related to the frequency shift values5. The maps clearly show that the simulation parameters are sufficient for distinguishing the first three relativistic images. The iron Kα line profiles that were also computed display significant secondary blueshifted horns related to secondary (first indirect) relativistic images (see right panels of Figs. 3 and 4).

thumbnail Fig. 2

Examples of the frequency shift maps for different distant views of the oscillating slender torus. The colour boxes on the right display the false colours scale of frequency shift values. The left column corresponds to the case of the ER axisymmetric dual mode. The right column corresponds to the case of the RP-like non-axisymmetric dual mode. The rows of the figure correspond to spin values a = 0, a = 0.5 and a = 0.96, respectively.

thumbnail Fig. 3

Simulations outputs in the case of the ER axisymmetric dual mode. Left panels: the amplitudes of prominent PSD peaks (see Table 1) as a function of distant observer inclination i. Right panels: iron Kα line profiles constructed for i∈(π12, π6, π4, π3, π2)\hbox{$i \in \left(\frac{\pi}{12},\, \frac{\pi}{6},\,\frac{\pi}{4},\,\frac{\pi}{3},\,\frac{\pi}{2}\right)$}. The rows of the picture correspond to the cases of spin values a = 0, a = 0.5, and a = 0.96, respectively (see Table 2).

thumbnail Fig. 4

Simulations outputs in the case of the RP-like non-axisymmetric dual mode. Left panels: the amplitudes of prominent PSD peaks (see Table 1) as a function of distant observer inclination i. Right panels: iron Kα line profiles constructed for i∈(π12, π6, π4, π3, π2)\hbox{$i \in \left(\frac{\pi}{12},\, \frac{\pi}{6},\,\frac{\pi}{4},\,\frac{\pi}{3},\,\frac{\pi}{2}\right)$}. The rows of the picture correspond to the cases of spin values a = 0, a = 0.5, and a = 0.96, respectively (see Table 3).

6. Results

6.1. Results for the ER axisymmetric setup

Table 2 summarises the parameters of the slender torus that oscillates in the pure epicyclic axisymmetric dual mode (mr = 0, mθ = 0) for three investigated values of the spin. The radial coordinate of equilibrium torus centre r0 given by relation (34) remains above both the black hole photosphere6 and the ergosphere for all such configurations.

Table 2

Values of parameters describing the investigated slender torus model for ER axisymmetric setup.

The lightcurve waveforms are influenced by a complex interplay of the general relativistic frequency shift, the time variation of the emitting torus surface area, and the time variation of the apparent torus area on the virtual detector screen (Bakala et al. 2015). All these effects strongly depend on the radial coordinate of the emission event, the inclination of the distant observer i, and the central black hole spin a. Nevertheless, the magnitude relations depicted in the left-hand panels of Fig. 3 exhibit certain identical qualitative features for all investigated spin values. The pair of peaks corresponding to radial νl and vertical νu torus oscillation frequency is dominant on a wide range of i. For this inclination range, the examined ER axisymmetric setup predicts twin peaks HF QPOs frequency ratio equal to 3:2 in accordance with expectations. The νl peak remains most prominent for low and medium values of distant observer inclination i. The magnitude of the νu peak grows with i becoming the most prominent for relatively high inclinations, but it rapidly falls for exact or almost exact equatorial observers. At the same time, the magnitude of the peak corresponding to 3νl, 2νu rapidly grows. Therefore, in the case of such observers, the examined torus configuration predicts a frequency ratio equal to 1/3 for the pair of the most distinguishable HF QPO peaks. In the case of zero or moderate spins (a = 0, a = 0.5) and small inclinations (i≤π12\hbox{$i \le \frac{\pi}{12}$}), the magnitude of the 2νl peak slightly exceeds the νl peak magnitude, and the predicted twin peaks HF QPOs frequency ratio value is equal to 1:2. As illustrated in the plots of magnitude relations (see left panels of Fig. 3), the spectral content of less distinct PSD peaks varies depending on values of i and a.

Like the power spectra behaviour, the iron Kα line profiles keep some identical qualitative features for all investigated spin values. Naturally, the energy span of line profiles is expanded and shifted down with decreasing r0. The dependence of the height of the primary blueshifted horns on i is the only qualitative difference observable for different spin values (see right panels of Fig. 3).

6.2. Results for the RP-like non-axisymmetric setup

Table 3 summarizes parameters of the slender torus oscillating in the RP-like non-axisymmetric dual mode (mr = −1, mθ = −2) for three investigated values of the spin. In the case of zero or moderate spin (a = 0, a = 0.5), the radial coordinate of equilibrium torus centre r0 given by relation (35) remains located above the black hole photosphere, as well as the ergosphere, while in the case of high spin (a = 0.96), the torus is located inside the ergopshere and therefore also deeply inside the photosphere. Moreover, in the case of high spin, the radial extent of the torus obtained as r0/ 10 exceeds the location of the cusp of equipotential surfaces (Blaes et al. 2006; Straub & Šrámková 2009). Such a torus configuration becomes unstable. Unfortunately, a surface area of the high spin stable configuration with maximum possible β = 7.0 × 10-5 is almost negligible, and emitted flux is comparable to the numerical error of the simulation. Therefore, we keep the torus radial extent equal to r0/ 10 and choose the unstable high spin configuration with β = 0.002.

Table 3

Values of parameters describing the investigated slender torus model for RP-like non-axisymmetric setup.

In the case of zero or moderate spin (a = 0, a = 0.5), the qualitative picture of power spectra and iron Kα line profiles behaviour is very similar to the case of the ER axisymmetric setup discussed in the previous section (see Fig. 4). The prediction for low inclination represents the main difference. In the Schwarzschild case, the pair of peaks corresponding to radial νl and vertical νu oscillation frequency also remains dominant for i≤π12\hbox{$i \le \frac{\pi}{12}$}, predicting the twin peaks HF QPOs frequency ratio equal to 3:2, as depicted in the top left panel of Fig. 4. In the case of a = 0.5 and a very small inclination, the magnitude of the νu−νl peak (instead of the 2νl peak acting the same way in the case of the ER axisymmetric setup) slightly exceeds the νl peak magnitude, and the predicted twin peaks HF QPOs frequency ratio is equal to 1:2 (see the middle left panel of Fig. 4).

The unstable high-spin configuration exhibits an entirely different picture, as shown in the bottom panels of Fig. 4. In the whole range of inclination, the pair of dominant PSD peaks corresponds to the radial νl frequency and its second harmonic 2νl. Therefore, in the unstable high spin case, the examined RP-like non-axisymmetric setup surprisingly predicts the twin peaks HF QPOs frequency ratio value that is only equal to 1:2. The dramatic change of the optical projection properties is documented by iron Kα line profiles in the bottom right-hand panel of Fig. 4. The energy span is significantly shifted down, and both primary and secondary blueshifted horns have comparable heights. The computed profiles also display numerical instabilities caused by a small emitting surface area of the unstable high spin torus configuration. The line profile related to i=π2\hbox{$i=\frac{\pi}{2}$} exhibits exceptional behaviour, because its extremely wide energy span reaches 11 keV and its primary blueshifted horn is absolutely dominant. The corresponding frequency shift map in the bottom right-hand panel of Fig. 2 also illustrates the equatorial optical projection of the torus located in the close vicinity of the Kerr black hole event horizon. It is clearly visible that the angular size of both secondary and tertiary relativistic images exceeds the angular size of the primary image. Moreover, despite the significant gravitational redshift, the high Keplerian orbital velocity causes a high Doppler blueshift for the left side of the torus projection corresponding to the extreme height of the primary blueshifted horn in the iron Kα line profile.

7. Conclusions and perspectives

The aim of this article has been to model twin peaks HF QPOs as a spectral impact of isotropically radiating slender tori oscillating in a dual mode regime in the close vicinity of Kerr black holes. Vincent et al. (2014) show that a significant fraction of the observed flux is regulated by the torus motion described by the lowest oscillation modes. We therefore examined two configurations of the dual oscillation regime based on the lowest radial and vertical oscillation modes with different azimuthal wave numbers. Appropriate frequency relations correspond to the two competing QPOs models, the epicyclic resonance (ER) HF QPOs model (Abramowicz & Kluźniak 2001) and a slightly modified relativistic precession (RP) QPOs model (Stella & Vietri 1999). We model twin peaks HF QPOs by the pair of the most prominent peaks in the obtained power spectra. Our results show that independently of the spin, the ER axisymmetric setup yields power spectra with the pair of dominant PSD peaks corresponding to the frequencies of radial and vertical oscillation modes with a proper ratio equal to 3:2, except some special cases of very high or very low distant observer inclinations, where higher harmonics becomes prominent. The predictions of the RP-like non-axisymmetric setup are almost identical to the ER case for zero or moderate spin configurations. An unstable high-spin RP-like configuration with the torus located in the ergosphere exhibits dominant PSD peaks pair corresponding to the frequency of radial oscillation modes and its second harmonics in the whole range of inclinations, so it predicts a constant frequency ratio equal to 1:2. The entire change of the optical projection is also documented by the different iron Kα line profiles with respect to the previous cases.

The analysis presented in the article primarily focused on the relative ratios of the amplitudes of the most prominent frequency peaks in the modelled power spectra. However, the absolute fractional rms of the amplitudes of HF QPOs peaks in the detected signal depends not only on the amplitudes of perturbation Ar,θ, but also on the relations of individual components of the whole total source flux. In Bakala et al. (2014) we defined an empirical model of total source flux, which mimics the so-called high steep power-law (HSPL) state in GRS 1905+105, including steep spectrum and power-law-dominated variability with an additional broad Lorentzian component at low frequencies (McClintock & Remillard 2006). Then we used this background to analyse the resolution of HF QPO peaks for a similar but simpler model of oscillating slender torus in the Schwarzschild geometry (Bursa et al. 2004), slowly passing the resonant orbit r0. Considering the capabilities of the RXTE and LOFT instruments simulated by their response matrices, we showed that the presently available observational technology enables a good detection of the pair of the most prominent peaks in such a modelled signal. Nevertheless, the behaviour of spectral content of less distinct PSD peaks probably remains the key task for the data analysis of future sensitive space observatory missions for X-ray timing, such as the proposed LOFT mission (see Bakala et al. 2014; Feroci et al. 2014; Karas et al. 2014, for details).

Our simulation yields iron Kα line profiles that are very different from the line profile integrated over the entire accretion disk. Therefore, the next related topic for future space X-ray missions can be sensitive frequency-resolved spectroscopy, which will be able to isolate the spectral component oscillating on the QPO frequency (see e.g. Axelsson et al. 2014; Revnivtsev et al. 1999). Phase-resolved spectroscopy that traces the iron line profile changes throughout an oscillation cycle could be another potentially interesting diagnostic tool. This idea has already been suggested for the case of low-frequency QPOs (e.g. Ingram & Done 2012b; Tsang & Butsky 2013), but its application for the studied model of HF QPO driven by slender torus oscillations will require a more detailed future study.

We assume an optically thick slender torus, and thus the influence of the torus opacity can also be the subject for our future research. It is possible to generalise the examined slender torus model by considering the pressure effects on the mode frequencies and the torus shape (Straub & Šrámková 2009). In our study, the location of the torus centre is empirically chosen using the observed twin peaks HF QPOs ratio. The resonant coupling of oscillation modes can prefer particular values of radial coordinate for amplification or excitation of QPOs (Horák 2008). Therefore, further important improvements in the simulations can incorporate mode-resonant coupling. Future implementation of improved models of non-slender tori into the used LSDplus code can be the next step towards more realistic results. A future detailed comparative study of spectral harmonic content can also be devoted to the possibility of distinguishing between QPOs models based on either accretion tori oscillations or the orbital motion of radiating blobs.

1

In the case of LMXBs, there are indications that the ratio of twin peak HF QPOs frequencies is not only clustered around 3:2, but 4:3 and 5:4 ratios are also observed (see e.g. Török et al. 2007, 2008a,b,c).

2

The slender torus geometry considered here accords well with the truncated disk model (see e.g. Done et al. 2007). Also, the power spectral fits of Ingram & Done (2012a) predict that the hot inner flow (corona) has a small scale height in the relevant spectral state.

3

Investigated torus model does not consider the presence of the resonant coupling of oscillation modes, which can cause amplification or excitation of QPOs for the preferred values of the radial coordinate (Horák 2008).

4

We assume tiny angular size of the torus image in the observer sky and therefore constant ΔΠ.

5

The frequency shift maps displayed in Fig. 2 are not zoomed and not positioned identically with respect to the projection of the whole observer sky.

6

Kerr black hole photosphere – a region of spherical unstable photon orbits reaches maximum extent in the equatorial plane between corotating and counter-rotating circular photon orbits, while it becomes infinitesimally thin on the polar axis (see e.g. Teo 2003, for details)

Acknowledgments

We acknowledge the Czech research grant GAČR 209/12/P740, Polish NCN UMO-2011/01/B/ST9/05439 grant and the internal grants of Silesian University in Opava IGS/11/2015 and SGS/11/2013.

References

  1. Abramowicz, M. A., & Fragile, P. C. 2013, Liv. Rev. Relativity, 16, 1 [Google Scholar]
  2. Abramowicz, M. A., & Kluźniak, W. 2001, A&A, 374, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Abramowicz, M. A., & Kluźniak, W. 2004, in X-ray Timing 2003: Rossi and Beyond, eds. P. Kaaret, F. K. Lamb, & J. H. Swank, AIP Conf. Ser., 714, 21 [Google Scholar]
  4. Abramowicz, M. A., & Kluźniak, W. 2005, Ap&SS, 300, 127 [NASA ADS] [CrossRef] [Google Scholar]
  5. Abramowicz, M. A., Bulik, T., Bursa, M., & Kluźniak, W. 2003a, A&A, 404, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Abramowicz, M. A., Karas, V., Kluźniak, W., Lee, W. H., & Rebusco, P. 2003b, PASJ, 55, 467 [NASA ADS] [CrossRef] [Google Scholar]
  7. Abramowicz, M. A., Blaes, O. M., Horák, J., Kluźniak, W., & Rebusco, P. 2006, Classical and Quantum Gravity, 23, 1689 [Google Scholar]
  8. Aliev, A. N. 2008, in The Eleventh Marcel Grossmann Meeting On Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories, ed. H. Kleinert, R. T. Jantzen, & R. Ruffini, 1057 [Google Scholar]
  9. Aliev, A. N., & Galtsov, D. V. 1981, General Relativity Gravitation, 13, 899 [Google Scholar]
  10. Alpar, M. A., & Shaham, J. 1985, Nature, 316, 239 [NASA ADS] [CrossRef] [Google Scholar]
  11. Axelsson, M., Done, C., & Hjalmarsdotter, L. 2014, MNRAS, 438, 657 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bakala, P., Čermák, P., Hledík, S., Stuchlík, Z., & Truparová, K. 2007, Centr. Eur. J. Phys., 5, 599 [NASA ADS] [Google Scholar]
  13. Bakala, P., Török, G., Karas, V., et al. 2014, MNRAS, 439, 1933 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bakala, P., Goluchová, K., Šrámková, E., et al. 2015, in IAU Symp. 313, eds. F. Massaro, C. C. Cheung, E. Lopez, & A. Siemiginowska, 380 [Google Scholar]
  15. Bambi, C. 2013, Phys. Rev. D, 87, 023007 [CrossRef] [Google Scholar]
  16. Basko, M. M. 1978, ApJ, 223, 268 [NASA ADS] [CrossRef] [Google Scholar]
  17. Beckwith, K., & Done, C. 2005, MNRAS, 359, 1217 [NASA ADS] [CrossRef] [Google Scholar]
  18. Belloni, T. M., Sanna, A., & Méndez, M. 2012, MNRAS, 426, 1701 [NASA ADS] [CrossRef] [Google Scholar]
  19. Blaes, O. M., Arras, P., & Fragile, P. C. 2006, MNRAS, 369, 1235 [NASA ADS] [CrossRef] [Google Scholar]
  20. Broderick, A. E., & Loeb, A. 2005, MNRAS, 363, 353 [NASA ADS] [CrossRef] [Google Scholar]
  21. Bursa, M., Abramowicz, M. A., Karas, V., & Kluźniak, W. 2004, ApJ, 617, L45 [NASA ADS] [CrossRef] [Google Scholar]
  22. Čadež, A., & Calvani, M. 2005, MNRAS, 363, 177 [NASA ADS] [CrossRef] [Google Scholar]
  23. Čadež, A., Calvani, M., & Kostić, U. 2008, A&A, 487, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Carter, B. 1968, Phys. Rev., 174, 1559 [NASA ADS] [CrossRef] [Google Scholar]
  25. Chan, C.-k., Psaltis, D., & Özel, F. 2013, ApJ, 777, 13 [NASA ADS] [CrossRef] [Google Scholar]
  26. Chandrasekhar, S. 1983, The mathematical theory of black holes (Oxford: Clarendon Press) [Google Scholar]
  27. Cunningham, C. T., & Bardeen, J. M. 1972, ApJ, 173, L137 [NASA ADS] [CrossRef] [Google Scholar]
  28. Cunningham, C. T., & Bardeen, J. M. 1973, ApJ, 183, 237 [NASA ADS] [CrossRef] [Google Scholar]
  29. Dexter, J., & Agol, E. 2009, ApJ, 696, 1616 [NASA ADS] [CrossRef] [Google Scholar]
  30. Done, C., Gierliński, M., & Kubota, A. 2007, A&ARv, 15, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Fabian, A. C., Rees, M. J., Stella, L., & White, N. E. 1989, MNRAS, 238, 729 [NASA ADS] [CrossRef] [Google Scholar]
  32. Feroci, M., den Herder, J. W., Bozzo, E., et al. 2014, in SPIE Conf. Ser., 9144, 2 [Google Scholar]
  33. Germanà, C. 2013, MNRAS, 430, L1 [NASA ADS] [CrossRef] [Google Scholar]
  34. Germanà, C., Kostić, U., Čadež, A., & Calvani, M. 2009, in AIP Conf. Ser. 1126, eds. J. Rodriguez & P. Ferrando, 367 [Google Scholar]
  35. Horák, J. 2008, A&A, 486, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Ingram, A., & Done, C. 2012a, MNRAS, 419, 2369 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ingram, A., & Done, C. 2012b, MNRAS, 427, 934 [NASA ADS] [CrossRef] [Google Scholar]
  38. Ingram, A., & Motta, S. 2014, MNRAS, 444, 2065 [NASA ADS] [CrossRef] [Google Scholar]
  39. Karas, V., Vokrouhlicky, D., & Polnarev, A. G. 1992, MNRAS, 259, 569 [NASA ADS] [CrossRef] [Google Scholar]
  40. Karas, V., Bakala, P., Torok, G., et al. 2014, Acta Polytechnica, 54, 191 [NASA ADS] [CrossRef] [Google Scholar]
  41. Kato, S. 2001, PASJ, 53, 1 [NASA ADS] [CrossRef] [Google Scholar]
  42. Kato, S. 2007, PASJ, 59, 451 [NASA ADS] [Google Scholar]
  43. Kluźniak, W., & Abramowicz, M. A. 2001, ArXiv e-prints [arXiv:astro-ph/0105057] [Google Scholar]
  44. Kostić, U., Čadež, A., Calvani, M., & Gomboc, A. 2009, A&A, 496, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Lai, D., Fu, W., Tsang, D., Horák, J., & Yu, C. 2013, in IAU Symp. 290, eds. C. M. Zhang, T. Belloni, M. Méndez, & S. N. Zhang, 57 [Google Scholar]
  46. Lamb, F. K., Shibazaki, N., Alpar, M. A., & Shaham, J. 1985, Nature, 317, 681 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mazur, G. P., Vincent, F. H., Johansson, M., et al. 2013, A&A, 554, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. McClintock, J. E., & Remillard, R. A. 2006, Black hole binaries, eds. W. H. G. Lewin & M. van der Klis, 157 [Google Scholar]
  49. Miller, M. C., Lamb, F. K., & Psaltis, D. 1998, ApJ, 508, 791 [NASA ADS] [CrossRef] [Google Scholar]
  50. Misner, C. W., Thorne, K. S., & Wheeler, J. A. 1973, Gravitation (San Francisco: Freeman) [Google Scholar]
  51. Morsink, S. M., & Stella, L. 1999, ApJ, 513, 827 [NASA ADS] [CrossRef] [Google Scholar]
  52. Motta, S. E., Belloni, T. M., Stella, L., Muñoz-Darias, T., & Fender, R. 2014, MNRAS, 437, 2554 [NASA ADS] [CrossRef] [Google Scholar]
  53. Mukhopadhyay, B. 2009, ApJ, 694, 387 [NASA ADS] [CrossRef] [Google Scholar]
  54. Papaloizou, J. C. B., & Pringle, J. E. 1984, MNRAS, 208, 721 [NASA ADS] [CrossRef] [Google Scholar]
  55. Pecháček, T., Karas, V., & Czerny, B. 2008, A&A, 487, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Pecháček, T., Goosmann, R. W., Karas, V., Czerny, B., & Dovčiak, M. 2013, A&A, 556, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Pétri, J. 2005, A&A, 439, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2002, Numerical recipes in C++: the art of scientific computing (New York: Cambridge University Press) [Google Scholar]
  59. Psaltis, D., Wijnands, R., Homan, J., et al. 1999, ApJ, 520, 763 [NASA ADS] [CrossRef] [Google Scholar]
  60. Rauch, K. P., & Blandford, R. D. 1994, ApJ, 421, 46 [NASA ADS] [CrossRef] [Google Scholar]
  61. Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
  62. Revnivtsev, M., Gilfanov, M., & Churazov, E. 1999, A&A, 347, L23 [NASA ADS] [Google Scholar]
  63. Rezzolla, L., Yoshida, S., & Zanotti, O. 2003, MNRAS, 344, 978 [NASA ADS] [CrossRef] [Google Scholar]
  64. Schee, J., & Stuchlík, Z. 2013, J. Cosmology Astropart. Phys., 4, 5 [NASA ADS] [CrossRef] [Google Scholar]
  65. Schnittman, J. D. 2006, Ph.D. Thesis, Massachusetts Institute of technology [Google Scholar]
  66. Schnittman, J. D., & Bertschinger, E. 2004, ApJ, 606, 1098 [NASA ADS] [CrossRef] [Google Scholar]
  67. Schnittman, J. D., & Rezzolla, L. 2006, ApJ, 637, L113 [NASA ADS] [CrossRef] [Google Scholar]
  68. Šrámková, E. 2005, Astron. Nachr., 326, 835 [NASA ADS] [CrossRef] [Google Scholar]
  69. Šrámková, E., Torkelsson, U., & Abramowicz, M. A. 2007, A&A, 467, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Stella, L., & Vietri, M. 1998, ApJ, 492, L59 [NASA ADS] [CrossRef] [Google Scholar]
  71. Stella, L., & Vietri, M. 1999, Phys. Rev. Lett., 82, 17 [NASA ADS] [CrossRef] [Google Scholar]
  72. Stella, L., & Vietri, M. 2002, in The Ninth Marcel Grossmann Meeting, eds. V. G. Gurzadyan, R. T. Jantzen, & R. Ruffini (Singapore: World Scientific), 426 [Google Scholar]
  73. Straub, O., & Šrámková, E. 2009, Classical and Quantum Gravity, 26, 055011 [Google Scholar]
  74. Stuchlík, Z., Konar, S., Miller, J. C., & Hledík, S. 2008, A&A, 489, 963 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Tagger, M., & Varnière, P. 2006, ApJ, 652, 1457 [NASA ADS] [CrossRef] [Google Scholar]
  76. Teo, E. 2003, General Relativity and Gravitation, 35, 1909 [NASA ADS] [CrossRef] [Google Scholar]
  77. Titarchuk, L., & Wood, K. 2002, ApJ, 577, L23 [NASA ADS] [CrossRef] [Google Scholar]
  78. Török, G. 2005, Astron. Nachr., 326, 856 [NASA ADS] [CrossRef] [Google Scholar]
  79. Török, G., & Stuchlík, Z. 2005, A&A, 437, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Török, G., Abramowicz, M. A., Kluźniak, W., & Stuchlík, Z. 2005, A&A, 436, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Török, G., Stuchlík, Z., & Bakala, P. 2007, Centr. Eur. J. Phys., 5, 457 [NASA ADS] [CrossRef] [Google Scholar]
  82. Török, G., Abramowicz, M. A., Bakala, P., et al. 2008a, Acta Astron., 58, 15 [NASA ADS] [Google Scholar]
  83. Török, G., Abramowicz, M. A., Bakala, P., et al. 2008b, Acta Astron., 58, 113 [NASA ADS] [Google Scholar]
  84. Török, G., Bakala, P., Stuchlík, Z., & Čech, P. 2008c, Acta Astron., 58, 1 [NASA ADS] [Google Scholar]
  85. Török, G., Bakala, P., Šrámková, E., Stuchlík, Z., & Urbanec, M. 2010, ApJ, 714, 748 [NASA ADS] [CrossRef] [Google Scholar]
  86. Török, G., Bakala, P., Šrámková, E., et al. 2012, ApJ, 760, 138 [NASA ADS] [CrossRef] [Google Scholar]
  87. Tsang, D., & Butsky, I. 2013, MNRAS, 435, 749 [NASA ADS] [CrossRef] [Google Scholar]
  88. Urbanec, M., Miller, J. C., & Stuchlík, Z. 2013, MNRAS, 433, 1903 [NASA ADS] [CrossRef] [Google Scholar]
  89. van der Klis, M. 2004, ArXiv e-prints [arXiv:astro-ph/0410551] [Google Scholar]
  90. Viergutz, S. U. 1993, A&A, 272, 355 [NASA ADS] [Google Scholar]
  91. Vincent, F. H., Paumard, T., Gourgoulhon, E., & Perrin, G. 2011, Classical and Quantum Gravity, 28, 225011 [NASA ADS] [CrossRef] [Google Scholar]
  92. Vincent, F. H., Mazur, G. P., Straub, O., et al. 2014, A&A, 563, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Yang, X.-L., & Wang, J.-C. 2014, A&A, 561, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Zhang, C.-M. 2005, Chin. J. Astron. Astrophys. Suppl., 5, 21 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Most prominent peaks observed in power density spectra of simulated lightcurves.

In the text
Table 2

Values of parameters describing the investigated slender torus model for ER axisymmetric setup.

In the text
Table 3

Values of parameters describing the investigated slender torus model for RP-like non-axisymmetric setup.

In the text

All Figures

thumbnail Fig. 1

Schematic ray-tracing geometry for the cases of a general observer and distant observer (robs → ∞).
In the text
thumbnail Fig. 2

Examples of the frequency shift maps for different distant views of the oscillating slender torus. The colour boxes on the right display the false colours scale of frequency shift values. The left column corresponds to the case of the ER axisymmetric dual mode. The right column corresponds to the case of the RP-like non-axisymmetric dual mode. The rows of the figure correspond to spin values a = 0, a = 0.5 and a = 0.96, respectively.

In the text
thumbnail Fig. 3

Simulations outputs in the case of the ER axisymmetric dual mode. Left panels: the amplitudes of prominent PSD peaks (see Table 1) as a function of distant observer inclination i. Right panels: iron Kα line profiles constructed for i∈(π12, π6, π4, π3, π2)\hbox{$i \in \left(\frac{\pi}{12},\, \frac{\pi}{6},\,\frac{\pi}{4},\,\frac{\pi}{3},\,\frac{\pi}{2}\right)$}. The rows of the picture correspond to the cases of spin values a = 0, a = 0.5, and a = 0.96, respectively (see Table 2).
In the text
thumbnail Fig. 4

Simulations outputs in the case of the RP-like non-axisymmetric dual mode. Left panels: the amplitudes of prominent PSD peaks (see Table 1) as a function of distant observer inclination i. Right panels: iron Kα line profiles constructed for i∈(π12, π6, π4, π3, π2)\hbox{$i \in \left(\frac{\pi}{12},\, \frac{\pi}{6},\,\frac{\pi}{4},\,\frac{\pi}{3},\,\frac{\pi}{2}\right)$}. The rows of the picture correspond to the cases of spin values a = 0, a = 0.5, and a = 0.96, respectively (see Table 3).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.