| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 12 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201525837 | |
| Published online | 26 August 2015 | |
Improving signal-to-noise in the direct imaging of exoplanets and circumstellar disks with MLOCI⋆
1 European Southern Observatory, Alonso de Cordova 3107, Vitacura, 19001 Casilla, Santiago Chile,
e-mail: zwahhaj@eso.org
2 Facultad de Ingenieria, Universidad Diego Portales. Av. Ejercito 441, Santiago, Chile
3 Sterrewacht Leiden, Universiteit Leiden, PO Box 9513, 2300 RA Leiden, The Netherlands
4 Departamento de Física y Astronomía, Universidad de Valparaíso, Valparaíso, Chile
5 Departamento de Astronomá, Universidad de Chile, Casilla 36-D, Santiago, Chile
6 Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
7 Institute for Astronomy, University of Edinburgh, Blackford Hill, Edinburgh EH9 3HJ, UK
8 Gemini Observatory, Southern Operations Center, c/o AURA, Casilla 603, La Serena, Chile
9 UMI-FCA, CNRS/INSU (UMI 3386), France
10 Millennium Nucleus “Protoplanetary Disks”, Chile
Received: 6 February 2015
Accepted: 14 May 2015
We present a new algorithm designed to improve the signal-to-noise ratio (S/N) of point and extended source detections around bright stars in direct imaging data.One of our innovations is that we insert simulated point sources into the science images, which we then try to recover with maximum S/N. This improves the S/N of real point sources elsewhere in the field. The algorithm, based on the locally optimized combination of images (LOCI) method, is called Matched LOCI or MLOCI. We show with Gemini Planet Imager (GPI) data on HD 135344 B and Near-Infrared Coronagraphic Imager (NICI) data on several stars that the new algorithm can improve the S/N of point source detections by 30–400% over past methods. We also find no increase in false detections rates. No prior knowledge of candidate companion locations is required to use MLOCI. On the other hand, while non-blind applications may yield linear combinations of science images that seem to increase the S/N of true sources by a factor >2, they can also yield false detections at high rates. This is a potential pitfall when trying to confirm marginal detections or to redetect point sources found in previous epochs. These findings are relevant to any method where the coefficients of the linear combination are considered tunable, e.g., LOCI and principal component analysis (PCA). Thus we recommend that false detection rates be analyzed when using these techniques.
Key words: planets and satellites: detection / instrumentation: adaptive optics / methods: data analysis / techniques: image processing
Based on observations obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (USA), the Science and Technology Facilities Council (UK), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), Ministério da Ciência e Tecnologia (Brazil) and Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina).
© ESO, 2015
1. Introduction
While more than 1700 planets have been detected by transit and radial velocity techniques, only about a dozen planetary-mass objects (≤13 MJup) have been directly imaged around stars to date1. However, this number is expected to increase significantly (e.g., McBride et al. 2011) since first light has just been obtained with the new extreme adaptive optics (AO) instruments, Gemini Planet Imager (GPI; Macintosh et al.2008), and SPHERE (Beuzit et al. 2010). A severe challenge in AO imaging arises from quasi-static speckles, which can emulate astronomical point sources for hour-long timescales (e.g., Marois et al. 2005). Besides high-order AO corrections and coronagraphy, the most powerful advances that overcome this sensitivity barrier are (1) angular differential imaging (ADI; Liu 2004; Marois et al. 2005), which decouples the sky rotation of the planet from the speckles; and (2) spectral difference imaging (SDI; Racine et al. 1999; Biller et al. 2007) and spectral deconvolution (Sparks & Ford 2002; Thatte et al. 2007), which decouple the star and planet spectrally, taking advantage of the fact that speckles move out radially with wavelength and that planet and stellar spectra differ.
 |
Fig. 1 Central steps of the MLOCI algorithm (see Sect. 2). Steps 2, 3, and 4, top row: a counterpart PSF is created for each science image. The counterpart PSF is such that its subtraction from the science preserves signal at 2 locations. Step 5, bottom row: each science image with reference fake sources and its counterpart PSF are derotated to align north upwards. |
To obtain the maximum signal-to-noise ratio (S/N) for true companions, the speckle structure, which is correlated over time and wavelength, must be subtracted. Thus, some science images must take negative weight in the linear combination to create the final reduced image. Tremendous effort has been dedicated to finding algorithms that optimize detections by varying the weights of science images. The most prominent of these have been the LOCI algorithm (Lafrenière et al. 2007) and the PCA-based algorithms, KLIP (Soummer et al. 2012) and PynPoint (Amara & Quanz 2012), which focus on minimizing speckle residuals. Subsequent improvements have concentrated on optimizing the S/N of point source recovery, e.g., damped LOCI, ALOCI, and TLOCI (Pueyo et al. 2012; Currie et al. 2013; Marois et al. 2014).
Our own experiments with data from the Gemini NICI Planet-Finding Campaign (Liu et al. 2010), based on blind recovery of simulated companions, showed no measurable improvement in achieved contrast using LOCI compared to conventional ADI (Wahhaj et al. 2013a). We found that the main problem with LOCI was that reductions in noise around detections were also accompanied by reductions in the signal. However, applications of LOCI to data from instruments other than NICI have been reported to improve the S/N of detections, although these typically do not employ prior image filtering (e.g., unsharp masking; Lafrenière et al. 2007; Bowler et al. 2015). Here, we present a LOCI variant that significantly improves S/N. We demonstrate the effectiveness of the algorithm using NICI Campaign datasets and the early science GPI dataset on HD 135344 B, a transition disk with strong evidence for ongoing planet formation. The science results from the GPI observations will be published in Ménard et al. (2015).
 |
Fig. 2 Final steps of the MLOCI algorithm (see Sect. 2). Steps 6 and 7, top row: instead of the usual difference image combination in ADI, all science with fakes and counterpart PSF images are combined to recover injected sources in the reference sector. Prior to the linear combination using coefficients from LOCI, we replace the science images with fakes with the original science images, so that the fake sources do not appear in the individual reductions. The fakes are, however, drawn in the figure above to show their changing locations. Steps 8, 9, and 10, bottom row: several such reductions, created through step 8, are combined to create the final reduction. The final reduction preserves point source signal, generally. |
2. Matched LOCI
The ADI reduction method is based on the principle that when the image rotator is turned off for an altitude-azimuth telescope, the sky rotates with respect to the detector at the Cassegrain focus, while the quasi-static speckle pattern caused by the telescope and instrument optics does not. At the Nasmyth focus, one achieves the same effect in an observing mode called pupil-tracking. Astrophysical sources are thus separated from the speckle pattern, which is isolated by median-combining a series of speckle-aligned images to create a reference point-spread function (PSF). This reference PSF is then subtracted from each science image. The difference images are then derotated to align the sky and stacked again to create the final reduced image. The details of our own implementation of regular ADI can be found in Wahhaj et al. (2013a). The LOCI algorithm differs in the PSF subtraction step where it subtracts the best linear combination of speckle-aligned images such that the root-mean square (RMS) in some region of the field of view (FoV) is minimized.
Our new algorithm, which we call MLOCI for matched LOCI, introduces three main innovations: 1) reference point sources are inserted into the science images, which we then try to recover with maximum S/N. This improves the recovery S/N of real point sources elsewhere in the images. 2) Strong negative point sources are inserted into each science image at the preselected reference positions. To create the best PSF for star subtraction for the chosen image, LOCI is then used to linearly combine the other science images and match this image. This generally preserves the point-source flux after PSF-subtraction. 3) Instead of subtracting matching PSFs immediately, they are derotated and aligned with their respective science images. Finally, all derotated science images and PSFs are linearly combined to directly match an image of the reference point sources, an image that otherwise contains no noise or signal. MLOCI is illustrated in Figs. 1 and 2. Below we list the steps of MLOCI in detail.
-
1.
A basic ADI reduction is initially applied to identify all candidate point sources with S/N> 2.
-
2.
For each science image, we define annuli with inner radius one full width at half maximum (FWHM) less than the radial coordinate of each candidate. We determine the optimum radial widths (W) of these annuli in Sect. 4. The annuli are divided into target sectors subtending 40°, which include the candidate point sources and for which the MLOCI results are obtained one by one. The other 320° of the annuli are defined as reference sectors into which we insert point sources at two (or three) chosen sky locations (see Fig. 1). Circular regions of radius 1 FHWM centered on the candidates are removed from the reference regions. In trying to recover the simulated point sources in the reference sectors, we aim to enhance the point source sensitivity in the target sectors.
-
3.
All images are unsharp-masked or catch-filtered (see Wahhaj et al. 2013a). For each science image, we create a counterpart where a point source is subtracted from the two (or three) sky locations chosen earlier in the reference sectors (see Fig. 1). The number of point sources subtracted and their intensity (or Pull; see Sect. 4) are found by experiments that we describe in Sect. 4. The point sources that we subtract are made to be azimuthally narrower then their radial extension. This is done to allow eventual ADI self-subtraction by our algorithm in a controlled manner. Such point sources have a positive core and negative wings along the azimuthal direction. Anticipating this shape and using it here, and when making the final reduced image, allows us to increase the S/N of real sources. To create these sources we smear Gaussian sources out over an angular range 30% less than the total rotation in the ADI data set. We then subtract the smeared images from the point sources. However, the sources are not allowed to shrink azimuthally to widths that are less than 0.7 times the radial FWHM. The 30% figure above was decided upon by trial and error.
-
4.
Next, LOCI is used to linearly combine the science images (with injected point sources in the reference region) to find the best match to each counterpart image to make counterpart PSFs. Only the science image corresponding to the counterpart image is excluded from the linear combination. There is no need for further image selection because the negative sources in the counterpart images protect against self-subtraction. The science images should be speckle-aligned at this stage. When there are several spectral channels, the images need to be spectrally deconvolved as described in Sect. 3. The matching is only done over the reference sector, not the target sector, which includes the candidate location.
-
5.
The science images are then derotated to align north upwards. Each counterpart PSF is derotated by the same angle as its science image.
-
6.
A single image with the injected sources in the reference sector with the same flux and sky locations (see Steps 2 and 3) is made. The image is otherwise empty. It contains no stars, and the background of this image is zero; i.e., it is noiseless (Fig. 2, top row, middle).
-
7.
Then LOCI is used to match this noiseless reference source image by linearly combining the derotated science images with reference sources, and counterpart PSFs (see Fig. 2). The result is the best possible recovery of the sources in the reference sector by the addition and subtraction of science images. The derotated science images are then replaced by the original science images without injected sources (also derotated). Next, the linear combination cofficients computed by LOCI are used to combine the counterpart PSFs and original science images. By using the best linear combination for the recovery of the reference sources, we induce improved detection of sources in the target sector. When there are hundreds of images to combine (too time-comsuming for LOCI to compute coefficients), we process subsets of the images and median combine the results.
-
8.
The sky locations of the injected sources are changed to positions that do not over-lap with the previous ones. The steps above are repeated to obtain five to ten different reductions. Since we use the original images without the source injections for the final combinations, these five to ten reductions only contain real astronomical sources and not the injected ones.
-
9.
The reductions above are then median-combined to create the final reduced image for a particular annular region.
-
10.
For X candidates, X annular reductions are made, the widths of which are at least as large as those of the matching annuli. The outer radius of these annuli are extended up to the matching annulus (inner radius) of the next candidate in radial separation. When the annular reductions overlap because of densely packed candidates, the overlapping pixels are median-combined.
It is important to remember that MLOCI only uses injected point sources to solve for the linear coefficients for image combination. Point sources are not injected at the locations of candidate companions but in the reference sectors that exclude the candidates.
We also present here an implementation of MLOCI for extended sources, which one could apply if there is any evidence of extended emission in a basic ADI reduction. However, in this implementation, the occurrence of false positives becomes a concern. Therefore, an MLOCI detection of a dataset devoid of signal should be performed to estimate the likelihood of false positives. Moreover, as a test, one can attempt to recover injected extended sources in empty data sets using MLOCI. This method is most promising when a library of PSFs from a different star is available as reference, thus allowing one to avoid self-subtraction of the extended source. However, such detailed analyses are deferred to a later publication.
Below we list the steps of MLOCI for extended source detection:
-
1.
A preliminary reduction (e.g., basic ADI) is done first toidentify all regions likely containing signal (e.g.,S/N> 2). These regions of the sky are defined as the target, while the regions that are likely devoid of signal are defined as background (e.g., S/N< 1). The two regions together make up the reference region and will be matched by MLOCI. Other non-reference regions in the image will not be matched. Although this step depends on prior estimates of the emissive and non-emissive regions around the target, we show that the final reduction is not very likely to yield false disk detections (see Sect. 4.3).
-
2.
For each science image, we create an rms map. To do so, the standard deviation of the pixel intensities in annular regions with widths of 2 pixels centered on the primary in the science image are calculated. These values are then placed in the rms map in all pixels of the corresponding annular regions. Next, for each science image, we create a counterpart where the local rms map is subtracted from the target region. This helps protect against ADI self-subtraction of any extended source in the target region, similar to Step 3 in the point source reduction.
-
3.
Then LOCI is used to linearly combine the original science images to find the best match to each counterpart image to make counterpart PSFs. As in the point-source reduction, only the corresponding science image is excluded from the linear combination. Also as before, the science images need to be speckle-aligned at this stage. The matching is done only over the reference region.
-
4.
The science images are then derotated to align north upwards. Each counterpart PSF is derotated by the same angle as its science image.
-
5.
The preliminary reduction is then set to zero in the background region to make the final counterpart.
-
6.
Then LOCI is used to match the final counterpart by linearly combining the derotated science images and counterpart PSFs. When there are hundreds of images (too many for LOCI), we process subsets of the images and median combine the results.
3. Observations and data reduction
We performed MLOCI reductions on ten methane-band (CH4S, λ = 1.578μm) datasets from the Gemini NICI Planet-Finding Campaign (2008–2012; Liu et al. 2010; Wahhaj et al. 2013b; Nielsen et al. 2013; Biller et al. 2013). The filter was designed to help detect methane, which is usually found in the atmospheres of cool substellar companions with surface temperatures <1400 K. In this work, the simultaneously exposed images in filter CH4L were not used for spectral differencing because we wanted to keep the analysis simple. However, since we used a single narrow-band (4% width) filter, we reach shallower contrasts than in the campaign. The campaign targets used were HD 107146, HD 25457, HD 53143, GJ 388, HD 31295, HIP 25486, HD 92945, HD 21997, HD 110058, and UY Pic, all observed between January and March of 2009. NICI was installed at the 8.1 m Gemini South Telescope and produced AO corrected images over a 18.4′′ × 18.4′′ FoV detector. The NICI plate scale was 17.96 mas/pixel. The campaign observations used a translucent coronagraphic mask (central attenuation factor =358; Wahhaj et al. 2011) with a half-power radius of 0.32′′. The median contrast achieved at ρ = 0.̋5 was 12.6 mag (Wahhaj et al. 2013a). We already demonstrated in Wahhaj et al. (2013a) that the LOCI pipeline does not perform better than regular ADI for NICI data.
We compared MLOCI reductions of the NICI datasets to both PCA reductions using the KLIP algorithm (see Soummer et al. 2012) and regular ADI reductions using the implementation described above. The PCA algorithm creates an orthogonal basis of images, which are then linearly combined to emulate the supplied PSF images. Moreover, the basis were ordered such that the first basis or mode is the best general match to the majority of the images, while each subsequent mode represents perturbations of decreasing importance. Thus fewer modes can be used in the hope of reducing noise without removing too much signal, thereby making an improvement over LOCI. The PSF subtraction can also be optimized for subregions of a science image. For our PCA reductions, we obtained the best results (best recovery S/N for injected companions) for a number of KLIP modes =8, and PSF subtraction optimized for annuli of width 20 pixels. The inner radius of the innermost annulus was set to 25 pixels.
In this paper, we also demonstrate MLOCI’s effectiveness for extended sources. We observed HD 135344 B in the J-band on April 21, 2014 UT as part of GPI Early Science (Program ID = GS-2014A-SV-402). HD 135344 B is a prime example of a transition disk suspected to harbor a substellar companion (a brown dwarf or a recently formed giant planet). Submillimeter images show a dust-depleted cavity with a radius of ~40 AU in a nearly face-on disk, while polarimetric differential imaging in the near-IR reveals two remarkable spiral arms extending from ~28 AU (inside the submillimeter cavity) to ~130 AU (Garufi et al. 2013).
 |
Fig. 3 All images as normalized by the rms over the full images. North up and east to the left. a) Simple stack of the HD 135344 B GPI J-band dataset scaled by ρ2 and spatially filtered to isolate features between 2–8 pixels in size. b) Regular ADI reduction and c) Channel 35 (λ = 1.337 μm) reduced with a non-blind variant of point-source MLOCI, targeting the SW spot. Here, the spot is treated the same as a reference source, and no other reference or target sources are used in the reduction. d) MLOCI matching regions: signal is preserved in the lightest regions. Noise is suppressed in medium blue regions. Darkest regions are not matched. e) MLOCI reduction matched to regions in d). Region within 240 mas of center divided by 5, to improve stretch. f) MLOCI reduction matched to a vertically flipped version of the map in d) but flipped vertically. This demonstrates that it is difficult to create false disks by MLOCI. |
 |
Fig. 4 Detection rates for the example case of 3σ signals and a detection threshold set at 2σ. Here, we illustrate the relationship between false positive rate (FPR), false detection rate (FDR), true detection rate (TDR) and true positive rate (TPR or completeness) and how they depend on true and false positives (TP shown in green and FP in red) and true and false negatives (TN shown in gray and FN shown in yellow). The FDR, which determines the telescope time spent following-up bogus detections, should be minimized. The FDR can be quite different from the FPR. |
 |
Fig. 5 Comparison of MLOCI reductions vs PCA and basic ADI reductions of NICI UY Pic data injected with simulated companions. The left panels in green show reductions for sky rotation equivalent to 0.35 × PSF FWHM (α = 0.35) of motion at 0.̋5 separation. The blue panels to the right show the ones for 1.25 × PSF FWHM of motion. The recovered companions can be seen at separations 0.̋5, 0.̋6, 0.̋7, and 0.̋8 with PA = 360, 270, 180, and 90° respectively. The images have been normalized to the peak flux of the recovered companion at the top position (color scale is linear). The S/N improvements for MLOCI over PCA were 1.3 to 2.3 for α = 0.35 and 1.3 to 1.9 for α = 1.25. The S/Ns from PCA and basic ADI reductions were within 10% of each other. |
 |
Fig. 6 Comparison of MLOCI to PCA and regular ADI for different pull factors (see Sect. 2). We attempted to recover simulated companions with contrasts of ~9−11 mag at 0.̋5 separation. We compare the 95% completeness contrast and completeness improvements for regular ADI, PCA, and MLOCI reductions. The subtraction annulus width W is set to 16, while the artificial sky motion α was set to 2.15 ×FWHM. |
 |
Fig. 7 Similar to Fig. 6. Comparison of MLOCI to PCA and regular ADI for different subtraction region widths and α = 2.15 and P = 3. |
 |
Fig. 8 Similar to Fig. 6. Comparison of MLOCI to PCA and regular ADI for different separations and α = 2.15, W = 16, and P = 3. |
 |
Fig. 9 Similar to Fig. 6. Comparison of MLOCI to PCA and regular ADI for different numbers of simulated companions and α = 2.15, W = 16, and P = 3. |
 |
Fig. 10 Similar to Fig. 6. Comparison of MLOCI to PCA and regular ADI for different amounts of sky rotation and P = 3 and W = 16. |
 |
Fig. 11 A demonstration that MLOCI does not increase false positive rates. The black dots show the measured signal to noise and PSF shape (same as fractional reduction in Sect. 4.1) of point sources injected at tests spots after 800 MLOCI reductions. The green dashed lines show the detection criteria defined in Sect. 4. The red dots show measurements for another 800 reductions where no signal was injected. No false positives were found; the red dots lie outside the green box and reasonably far from the detection limits. Moreover, the standard deviations of the black and red S/N distributions are 1.2 and 1, respectively. |
We obtained images from the integral field spectrograph (IFS) in 37 spectral channels from λ = 1.1–1.35 μm using GPI’s unprecedented AO capabilities. The star was placed behind a coronagraphic mask of radius 92 mas and thus a properly detected point source has projected separation, ρ≥ 112 mas (since J-band resolution is ~40 mas2). The IFS has a plate scale of 14.3 mas/pixel and a 2.8′′ × 2.8′′ FoV. The telescope rotator was turned off, allowing the sky to rotate on the detector through 35°, so that the speckle pattern produced by the telescope and instrument optics would be decoupled from real astronomical sources. This ensures a total azimuthal sky motion of 1.7 × FWHM at 112 mas (and 2 × FWHM at 130 mas). We obtained 39 sixty-second exposures. A total of 50 min of telescope time, excluding acquisition, was used. A speckle at 112 mas should move outward by only 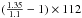 mas = 25.5 mas (<1 × FHWM) across images obtained over λ = 1.1–1.35 μm, and thus we do not expect much contrast gain from spectral deconvolution at this separation.
mas = 25.5 mas (<1 × FHWM) across images obtained over λ = 1.1–1.35 μm, and thus we do not expect much contrast gain from spectral deconvolution at this separation.
We used the GPI pipeline (Maire et al. 2010) to produce wavelength-calibrated spectral cubes with bad-pixel removal, de-striping, flat-fielding, non-linearity, and persistence corrections. The centroid of each of the 37 × 39 = 1443 images are found by averaging the coordinates of the peaks of the four GPI satellites spots3. The centroids of the spots were estimated using the center of mass IDL routine bscentrd.pro. The ADI datasets from each spectral channel were reduced separately using the pipeline described in Wahhaj et al. (2013a). However, we did not spatially filter the science images. Also, the reference PSFs were not translated to optimize the fit to the science images before subtraction, but only scaled in intensity to minimize the rms between ρ= 70–210 mas. The 37 ADI reductions from each of the spectral channels were then median-combined.
For the MLOCI reduction, we created counterpart PSFs for each of the 1443 science images. Before combining science images to create the counterpart PSFs, they have to be spectrally deconvolved. That is, to match an image in the ith channel, the science images are magnified by a factor λi/λj, where λi and λj are the central wavelengths of the ith and jth channels, respectively. The science images and their PSF counterparts images are then derotated to align north upwards.
We then use LOCI again to match the adjusted preliminary reduction, by linearly combining the science images and the counterpart PSFs. We have two counterpart PSFs for each science image: one made from images in the same spectral channel and the other from images with the same orientation on detector. In the last step, the 1443×3 science and counterpart PSF images can be combined using LOCI to match the final counterpart (see Sect. 2). However, this is often too many images for LOCI to combine, so instead we sequentially combine all images (science and two counterpart PSFs) in the jth channel and jth orientation with (37+39) × 3 = 228 images in each combination. See Fig. 3 for the reduction of the GPI data.
4. Results
4.1. Recovery of simulated companions
To tune MLOCI and measure its optimum performance, we insert simulated companions into our ten NICI datasets and recover them using MLOCI. We place the companions at 0.̋5−1.̋0 separations from the primary (where sensitivity is speckle-limited) with contrasts just below the 5σ detection limit for regular ADI reduction. For each data set between 0.̋5−1.̋0, we have roughly 800 independent sky locations at which to do this test, given that the FWHM of the NICI H-band PSF is ~55 mas. As described in Sect. 2, injected test companions are bounded by target sectors, while two or three point sources are inserted into the corresponding reference sectors (annulus − target sector) to aid MLOCI in preserving the point source signal. Our aim is to compare the S/N of simulated companions as recovered by MLOCI to the S/N as in recoveries by ADI and PCA reductions. We measure MLOCI’s false positive rate by repeating the reductions without simulated companions at the test locations.
First, we find the best reduction parameters for MLOCI given different amounts of sky rotations in an ADI dataset. We multiply the true position angles (PA) of the FoV by a negative number to misalign the images as done in Wahhaj et al. (2013a) so that any real astronomical sources will be mostly removed in a median combination of the images. To simulate different amounts of sky rotation, we choose five values of this negative number so that the total sky motions, which we call α, are 0.35, 1.25, 2.15, 3.1 or 4.0 × FWHM at the separations of interest. We had to use companions that are 2 and 0.5 mag brighter for α = 0.35 and 1.25 ×FWHM, respectively, because of reduced sensitivity in these cases due to large self-subtraction factors. We also vary W, the width of the reference sectors, over 4, 8, 16, 32, and 64 pixels and P the pull over 1, 2, 3, 4, and 5. Here, P is the brightness relative to the local rms, of the point sources that are subtracted from the reference sectors (see Sect. 2). Reductions of the UY Pic dataset by varying the parameters over this grid of values show that optimum settings are near W = 16, P = 3, while two simulated companions in the reference sector to assist MLOCI are adequate (see Sect. 4.2).
Using the above parameters, we show two MLOCI reductions (for α = 0.35 and 1.25) of the UY Pic (K0V, H = 5.9 mag, age ~70 Myr; López-Santiago et al. 2006) data set along with ADI and PCA reductions (see Fig. 5). In these reductions, simulated companions were placed at separations 0.̋5, 0.̋6, 0.̋7, and 0.̋8 and at PAs 360, 270, 180, and 90° just below the detection limits of an initial ADI reduction. The S/N improvement factors achieved for MLOCI over ADI and PCA range from 1.3 to 2.3.
In the S/N calculations, for the noise we use the rms in an annulus of width 2 ×FWHM centered on the test locations but exclude circular regions of diameter 1 ×FWHM around them. The signal is just the intensity at the test locations minus the median intensity in the noise region. To decide whether a source in the reduced images is a detection based on shape, we calculate the fractional reduction in the rms in a box of size 2 ×FWHM + 1 pixels when an optimally scaled Gaussian PSF is subtracted from the source. Here FWHM is estimated for the source, first. When the fractional reduction is >0.3 and the S/N is 5, we consider the source a detection. The fractional reduction (or shape criteria) judges a 5σ signal as true >99% of the time with a negligible false detection rate (FDR; sometimes termed false discovery rate) in our tests. We use this criteria rather than the one in Wahhaj et al. (2013a), because it has a clearer interpretation.
In the example MLOCI reductions of Fig. 5, no other sources, besides the ones that were injected into the data, were recovered according to the detections criteria specified above. Although MLOCI can improve S/N by a factor >2, we need to check that the FDR is not elevated compared to ADI. The FDR is the rate (or fraction) of detections that are incorrect; i.e., they do not result from a real or injected signal. It is important that this number is low, so that negligible time is wasted in follow-up observations trying to confirm false detections. The FDR is also different from FPR, the false positive rate (see Fig. 4). Next, we discuss FDR for MLOCI reductions.
4.2. Contrast, S/N, completeness and false detection rates
Before presenting an analysis of our detection statistics, we discuss the relationship between frequently used terms in the literature. After ADI processing of AO images, the residual intensity statistics is nearly Gaussian (Mawet et al. 2014, see also for detection statistics at 1–3 λ/D from the primary). A signal S embedded in Gaussian noise with standard deviation, σ = 1, when detected using a signal threshold T, will be recovered at a completeness (or true positive rate) of 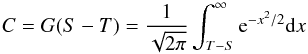 (1)with inverse function, G′(C) = S − T. This is because the real signal is redistributed owing to the noise in a Gaussian manner (see Fig. 4). In other words, the completeness is the fraction of the real (or injected) signal above a level, S, that is detected by a method. The FDR, which we measure as the number of bogus detections or the number of detections in the absence of signal, is theoretically FPR/(FPR+C), where the FPR is G( − T).
(1)with inverse function, G′(C) = S − T. This is because the real signal is redistributed owing to the noise in a Gaussian manner (see Fig. 4). In other words, the completeness is the fraction of the real (or injected) signal above a level, S, that is detected by a method. The FDR, which we measure as the number of bogus detections or the number of detections in the absence of signal, is theoretically FPR/(FPR+C), where the FPR is G( − T).
Since there is a one-to-one correspondence between S/N improvement and contrast improvement, (Δcontrast = 2.5 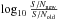 mag), we have only plotted contrast improvements. According to Eq. (1), an improvement in S/N from five to ten corresponds to improvement in completeness from 50% to nearly 100% (to within 10-6), for T = 5. Thus, completeness improvements quickly become insensitive to S/N improvements. Nevertheless, since it is interesting to show the improvement in the fraction of sources recovered, we compared the completeness for PCA and basic ADI at the threshold where MLOCI yields 50%.
mag), we have only plotted contrast improvements. According to Eq. (1), an improvement in S/N from five to ten corresponds to improvement in completeness from 50% to nearly 100% (to within 10-6), for T = 5. Thus, completeness improvements quickly become insensitive to S/N improvements. Nevertheless, since it is interesting to show the improvement in the fraction of sources recovered, we compared the completeness for PCA and basic ADI at the threshold where MLOCI yields 50%.
In Figs. 6–10, we compare average detection statistics from our ten NICI datasets for basic ADI, PCA, and MLOCI for different reduction parameters. In Fig. 6, we see that the performance of MLOCI is not very sensitive to P, the relative intensity of the negative sources, generally yielding contrast improvements of 0.3–0.4 mag. The plots are made for α = 2.15 and optimum parameter settings W = 16 and N = 2. However, for very large P (e.g., 10–100) we have found that the performance of MLOCI does deteriorate. Moreover, the counterpart PSFs begin to look similar to each other, instead of the science images that they are being matched to. This is because LOCI strongly biases the linear combination to match the negative sources in the counterpart images. The completeness improvement for MLOCI at the chosen threshold is usually 50%. The ADI and PCA performances are nearly equal to each other.
From our reduction experiments, we can estimate the accuracy of the photometric measurements allowed by MLOCI. The systematic uncertainty of the photometry can be estimated by the change in the contrast (or flux) before and after recovery, between the companion in the test sector to the two point sources in the reference sector. This systematic is essentially a flux loss and has to be corrected for when performing photometry. Since the reduction is done ten times with the reference companions in different positions, we can also estimate the random uncertainty by calculating the standard deviation of the contrast after recovery between the two sets of companions. When an actual companion is detected in a real dataset, we can estimate photometric uncertainties and systematic errors by injecting companions at other PAs at the same separation and performing MLOCI reductions to recover them. In the bottom panel of Fig. 6, we see that while the photometric uncertainty is insensitive to P (variation of ~13% in these cases), the systematic error increases with increasing P. Since the systematic error in photometry can be corrected for, we select P = 3 for its superior contrast performance, although nearby values of P give very similar performances.
In Figs. 6–8, we see that the contrast (and completeness) improvements are not very sensitive to the width of the reference sector or the number of companions used as reference or to the separation of the recovered companions from the primary. However, Fig. 10 shows that for very small sky rotation (α = 0.35), the contrast gain due to MLOCI is much greater (~1.4 mag). Here, PCA also shows a 0.5 mag gain over ADI. The variation in photometric uncertainties over these experiments is small. Finally, for simulated companions of brightness near the sensitivity limits of the reductions, preliminary investigation shows no change in optimum MLOCI parameters or performance with companion brightness.
In Fig. 11, we show attempts at measuring the source properties at the test locations after 800 MLOCI reductions of the UY Pic data set when no actual signal has been injected. According to the previously defined detection criteria in Sect. 4.1, none of the measurements indicated a detection, and thus there were no false positives. Moreover, the standard deviation of the S/N distribution was 1.0, showing that the false positive rate is not elevated above what is expected. A higher false positive rate would indicate that while the reduction method may produce detections with seemingly high S/N, the noise is in fact not being calculated correctly. For our 800 test locations, 38 returned a S/N> 2 when no simulated signal was present. Thus for an image with 800 resolution elements, ~38 target regions would be defined when applying MLOCI.
We also performed non-blind reduction experiments where the test companion in the target region and the reference companions are treated in the same way by MLOCI, using negative sources in all locations when creating the counterpart PSFs and/or positive sources in the noiseless counterpart when finally combining all the images. In these cases, the apparent contrast improvement was on average 0.75 mag. However, using the best algorithm parameters, we were only able to reduce the false detection rate to 1%. Poor parameters could yield false detection rates >20%. Thus, MLOCI must be kept blind to any suspected companion, except when informed by another blind process, which in our case is a basic ADI reduction. By the same logic, other versions of LOCI and PCA can also accidentally create false detections, since no restrictions on the allowed linear combinations are generally imposed when constructing reference images. This is an especially unpleasant possibility when trying to redetect a companion marginally detected in an earlier epoch. We therefore strongly recommend that FDRs be provided for any reduction method.
4.3. GPI early science data
Here, we describe the results of MLOCI and ADI processing of the GPI data on HD 135344 B. In Fig. 3a, we show a de-rotated median combination of all the channels without PSF subtraction, but scaled in intensity by ρ2, and then bandpass-filtered to isolate spatial features between two and eight pixels. We easily see the spiral arms, which were discovered in Muto et al. (2012), extending out to 0.9′′, and the cavity inside 0.2′′. However, we do not see their inner ring where the spiral arms begin. We do see a bright rim at 0.15′′ separation around the coronagraphic mask. Since, there is presumably no self-subtraction of the disk (no ADI) in this image, we use this image to identify reliable signal and background regions for MLOCI (Fig. 3d).
In the regular ADI reduction (Fig. 3b), we find some features at 110–170 mas separations with S/N = 3–5 (ΔJ = 8−9.5 mag), particularly two radially extended spots to the NE and SW. As discussed in Menard et al. (in prep.), while these could prove to be accretion streams from the disk onto the star, this is currently uncertain because of the small amount of sky motion (1.7–2 ×FWHM) at the relevant separation and similar PSF features in the unreduced images near mask (see Fig. 3a). Moreover, GPI images of HR 4796 A (Perrin et al. 2015) also show similar residuals near the mask.
We find that particular caution needs to be exercised with the point-source version of MLOCI when there is signal in the FoV, which is extended azimuthally, as in the case of HD 135344 B. When we try to target each spot separately with a non-blind variant of point-source MLOCI, we obtain isolated point sources, admittedly with large FWHM, while the rest of the disk disappears (see Fig. 3c). In this aggressive application of the MLOCI concept, the targeted source is treated the same as a reference with the exception that we do not at any stage inject a positive source into its corresponding sky locations. No other reference or target sources are used. This result demonstrates the ability of non-blind algorithms that allow free linear combinations of science images to produce misleading features, especially in the case where disk emission may exist. In the absence of disk emission, we have found that the most conservative non-blind methods create fewer false positives but are still at elevated levels compared to ADI.
However, the MLOCI algorithm for extended sources does have the special ability to improve the S/N of any feature suspected in a dataset, be it mutiple companions or an entire disk. To demonstrate this potential of the algorithm, we used MLOCI (P = 3; extended-source reduction as described in Sects. 2 and 3) to optimize the S/N according to regions selected in Fig. 3d. Indeed, the spiral and the suspected streamers are much enhanced in the MLOCI reduction (see Fig. 3e). When we flip the matching regions vertically so that they do not match with the real disk emission, MLOCI yields no disk (Fig. 3f). Thus MLOCI is not likely to yield false disk detections.
5. Conclusions
We have presented a version of the LOCI algorithm that significantly improves the S/N of both point and extended sources. This algorithm, called matched LOCI or MLOCI, can be applied to both ADI and IFS data. The only difference is that, in the PSF construction step of image processing, the images have to be pupil-aligned in the former and both pupil and spectrally aligned in the latter. The contrast gain over both regular ADI
and PCA in NICI data was 0.3–1.4 mag. This is especially interesting, since it was shown that LOCI itself provides no gain over regular ADI processing for NICI data (Wahhaj et al. 2013a). While we found that LOCI could reduce the speckle noise in the final reduced image, it also reduced the signal of test companions. We expect similar gains in contrast from applications of MLOCI to data from other instruments, because the novel ways in which we preserve signal and use reference sources to more directly increase S/N are not implemented in versions of PCA, LOCI, and other ADI algorithms presented to date.
We showed how MLOCI can be used to detect disks using GPI data, recovering new streamer-like features that need new observations before they can be confirmed. Thus MLOCI can be a powerful tool for detecting companions and disks in the current direct imaging campaigns with GPI and SPHERE.
While the false detection rate is low for blind MLOCI, we find that for non-blind MLOCI for both NICI and GPI data, the false detection rate (FDR) can in some cases be much higher. The FDR is even more for when there is azimuthally distributed diffuse light in the FoV. Thus, in non-blind variants of LOCI and PCA algorithms high FDRs may also arise. Therefore, we strongly recommend that FDRs be measured whenever these methods are used.
Acknowledgments
Our research has employed the 2MASS data products; NASA’s Astrophysical Data System; the SIMBAD database operated at the CDS, Strasbourg, France. L.A.C. was supported by ALMA-CONICYT grant number 31120009 and CONICYT-FONDECYT grant number 1140109. L.A.C., M.R.S., H.C., and S.C. acknowledge support from the Millennium Science Initiative (Chilean Ministry of Economy), through grant Nucleus RC13007. H.C. also thanks ALMA/CONICYT (grants 31100025 and 31130027) for their support.
References
- Amara, A., & Quanz, S. P. 2012, MNRAS, 427, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Beuzit, J.-L., Boccaletti, A., Feldt, M., et al. 2010, in Pathways Towards Habitable Planets, eds. V. Coudé Du Foresto, D. M. Gelino, & I. Ribas, ASP Conf. Ser., 430, 231 [Google Scholar]
- Biller, B. A., Close, L. M., Masciadri, E., et al. 2007, ApJS, 173, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Biller, B. A., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 777, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Bowler, B. P., Liu, M. C., Shkolnik, E. L., & Tamura, M. 2015, ApJS, 216, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Currie, T., Burrows, A., Madhusudhan, N., et al. 2013, ApJ, 776, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Garufi, A., Quanz, S. P., Avenhaus, H., et al. 2013, A&A, 560, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lafrenière, D., Marois, C., Doyon, R., Nadeau, D., & Artigau, É. 2007, ApJ, 660, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C. 2004, Science, 305, 1442 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C., Wahhaj, Z., Biller, B. A., et al. 2010, in SPIE Conf. Ser., 7736 [Google Scholar]
- López-Santiago, J., Montes, D., Crespo-Chacón, I., & Fernández-Figueroa, M. J. 2006, ApJ, 643, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Macintosh, B. A., Graham, J. R., Palmer, D. W., et al. 2008, in SPIE Conf. Ser., 7015 [Google Scholar]
- Maire, J., Perrin, M. D., Doyon, R., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
- Marois, C., Doyon, R., Racine, R., et al. 2005, J. Roy. Astron. Soc. Can., 99, 130 [NASA ADS] [Google Scholar]
- Marois, C., Correia, C., Galicher, R., et al. 2014, Proc. SPIE, 9148, 91480U [CrossRef] [Google Scholar]
- Mawet, D., Milli, J., Wahhaj, Z., et al. 2014, ApJ, 792, 97 [NASA ADS] [CrossRef] [Google Scholar]
- McBride, J., Graham, J. R., Macintosh, B., et al. 2011, PASP, 123, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, E. L., Liu, M. C., Wahhaj, Z., et al. 2013, ApJ, 776, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Duchene, G., Millar-Blanchaer, M., et al. 2015, ApJ, 799, 182 [Google Scholar]
- Pueyo, L., Crepp, J. R., Vasisht, G., et al. 2012, ApJS, 199, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Racine, R., Walker, G. A. H., Nadeau, D., Doyon, R., & Marois, C. 1999, PASP, 111, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Soummer, R., Pueyo, L., & Larkin, J. 2012, ApJ, 755, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. B., & Ford, H. C. 2002, ApJ, 578, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Thatte, N., Abuter, R., Tecza, M., et al. 2007, MNRAS, 378, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2011, ApJ, 729, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Biller, B. A., et al. 2013a, ApJ, 779, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Wahhaj, Z., Liu, M. C., Nielsen, E. L., et al. 2013b, ApJ, 773, 179 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Central steps of the MLOCI algorithm (see Sect. 2). Steps 2, 3, and 4, top row: a counterpart PSF is created for each science image. The counterpart PSF is such that its subtraction from the science preserves signal at 2 locations. Step 5, bottom row: each science image with reference fake sources and its counterpart PSF are derotated to align north upwards. |
| In the text | |
 |
Fig. 2 Final steps of the MLOCI algorithm (see Sect. 2). Steps 6 and 7, top row: instead of the usual difference image combination in ADI, all science with fakes and counterpart PSF images are combined to recover injected sources in the reference sector. Prior to the linear combination using coefficients from LOCI, we replace the science images with fakes with the original science images, so that the fake sources do not appear in the individual reductions. The fakes are, however, drawn in the figure above to show their changing locations. Steps 8, 9, and 10, bottom row: several such reductions, created through step 8, are combined to create the final reduction. The final reduction preserves point source signal, generally. |
| In the text | |
 |
Fig. 3 All images as normalized by the rms over the full images. North up and east to the left. a) Simple stack of the HD 135344 B GPI J-band dataset scaled by ρ2 and spatially filtered to isolate features between 2–8 pixels in size. b) Regular ADI reduction and c) Channel 35 (λ = 1.337 μm) reduced with a non-blind variant of point-source MLOCI, targeting the SW spot. Here, the spot is treated the same as a reference source, and no other reference or target sources are used in the reduction. d) MLOCI matching regions: signal is preserved in the lightest regions. Noise is suppressed in medium blue regions. Darkest regions are not matched. e) MLOCI reduction matched to regions in d). Region within 240 mas of center divided by 5, to improve stretch. f) MLOCI reduction matched to a vertically flipped version of the map in d) but flipped vertically. This demonstrates that it is difficult to create false disks by MLOCI. |
| In the text | |
 |
Fig. 4 Detection rates for the example case of 3σ signals and a detection threshold set at 2σ. Here, we illustrate the relationship between false positive rate (FPR), false detection rate (FDR), true detection rate (TDR) and true positive rate (TPR or completeness) and how they depend on true and false positives (TP shown in green and FP in red) and true and false negatives (TN shown in gray and FN shown in yellow). The FDR, which determines the telescope time spent following-up bogus detections, should be minimized. The FDR can be quite different from the FPR. |
| In the text | |
 |
Fig. 5 Comparison of MLOCI reductions vs PCA and basic ADI reductions of NICI UY Pic data injected with simulated companions. The left panels in green show reductions for sky rotation equivalent to 0.35 × PSF FWHM (α = 0.35) of motion at 0.̋5 separation. The blue panels to the right show the ones for 1.25 × PSF FWHM of motion. The recovered companions can be seen at separations 0.̋5, 0.̋6, 0.̋7, and 0.̋8 with PA = 360, 270, 180, and 90° respectively. The images have been normalized to the peak flux of the recovered companion at the top position (color scale is linear). The S/N improvements for MLOCI over PCA were 1.3 to 2.3 for α = 0.35 and 1.3 to 1.9 for α = 1.25. The S/Ns from PCA and basic ADI reductions were within 10% of each other. |
| In the text | |
 |
Fig. 6 Comparison of MLOCI to PCA and regular ADI for different pull factors (see Sect. 2). We attempted to recover simulated companions with contrasts of ~9−11 mag at 0.̋5 separation. We compare the 95% completeness contrast and completeness improvements for regular ADI, PCA, and MLOCI reductions. The subtraction annulus width W is set to 16, while the artificial sky motion α was set to 2.15 ×FWHM. |
| In the text | |
 |
Fig. 7 Similar to Fig. 6. Comparison of MLOCI to PCA and regular ADI for different subtraction region widths and α = 2.15 and P = 3. |
| In the text | |
 |
Fig. 8 Similar to Fig. 6. Comparison of MLOCI to PCA and regular ADI for different separations and α = 2.15, W = 16, and P = 3. |
| In the text | |
 |
Fig. 9 Similar to Fig. 6. Comparison of MLOCI to PCA and regular ADI for different numbers of simulated companions and α = 2.15, W = 16, and P = 3. |
| In the text | |
 |
Fig. 10 Similar to Fig. 6. Comparison of MLOCI to PCA and regular ADI for different amounts of sky rotation and P = 3 and W = 16. |
| In the text | |
 |
Fig. 11 A demonstration that MLOCI does not increase false positive rates. The black dots show the measured signal to noise and PSF shape (same as fractional reduction in Sect. 4.1) of point sources injected at tests spots after 800 MLOCI reductions. The green dashed lines show the detection criteria defined in Sect. 4. The red dots show measurements for another 800 reductions where no signal was injected. No false positives were found; the red dots lie outside the green box and reasonably far from the detection limits. Moreover, the standard deviations of the black and red S/N distributions are 1.2 and 1, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


