| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 9 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201425579 | |
| Published online | 15 September 2015 | |
When is pile-up important in the XMM-Newton EPIC cameras?
1
European Space Astronomy Centre of ESA,
PO Box 78, Villanueva de la
Cañada, 28691
Madrid,
Spain
2
Institute of Astronomy, Madingley Rd, Cambridge, CB3
0HA, UK
e-mail:
pj253@ast.cam.ac.uk
Received: 23 December 2014
Accepted: 23 June 2015
Context. Pile-up in X-ray charged couple device (CCD) detectors is defined as the reconstruction of independent events in the same detection cell as a single event during a read-out cycle. Pile-up can seriously compromise the spectral performance, modifying both the flux and the spectral shape of celestial sources.
Aims. In this paper we define rigorous metrics to characterise the effect of pile-up in terms of flux loss and spectral distortion.
Methods. We extend analytical formulae derived for pile-up on CCD detectors with the inclusion of the calibrated energy-dependence of the point spread function. We validated our analytical results through both Monte-Carlo simulations of the EPIC cameras on-board XMM-Newton and comparison with pile-up diagnostics in observed data.
Results. We estimate new count rate levels corresponding to a given degree of flux loss and spectral distortion for each EPIC imaging acquisition mode and provide guidance to observers wishing to estimate these values in their own observations.
Conclusions. We strongly recommend using these thresholds in planning future observations with the EPIC cameras.
Key words: instrumentation: detectors / X-rays: general
© ESO, 2015
1. Introduction on pile-up
In this paper we discuss pile-up in X-ray charged couple device (CCD) detectors, in particular in the European Photon Imaging Cameras (EPIC; Strüder et al. 2001; Turner et al. 2001) on board XMM-Newton (Jansen et al. 2001).
Pile-up refers to overexposure of the CCD, occurring when two or more independent photons arrive at nearby pixels within one read-out cycle. The photons are erroneously interpreted as one single event, whose energy is the sum of the energies of the individual incoming photons. Pile-up distorts the spectral shape in three, not necessarily exclusive, ways:
-
1.
by hardening the observed spectrum with respect to the intrinsic source (because events are shifted to higher energies),
-
2.
by suppressing flux due to the creation of invalid patterns, or through increasing an event’s energy beyond the on board energy rejection threshold,
-
3.
by joining separate mono-pixel events into a single multi-pixel event (pattern migration).
Pile-up can be mitigated in affected observations by extracting spectra corresponding to events where the electron cloud is confined to a single pixel. The best way to avoid the consequences of pile-up however is to avoid pile-up altogether, by selecting the count-rate dependent instrument mode appropriate for each specific source. This papers aims at providing guidelines for such a choice.
The EPIC cameras allow several modes of data acquisition. In broad terms, both cameras can be operated in Full Frame or Partial Window modes. In Full Frame (and Extended Full Frame for EPIC-pn only) all pixels of all CCDs are read out and the full field-of-view is covered. In Partial Window modes only subsections of the CCD are used, trading off a smaller field-of-view for a faster read-out cycle, reducing the probability of pile-up. Fast Modes are also available, where an even faster read-out cycle is obtained by sacrificing one dimension of spatial information. These will not be discussed here but we direct interested readers to a discussion on pile-up in EPIC-pn Timing Mode in Guainazzi et al. (2014). Readers are referred to the XMM-Newton User’s Handbook1 (XMM-UH) for a more detailed description of the EPIC instrumental modes.
The paper is structured as follows. In Sect. 2 we define useful metrics for describing pile-up and describe our two modelling methods: a set of analytic equations, and a stochastic simulator. In Sect. 3 we test the simulator by comparison with pile-up diagnostics as measured in a large sample of XMM-Newton observations. In Sect. 4 we first derive new count rate thresholds for use in observation planning, and list instructions for users who wish to quantify pile-up in their own observations.
2. Pile-up modelling
The XMM-UH contains recommended flux limits below which the effects of pile-up should be less than 1%. It was unclear whether this limit referred to flux loss, spectral distortion or some combination of the two. In this section we define quantitative metrics of these phenomena.
An X-ray photon arriving at the CCD array will excite a charge cloud, which may either concentrate in a single pixel or spread over several adjacent pixels. The distribution of pixels over which a charge cloud spreads is known as the pattern in XMM-Newton/EPIC terminology (likewise grade for Chandra/ACIS). Examples are shown in Fig. 1. A given photon can stochastically give rise to a variety of patterns, the probability of each pattern being a function of the photon’s energy. Generally, higher energy photons are more likely to produce larger patterns.
For a particular instrument, we call the set of patterns employed for standard data analysis good patterns. Good patterns for EPIC-pn are the singles and doubles, whereas for EPIC-MOS they are singles, doubles, triples, and quadruples. Bad patterns are those that are not good. They are not used for data analysis for two reasons. EPIC-pn does not support the calibration of triples and quadruples since these constitute a negligible fraction of all events. Other bad patterns have a significant probability of arising from non X-ray sources (e.g. cosmic rays) hence their exclusion increases the signal to noise ratio of the data.
 |
Fig. 1 Examples of EPIC pattern classifications. In each case the dark red pixel contains maximum charge, light red pixels have charge above a threshold value whereas white pixels are necessarily below this threshold. Grey pixels do not influence the pattern classification of the event. |
If two or more photons pile-up and their combined pattern is bad, the resulting event will be rejected and the photon counts will be lost. The other possibility is that they combine to give a good pattern. In this case the piled-up event will erroneously be identified as a single photon X-ray event whose energy is the sum of the energies of the incident photons. All but one of the counts are lost, and one is recorded albeit at the incorrect energy. Both possibilities contribute to flux loss, and the second to spectral distortion. We quantify these effects as
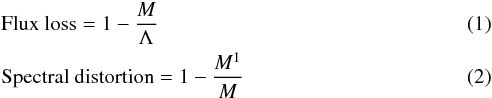 where M is the measured count rate of good patterns, Λ is the expected count rate of good patterns given no pile-up, and M1 is the count rate of good patterns formed from exactly one photon. In other words, flux loss is the fraction of useful data we have lost, and spectral distortion is the fraction of the remaining useful data which is at the wrong energy. M, Λ and M1 all depend on the spectrum and brightness of the observed source, as well as the instrument and operational mode employed.
where M is the measured count rate of good patterns, Λ is the expected count rate of good patterns given no pile-up, and M1 is the count rate of good patterns formed from exactly one photon. In other words, flux loss is the fraction of useful data we have lost, and spectral distortion is the fraction of the remaining useful data which is at the wrong energy. M, Λ and M1 all depend on the spectrum and brightness of the observed source, as well as the instrument and operational mode employed.
M can be measured in observed data. If we know the spectrum and brightness of the source, f(E) (photons cm-2 s-1 keV-1), then it is straightforward to calculate Λ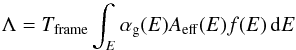 (3)where Aeff(E) is the effective area of the detector, αg(E) the fraction of photons which will create a good pattern and Tframe the frame time for a particular instrument mode. Of course f(E) is never known a priori, and the standard procedure for inferring it implicitly assumes no pile-up. Furthermore it is impossible to tell if a particular event has been formed from one or multiple photons, making M1 inaccessible from data alone. Hence to calculate flux loss and spectral distortion we must model the pile-up phenomenon starting from a known choice of f(E). We do this in two independent ways.
(3)where Aeff(E) is the effective area of the detector, αg(E) the fraction of photons which will create a good pattern and Tframe the frame time for a particular instrument mode. Of course f(E) is never known a priori, and the standard procedure for inferring it implicitly assumes no pile-up. Furthermore it is impossible to tell if a particular event has been formed from one or multiple photons, making M1 inaccessible from data alone. Hence to calculate flux loss and spectral distortion we must model the pile-up phenomenon starting from a known choice of f(E). We do this in two independent ways.
2.1. Analytic pile-up equations
Ballet (1999) presents a set of analytical equations for calculating flux loss and spectral distortion for detectors with pixels small compared to the point spread function (PSF) of the telescope, such as EPIC-MOS. In Ballet (2001) this is generalised to cases where the pixel size is comparable to the PSF, as is the case for EPIC-pn. Here we further extend these equations to take into account the energy dependence of the current EPIC PSF models (Read et al. 2011). We outline the updated equations here, a more detailed explanation can be found in the original works. We use the phrasing photon with pattern p to mean a photon whose charge cloud will spread over pixels with pattern p.
Say the detector has energy dependent PSF given by g(x,y,E) normalised such that ∑ x,yg(x,y,E) = 1. Then for some source spectrum f(E) the expected number of photons arriving per frame at pixel (x,y) with pattern p is given by 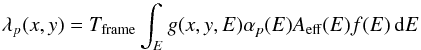 (4)where Tframe, Aeff(E) are as in Eq. (3) and αp(E) is the the fraction of photons with pattern p as a function of E. Now consider a quantity related to λp(x,y). Let mp(x,y) be the probability of observing an event of pattern p in pixel (x,y) in one frame. In the low flux limit, mp(x,y) and λp(x,y) coincide. But as flux increases and pile-up occurs, mp(x,y) becomes the product of two probabilities: firstly, that pattern p is created in pixel (x,y), and secondly that it is not destroyed by other photons’ charge clouds entering a buffer zone of pixels surrounding p.
(4)where Tframe, Aeff(E) are as in Eq. (3) and αp(E) is the the fraction of photons with pattern p as a function of E. Now consider a quantity related to λp(x,y). Let mp(x,y) be the probability of observing an event of pattern p in pixel (x,y) in one frame. In the low flux limit, mp(x,y) and λp(x,y) coincide. But as flux increases and pile-up occurs, mp(x,y) becomes the product of two probabilities: firstly, that pattern p is created in pixel (x,y), and secondly that it is not destroyed by other photons’ charge clouds entering a buffer zone of pixels surrounding p.
Consider the simplest pattern p = s, a single pixel. The condition necessary for creating s in (x,y) is that one or more photons with pattern s land in (x,y). Given that photon arrival times are Poisson distributed this probability is given by 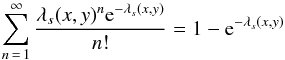 (5)The necessary condition for not destroying this pattern is that no photon’s charge cloud spills into the 8 pixels surrounding (x,y). This defines an exclusion zone Es,p for each p inside which we insist no photon with pattern p may land. Some examples of exclusion zones are shown in Fig. 2. The probability this condition is met is then a product of Poisson zero occupancy probabilities over all patterns and their associated exclusion zones. Finally ms(x,y) is given by the product
(5)The necessary condition for not destroying this pattern is that no photon’s charge cloud spills into the 8 pixels surrounding (x,y). This defines an exclusion zone Es,p for each p inside which we insist no photon with pattern p may land. Some examples of exclusion zones are shown in Fig. 2. The probability this condition is met is then a product of Poisson zero occupancy probabilities over all patterns and their associated exclusion zones. Finally ms(x,y) is given by the product 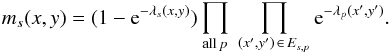 (6)If we insist that the event is not piled-up (i.e. that it is formed from exactly one photon) the probability of observation is given by
(6)If we insist that the event is not piled-up (i.e. that it is formed from exactly one photon) the probability of observation is given by 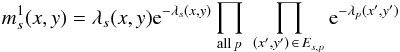 (7)where we have retained only first term of the sum in expression 5.
(7)where we have retained only first term of the sum in expression 5.
 |
Fig. 2 For the single (s), double (d) and triple (t) patterns with orientations as in Fig. 1 we show exclusion zones Ep,q in red. A photon with pattern q landing in Ep,q would destroy an event of pattern p whose maximum charge is in the central pixel. |
For larger patterns we derive similar expressions in Appendix A. The creation probabilities become more complex since there are more ways than one to create a large pattern from smaller ones. For example a double pattern d can be created by a photon whose pattern is a genuine double, or by adjacent singles, or by a single on top of a double. We must include all of these possibilities in md(x,y) and explicitly exclude all but one of these in 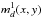 . Hence the expressions grow quickly but are readily computable. The global quantities Λ, M and M1 in Eqs. (1) and (2) are found by summing λp(x,y), mp(x,y) and
. Hence the expressions grow quickly but are readily computable. The global quantities Λ, M and M1 in Eqs. (1) and (2) are found by summing λp(x,y), mp(x,y) and 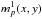 respectively over all good patterns and a desired extraction region.
respectively over all good patterns and a desired extraction region.
Aside from the integration of an energy dependent PSF, another addition to our implementation of the equations is the treatment of photons which give rise to bad patterns. For EPIC-pn these produce triple and quadruple patterns, and comprise a small proportion of the total number of photons at all energies (~1% at 1 keV rising to ~5% at 10 keV). For EPIC-MOS they are more prominent at high energies (~1% at 4 keV rising steadily to ~60% at 10 keV) and the offending pattern is a 3 × 3 grid of pixels (panel (f) in Fig. 1). Although we are not interested directly in the count rates of bad patterns we must consider them due to their capacity to pile-up with the good patterns we are interested in, which enter the expressions via the Eqs. (6) and (7).
2.2. The EPIC event simulator
The EPIC event simulator is an IDL-based code which traces incoming photons from their impact on the EPIC-pn or EPIC-MOS cameras through to their final recognition as good or bad events. The code uses stochastic numerical modelling to assign parameters for all incoming photons. A probability distribution is generated from the latest XMM-Newton calibration files (CCF in XMM-Newton terminology) for each property. An alternative approach, involving a detailed physical modelling of the mirrors and detection hardware, is provided by the ray tracing software SCISIM (Gabriel et al. 2005) which has also been adopted for the analogous pile-up simulator for the Swift-XRT detector (Beardmore et al., in prep.). The EPIC event simulator uses the frame as the basic integration unit, generating photons within the frame, adding the charges into an image and storing any resulting good events.
The flow of information, generated and captured during a single simulated frame is shown schematically in Fig. 3.
Each simulated run is controlled by a set of parameters: the total count rate ΛT, the source spectrum f(E), the required camera and the number of frames over which to run the simulation. The simulator generates input events, comprising all the possible patterns, good and bad, from the incoming photons and combines them to form output events. The total count rate, which includes all patterns (good and bad), is related to the count rate of good-pattern only events by: 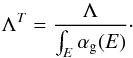 (8)The simulator supports a source spectrum consisting of a power-law or Gaussian, optionally modified by exponential absorption (corresponding to the Xspec models pow(Γ), Gauss(El,s) and expabs(Ec) respectively where Γ,El,s and Ec are the power-law slope, Gaussian energy and width, and absorption e-folding energy, respectively). Alternatively it may be provided in a file containing counts against energy.
(8)The simulator supports a source spectrum consisting of a power-law or Gaussian, optionally modified by exponential absorption (corresponding to the Xspec models pow(Γ), Gauss(El,s) and expabs(Ec) respectively where Γ,El,s and Ec are the power-law slope, Gaussian energy and width, and absorption e-folding energy, respectively). Alternatively it may be provided in a file containing counts against energy.
For each frame, the number of incident photons is selected from a Poisson distribution whose mean is the count rate, ΛT. Photon energies are assigned from a distribution given by the product of f(E) and the effective area A(E).
 |
Fig. 3 A schematic diagram of the flow of generated and detected events from a single frame in the EPIC event simulator |
A spatial pixel (x,y) is randomly selected for the event centre from the distribution given by the PSF at this energy, and a pattern selected using the calibrated pattern fractions for this energy. As the pattern fractions for bad patterns are not well calibrated, we simply model all bad-pattern events as quadruple-pixel events. The redistribution function, ψ(E), is used to select a pulse invariant (P.I.) channel, C. The actual distribution of charge between primary and secondary pixels of a multi-pixel event has not yet been calibrated for XMM-Newton. Physically, a charge cloud is generated in the primary pixel and diffuses into secondary pixels in a manner which depends in detail on the physics of the CCD (Pavlov & Nousek 1999; Townsley et al. 2002). For the purposes of calculating pile-up from this simulator it is the summation of the total charge, C, from each event which is important, rather than the charges in the individual pixels. For simplicity, the simulator models individual pixel charges by assuming that the probability of the charge in each pixel (Ci) is uniformly spread between Ci = Cth ⇒ C, where Cth is the threshold energy below which a charge is ignored and where for an event of n pixels 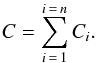 (9)This approximation results in secondary pixels having, on average, a higher charge in the simulation than they would have in reality but there is no effect on the total summed charge.
(9)This approximation results in secondary pixels having, on average, a higher charge in the simulation than they would have in reality but there is no effect on the total summed charge.
By obtaining the charge statistically from the redistribution function, rather than by a physical model, we only consider those pixels whose charge is above the detection threshold. Hence, we ignore the possibility of a pixel receiving two or more below-threshold charges and becoming an above-threshold pixel. Such an occurrence would change the energy and pattern of a final piled-up event and could turn it from being a good to a bad event. We estimate that the probability of this happening is small and that this omission will not significantly affect the final result.
Simulations may be run for any detector position or observing mode by supplying the appropriate RMF, ARF and PSF functions.
The charges falling in each of the pixels during the frame are summed to produce a charge image where spatially overlapping events produce pile-up as described in Sect. 2. The image is fed into a pattern recognition algorithm which separates contiguous regions of charge into individual events (see Fig. 1). The properties; x/y position, pattern, frame number and total charge, of the good events are stored in an event list. A selection, optionally using a particular set of patterns or a spatial region, may then be taken from the event list to produce a spectrum.
3. Diagonal events: an empirical pile-up test
Diagonal events are produced almost exclusively from the pile-up of two single pixel events, and hence can serve as a useful, empirical diagnostic of the level of pile-up in a dataset (Molendi & Sembay 2003). Here we quantify this phenomena in real and simulated observations to demonstrate the validity of the pile-up simulator described above.
We use the XMM-Newton Cross-calibration sample (XCAL hereafter), a compilation of over 250 observations performed over the mission and routinely used for calibration and cross-calibration purposes (Stuhlinger et al. 2010). These are mainly bright sources with astrophysically well defined (albeit not necessarily fully understood) astrophysical models. They have been mainly observed in windowed (i.e. Large or Small Window) EPIC instrumental modes to mitigate pile-up, however many of them are still affected to some level. This makes the XCAL an ideal sample for our study.
We estimate the fraction of diagonal events for the XCAL sample as the PSF-weighted mean of the image obtained by dividing an image of diagonal events [selectlib expression: (FLAG & 0x1)!=0 && (FLAG & 0x766ba000)==0] by an image extracted from bona fide X-ray events (PATTERNs from 0 to 12 inclusive). The image is smoothed with a 2-pixel wide boxcar function to avoid the maximum intensity peak being significantly affected by pixel-to-pixel fluctuations. Statistical errors are calculated by propagating the Poisson error on each pixel via the Gehrels (1986) prescription. The test is only performed for the EPIC-MOS cameras, and for observations taken in Small Window mode (the XCAL sample for other instrumental modes being significantly smaller). Results are shown in green in Fig. 4, as a function of the full energy band (0.2−12 keV) observed count rate of PATTERN < 13 EPIC-MOS events.
 |
Fig. 4 Green circles: MOS fraction of diagonal to good patterns as a function of the observed count rate for the MOS1 (left) and MOS2 (right) cameras in Small Window exposures as measured in the XCAL sample. The dotted lines are curves fitted to the data points for clarity. Arrows indicate upper limits. The red squares are predictions from the pile-up simulator. |
We also predict values of the diagonal fraction using the pile-up simulator. We do this for a fixed spectral model expabs(Ec = 0.5 keV)*pow(Γ = 1.7), over a range of incoming photon rates which give rise to observed count rates of good patterns overlapping with those present in the XCAL sample. The results are shown as red squares in Fig. 4.
We see good agreement between the simulated and observed results. The simulator correctly predicts a turn-over in the diagonal fraction at 60 counts per second, above which pile-up destroys diagonal events faster than it creates them. A small (~1.0%) vertical offset between the predicted and observed values could be explained by a bias due to our chosen spectral model, or a small number of real diagonal events (i.e. not produced via pile-up) which exist in the data but are not included in the simulations.
This gives us much confidence in the faithfulness of the pile-up simulator. It is also possible to predict the value of the diagonal fraction using the pile-up equations, however we will demonstrate below (see Fig. 5) that the equations produce results in good agreement with the simulator.
4. Results
Here we calculate flux loss and spectral distortion as defined in Eqs. (1) and (2) using the two modelling methods described in Sect. 2. We do this for four spectral models over a range of source fluxes. We parameterise source brightness using the quantity 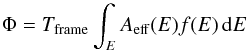 (10)which corresponds to total number of photons arriving at the detector per frame.The four models we test span the possible range of spectral hardness and are listed in Table 1. As spectral shape only enters the pile-up equations through the generated pattern fractions, in Table 1 we also show the fraction of incoming photons that would give rise to single and double patterns in the no-pile up case (αs and αd). For generic pattern p, αp is given by
(10)which corresponds to total number of photons arriving at the detector per frame.The four models we test span the possible range of spectral hardness and are listed in Table 1. As spectral shape only enters the pile-up equations through the generated pattern fractions, in Table 1 we also show the fraction of incoming photons that would give rise to single and double patterns in the no-pile up case (αs and αd). For generic pattern p, αp is given by 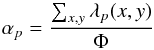 (11)where λp(x,y) is defined in Eq. (4), Φ in Eq. (10) and the sum is performed over the entire PSF.
(11)where λp(x,y) is defined in Eq. (4), Φ in Eq. (10) and the sum is performed over the entire PSF.
Simulated spectral models.
We calculate flux loss and spectral distortion inside a 30 arcsec radius circle centred on the source position. We do this first by using the equations over a continuous range of Φ, and then by performing 32 simulations each for EPIC-pn/-MOS, for 8 values of Φ, with each simulation using 100 000 incoming photons. The results are shown in Fig. 5.
 |
Fig. 5 Flux loss and spectral distortion as a function of the incoming number of photons per frame (i.e. not the observed count rate) inside a 30-arcsec extraction circle. For four spectral models (shown in different colours, with flux loss increasing and spectral distortion decreasing at fixed Φ for increasing spectral hardness) for both EPIC-pn (left) and EPIC-MOS (right). Solid coloured lines show the equation results, data points are the simulator results. Error-bars estimate the stochastic error in the simulations. Dashed vertical lines represent the old PHSTools-based flux thresholds. Dotted vertical lines represent the two new simulator-based flux thresholds. Coloured dashed lines show spectral distortion for spectra of single pixel patterns only. |
Two new EPIC flux limit thresholds (units photons s-1): one conservative (permitting 2−3% flux loss and <1% spectral distortion) and one tolerant (4−6% and 1−1.5% equivalently).
The simulator and equation outputs agree very well, giving us confidence in both modelling methods. We see that flux loss is always worse than spectral distortion: typically, we can expect to have lost 5 times as many photon counts than are present in our data at the incorrect energy. Flux loss increases with spectral hardness, whereas spectral distortion decreases. These trends make sense since harder spectra produce more multi-pixel patterns which have a greater capacity for destruction, whereas softer spectra create more single pixel patterns which can pile-up with an existing event with less chance of destroying it.
4.1. Flux thresholds
We can now derive flux thresholds to be used for observation planning purposes.
At the previous flux thresholds recommended by e.g. XMM-Newton PHSTools software (shown as dashed vertical lines in Fig. 5), EPIC-pn suffers 6−10% flux loss and 1.5−2.5% spectral distortion, and EPIC-MOS (ignoring the outlying Very Hard model) suffers 2−4% flux loss and 0.7−0.9% spectral distortion. We provide new limits based on the pile-up simulator and equations satisfying the following criteria: a conservative limit where 2−3% flux loss and less than 1% spectral distortion is incurred, and a tolerant limit allowing for 4−6% flux loss and 1−1.5% spectral distortion. Values for these limits scaled by the frame rate of each science mode of the EPIC-cameras are shown in Table 2.
These new thresholds were made available to the astronomical community prior to the 2013 Announcement for Opportunity through the accompanying user documentation (XMM-UH). For EPIC-MOS the old flux threshold lies between the new recomendations, suggesting that the old threshold was a reasonable estimate. This is not the case for EPIC-pn where the new thresholds are significantly lower than the previous one.
4.2. Spectral distortions
We now perform fits to spectra extracted from the simulated event files for the Hard spectral model. These numbers are purely representative and will depend strongly on the spectral model in question.
For both instruments, we consider events inside a 30 arcsec extraction radius, with energies between 0.5−10 keV and extract two spectra: one using the set of all good patterns, one using only single pixel events. We fit the piled-up spectra with the input spectral model phabs(nH)*pow(Γ) and report the differences ΔΓ = Γp − Γ0 and ℛnH = nH,p/nH,0 where subscripts 0,p correspond to the input parameters and the best-fit piled-up parameters respectively. Errors on these quantities arising from the finite number of photons (100 000) used in the simulation are also reported. In each case we report two results: the values at the conservative simulator-based flux limit, followed by the PHSTOOLS-based limit in brackets.
For spectra extracted using all good patterns, EPIC-MOS incurs hardening of the power-law slope ΔΓ = 0.10 ± 0.01(0.14 ± 0.1) and reduction in absorbing column density of ℛnH = 0.96 ± 0.01(0.91 ± 0.01). For EPIC-pn the numbers are ΔΓ = 0.10 ± 0.02(0.30 ± 0.04) and ℛnH = 0.94 ± 0.01(0.88 ± 0.02). For spectra extracted using just single pixel events, for EPIC-MOS ΔΓ = 0.01 ± 0.03(0.02 ± 0.03) and ℛnH = 1.03 ± 0.03(0.99 ± 0.03). For EPIC-pn ΔΓ = 0.02 ± 0.03(0.03 ± 0.03) and ℛnH = 1.01 ± 0.03(1.03 ± 0.03). We see that, for the number of photons used here, the recovered spectral parameters are consistent with the input into the simulations when just single pattern events are used.
In Fig. 5 we also show the spectral distortion incurred when only single pattern events are used (i.e. as in Eq. (2) but now just considering count rates of single pattern events). For all spectral models at all count rates shown we see that when considering just single pattern events, the fraction of observed counts at the wrong energy is <1% for EPIC-pn and <0.3% for EPIC-MOS. This supports the recommendation that spectral analysis can safely be performed using just single pixel events even in moderately piled-up data.
We further note that we have defined flux loss as the fractional loss of photon counts. The reduction in flux as measured by a spectral fit will depend on this number but also on the spectral distortions. For example in the fits described above, the best-fit model normalisations decrease by 10−20% due to pile-up despite incurring flux losses (as defined here) between 2−7%. The question of correct spectral fitting with piled-up data is beyond the scope of the current work, however solutions have been developed in Davis (2001) and Ballet (2003).
 |
Fig. 6 As Fig. 5 but given as a function of the observed count rate of good patterns per frame, and only showing the results using the pile-up equations (excluding the simulator results for clarity). For four spectral models (shown in different colours, with flux loss increasing and spectral distortion decreasing at fixed count rate for increasing spectral hardness). |
4.3. Estimating pile-up in your own data
We now describe how users interested in estimating meaningful pile-up diagnostics in their own data may proceed. Figure 5 shows the effects of pile-up as a function of the incoming number of photons per frame. In Fig. 6 we transform the x-axis into a directly observable quatity: the count rate (i.e. after pile-up) of good patterns. In practical terms, this figure can be used to quantify pile-up as follows:
-
1.
produce an event file (e.g. through the SAS reduction meta-tasks epproc or emproc) and evselect from a 30 arcsec radius circle around the source, of all energies but only good patterns (PATTERNs 0−12 and #XMMEA_EM for EPIC-MOS, PATTERNs 0−4 and FLAG==0 for EPIC-pn);
-
2.
calculate the number of total counts in the events list (e.g. through the FTOOLS task fstatistics);
-
3.
divide the number of counts by the ONTIME keyword in the event list header to give observed counts per second;
-
4.
multiply by the appropriate frame time as found in Table 2 to give observed number of counts per frame;
-
5.
approximate the spectral hardness of the source by comparison with the models listed in Table 1;
-
6.
derive the flux loss and spectral distortion from Fig. 6.
Step 5 may be performed more quantitatively by picking a spectral model roughly representative of your source (or indeed fitting a spectral model to a spectrum extracted just using single pattern events) then, by using Eq. (11), calculating for this model the fraction of photons which would give rise to single and double events in the no pile-up case. These may be cross referenced with the values given in Table 1 to determine the appropriate hardness. We expect most spectra to lie somewhere between the Hard and Soft cases (the Very Hard and Very Soft cases being at the extremes of realistic spectra). The uncertainty in the intrinsic spectral model dominates the error in these estimates of the effects of pile up.
5. Conclusions
In this paper we define rigorous metrics from first principles to characterise the effect of pile-up in X-ray CCD cameras. Our work extends the pioneering studies of Ballet (1999, 2001) by explicitly including the energy dependence of the telescope PSF. This allows us to extend the analytical formulas original developed by Ballet to the state-of-the-art energy-dependent PSF calibration (Read et al. 2011).
We characterise the effect of pile-up through two quantities: flux loss and spectral distortion. We validated our analytical results against the predictions of a novel event simulator, also described in this paper, that makes use of the most recent EPIC in-flight calibrations. We also demonstrate that the simulator is able to predict the behaviour of pile-up diagnostics based on the rate of diagonal event as measured in a sample of real observations.
We calculated count rate thresholds for all EPIC imaging instrumental modes under a wide range of spectral shapes. Our calculations (Table 2) improve previous estimates, unveiling that pile-up may have been slightly underestimated in the past. The new thresholds were made available to the astronomical community prior to the 2013 Announcement for Opportunity through the accompanying user documentation (XMM-UH).
The instrument mode dependent count rate thresholds presented in this paper shall be used in planning XMM-Newton observations of celestial sources to optimise the instrumental configuration, and prevent pile-up in real data, or at least limit it to an acceptable level depending on the observation’s scientific goals.
Acknowledgments
Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. We acknowledge support from the Faculty of the European Space Astronomy Centre (ESAC). We thank Andy Pollock for useful discussions and the referee, Andy Beardmore, for comments which significantly improved the paper.
References
- Ballet, J. 1999, A&AS, 135, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballet, J. 2001, ASPC, 238, 381 [Google Scholar]
- Ballet, J. 2003, Adv. Space Res., 32, 2077 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, J. E. 2001, ApJ, 562, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, C., Ibarra Ibaibarriaga, A., & Hoar, J. 2005, in UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XIV, ed. O. H. W. Siegmund, SPIE Conf. Ser., 5898, 469 [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Guainazzi, S., Kirsch, M., Haberl, F., et al. 2014, XMM-SOC-CAL-TN-0083, available at http://xmm2.esac.esa.int/docs/documents/CAL-TN-0083.pdf [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molendi, S. & Sembay, S. 2003, XMM-SOC-CAL-TN-0036, available at http://xmm2.esac.esa.int/docs/documents/CAL-TN-0036-1-0.ps.gz [Google Scholar]
- Pavlov, G. G. & Nousek, J. A. 1999, Nucl. Instr. Meth. Phys. Res. A, 428, 348 [Google Scholar]
- Read, A. M., Rosen, S. R., Saxton, R. D., & Ramirez, J. 2011, A&A, 534, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stuhlinger, M., et al. 2010, XMM-SOC-CAL-TN-0052, available at http://xmm2.esac.esa.int/docs/documents/CAL-TN-0052.ps.gz [Google Scholar]
- Townsley, L. K., Broos, P. S., Chartas, G., et al. 2002, Nucl. Instrum. Methods Phys. Res. A, 486, 716 [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Equations for arbitrary pattern
Creation probabilities for good XMM/EPIC patterns.
Here we detail the equations equivalent to Eqs. (6) and (7) for patterns larger than a single pixel i.e. for an arbitrary pattern p we write expressions for (i) mp(x,y) and (ii) 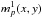 . These are, respectively, the probabilities of observing in pixel (x,y) during one frame (i) an event of pattern p; and (ii) an un piled-up event of pattern p. This is based on the work of Ballet (1999, 2001) and updated here to include an energy dependent PSF and a notation which is easily generalised for arbitrary patterns which, in particular, allows us to easily consider the effect of photons which generate bad patterns on the observed count rates of good patterns.
. These are, respectively, the probabilities of observing in pixel (x,y) during one frame (i) an event of pattern p; and (ii) an un piled-up event of pattern p. This is based on the work of Ballet (1999, 2001) and updated here to include an energy dependent PSF and a notation which is easily generalised for arbitrary patterns which, in particular, allows us to easily consider the effect of photons which generate bad patterns on the observed count rates of good patterns.
Define the set P of all possible patterns − both good and bad − with each pattern p ∈ P represented by a binary 2D array, where p(x,y) = 1 for pixels with charge above the detection threshold, 0 elsewhere, and (x,y) = (0,0) is the pattern’s primary pixel (i.e. the one containing the greatest charge). For each p we also define the buffer zone 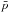 where
where 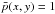 if max(|x − xi | , | y − yi|) = 1 for any i such that p(xi,yi) = 1, and
if max(|x − xi | , | y − yi|) = 1 for any i such that p(xi,yi) = 1, and 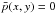 otherwise. Pixels in the buffer zone must contain charge below the detection threshold or the pattern p will be destroyed.
otherwise. Pixels in the buffer zone must contain charge below the detection threshold or the pattern p will be destroyed.
For every pair of patterns p,q we now define two more binary arrays, the exclusion zone Ep,q and the target zone Tp,q. Consider an event of pattern p in the pixel (x,y) = (0,0). If the primary pixel of a pattern q event arrives in a pixel where Ep,q(x,y) = 1, the pattern p event will be destroyed. If it arrives in a pixel where Tp,q(x,y) = 1 then the pattern p event will not be destroyed, but will become piled-up, with energy equal to the sum of the energies of p and q. We can write the following conditions to compute these two arrays 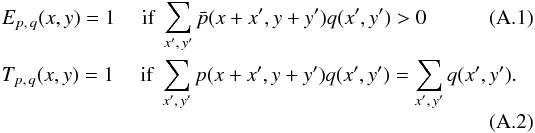 The probability that we observe an event of a pattern p in (x,y)− which we call mp(x,y)− is the product of the probabilities that we create this event and subsequently do not destroy it. Expressions for the probability of creating pattern p in (x,y)− which we call cp(x,y)− are listed for good patterns in Table A.1. A multi-pixel pattern may be created by combining smaller patterns, and the number of ways this is possible grows quickly with pattern size, hence the expressions for cp(x,y) become large. Full derivations can be found in the original works. The probability that we do not destroy pattern p comes from insisting that the buffer zone remains empty, which is the product of Poisson null occupancy probabilities over the exclusion zones Ep,q. This gives the following expression for mp(x,y), where the product over Ep,q (and likewise below for Tp,q) is shorthand for the product over all (x′,y′) where Ep,q(x′,y′) = 1
The probability that we observe an event of a pattern p in (x,y)− which we call mp(x,y)− is the product of the probabilities that we create this event and subsequently do not destroy it. Expressions for the probability of creating pattern p in (x,y)− which we call cp(x,y)− are listed for good patterns in Table A.1. A multi-pixel pattern may be created by combining smaller patterns, and the number of ways this is possible grows quickly with pattern size, hence the expressions for cp(x,y) become large. Full derivations can be found in the original works. The probability that we do not destroy pattern p comes from insisting that the buffer zone remains empty, which is the product of Poisson null occupancy probabilities over the exclusion zones Ep,q. This gives the following expression for mp(x,y), where the product over Ep,q (and likewise below for Tp,q) is shorthand for the product over all (x′,y′) where Ep,q(x′,y′) = 1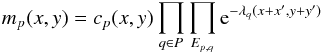 (A.3)λq(x,y) is given by Eq. (4) and depends on the PSF, effective area, and pattern fraction of the instrument as well as a spectral model for the observed source.
(A.3)λq(x,y) is given by Eq. (4) and depends on the PSF, effective area, and pattern fraction of the instrument as well as a spectral model for the observed source.
The un piled-up count rate is found replacing cp(x,y) in the above expression with the probability that the event is created from exactly one photon, which we call 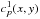 . This requires that the target zone remains unoccupied barring exactly one photon of the desired pattern p. Inserting Poisson probabilities gives the following expression for
. This requires that the target zone remains unoccupied barring exactly one photon of the desired pattern p. Inserting Poisson probabilities gives the following expression for 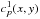 (and thus
(and thus 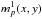 ) where the product over q ∈ { P − p } means multiplication over all patterns other than p
) where the product over q ∈ { P − p } means multiplication over all patterns other than p![\appendix \setcounter{section}{1} \begin{eqnarray} &&c^1_p(x,y) = \lambda_p(x,y){\rm e}^{-\lambda_p(x,y)} \prod_{q\,\in\, \{P-p\}} \prod_{T_{p,q}} {\rm e}^{-\lambda_q(x+x',y+y')} \\[3mm] &&m^1_p(x,y) = c^1_p(x,y) \prod_{q\,\in\, P} \prod_{E_{p,q}} {\rm e}^{-\lambda_q(x+x',y+y')}. \end{eqnarray}](/articles/aa/full_html/2015/09/aa25579-14/aa25579-14-eq127.png) The global quantities M and M1 defining flux loss and spectral distortion via Eqs. (1) and (2) are then found by summing the local, pattern dependent quantities mp(x,y) and
The global quantities M and M1 defining flux loss and spectral distortion via Eqs. (1) and (2) are then found by summing the local, pattern dependent quantities mp(x,y) and 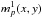 over the desired set of patterns, and pixels corresponding to the region of the PSF where spectral data are extracted.
over the desired set of patterns, and pixels corresponding to the region of the PSF where spectral data are extracted.
All Tables
Two new EPIC flux limit thresholds (units photons s-1): one conservative (permitting 2−3% flux loss and <1% spectral distortion) and one tolerant (4−6% and 1−1.5% equivalently).
All Figures
 |
Fig. 1 Examples of EPIC pattern classifications. In each case the dark red pixel contains maximum charge, light red pixels have charge above a threshold value whereas white pixels are necessarily below this threshold. Grey pixels do not influence the pattern classification of the event. |
| In the text | |
 |
Fig. 2 For the single (s), double (d) and triple (t) patterns with orientations as in Fig. 1 we show exclusion zones Ep,q in red. A photon with pattern q landing in Ep,q would destroy an event of pattern p whose maximum charge is in the central pixel. |
| In the text | |
 |
Fig. 3 A schematic diagram of the flow of generated and detected events from a single frame in the EPIC event simulator |
| In the text | |
 |
Fig. 4 Green circles: MOS fraction of diagonal to good patterns as a function of the observed count rate for the MOS1 (left) and MOS2 (right) cameras in Small Window exposures as measured in the XCAL sample. The dotted lines are curves fitted to the data points for clarity. Arrows indicate upper limits. The red squares are predictions from the pile-up simulator. |
| In the text | |
 |
Fig. 5 Flux loss and spectral distortion as a function of the incoming number of photons per frame (i.e. not the observed count rate) inside a 30-arcsec extraction circle. For four spectral models (shown in different colours, with flux loss increasing and spectral distortion decreasing at fixed Φ for increasing spectral hardness) for both EPIC-pn (left) and EPIC-MOS (right). Solid coloured lines show the equation results, data points are the simulator results. Error-bars estimate the stochastic error in the simulations. Dashed vertical lines represent the old PHSTools-based flux thresholds. Dotted vertical lines represent the two new simulator-based flux thresholds. Coloured dashed lines show spectral distortion for spectra of single pixel patterns only. |
| In the text | |
 |
Fig. 6 As Fig. 5 but given as a function of the observed count rate of good patterns per frame, and only showing the results using the pile-up equations (excluding the simulator results for clarity). For four spectral models (shown in different colours, with flux loss increasing and spectral distortion decreasing at fixed count rate for increasing spectral hardness). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


