| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526268 | |
| Published online | 07 August 2015 | |
Shape and solar phase angle effects on the taxonomic classification of asteroids
Observatório Nacional, rua Gal. José Cristino 77, São Cristóvão, 20921-400 Rio de Janeiro, Brazil
e-mail: carvano@on.br
Received: 7 April 2015
Accepted: 29 May 2015
Context. The taxonomic classification of SDSS observations of asteroids show a dependency on the phase angle of the observations.
Aims. We aim to quantify this dependence and use Hapke models to investigate its cause.
Methods. Statistical methods were used to characterize the taxonomic variation with phase angle. The effect of several Hapke parameters on the spectral slope and band depth of synthetic spectra for a slab and for ellipsoids with different oblatenesses were then analyzed.
Results. Effects linked to body shape and the solar phase function and macroscopic roughness can alter key spectral parameters that are related to the taxonomic classification depending on the solar phase angle, rotational phase of the observation, and shape of the asteroid. Depending on the oblateness of the body, shape effects are similar to phase effects.
Key words: minor planets, asteroids: general / methods: statistical / methods: analytical
© ESO, 2015
1. Introduction
Asteroid taxonomy is the effort of grouping asteroids into classes based on similarities of a number of their observational properties (Tholen & Barucci 1989). The most frequently used properties include measurements of their spectral reflectance (by means of low-resolution spectra, spectro-photometry, or colors) and geometric albedo. The usefulness of asteroid taxonomic classes derived in this way relies on the assumption that the classes bear some correspondence to the mineralogy of the asteroids, and on the fact that such a classification can be made using types of observations that are currently available for a large number of asteroids. Therefore, asteroid taxonomy can be used to infer trends in the distribution of compositions in the Main belt and other populations (Mothé-Diniz et al. 2003; DeMeo & Carry 2013), as an additional parameter in defining asteroid families (Cellino et al. 2002; Mothé-Diniz et al. 2005), and as a selection tool to identify candidates for more detailed observations (Roig & Gil-Hutton 2006; Moskovitz et al. 2008; DeMeo et al. 2014). However, the fact that the correspondence between taxonomic class and composition is far from perfect is still sometimes overlooked in the literature. Although a taxonomic classification narrows down the possible mineralogies of a given asteroid, it will seldom point unequivocally to one particular mineralogy. This has a number of reasons, some linked to the intrinsic difficulty involved in the remote characterization of the mineralogy of an asteroid, since it depends on the presence of absorption bands in its reflectance spectrum which may be absent or not completely sampled by the observations used to derive taxonomy. Another problem here is the exposure of the material on the surface of the asteroid to space weathering effects, such as solar wind implantation and micro-meteorite bombardment, which can change the optical properties of the material. Finally, the overall shape of the reflectance spectrum of an asteroid is also affected by the geometry of the observation, as well as by its shape.
While analyzing the distribution of SDSS-based taxonomies (Carvano et al. 2010; Hasselmann et al. 2011) in the Vesta family, Jasmim et al. (2013) recently noted a considerable number of asteroids classified as Qp, along with the dominant Vp class. Mineralogy inferred from near-infrared (NIR) spectra of a sample of Vp and Qp in the family showed that although the Qp asteroids presented a shallower 1 μm band than the Vp asteroids, their silicate mineralogy was essentially the same. Interestingly, however, it was noted that the distribution in solar phase angle of the asteroids classified as Qp was markedly different from the Vp asteroids in the family, with the Qp class showing a clear concentration around low phase angles.
In this work we analyze how the classification of asteroids observed by the Sloan Digital Sky Survey (SDSS) is affected by the solar phase angle of the observation and discuss the possible causes of this behavior using Hapke bidirectional reflectance models (Hapke 2012b). In Sect. 2 we analyze the distribution in phase of the main taxonomic classes of asteroids observed by the SDSS (Jurić et al. 2002) and also the correlation with phase angle of the spectral parameters (spectral slope and band depth) that most affect the taxonomic classification of asteroid spectra. In Sect. 3 we analyze how the several parameters that control the phase dependency of the reflectance in Hapke model affect the spectral slope of synthetic spectra, considering the effects of the shape of the asteroids, and the results are further discussed and summarized in Sect. 4.
2. Phase effects in SDSS data
 |
Fig. 1 Distribution in phase angle of the observation of asteroids classified as CP, Xp, Dp, Qp, Sp, and Vp, compared with all SDSS observations classified by Carvano et al. (2010). The number of observations involved in each distribution is given in parenthesis. |
 |
Fig. 2 Template spectra of the taxonomic classes defined in Carvano et al. (2010). |
2.1. Effects on taxonomic classification
Figure 1 shows the distribution on solar phase angle of SDSS observations of asteroids that were classified by Carvano et al. (2010) as CP, Xp, Dp, Qp, Sp, or Vp. These classes sample well the main features that dominate the shape of the visible spectra of most asteroids. The Qp, Vp, and Sp classes are characterized by a broad 1 μm band that is caused by the presence of olivine and or pyroxenes, whose wing in the reflectance spectra derived from SDSS color is seen as a sharp drop in the reflectance beyond 0.7 μm. Vp spectra tend to be somewhat red before 0.7 μm and show a steep fall in reflectance due to a deep 1 μm band, while spectra of the Qp are less red before 0.7 μm and have a fainter band; the Sp class, on the other hand, are redder before 0.7 μm, but show a much shallower band. The Cp, Xp, and Dp classes, on the other hand, have no band in their visible spectra and differ only by their spectral slope: for Cp it ranges from bluish to flat, Xp have moderately red spectra, and Dp have redder spectra, with higher positive spectral slope. The template spectra for each class are shown in Fig. 2.
In Fig. 1 we compare the distribution of those classes in phase angle to the distribution of all observations that were classified by Carvano et al. (2010). The similarities of the distributions were quantified using a Kolmogorov-Smirnov test, which assesses the hypothesis that two samples have the same distribution. This yields the probability pKS of the veracity of that hypothesis. A value of pKS higher than the considered significance level (usually %1 or %5) would then mean that the two samples cannot be distinguished statistically. If the classification were not affected by the phase angle of the observation, the distribution of all classes are expected to be identical to the distribution of the whole sample. That is not what happens, however. From Fig. 1 is clear that there is an excess of observations classified as Qp at low phase angles and a deficit of observations with this classification at higher phase angles, with the reverse occurring for the Sp and Vp classes. This effect was originally noted by Jasmim et al. (2013) when analyzing Qp asteroids in the Vesta family. Considering the classes without band, the observations classified as Cp are also more frequent at low phase angles and missing at higher phase angles, while the opposite is true for the observations with Dp class, and the distribution of observations with Xp class more closely reproduces the distribution of all observations. Except for Xp class, which has a pKS = 0.507, all others have pKS ≈ 0.0, which means that their distributions in phase are statistically different from the distribution of the whole sample.
 |
Fig. 3 Distribution of Pearson’s correlation coefficient between the phase angle of observation and the spectral parameter slope1 and bd for classified asteroids that were observed more than four times, spanning a phase angle interval greater than 10°. |
Distribution of correlations between spectral parameters and phase angle of observation.
These effects are in principle consistent with what is expected from phase reddening effects (Millis et al. 1976; Gradie & Veverka 1986; Sanchez et al. 2013; Reddy et al. 2015). Essentially, we could explain the discrepancies in the phase angle distributions by assuming that objects with mineralogies that would yield spectra compatible with S or V (but close to the limits of the QP class), at intermediate phase angles would exhibit spectra compatible with Qp class at lower phase angles, and vice versa. Similarly, objects with spectra that are borderline between Cp and Xp would show as Cp class at low phase angle and Xp class at higher phase angles, while objects with borderline spectra between Xp and Dp would appear as Xp class at low phase angles and as Dp class at higher values.
2.2. Effects on spectral parameters
To understand how variations of phase angles affect the reflectance spectra of individual asteroids listed in the SDSS with multiple observations, we used the reflectance spectra derived from SDSS colors to define two parameters. The first, slope, measures the reddening of the visible part of the spectra and is defined as the gradient of the reflectance between SDSS filters g′ and i′: 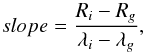 (1)where R and λ are the reflectance and central wavelength in microns of the filters. The second parameter, which measures the depth of the 1 μm and, is simply the difference of the reflectances between the z′ and i′ filters,
(1)where R and λ are the reflectance and central wavelength in microns of the filters. The second parameter, which measures the depth of the 1 μm and, is simply the difference of the reflectances between the z′ and i′ filters, 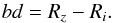 (2)This last parameter is only meaningful for classes with this feature, while slope is a valid indicator of reddening for all classes. To calculate these parameters, we first normalized the reflectance spectra at the r′ filter, following the convention usually adopted for the SDSS asteroid data.
(2)This last parameter is only meaningful for classes with this feature, while slope is a valid indicator of reddening for all classes. To calculate these parameters, we first normalized the reflectance spectra at the r′ filter, following the convention usually adopted for the SDSS asteroid data.
These parameters were calculated for all observations of asteroids with SDSS classification that were observed at least three times, spanning a range of phase angles larger than 10 deg (Hasselmann et al. 2011); then we used the Pearson rank order correlation coefficient P for each asteroid to assess the existence of a correlation between each parameter and the phase angle. Figure 3 show the distribution of the correlation coefficient of slope for all asteroids that satisfy the mentioned criteria (2077 objects) and for subsamples of Cp, Xp, or Dp class asteroids (626) and Vp, Sp or Qp class asteroids (1164). We also show the distribution of the correlation coefficient for ΔRiz for the last subsample. If we consider that values of P> 0.2 indicate a statistically meaningful correlation, values −0.2 ≤ P ≤ 0.2 indicate the absence of any meaningful correlation, and that P< −0.2 indicates a statistically meaningful anticorrelation, then the number of asteroids in each case is given in Table 1 for the four samples displayed in Fig. 3. From these numbers it is clear that most asteroids in the sample tend to be redder at higher phase angles, and that for the classes showing a 1 μm band, most show increasing band depth with increasing phase angle. This predominance of positive correlations for both band depth and spectral slope might suffice to explain the offsets in the distribution of classes in phase angle that were shown in Sect. 2.1.
However, for both parameters there is a significant fraction in each sample for which there seems to be no correlation at all, and a similar number seem to display an anticorrelation between the parameters and the phase angle. Figure 4 shows examples of the variation of slope with phase angle for two asteroids. In Fig. 4a we show an S-type asteroid that has a clear correlation between Slope and phase angle. Even so, there is considerable scatter in the Slope values; it is greater than the calculated uncertainty for the parameter. Figure 4b shows a C-type asteroid without a clear correlation and with a scatter again greater than the uncertainties in the data.
 |
Fig. 4 Variation of slope with phase angle for panel a) the S-type asteroid (728) Leonisis and panel b) the C-type asteroid (9396) Yamaneakisato. |
3. Hapke models
To gain a better understanding of the effects of observation geometry and shape on the SDSS spectra, we used the Hapke theory to model the bidirectional reflectance of asteroids. Hapke bi-directional reflectance models consist of analytic approximations to the solution of the radiative transfer equation on a plane, semi-infinite particulate medium, modified to include some semi-empirical terms to account for additional physical effects (Hapke 1993). The latest version of Hapke’s formula for the bidirectional reflectance includes parameters to describe the effects of solar phase, porosity, macroscopic roughness, shadow-hiding, and coherent backscatter (Hapke 1984, 1986, 2002, 2008).
The parameters that control the variation of the reflectance spectra with phase angle are related to the phase function of the material, to the opposition effect, and to the macroscopic roughness of the surface. The adopted expression for the bidirectional reflectance is then![\begin{equation} \label{IMSA} r_{\lambda}=\frac{w_{\lambda}}{4\pi}\frac{\mu_0}{\mu_0+\mu}\left[p(g)B_{\rm SH}(g)+M(w_{\lambda},\mu_0,\mu)\right]S(\theta, \psi,\mu_0,\mu) . \end{equation}](/articles/aa/full_html/2015/08/aa26268-15/aa26268-15-eq35.png) (3)In this expression, wλ is the average volumetric single-scatter albedo of the material at the wavelength λ, p is the phase function, g is the phase angle, μ0 and μ are the cosines of the angle between the illumination and observation directions with the normal of surface of the medium, M is the multiple scattering function (Hapke 2002), BSH is the function for the shadow-hiding opposition effect (Hapke 1986), and S is the shadowing function (Hapke 1984).
(3)In this expression, wλ is the average volumetric single-scatter albedo of the material at the wavelength λ, p is the phase function, g is the phase angle, μ0 and μ are the cosines of the angle between the illumination and observation directions with the normal of surface of the medium, M is the multiple scattering function (Hapke 2002), BSH is the function for the shadow-hiding opposition effect (Hapke 1986), and S is the shadowing function (Hapke 1984).
For planetary applications, the most frequently adopted phase function is the empirical Henyey-Greenstein function, and here we use the double-lobed version of this function (Hapke 2002), 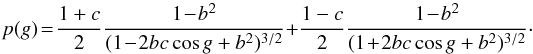 (4)The parameters in this function are related to the asymmetric cosine ε of the medium as ε = −bc. Laboratory measurements suggest that for particles within a wide range of compositions and textures, b and c follow an empirical relation (Hapke 2012a):
(4)The parameters in this function are related to the asymmetric cosine ε of the medium as ε = −bc. Laboratory measurements suggest that for particles within a wide range of compositions and textures, b and c follow an empirical relation (Hapke 2012a):![\begin{equation} b=\left[\frac{1}{17.4}\ln\left(\frac{3.29}{0.908+c}\right)\right]^{1/2}\cdot \end{equation}](/articles/aa/full_html/2015/08/aa26268-15/aa26268-15-eq48.png) (5)\label{bc}The multiple scattering function is given by
(5)\label{bc}The multiple scattering function is given by ![\begin{eqnarray} \begin{split} M(w_{\lambda},\mu_0,\mu)=P(\mu_0)\left[H(\mu)-1\right]+P(\mu)\left[H(\mu_0)-1\right] \\ +{\cal P }\left[H(\mu) - 1\right]\left[H(\mu_0)-1 \right] \end{split} . \end{eqnarray}](/articles/aa/full_html/2015/08/aa26268-15/aa26268-15-eq49.png) (6)Here, H is the Ambartsumian-Chandrasekhar function, which also depends on wλ and is calculate here as
(6)Here, H is the Ambartsumian-Chandrasekhar function, which also depends on wλ and is calculate here as ![\begin{equation} H(x)=\left[1-w_{\lambda}x\left(r_0+\frac{1-2r_0 x}{2}\ln \frac{1+x}{x}\right)\right]^{-1} , \end{equation}](/articles/aa/full_html/2015/08/aa26268-15/aa26268-15-eq51.png) (7)where
(7)where 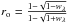 . The functions P and
. The functions P and 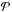 are calculated using a Legendre polynomial expansion of the phase function (Hapke 2002) and therefore implicitly depend on its coefficients (but not on the phase angle).
are calculated using a Legendre polynomial expansion of the phase function (Hapke 2002) and therefore implicitly depend on its coefficients (but not on the phase angle).
The shadowing function S describes the macroscopic roughness effect and has an explicit dependency on the azimuth angle ψ, which is a function of the phase angle and the incidence and emergence angles. The magnitude of this effect increases with the mean slope angle of the surface (or roughness parameter), 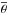 . We modeled the opposition effect using only the shadow-hiding function:
. We modeled the opposition effect using only the shadow-hiding function: ![\begin{equation} B_{\rm SH}=1+B_{S0}\left[1+\frac{1}{h_{\rm s}}\tan(g/2)\right]^{-1} , \end{equation}](/articles/aa/full_html/2015/08/aa26268-15/aa26268-15-eq56.png) (8)where BS0 is the amplitude of the opposition effect and hs is its angular width.
(8)where BS0 is the amplitude of the opposition effect and hs is its angular width.
Equation (3) models the bidirectional reflectance of a plane slab with well-defined illumination and observation angles. For Earth-based observations of asteroids, on the other hand, the observables are integrated over the visible and illuminated portions of the body. To model the shape effects, we considered shape models of asteroids made of triangular facets, with the reflectance of each facet described by Eq. (3), and the observed reflectance is the sum of the contribution of each facet, whose illumination and observation cosine are functions of the direction of the observer and the Sun, the direction of the rotation pole of the asteroid, and the position of the facet in the asteroid.
For particles that are larger than the wavelength, the single-scatter albedo can be calculated with a geometric optics approximation as a function of the optical constants of the material (which in turn also depends on the wavelength) and the size of particle.
In principle, the phase parameters depend on the properties of the material through the optical constants (Hapke 2012b), and as consequence, these parameters should also depend on the wavelength. To separate the effects of the phase parameters on the final spectra, however, we considered here that they are independent of wavelength and related through Eq. (3). To simulate spectra with a 1 μm band, we used the optical constants for pure olivine (Fa = 1) derived by Trang et al. (2011), with particles with diameters d = 50 μm. We then computed bidirectional reflectance spectra for a range of phase parameters and geometries and calculated the resulting Slope and band depth. We considered the cases of materials that are backward-scattering (b = 0.2), forward-scattering (b = 0.7), and a material with intermediate properties (b = 0.5).
 |
Fig. 5 Panel a) reflectance spectra of a slab for b = 0.2 for phase angles between 0° and 60°; panel b) same for b = 0.7; panel c) slope as function of phase angle for b ∈ [0.2,0.5,0.7] . |
3.1. Plane slab
Figure 5 shows the how the bireflectance spectra of a slab vary as a function of phase angle and phase parameters. Here we did not consider macroscopic roughness or opposition effects. Figures 5a and b shows the normalized bidirectional reflectance spectra for phase angles between 0° and 60° using b = 0.2 and b = 0.7, respectively. It is clear here that the shape of the spectra changes very little with phase angle for backward-scattering materials, while the variations are more considerable for forward-scattering surfaces. Figure 5c shows how these variations affect the slope of the spectra; the band depth variations are highly correlated with variations of the slope. For a backward-scattering surface (b = 0.2), the slope is anticorrelated with phase angle, decreasing smoothly with increasing phase angles. A similar behavior is observed for materials with b = 0.5. For forward-scattering material (b = 0.7), on the other hand, the slope increases with phase angle until g ≈ 30°, but eventually starts decreasing after g ≈ 40°.
Therefore, the results obtained for a slab suggest that for phase angles up to 30°, a positive correlation of slope and band depth will occur for forward-scattering material, while for backward-scattering material and materials with intermediate properties, these parameters will be anticorrelated with phase angle.
3.2. Shape effects
To understand how the shape of the body may affect these results, we modeled the bireflectance spectra of ellipsoids, which can be described by three axis a1, a2, and a3, considering the case where the larger axis a1 = 1 and a2 = a3, such that the shape is completely described by the a2/a1 ratio. To fully describe the orientation of each facet of the spheroid with respect to the observer and the Sun, it is also necessary to specify the direction of the rotation pole of the body, as well as the rotational angle from a fixed position on the body to the line of sight. We considered here the case where the rotation pole is perpendicular to the line of sight and the rotational angle is zero in one direction along the larger axis of the spheroid.
 |
Fig. 6 Panel a) Reflectance spectra of a spheroid with a2/a1 = 0.9 for b = 0.2 for phase angles between 0° and 60°; panel b) same for b = 0.7; panel c) slope as function of phase angle for b ∈ [0.2,0.5,0.7] . |
 |
Fig. 7 Panel a) Reflectance spectra of a spheroid with a2/a1 = 0.2 for b = 0.2 for phase angles between 0° and 60°; panel b) same for b = 0.7; panel c) slope as function of phase angle for b ∈ [0.2,0.5,0.7] . |
 |
Fig. 8 Panel a) Slope as a funcion of fase angle, considering rugosity for several values of |
 |
Fig. 9 Panel a) slope as funcion of fase angle, considering a shadow-hidding opposition effect with BS0 = 1.1 and several values of hs for a spheroid with a2/a1 = 0.9 and b = 0.5 for phase angles between 0° and 60°. The curve maked with hs = 0.0 does not include the opposition effect. Panel b) The same for a2/a1 = 0.2. |
 |
Fig. 10 Variation of the spectral slope with rotation for b = 0.5 and different values of a2/a1. |
Figure 6 shows the same plots as Fig. 5, except that now we consider a nearly spherical ellipsoid (a2/a1 = 0.9) seen at a rotational angle of 10°. For the back-scattering material the spectral slope shows no correlation with phase angle, remaining essentially constant for phase angles up to 60°. In contrast, forward-scattering materials show an increase of the spectral slope up to g ≈ 40° that is steeper than what is observed for a slab, with the spectral slope becoming essentially constant for larger phase angles. The same qualitative behavior is now seen for b = 0.5, but with a much fainter gradient before g ≈ 40°. For an extremely elongated body with a2/a1 = 0.2 (Fig. 7), the variations of shape of the spectra with phase angle are more pronounced than for the slab for both backward- and forward-scattering materials. The spectral parameters show an anticorrelation for phase angles smaller than 10°, which becomes a positive correlation up to g ≈ 50°, and then again turns to anticorrelation for larger phase angles. The positive correlations become steeper as one goes from backward-scattering to forward-scattering materials.
These qualitative behaviors are only slightly modified by the addition of macroscopic roughness and opposition effects. Figure 8 shows the behavior of the spectral slope with phase angle for mean surface slopes from 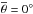 to
to 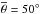 , considering b = 0 and different body shapes. The overall effect of the macroscopic roughness is to slightly increase the gradient of the spectral slope with phase angle (more noticeably at larger phase angles), and the magnitude of this increase becomes more important for more elongated bodies. The effect of the shadow-hiding opposition effect is shown in Fig. 9. This effect causes a decrease in the observed spectral slope that becomes more important at small phase angles and results in an overall increase in the gradient of the spectral slope with respect to the phase angle.
, considering b = 0 and different body shapes. The overall effect of the macroscopic roughness is to slightly increase the gradient of the spectral slope with phase angle (more noticeably at larger phase angles), and the magnitude of this increase becomes more important for more elongated bodies. The effect of the shadow-hiding opposition effect is shown in Fig. 9. This effect causes a decrease in the observed spectral slope that becomes more important at small phase angles and results in an overall increase in the gradient of the spectral slope with respect to the phase angle.
It is also important to consider how the shape of the spectra is affected by the change in rotational aspect. Figure 10 shows for different a2/a1 ratios the variation of spectral slope with rotational angle for a phase angle fixed at g = 20°. The overall behavior of both parameters with rotational angle does not depend on whether the material is forward- or backward-scattering, but, as expected, it depends very strongly on a2/a1, while it is negligible for a near-spherical and quite significant for the elongated bodies. For both parameters, the amount of the variation with rotation can be similar to the variation attributable to changes in phase angle, depending on the scattering properties of the material and the shape of the body.
4. Discussion
From the discussions in the previous section it is clear that the variations of spectral slope and band depth that should influence the dependence of the taxonomic classification of asteroids with phase angle presented in Sect. 2 are primarily controlled by the phase function parameters, but that the shape of the body is an important source of variation as well. For a plane-parallel medium, the dependence of the spectral slope with phase angle goes from anticorrelation for backward-scattering materials to positive correlation for forward-scattering materials. However, no anticorrelation is seen once a convex shape is assumed. In this case, there is essentially no correlation between spectral slope and phase angle for more extreme backward-scattering surfaces, and progressively steeper positive correlations as the surface becomes more forward-scattering. In addition, more elongated bodies would in principle show steeper gradients, and the addition of opposition and macroscopic roughness effects would also produce a steeper phase reddening. All these effects are compatible with the observed dependency of taxonomic classification with phase angle, and with the fact that most of SDSS asteroids with observations on multiple phase angles either present a positive correlation of the spectral slope with phase angle or no correlation; the latter case would be consistent with more backward-scattering surfaces. It is also possible to understand the existence of objects with an anticorrelation of spectral slope and band depth with phase angle as a consequence of the dependence that these parameters have on the rotational and aspect angle of each observation. This is because for more elongated bodies, the variation of these parameters with rotational angle is comparable with the magnitude of the variation caused by changes in the phase angle of the observations. Since the asteroids were observed by SDSS at essentially random configurations in terms of rotational, aspect, and phase angles, the combined effects of these parameters on the observed spectra for more elongated bodies could produce the observed negative correlations and the absence of correlations.
5. Conclusions
We have analyzed the influence of the solar phase angle on the taxonomic classification of SDSS observations of asteroids. Our main results are listed below.
- 1.
The distribution in phase angle of SDSS observations ofasteroids classified in most of the major taxonomic classes showstrends that are consistent with an increase in spectral slope andband depth with increasing phase angle.
- 2.
Although the majority of asteroids with SDSS observations over multiple phase angles show a positive correlation of both spectral slope and band depth and phase angle, there are many asteroids for which these parameters have no correlation and even negative correlations with phase angle.
-
The dependence of the spectral slope with phase angle is most affected by the parameters of the phase function. The amount of reddening with phase angle increases as the material becomes more forward scattering, while surfaces that show extreme backward scattering may present a negative correlation between spectral slope and phase angle.
-
The shape of the target also strongly affects the dependence between spectral slope and phase angle:
-
The phase reddening increases for more elongated bodies.
-
Ellipsoids with extreme backward-scattering surfaces show, at most, no correlation between spectral slope and phase angle, instead of the negative correlation seen for plane slabs.
-
For elongated bodies the measured spectral slope is also a function of the aspect and rotational angles of the observation, and the variation in spectral slope that is due to changes in the rotational angle is similar to the variation that is due to phase angle.
-
Both opposition effects and macroscopic roughness contributeto increase the phase reddening, and together they may result in anincrease in the spectral slope with phase angle even for a spherecovered in backward-scattering material.
Therefore, the observational circumstances and shape of the body may affect the spectral parameters that are related to taxonomic classifications. For most asteroids, the magnitude of these effects is probably small, but it might change the taxonomic classification of observations in some instances. Attempts to correct for these effects in a proper way would require knowledge about not only the scattering properties of the material on the surface of the bodies, but also about their shapes and rotation poles. These parameters are not known at this point for the vast majority of the asteroids with SDSS observations. In the end, however, this kind of correction is not really necessary for most of the meaningful uses of taxonomy. Although phase and shape effects can blur the lines between taxonomic classes, it must be realized that these lines, although useful as references, lack any strict meaning in terms of defining the mineralogical composition of an asteroid. It suffices then to take the effects we showed here into account when trying to interpret the taxonomic classification of asteroids in any given context.
Acknowledgments
J.M.C. would like to thank CNPq and CAPES for supporting this work through diverse fellowships and grants. J.A.G.D. would like to thank CAPES for supporting his work with a PhD fellowship.
References
- Carvano, J. M., Hasselmann, P. H., Lazzaro, D., & Mothé-Diniz, T. 2010, A&A, 510, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cellino, A., Bus, S. J., Doressoundiram, A., & Lazzaro, D. 2002, Asteroids III (Tucson: University of Arizona Press), 633 [Google Scholar]
- DeMeo, F. E., & Carry, B. 2013, Icarus, 226, 723 [NASA ADS] [CrossRef] [Google Scholar]
- DeMeo, F. E., Binzel, R. P., Carry, B., Polishook, D., & Moskovitz, N. A. 2014, Icarus, 229, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Gradie, J., & Veverka, J. 1986, Icarus, 66, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1984, Icarus, 59, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1986, Icarus, 67, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 1993, Theory of reflectance and emittance spectroscopy (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Hapke, B. 2002, Icarus, 157, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 2008, Icarus, 195, 918 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 2012a, Icarus, 221, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Hapke, B. 2012b, Theory of reflectance and emittance spectroscopy, 2nd edn. [Google Scholar]
- Hasselmann, P. H., Carvano, J. M., & Lazzaro, D. 2011, NASA Planetary Data System, 145 [Google Scholar]
- Jasmim, F. L., Lazzaro, D., Carvano, J. M. F., Mothé-Diniz, T., & Hasselmann, P. H. 2013, A&A, 552, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jurić, M., Ž. Ivezić, & Lupton, R. H. 2002, in BAAS, 34, 1172 [Google Scholar]
- Millis, R. L., Bowell, E., & Thompson, D. T. 1976, Icarus, 28, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Moskovitz, N. A., Jedicke, R., Gaidos, E., et al. 2008, Icarus, 198, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Mothé-Diniz, T., Carvano, J. M. Á., & Lazzaro, D. 2003, Icarus, 162, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Mothé-Diniz, T., Roig, F., & Carvano, J. M. 2005, Icarus, 174, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, V., Dunn, T. L., College, C., et al. 2015, in Asteroids IV, Space Sci. Ser. (University of Arizona Press), in press [arXiv:1502.05008] [Google Scholar]
- Roig, F., & Gil-Hutton, R. 2006, Icarus, 183, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, J. A., Michelsen, R., Reddy, V., & Nathues, A. 2013, Icarus, 225, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Tholen, D. J., & Barucci, M. A. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews, 298 [Google Scholar]
- Trang, D., Lucey, P. G., & Gillis-Davis, J. J. 2011, in Lunar and Planetary Sci. Conf., 42, 2745 [Google Scholar]
All Tables
Distribution of correlations between spectral parameters and phase angle of observation.
All Figures
 |
Fig. 1 Distribution in phase angle of the observation of asteroids classified as CP, Xp, Dp, Qp, Sp, and Vp, compared with all SDSS observations classified by Carvano et al. (2010). The number of observations involved in each distribution is given in parenthesis. |
| In the text | |
 |
Fig. 2 Template spectra of the taxonomic classes defined in Carvano et al. (2010). |
| In the text | |
 |
Fig. 3 Distribution of Pearson’s correlation coefficient between the phase angle of observation and the spectral parameter slope1 and bd for classified asteroids that were observed more than four times, spanning a phase angle interval greater than 10°. |
| In the text | |
 |
Fig. 4 Variation of slope with phase angle for panel a) the S-type asteroid (728) Leonisis and panel b) the C-type asteroid (9396) Yamaneakisato. |
| In the text | |
 |
Fig. 5 Panel a) reflectance spectra of a slab for b = 0.2 for phase angles between 0° and 60°; panel b) same for b = 0.7; panel c) slope as function of phase angle for b ∈ [0.2,0.5,0.7] . |
| In the text | |
 |
Fig. 6 Panel a) Reflectance spectra of a spheroid with a2/a1 = 0.9 for b = 0.2 for phase angles between 0° and 60°; panel b) same for b = 0.7; panel c) slope as function of phase angle for b ∈ [0.2,0.5,0.7] . |
| In the text | |
 |
Fig. 7 Panel a) Reflectance spectra of a spheroid with a2/a1 = 0.2 for b = 0.2 for phase angles between 0° and 60°; panel b) same for b = 0.7; panel c) slope as function of phase angle for b ∈ [0.2,0.5,0.7] . |
| In the text | |
 |
Fig. 8 Panel a) Slope as a funcion of fase angle, considering rugosity for several values of |
| In the text | |
 |
Fig. 9 Panel a) slope as funcion of fase angle, considering a shadow-hidding opposition effect with BS0 = 1.1 and several values of hs for a spheroid with a2/a1 = 0.9 and b = 0.5 for phase angles between 0° and 60°. The curve maked with hs = 0.0 does not include the opposition effect. Panel b) The same for a2/a1 = 0.2. |
| In the text | |
 |
Fig. 10 Variation of the spectral slope with rotation for b = 0.5 and different values of a2/a1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


