| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526264 | |
| Published online | 07 August 2015 | |
Underlying particle spectrum of Mkn 421 during the huge X-ray flare in April 2013
1 Tata Institute of Fundamental Research, Homi Bhabha Road, Colaba, 400 005 Mumbai, India
e-mail: atreyee@tifr.res.in
2 Inter-University Center for Astronomy and Astrophysics, Post Bag 4, Ganeshkhind, 411007 Pune, India
3 Now at ETH Zurich, Institute for Particle Physics, Otto-Stern-Weg 5, 8093 Zurich, Switzerland
Received: 6 April 2015
Accepted: 9 June 2015
Context. In April 2013, the nearby TeV blazar, Mkn 421, showed one of the largest flares in X-rays in the past decade.
Aims. We study all multiwavelength data available during MJD 56 392 to 56 403, with special emphasis on X-ray data to understand the underlying particle energy distribution.
Methods. We studied the correlations between the UV and gamma-ray bands with the X-ray band using the z-transformed discrete correlation function. We modelled the underlying particle energy spectrum with a single population of electrons emitting synchrotron radiation, and statistically fitted the simultaneous time-resolved data from Swift-XRT and NuSTAR.
Results. The flux varied rapidly in the X-ray band, with a minimum doubling timescale of 1.69 ± 0.13 h. There were no corresponding flares in UV and gamma-ray bands. The variability in UV and gamma rays was relatively modest with ~8% and ~16%, respectively, and no significant correlation was found with the X-ray light curve. The observed X-ray spectrum shows a clear curvature that can be fit by a log parabolic spectral form. This is best explained as originating from a log parabolic electron spectrum. However, a broken power law or a power law with an exponentially falling electron distribution cannot be ruled out either. Moreover, the excellent broadband spectrum from 0.3–79 keV allows us to make predictions of the UV flux. We find that this prediction is compatible with the observed flux during the low state in X-rays. However, during the X-ray flares, depending on the adopted model, the predicted flux is a factor of 2–50 lower than the observed one. This suggests that the X-ray flares are probably caused by a separate population that does not contribute significantly to the radiation at lower energies. Alternatively, the underlying particle spectrum can be much more complex than those explored in this work.
Key words: BL Lacertae objects: individual: Mkn 421 / galaxies: active / X-rays: galaxies / radiation mechanisms: non-thermal
© ESO, 2015
1. Introduction
According to the unification scheme of active galactic nuclei (AGNs) by Urry & Padovani (1995), blazars are a subclass of AGNs with a relativistic jet aligned close to the line of sight. Blazars are further subdivided into BL lacertae (BL Lac) and flat-spectrum radio quasaars (FSRQs), where BL Lacs are characterized by the absence of (or very weak) emission lines. They show high optical polarization, intense and highly variable non-thermal radiation throughout the entire electromagnetic spectra on timescales extending from minutes to years, apparent super-luminal motion in radio maps, large Doppler factors, and beaming effects. The broadband spectral energy distribution (SED) of blazars is characterized by two peaks, one in the IR – X-ray regime, and the second one in the γ-ray regime. According to the location of the first peak, BL Lacs are further classified into low-energy peaked BL Lacs (LBLs) and high-energy peaked BL Lacs (HBLs; Padovani & Giommi 1995). Both leptonic and hadronic models have been used to explain the broadband SED with varying degrees of success. The origin of the low-energy component is well established to be caused by synchrotron emission from relativistic electrons gyrating in the magnetic field of the jet. However, the physical mechanisms responsible for the high-energy emission are still under debate. It can be produced either through inverse Compton (IC) scattering of low-frequency photons by the same electrons responsible for the synchrotron emission (leptonic models), or through hadronic processes initiated by relativistic protons, neutral and charged pion decays, or muon cascades (hadronic models). The seed photons for IC in leptonic models can be either the synchrotron photons themselves (synchrotron self-Compton, SSC) or from external sources such as the broad line region (BLR), the accretion disc, and the cosmic microwave background (external Compton, EC). For a comprehensive review of these mechanisms, see Böttcher (2007).
Mkn 421 is the closest (z = 0.031) and the best-studied TeV blazar. It was also the first detected extragalactic TeV source (Punch et al. 1992), and one of the brightest BL Lac objects seen in the UV and X-ray bands. It is an HBL, with the synchrotron spectrum peaking in the X-ray regime. Moreover, the X-ray emission is known to be highly correlated with the TeV emission (Błażejowski et al. 2005; Katarzynski et al. 2005; Qian et al. 1998), but like other HBLs, shows moderate correlation with the GeV emission (Li et al. 2013). It is highly variable and has been well studied during its flaring episodes by several authors (Aleksić et al. 2010, 2012; Shukla et al. 2012; Isobe et al. 2010; Krawczynski et al. 2001; Acciari et al. 2009; Ushio et al. 2009; Tramacere et al. 2009; Horan et al. 2009; Lichti et al. 2008; Fossati et al. 2008; Albert et al. 2007; Brinkmann et al. 2003). A detailed study of its quiescent state emission has been performed by Abdo et al. (2011) with the best-sampled SED to date.
In April 2013, Mkn 421 underwent one of the largest X-ray flares ever recorded in the past decade (Pian et al. 2014). The source was simultaneously observed by Swift and NuSTAR during this flaring episode, and we use these observations to study the spectral variations. To strengthen our study further, we supplement the X-ray information with other available multiwavelength observations.
The main focus of our work is the joint spectral fitting of the Nuclear Spectroscopic Telescope Array NuSTAR the Swift-XRT telescopes, and using this, we investigate the underlying particle energy spectrum. The high photon statistics during the flare, coupled with the excellent spectral response of Swift-XRT and NuSTAR, gives us a rich X-ray spectrum from 0.3−79 keV to explore. A study of the quiescent state of Mkn 421 using NuSTAR data was performed by Baloković et al. (2013). In Sect. 2 we describe the data reduction techniques from the various instruments. Section 3 lists the multiwavelength temporal results, while the X-ray spectral modelling is described in Sect. 4. We discuss the implications of the results in Sect. 5.
2. Multiwavelength observations and data analysis
The huge X-ray flare of Mkn 421 in April 2013 (2013 April 10 to 21; MJD 56 392−56 403) was simultaneously observed by the NuSTAR and Swift X-ray and UV telescopes. The γ-ray behaviour of this source during this flare was obtained by analysing Fermi-LAT observations. In addition, we included the X-ray observations by the Monitor of All-sky X-ray Image (MAXI) telescope and optical observations by SPOL CCD Imaging/ Spectropolarimeter at Steward Observatory for the present study. The analysis procedures of these observations are described below.
2.1. Fermi-large area telescope observations
The Fermi-LAT data used in this work were collected covering the period of the X-ray outburst (MJD 56 390−56 403). The standard data analysis procedure as mentioned in the Fermi-LAT documentation1 was employed. Events belonging to the energy range 0.2−300 GeV and SOURCE class were used. To select good time intervals, a filter “DATA_QUAL>0” && “LAT_CONFIG==1” was chosen, and only events with zenith angles smaller than 105° were selected to avoid contamination from the Earth limb γ-rays. The Galactic diffuse emission component gll_iem_v05_rev1.fits and an isotropic component iso_source_v05_rev1.txt were used as background models. The unbinned likelihood method included in the pylikelihood library of Science Tools (v9r33p0) and the post-launch instrument response functions P7REP_SOURCE_V15 were used for the analysis. All the sources lying within 10° region of interest (ROI) centred at the position of Mkn 421 and defined in the second Fermi-LAT catalogue (Nolan et al. 2012) were included in the xml file. All the parameters except for the scaling factor of the sources within the ROI were allowed to vary during the likelihood fitting. For sources between 10° to 20° from the centre, all parameters were kept frozen at the default values. The source was modelled by a power law as in the 2FGL catalogue.
Details of NuSTAR pointings.
Details of Swift pointings.
2.2. NuSTAR observations
NuSTAR (Harrison et al. 2013) features the first focussing X-ray telescope to extend high sensitivity beyond 10 keV. There were 11 NuSTAR pointings at the dates of interest, the details of which are given in Table 1. The NuSTAR data were processed with the NuSTARDAS software package v.1.4.1 available within HEASOFT package (6.16). The latest CALDB (v.20140414) was used. After running nupipeline v.0.4.3 on each observation, nuproducts v.0.2.8 was used to obtain the light curves and spectra. Circular regions of 12 pixels centred on Mkn 421 and of 40 pixels centred on 165.96, 38.17 were used as source and background regions, respectively. The spectra from the two detectors A and B were combined using addascaspec and were then grouped (using the tool grppha v.3.0.1) to ensure a minimum of 30 counts in each bin. To achieve strict simultaneity with Swift-XRT observations, observation id 60002023025 was broken into four parts 56 393.15591890 to 56 393.29538714, 56 393.29538714 to 56 393.91093765, 56 393.91093765 to 56 393.96788711, and 56 393.96788711 to 56 394.37822500 MJD.
2.3. Swift observations
There were 15 Swift pointings at the dates of interest, the details of which are given in Table 2. Publicly available daily binned source counts were taken from the Swift-BAT webpage2.
The XRT data (Burrows et al. 2005) were processed with the XRTDAS software package (v.3.0.0) available within HEASOFT package (6.16). Event files were cleaned and calibrated using standard procedures (xrtpipeline v.0.13.0), and xrtproducts v.0.4.2 was used to obtain the light curves and spectra. Standard grade selections of 0−12 in the Windowed Timing (WT) mode were used. Circular regions of 20 pixels centred on Mkn 421 (at 166.113 and Dec 38.208) and of 40 pixels centred at 166.15, 38.17 were used as source and background regions, respectively. For the observations affected by pileup (counts >100 c/s) (Romano et al. 2006), an annular region with an inner radius of 2 pixels and an outer radius of 20 pixels was taken as the source region. The light curves were finally corrected for telescope vignetting and PSF losses with the tool xrtlccorr v.0.3.8. The spectra were grouped to ensure a minimum of 30 counts in each bin by using the tool grppha v.3.0.1.
Swift-UVOT (Roming et al. 2005) operated in imaging mode during this period, and for most of the observations, cycled through the UV filters UW1, UW2, and UM2. The tool uvotsource v.3.3 was used to extract the fluxes from each of the images using aperture photometry. The observed magnitudes were corrected for Galactic extinction (EB−V = 0.019 mag) using the dust maps of Schlegel et al. (1998) and converted to flux units using the zero-point magnitudes and conversion factors of Breeveld et al. (2011). The tool flx2xsp v.2.1 was used to convert the fluxes to pha files for use in XSPEC.
 |
Fig. 1 Multiwavelength light curve during MJD 56 390 to 56 403 showing: in panel 1 the V-band magnitude, in panel 2 the UV flux in mJy, in panel 3 the degree and angle of optical polarization, in panel 4 the Swift-XRT flux in counts/s, in panel 5 the MAXI flux in counts/s, in panel 6 the NuSTAR flux in counts/s, in panel 7 the Swift-BAT flux in counts/s, and in panel 8 the Fermi-LAT flux in ph/cm2/s. One Swift-XRT (or NuSTAR) point is plotted for each snapshot. |
 |
Fig. 2 Hardness ratio as observed by NuSTAR FPMA. The upper panel shows the hardness ratio, and the lower panel the flux(counts/s). There is a trend of spectral hardening with flux. |
 |
Fig. 3 Thirteen time bins for which spectra have been extracted. |
Reduced χ2 values for the various time bins (f1 to f13), as marked in Fig. 3, for the different models of the photon spectrum (broken power-law (bknpo) and log parabola (logpar)) and the particle spectrum (cutoff power law, bknpo and log parabola), respectively.
Best-fit parameters of the log parabolic photon and particle spectrum.
 |
Fig. 4 Cross plot of parameters for the logparabolic photon (green stars) and particle (red circles) spectrum. The peak curvature Ep clearly anti-correlates with alpha and strongly correlates with the flux. However, there is no correlation between Ep and the curvature parameter β, or between β and α. |
 |
Fig. 5 Cross plot of the two indices of the broken power-law particle spectrum. The green points are not from combined spectrum, but are NuSTAR only and Swift-XRT only (see text). |
 |
Fig. 6 Observed X-ray and UV spectrum during two states. While the X-ray flux changes by more than a factor of 10, the UV flux remains constant. |
 |
Fig. 7 Fitted spectrum and residuals for the three models for state f6. The differences start showing up above 50 keV. |
2.4. Other multiwavelength data
Publicly available daily binned source counts were plotted for MAXI3. As a part of the Fermi multiwavelength support program, the SPOL CCD Imaging/Spectropolarimeter at the Steward Observatory at the University of Arizona (Smith et al. 2009) regularly observes Mkn 421. The publicly available optical V-band photometric and linear polarization data were downloaded from their website4.
3. Multiwavelength temporal study
The multiwavelength light curve for the ten-day period is plotted in Fig. 1 from optical to gamma ray energies, along with the optical polarization measurements. While there were two huge flares in X-rays (on MJD 56 395 and 56 397), where the flux increased by a factor of 10, the fluxes in the other bands were not very variable on the timescale of days. We computed the z-transformed discrete correlation using a freely available Fortran 90 code with the details of the method employed described in Alexander (1997). We found no lag between the soft (0.3−10 keV, Swift-XRT) and the hard X-ray (3.0−79 keV NuSTAR) bands. There is no correlation seen between the UV flux and the X-ray flux, (zdcfmax = 0.62 ± 2.3, at a lag of 2.2 days). Moreover, while the UV flux does not show a correlation with the optical polarization (zdcfmax = 0.61 ± 1.1, at a lag of 2.4 days), the X-ray flux shows a tighter correlation (zdcfmax = 0.81 ± 0.6, at a lag of 3.5 days) with the latter. There was also a strong change in the angle of polarization during the two X-ray flares.
The hardness ratios (computed here as the ratio between the 10–79 keV count rate and the 3–10 keV count rate Tomsick et al. 2014) are plotted in Fig. 2. A trend of spectral hardening with increasing flux (Spearman rank correlation, rs = 0.58, p = 5.0 × 10-8) is observed, and the same is often reported for this source (e.g. Baloković et al. 2013; Brinkmann et al. 2001). Moreover, the correlation is much tighter during the rising part of the two flares (rs = 0.92, p = 4.0 × 10-5). These interesting features allow us to perform a more detailed spectral study, which we describe in Sect. 4.
The fractional variability amplitude parameter Fvar (Vaughan et al. 2003; Chitnis et al. 2009), computed on daily timescales, was used to quantify the multiwavelength variability. It is calculated as 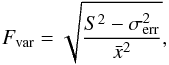 (1)where
(1)where 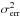 is the mean square error,
is the mean square error, 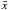 the unweighted sample mean, and S2 the sample variance. The error on Fvar is given as
the unweighted sample mean, and S2 the sample variance. The error on Fvar is given as 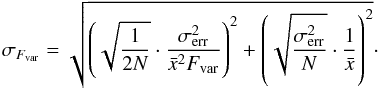 (2)Here, N is the number of points.
(2)Here, N is the number of points.
The variability amplitude is highest for the X-ray bands (Fvar ~ 0.75 ± 0.10) and significantly lower for the UV bands (Fvar ~ 0.08 ± 0.02), suggesting that the emission may probably arise from different components in the two bands. The variability in the GeV range is also weak (Fvar ~ 0.16 ± 0.07). This contradicts the general trend found in blazars that Fvar is highest for the γ-ray band and decreases with frequency (Zhang et al. 2005; Paliya et al. 2015).
We scanned the Swift-XRT and the NuSTAR light curves for the shortest flux-doubling timescale using the following equation (Foschini et al. 2011): 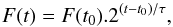 (3)where F(t) and F(t0) are the fluxes at time t and t0, respectively, and τ is the characteristic doubling or halving timescale. The fastest observed variability in the NuSTAR band is 1.69 ± 0.08 h between MJD 97.06438 to 97.08573. This is similar to the very fast variability observed in this source with the Beppo-SAX (Fossati et al. 2000a).
(3)where F(t) and F(t0) are the fluxes at time t and t0, respectively, and τ is the characteristic doubling or halving timescale. The fastest observed variability in the NuSTAR band is 1.69 ± 0.08 h between MJD 97.06438 to 97.08573. This is similar to the very fast variability observed in this source with the Beppo-SAX (Fossati et al. 2000a).
This study was only performed for those periods where the flux difference was significant, at least at the 3σ level.
4. X-ray spectral analysis
The close simultaneity between Swift-XRT and NuSTAR observations allows us to perform a joint spectral fitting using XSPEC package v.12.8.2. The time periods that were fitted together are shown in Fig. 3. The bin widths were selected as one bin per Swift-XRT observation (except for Obs. id. 00035014062 and 00035014069, which lasted only for a few minutes), leading to 13 time bins that we denote as f1–f13. The state f3 has no Swift-XRT data, whereas the state f13 has no NuSTAR data. Again in Table 3 we list the Swift-XRT and corresponding NuSTAR data that were combined.
While fitting the broadband X-ray spectrum (0.3−79 keV), the XRT and the NuSTAR spectral parameters were tied to each other, except for the relative normalization between the two instruments. To correct for the line-of-sight absorption of soft X-rays due to the interstellar gas, the neutral hydrogen column density was fixed at NH = 1.92 × 1020 cm-2 (Kalberla et al. 2005).
4.1. Fitting the photon spectrum
It is known that the X-ray spectrum of Mkn 421 shows significant curvature (Fossati et al. 2000b; Massaro et al. 2004), and consistently, we also note that the data cannot be fitted satisfactorily by a simple power law. On the other hand, a power law with an exponential cutoff gives a much steeper curvature than observed, yielding unacceptable fits. A sharp broken power-law also gives high χ2 values in most cases, which suggests a smooth intrinsic curvature in the spectrum. Following (Massaro et al. 2004; Tramacere et al. 2007), we therefore fitted the observed spectrum with a log parabola given by 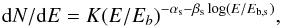 (4)where αs gives the spectral index at Eb,s. The point of maximum curvature, Ep,s is given by
(4)where αs gives the spectral index at Eb,s. The point of maximum curvature, Ep,s is given by 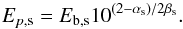 (5)During fitting, Eb,s was fixed at 1 keV. In Table 3 we list the resulting reduced χ2s for the case of the broken power-law and the log parabola models; while in Table 4 we report the fit parameters corresponding to the latter model.
(5)During fitting, Eb,s was fixed at 1 keV. In Table 3 we list the resulting reduced χ2s for the case of the broken power-law and the log parabola models; while in Table 4 we report the fit parameters corresponding to the latter model.
Interestingly, there is a strong anti-correlation between αs and flux (rs = −0.98, p< 2.2 × 10-16) and a strong correlation between flux and Ep,s (rs = 0.97, p< 2.2 × 10-16), which implies that during flares, the spectral index at 1 keV hardens and the peak of the spectrum shifts to higher energies. This behaviour of the source has often been reported (Massaro et al. 2004, 2008). In addition, there was no correlation between αs and βs (rs = −0.35, p = 0.24), which was reported by Massaro et al. (2004). We also noted that there is no correlation observed between the curvature parameter β and the peak of the curvature Ep (rs = 0.63, p = 0.02). These cross plots are shown in Fig. 4.
4.2. Emitting particle distribution
The excellent spectral resolution of NuSTAR gives us an unprecedented view of the high-energy X-ray behaviour beyond 20 keV. Coupled with Swift-XRT, we have, for the first time, an uninterrupted, well-resolved spectrum from 0.3−79 keV. This allows us to go beyond only fitting the photon spectrum with various spectral forms. Instead, we here study the underlying particle distributions that give rise to the observed photon spectrum.
We considered the case where X-ray emission arises from a relativistic distribution of electrons emitting synchrotron radiation. The electrons are confined within a spherical zone of radius R filled with a tangled magnetic field B. As a result of the relativistic motion of the jet, the radiation is boosted along our line of sight by a Doppler factor δ. A good sampling of the entire SED from radio to γ-rays allows one to perform a reasonable estimation of these physical parameters (Tavecchio et al. 1998). For synchrotron emission alone, R, B, and δ will only decide the spectral normalization. On the other hand, the shape of the observed spectrum is determined by the corresponding form of the underlying particle spectrum. To obtain further insight into the emitting particle distribution, we developed synchrotron emission models with different particle distribution and incorporated them into XSPEC spectral fitting software. In particular, we here considered the following particle distributions:
(i): Simple power law (SPL): in this case, we assume the electrondistribution to be a simple power law with a sharp high-energycutoff, given by 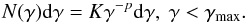 (6)Here γmc2 is the energy of the emitting electron, p is the particle spectral index, K is the normalization, and γmaxmc2 is the cut-off energy. Of these parameters, p and γmax are chosen as the free parameters.
(6)Here γmc2 is the energy of the emitting electron, p is the particle spectral index, K is the normalization, and γmaxmc2 is the cut-off energy. Of these parameters, p and γmax are chosen as the free parameters.
(ii): Cutoff power law (CPL): here the underlying particle distribution is assumed to be a power law with index p and an exponential cutoff above energy γmmc2 given by 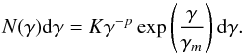 (7)For this distribution, p and γm are chosen as the free parameters.
(7)For this distribution, p and γm are chosen as the free parameters.
(iii): Broken power-law (BPL): the particle distribution in this case is described by a broken power-law with indices p1 and p2 with a break at energy γb given by 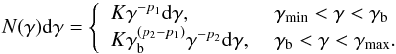 (8)Here, p1, p2 and γb are chosen as the free parameters.
(8)Here, p1, p2 and γb are chosen as the free parameters.
(iv): Log parabola (LP): for this case, the particle distribution is chosen to be a log parabola, given by 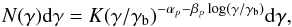 (9)with αp and βp chosen as the free parameters.
(9)with αp and βp chosen as the free parameters.
5. Discussions and conclusions
We performed a detailed study of the bright X-ray flare of Mkn 421 observed in April 2013 along with information available at other wavebands. The X-ray flare is not significantly correlated with the UV and, in addition, the variability amplitude of the former is considerably larger than the latter. This suggests that the X-ray and UV emission probably belongs to emission from different particle distributions.
A detailed spectral analysis of the X-ray observations over different time periods during the flare suggests that the emission arises from a synchrotron mechanism from log parabola particle distribution. Although this particle distribution can be statistically more appealing, a broken power-law particle spectrum cannot be excluded. Furthermore, we extended the best-fit LP and BPL particle distributions to low energies and predicted the UV synchrotron flux. During low X-ray flux states, the predicted UV flux agrees reasonably well with the observed flux. However, at high X-ray flux states, the observed UV flux is significantly higher that the predicted one by a factor of 2−50, with the larger deviations corresponding to the LP model. In addition, the variability of the predicted UV flux is much higher (Fvar,pred = 1.10 ± 0.10) than the one obtained from the observed UV flux. This study again questions the similar origin of X-ray and UV emission.
A plausible interpretation of this inconsistency between X-ray and UV fluxes can be made by associating the UV emission from the putative accretion disk. However, such thermal emission from the disc was never a important contribution in the UV bands for Mkn 421 (Abdo et al. 2011), and the UV spectral detail is not sufficient to support this interpretation (Fig. 6). Alternatively, the underlying particle distribution might be more complex than those we studied. Nevertheless, such a particle distribution demands a concave spectrum, which is not possible with our present understanding of particle acceleration (Sahayanathan 2008). Hence, we attribute this unusual X-ray – UV behaviour of the source to a two-population electron distribution. A similar conclusion was obtained by Aleksić et al. (2015) by studying a flare of the same source in March 2010. Such different electron distributions can be obtained if multiple emission regions are involved in the emission process. If the flaring region is located at the recollimation zone of the jet, then a compact emission region can be created where the recollimation shock meets the jet axis (Tavecchio et al. 2011; Kushwaha et al. 2014). Alternatively, episodic particle acceleration as suggested by Perlman et al. (2006) might be the reason for the second particle distribution. Perlman et al. (2005) have shown that this can also explain the relatively weaker variability of the optical/UV bands as compared to the X-ray.
Pian et al. (2014) studied the same flare, starting from MJD 56 397, with an emphasis on INTEGRAL and Fermi-LAT data. They also found trends of spectral hardening with flux. However, unlike our results, the INTEGRAL spectral data could be well fitted by a broken power-law spectral form. They modelled the broadband SED with a simple one-zone SSC model and required strong variations in the magnetic fields and Doppler factors to sucessfully fit the SED of different states. In addition, our results do not match those of Massaro et al. (2004) because we found no correlation between αs and βs. Thus, our results are inconsistent with statistical particle acceleration.
Our results indicate the potential of using broadband X-ray data to constrain the underlying particle spectrum and distinguish separate variable spectral components, especially if there are simultaneous data in other wavebands. Figure 7 shows the energy spectrum (in νFν) and the residuals for the BPL, the CPL and the LP for the state f6. While the residuals show structure as a function of energy for energies <0.7 keV, especially for the CPL and the BPL, the data and model agree within 10% at these energies. Moreover, we also implemented a fit at energies <0.7 keV and verified that our results do not change significantly. Thus, this effect is unlikely to be a serious source of error in this work. More importantly, there is a clear systematic deviation from the data for the BPL and the CPL at the higher energies, beyond 50 keV. The forthcoming satellite ASTROSAT (Singh et al. 2014), with its wide-band X-ray coverage and simultaneous optical-UV measurement is expected to enable significant breakthroughs in this field.
Acknowledgments
A. Sinha would like to thank Sunder Sahayanathan from the Bhabha Atomic Research Center, Mumbai, for helpful discussions and comments. This research has made use of data, software and/or web tools obtained from NASAs High Energy Astrophysics Science Archive Research Center (HEASARC), a service of Goddard Space Flight Center and the Smithsonian Astrophysical Observatory. Part of this work is based on archival data, software, or online services provided by the ASI Science Data Center (ASDC). This research has made use of the XRT Data Analysis Software (XRTDAS) developed under the responsibility the ASI Science Data Center (ASDC), Italy, and the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center (ASDC, Italy) and the California Institute of Technology (Caltech, USA). Data from the Steward Observatory spectropolarimetric monitoring project were used. This program is supported by Fermi Guest Investigator grants NNX08AW56G, NNX09AU10G, and NNX12AO93G.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 736, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Acciari, V. A., Aliu, E., Aune, T., et al. 2009, ApJ, 703, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, J., Aliu, E., Anderhub, H., et al. 2007, ApJ, 663, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Aleksić, J., Anderhub, H., Antonelli, L. A., et al. 2010, A&A, 519, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Alvarez, E. A., Antonelli, L. A., et al. 2012, A&A, 542, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2015, A&A, 578, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, T. 1997, in Astronomical Time Series, eds. D. Maoz, A. Sternberg, & E. M. Leibowitz, Astrophys. Space Sci. Lib., 218, 163 [Google Scholar]
- Baloković, M., Ajello, M., Blandford, R. D., et al. 2013, Eur. Phys. J. Web Conf., 61, 4013 [CrossRef] [EDP Sciences] [Google Scholar]
- Błażejowski, M., Blaylock, G., Bond, I. H., et al. 2005, ApJ, 630, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Böttcher, M. 2007, Ap&SS, 307, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, in AIP Conf. Ser. 1358, eds. J. E. McEnery, J. L. Racusin, & N. Gehrels, 373 [Google Scholar]
- Brinkmann, W., Papadakis, I. E., den Herder, J. W. A., & Haberl, F. 2003, A&A, 402, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Chitnis, V. R., Pendharkar, J. K., Bose, D., et al. 2009, ApJ, 698, 1207 [NASA ADS] [CrossRef] [Google Scholar]
- Foschini, L., Ghisellini, G., Tavecchio, F., Bonnoli, G., & Stamerra, A. 2011, A&A, 530, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fossati, G., Celotti, A., Chiaberge, M., et al. 2000a, ApJ, 541, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, G., Celotti, A., Chiaberge, M., et al. 2000b, ApJ, 541, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, G., Buckley, J. H., Bond, I. H., et al. 2008, ApJ, 677, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Horan, D., Acciari, V. A., Bradbury, S. M., et al. 2009, ApJ, 695, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, N., Sugimori, K., Kawai, N., et al. 2010, PASJ, 62, L55 [NASA ADS] [Google Scholar]
- Katarzynski, K., Ghisellini, G., Tavecchio, F., et al. 2005, A&A, 433, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krawczynski, H., Sambruna, R., Kohnle, A., et al. 2001, ApJ, 559, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Kushwaha, P., Sahayanathan, S., Lekshmi, R., et al. 2014, MNRAS, 442, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Li, B., Zhang, H., Zhang, X., et al. 2013, Ap&SS, 347, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Lichti, G. G., Bottacini, E., Ajello, M., et al. 2008, A&A, 486, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, E., Perri, M., Giommi, P., & Nesci, R. 2004, A&A, 413, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, F., Tramacere, A., Cavaliere, A., Perri, M., & Giommi, P. 2008, A&A, 478, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., & Giommi, P. 1995, ApJ, 444, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Paliya, V. S., Sahayanathan, S., & Stalin, C. S. 2015, ApJ, 803, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Madejski, G., Georganopoulos, M., et al. 2005, ApJ, 625, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Daugherty, T., Georganopoulos, M., et al. 2006, in Blazar Variability Workshop II: Entering the GLAST Era, eds. H. R. Miller, K. Marshall, J. R. Webb, & M. F. Aller, ASP Conf. Ser., 350, 191 [Google Scholar]
- Pian, E., Türler, M., Fiocchi, M., et al. 2014, A&A, 570, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Punch, M., Akerlof, C. W., Cawley, M. F., et al. 1992, Nature, 358, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, Shan-jie, Zhang, Xi-zhen, Witzel, A., et al. 1998, Chin. Astron. Astrophys., 22, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Campana, S., Chincarini, G., et al. 2006, A&A, 456, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roming, P. W. A., Kennedy, T. E., Mason, K. O., et al. 2005, Space Sci. Rev., 120, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Sahayanathan, S. 2008, MNRAS, 388, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shukla, A., Chitnis, V. R., Vishwanath, P. R., et al. 2012, A&A, 541, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singh, K. P., Tandon, S. N., Agrawal, P. C., et al. 2014, SPIE Conf. Ser., 9144, 1 [NASA ADS] [Google Scholar]
- Smith, P. S., Montiel, E., Rightley, S., et al. 2009, Fermi Symposium, eConf Proceedings C091122 [arXiv:0912.3621] [Google Scholar]
- Tavecchio, F., Maraschi, L., & Ghisellini, G. 1998, ApJ, 509, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., Becerra-Gonzalez, J., Ghisellini, G., et al. 2011, A&A, 534, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomsick, J. A., Nowak, M. A., Parker, M., et al. 2014, ApJ, 780, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Tramacere, A., Giommi, P., Massaro, E., et al. 2007, A&A, 467, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramacere, A., Giommi, P., Perri, M., Verrecchia, F., & Tosti, G. 2009, A&A, 501, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Ushio, M., Tanaka, T., Madejski, G., et al. 2009, ApJ, 699, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- W., Brinkmann, S., Sembay, R. G., Griffiths, et al. 2001, A&A, 365, L162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y. H., Treves, A., Celotti, A., Qin, Y. P., & Bai, J. M. 2005, ApJ, 629, 686 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Reduced χ2 values for the various time bins (f1 to f13), as marked in Fig. 3, for the different models of the photon spectrum (broken power-law (bknpo) and log parabola (logpar)) and the particle spectrum (cutoff power law, bknpo and log parabola), respectively.
All Figures
 |
Fig. 1 Multiwavelength light curve during MJD 56 390 to 56 403 showing: in panel 1 the V-band magnitude, in panel 2 the UV flux in mJy, in panel 3 the degree and angle of optical polarization, in panel 4 the Swift-XRT flux in counts/s, in panel 5 the MAXI flux in counts/s, in panel 6 the NuSTAR flux in counts/s, in panel 7 the Swift-BAT flux in counts/s, and in panel 8 the Fermi-LAT flux in ph/cm2/s. One Swift-XRT (or NuSTAR) point is plotted for each snapshot. |
| In the text | |
 |
Fig. 2 Hardness ratio as observed by NuSTAR FPMA. The upper panel shows the hardness ratio, and the lower panel the flux(counts/s). There is a trend of spectral hardening with flux. |
| In the text | |
 |
Fig. 3 Thirteen time bins for which spectra have been extracted. |
| In the text | |
 |
Fig. 4 Cross plot of parameters for the logparabolic photon (green stars) and particle (red circles) spectrum. The peak curvature Ep clearly anti-correlates with alpha and strongly correlates with the flux. However, there is no correlation between Ep and the curvature parameter β, or between β and α. |
| In the text | |
 |
Fig. 5 Cross plot of the two indices of the broken power-law particle spectrum. The green points are not from combined spectrum, but are NuSTAR only and Swift-XRT only (see text). |
| In the text | |
 |
Fig. 6 Observed X-ray and UV spectrum during two states. While the X-ray flux changes by more than a factor of 10, the UV flux remains constant. |
| In the text | |
 |
Fig. 7 Fitted spectrum and residuals for the three models for state f6. The differences start showing up above 50 keV. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


