EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 579 (July 2015) A&A, 579 (2015) A125 Full HTML
Free Access
Issue
A&A
Volume 579, July 2015
Article Number A125
Number of page(s) 6
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201526548
Published online 15 July 2015

© ESO, 2015

1. Introduction

Around 180 molecular species have been detected so far in the interstellar medium, and the list is increasing every year. These detections suggest a much richer chemistry than previously expected in the interstellar medium. One of the most complex questions in interstellar chemistry concerns the possible existence of bio-molecules. Undoubtedly, finding bio-molecules in the interstellar medium would have a deep impact on our vision of the origin of life. It is not surprising that so much effort has been devoted to finding amino acids, the basic building blocks of proteins, in astronomical sources. In particular, the simplest amino acid, glycine, has been searched for recursively, although with no success so far (Hollis et al. 1980; Snyder et al. 1983, 2005; Ceccarelli et al. 2000; Hollis et al. 2003a,b; Kuan et al. 2003; Jones et al. 2007; Cunningham et al. 2007).

Nevertheless, there is observational evidence of amino acids in extraterrestrial objects, such as meteorites (Cronin & Pizarello 1997; Ehrenfreund et al. 2001; Glavin et al. 2010; Burton et al. 2013) or comets (Elsila et al. 2009). Furthermore, different experiments have shown the formation of amino acids after UV irradiation of interstellar ice analogues (Bernstein et al. 2002; Muñoz-Caro et al. 2002; Holtom et al. 2005; Elsila et al. 2007). Therefore, even though no conclusive detection of an amino acid in the interstellar medium has been reported, it is conceivable that they could be present in space. A recent three-phase (gas-phase, grain-surface, and bulk-ice) chemical model of hot cores (Garrod 2013) predicts that detection of glycine with instruments like ALMA that have greater sensitivity and spatial resolution could be plausible.

To ascertain whether amino acids could be possible interstellar molecules, a crucial point is how they could be synthesized in the interstellar medium. In view of the experimental results mentioned earlier, a possible way of obtaining amino acids is through reactions on the surface of interstellar dust particles. Different theoretical studies have been carried out on possible synthetic pathways taking place on the surface of interstellar grains leading to precursors of glycine (Woon 2001, 2002a,b; Rimola et al. 2010, 2012). In most of these studies, the reactions that were considered involved radical species.

In addition, amino acids could also be formed through gas phase reactions. Several proposals of different neutral-neutral reactions have been made (Hoyle 1976; Maeda & Ohno 2004a,b, 2006; Basiuk & Kobayashi 2004; Andreazza et al. 2006). In some cases theoretical studies have been carried out (Basiuk & Bogillo 2000; Basiuk 2001) that conclude that these processes are not feasible under interstellar conditions. Ion-molecule reactions are more promising, since in many cases they are more likely to proceed without involving energy barriers. Different ion-molecule processes have been invoked as possible sources of glycine precursors. Experimental (Jackson et al. 2005a,b) and theoretical (Largo et al. 2004, 2008, 2010) studies of the reactions of ammonia cations with formic and acetic acids and of different neutrals with amines have been carried out. Some of these reactions involve significant barriers, whereas other barrier-free processes leading to precursors of glycine are less favorable than other competing channels.

Precursors of glycine and alanine were obtained in experiments involving ion-molecule reactions of hydroxylamine derivatives and carboxylic acids (Blagojevic et al. 2003; Snow et al. 2007). However, a recent theoretical study (Barrientos et al. 2012) has concluded that production of glycine from the reaction of either cationic or protonated hydroxylamine should be fairly inefficient under interstellar conditions, a result which agrees with a recently model developed by Garrod (2013). Therefore, until now there seems to be no successful proposal for a gas-phase reaction that could lead to precursors of interstellar glycine.

In the present work we perform a theoretical study of the viability of the ion-molecule reaction involving protonated aminomethanol and formic acid in space. This reaction has been proposed by other authors as one route toward producing glycine in the interstellar medium (Charnley 1999; Charnley et al. 2001; Kuan et al. 2003). However, to the best of our knowledge, this reaction has not been previously studied theoretically or experimentally. The paper is structured as follows. In the second section, we introduce the computational methods used in our study. Section 3 first presents the protonation of aminomethanol under interstellar conditions, and then the potential energy surface of the reaction of protonated aminomethanol with formic acid is analyzed. In the last section, we summarize the main findings of our study.

2. Computational methods

The characterization of stationary points on the potential energy surface for the reaction of aminomethanol with formic acid employed similar theoretical methods to our previous work on related systems (Barrientos et al. 2012; Largo et al. 2008, 2010), since these methods provide reliable enough results. Geometrical parameters of the different species were obtained at the second-order Moller-Plesset level (MP2) by employing the correlation-consistent polarized valence triple-zeta (cc-pVTZ) basis set developed by Dunning (1989) and Kendall et al. (1992). Harmonic vibrational frequencies were computed at the same level of theory as for the different optimized structures. This allows the zero-point vibrational energy correction (ZPE) to be estimated and the nature of the stationary points located on the potential energy surface to be confirmed, which is either a true minimum (all vibrational frequencies real) or a transition state (one of the frequencies, and just one, imaginary). Intrinsic-reaction coordinate (IRC) calculations (Gonzalez & Schelegel 1990; Gonzalez et al. 1989) were also carried out to check that the transition structures obtained correspond to the desired process.

Electronic energies were refined, over the MP2/cc-pVTZ geometries, through single-point calculations at the coupled-cluster single and double excitation model augmented with a non-iterative triple excitation correction. This is usually referred to as CCSD(T) level (Raghavachari et al. 1989). In these calculations, the aug-cc-pVTZ basis set (Dunning 1989; Kendall et al. 1992), which also includes diffuse functions, was employed.

The same levels of theory were employed in the study of aminomethanol protonation but for these systems, given their size, the MP2 geometry optimization was also carried out with the aug-cc-pVTZ basis set. For these geometries single-point calculations at the CCSD(T) were performed with the aug-cc-pVQZ basis set (correlation-consistent polarized valence quadruple-zeta including diffuse functions Dunning 1989; Kendall et al. 1992). All calculations reported in this work were carried out with the Gaussian-09 program package (Frisch at al. 2010).

3. Results and discussion

Formic acid (HCOOH) is a molecule present in the interstellar medium (Zuckerman et al. 1971; Winnewisser & Churchwell 1975) that can evolve to more complex systems. Despite, aminomethanol (NH2CH2OH) is considered to be a key prebiotic interstellar molecule, it remains undetected in space, in part because of the difficulties synthethizing it in terrestrial laboratories, which makes it difficult to obtain a complete spectroscopic characterization. It has been predicted that aminomethanol is formed in interstellar ices through a radical-radical reaction between NH2 and CH2OH, which are created in the photolysis of ammonia and methanol, respectively (Garrod et al. 2008). The experimental work of Bossa et al. (2009) shows that aminomethanol is formed from the thermal reaction of NH3 and H2CO in interstellar-ice analogues at low temperatures. They conclude that NH2CH2OH should be detectable in the gas phase in warm environments where the icy material is desorbed. From a theoretical point of view, inserting O(1D) into the C-H bond of methyl amine gives aminomethanol as the most energetically favored pathway (Hays & Widicus Weaver 2013). A simulation of the spectrum of aminomethanol based on its optimized geometry has also been reported. Feldmann et al. (2005) analyzed the stability of aminomethanol with respect to the loss of one water molecule and its conversion to methanimine. The calculated barrier height (about 55 kcal/mol) indicates that aminomethanol is stable in relation to this process. Finally, the water-catalyzed reaction of formaldehyde and ammonia for generating NH2CH2OH has been also studied (Courmier et al. 2005).

3.1. Protonation of aminomethanol

Before analyzing the reaction of protonated aminomethanol with formic acid, we briefly discuss the protonation of aminomethanol. Proton transfer processes are common in the interstellar medium where H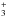+3\hbox{$_{3}^{+}$} is abundant. If aminomethanol is present in the gas phase, two different isomers could be obtained upon protonation: NH3CH2OH+ if protonation takes place at the nitrogen atom, and NH2CH2OH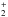+2\hbox{$_{2}^{+}$} when the proton is attached to the oxygen atom.

The most relevant geometrical parameters for both isomers are collected in Fig. 1. Protonation of aminomethanol at the nitrogen atom is slightly more favorable than protonation at oxygen one, since NH3CH2OH+ is located 0.96 kcal/mol lower in energy than NH2CH2OH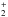+2\hbox{$_{2}^{+}$} at the CCSD(T)/aug-cc-pVQZ//MP2/aug-cc-pVTZ level. Proton affinities for aminomethanol are shown in Table 1. Considering the similar stability of both protonated isomers, the proton affinities are close for protonation at either a nitrogen or an oxygen atom. In both cases, proton affinities are relatively high if comparison is made to the values of some abundant interstellar molecules. For example, the proton affinities of H2, CO, and, C2H2 are 100, 143, and 152 kcal/mol, respectively. Therefore NH2CH2OH should react quite easily in proton-rich interstellar media to give the protonated species.

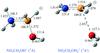thumbnail Fig. 1

MP2/aug-cc-pVTZ optimized geometries for the NH3CH2OH+ and NH2CH2OH+2\hbox{$_{2}^{+}$} isomers. Distances are given in angstroms and angles in degrees.

We have also considered the isomerization process between both isomers of protonated aminomethanol, and the results are summarized in Fig. 2. The conversion barrier of N-protonated into O-protonated aminomethanol is 30.10 kcal/mol (corresponding to a temperature of 15 100 K) at the CCSD(T)/aug-cc-pVQZ//MP2/aug-cc-pVTZ level. Consequently, the two protonated forms may coexist in the interstellar medium, and both isomers could be considered as reactants. A similar situation is reported by Snow et al. (2007) in the case of hydroxylamine.

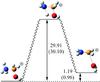thumbnail Fig. 2

Energy profile in kcal/mol for the isomerization of protonated aminomethanol. Relative energies are calculated with respect to N-protonated aminomethanol at the CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ and CCSD(T)/aug-cc-pVQZ//MP2/aug-cc-pVTZ (in parentheses) levels.

It can be seen from Table 1 and Fig. 2 that similar results are obtained at both the CCSD(T)/aug-cc-pVQZ//MP2/aug-cc-pVTZ and CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ levels. Energy differences are in all cases less than 1 kcal/mol; therefore, the second approach seems to be reliable in the study of this kind of system and is employed for characterizing stationary points on the potential energy surface of the reaction between protonated aminomethanol and formic acid.

3.2. Reaction of protonated aminomethanol and formic acid

Table 1

Proton affinities (PA) in kcal/mol for aminomethanol at 298 K calculated at different levels of theory.

Table 2

Relative energies (in kcal/mol) with respect to reactants at the MP2/cc-pVTZ//MP2/cc-pVTZ (ΔE MP2) and CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ (ΔE CCSD(T)) levels of theory for the possible products of the reaction between protonated aminomethanol and formic acid.

In this section we report the theoretical results for the ion-molecule reaction of protonated aminomethanol and formic acid. Table 2 summarizes the calculated reaction energies for different products. We have included only those products that were reached from the reactants.

From a qualitative point of view, the MP2 and CCSD(T) values shown in Table 2 are rather similar. First, we can point out that proton transfer from protonated aminomethanol to HCOOH is endothermic (ΔE = 32.83 kcal/mol at the CCSD(T) level). Therefore, simple proton transfer is not a viable process, and only transformation reactions of formic acid into more complex systems could be feasible processes in the gas phase. One possible product for the reaction between protonated aminomethanol and formic acid is the formation of protonated glycine and elimination of a water molecule. As seen in Table 2, only formation of N-protonated glycine (NH3CH2COOH+ (pg1)), the most stable isomer of protonated glycine (Lattelais et al. 2011), is an exothermic process (ΔE = − 16.46 kcal/mol at the CCSD(T) level). O-protonated glycine NH2CH2C(OH)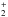+2\hbox{$_{2}^{+}$} (pg3) is located 11.32 kcal/mol above the most stable reactants at the CCSD(T) level, which is an endothermic process. Formation of other protonated isomers of glycine (isomers pg2 and pg4) are also endothermic processes. Protonated glycolic acid, OHCH2C(OH)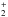+2\hbox{$_{2}^{+}$}, can be obtained from the title reaction by the elimination of a molecule of ammonia, but this product is located 7.92 kcal/mol above the most stable reactants. We have seen in the previous section that the energy difference between both isomers of protonated aminometanol is quite small (about 1 kcal/mol), so the viability of the different processes is the same when both are considered as reactants. We can conclude that from a thermodynamic point of view, only formation of N-protonated glycine is viable in space conditions.

To assess the role of these reactions in the formation of protonated glycine in the interstellar medium, a detailed study of the corresponding potential energy surface is necessary. This allows us to know if a process is barrier free and, therefore, viable from a kinetic point of view. It should be pointed out that even if the reaction between formic acid and protonated aminomethanol is barrierless, additional considerations are needed to establish that this reaction could play an important role in the synthesis of glycine. In this way, a key factor is knowing the branching ratio leading from protonated glycine to glycine and hydrogen atom in the dissociative recombination reaction of protonated glycine with free electrons. An example of the relevance of determining branching ratios is given in the study of the dissociative recombination of protonated methanol (Geppert et al. 2006). We searched for possible intermediates for the reactions of NH3CH2OH+ and NH2CH2OH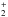+2\hbox{$_{2}^{+}$} with formic acid, and the corresponding transition states connecting these intermediates have also been characterized. All intermediates considered in the present work have vibrational frequencies that are real, thus corresponding to true minima on the potential energy surface. On the other hand, all transition states have just one imaginary frequency that is associated to the corresponding reaction coordinate in each case. In addition, IRC calculations confirm a correct connection. When we take the multiplicity of reactants into account, the reaction takes place on the singlet potential energy surface. The energy profile for the reaction NH3CH2COOH+(NH2CH2C(OH)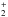+2\hbox{$_{2}^{+}$}) + HCOOH is shown in Fig. 3. The energy values reported in Fig. 3 correspond to the CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ level.

thumbnail Fig. 3

Energy profile in kcal/mol for the reaction of NH3CH2OH+(NH2CH2OH+2\hbox{$_{2}^{+}$}) with HCOOH at the CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ level (including zero-point vibrational energy differences).

The reaction of N-protonated aminomethanol with HCOOH starts with the formation of an ion-molecule complex I1(1A) obtained through the interaction between one of the hydrogen atoms bonded to nitrogen in NH3CH2OH+ with the carbonyl oxygen of formic acid. This intermediate is located −18.80 kcal/mol below the reactants at the CCSD(T)/aug-cc-pVTZ level. Hydrogen-atom migration from CH2 to OH gives I2(1A) that involves transition state TS1(1A). This intermediate evolves to I3(1A) through transition state TS2(1A), where a proton transfer to carbonyl oxygen and simultaneous formation of a C-C bond take place. As can be seen in Fig. 3, both transition states, TS1(1A) and TS2(1A), and intermediate I2(1A) are located clearly above the reactants (64.10 kcal/mol, 50.84 kcal/mol, and 45.65 kcal/mol at the CCSD(T)/aug-cc-pVTZ level, respectively), whereas intermediate I3(1A) is located 11.47 kcal/mol below the reactants at the same level. We have found that both carbon atoms should be activated for a C-C bond to be formed. These activation processes involve a clear energy barrier (above 32 000 K). Intermediate I3(1A) could evolve protonated glycine through patha.1, which can be summarized as 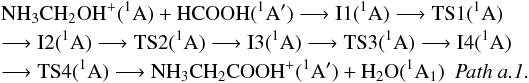NH3CH2OH+(1A)+HCOOH(1A′)−→I1(1A)−→TS1(1A)−→I2(1A)−→TS2(1A)−→I3(1A)−→TS3(1A)−→I4(1A)−→TS4(1A)−→NH3CH2COOH+(1A′)+H2O(1A1)Patha.1.\begin{eqnarray*} &&{\rm NH_{3}CH_{2}OH^{+}(^{1}A) + HCOOH(^{1}A') \longrightarrow I1(^{1}A) \longrightarrow TS1(^{1}A)} \\&&\longrightarrow\rm I2(^{1}A) \longrightarrow TS2(^{1}A) \longrightarrow I3(^{1}A) \longrightarrow TS3(^{1}A) \longrightarrow I4(^{1}A)\\&&\longrightarrow\rm TS4(^{1}A) \longrightarrow NH_{3}CH_{2}COOH^{+}(^{1}A') + H_{2}O(^{1}A_{1})\ \ \textit{Path a.1}. \end{eqnarray*}Once I3(1A) is reached, the simultaneous migration of both a hydrogen atom and the NH3 group through transition state TS3(1A) leads to intermediate I4(1A) located −13.60 kcal/mol below the reactants at the CCSD(T)/aug-cc-pVTZ level. The elimination of one water molecule and subsequent migration of NH3 group involving transition state TS4(1A) give the most stable isomer of protonated glycine (pg1). Transition states TS3(1A) and TS4(1A) are clearly located above the reactants (see Fig. 3). Even if the process described in patha.1 is clearly exothermic, it implies a net activation barrier, so it is not viable under interstellar conditions.

The loss of a NH3 molecule from intermediate I4(1A) leads to protonated glycolic acid (patha.2), which is an endothermic product. From this intermediate, this process follows the same steps as patha.1. It is therefore not allowed in space because it implies significant energy barriers.

Other possible evolution paths have been considered from intermediate I3(1A). Considering this intermediate, the migration of a hydrogen atom from nitrogen to oxygen through transition state TS5(1A) leads to intermediate I5(1A). From I5(1A), two different isomers of protonated glycine (pg2 and pg3) could be reached through pathsb.1 and b.2. In both cases, the full process is endothermic and presents a high energy barrier. Finally, the loss of a H2O molecule from I3(1A) gives another isomer of protonated glycine (pg4) involving transition state TS7(1A) (pathc). This path is clearly not viable under interstellar conditions given its endothermicity and high energy barrier.

When we start the reaction by considering the less stable isomer of protonated aminomethanol, the direct interaction of NH2CH2OH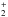+2\hbox{$_{2}^{+}$} with formic acid gives the ion-molecule intermediate I7(1A), which is located 10.19 kcal/mol below the reactants at the CCSD(T)/aug-cc-pVTZ level. As can be seen in Fig. 3, the initial ion-molecule complex is more stable when the reaction is initiated by N-protonated aminomethanol (about 8.61 kcal/mol at the CCSD(T)/aug-cc-pVTZ level). From intermediate I7(1A), the activation of the carbon atom in the NH2CH2OH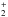+2\hbox{$_{2}^{+}$} fragment takes place through transition state TS8(1A) where one hydrogen atom migrates from a carbon atom to a nitrogen one, reaching the same intermediate that in the case of N-protonated aminomethanol, I2(1A), pathd: 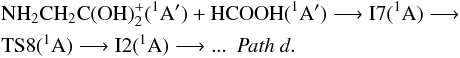NH2CH2C(OH)2+(1A′)+HCOOH(1A′)−→I7(1A)−→TS8(1A)−→I2(1A)−→...Pathd.\begin{eqnarray*} &&{\rm NH_{2}CH_{2}C(OH)_{2}^{+}(^{1}A') + HCOOH(^{1}A') \longrightarrow I7(^{1}A) \longrightarrow}\\ &&\rm TS8(^{1}A) \longrightarrow I2(^{1}A) \longrightarrow ...\ \ \textit{Path d}. \end{eqnarray*}Transition state TS8(1A) is clearly located above the reactants (73.76 kcal/mol or 37 100 K at the CCSD(T)/aug-cc-pVTZ level), therefore subsequent processes imply a net activation barrier and are not viable under interstellar conditions.

From the analysis of the potential energy surface of the reaction between both isomers of protonated aminomethanol and formic acid, we notice that even if formation of the most stable isomer of protonated glycine (pg1) is an exothermic process, a net activation barrier is found in the paths that lead to this product.

4. Conclusions

We have carried out a theoretical study of the reaction between protonated aminomethanol and formic acid. The different intermediate species, as well as the most relevant transition states for these reactions, were characterized. In addition, we considered the protonation of aminomethanol.

Proton affinities for the protonation of aminomethanol either in a nitrogen or an oxygen atom are relatively high (210.31 and 209.35 kcal/mol at the CCSD(T)/aug-cc-pVQZ level, respectively), therefore NH2CH2OH should react quite easily in proton-rich interstellar media to yield the protonated species. The conversion barrier of N-protonated into O-protonated aminomethanol is calculated to be 15 100 K at the CCSD(T)/aug-cc-pVQZ level. Consequently, the two protonated forms may coexist in the interstellar medium, and both isomers could be considered as reactants.

A priori, and just from a thermodynamic analysis, the reaction between protonated aminomethanol and formic acid to give N-protonated glycine (pg1) should be feasible under interstellar conditions, since it is an exothermic process (ΔE = − 16.46 kcal/mol at the CCSD(T)/aug-cc-pVTZ level). A detailed study of the corresponding potential energy surface was reported to explore the viability of these reactions in the interstellar medium and their possible role in forming protonated glycine in space. From the analysis of the potential energy surface we can conclude that even if formation of the most stable isomer of protonated glycine is an exothermic process, a significant net activation barrier (about 64 kcal/mol at the CCSD(T)/aug-cc-pVTZ level corresponding to a temperature of 32 000 K) is found in the paths leading to this product.

Therefore, we conclude that the reaction of protonated aminomethanol with formic acid, which has been invoked as a possible source of interstellar glycine, does not seem viable in the interstellar medium. This particular case is a clear example that a theoretical detailed study of the potential energy surface is needed to establish the relevance of any process in the interstellar medium.

Acknowledgments

This research has been supported by the Junta de Castilla y León (Spain; Grant No. VA077U13).

References

  1. Andreazza, H. J., Fitzgerald, M., & Bowie, J. H. 2006, Org. Biomol. Chem., 4, 2466 [CrossRef] [Google Scholar]
  2. Barrientos, C., Redondo, P., Largo, L., Rayon, V. M., & Largo, A. 2012, ApJ, 748, 99 [NASA ADS] [CrossRef] [Google Scholar]
  3. Basiuk, V. A. 2001, J. Phys. Chem. A, 105, 4252 [CrossRef] [Google Scholar]
  4. Basiuk, V. A., & Bogillo, V. I. 2000, Adv. Space Res., 30, 1439 [NASA ADS] [CrossRef] [Google Scholar]
  5. Basiuk, V. A., & Kobayashi, Y. 2004, Int. J. Quantum Chem., 99, 92 [CrossRef] [Google Scholar]
  6. Bernstein, M. P., Dworkin, J. P., Sandford, S. A., Cooper, G. W., & Allamandola, L. J. 2002, Nature, 416, 401 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Blagojevic, V., Petrie, S., & Bohme, D. K. 2003, MNRAS, 339, L7 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bossa, J. B., Theule, P., Duvernay, F., & Chiavassa, T. 2009, ApJ, 707, 1524 [NASA ADS] [CrossRef] [Google Scholar]
  9. Burton, A. S., Elsila, J. E., Hein, J. E., et al. 2013, Meteorit. Planet. Sci., 48, 390 [NASA ADS] [CrossRef] [Google Scholar]
  10. Ceccarelli, C., Loinard, L., Castets, A., Faure, A., & Leffloch, B. 2000, A&A, 362, 1122 [NASA ADS] [Google Scholar]
  11. Charnley, S. B. 1999, in The Bridge Between the Big Bang and Biology, ed. F. Giovannelli (Rome: CNR), 139 [Google Scholar]
  12. Charnley, S. B., Ehrenfreund, P., & Kuan, Y.-J. 2001, Spectrochim. Acta A, 57, 685 [Google Scholar]
  13. Courmier, D., Gardebien, F., Minot, C., & St.-Amant, A. 2005, Chem. Phys. Lett., 405, 357 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cronin, J. R., & Pizzarello, S. 1997, Science, 275, 951 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  15. Cunningham, M. R., Jones, P. A., Godfrey, P. D., et al. 2007, MNRAS, 376, 1201 [NASA ADS] [CrossRef] [Google Scholar]
  16. Dunning, T. H. 1989, J. Chem. Phys., 90, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  17. Ehrenfreund, P., Glavin, D. P., Botta, O., Cooper, G., & Bada, J. L. 2001, PNAS, 98, 2138 [Google Scholar]
  18. Elsila, J. E., Dworkin, J. P., Bernstein, M. P., Martin, M. P., & Sandford, S. A. 2007, ApJ, 660, 911 [NASA ADS] [CrossRef] [Google Scholar]
  19. Elsila, J. E., Glavin, D. P., & Dworkin, J. P. 2009, Meteorit. Planet. Sci., 44, 1323 [NASA ADS] [CrossRef] [Google Scholar]
  20. Feldmann, M. T., Widicus, S. L., Blake, G. A., Kent IV, D. R., & Goddard III, W. A. 2005, J. Chem. Phys., 123, 034304 [NASA ADS] [CrossRef] [Google Scholar]
  21. Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2010, Gaussian 09, Gaussian Inc, Wallingford CT [Google Scholar]
  22. Garrod, R. T. 2013, ApJ, 765, 60 [Google Scholar]
  23. Garrod, R. T., Widicus Weaver, S. L., & Herbst, E. 2008, ApJ, 682, 283 [NASA ADS] [CrossRef] [Google Scholar]
  24. Geppert, W. D., Hamberg, M., Thomas, R. D., et al. 2006, Faraday Discuss., 133, 177 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  25. Glavin, D. P., Aubrey, A. D., Callahan, M. P., et al. 2010, Meteorit. Planet. Sci, 45, 1695 [NASA ADS] [CrossRef] [Google Scholar]
  26. Gonzalez, C., & Schelegel, H. B. 1989, J. Chem. Phys., 90, 2154 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gonzalez, C., & Schelegel, H. B. 1990, J. Phys. Chem., 94, 5523 [CrossRef] [Google Scholar]
  28. Hays, B. M., & Widicus Weaver, S. L. 2013, J. Phys. Chem. A, 117, 7142 [NASA ADS] [CrossRef] [Google Scholar]
  29. Hollis, J. M., Snyder, L. E., Suenram, R. D., & Lovas, F. J. 1980, ApJ, 241, 1001 [NASA ADS] [CrossRef] [Google Scholar]
  30. Hollis, J. M., Pedelty, J. A., Boboltz, D. A., et al. 2003a, ApJ, 596, L235 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hollis, J. M., Pedelty, J. A., Snyder, L. E., et al. 2003b, ApJ, 588, 353 [NASA ADS] [CrossRef] [Google Scholar]
  32. Holtom, P. D., Bennett, C. J., Osamura, Y., Mason, N. J., & Kaiser, R. I. 2005, ApJ, 626, 940 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hoyle, F., & Wickramasinghe, N. C. 1976, Nature, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]
  34. Jackson, D. M., Stibrich, N. J., Adams, N. G., & Babcock, L. M. 2005a, Int. Mass. Spectrom., 243, 115 [CrossRef] [Google Scholar]
  35. Jackson, D. M., Stibrich, N. J., McLain, J. L., et al. 2005b, Int. Mass. Spectrom., 247, 55 [CrossRef] [Google Scholar]
  36. Jones, P. A., Cunningham, M. R., Godfrey, P. D., & Cragg, D. M. 2007, MNRAS, 374, 579 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kendall, R. A., Dunning, T. H., & Harrison, R. J. 1992, J. Chem. Phys., 96, 6796 [NASA ADS] [CrossRef] [Google Scholar]
  38. Kuan, Y.-J., Charnley, S. B., Huang, H-C., Tseng, W-L., & Kisiel, Z. 2003, ApJ, 593, 848 [NASA ADS] [CrossRef] [Google Scholar]
  39. Largo, A., Redondo, P. & Barrientos, C. 2004, Int. J. Quantum Chem., 98, 355 [Google Scholar]
  40. Largo, L., Rayón, V. M., Barrientos, C., Largo, A., & Redondo, P. 2008, J. Chem. Theory Comput., 4, 2085 [CrossRef] [Google Scholar]
  41. Largo, L., Redondo, P., Rayón, V. M., Largo, A., & Barrientos, C. 2010, A&A, 516, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Lattelais, M., Pauzat, F., Pilme, J., Ellinger, Y., & Ceccarelli, C. 2011, A&A, 532, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Maeda, S., & Ohno, K. 2004a, Chem. Phys. Lett., 398, 240 [NASA ADS] [CrossRef] [Google Scholar]
  44. Maeda, S., & Ohno, K. 2004b, Chem. Lett., 33, 1372 [CrossRef] [Google Scholar]
  45. Maeda, S., & Ohno, K. 2006, ApJ, 640, 823 [NASA ADS] [CrossRef] [Google Scholar]
  46. Muñoz-Caro, G. M., Meierhenrich, U. J., Schutte, W. A., et al. 2002, Nature, 416, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  47. Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, Chem. Phys. Lett., 157, 479 [NASA ADS] [CrossRef] [Google Scholar]
  48. Rimola, A., Sodupe, M., & Ugliengo, P. 2010, Phys. Chem. Chem. Phys., 12, 5285 [CrossRef] [PubMed] [Google Scholar]
  49. Rimola, A., Sodupe, M., & Ugliengo, P. 2012, ApJ, 754, 24 [NASA ADS] [CrossRef] [Google Scholar]
  50. Snow, J. L., Orlova, G., Blagojevic, V., & Bohme, D. K. 2007, J. Am. Chem. Soc., 129, 9910 [CrossRef] [PubMed] [Google Scholar]
  51. Snyder, LE., Hollis, J. M., Suenram, R. D., et al. 1983, ApJ, 268, 123 [NASA ADS] [CrossRef] [Google Scholar]
  52. Snyder, L. E., Lovas, F. J., Hollis, J. M., et al. 2005, ApJ, 619, 914 [NASA ADS] [CrossRef] [Google Scholar]
  53. Winnewisser, G., & Churchwell, E. 1975, ApJ, 200, L33 [NASA ADS] [CrossRef] [Google Scholar]
  54. Woon, D. E. 2001, J. Phys. Chem. A, 105, 9478 [CrossRef] [Google Scholar]
  55. Woon, D. E. 2002a, ApJ, 571, L177 [NASA ADS] [CrossRef] [Google Scholar]
  56. Woon, D. E. 2002b, Int. J. Quant. Chem., 88, 226 [CrossRef] [Google Scholar]
  57. Zuckerman, B., Ball, J. A., & Gottlieb, C. A. 1971, ApJ, 163, L41 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Proton affinities (PA) in kcal/mol for aminomethanol at 298 K calculated at different levels of theory.

In the text
Table 2

Relative energies (in kcal/mol) with respect to reactants at the MP2/cc-pVTZ//MP2/cc-pVTZ (ΔE MP2) and CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ (ΔE CCSD(T)) levels of theory for the possible products of the reaction between protonated aminomethanol and formic acid.

In the text

All Figures

thumbnail Fig. 1

MP2/aug-cc-pVTZ optimized geometries for the NH3CH2OH+ and NH2CH2OH+2\hbox{$_{2}^{+}$} isomers. Distances are given in angstroms and angles in degrees.
In the text
thumbnail Fig. 2

Energy profile in kcal/mol for the isomerization of protonated aminomethanol. Relative energies are calculated with respect to N-protonated aminomethanol at the CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ and CCSD(T)/aug-cc-pVQZ//MP2/aug-cc-pVTZ (in parentheses) levels.
In the text
thumbnail Fig. 3

Energy profile in kcal/mol for the reaction of NH3CH2OH+(NH2CH2OH+2\hbox{$_{2}^{+}$}) with HCOOH at the CCSD(T)/aug-cc-pVTZ//MP2/cc-pVTZ level (including zero-point vibrational energy differences).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.