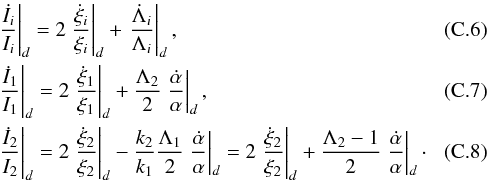| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A128 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526285 | |
| Published online | 16 July 2015 | |
Stability of resonant configurations during the migration of planets and constraints on disk-planet interactions
1
Observatoire de l’Université de Genève,
51 chemin des Maillettes,
1290
Sauverny,
Switzerland
e-mail:
jean-baptiste.delisle@unige.ch
2
ASD, IMCCE-CNRS UMR 8028, Observatoire de Paris, UPMC,
77 Av. Denfert-Rochereau,
75014
Paris,
France
3
CIDMA, Departamento de Física, Universidade de
Aveiro, Campus de
Santiago, 3810-193
Aveiro,
Portugal
Received: 8 April 2015
Accepted: 12 June 2015
We study the stability of mean-motion resonances (MMR) between two planets during their migration in a protoplanetary disk. We use an analytical model of resonances and describe the effect of the disk by a migration timescale (Tm,i) and an eccentricity damping timescale (Te,i) for each planet (i = 1,2 for the inner and outer planets, respectively). We show that the resonant configuration is stable if Te,1/Te,2> (e1/e2)2. This general result can be used to put constraints on specific models of disk-planet interactions. For instance, using classical prescriptions for type-I migration, we show that when the angular momentum deficit (AMD) of the inner orbit is greater than the outer’s orbit AMD, resonant systems must have a locally inverted disk density profile to stay locked in resonance during the migration. This inversion is very atypical of type-I migration and our criterion can thus provide an evidence against classical type-I migration. That is indeed the case for the Jupiter-mass resonant systems HD 60532b, c (3:1 MMR), GJ 876b, c (2:1 MMR), and HD 45364b, c (3:2 MMR). This result may be evidence of type-II migration (gap-opening planets), which is compatible with the high masses of these planets.
Key words: celestial mechanics / planets and satellites: dynamical evolution and stability / planet-disk interactions
© ESO, 2015
1. Introduction
In Delisle et al. (2014), we showed that tidal dissipation raised by the star on two resonant planets can produce three kinds of distinct evolutions depending on the relative strength of the dissipation in both planets. The three different outcomes of this tidal process are systems that stay in resonance, systems that leave the resonance with an increasing period ratio (Pout/Pin), and systems that leave the resonance with a decreasing period ratio. For known near resonant systems, the comparison of the period ratio of the planets with respect to the nominal resonant value helps to put constraints on the tidal dissipation undergone by each planet and thus on the nature of the planets (see Delisle et al. 2014). In this article, we generalize our reasoning to other forms of dissipation, in particular to disk-planet interactions.
Disk-planet interactions can induce migration of the planets (e.g., Goldreich & Tremaine 1979). In the case of convergent migration (i.e., decreasing period ratio), the planets can be locked in resonance (e.g., Weidenschilling & Davis 1985). Two planets that are locked in resonance have their eccentricities excited on the migration timescale (e.g., Weidenschilling & Davis 1985). However, disk-planet interactions also induce exponential eccentricity damping. Depending on the respective timescales of the migration and eccentricity damping, the system can reach a stationary state in which eccentricities stay constant (Lee & Peale 2002). The semi-major axes continue to evolve, but the semi-major axis ratio (or period ratio) stays locked at the resonant value. Recently, Goldreich & Schlichting (2014) have shown that this equilibrium is unstable in the case of the circular restricted three-body problem where the inner planet has negligible mass. This means that after the resonance locking, the eccentricity of the inner planet reaches an equilibrium value but then undergoes larger and larger oscillations around this equilibrium value until the system reaches the resonance separatrix and leaves the resonance. Then, the period ratio is no longer locked at the resonant value, and the convergent migration continues (decreasing period ratio) until the system reaches another resonance. The timescale of the resonance escape is given by the eccentricity damping timescale and is thus short compared to the migration timescale (see Goldreich & Schlichting 2014). Therefore, Goldreich & Schlichting (2014) conclude that when the disk disappears and the migration stops, only a few systems should be observed in resonance. However, this conclusion is mainly based on a particular case in which the mass of the inner planet is much lower than the mass of the outer planet whose eccentricity is negligible, and the migration and damping forces are only undergone by the inner planet. As shown in Delisle et al. (2014), the evolution of a resonant system under dissipation strongly depends on which planet is affected by the dissipation. In this paper we study a more general case in which both planets have masses, eccentricities, and undergo dissipative forces.
In Sect. 2 we introduce the notations and the model of the resonant motion in the conservative case that we developed in Delisle et al. (2014). In Sect. 3 we study the dissipative evolution of resonant planets in a very general framework (Sect. 3.1), and we apply this modeling to disk-planet interactions (Sect. 3.2). In Sect. 4 we show how our model can be used to put constraints on disk properties for observed resonant systems. In Sect. 5 we apply these analytical constraints to selected examples and compare them to numerical simulations. We specifically study HD 60532b, c (3:1 resonance, Sect. 5.1) GJ 876b, c (2:1 resonance, Sect. 5.2), and HD 45364b, c (3:2 resonance, Sect. 5.3).
2. Resonant motion in the conservative case
In the following, we refer to the star as Body 0, to the inner planet as Body 1, and to the outer planet as Body 2. We denote mi as the masses of the three bodies and introduce 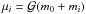 and βi = m0mi/ (m0 + mi), where
and βi = m0mi/ (m0 + mi), where 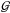 is the gravitational constant. We only consider the planar case in this study.
is the gravitational constant. We only consider the planar case in this study.
In Delisle et al. (2014) we constructed a simplified and integrable model of the resonant motion in the conservative and planar case. The main simplification of this model is to assume that the eccentricity ratio (e1/e2) stays close to the forced eccentricities ratio (e1,ell/e2,ell). These forced eccentricities correspond to the eccentricities at the elliptical fixed point at the resonance libration center. With this assumption, and assuming moderate eccentricities1, the Hamiltonian of the system can be simplified (see Delisle et al. 2014) to the following simple pendulum Hamiltonian 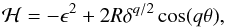 (1)where q is the degree of the resonance (q = k2 − k1 for a k2:k1 resonance), ϵ is the action coordinate that provides a measure of the distance to the exact commensurability, and θ is the unique resonant angle in this simplified model. This angle is a combination of both usual resonant angles (
(1)where q is the degree of the resonance (q = k2 − k1 for a k2:k1 resonance), ϵ is the action coordinate that provides a measure of the distance to the exact commensurability, and θ is the unique resonant angle in this simplified model. This angle is a combination of both usual resonant angles (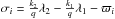 , see Appendix B, Eqs. (B.4) and (B.6), and Delisle et al. 2014). Here, R is a constant that depends on the masses of the bodies and on the considered resonance (see Delisle et al. 2014), and δ is a constant of motion (parameter of the model). We have
, see Appendix B, Eqs. (B.4) and (B.6), and Delisle et al. 2014). Here, R is a constant that depends on the masses of the bodies and on the considered resonance (see Delisle et al. 2014), and δ is a constant of motion (parameter of the model). We have  where Λi is the renormalized circular angular momentum of planet i, and Gi its renormalized angular momentum (see Appendix A and Delisle et al. 2014). The subscript 0 denotes the values at the exact commensurability. The quantities Λi only depend on the semi-major axis ratio α = a1/a2
where Λi is the renormalized circular angular momentum of planet i, and Gi its renormalized angular momentum (see Appendix A and Delisle et al. 2014). The subscript 0 denotes the values at the exact commensurability. The quantities Λi only depend on the semi-major axis ratio α = a1/a2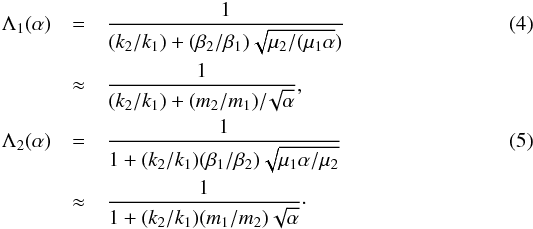 At the exact commensurability, we have
At the exact commensurability, we have 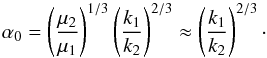 (6)The quantities Gi depend on α and on the planet eccentricities
(6)The quantities Gi depend on α and on the planet eccentricities 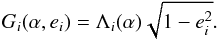 (7)We denote Ii as the renormalized angular momentum deficit (AMD) of planet i (Laskar 1997, 2000)
(7)We denote Ii as the renormalized angular momentum deficit (AMD) of planet i (Laskar 1997, 2000) 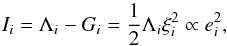 (8)with
(8)with 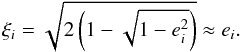 (9)The simplifying assumption introduced in Delisle et al. (2014) implies (see also Appendix B)
(9)The simplifying assumption introduced in Delisle et al. (2014) implies (see also Appendix B) 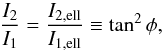 (10)where φ is a constant angle and Ii,ell are values of the renormalized AMD at the center of the resonance (elliptical fixed point, see Delisle et al. 2014). We also denote
(10)where φ is a constant angle and Ii,ell are values of the renormalized AMD at the center of the resonance (elliptical fixed point, see Delisle et al. 2014). We also denote 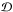 as the renormalized total AMD
as the renormalized total AMD  (11)The parameter δ corresponds to the renormalized total AMD at the exact commensurability (
(11)The parameter δ corresponds to the renormalized total AMD at the exact commensurability (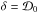 ). Thus, for a resonant system, δ provides a measure of the planet eccentricities (δ ∝ e2, see Eq. (8)). Figure 1 shows the phase space corresponding to Hamiltonian (1). The width of the resonant area is proportional to δq/ 4 ∝ eq/ 2 for a resonance of order q (see Fig. 1). For a resonant system, in the regime of moderate eccentricities, a measure (between 0 and 1) of the relative amplitude of libration (amplitude of libration versus resonance width) is given by (see Delisle et al. 2014)
). Thus, for a resonant system, δ provides a measure of the planet eccentricities (δ ∝ e2, see Eq. (8)). Figure 1 shows the phase space corresponding to Hamiltonian (1). The width of the resonant area is proportional to δq/ 4 ∝ eq/ 2 for a resonance of order q (see Fig. 1). For a resonant system, in the regime of moderate eccentricities, a measure (between 0 and 1) of the relative amplitude of libration (amplitude of libration versus resonance width) is given by (see Delisle et al. 2014) 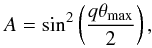 (12)where θmax is the maximum value reached by the resonant angle θ during a libration period (see Fig. 1).
(12)where θmax is the maximum value reached by the resonant angle θ during a libration period (see Fig. 1).
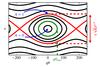 |
Fig. 1 Phase space of a resonance of order q in the simplified pendulum-like approximation (Hamiltonian (1)). θ is the unique resonant angle and ϵ its conjugated action. The separatrix is highlighted in red. The amplitude A (defined with θmax see Eq. (12)) is 0 at the center of the resonance (elliptical fixed point) and 1 at the separatrix. |
Our simplifying assumption (eccentricity ratio close to the forced eccentricities ratio) is verified well when the amplitude of libration is small (A ≪ 1) and the system stays close to the elliptical fixed point. For high amplitude of libration (A ~ 1), the eccentricity ratio undergoes oscillations around the forced value, and our model only provides a first approximation of the motion (see Delisle et al. 2014).
3. Resonant motion in the dissipative case
In this section we describe the evolution of a resonant system undergoing dissipation. The main parameters that have to be tracked during this evolution are the parameter δ, which describes the evolution of the phase space (and of the eccentricities for resonant systems) and the relative amplitude A, which describes the spiraling of the trajectory with respect to the separatrix of the resonance.
3.1. General case
We now consider a dissipative force acting on the semi-major axes and the eccentricities of both planets. We first consider a very general case and do not assume a particular form for this dissipation, except that it acts on a long timescale. The evolution of the system can be described by the three following timescales (which may depend on the eccentricities and semi-major axes of the planets): 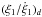 ,
, 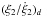 ,
, 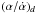 . For sufficiently small eccentricities, we have ξi ≈ ei, and
. For sufficiently small eccentricities, we have ξi ≈ ei, and 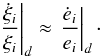 (13)The evolution of the parameter δ that drives the evolution of the phase space (and of the eccentricities for resonant systems) is given by (see Appendix C)
(13)The evolution of the parameter δ that drives the evolution of the phase space (and of the eccentricities for resonant systems) is given by (see Appendix C) ![\begin{eqnarray} \label{eq:ddeltadt} \dot{\delta}|_d &=& 2 \left(\cos^2\phi \left.\frac{\dot{\xi}_1}{\xi_1}\right|_d + \sin^2\phi \left.\frac{\dot{\xi}_2}{\xi_2}\right|_d \right) \mathcal{D}\nonumber \\[2mm] && + \frac{\Lambda_2 - \sin^2\phi}{2} \left.\frac{\dot{\alpha}}{\alpha}\right|_d \mathcal{D} + \frac{q}{k_1} \frac{\Lambda_1\Lambda_2}{2} \left.\frac{\dot{\alpha}}{\alpha}\right|_d\cdot \end{eqnarray}](/articles/aa/full_html/2015/07/aa26285-15/aa26285-15-eq52.png) (14)For a resonant system, the evolution of the relative amplitude of libration reads as (see Delisle et al. 2014, Appendix A)
(14)For a resonant system, the evolution of the relative amplitude of libration reads as (see Delisle et al. 2014, Appendix A) 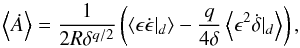 (15)with
(15)with 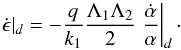 (16)
(16)
3.2. Disk-planet interactions
We now apply Eqs. (14), (15) to the specific case of disk-planet interactions. Because of these interactions, the planets undergo a torque that induces a modification in their orbital elements and subsequent migration in the disk (e.g., Goldreich & Tremaine 1979, 1980). In particular, the angular momentum of each planet evolves on an exponential timescale Tm,i owing to this migration, while eccentricities evolve on an exponential timescale Te,i (e.g., Papaloizou & Larwood 2000; Terquem & Papaloizou 2007; Goldreich & Schlichting 2014):  where Ĝi is the angular momentum of planet i. From these simple decay laws, we can deduce the evolution of the parameters of interest for resonant systems (
where Ĝi is the angular momentum of planet i. From these simple decay laws, we can deduce the evolution of the parameters of interest for resonant systems (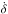 and Ȧ, see Sect. 3.1). We have
and Ȧ, see Sect. 3.1). We have 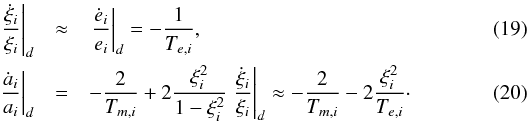 The evolution of the semi-major axis ratio is thus governed by
The evolution of the semi-major axis ratio is thus governed by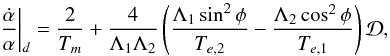 (21)with
(21)with 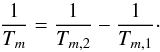 (22)From Eq. (14) we obtain
(22)From Eq. (14) we obtain ![\begin{eqnarray} \dot{\delta}|_d &=& \frac{q}{k_1} \frac{\Lambda_1\Lambda_2}{T_m} + \frac{\Lambda_2-\sin^2\phi}{T_m} \mathcal{D} - 2 \left(\frac{\cos^2\phi}{T_{e,1}}+\frac{\sin^2\phi}{T_{e,2}}\right) \mathcal{D} \nonumber\\ && +\, 2 \frac{q}{k_1} \left(\frac{\Lambda_1\sin^2\phi}{T_{e,2}} - \frac{\Lambda_1\cos^2\phi}{T_{e,1}} \right) \mathcal{D} \label{eq:diskdelta}\nonumber\\ &=& \frac{q}{k_1}\frac{\Lambda_1\Lambda_2}{T_m} - \mathcal{D} \left[ 2 (\Lambda_1+\Lambda_2) \left( \frac{k_2}{k_1} \frac{\cos^2\phi}{T_{e,1}} + \frac{\sin^2\phi}{T_{e,2}} \right)\right.\nonumber\\ && \qquad \left. - \frac{\Lambda_2-\sin^2\phi}{T_m}\right] , \end{eqnarray}](/articles/aa/full_html/2015/07/aa26285-15/aa26285-15-eq62.png) (23)where we neglect second order terms in
(23)where we neglect second order terms in 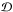 (
(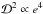 ). We now introduce
). We now introduce 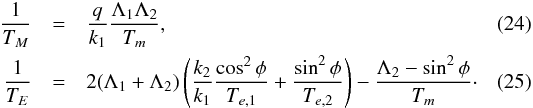 We thus have
We thus have  The damping timescale is often much shorter than the migration timescale (Te,i ≪ Tm,i, e.g., Goldreich & Tremaine 1980), thus
The damping timescale is often much shorter than the migration timescale (Te,i ≪ Tm,i, e.g., Goldreich & Tremaine 1980), thus 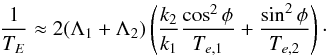 (28)The timescales TE, TM can be expressed using more usual notations
(28)The timescales TE, TM can be expressed using more usual notations 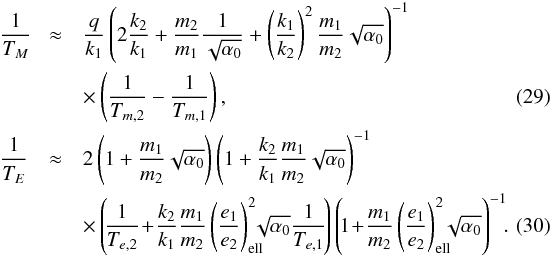 Depending on the values of TM and TE, different evolution scenarios for δ are possible. All these equations remain valid for TM and TE negative. In most cases the disk induces a damping of eccentricities (Te,i> 0, thus TE> 0), but some studies (e.g., Goldreich & Sari 2003) suggest that an excitation of the eccentricities by the disk is possible (Te,i< 0, thus TE< 0). The timescale TM is positive if the period ratio between the planets (P2/P1) decreases (convergent migration). But if the planets undergo divergent migration (P2/P1 increases), TM is negative. This does not depend on the absolute direction (inward or outward) of the migration of the planets in the disk but only on the evolution of their period ratio.
Depending on the values of TM and TE, different evolution scenarios for δ are possible. All these equations remain valid for TM and TE negative. In most cases the disk induces a damping of eccentricities (Te,i> 0, thus TE> 0), but some studies (e.g., Goldreich & Sari 2003) suggest that an excitation of the eccentricities by the disk is possible (Te,i< 0, thus TE< 0). The timescale TM is positive if the period ratio between the planets (P2/P1) decreases (convergent migration). But if the planets undergo divergent migration (P2/P1 increases), TM is negative. This does not depend on the absolute direction (inward or outward) of the migration of the planets in the disk but only on the evolution of their period ratio.
In the case of divergent migration, the planets cannot get trapped in resonance (e.g., Henrard & Lemaitre 1983). The system always ends up with a period ratio higher than the resonant value, and this does not depend on the damping or excitation of eccentricities.
The case of convergent migration is more interesting. If the initial period ratio is higher than the resonant value, the planets can be locked in resonance. This induces an excitation of the eccentricities of the planets (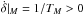 ). If TE< 0 (excitation of eccentricities by the disk) or TE ≫ TM (inefficient damping), δ (as well as the eccentricities) does not stop increasing. When eccentricities reach values that are too high, the system becomes unstable, and the resonant configuration is broken.
). If TE< 0 (excitation of eccentricities by the disk) or TE ≫ TM (inefficient damping), δ (as well as the eccentricities) does not stop increasing. When eccentricities reach values that are too high, the system becomes unstable, and the resonant configuration is broken.
The most common scenario is the case of efficient damping of eccentricities (0 <TE ≲ TM). In this case, δ reaches an equilibrium value (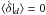 , see Eq. (27))
, see Eq. (27)) 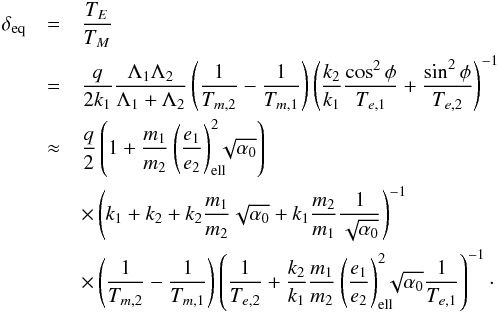 (31)However, as shown by Goldreich & Schlichting (2014) for the restricted three body problem, this equilibrium can be unstable. Even if the parameter δ reaches the equilibrium δeq and the phase space of the system stops evolving, the amplitude of libration can increase until the system crosses the separatrix and escapes from resonance.
(31)However, as shown by Goldreich & Schlichting (2014) for the restricted three body problem, this equilibrium can be unstable. Even if the parameter δ reaches the equilibrium δeq and the phase space of the system stops evolving, the amplitude of libration can increase until the system crosses the separatrix and escapes from resonance.
We now compute the evolution of this amplitude of libration. According to Eq. (15), we need to compute 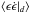 and
and 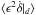 . We have
. We have 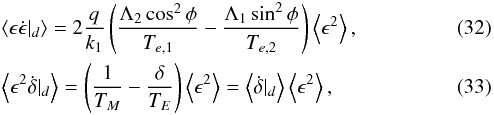 where ⟨ ϵ2 ⟩ can be computed using elliptic integrals (see Delisle et al. 2014)
where ⟨ ϵ2 ⟩ can be computed using elliptic integrals (see Delisle et al. 2014) 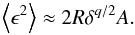 (34)The first term (
(34)The first term (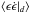 ) does not depend on the migration timescale but only on the damping timescale. The second term (
) does not depend on the migration timescale but only on the damping timescale. The second term (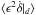 ) vanishes when the system reaches the equilibrium δ = δeq, since
) vanishes when the system reaches the equilibrium δ = δeq, since 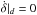 . This is not surprising because the first term describes the evolution of the absolute amplitude of libration ϵ2, while the second one describes the evolution of the resonance width, which does not evolve if the phase space does not evolve (constant δ). Finally, we obtain (see Eq. (15))
. This is not surprising because the first term describes the evolution of the absolute amplitude of libration ϵ2, while the second one describes the evolution of the resonance width, which does not evolve if the phase space does not evolve (constant δ). Finally, we obtain (see Eq. (15)) 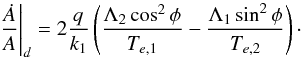 (35)The amplitude of libration increases if
(35)The amplitude of libration increases if 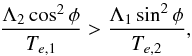 (36)which is equivalent to
(36)which is equivalent to 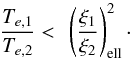 (37)Using ξi ≈ ei, this gives
(37)Using ξi ≈ ei, this gives 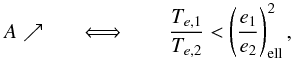 (38)where the eccentricity ratio is evaluated at the elliptical fixed point (ell subscript) at the center of the resonance. In the circular restricted case studied by Goldreich & Schlichting (2014), e2 = 0 and Te,2 = +∞, so the amplitude always increases (Eq. (38)) and the equilibrium is unstable. However, in the opposite restricted case (e1 = 0 and Te,1 = +∞), which was not addressed in Goldreich & Schlichting (2014), the amplitude always decreases (Eq. (38)) leading to a stable equilibrium.
(38)where the eccentricity ratio is evaluated at the elliptical fixed point (ell subscript) at the center of the resonance. In the circular restricted case studied by Goldreich & Schlichting (2014), e2 = 0 and Te,2 = +∞, so the amplitude always increases (Eq. (38)) and the equilibrium is unstable. However, in the opposite restricted case (e1 = 0 and Te,1 = +∞), which was not addressed in Goldreich & Schlichting (2014), the amplitude always decreases (Eq. (38)) leading to a stable equilibrium.
This result is based on our approximation that the eccentricity ratio remains close to the forced value (value at the elliptical fixed point). This is verified for a small amplitude of libration, but when the amplitude increases, the eccentricity ratio oscillates and may differ significantly from the forced value. Our model thus only provides a first approximation of the mean value of this ratio in the case of a high amplitude of libration.
To sum up, the evolution of a resonant pair of planets undergoing disk-planet interactions mainly depends on two parameters: TE/TM (damping vs. migration timescale) and Te,1/Te,2 (damping in inner planet vs. outer planet). The ratio TE/TM governs the equilibrium eccentricities of the planets (see Eqs. (27), (31)). The ratio Te,1/Te,2 governs the stability of this equilibrium (see Eqs. (35), (38)).
4. Constraints on disk properties
In this section, we show how the classification of the outcome of disk-planet interactions can be used to put constraints on the dissipative forces undergone by the planets and thus on some disk properties. More precisely, if a system is currently observed to harbor two planets locked in a mean-motion resonance (MMR), it is probable that this resonant configuration was stable (or unstable but with a very long timescale) when the disk was present. We could imagine that the configuration was highly unstable, but the protoplanetary disk disappeared before the system had time to escape from resonance. However, this would require a fine tuning of the disk disappearing timing. Thus the amplitude of libration was probably either decreasing or increasing on a very long timescale. This induces that 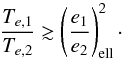 (39)Moreover, a small amplitude of libration is probably the sign of a damping of the amplitude on a short timescale
(39)Moreover, a small amplitude of libration is probably the sign of a damping of the amplitude on a short timescale 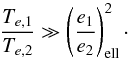 (40)On the opposite, a large amplitude of libration could be the sign of a long timescale of amplitude damping or a long timescale of amplitude excitation. Indeed, if the amplitude was increasing fast, the system should not be observed in resonance. If it was decreasing fast, the observed amplitude should be very small. However, another mechanism may be responsible for the excitation of the amplitude of libration, possibly after the disk disappears (e.g., presence of a third planet in the system). Thus we cannot exclude the case of a fast damping of the amplitude of libration, even in the case of an observed large amplitude,
(40)On the opposite, a large amplitude of libration could be the sign of a long timescale of amplitude damping or a long timescale of amplitude excitation. Indeed, if the amplitude was increasing fast, the system should not be observed in resonance. If it was decreasing fast, the observed amplitude should be very small. However, another mechanism may be responsible for the excitation of the amplitude of libration, possibly after the disk disappears (e.g., presence of a third planet in the system). Thus we cannot exclude the case of a fast damping of the amplitude of libration, even in the case of an observed large amplitude, 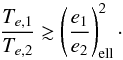 (41)In addition to the constraints obtained from the observed amplitude of libration, the observed values of both eccentricities is also an important information. If the planets did not undergo other sources of dissipation after the disk had disappeared, the present eccentricities should still correspond to the equilibrium ones. For close-in planets, the tides raised by the star on the planets induce a significant dissipative evolution of the system after the disk disappeared (e.g., Delisle & Laskar 2014). Therefore, this reasoning only applies for systems farther from the star for which tidal interactions have a negligible effect on the orbits over the age of the system. We recall that the equilibrium eccentricities are given by (Eq. (31)):
(41)In addition to the constraints obtained from the observed amplitude of libration, the observed values of both eccentricities is also an important information. If the planets did not undergo other sources of dissipation after the disk had disappeared, the present eccentricities should still correspond to the equilibrium ones. For close-in planets, the tides raised by the star on the planets induce a significant dissipative evolution of the system after the disk disappeared (e.g., Delisle & Laskar 2014). Therefore, this reasoning only applies for systems farther from the star for which tidal interactions have a negligible effect on the orbits over the age of the system. We recall that the equilibrium eccentricities are given by (Eq. (31)): 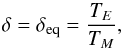 (42)with
(42)with 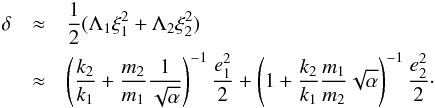 (43)Here, δ can be computed from the known (observed) orbital elements of the planets. Thus, the ratio TE/TM of the damping and migration timescales is constrained by the observations. This ratio depends on the four timescales (Te,1, Te,2, Tm,1, and Tm,2) of the model (see Eq. (31)), which themselves depend on the properties of the disk and the planets. There is a wide diversity of disk models in the literature, which would result in significantly different migration and damping timescales for each planet. Our analytical model is very general and can handle these different models as long as expressions for Te,1, Te,2, Tm,1, and Tm,2 are available.
(43)Here, δ can be computed from the known (observed) orbital elements of the planets. Thus, the ratio TE/TM of the damping and migration timescales is constrained by the observations. This ratio depends on the four timescales (Te,1, Te,2, Tm,1, and Tm,2) of the model (see Eq. (31)), which themselves depend on the properties of the disk and the planets. There is a wide diversity of disk models in the literature, which would result in significantly different migration and damping timescales for each planet. Our analytical model is very general and can handle these different models as long as expressions for Te,1, Te,2, Tm,1, and Tm,2 are available.
We consider here the case of type-I migration to illustrate the possibility of constraining the disk properties for observed systems. Following the prescriptions of Kley & Nelson (2012), we have 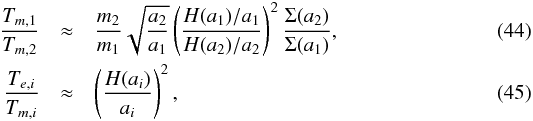 where H(a) is the local disk scale height and Σ(a) ∝ a− βΣ its local surface density. The standard MMSN (minimum mass solar nebula) model assumes Σ ∝ a− 3 / 2 (βΣ = 3 / 2). The disk aspect ratio, H/a, is often assumed to be roughly constant and of the order of 0.05 (e.g., Kley & Nelson 2012). Using these assumptions we obtain
where H(a) is the local disk scale height and Σ(a) ∝ a− βΣ its local surface density. The standard MMSN (minimum mass solar nebula) model assumes Σ ∝ a− 3 / 2 (βΣ = 3 / 2). The disk aspect ratio, H/a, is often assumed to be roughly constant and of the order of 0.05 (e.g., Kley & Nelson 2012). Using these assumptions we obtain 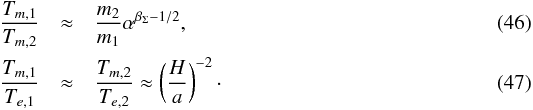 For the sake of brevity, we introduce
For the sake of brevity, we introduce 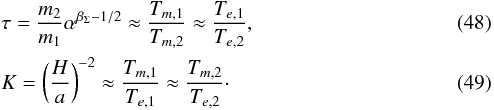 If the system is observed with a small amplitude of libration in the resonance, we have (Eq. (40))
If the system is observed with a small amplitude of libration in the resonance, we have (Eq. (40)) 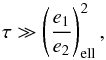 (50)and if the amplitude is large we have (Eq. (41))
(50)and if the amplitude is large we have (Eq. (41)) 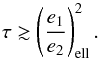 (51)The lower limit we obtain for τ corresponds to an upper limit for the density profile exponent βΣ (see Eq. (48)). In particular, if
(51)The lower limit we obtain for τ corresponds to an upper limit for the density profile exponent βΣ (see Eq. (48)). In particular, if 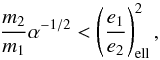 (52)then the density profile of the disk must be inverted (βΣ< 0, i.e., the surface density increases with the distance to the star) for the system to be stable in resonance. The condition of Eq. (52) is roughly equivalent to
(52)then the density profile of the disk must be inverted (βΣ< 0, i.e., the surface density increases with the distance to the star) for the system to be stable in resonance. The condition of Eq. (52) is roughly equivalent to 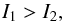 (53)where I1 and I2 are the AMD of both planets.
(53)where I1 and I2 are the AMD of both planets.
We recall that in order to be captured in resonance, the planets must undergo convergent migration (e.g., Henrard & Lemaitre 1983). This puts another constraint on the parameter τ (see Eq. (48)) 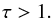 (54)Again, this corresponds to an upper limit for βΣ, and if
(54)Again, this corresponds to an upper limit for βΣ, and if  (55)then the density profile of the disk must be inverted (βΣ< 0) for the planets to undergo convergent migration. The condition of Eq. (55) is roughly equivalent to
(55)then the density profile of the disk must be inverted (βΣ< 0) for the planets to undergo convergent migration. The condition of Eq. (55) is roughly equivalent to 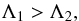 (56)where Λ1 and Λ2 are the circular angular momenta of both planets.
(56)where Λ1 and Λ2 are the circular angular momenta of both planets.
The constraint provided by the observation of the equilibrium eccentricities reads as (see Eq. (31)) 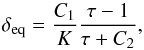 (57)with
(57)with 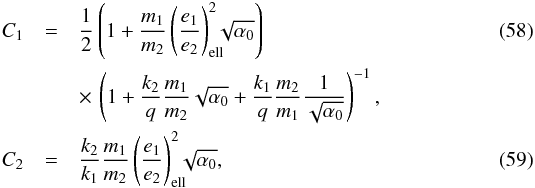 and δeq is given by Eq. (43). We thus have
and δeq is given by Eq. (43). We thus have 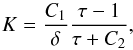 (60)where C1, C2, and δ can all be derived from the observations. We note that K is an increasing function of τ (Eq. (60)), so our analytical criterion for stability provides a lower bound for both τ and K.
(60)where C1, C2, and δ can all be derived from the observations. We note that K is an increasing function of τ (Eq. (60)), so our analytical criterion for stability provides a lower bound for both τ and K.
5. Application to observed resonant systems
In the following we apply our analytical criteria to systems that are observed in resonance. We also performed N-body simulations with the additional migration and damping forces exerted by the disk on the planets. We used the ODEX integrator (e.g., Hairer et al. 2010), and the dissipative timescales Tm,i (angular momentum evolution) and Te,i (eccentricity evolution) are fixed for each planet and each simulation.
Many multiplanetary systems are observed close to different MMR (period ratio close to a resonant value). However, only a few of them have a determination of the planets orbital parameters that is precise enough to distinguish between resonant motion and near-resonant motion. To our knowledge, all known resonant planet pairs are giant planets (better precision of orbital parameters). We thus selected three of these resonant giant planet pairs to illustrate our model.
Giant planets are believed to undergo type-II migration. Our analytical model is very general and can take any prescription for the evolution of the angular momentum and the eccentricity of each planet into account. We did not find a simple analytical prescription for type-II migration in the literature. Indeed type-II migration is a more complex (nonlinear) mechanism than type-I migration, and it is not yet well understood. In particular, the timescale of type-II migration is still being discussed (e.g., Duffell et al. 2014; Dürmann & Kley 2015). However, the effect of type-II migration is expected to be similar to type-I migration (i.e., inward migration and damping of eccentricities, e.g., Bitsch & Kley 2010). The main difference is that the disk profile is affected by the presence of the planets (gap around the planets), so the timescales of migration and damping are slowed down. We thus chose to apply type-I migration prescriptions for our study of these giant planets resonant systems as a first approximation.
Orbital parameters of HD 60532b,c used in this study (taken from Laskar & Correia 2009).
 |
Fig. 2 Semi-major axes, period ratio, eccentricities, eccentricity ratio, and angles evolution for simulations of HD 60532b, c with different dissipation timescale ratios τ = Te,1/Te,2 = Tm,1/Tm,2. The ratio K = Tm,i/Te,i is set according to Eq. (60) to reproduce the observed equilibrium eccentricities. We used τ = +∞, 10, 8, 4 with K = 70, 34, 30, 17, respectively, for the four shown simulations (four columns). The amplitude of libration decreases for the first two simulations (τ = +∞, 10) and increases for the last two (τ = 8, 4). The value given by our analytical criterion for the transition between decreasing and increasing amplitude is τ ~ 9. |
5.1. HD 60532b, c: 3:1 MMR, large amplitude of libration
The star HD 60532 hosts two planets (see Desort et al. 2008) that exhibit a 3:1 period ratio. Laskar & Correia (2009) performed a dynamical study of the system and confirm the 3:1 MMR between the planets with a large amplitude of libration (~40°). We reproduced the orbital elements of the planets (taken from Laskar & Correia 2009) in Table 1. For this system, the forced eccentricity ratio (ratio of eccentricity at the center of the resonance) is 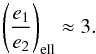 (61)Since the system is observed with a large amplitude of libration, the stability constraint gives (Eq. (51))
(61)Since the system is observed with a large amplitude of libration, the stability constraint gives (Eq. (51)) 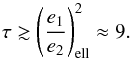 (62)This value is much greater than one, so the condition of convergent migration is fulfilled (see Eq. (54)). This value of τ corresponds to a surface density profile exponent of (see Eq. (48))
(62)This value is much greater than one, so the condition of convergent migration is fulfilled (see Eq. (54)). This value of τ corresponds to a surface density profile exponent of (see Eq. (48))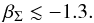 (63)We recall that for the MMSN model, βΣ = 3 / 2. The negative value we obtain corresponds to an inverted density profile. This inverted density profile is very atypical for type-I migration. This result is thus proof that the planets did not undergo classical type-I migration. This is not surprising since giant planets are expected to open a gap and undergo type-II migration. Our results also constrain a type-II migration scenario. Indeed, independently of the migration prescriptions, for the resonance to be stable, the damping of the outer eccentricity must be much more efficient than the inner eccentricity damping (Te,1/Te,2 ≳ 9). One would need prescriptions for type-II migration to relate this result to some disk and/or planets properties.
(63)We recall that for the MMSN model, βΣ = 3 / 2. The negative value we obtain corresponds to an inverted density profile. This inverted density profile is very atypical for type-I migration. This result is thus proof that the planets did not undergo classical type-I migration. This is not surprising since giant planets are expected to open a gap and undergo type-II migration. Our results also constrain a type-II migration scenario. Indeed, independently of the migration prescriptions, for the resonance to be stable, the damping of the outer eccentricity must be much more efficient than the inner eccentricity damping (Te,1/Te,2 ≳ 9). One would need prescriptions for type-II migration to relate this result to some disk and/or planets properties.
From the observed orbital elements we obtain (see Eqs. (43), (58), and (59))  Using τ ≳ 9, the current eccentricities should be reproduced with (see Eq. (60))
Using τ ≳ 9, the current eccentricities should be reproduced with (see Eq. (60)) 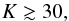 (67)which corresponds to an aspect ratio of (see Eq. (49))
(67)which corresponds to an aspect ratio of (see Eq. (49)) 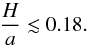 (68)We performed numerical simulations with different values of τ. For each simulation, the value of K is computed using Eq. (60), in order to reproduce the equilibrium eccentricities. We fixed Tm,2 = 5 × 105 yr for all simulations and integrated the system for 106 yr. We thus have Tm,1 = 5 × 105τ yr, Te,2 = 5 × 105/K yr, Te,1 = 5 × 105τ/K yr. The semi-major axes are initially 10 and 22 au, such that the system is initially outside of the 3:1 resonance with a period ratio of about 3.3. Both eccentricities are initially set to 0.001 with anti-aligned periastrons and coplanar orbits. The planets are initially at periastrons (zero anomalies). The evolution of the semi-major axes, the period ratio, the eccentricities, the eccentricity ratio, and the angles are shown in Fig. 2. These simulations confirm our analytical results: for τ< 9, the amplitude of libration decreases, and for τ> 9 the amplitude increases (see Fig. 2).
(68)We performed numerical simulations with different values of τ. For each simulation, the value of K is computed using Eq. (60), in order to reproduce the equilibrium eccentricities. We fixed Tm,2 = 5 × 105 yr for all simulations and integrated the system for 106 yr. We thus have Tm,1 = 5 × 105τ yr, Te,2 = 5 × 105/K yr, Te,1 = 5 × 105τ/K yr. The semi-major axes are initially 10 and 22 au, such that the system is initially outside of the 3:1 resonance with a period ratio of about 3.3. Both eccentricities are initially set to 0.001 with anti-aligned periastrons and coplanar orbits. The planets are initially at periastrons (zero anomalies). The evolution of the semi-major axes, the period ratio, the eccentricities, the eccentricity ratio, and the angles are shown in Fig. 2. These simulations confirm our analytical results: for τ< 9, the amplitude of libration decreases, and for τ> 9 the amplitude increases (see Fig. 2).
Orbital parameters of GJ 876b, c used in this study (taken from Correia et al. 2010).
5.2. GJ 876b, c: 2:1 MMR, small amplitude of libration
GJ 876 is an M dwarf that hosts four planets (Delfosse et al. 1998; Marcy et al. 1998, 2001; Rivera et al. 2010). The planets b and c, in which we are interested here (see Table 2 for orbital elements), are Jupiter-mass planets embedded in a 2:1 MMR, while d and e are much less massive. A small amplitude of libration is observed (~5°, see Correia et al. 2010) for the 2:1 resonance between GJ 876b, c. The forced eccentricity ratio is 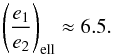 (69)Since the system is observed with a small amplitude of libration, the stability constraint gives (Eq. (50))
(69)Since the system is observed with a small amplitude of libration, the stability constraint gives (Eq. (50))  (70)As for HD 60532b, c, the condition of convergent migration is fulfilled (see Eq. (54)). The surface density profile exponent is (see Eq. (48))
(70)As for HD 60532b, c, the condition of convergent migration is fulfilled (see Eq. (54)). The surface density profile exponent is (see Eq. (48)) 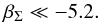 (71)We again obtain a negative value that corresponds to an inverted profile. We have (see Eqs. (43), (58), and (59))
(71)We again obtain a negative value that corresponds to an inverted profile. We have (see Eqs. (43), (58), and (59))  Using these values and τ ≫ 42, we obtain (see Eq. (60))
Using these values and τ ≫ 42, we obtain (see Eq. (60)) 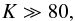 (75)which corresponds to an aspect ratio of (see Eq. (49))
(75)which corresponds to an aspect ratio of (see Eq. (49)) 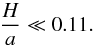 (76)As for HD 60532b, c, we performed numerical simulations with different values of τ (and adjusted values of K given by Eq. (60)). The semi-major axes are initially 2 and 3.5 au (period ratio of about 2.3), and the eccentricities are 0.001 with anti-aligned periastrons and coplanar orbits. The planets are initially at periastrons (zero anomalies). The evolution of the semi-major axes, the period ratio, the eccentricities, the eccentricity ratio, and the angles are shown in Fig. 3. The transition between decreasing and increasing amplitude of libration happens around τ ≈ 20 (see Fig. 3), while our analytical criterion gives a value of 42. Taking this refined value for τ, the condition for reproducing the observed system with type-I migration reads as
(76)As for HD 60532b, c, we performed numerical simulations with different values of τ (and adjusted values of K given by Eq. (60)). The semi-major axes are initially 2 and 3.5 au (period ratio of about 2.3), and the eccentricities are 0.001 with anti-aligned periastrons and coplanar orbits. The planets are initially at periastrons (zero anomalies). The evolution of the semi-major axes, the period ratio, the eccentricities, the eccentricity ratio, and the angles are shown in Fig. 3. The transition between decreasing and increasing amplitude of libration happens around τ ≈ 20 (see Fig. 3), while our analytical criterion gives a value of 42. Taking this refined value for τ, the condition for reproducing the observed system with type-I migration reads as  The density profile still needs to be inverted (βΣ< 0), and the overall conclusions are the same.
The density profile still needs to be inverted (βΣ< 0), and the overall conclusions are the same.
 |
Fig. 3 Same as Fig. 2 but for GJ 876b, c. We used τ = +∞, 20, 10, 5 with K = 130, 58, 36, 19, respectively, for the four shown simulations (four columns). The last simulation (τ = 5, K = 19) ended before 106 yr (around 8 × 105 yr) because of orbital instability when the system escaped from resonance. The amplitude of libration decreases for the first two simulations (τ = +∞, 20) and increases for the last two (τ = 10, 5). The value given by our analytical criterion for the transition between decreasing and increasing amplitude is τ ~ 42. |
Lee & Peale (2002) studied capture scenarios for this system using a slightly different model for the migration and damping and did not observe any evolution of the libration amplitude in their simulations. The authors used constant semi-major axis (Ta,i) and eccentricity (Te,i) damping timescales for each planet. In our study we followed the prescriptions of Papaloizou & Larwood (2000; see also Goldreich & Schlichting 2014) and considered constant angular momentum (Tm,i) and eccentricity (Te,i) damping timescales. We replaced these prescriptions with Lee & Peale (2002) prescriptions for the disk-planet interactions in our analytical model (following the same scheme as described in Sect. 3.2). We found that the amplitude of libration does not evolve in this case (in agreement with Lee & Peale 2002 simulations). This difference between both prescriptions has important consequences since in the case of the Lee & Peale (2002) prescriptions, two initially resonant planets will stay locked in resonance forever, while with the prescriptions we used, the amplitude of libration can increase and the system can escape from resonance. The main difference between both prescriptions comes from the fact that with Lee & Peale (2002) prescriptions, the eccentricity damping does not affect the semi-major axes, while in our model the eccentricity damping terms contribute to the semi-major axes evolution (see Eq. (20)). Disk-planet interaction models suggest that the semi-major axes evolution are indeed influenced by the eccentricity damping effect of the disk (see Goldreich & Schlichting 2014). We thus follow these prescriptions in our study.
Orbital parameters of HD 45364b, c used in this study (taken from Correia et al. 2009).
 |
Fig. 4 Same as Fig. 2 but for HD 45364b, c. We used τ = +∞, 15, 5, 2 with K = 15, 12, 8, 3.5, respectively, for the four shown simulations (four columns). The amplitude of libration decreases for the first two simulations (τ = +∞, 15) and increases for the last two (τ = 5, 2). The value given by our analytical criterion for the transition between decreasing and increasing amplitude is τ ~ 6.3. |
5.3. HD 45364b, c: 3:2 MMR, large amplitude of libration
The star HD 45364 hosts two planets (Correia et al. 2009) embedded in a 3:2 MMR (see Table 3 for orbital elements). The forced eccentricity ratio is 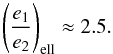 (80)A large amplitude of libration is observed (~70°, see Correia et al. 2009), therefore, the stability constraint gives (Eq. (51))
(80)A large amplitude of libration is observed (~70°, see Correia et al. 2009), therefore, the stability constraint gives (Eq. (51)) 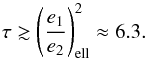 (81)The condition of convergent migration is fulfilled (see Eq. (54)). The surface density profile exponent is (see Eq. (48))
(81)The condition of convergent migration is fulfilled (see Eq. (54)). The surface density profile exponent is (see Eq. (48)) 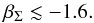 (82)We again obtain a negative value that corresponds to an inverted profile. We have (see Eqs. (43), (58), and (59))
(82)We again obtain a negative value that corresponds to an inverted profile. We have (see Eqs. (43), (58), and (59))  Using these values and τ ≳ 6.3, we obtain (see Eq. (60))
Using these values and τ ≳ 6.3, we obtain (see Eq. (60)) 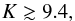 (86)which corresponds to an aspect ratio of (see Eq. (49))
(86)which corresponds to an aspect ratio of (see Eq. (49)) 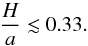 (87)We performed numerical simulations with different values of τ and K (given by Eq. (60)). The semi-major axes are initially 10 and 14 au (period ratio of about 1.65), the eccentricities are 0.001 with anti-aligned periastrons and coplanar orbits. The planets are initially at periastrons (zero anomalies). The evolution of the semi-major axes, the period ratio, the eccentricities, the eccentricity ratio, and the angles are shown in Fig. 4. According to our simulations, the amplitude of libration increases for τ ≲ 10 (transition between 5−15, see Fig. 4), which is comparable to our analytical result (τ ≲ 6.3).
(87)We performed numerical simulations with different values of τ and K (given by Eq. (60)). The semi-major axes are initially 10 and 14 au (period ratio of about 1.65), the eccentricities are 0.001 with anti-aligned periastrons and coplanar orbits. The planets are initially at periastrons (zero anomalies). The evolution of the semi-major axes, the period ratio, the eccentricities, the eccentricity ratio, and the angles are shown in Fig. 4. According to our simulations, the amplitude of libration increases for τ ≲ 10 (transition between 5−15, see Fig. 4), which is comparable to our analytical result (τ ≲ 6.3).
It may seem surprising that the amplitude of libration does not increase much more rapidly for τ = 2 than for τ = 5 (see Fig. 4). Indeed, our study shows that the smaller τ is, the more unstable the resonant configuration (Eq. (35)). However, the evolution of the amplitude of libration not only depends on the ratio τ = Te,1/Te,2, but also on the absolute values of these damping timescales (see Eq. (35)). In our simulations, we fixed the migration timescale for the outer planet (Tm,2) and varied the three other timescales: Tm,1 = τTm,2, Te,2 = Tm,2/K, Te,1 = τTm,2/K. The damping timescales are thus much longer for the simulation with τ = 2 (K = 3.5) than for τ = 5 (K = 8), in order to reproduce the same equilibrium eccentricities. This tends to slow down the increase in the amplitude of libration and compensates for the acceleration provided by decreasing τ.
6. Conclusion
We obtained a simple analytical criterion for the stability of the resonant configuration between two planets during their migration in a protoplanetary disk. We used the simplified integrable model of MMRs that we developed in Delisle et al. (2014) and modeled the dissipative effect of the disk on the planets by four distinct timescales: Tm,1, Tm,2 (migration of both planets), and Te,1, Te,2 (damping of both eccentricities). As shown by Lee & Peale (2002), migrating planets that are captured in resonance have their eccentricities excited by the migration forces of the disk. The eccentricities reach equilibrium values between the migration and damping forces. However, this equilibrium can be unstable, in which case the amplitude of libration in the resonance increases until the system crosses the separatrix and escapes from resonance (Goldreich & Schlichting 2014). We showed here that the equilibrium is stable on the condition that 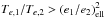 (ratio of equilibrium eccentricities). For observed resonant systems, it is probable that the equilibrium was stable during the migration phase. Otherwise, the planets would have escaped from resonance. This result allows one to put constraints on the damping forces undergone by the planets. For instance, using prescriptions for type-I migration, we show that a locally inverted profile is needed for resonant systems for which the inner planet AMD is greater than the outer planet AMD. We applied our analytical criterion to HD 60532b, c (3:1 MMR), GJ 876b, c (2:1 MMR), and HD 45364b, c (3:2 MMR). We showed for all studied systems that if the planets had undergone type I migration, an inverted density profile would be required for the resonant configuration to be stable. All these planets are Jupiter-mass planets and are thus believed to open a gap in the disk and undergo type-II migration. Our results confirm that classical type-I migration cannot reproduce the observed systems.
(ratio of equilibrium eccentricities). For observed resonant systems, it is probable that the equilibrium was stable during the migration phase. Otherwise, the planets would have escaped from resonance. This result allows one to put constraints on the damping forces undergone by the planets. For instance, using prescriptions for type-I migration, we show that a locally inverted profile is needed for resonant systems for which the inner planet AMD is greater than the outer planet AMD. We applied our analytical criterion to HD 60532b, c (3:1 MMR), GJ 876b, c (2:1 MMR), and HD 45364b, c (3:2 MMR). We showed for all studied systems that if the planets had undergone type I migration, an inverted density profile would be required for the resonant configuration to be stable. All these planets are Jupiter-mass planets and are thus believed to open a gap in the disk and undergo type-II migration. Our results confirm that classical type-I migration cannot reproduce the observed systems.
Our model is very general and is not restricted to type-I migration. Considering a scenario of type-II migration that is much more realistic for the studied systems, our model still gives constraints on the migration process and especially on the eccentricity damping undergone by each planet. However, we could not find a simple analytical prescription for type-II migration in the literature and thus could not derive constraints on the disk properties in this case. Having analytical prescriptions for type-II migration would allow a more detailed analysis of these systems.
It would also be very interesting in the future to study small planets in resonance (with precise enough determination of orbital parameters to be sure of the resonant motion). Indeed, for small planets, a type-I migration scenario is more realistic. In this case, a local inversion of the density profile (as needed for the three systems of this study) would be more surprising.
The pendulum approximation of resonances is obtained using an analytical expansion in power series of eccentricities and is thus not valid at high eccentricities. Moreover, when eccentricities are vanishing, the phase space bifurcates, and a better approximation is given by the second fundamental model of resonances (see Henrard & Lemaitre 1983; Delisle et al. 2012).
Acknowledgments
We thank Rosemary Mardling, Yann Alibert, Wilhelm Kley, and the anonymous referee for useful advice. This work has been carried out in part within the framework of the National Center for Competence in Research PlanetS supported by the Swiss National Science Foundation. This work has been supported by PNP-CNRS, CS of the Paris Observatory, and the PICS05998 France-Portugal program. J.B.D. acknowledges the financial support of the SNSF. A.C. acknowledges support from CIDMA strategic project UID/MAT/04106/2013.
References
- Bitsch, B., & Kley, W. 2010, A&A, 523, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Udry, S., Mayor, M., et al. 2009, A&A, 496, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, A. C. M., Couetdic, J., Laskar, J., et al. 2010, A&A, 511, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delfosse, X., Forveille, T., Mayor, M., et al. 1998, A&A, 338, L67 [Google Scholar]
- Delisle, J.-B., & Laskar, J. 2014, A&A, 570, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delisle, J.-B., Laskar, J., Correia, A. C. M., & Boué, G. 2012, A&A, 546, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delisle, J.-B., Laskar, J., & Correia, A. C. M. 2014, A&A, 566, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desort, M., Lagrange, A.-M., Galland, F., et al. 2008, A&A, 491, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duffell, P. C., Haiman, Z., MacFadyen, A. I., D’Orazio, D. J., & Farris, B. D. 2014, ApJ, 792, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Dürmann, C., & Kley, W. 2015, A&A, 574, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Sari, R. 2003, ApJ, 585, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Schlichting, H. E. 2014, AJ, 147, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1980, ApJ, 241, 425 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hairer, E., Nørsett, S. P., & Wanner, G. 2010, Solving Ordinary Differential Equations I: Nonstiff Problems (Springer) [Google Scholar]
- Henrard, J., & Lemaitre, A. 1983, Celest. Mech., 30, 197 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1997, A&A, 317, L75 [NASA ADS] [Google Scholar]
- Laskar, J. 2000, Phys. Rev. Lett., 84, 3240 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Laskar, J., & Correia, A. C. M. 2009, A&A, 496, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. H., & Peale, S. J. 2002, ApJ, 567, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Butler, R. P., Vogt, S. S., Fischer, D., & Lissauer, J. J. 1998, ApJ, 505, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Butler, R. P., Fischer, D., et al. 2001, ApJ, 556, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Larwood, J. D. 2000, MNRAS, 315, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera, E. J., Laughlin, G., Butler, R. P., et al. 2010, ApJ, 719, 890 [Google Scholar]
- Terquem, C., & Papaloizou, J. C. B. 2007, ApJ, 654, 1110 [NASA ADS] [CrossRef] [Google Scholar]
- Weidenschilling, S. J., & Davis, D. R. 1985, Icarus, 62, 16 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Renormalization of coordinates
The renormalized variables are constructed by dividing all actions by the following constant of motion (see Delisle et al. 2012, 2014) 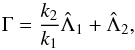 (A.1)where
(A.1)where 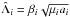 is the circular angular momentum of the planet i. When denoting the initial actions with a hat, the renormalized ones are defined by
is the circular angular momentum of the planet i. When denoting the initial actions with a hat, the renormalized ones are defined by ![\appendix \setcounter{section}{1} \begin{eqnarray} &&\Lambda_i = \frac{\hat{\Lambda}_i}{\Gamma},\\[1mm] && G_i = \frac{\hat{G}_i}{\Gamma},\\[1mm] && I_i = \frac{\hat{I}_i}{\Gamma},\\[1mm] && \mathcal{D} = \frac{\hat{\mathcal{D}}}{\Gamma},\\[1mm] && \delta = \frac{\hat{\delta}}{\Gamma}\cdot \end{eqnarray}](/articles/aa/full_html/2015/07/aa26285-15/aa26285-15-eq237.png) Expressions (4) and (5) are straightforwardly derived from these definitions.
Expressions (4) and (5) are straightforwardly derived from these definitions.
The Hamiltonian and the time also have to be renormalized (see Delisle et al. 2012, 2014) in order to preserve Hamiltonian properties. However, in this study, we consider dissipative forces that act on the system on very long timescales. As long as the conservative timescale remains much shorter than the dissipation timescale, the long-term evolution of the system is described well by the mean effect of the dissipation on the conservative timescale. Therefore, the rescaling of this conservative timescale will not influence the long-term evolution of the system.
Appendix B: Reducing to an integrable problem
In the general case, the motion of two planets in a k2:k1 resonance is described by two degrees of freedom, i.e. both resonant angles, 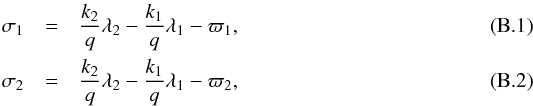 and both actions I1, I2. We denote xi as the complex Cartesian coordinates associated to these action-angle coordinates
and both actions I1, I2. We denote xi as the complex Cartesian coordinates associated to these action-angle coordinates 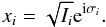 (B.3)The simplifying assumption introduced in Delisle et al. (2014) allows this generally non-integrable problem to be reduced to a single degree of freedom (thus integrable). The only remaining resonant angle is θ and the associated action is
(B.3)The simplifying assumption introduced in Delisle et al. (2014) allows this generally non-integrable problem to be reduced to a single degree of freedom (thus integrable). The only remaining resonant angle is θ and the associated action is 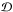 . If denoting u the related complex Cartesian coordinate
. If denoting u the related complex Cartesian coordinate 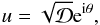 (B.4)the simplifying assumption reads as
(B.4)the simplifying assumption reads as 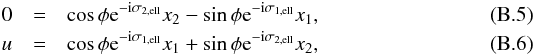 where φ, σ1,ell, and σ2,ell are constant angles defined such that the libration center is directed toward u (see Delisle et al. 2014). Equation (B.6) shows how the simplified one degree of freedom model mixes both initial degrees of freedom, and especially how the resonant angle θ mixes both initial resonant angles σ1, σ2. Equation (10) directly results from Eq. (B.5).
where φ, σ1,ell, and σ2,ell are constant angles defined such that the libration center is directed toward u (see Delisle et al. 2014). Equation (B.6) shows how the simplified one degree of freedom model mixes both initial degrees of freedom, and especially how the resonant angle θ mixes both initial resonant angles σ1, σ2. Equation (10) directly results from Eq. (B.5).
Appendix C: Evolution of the parameter δ under dissipation
In this section we show how to compute the evolution of the parameter δ (Eq. (14)) under a dissipation affecting the semi-major axes and eccentricities of the planets. The evolution of the renormalized circular angular momenta only depends on 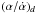 . These renormalized quantities are constructed such that (see Appendix A and Delisle et al. 2014)
. These renormalized quantities are constructed such that (see Appendix A and Delisle et al. 2014) 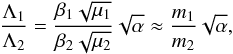 (C.1)and
(C.1)and 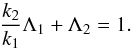 (C.2)We deduce
(C.2)We deduce 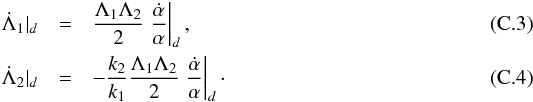 The evolution of ϵ is then straightforward (see Eq. (2))
The evolution of ϵ is then straightforward (see Eq. (2)) 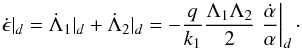 (C.5)The evolution of the renormalized deficit of angular momentum Ii is given by
(C.5)The evolution of the renormalized deficit of angular momentum Ii is given by
We thus deduce 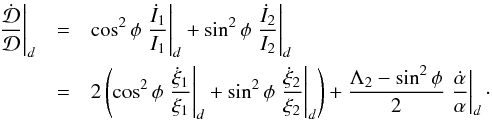 (C.9)Finally, we have
(C.9)Finally, we have 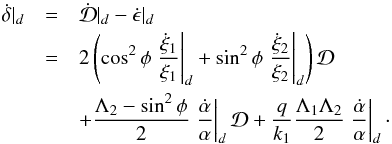 (C.10)
(C.10)
All Tables
Orbital parameters of HD 60532b,c used in this study (taken from Laskar & Correia 2009).
Orbital parameters of GJ 876b, c used in this study (taken from Correia et al. 2010).
Orbital parameters of HD 45364b, c used in this study (taken from Correia et al. 2009).
All Figures
 |
Fig. 1 Phase space of a resonance of order q in the simplified pendulum-like approximation (Hamiltonian (1)). θ is the unique resonant angle and ϵ its conjugated action. The separatrix is highlighted in red. The amplitude A (defined with θmax see Eq. (12)) is 0 at the center of the resonance (elliptical fixed point) and 1 at the separatrix. |
| In the text | |
 |
Fig. 2 Semi-major axes, period ratio, eccentricities, eccentricity ratio, and angles evolution for simulations of HD 60532b, c with different dissipation timescale ratios τ = Te,1/Te,2 = Tm,1/Tm,2. The ratio K = Tm,i/Te,i is set according to Eq. (60) to reproduce the observed equilibrium eccentricities. We used τ = +∞, 10, 8, 4 with K = 70, 34, 30, 17, respectively, for the four shown simulations (four columns). The amplitude of libration decreases for the first two simulations (τ = +∞, 10) and increases for the last two (τ = 8, 4). The value given by our analytical criterion for the transition between decreasing and increasing amplitude is τ ~ 9. |
| In the text | |
 |
Fig. 3 Same as Fig. 2 but for GJ 876b, c. We used τ = +∞, 20, 10, 5 with K = 130, 58, 36, 19, respectively, for the four shown simulations (four columns). The last simulation (τ = 5, K = 19) ended before 106 yr (around 8 × 105 yr) because of orbital instability when the system escaped from resonance. The amplitude of libration decreases for the first two simulations (τ = +∞, 20) and increases for the last two (τ = 10, 5). The value given by our analytical criterion for the transition between decreasing and increasing amplitude is τ ~ 42. |
| In the text | |
 |
Fig. 4 Same as Fig. 2 but for HD 45364b, c. We used τ = +∞, 15, 5, 2 with K = 15, 12, 8, 3.5, respectively, for the four shown simulations (four columns). The amplitude of libration decreases for the first two simulations (τ = +∞, 15) and increases for the last two (τ = 5, 2). The value given by our analytical criterion for the transition between decreasing and increasing amplitude is τ ~ 6.3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.