| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201525688 | |
| Published online | 10 July 2015 | |
Angular momentum transport and large eddy simulations in magnetorotational turbulence: the small Pm limit
1 Laboratoire AIM, CEA/DSM-CNRS-Université Paris 7, Irfu/Service d’Astrophysique, CEA-Saclay, 91191 Gif-sur-Yvette, France
e-mail: heloise.meheut@cea.fr
2 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
3 CNRS, IPAG, 38000 Grenoble, France
Received: 19 January 2015
Accepted: 19 May 2015
Context. Angular momentum transport in accretion discs is often believed to be due to magnetohydrodynamic turbulence mediated by the magnetorotational instability (MRI). Despite an abundant literature on the MRI, the parameters governing the saturation amplitude of the turbulence are poorly understood and the existence of an asymptotic behaviour in the Ohmic diffusion regime has not been clearly established.
Aims. We investigate the properties of the turbulent state in the small magnetic Prandtl number limit. Since this is extremely computationally expensive, we also study the relevance and range of applicability of the most common subgrid scale models for this problem.
Methods. Unstratified shearing box simulations are performed both in the compressible and incompressible limits, with a resolution up to 800 cells per disc scale height. This is the highest resolution ever attained for a simulation of MRI turbulence. Different magnetic field geometry and a wide range of dimensionless dissipative coefficients are considered. We also systematically investigate the relevance of using large eddy simulations (LES) in place of direct numerical simulations.
Results. In the presence of a mean magnetic field threading the domain, angular momentum transport converges to a finite value in the small Pm limit. When the mean vertical field amplitude is such that β (the ratio between the thermal and magnetic pressure) equals 103, we find α ~ 3.2 × 10-2 when Pm approaches zero. In the case of a mean toroidal field for which β = 100, we find α ~ 1.8 × 10-2 in the same limit. Implicit LES and the Chollet-Lesieur closure model both reproduce these results for the α parameter and the power spectra. A reduction in computational cost by a factor of at least 16 (and up to 256) is achieved when using such methods.
Conclusions. MRI turbulence operates efficiently in the small Pm limit provided there is a mean magnetic field. Implicit LES offers a practical and efficient means of investigation of this regime but should be used with care, particularly in the case of a vertical field. The Chollet-Lesieur closure model is perfectly suited for simulations done with a spectral code.
Key words: accretion, accretion disks / magnetohydrodynamics (MHD) / turbulence / protoplanetary disks / methods: numerical
© ESO, 2015
1. Introduction
Determining the rate of angular momentum transport in accretion discs is considered to be one of the most important unsolved astrophysical questions. Accretion is believed to be at the origin of the radiation emitted by some of the most luminous sources in the universe from active galactic nuclei to X-ray binaries and is also a major process at work during planet formation in protoplanetary discs (Frank et al. 2002). In addition, accretion discs are ubiquitous in the universe and affect the dynamics, evolution, and appearance of multiple astrophysical objects at all spatial and energy scales. The accretion rate can be indirectly constrained by the luminosity of high-energy sources or the lifetime of protoplanetary discs, and, if the transport process is modelled by an α viscosity (Shakura & Sunyaev 1973), such an estimate gives 0.01 <α< 0.4 depending on the system considered (King et al. 2007).
The physical origin of angular momentum transport has to be understood to explain such an efficient radial angular momentum transport. Currently, the most widely accepted mechanism is magnetohydrodynamic (MHD) turbulence induced by the non-linear evolution of the magneto-rotational instability (MRI, Balbus & Hawley 1991). That instability along with its non-linear development has been extensively studied in the last two decades (Balbus & Hawley 1998; Balbus 2003; Fromang 2013). Using local simulations performed in the framework of the shearing box, Hawley et al. (1995) quickly established that the MRI develops into vigorous MHD turbulence that efficiently transports angular momentum outward, a result that was later confirmed to be independent of the field geometry (Hawley et al. 1996) or to the background disc stratification (Brandenburg et al. 1995; Stone et al. 1996). Only recently has the sensitivity of MRI-driven MHD turbulence saturation to small-scale dissipation in such idealized simulations been identified: when magnetic field diffusion is dominated by an ohmic resistivity η, α is an increasing function of the magnetic Prandtl number Pm, the ratio between the kinematic viscosity ν and η. This is the case both in the presence of a mean vertical magnetic field (Lesur & Longaretti 2007) and of a mean azimuthal magnetic field (Simon & Hawley 2009). Such a “Pm-effect” has a significant impact on the rate of angular momentum transport measured in homogeneous shearing box simulations: in the case of a mean vertical field such that the plasma β parameter (defined in Sect. 2.4) amounts to 103, Longaretti & Lesur (2010) showed that α varies by a factor of about 5 when Pm only varies between 1/4 and 4, without any sign of the relation flattening at either range. The dynamo case (i.e. no mean magnetic field threading the computational domain) also displays a high sensitivity to Pm (Fromang et al. 2007; Simon & Hawley 2009; Guan et al. 2009; Bodo et al. 2011) that persists when density stratification is included (Simon et al. 2011). In this dynamo regime and without stratification, the effect is even stronger and dynamo action is suppressed for Pm values smaller than unity, in which case the flow remains laminar, i.e. α goes to zero. A clear understanding of the origin of the effect of Pm on the rate of angular momentum transport is still lacking and is currently a matter of active research. The first results, based on methods borrowed from the fluid community (Herault et al. 2011; Riols et al. 2013) are promising (Riols et al. 2015) and should be extended to more realistic geometries and dimensionless numbers.
Taken together, the results described above question the relevance of MRI-driven MHD turbulence as the dominant transport mechanism in accretion discs where the Prandtl number can be orders of magnitude lower (Pm ≪ 1) than has been explored in published simulations (Balbus & Henri 2008). There is clearly the possibility that α becomes vanishingly small as Pm decreases to small but astrophysically relevant values. The first goal of this paper is to investigate this asymptotic behaviour by means of high-resolution simulations performed in the homogeneous shearing box. In doing so, we will leave aside the dynamo case and focus on vertical and azimuthal mean field configurations. Using high-resolution simulations (such that the coverage in Pm now extends over more than two orders of magnitudes, from 10-2 to 4), we will show that α asymptotically converges to a well-defined finite value in both cases. However, the computational cost associated with such simulations is extremely high (for example, 15 million CPU hours are needed to complete the 10003 simulation we describe in Sect. 3.1.1 on a BlueGen/Q machine ranked 42nd on the Top500 supercomputing website in November 20141). In practice, such a high cost is prohibitive if one wants to perform a parameter survey in the asymptotic regime with additional physics included and simply prevents global simulations from being performed in that limit. The second goal of this paper is thus to investigate the possibility of using sub-grid scale models as a means of reducing the computational cost associated with MHD turbulence simulations in the small Pm limit.
Recent years have seen significant progress in our understanding of the consequences of ambipolar diffusion (Bai & Stone 2011, 2013; Simon et al. 2013) and the Hall effect (Kunz & Lesur 2013; Lesur et al. 2014; Bai 2015), both of which are particularly important in shaping the structure of protoplanetary discs. In this paper we will restrict our attention to Ohmic resistivity as the sole source of magnetic field dissipation. Such a regime is relevant in order to describe the very inner parts of protoplanetary discs (at stellar distances of a few tens of an AU) and also cataclysmic variable (CV) discs and the outer parts of X-ray binary discs (Balbus & Henri 2008). In principle, the analysis we present here should also be carried for such cases where ambipolar diffusion or the Hall effect is the dominant magnetic field diffusion processes.
The plan of the paper is as follows. In the following section, the equations and numerical methods are given. Section 3 presents our results, focusing first on simulations that explicitly resolve the small dissipative scales (Sect. 3.1) and then on two different methods for performing large eddy simulations (LES) in Sect. 3.2. We finally conclude and discuss the implications of our work in Sect. 4.
2. Methods
2.1. Equations and notations
In this paper we use the shearing box approximation (Hawley et al. 1995). Namely, we compute the evolution of the fluid in a small box centred at a radius r0 of the disc and rotating at the same velocity as the fluid at r = r0. As the size of the box is small compared to the radial position, the curvature terms of the standard fluid equations can be simplified (Hawley & Balbus 1992). We thus use Cartesian coordinates (x,y,z) with unit vectors (i,j,k). In this coordinate system, we denote (Lx,Ly,Lz) the size of the computational box. Neglecting the vertical component of the gravitational acceleration, we solve the following set of equations, 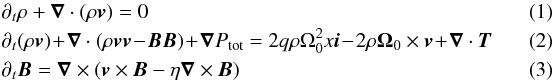 where ρ is the fluid density, v its velocity in the rotating frame, B is the magnetic field, and Ω0 is the angular velocity of the fluid at r0 corresponding to the angular velocity of the box; q stands for the background Keplerian shear and is taken as equal to 1.5 throughout this paper; Ptot is the total pressure, the sum of the thermal pressure P and the magnetic pressure B2/ 2. Explicit dissipation is accounted for through the Ohmic resistivity η and the kinematic viscosity ν that enters in the viscous stress tensor T defined as
where ρ is the fluid density, v its velocity in the rotating frame, B is the magnetic field, and Ω0 is the angular velocity of the fluid at r0 corresponding to the angular velocity of the box; q stands for the background Keplerian shear and is taken as equal to 1.5 throughout this paper; Ptot is the total pressure, the sum of the thermal pressure P and the magnetic pressure B2/ 2. Explicit dissipation is accounted for through the Ohmic resistivity η and the kinematic viscosity ν that enters in the viscous stress tensor T defined as 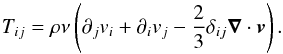 (4)The amplitude of viscosity and resistivity are set using the magnitude of the Reynolds number Re and magnetic Reynolds number Rm with the relations
(4)The amplitude of viscosity and resistivity are set using the magnitude of the Reynolds number Re and magnetic Reynolds number Rm with the relations 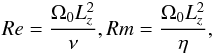 which can also serve as an alternative definition for the magnetic Prandtl number Pm already given in the introduction:
which can also serve as an alternative definition for the magnetic Prandtl number Pm already given in the introduction: 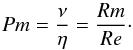 (5)We performed simulations that consider two different flavours of the system of Eqs. (1)–(3). First, we solved the above equations in the incompressible limit. In this case, the density is constant and Eq. (1) reduces to ∇·v = 0. We used the code SNOOPY in that case (see Sect. 2.2). In the second type of simulations, we solved the full set of equations (and refer to that case as the compressible simulations) using the code RAMSES (Sect. 2.3). We briefly describe below the two codes and the specificities of each set of simulations.
(5)We performed simulations that consider two different flavours of the system of Eqs. (1)–(3). First, we solved the above equations in the incompressible limit. In this case, the density is constant and Eq. (1) reduces to ∇·v = 0. We used the code SNOOPY in that case (see Sect. 2.2). In the second type of simulations, we solved the full set of equations (and refer to that case as the compressible simulations) using the code RAMSES (Sect. 2.3). We briefly describe below the two codes and the specificities of each set of simulations.
2.2. Incompressible simulations: the SNOOPY code
The SNOOPY code is a pseudo-spectral code that solves the incompressible MHD equations in a Fourier basis. It uses a low-storage third-order Runge-Kutta integrator and works in a sheared frame comoving with the mean flow, which is equivalent to a third-order Fargo scheme (Masset 2000). SNOOPY uses a 3/2 antialiasing rule to eliminate the excitation of spurious modes during the computation of quadratic non-linearities.
The use of a sheared Fourier basis makes the boundary conditions periodic in the y- and z-directions and shear-periodic in the x-direction. SNOOPY conserves linear momentum and magnetic flux down to machine precision. Since spectral methods are inherently diffusion free and energy conserving, the addition of dissipation is required to mimic the damping due to small scale dissipation processes2. In SNOOPY, one can choose second-order diffusion operators, hyperdiffusion operators, or Chollet & Lesieur (1981) subgrid models (see Sect. 3.2.1).
2.3. Compressible simulations: the RAMSES code
The RAMSES code is a finite volume code that solves the compressible MHD equations on a Cartesian grid (Teyssier 2002; Fromang et al. 2006) using the constrained transport algorithm (Evans & Hawley 1988). We use a version of the code for which the grid is uniform (i.e. without the adaptive mesh refinement). The source terms associated with the tidal potential are included as described by Stone & Gardiner (2010). We use the HLLD Riemann solver (Miyoshi & Kusano 2005) with monotonized central slope limiter, shearing box boundary conditions in the x-direction (Hawley et al. 1995), and periodic boundary conditions in the y- and z-directions. For extended box sizes such as used in the mean vertical field case (see Sect. 2.4), it has been found that radially variable numerical dissipation causes the turbulent stress to vary accross the box. To avoid that problem, we used the FARGO algorithm (Masset 2000; Stone & Gardiner 2010) in that case, which also improves the efficiency of the code through an increase in the timestep.
Throughout this paper, we use an isothermal equation of state to close the system of MHD equations in compressible simulations, such that 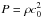 , where c0 stands for the constant sound speed. We start the simulation with an initial uniform density ρ = ρ0 and choose Lz = H = c0/ Ω0, where H is the disc scale height.
, where c0 stands for the constant sound speed. We start the simulation with an initial uniform density ρ = ρ0 and choose Lz = H = c0/ Ω0, where H is the disc scale height.
2.4. Models parameters
We start the simulations with a uniform initial magnetic field: 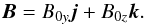 (6)Two different initial magnetic configurations are considered in the following, namely pure azimuthal field (B0z = 0) simulations and pure vertical field simulations (B0y = 0). The strength of the magnetic field is defined using the plasma parameter βi that is given by
(6)Two different initial magnetic configurations are considered in the following, namely pure azimuthal field (B0z = 0) simulations and pure vertical field simulations (B0y = 0). The strength of the magnetic field is defined using the plasma parameter βi that is given by  For the mean azimuthal (resp. vertical) magnetic field simulations, we used βy = 112.5 (resp. βz = 103). At the start of each run, small amplitude random velocity perturbations are added on the three velocity components with an amplitude equal to 1% of the sound speed in compressible runs. In incompressible simulations both velocity and magnetic random perturbations are added with an amplitude of 0.1ΩLz.
For the mean azimuthal (resp. vertical) magnetic field simulations, we used βy = 112.5 (resp. βz = 103). At the start of each run, small amplitude random velocity perturbations are added on the three velocity components with an amplitude equal to 1% of the sound speed in compressible runs. In incompressible simulations both velocity and magnetic random perturbations are added with an amplitude of 0.1ΩLz.
The size of the computational box is either (Lz,4Lz,Lz) for the simulations with a mean azimuthal magnetic field, or (4Lz,4Lz,Lz) for the simulations with a mean vertical magnetic field. In the latter case, it is indeed well known that boxes with Lx = Lz artificially enhance the importance of recurrent bursts in the flow structure (Bodo et al. 2008; Johansen et al. 2009). In such box sizes and with such vertical magnetic field, Bai & Stone (2014) recently reported zonal flows. We also found such structures in our simulations.
The resolution varies from 32 cells per unit length up to 800 cells per unit length. Such high resolutions allow us to reach the largest Reynolds number (run Y-C-Re85000, Re = 85 000) and the smallest Prandtl number (run Z-I-Re40000, Pm = 0.01) ever published. As larger structures are expected in the y-direction, we typically use a resolution that is twice as coarse in that direction.
RAMSES runs with a mean azimuthal field.
3. Results
The whole set of runs discussed in the remainder of this paper is listed in Tables 1−3, where the first column provides the simulation labels. Runs starting with a pure azimuthal (vertical) magnetic field are labelled with the letter “Y” (“Z”). Likewise, compressible (incompressible) simulations are labelled with the letter “C” (“I”). Large eddy simulations are labelled either “ILES” or “CL” depending on the subgrid scale model that is used (see Sect. 3.2). The remaining columns in Tables 1−3 give the run resolution (Col. 2) and duration TRun (Col. 3), the Reynolds number (Col. 4), the magnetic Reynolds number (Col. 5), the magnetic Prandtl number (Col. 6), and α (Col. 7), which is the sum of αRey (Col. 8) and αMax (Col. 9). The last two are defined by the following relations: ![\begin{eqnarray} \alpha_{\rm Rey} = \left\{ \begin{array}{l l} \frac{\langle \rho \delta v_r \delta u_\phi\rangle}{P_0} \,& \quad \text{in compressible runs,}\\ \frac{\langle\delta v_r \delta u_\phi\rangle}{(\Omega Lz)^2} & \quad \text{in incompressible runs,}\\ \end{array} \right. \\[1mm] \alpha_{\rm Max} = \left\{ \begin{array}{l l} -\frac{\langle B_rB_\phi\rangle}{P_0} \,& \quad \text{in compressible runs,}\\ -\frac{\langle B_rB_\phi\rangle}{\rho_0(\Omega Lz)^2} & \quad \text{in incompressible runs.}\\ \end{array} \right. \label{eq:alphamax} \end{eqnarray}](/articles/aa/full_html/2015/07/aa25688-15/aa25688-15-eq152.png) Here ⟨ . ⟩ denotes an average over the shearing box volume and over time and δv is the velocity difference to the laminar sheared flow. Except for the shortest runs (see Sect. 3.1.1), the turbulent transport rates as measured by the α parameters are time averaged over the last 60 orbits of the models. The last column gives the ratio between magnetic and hydrodynamic transport rate.
Here ⟨ . ⟩ denotes an average over the shearing box volume and over time and δv is the velocity difference to the laminar sheared flow. Except for the shortest runs (see Sect. 3.1.1), the turbulent transport rates as measured by the α parameters are time averaged over the last 60 orbits of the models. The last column gives the ratio between magnetic and hydrodynamic transport rate.
3.1. Direct numerical simulations in the small Pm regime
In this section, we present the results of the resolved simulations (meaning that kinematic viscosity and ohmic resistivity are explicitly included in the calculation), focusing on the rate of angular momentum transport and on the power spectra of the turbulent flow.
 |
Fig. 1 Top panel: time evolution of α in model Y-C-Re85000 for which Pm = 0.03. The initial 15 orbits were performed in the ideal MHD regime, before including explicit diffusion coefficients. The hatched region represents the time interval over which the angular momentum transport is averaged. Bottom panel: Y-C-Re85000 run, kinetic (solid green line) and magnetic energy (dashed blue line) power spectrum. |
3.1.1. A 10003 MRI simulation
Because of the tremendous computational cost that was associated with that simulation, we start with a description of model Y-C-Re85000, performed with RAMSES. In this model, Re = 85 000 and Pm = 0.03. This simulation was performed with a resolution (Nx,Ny,Nz) = (800,1600,800). Based on past experience and published results of simulations using the same set-up at a lower Reynolds number with a similar code (Simon & Hawley 2009), we are confident that the small scales of the flow are properly accounted for in this simulation. In the x- and z-directions, the number of cells thus amounts to 800 cells per disc scale height, which is the highest resolution ever achieved of MRI-driven MHD turbulence with a second-order compressible code. This gigantic simulation was run at the IDRIS supercomputing centre on the BlueGen-Q machine Turing, using 32 768 cores. We found that the most efficient configuration was to use 4 threads per core, meaning that a total of 131 072 threads (or, equivalently, MPI sub-domains) were used. We used approximately 10 h of CPU time per timestep. Running the simulation for over 35 orbits (~106 timesteps) thus required about 107 h of CPU time, corresponding to 300 h of wall clock time (i.e. about two weeks).
As described by Simon & Hawley (2009), in the presence of a mean azimuthal magnetic field, resistivity can prevent the linear instability from transiting to a turbulent state when the simulation starts from a laminar flow, even though it is found to remain turbulent on long timescales when that linear phase is bypassed. We thus adopted the method described by these authors and performed the run in two steps. We first solved the ideal MHD equations (i.e. with vanishing viscosity and resistivity parameters). The only dissipative effects are numerical in origin during that part of the calculation. A turbulent state is reached after ~10 orbits. The turbulent transport as measured by α displays fluctuations around a well-defined mean value of about 6 × 10-2 for the next few orbits (see Fig. 1, top panel). At t = 15, we restarted the simulation for an additional 20 orbits with dissipation coefficients such that Re = 85 000 and Pm = 0.03. As seen in the top panel of Fig. 1, the turbulence amplitude is quickly modified by the presence of those dissipation coefficients and reaches a new steady state after a few additional orbits3. The nature of the flow is illustrated by a series of snapshots of the last time step of the run in Fig. 2. On the density plot one can recognize large-scale density waves and low-amplitude shocks. The turbulent magnetic field is dominated by large-scale structures. On the contrary, the velocity snapshot shows both large- and small-scale structures, as expected given the very small Pm used here.
We next averaged the transport rate after the system had reached a quasi-steady state and until the end of the simulation. This period corresponds to t> 21 orbits and is hatched in Fig. 1 (top panel). The values of αRey, αMax, and α that we obtained are 4.6 × 10-3, 1.3 × 10-2, and 1.8 × 10-2, respectively (see also Table 1). This α value is comparable to the one reported by Simon & Hawley (2009) for their most resolved run, for which Pm = 0.25, Rm = 3200, and β = 450. The Maxwell and Reynolds stresses display a ratio of ~3 that is typical of such simulations. There is of course a degree of arbitrariness regarding the exact time at which we decide that the system has reached the “quasi-steady state” and start averaging. We have checked that the statistics we consider do not vary significantly when making modest changes to the averaging period. For example, we find α = 1.9 × 10-2 and α = 1.8 × 10-2 when averaging over the periods t> 18 and t> 25 orbits, respectively. This is only a variation of 7% and it gives an idea of the uncertainty associated with that measurement.
 |
Fig. 2 From left to right, 3D snapshots of ρ, By, and vz in model Y-C-Re85000 at the end of the simulation. |
To obtain a more accurate view of the energy budget at each scale, we also show in Fig. 1 (bottom panel) the time averaged power spectra. Because of the shearing box boundary conditions, we consider time dependent unsheared wave vector k and the shell filter decomposition of the physical variables (Hawley et al. 1995). Because the decomposition is spherically symmetric, this method filters out the information about the flow anisotropy, which is known to be significant for MRI-driven turbulence (see Murphy & Pessah 2015; Fig. 3 in Lesur & Longaretti 2011, and Sect. 3.2.1). For each wavenumber, the kinetic and magnetic energy are then given by  respectively, where the bar denotes an average over time. Magnetic energy dominates at large scales (k′< 15, where we have defined k′ = k/ 2π so that it corresponds to scales l′>H/ 15), while kinetic energy dominates at smaller scales. This is a signature of the small Pm value of the simulation, which implies that the resistive dissipation length is larger than the viscous dissipation length (Schekochihin et al. 2004). At small scales, the motions essentially correspond to hydrodynamic turbulence associated with a forward cascade (Lesur & Longaretti 2011). We will exploit this scale separation in Sect. 3.2 when designing subgrid scale models for the hydrodynamic part of the flow. The kinetic energy power spectrum follows a power law with exponent −3/2 over the range 2 <k′< 20, thus covering one order in magnitude in spatial scales. The same exponent has been reported recently in other high-resolution simulations of MRI-driven MHD turbulence both in the dynamo regime (Fromang 2010) and in the presence of a net vertical field (Lesur & Longaretti 2011), suggesting it is a general feature of the flow. We note that homogeneous forced MHD turbulence also displays the same exponent (Mason et al. 2008), although the result is still debated (Beresnyak 2014). The surprising result here is that the magnetic energy does not show any obvious signature of a power-law regime, contrary to the case of homogeneous and driven MHD turbulence, while still being comparable in magnitude with EK. More work is needed to clarify the reason for this discrepancy and to better understand the origin of the −3/2 exponent that is obtained in the case of MRI-driven MHD turbulence.
respectively, where the bar denotes an average over time. Magnetic energy dominates at large scales (k′< 15, where we have defined k′ = k/ 2π so that it corresponds to scales l′>H/ 15), while kinetic energy dominates at smaller scales. This is a signature of the small Pm value of the simulation, which implies that the resistive dissipation length is larger than the viscous dissipation length (Schekochihin et al. 2004). At small scales, the motions essentially correspond to hydrodynamic turbulence associated with a forward cascade (Lesur & Longaretti 2011). We will exploit this scale separation in Sect. 3.2 when designing subgrid scale models for the hydrodynamic part of the flow. The kinetic energy power spectrum follows a power law with exponent −3/2 over the range 2 <k′< 20, thus covering one order in magnitude in spatial scales. The same exponent has been reported recently in other high-resolution simulations of MRI-driven MHD turbulence both in the dynamo regime (Fromang 2010) and in the presence of a net vertical field (Lesur & Longaretti 2011), suggesting it is a general feature of the flow. We note that homogeneous forced MHD turbulence also displays the same exponent (Mason et al. 2008), although the result is still debated (Beresnyak 2014). The surprising result here is that the magnetic energy does not show any obvious signature of a power-law regime, contrary to the case of homogeneous and driven MHD turbulence, while still being comparable in magnitude with EK. More work is needed to clarify the reason for this discrepancy and to better understand the origin of the −3/2 exponent that is obtained in the case of MRI-driven MHD turbulence.
 |
Fig. 3 Mean value of the angular momentum transport (measured by means of α) for the mean toroidal field simulations (blue circles), the mean vertical field simulations performed with RAMSES (green filled circles), and with SNOOPY (green filled squares). The dashed lines are power-law functions that approximately describe the data (see text). |
3.1.2. Angular momentum transport
We plot in Fig. 3 the total averaged stress α for all the resolved simulations we performed. Error bars σα are estimated with the method presented in Longaretti & Lesur (2010). In general, we find σα ~ 5 × 10-3 for the vertical field model (thus giving σα/α ~ 5%). This is consistent with the estimate of Longaretti & Lesur (2010). The error estimate is smaller in the azimuthal field case, for which we obtained σα ~ 10-3, which corresponds to σα/α ~ 1%. We note that we could not apply the same method for model Y-C-Re85000 because of the short duration of the integration in that case. A simple standard deviation is thus plotted instead and explains the larger error bar for that particular model.
In agreement with previous results (see Sect. 1) we find that α increases with Pm. However, the main result of Fig. 3 (and the main result of the paper) is that there is now convincing evidence of the convergence of the angular momentum transport rate at small Pm toward a well-defined, non-zero value. This is the case for both field geometries.
The azimuthal field case:
in this case, and with constant Rm and β, we find that a fit to the data is given by the formula 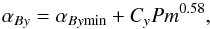 (13)with the values4 of αBymin = 1.8 × 10-2 and Cy = 5.5 × 10-3. This means that a good estimate of α is already obtained at Pm = 0.2 for which a resolution of 128 cells per unit length is sufficient. Indeed, we obtained α = 1.8 × 10-2 which is equal to the asymptotic value of α at vanishingly low Pm.
(13)with the values4 of αBymin = 1.8 × 10-2 and Cy = 5.5 × 10-3. This means that a good estimate of α is already obtained at Pm = 0.2 for which a resolution of 128 cells per unit length is sufficient. Indeed, we obtained α = 1.8 × 10-2 which is equal to the asymptotic value of α at vanishingly low Pm.
 |
Fig. 4 Left panel: time history of α (blue curve), αMax (red curve), and αRey (green curve) in model Z-C-Re3000. Right panel: scatter plot showing the total angular momentum transport rate α as a function of αaxi which measures the angular momentum transport due to |
The vertical field case:
here, we find a somewhat larger transport coefficient that can be fitted by the relation 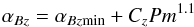 (14)with αBzmin = 3.2 × 10-2 and Cz = 3.3 × 10-2, with fixed Rm and β. Moreover, there is good agreement between the compressible and incompressible approach in this vertical field case: for both flow types the simulations converge at small Pm toward the same α. As is true for the azimuthal field case, a good estimate of the asymptotic rate of angular momentum transport is already obtained for Pm = 0.13 (using a resolution of 128 cells per unit length), for which we found α = 3.7 × 10-2, i.e. a value that differs by about 15% from the asymptotic limit.
(14)with αBzmin = 3.2 × 10-2 and Cz = 3.3 × 10-2, with fixed Rm and β. Moreover, there is good agreement between the compressible and incompressible approach in this vertical field case: for both flow types the simulations converge at small Pm toward the same α. As is true for the azimuthal field case, a good estimate of the asymptotic rate of angular momentum transport is already obtained for Pm = 0.13 (using a resolution of 128 cells per unit length), for which we found α = 3.7 × 10-2, i.e. a value that differs by about 15% from the asymptotic limit.
As already noted (Sect. 2.4), in the presence of a vertical magnetic field we find that the time history of α displays significant variability. This is illustrated in Fig. 4 (left panel) for the particular case of model Z-C-Re3000 (Pm = 0.13): while the time averaged transport rate amounts to α = 3.7 × 10-2 in that case, there are numerous peaks during which it reaches values as high as 0.1 that occur with a typical period of about 5 to 10 orbits. Such bursts are not unheard of in unstratified shearing boxes with a mean vertical field (Bodo et al. 2008; Latter et al. 2009) and have been attributed to recurrent “channel-like” modes associated with the MRI. For the set of parameters we have considered here, the time history of α suggests that they contribute significantly to the turbulent transport. In an attempt to quantify that contribution, for model Z-C-Re3000 we have calculated the value αaxi of the transport that is due to axisymmetric channel-like modes (for which 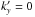 and
and 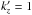 ) for 120 dumps evenly spaced between t = 40 and t = 100. The mean value of αaxi, averaged over all the dumps of the simulation, amounts to 1.2 × 10-2; this means that axisymmetric modes with
) for 120 dumps evenly spaced between t = 40 and t = 100. The mean value of αaxi, averaged over all the dumps of the simulation, amounts to 1.2 × 10-2; this means that axisymmetric modes with 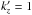 account for ~30% of the angular momentum transport. In agreement with the results of Longaretti & Lesur (2010), angular momentum transport is dominated on average by non-axisymmetric modes even if the contribution of channel-like modes is significant. The scatter plot showing the relation between α and αaxi for those 120 dumps is shown in the right panel of Fig. 4, along with an indicative fit of the data given by
account for ~30% of the angular momentum transport. In agreement with the results of Longaretti & Lesur (2010), angular momentum transport is dominated on average by non-axisymmetric modes even if the contribution of channel-like modes is significant. The scatter plot showing the relation between α and αaxi for those 120 dumps is shown in the right panel of Fig. 4, along with an indicative fit of the data given by 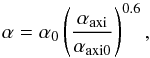 (15)with α0 = 10-2 and αaxi0 = 10-3. The positive correlation between α and αaxi indicates that the relative contribution of the transport mediated by axisymmetric modes with
(15)with α0 = 10-2 and αaxi0 = 10-3. The positive correlation between α and αaxi indicates that the relative contribution of the transport mediated by axisymmetric modes with 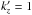 increases during the bursts of activity. For example, αaxi amounts to only about 10% of the transport when α = 10-2 but, as indicated by Eq. (15), can contribute up to 50% of the turbulent activity when α = 0.1. These variations are consistent with the results of Latter et al. (2009) and with the idea that the bursts seen in Fig. 4 are due to large-scale channel-like modes (Bodo et al. 2008). We have repeated the same analysis for all the models and we have found a weak dependance of the relative fraction of axisymmetric transport with Pm: αaxi/α = 0.39, 0.34, 0.32, and 0.29, respectively for Pm = 1, 0.5, 0.13, and 0.05 and similar results for the incompressible runs with αaxi/α = 0.38, 0.35, respectively for Pm = 0.02 and 0.01.
increases during the bursts of activity. For example, αaxi amounts to only about 10% of the transport when α = 10-2 but, as indicated by Eq. (15), can contribute up to 50% of the turbulent activity when α = 0.1. These variations are consistent with the results of Latter et al. (2009) and with the idea that the bursts seen in Fig. 4 are due to large-scale channel-like modes (Bodo et al. 2008). We have repeated the same analysis for all the models and we have found a weak dependance of the relative fraction of axisymmetric transport with Pm: αaxi/α = 0.39, 0.34, 0.32, and 0.29, respectively for Pm = 1, 0.5, 0.13, and 0.05 and similar results for the incompressible runs with αaxi/α = 0.38, 0.35, respectively for Pm = 0.02 and 0.01.
 |
Fig. 5 Time history of αMax (blue curve) and αRey (green curve) in model Z-C-Re3000. |
It is also noteworthy that the angular momentum transport in the presence of a vertical field is equally due to Maxwell and Reynolds stresses in the compressible simulation, whereas the classical ratio of approximately 3 is obtained in an incompressible fluid or with an azimuthal field configuration for the specific values of β and Rm chosen in our investigation. The exact value of the Maxwell-to-Reynolds stress ratio (R) are given in the last column of Tables 1−3. In an attempt to have a better understanding of the relative contribution of Maxwell and Reynolds stresses, we plot in Fig. 5 their time history over two burst cycles for the particular case of model Z-C-Re3000. This plot reveals that the Reynolds stress is larger than the Maxwell stress during the decaying part of the burst when the channel-like modes (with ky = 0 and kz = 1) are destroyed by the non-linear turbulent dynamics. The computation of the contribution of the axisymmetric modes shows that the Maxwell transport is dominated by channel-like modes whereas the Reynolds transport is due to non-axisymmetric modes. Because of the difference between the incompressible and compressible runs, we further speculate that such a destruction is associated with the excitation of compressible modes such as density waves. However, this detailed study is not directly related to the angular momentum transport rate and is beyond the scope of this paper.
3.2. Large eddy simulations in the small Pm limit
The previous results have shown that angular momentum transport converges toward a well-defined limit at small Pm. However, such simulations are very computationally expensive. Here, we investigate the possibility of using a subgrid scale model instead of standard kinematic viscosity. The aim is to reduce the computational cost of the simulations without compromising the physics one may want to consider, such as the accretion rate or the turbulent power spectra.
Historically, the study of small Pm flows has mostly relied on simulations using hyperviscosity such as geodynamo models (Glatzmaiers & Roberts 1995) or small-scale dynamo theory (Schekochihin et al. 2007). However, hyperviscosity is known to produce numerous artefacts in hydrodynamic turbulence, such as spectral bottlenecks, reduced intermittency, and spurious isotropization (Frisch et al. 2008). For this reason, we instead focus on LES in which the dissipation adapts dynamically to the turbulent cascade initiated by the large scales, thereby limiting the artefacts commonly due to hyperviscosity.
Large eddy simulations are routinely used in industrial applications to model flows at high Re. However, their MHD counterparts are not widespread, the reason being the higher complexity of the MHD turbulent cascade compared to the purely hydrodynamic cascade. Several subgrid-MHD models have been discussed in the literature including Smagorinsky-type models (Smagorinsky 1963; Yoshizawa 1987) which can be used in finite difference/volume codes and Chollet & Lesieur-type models (Chollet & Lesieur 1981; Baerenzung et al. 2008) targeted to spectral methods. However, most of these models are still under development and their applicability to Pm ≪ 1 flows is yet to be proven.
In this work we have chosen to use well-known hydrodynamical subgrid models to treat the kinetic turbulent cascade only, leaving the induction equation with standard Ohmic resistivity. This approach is valid provided that the subgrid model is introduced at a scale much smaller than the resistive scale, so that the energy cascade is mostly hydrodynamical. Moreover, it has the advantage of using well-tested subgrid models, which are reasonably simple to implement numerically. This type of method has already been used to study Taylor-Green flows (Ponty et al. 2004) and dynamo action (Ponty et al. 2005) in the limit Pm → 0. We therefore reproduce this approach using very similar tools in the MRI turbulence context.
3.2.1. Chollet-Lesieur model in incompressible simulations
Since our incompressible simulations are done with a spectral code, we have used the spectral subgrid model of Chollet & Lesieur (1981, hereafter CL) to perform our incompressible LES. This model replaces the standard viscosity ν by the following expression in Fourier space, ![\begin{equation} \nu_\mathrm{CL}(k)=\Bigg(\frac{E(k_{\rm c})}{k_{\rm c}}\Bigg)^{1/2}\Big(0.267+9.21\exp[-3.03k_{\rm c}/k]\Big) \end{equation}](/articles/aa/full_html/2015/07/aa25688-15/aa25688-15-eq240.png) (16)where kc is the cutoff scale and E(kc) is the kinetic energy at the cutoff scale5. This expression encloses long-range non-linear interactions via a constant viscosity at k ≪ kc and a cusp due to local energy transfers close to the cutoff scale kc. Interestingly, kc is the only free parameter of this model. The amount of viscosity itself is automatically adjusted according to the amount of energy at the cutoff scale. It should be emphasized that this expression is only valid for 3D homogeneous and isotropic Kolmogorov turbulence. In principle, it is therefore not applicable to turbulent shear flows found in shearing box models since such flows are anisotropic (see Sect. 3.1.1). As a first attempt to quantify this anisotropy, we proceed as follows. We define a decomposition in spherical harmonics6 such that
(16)where kc is the cutoff scale and E(kc) is the kinetic energy at the cutoff scale5. This expression encloses long-range non-linear interactions via a constant viscosity at k ≪ kc and a cusp due to local energy transfers close to the cutoff scale kc. Interestingly, kc is the only free parameter of this model. The amount of viscosity itself is automatically adjusted according to the amount of energy at the cutoff scale. It should be emphasized that this expression is only valid for 3D homogeneous and isotropic Kolmogorov turbulence. In principle, it is therefore not applicable to turbulent shear flows found in shearing box models since such flows are anisotropic (see Sect. 3.1.1). As a first attempt to quantify this anisotropy, we proceed as follows. We define a decomposition in spherical harmonics6 such that 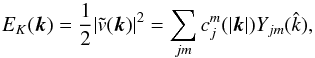 (17)and similarly for the magnetic energy. We focus on the l = 2 coefficients of the decomposition and define:
(17)and similarly for the magnetic energy. We focus on the l = 2 coefficients of the decomposition and define: 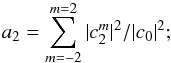 (18)here a2 takes significant values when there are strong variations of the energy over the shell or, in other words, when the flow displays anisotropy at that scale. As shown in Fig. 7, it decreases with k, but is still high at small scales for the kinetic energy. Nevertheless, we will see that the Chollet-Lesieur model gives satisfactory results.
(18)here a2 takes significant values when there are strong variations of the energy over the shell or, in other words, when the flow displays anisotropy at that scale. As shown in Fig. 7, it decreases with k, but is still high at small scales for the kinetic energy. Nevertheless, we will see that the Chollet-Lesieur model gives satisfactory results.
 |
Fig. 6 Mean value of the angular momentum transport (measured by means of α) for the mean toroidal field LES simulation (implicit LES blue circles), the mean vertical field LES simulation performed with RAMSES (implicit LES, green filled circles), and with SNOOPY (Chollet-Lesieur LES, green filled squares). The resolution is given in number of cells per scale height. The dashed lines represent the asymptotic limits obtained with DNS. |
 |
Fig. 7 Estimate of the anisotropy at each scale. For each wavenumber, the energy is decomposed into spherical harmonics; the anisotropy is estimated from the sum of the second-order coefficients normalized by the isotropic coefficient. |
We have performed several simulations using the CL subgrid model, varying kc and the resolution (runs Z-CL-XXX-X). Models labelled a have kc/kmax = 0.75 and models labelled b have kc/kmax = 1, where kmax is the maximum accessible wavenumber of the simulation (Table 3). As plotted in Fig. 6 (green squares), all of our models recover the statistical results of direct numerical simulations (DNS) with a reduced resolution. These encouraging results are confirmed by turbulent spectra compared to DNS simulation (Fig. 8). We find that both kinetic and magnetic spectra agree to less than 10% down to k ~ 20 with the highest resolution DNS Z-I-Re40000. We also find that simulations with k/kc = 0.75 exhibit the same convergence properties, at least for the resolution we studied. Therefore, the cutoff scale does not seem to have much impact on these results, provided it is below the resistive dissipation scale. These results demonstrate that CL models can be used efficiently to study low Pm flows with a gain in resolution of at least a factor of 2 associated with a gain in computation time of at least a factor of 20.
 |
Fig. 8 Ratio of power spectra of kinetic energy (top) and magnetic energy (bottom) obtained with a Chollet-Lesieur subgrid model with kc/kmax = 1 and full DNS calculation at Re = 40 000. |
 |
Fig. 9 Ratio between the power spectra obtained with RAMSES in the ILES (green, red, blue, and dotted curves and model Y-C-Re85000 in the azimuthal magnetic field cases. Top panel is for kinetic energy power spectrum and bottom panel for magnetic energy power spectrum. In both panels, the black horizontal line marks the location of the unity ratio. |
3.2.2. Implicit LES in compressible simulations
In the small Pm limit, the simplest possible subgrid scale model when using finite volume codes is certainly the so-called “Implicit LES” (ILES). The idea is to capture Ohmic resistivity explicitly in the simulation (since it occurs at large scale) but let numerical dissipation handle kinetic energy dissipation at small scales. This method has already been used in some previous works (Fleming et al. 2000; Inutsuka & Sano 2005; Okuzumi & Hirose 2011; Flock et al. 2012, 2015), but its range of validity has never been systematically and quantitatively investigated. In this section, we compare the results of such simulations performed with RAMSES at various resolutions with the results presented in Sect. 3.1.
The azimuthal field case:
the magnetic Reynolds number is here fixed to Rm = 2600 as it was for DNS. We performed a series of simulations with resolutions ranging from 64 to 256 cells per scale height. For all cases, we obtain α = 1.8 × 10-2, in very good agreement with our best resolved simulations at Pm = 0.03 (see Fig. 6). We then compared the kinetic and magnetic energy power spectra in these simulations with the spectra obtained in the DNS with the lowest Prandlt number (Y-C-Re85000). In the upper panel (resp. lower panel) of Fig. 9, we plot the ratio of the kinetic (resp. magnetic) power spectra between the ILES and the DNS. The runs give an acceptable agreement with the DNS at all available scales (except at small scales in the kinetic energy, which is a result of the different hydrodynamical dissipation): at all resolutions, the deviations to the DNS run for k′< 10 for both the kinetic and the magnetic energy spectra, are at most of the order of 15%.
The vertical field case:
the resolution in this case was varied from 32 cells per scale height to 256 cells per scale height. As can be seen in Fig. 6, α decreases as resolution increases, most likely as a result of the decrease of the effective numerical viscosity, and converges to the value determined by the DNS simulations. Quite surprisingly, however, the convergence as resolution is increased toward the asymptotic value of α at low Pm is slower than the azimuthal field case, even though Rm is much larger in that case. Indeed, with 64 cells per scale height, the difference between the two α values is still approximately 20%, while it has reached convergence in the case of a mean By. This is probably due to the stress dependence with Pm being steeper in the presence of a mean vertical field. In any case, 128 cells per scale height are needed to reach the asymptotic α value to less than 10%. We note that this is still a gain of a factor of 16 in computing time. The power spectra displayed in Fig. 10 confirm that result: there is a difference of about 50% between the power spectra of the ILES and the DNS at large scale for a resolution of 32 cells per scale height. Even the largest resolution reveals differences of up to 20% in both the kinetic and magnetic power spectra, even if the largest scales are converged to better than 10%, as is expected from the good agreement between the transport coefficients in both simulations (Fig. 6).
4. Conclusions
We briefly summarize the main results and ideas of the paper and discuss some of their limitations.
Our main goal was to investigate the properties of the turbulent state in the small magnetic Prandtl number limit by mean of local DNS simulations. We showed that in the presence of a mean magnetic field threading the domain, angular momentum transport converges to a finite value in the small Pm limit. This result is valid both with a vertical and with an azimuthal mean magnetic field with the asymptotic values at small Pm being, respectively, α = 1.8 × 10-2 with Rm = 2600 and βy ~ 102 and α = 3.2 × 10-2 with Rm = 400 and βz = 103. The obtained values with our set of parameters are consistent with the estimations computed from the lifetime and accretion rate of protoplanetary discs (α is a few 10-2). Obviously, a word of care is in order here: the magnetization of accretion discs, such as protoplanetary discs, is only loosely constrained and the value of the β parameter is unknown. The value of α is known to strongly depend on the field strength, with α proportional to β− 1/2 (Hawley et al. 1995) or β-1 (Bodo et al. 2011) in the vertical field case. Similarly, we can expect angular momentum transport to increase with the magnetic Reynolds number (Longaretti & Lesur 2010). The asymptotic values of the angular momentum rate we obtained are thus only valid for the β and Rm parameters we considered, and with a scaling that remains to be determined in the small Pm limit.
In the case of the compressible simulations with a mean vertical field, we obtained a surprising ratio of Maxwell to Reynolds stress of about 1. Notwithstanding any possible dependance with β and Rm, we noticed that this ratio is related to the compressibility of the fluid as a more usual value of about 3 is obtained in the incompressible runs. It is also related to the bursty behaviour of these two stresses: whereas a usual value is obtained in the growing phase of the bursts, the Reynolds stress dominates during its decreasing parts, resulting in a mean R value of about 1. This result is specific to the compressible simulations, but it implies that neither the Reynolds stress nor the Maxwell stress converges to the same value in compressible and incompressible simulations at low Pm. In fact, both stresses differ by about 50%, which we show can be attributed to their different behaviour during the bursts. It is possible that the convergence of α at low Pm to the same value with this two types of flow is fortuitous. In order to solve that issue, higher Rm simulations are needed but are currently very costly.
Next, we investigated the interest of using large eddy simulations both in spectral and real spaces for such simulations. The simplest approach is to consider the implicit LES method. As expected, in all cases the smallest scales are not correctly handled, but it is possible to reproduce the large-scale energy spectra by using a resolution that is high enough. To obtain an error smaller than 20% on α, the needed resolution corresponds to a fourth of the resolution needed when explicit viscosity is included. This corresponds to a decrease in CPU time of a factor of 256. To limit the computational cost of a simulation of a turbulent flow, explicit subgrid scale (SGS) models are also usually considered. The anisotropy of the rotating sheared flow and the turbulent cascade, which differs from the Kolmogorov cascade, may indicate that simple SGS approaches are not well suited for MRI turbulence simulations. We tested the Chollet-Lesieur method which is used in spectral space and is applied directly on the spectrum components. This method is local in frequency space, the effective viscosity being a function of the wave number, and there is a limited inclusion of the backscatter. We found that good results are also obtained with the Chollet-Lesieur approach notwithstanding the anisotropy of the flow at small scales.
Despite such positive results, a word of care is in order here. Although we showed that these methods are efficient at decreasing the computational cost of MRI turbulence simulations, the needed resolution is still significant. For a magnetic Reynolds number Rm = 400 with a vertical mean magnetic field, the required resolution is 64 pts/H. This Rm is low compared to the values that are often chosen in the literature for which an even higher resolution is then necessary. To reach a turbulent flow dominated by Ohmic dissipation, a resolution of at least 256 pts/H will be needed for Rm values of a few thousands. Moreover, we considered only two diagnostics, namely the angular momentum transport rate and the power spectra, to reach this conclusion and other diagnostics, such as helicity or correlation functions, were not considered. Such statistical quantities may well be incorrectly described in our LES for the resolutions we used. More generally, with such reduced resolutions, any small scale process is not correctly handled, and for instance the study of collision of grains in protoplanetary discs or magnetic reconnection cannot be studied in such simulations.
Overall we still conclude that LES can be used to limit the computational time of future simulations. Future works should account for density stratification, which will be particularly relevant in the context of global simulations. Large-scale phenomena such as the ones identified in the “butterflies diagrams” can strongly modify the flow properties and are likely to affect the LES approach. Dedicated simulations should be performed to quantify the interest of such methods in this case.
The numerical stability of the scheme does not require any dissipation. However, the absence of dissipation in a turbulent flow naturally leads to thermalization, a situation which does not occur in natural systems, which always exhibit dissipation processes. Numerical dissipation is therefore required on physical grounds to break the thermodynamic equilibrium and create the well-known energy cascade picture.
The asymptotic transport values αBymin and αBzmin depend in principle on Rm and β. See the discussion in Sect. 4.
Several forms for the CL viscosity may be found in the literature since this expression is a fit to numerical EDQNM (eddy-damped quasi-normal Markovian) calculations. Our expression comes from the asymptotic viscosity of Chollet & Lesieur (1981) and a fit close to kc of Sagaut (2006).
This use of spherical harmonics to estimate the anisotropy of turbulence is a standard procedure for the study of sheared flows (e.g. Biferale & Vergassola 2001).
Acknowledgments
H.M., S.F., and M.J. acknowledge funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007−2013)/ERC Grant agreement No. 258729. G.L. acknowledges support by the European Community via contract PCIG09-GA-2011-294110. The simulations presented in this paper were granted access to the HPC resources of CCRT under the allocation x2012042231 made by GENCI (Grand Équipement National de Calcul Intensif).
References
- Baerenzung, J., Politano, H., Ponty, Y., & Pouquet, A. 2008, Phys. Rev. E, 77, 046303 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bai, X.-N. 2015, ApJ, 798, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2011, ApJ, 736, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2013, ApJ, 769, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2014, ApJ, 796, 31 [Google Scholar]
- Balbus, S. A. 2003, ARA&A, 41, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Balbus, S. A., & Henri, P. 2008, ApJ, 674, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Beresnyak, A. 2014, ApJ, 784, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Biferale, L., & Vergassola, M. 2001, Phys. Fluids, 13, 2139 [NASA ADS] [CrossRef] [Google Scholar]
- Bodo, G., Mignone, A., Cattaneo, F., Rossi, P., & Ferrari, A. 2008, A&A, 487, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodo, G., Cattaneo, F., Ferrari, A., Mignone, A., & Rossi, P. 2011, ApJ, 739, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Nordlund, A., Stein, R. F., & Torkelsson, U. 1995, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Chollet, J.-P., & Lesieur, M. 1981, J. Atmosph. Science, 38, 2747 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [Google Scholar]
- Fleming, T. P., Stone, J. M., & Hawley, J. F. 2000, ApJ, 530, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Henning, T., & Klahr, H. 2012, ApJ, 761, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Ruge, J. P., Dzyurkevich, N., et al. 2015, A&A, 574, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics: Third Edition (Cambridge University Press) [Google Scholar]
- Frisch, U., Kurien, S., Pandit, R., et al. 2008, Phys. Rev. Lett., 101, 144501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fromang, S. 2010, A&A, 514, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S. 2013, EAS Pub. Ser., 62, 95 [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fromang, S., Papaloizou, J., Lesur, G., & Heinemann, T. 2007, A&A, 476, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glatzmaiers, G. A., & Roberts, P. H. 1995, Nature, 377, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Guan, X., Gammie, C. F., Simon, J. B., & Johnson, B. M. 2009, ApJ, 694, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., & Balbus, S. A. 1992, ApJ, 400, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 464, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Herault, J., Rincon, F., Cossu, C., et al. 2011, Phys. Rev. E, 84, 036321 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-i., & Sano, T. 2005, ApJ, 628, L155 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Youdin, A., & Klahr, H. 2009, ApJ, 697, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Pringle, J. E., & Livio, M. 2007, MNRAS, 376, 1740 [NASA ADS] [CrossRef] [Google Scholar]
- Kunz, M. W., & Lesur, G. 2013, MNRAS, 434, 2295 [NASA ADS] [CrossRef] [Google Scholar]
- Latter, H. N., Lesaffre, P., & Balbus, S. A. 2009, MNRAS, 394, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2007, MNRAS, 378, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2011, A&A, 528, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., Kunz, M. W., & Fromang, S. 2014, A&A, 566, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longaretti, P.-Y., & Lesur, G. 2010, A&A, 516, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, J., Cattaneo, F., & Boldyrev, S. 2008, Phys. Rev. E, 77, 036403 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyoshi, T., & Kusano, K. 2005, J. Comput. Phys., 208, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, G. C., & Pessah, M. E. 2015, ApJ, 802, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., & Hirose, S. 2011, ApJ, 742, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ponty, Y., Politano, H., & Pinton, J.-F. 2004, Phys. Rev. Lett., 92, 144503 [NASA ADS] [CrossRef] [Google Scholar]
- Ponty, Y., Mininni, P. D., Montgomery, D. C., et al. 2005, Phys. Rev. Lett., 94, 164502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Riols, A., Rincon, F., Cossu, C., et al. 2013, J. Fluid Mech., 731, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Riols, A., Rincon, F., Cossu, C., et al. 2015, A&A, 575, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sagaut, P. 2006, Large Eddy Simulation for Incompressible Flows (Springer) [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L., & McWilliams, J. C. 2004, ApJ, 612, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Iskakov, A. B., Cowley, S. C., et al. 2007, New J. Phys., 9, 300 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Simon, J. B., & Hawley, J. F. 2009, ApJ, 707, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Hawley, J. F., & Beckwith, K. 2011, ApJ, 730, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, J. B., Bai, X.-N., Armitage, P. J., Stone, J. M., & Beckwith, K. 2013, ApJ, 775, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Smagorinsky, J. 1963, Mon. Weather Rev., 91, 99 [Google Scholar]
- Stone, J. M., & Gardiner, T. A. 2010, ApJS, 189, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1996, ApJ, 463, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoshizawa, A. 1987, Phys. Fluids, 30, 1089 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top panel: time evolution of α in model Y-C-Re85000 for which Pm = 0.03. The initial 15 orbits were performed in the ideal MHD regime, before including explicit diffusion coefficients. The hatched region represents the time interval over which the angular momentum transport is averaged. Bottom panel: Y-C-Re85000 run, kinetic (solid green line) and magnetic energy (dashed blue line) power spectrum. |
| In the text | |
 |
Fig. 2 From left to right, 3D snapshots of ρ, By, and vz in model Y-C-Re85000 at the end of the simulation. |
| In the text | |
 |
Fig. 3 Mean value of the angular momentum transport (measured by means of α) for the mean toroidal field simulations (blue circles), the mean vertical field simulations performed with RAMSES (green filled circles), and with SNOOPY (green filled squares). The dashed lines are power-law functions that approximately describe the data (see text). |
| In the text | |
 |
Fig. 4 Left panel: time history of α (blue curve), αMax (red curve), and αRey (green curve) in model Z-C-Re3000. Right panel: scatter plot showing the total angular momentum transport rate α as a function of αaxi which measures the angular momentum transport due to |
| In the text | |
 |
Fig. 5 Time history of αMax (blue curve) and αRey (green curve) in model Z-C-Re3000. |
| In the text | |
 |
Fig. 6 Mean value of the angular momentum transport (measured by means of α) for the mean toroidal field LES simulation (implicit LES blue circles), the mean vertical field LES simulation performed with RAMSES (implicit LES, green filled circles), and with SNOOPY (Chollet-Lesieur LES, green filled squares). The resolution is given in number of cells per scale height. The dashed lines represent the asymptotic limits obtained with DNS. |
| In the text | |
 |
Fig. 7 Estimate of the anisotropy at each scale. For each wavenumber, the energy is decomposed into spherical harmonics; the anisotropy is estimated from the sum of the second-order coefficients normalized by the isotropic coefficient. |
| In the text | |
 |
Fig. 8 Ratio of power spectra of kinetic energy (top) and magnetic energy (bottom) obtained with a Chollet-Lesieur subgrid model with kc/kmax = 1 and full DNS calculation at Re = 40 000. |
| In the text | |
 |
Fig. 9 Ratio between the power spectra obtained with RAMSES in the ILES (green, red, blue, and dotted curves and model Y-C-Re85000 in the azimuthal magnetic field cases. Top panel is for kinetic energy power spectrum and bottom panel for magnetic energy power spectrum. In both panels, the black horizontal line marks the location of the unity ratio. |
| In the text | |
 |
Fig. 10 Same as Fig. 9, but for the vertical field case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


