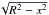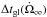| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 6 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201525667 | |
| Published online | 03 June 2015 | |
Properties and observability of glitches and anti-glitches in accreting pulsars
1 Institut für Astronomie und Astrophysik, Eberhard Karls Universität, Sand 1, 72076 Tübingen, Germany
e-mail: ducci@astro.uni-tuebingen.de
2 ISDC Data Center for Astrophysics, Université de Genève, 16 chemin d’Écogia, 1290 Versoix, Switzerland
3 Dipartimento di Fisica, Università degli Studi di Milano, via Celoria 16, 20133 Milano, Italy
4 Istituto Nazionale di Fisica Nucleare, sezione di Milano, via Celoria 16, 20133 Milano, Italy
5 INAF–Istituto di Astrofisica Spaziale e Fisica Cosmica, via E. Bassini 15, 20133 Milano, Italy
Received: 15 January 2015
Accepted: 29 April 2015
Several glitches have been observed in young, isolated radio pulsars, while a clear detection in accretion-powered X-ray pulsars is still lacking. We use the Pizzochero snowplow model for pulsar glitches as well as starquake models to determine for the first time the expected properties of glitches in accreting pulsars and their observability. Since some accreting pulsars show accretion-induced long-term spin-up, we also investigate the possibility that anti-glitches occur in these stars. We find that glitches caused by quakes in a slow accreting neutron star are very rare and their detection extremely unlikely. On the contrary, glitches and anti-glitches caused by a transfer of angular momentum between the superfluid neutron vortices and the non-superfluid component may take place in accreting pulsars more often. We calculate the maximum jump in angular velocity of an anti-glitch and we find that it is expected to be ΔΩa − gl ≈ 10-5 − 10-4 rad s-1. We also note that since accreting pulsars usually have rotational angular velocities lower than those of isolated glitching pulsars, both glitches and anti-glitches are expected to have long rise and recovery timescales compared to isolated glitching pulsars, with glitches and anti-glitches appearing as a simple step in angular velocity. Among accreting pulsars, we find that GX 1+4 is the best candidate for the detection of glitches with currently operating X-ray instruments and future missions such as the proposed Large Observatory for X-ray Timing (LOFT).
Key words: accretion, accretion disks / dense matter / stars: neutron / X-rays: binaries / X-rays: individuals: GX 1+4
© ESO, 2015
1. Introduction
Isolated pulsars are considered remarkably stable rotators showing long-term spin-down caused by the emission of electromagnetic dipole radiation, relativistic outflows, and possibly gravitational waves (Aasi et al. 2015). However, they have sometimes been observed to glitch. Glitches are sudden increases in the spin rate followed by a relaxation toward a steadily, long-term, decreasing spin rate. They have been observed in over 100 isolated radio pulsars and magnetars (see, e.g., Espinoza et al. 2011; Yu et al. 2013; Dib et al. 2008), with jumps in angular velocity up to ΔΩgl ≈ 10-4 rad s-1.
There are two main models to explain glitches: the starquake glitch model (e.g., Baym & Pines 1971) and the superfluid vortex unpinning model (Anderson & Itoh 1975; see also Haskell & Melatos 2015, for a recent review on models of pulsar glitches). In the starquake glitch model of Baym & Pines (1971), a rapidly rotating pulsar has an oblate crust that deforms toward an almost spherical shape as the pulsar slows down. This leads to a sudden crack in the crust and a decrease in the moment of inertia resulting in a sudden increase in the angular velocity of the star. In the model proposed by Anderson & Itoh (1975) the glitch is caused by a sudden unpinning of neutron superfluid vortices from the lattice nuclei in different regions of the interior of a neutron star (NS). The angular momentum stored in the superfluid vortices is then transferred to the non-superfluid component of the star, leading to the observed fast spin-up of the NS rotation angular velocity.
No clear observational evidence that accreting NSs experience glitches has been presented so far. Nonetheless, they have been proposed as a possible explanation of the peculiar timing behavior of some accreting pulsars. Galloway et al. (2004) observed a sudden spin-up (with a fractional change in frequency of ~3.7 × 10-5 in ≲10 h) in the accreting 18.7 s pulsar KS 1947+300 with RXTE, that was interpreted as a glitch event. Contrary to what happens in the classical glitch scenario, the sudden spin-up was observed when the NS was already spinning up because of the transfer of angular momentum from the accretion disk. Galloway et al. (2004) did not rule out the possibility that the sudden spin-up was caused by a short episode of enhanced accretion. Klochkov et al. (2009) studied the pulse period variations of Her X−1 using Swift/BAT data. They found two spin-down episodes followed by spin-up intervals where the spin period increased exponentially, a phenomenon typical of the post-glitch recovery stage, but with an opposite sign.
Observations of glitching pulsars showed that the glitch frequency increases with the long-term spin-down rate (Espinoza et al. 2011). Since the spin-down caused by electromagnetic braking decreases as pulsars age, the detection of glitches in old pulsars (>104 yr, Espinoza et al. 2011), such as accreting pulsars in X-ray binaries, is expected to drop. In this paper we show that glitch frequency in accreting pulsars in X-ray binaries can actually be higher than expected for old pulsars. The aim of this paper is to assess the conditions under which glitches are more likely to occur in an accreting pulsar and investigate, for the first time, the expected properties of glitches in these objects.
In Sect. 2 we calculate the expected jump in angular velocity and the interglitch interval in the starquake and superfluid vortex scenarios, assuming that glitches occur during a long-term spin-down. Then, we investigate the properties of anti-glitches (sudden spin-down) during long-term spin-up of the NS. We modified the model of Pizzochero (2011) to calculate the jump in angular velocity in this scenario. In Sect. 3 we discuss the observability of glitches and anti-glitches in accreting X-ray pulsars.
2. Properties of glitches in accreting pulsars
Pulsars in X-ray binary systems (XRBs) can experience spin-up and spin-down caused by the interaction between the accretion flow and the magnetosphere of the NS (Pringle & Rees 1972; Rappaport & Joss 1977). The interaction may occur directly from the wind of the donor star or through an accretion disk (e.g., Bildsten et al. 1997, and references therein). In some XRBs (see examples in Table 1) the accretion torque is responsible for variations of the angular velocity of the NS of magnitude comparable to that caused by the electromagnetic braking torque in young, glitching pulsars (10-15−10-10 rad s-2, Lyne et al. 2000 and, for comparison, Table 1). Since the rate of glitches increases with the spin-down rate (see following sections), glitches in XRBs should be quite frequent. In the next sections we derive their main properties in different scenarios.
Rotational parameters and luminosities of four accreting pulsars showing among the largest and stable spin-down rates (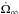 ) in XRBs.
) in XRBs.
2.1. Starquake glitch scenario
The Baym-Pines model allows the time Δtq to the next quake to be estimated from the magnitude of the preceeding one through the equation 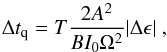 (1)where
(1)where 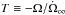 is the characteristic timescale at which the pulsar slows down because of the loss of rotational energy, Ω is the rotational angular velocity of the NS,
is the characteristic timescale at which the pulsar slows down because of the loss of rotational energy, Ω is the rotational angular velocity of the NS, 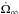 is the long-term spin-down rate, | Δϵ | is the reduction in oblateness ϵ caused by the quake in the previous glitch, A and B are coefficients describing respectively the gravitational and elastic energy stored in the NS as a result of its rotation, and I0 is the moment of inertia. The values of A, B, and I0 depend on the equation of state (EoS) of the neutron star core and on the crust model adopted. Here we adopt the parameters obtained by Pandharipande et al. (1976) and Zdunik et al. (2008), which updated the Baym-Pines model using different EoSs and crust models.
is the long-term spin-down rate, | Δϵ | is the reduction in oblateness ϵ caused by the quake in the previous glitch, A and B are coefficients describing respectively the gravitational and elastic energy stored in the NS as a result of its rotation, and I0 is the moment of inertia. The values of A, B, and I0 depend on the equation of state (EoS) of the neutron star core and on the crust model adopted. Here we adopt the parameters obtained by Pandharipande et al. (1976) and Zdunik et al. (2008), which updated the Baym-Pines model using different EoSs and crust models.
We assume different values of Δϵ ranging from 10-10 to 10-6 (which are the typical values of glitches observed in isolated pulsars). We use Ω and 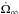 of the four XRBs in Table 1. We find that for any value of Ω,
of the four XRBs in Table 1. We find that for any value of Ω, 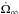 , A, B, I0, and Δϵ, Δtq is always greater than 105 yr. The value of Δtq can be ≪105 yr for Δϵ ≪ 10-10. However, starquakes with such small Δϵ would be difficult to detect. Therefore, the detection of a glitch produced by a starquake in an accreting pulsar is extremely unlikely. Moreover, Zdunik et al. (2008) showed that an accreted crust is softer to an elastic deformation than the crust of an isolated pulsar1. As a consequence, Δtq would be longer and glitches caused by quakes rarer.
, A, B, I0, and Δϵ, Δtq is always greater than 105 yr. The value of Δtq can be ≪105 yr for Δϵ ≪ 10-10. However, starquakes with such small Δϵ would be difficult to detect. Therefore, the detection of a glitch produced by a starquake in an accreting pulsar is extremely unlikely. Moreover, Zdunik et al. (2008) showed that an accreted crust is softer to an elastic deformation than the crust of an isolated pulsar1. As a consequence, Δtq would be longer and glitches caused by quakes rarer.
2.2. Superfluid vortex scenario
Our calculation of the interval between glitches Δtgl and of the jump in angular velocity ΔΩgl of accreting pulsars in the superfluid vortex scenario is based on the “snowplow” model of Pizzochero (2011). In this model, the matter of the NS is divided into two components: the neutron superfluid and the normal component (charged components that corotate with the pulsar magnetic field). In the core (r<Rc ≈ 9.3 km) and inner crust (Rc<r<R = 10 km) the rotating superfluid is organized as an array of vortices parallel to the spin axis of the NS2. The vortices are pinned to the crustal lattice of ions, but are not coupled with the normal component of the star. Therefore, although the crust spins-down because of the electromagnetic braking, the superfluid conserves its angular momentum3. As the NS spins down, a rotational lag builds up between the superfluid vortices and the normal component. When it reaches a critical value, a hydrodynamical force acting on vortices, the Magnus force, unpins and moves them out. The Pizzochero (2011) model introduces for the first time a density profile of the pinning force with maximum value fm = 1.1 × 1015 dyn cm-1 at densities ρm ≈ 0.2ρ0, where ρ0 = 2.8 × 1014 g cm-3 is the nuclear saturation density. Because of the shape of the density profile of the pinning force, the critical rotational lag for depinning is maximum at xm ≈ 9.7 km (in cylindrical coordinates, with the z-axis parallel to the spin axis). Therefore, vortices from x<xm accumulates in a vortex sheet at xm. When the rotational lag at xm reaches the critical value, the vortex sheet suddenly moves out and exchanges the stored angular momentum with the normal component, causing a glitch.
With this model it is possible to determine the fraction of vortices pinned to the lattice nuclei in different regions of the interior of a neutron star and the timescale of the pinning−unpinning process. The model can be used to predict the interval between glitches Δtgl, the jump in angular velocity ΔΩgl and the jump in angular acceleration 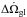 during a glitch.
during a glitch.
We leave the observables Ω and 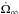 as well as the two free parameters of the model fm and Ygl free to vary. The parameter Ygl describes the fraction of vorticity coupled to the normal crust on timescales of the glitch rise time (≲40 s; Dodson et al. 2002).
as well as the two free parameters of the model fm and Ygl free to vary. The parameter Ygl describes the fraction of vorticity coupled to the normal crust on timescales of the glitch rise time (≲40 s; Dodson et al. 2002).
According to Pizzochero (2011), the interval between glitches can be expressed as 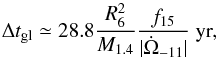 (2)where R6 = RNS/ 106 cm, M1.4 = MNS/ 1.4 M⊙, f15 = fm/1015 dyn cm-1, and
(2)where R6 = RNS/ 106 cm, M1.4 = MNS/ 1.4 M⊙, f15 = fm/1015 dyn cm-1, and 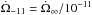 rad s-2.
rad s-2.
When 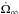 increases, Δtgl decreases resulting in a larger probability that a glitch will be observed. Indeed, the greater the spin-down rate of the crust, the more quickly the critical rotational lag for depinning will be reached. In addition, Eq. (2) shows that when fm increases, Δtgl also increases owing to the larger unpinning critical lag required by the Magnus forces acting on the neutron vortices to overcome the pinning force.
increases, Δtgl decreases resulting in a larger probability that a glitch will be observed. Indeed, the greater the spin-down rate of the crust, the more quickly the critical rotational lag for depinning will be reached. In addition, Eq. (2) shows that when fm increases, Δtgl also increases owing to the larger unpinning critical lag required by the Magnus forces acting on the neutron vortices to overcome the pinning force.
The jump in angular velocity is given by (Pizzochero 2011), ![\begin{equation} \label{eq. delta omega_gl} \Delta \Omega_{\rm gl} \simeq 1.25 \times 10^{-4} \frac{Q_{0.95}R_6^2f_{15}}{M_{1.4}[1 - Q_{0.95}(1-Y_{0.05})]} \mbox{ rad s}^{-1} , \end{equation}](/articles/aa/full_html/2015/06/aa25667-15/aa25667-15-eq71.png) (3)where Q0.95 = Q/ 0.95 (Zuo et al. 2004), Q is the superfluid fraction of the star, and Y0.05 = Ygl/ 0.05 (Pizzochero 2011).
(3)where Q0.95 = Q/ 0.95 (Zuo et al. 2004), Q is the superfluid fraction of the star, and Y0.05 = Ygl/ 0.05 (Pizzochero 2011).
When fm increases, ΔΩgl increases because of the larger number of neutron vortices unpinned simultaneously (see Pizzochero 2011). Equation (3) also shows that when Ygl increases, ΔΩgl decreases because of the reduced number of vortices storing angular momentum coupled to the normal component of the neutron star.
Since accreting pulsars usually have angular velocities smaller than those of isolated pulsars, we expect the glitch rise time and the recovery time after glitch4 to be longer in accreting pulsars. Indeed, these timescales depend on the coupling timescale between the superfluid and the normal component, which is inversely proportional to the angular velocity of the NS: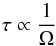 (4)(see, e.g., Haskell & Antonopoulou 2014 and references therein). Therefore, since the glitch rise time of Vela pulsar (ΩVela = 70 rad s-1) is τVela ≈ 1 − 10 s (Haskell et al. 2012), in a slow rotator such as GX 1+4 it would be τGX1 + 4 ≈ 103 − 104 s. Similarly, the recovery timescales of slow rotators become longer as well. The glitch is expected to appear as a simple step in angular velocity.
(4)(see, e.g., Haskell & Antonopoulou 2014 and references therein). Therefore, since the glitch rise time of Vela pulsar (ΩVela = 70 rad s-1) is τVela ≈ 1 − 10 s (Haskell et al. 2012), in a slow rotator such as GX 1+4 it would be τGX1 + 4 ≈ 103 − 104 s. Similarly, the recovery timescales of slow rotators become longer as well. The glitch is expected to appear as a simple step in angular velocity.
Glitches with relaxation timescales longer than those of Vela pulsar have been observed in some slower anomalous X-ray pulsars (Haskell & Antonopoulou 2014; Dib et al. 2008). The glitch rise time has not yet been measured. An upper-limit of ~40 s has been placed by Dodson et al. (2002) for Vela pulsar.
2.3. Anti-glitch scenario
Some XRBs show long-term spin-ups with timescales on the order of ~10 years (e.g., 12 yr of 4U 1626−67; Chakrabarty et al. 1997 and referencese therein), and rates up to 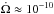 rad s-2 (e.g., KS 1947+300; Galloway et al. 2004). In principle they are good candidates for experiencing the anti-glitch scenario proposed by Pines et al. (1980), in which a pulsar can show a sudden spin-down caused by a mechanism of angular momentum transfer similar to that of glitches.
rad s-2 (e.g., KS 1947+300; Galloway et al. 2004). In principle they are good candidates for experiencing the anti-glitch scenario proposed by Pines et al. (1980), in which a pulsar can show a sudden spin-down caused by a mechanism of angular momentum transfer similar to that of glitches.
Here we adapt the snowplow model of Pizzochero (2011) to the scenario proposed by Pines et al. (1980) to calculate the expected jump in angular velocity caused by an anti-glitch ΔΩa − gl. Hereafter we will use cylindrical coordinates as shown in Fig. 1.
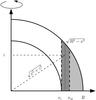 |
Fig. 1 Schematic representation of the cylindrical geometry assumed in Sect. 2.3. The z-axis is parallel to the spin-axis of the NS. The dotted line shows a vortex line with half length |
In the glitch scenario, when the pulsar slows down, vortices from the core region are expelled outward, allowing the angular momentum of the core to rebalance easily, while the vortices in excess are accumulated at the boundary xc and then expelled outward as vortex sheet. In the anti-glitch scenario, on the contrary, the crust accelerates. Before the anti-glitch, new vortices are created at R, near the equator, as the star accelerates. They are accumulated in a vortex sheet by the external depinning front5 that moves inward from R to xm. In the meantime, as the internal depinning front moves across the region x<xm, the vorticity moves from the inner crust to the core and rebalances the angular momentum in the core region. Since the number of vortices within xm does not change, their accumulation in the core region must correspond to a depletion in the regions of the inner crust with lower pinning potential, which is around xc, the boundary between the two regions (see Pizzochero 2011 and Figs. 1 and 3 therein). We assume that when the vortices accumulated at xm by the external depinning front are released simultaneously, they fill the depleted region around xc. Hence, the transfer of angular momentum will take place in the region xc ≲ x ≲ xm. We point out that the minimum (xmin) and maximum (xmax) radii of the depletion region are unknown. A precise estimate of these values requires a detailed study of vortex dynamics. Nonetheless, it is still possible to roughly estimate the order of magnitude of the jump in angular velocity caused by an anti-glitch relying on a few reasonable assumptions on xmin and xmax as described below.
According to Seveso et al. (2012), the angular velocity of the superfluid component of the star Ωs(x) is given by 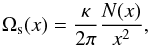 (5)where N(x) is the number of vortices in a cylindrical region of radius x, κ = πħ /mN, and mN is the mass of a neutron. Using Eq. (5), the number of vortices removed from the region xm<x<R and accumulated at xm before the anti-glitch is
(5)where N(x) is the number of vortices in a cylindrical region of radius x, κ = πħ /mN, and mN is the mass of a neutron. Using Eq. (5), the number of vortices removed from the region xm<x<R and accumulated at xm before the anti-glitch is 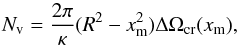 (6)where ΔΩcr(xm) is the critical rotational lag for depinning at xm. Since we do not know the exact size of the re-coupling region, we calculate the angular momentum released during the anti-glitch ΔLa − gl based on two different assumptions. In the first case we assume that Nv vortices will be uniformly distributed in xmin<x<xm by integrating
(6)where ΔΩcr(xm) is the critical rotational lag for depinning at xm. Since we do not know the exact size of the re-coupling region, we calculate the angular momentum released during the anti-glitch ΔLa − gl based on two different assumptions. In the first case we assume that Nv vortices will be uniformly distributed in xmin<x<xm by integrating 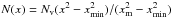 , where xmin corresponds to the minimum radius of the depletion zone around the boundary xc. From the definition dL = ΩsdIs, ΔLa − gl can be expressed as
, where xmin corresponds to the minimum radius of the depletion zone around the boundary xc. From the definition dL = ΩsdIs, ΔLa − gl can be expressed as 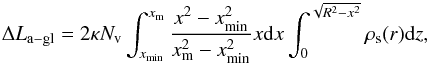 (7)where
(7)where 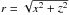 and
and 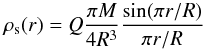 is the superfluid density profile (Pizzochero 2011). In the second case, we assume that Nv vortices will be uniformly distributed in xc<x<xmax (xmax<xm), where the pinning potential is lower. In this case, ΔLa − gl is
is the superfluid density profile (Pizzochero 2011). In the second case, we assume that Nv vortices will be uniformly distributed in xc<x<xmax (xmax<xm), where the pinning potential is lower. In this case, ΔLa − gl is 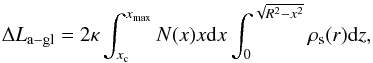 (8)where
(8)where 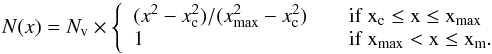 (9)The jump in angular velocity of the normal component of the NS caused by the anti-glitch is thus given by
(9)The jump in angular velocity of the normal component of the NS caused by the anti-glitch is thus given by ![\begin{equation} \label{eq domega_agl} \Delta \Omega_{\rm a-gl} = \frac{\Delta L_{\rm a-gl}}{I_{\rm tot}[1-Q(1-Y_{\rm gl})]} , \end{equation}](/articles/aa/full_html/2015/06/aa25667-15/aa25667-15-eq109.png) (10)where Itot is the total momentum of inertia of the NS. In Eqs. (7) and (8) we integrate on the cylindrical regions xmin<x<xm and xc<x<xmax, where xmin and xmax are unknown. Under the reasonable assumption that xmin and xmax are close to xc, where the pinning potential of the inner crust is lower, we find that | ΔΩa − gl | is approximately 10-5 − 10-4 rad s-1 assuming fm = 1.1 × 1015 dyn cm-1 and Ygl = 0.05.
(10)where Itot is the total momentum of inertia of the NS. In Eqs. (7) and (8) we integrate on the cylindrical regions xmin<x<xm and xc<x<xmax, where xmin and xmax are unknown. Under the reasonable assumption that xmin and xmax are close to xc, where the pinning potential of the inner crust is lower, we find that | ΔΩa − gl | is approximately 10-5 − 10-4 rad s-1 assuming fm = 1.1 × 1015 dyn cm-1 and Ygl = 0.05.
We note that Eq. (2) can also be used to describe the interval between anti-glitches. Indeed, Δtgl is the time required to reach the critical rotational lag for depinning, no matter whether the rotational lag between the superfluid vortices and the normal component has been built through a long-term spin-down or a long-term spin-up. Hereafter we will use Δtgl both for glitches and for anti-glitches.
3. Observability
The results of the previous section indicate that, in the case of accreting pulsars, glitches (anti-glitches) should have maximum jumps in angular velocity ΔΩgl ≈ 1.3 × 10-4 rad s-1 (ΔΩa − gl ≈ 10-5 − 10-4 rad s-1), rise time τrise ≈ (102 − 103)Ω-1 s, and long recovery timescales making them appear as simple steps in angular velocity leaving 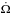 nearly unchanged.
nearly unchanged.
In accreting pulsars, accretion torque variations (including sign reversals) result in changes in the NS angular velocity. Several transitions between spin-up and spin-down have been observed (Nelson et al. 1997) and have been explained so far with sharp changes in the coupling between the matter flowing toward the NS and the magnetosphere. Several models have been proposed both for disk- and wind-fed pulsars (e.g., Zhang & Li 2010 and references therein; Wang 1981). However, a widely accepted model does not yet exist. The timescale t∞ between two torque reversals varies from source to source. Some pulsars show numerous torque reversals with moderate spin period derivative (e.g., Vela X−1, Her X−1; Bildsten et al. 1997), others show quasi-periodic torque reversals superimposed on a long-term spin-up trend (e.g., OAO 1657−415, Barnstedt et al. 2008; EXO 2030+375, Fermi/GBM6; SAX J2103.5+4545, Camero et al. 2014), while others show steady spin-up or spin-down sporadically interrupted by a torque reversal (e.g., GX 1+4, González-Galán et al. 2012; 4U 1626−67, Beri et al. 2014; 4U 1907+09, Inam et al. 2009).
 |
Fig. 2 Δtgl − t∞ diagram of 13 accreting pulsars. Black refers to spin-down, blue to spin-up. Pulsars with horizontal arrows experience a “random walk” of the spin period, and so the value Δtgl reported in the diagram is a lower-limit. Pulsars with vertical arrows have ongoing spin-up or spin-down. We obtained t∞ and |
It is interesting to compare, for each pulsar, t∞ with Δtgl, the time needed to reach the critical rotational lag for depinning. The accreting pulsars with sufficiently long time intervals of spin-down or spin-up (i.e., with t∞ ≳ Δtgl) are those more likely to experience glitches or anti-glitches. In Fig. 2 we show t∞ and Δtgl for a sample of accreting pulsars. We calculate Δtgl from 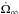 using Eq. (2) and obtain t∞ and
using Eq. (2) and obtain t∞ and 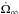 from previous works or from the Fermi/GBM monitoring archive. Black symbols refer to the values observed during a long-term spin-down, while those obtained during a long-term spin-up are plotted in blue (for some pulsars, e.g., 4U 1626−67, both spin-up and spin-down episodes have been observed, hence both cases are indicated). For those pulsars that exhibit quasi-periodic torque reversals superimposed on a long-term spin-up, namely OAO 1657−415, EXO 2030+375, and SAX J2103.5+4545, we use t∞ and Δtgl related to the long-term spin-up. For persistent pulsars that show a “random walk” of the spin period with several torque reversals and moderate
from previous works or from the Fermi/GBM monitoring archive. Black symbols refer to the values observed during a long-term spin-down, while those obtained during a long-term spin-up are plotted in blue (for some pulsars, e.g., 4U 1626−67, both spin-up and spin-down episodes have been observed, hence both cases are indicated). For those pulsars that exhibit quasi-periodic torque reversals superimposed on a long-term spin-up, namely OAO 1657−415, EXO 2030+375, and SAX J2103.5+4545, we use t∞ and Δtgl related to the long-term spin-up. For persistent pulsars that show a “random walk” of the spin period with several torque reversals and moderate 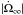 (Vela X−1, Cen X−3, Her X−1), we give the lower-limits on Δtgl. We show the lower-limits on t∞ for pulsars with spin-up or spin-down that are still ongoing (GX 1+4, OAO 1657−415, SAX J2103.5+4545, spin-up of 4U 1626−67, and EXO 2030+375). GX 1+4 has t∞> Δtgl, making it the best candidate for observing glitches. Other good candidates are 4U 1626−67 and OAO 1657−415, with t∞ ≈ Δtgl. We point out that, in principle, all the accreting pulsars can experience glitches or anti-glitches, although with a lower probability. Indeed, they have long spin period evolutions (104 − 106 yr) during which they might have built up a rotational lag for depinning close to the critical value.
(Vela X−1, Cen X−3, Her X−1), we give the lower-limits on Δtgl. We show the lower-limits on t∞ for pulsars with spin-up or spin-down that are still ongoing (GX 1+4, OAO 1657−415, SAX J2103.5+4545, spin-up of 4U 1626−67, and EXO 2030+375). GX 1+4 has t∞> Δtgl, making it the best candidate for observing glitches. Other good candidates are 4U 1626−67 and OAO 1657−415, with t∞ ≈ Δtgl. We point out that, in principle, all the accreting pulsars can experience glitches or anti-glitches, although with a lower probability. Indeed, they have long spin period evolutions (104 − 106 yr) during which they might have built up a rotational lag for depinning close to the critical value.
While glitches are traditionally observed with radio observations, the numerous examples of glitches seen in magnetars clearly show that they can also be detected by X-ray observatories (e.g., Kaspi et al. 2000). The size of the jumps in angular velocity observed in the magnetars is the same or smaller than that expected in accreting pulsars (ΔΩ ≈ 10-7 − 10-4 rad s-1, Şaşmaz Muş & Göğüş 2013 and references therein).
A suitable spacing of the observations, allowing phase-connected timing ephemeris to be derived, is required in order to detect glitches and to distinguish them from other timing irregularities induced by variations in the accretion torque. The observation of correlated changes in the source flux should help to recognize accretion-induced torque variations. Existing instruments with a wide field of view, such as the Fermi/GBM, Swift/BAT, and INTEGRAL/IBIS are already providing repeated observations of the brightest X-ray pulsars that could be used to search for glitches, but the observing strategy of these satellites has not been optimized in this respect. In the future, a relevant contribution in this field could be given by the LOFT mission, proposed in the context of the European Space Agency science program (Feroci et al. 2014). The Large Area Detector (LAD) instrument on LOFT will be able to detect the pulsations of bright sources like 4U 1626−67 or GX 1+4 in observations of only a few kiloseconds. A program of suitably spaced monitoring observations will be easily implemented, also exploiting the frequent coverage of the Galactic plane with the LOFT Wide Field X-ray monitor.
4. Conclusions
We use starquake and superfluid vortex models to outline for the first time the expected observational properties of glitches in accreting pulsars.
We find that glitches caused by quakes of the crust in an accreting slow pulsar are very rare and their detection unlikely. On the contrary, glitches caused by the transfer of angular momentum between the superfluid and the normal components may take place more often. In the superfluid vortex scenario they can have maximum jump in angular velocity ΔΩgl ≈ 1.3 × 10-4 rad s-1. Some accreting pulsars show long-term spin-up periods during which they may undergo anti-glitches. Therefore, we modify the snowplow model of Pizzochero (2011) on the basis of the anti-glitch scenario proposed by Pines et al. (1980) to determine the expected properties of anti-glitches in these objects. We find that anti-glitches in accreting pulsars have maximum jumps in angular velocity of about the same order of magnitude or ten times smaller than ΔΩgl. Both glitches and anti-glitches are expected to have long rise times (τrise ≈ 102 − 103Ω-1 s) and long recovery timescales, with the glitch appearing as a simple step in angular velocity.
By comparing the timescales between two consecutive torque reversals t∞ and the interglitch timescale Δtgl of a sample of accreting pulsars, we find that GX 1+4 has t∞> Δtgl (see Fig. 2). It is therefore the best candidate for observing glitches. Other good candidates with t∞ ≈ Δtgl are 4U 1626−67 and OAO 1657−415. These sources can be monitored to search for glitches and anti-glitches with the currently operating X-ray instruments and represent good targets for future missions devoted to X-ray timing such as the proposed LOFT.
Zdunik et al. (2008) pointed out that the calculations for the elastic properties of accreted crusts are subject to high uncertainties, and therefore they must be taken with caution.
The value Rc = 9.3 km is obtained assuming a n = 1 polytropic density profile to describe the core and inner crust, with R = 10 km and M = 1.4 M⊙ for the radius of the inner crust and mass of the neutron star (see Pizzochero 2011).
The post-glitch recovery stage, which follows the sudden spin-up, is characterized by a quasi-exponential relaxation of the angular velocity time derivative of the star toward the spin-down rate which the pulsar would have had in the absence of the glitch (Baym et al. 1969; Alpar et al. 1984; Jones 1990).
At any time t before the glitch, the external and internal depinning fronts represent the radial distance xext(t) and xint(t) (with xext(t) >xm for the external depinning front and xint(t) <xm for the internal depinning front) where the rotational lag ΔΩ = Ωs(x) − Ω between the local superfluid angular velocity Ωs(x) and that of the normal component Ω is equal to the critical lag for depinning ΔΩcr. As the star spins up, a rotational lag builds up between the superfluid vortices and the normal component. The critical lag for depinning is highest at xm. Therefore, the external depinning front moves inward and the internal depinning front outward, both to xm. Since the NS spins up, the relative velocity vL − vs of the vortex lines pinned to the lattice (vL) with respect to the superfluid (vs) increases. The Magnus force acting on the vortices is given by
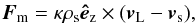 where êz is the unit vector pointing along the rotation axis. Because of the direction of Fm, the vortices unpinned by the external and internal depinning fronts move inward (while in the glitch scenario, they move outward).
where êz is the unit vector pointing along the rotation axis. Because of the direction of Fm, the vortices unpinned by the external and internal depinning fronts move inward (while in the glitch scenario, they move outward).
The Fermi team provides the pulse frequency history of the accreting pulsars monitored with the Gamma-ray Burst Monitor (GBM) on board the Fermi satellite since its launch (June 11, 2008). Preliminary results are available for download from the website http://gammaray.nsstc.nasa.gov/gbm/science/pulsars.html
Acknowledgments
We thank the anonymous referee for constructive comments that helped to improve the paper. This work is partially supported by the Bundesministerium für Wirtschaft und Technologie through the Deutsches Zentrum für Luft und Raumfahrt (grant FKZ 50 OG 1301). V.D. and A.S. thank the Deutsches Zentrum für Luft- und Raumfahrt (DLR) and Deutsche Forschungsgemeinschaft (DFG) for financial support (grant DLR 50 OR 0702). Partial support comes from NewCompStar, COST Action MP1304. Part of this work is based on the publicly available “GBM Accreting Pulsar Histories” provided by the Fermi team.
References
- Aasi, J., Abbott, B. P., Abbott, R., et al. (LIGO and Virgo Collaborations) 2015, Phys. Rev. D, 91, 022004 [NASA ADS] [CrossRef] [Google Scholar]
- Alpar, M. A., Pines, D., Anderson, P. W., & Shaham, J. 1984, ApJ, 276, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, P. W., & Itoh, N. 1975, Nature, 256, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Barnstedt, J., Staubert, R., Santangelo, A., et al. 2008, A&A, 486, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baym, G., & Pines, D. 1971, Ann. Phys., 66, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., Pethick, C., Pines, D., & Ruderman, M. 1969, Nature, 224, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Beri, A., Jain, C., Paul, B., & Raichur, H. 2014, MNRAS, 439, 1940 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Camero, A., Zurita, C., Gutiérrez-Soto, J., et al. 2014, A&A, 568, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chakrabarty, D., Bildsten, L., Grunsfeld, J. M., et al. 1997, ApJ, 474, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, R., Kaspi, V. M., & Gavriil, F. P. 2008, ApJ, 673, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson, R. G., McCulloch, P. M., & Lewis, D. R. 2002, ApJ, 564, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Espinoza, C. M., Lyne, A. G., Stappers, B. W., & Kramer, M. 2011, MNRAS, 414, 1679 [NASA ADS] [CrossRef] [Google Scholar]
- Feroci, M., den Herder, J. W., Bozzo, E., et al. 2014, SPIE Conf. Ser., 9144, 2 [Google Scholar]
- Galloway, D. K., Morgan, E. H., & Levine, A. M. 2004, ApJ, 613, 1164 [NASA ADS] [CrossRef] [Google Scholar]
- González-Galán, A., Kuulkers, E., Kretschmar, P., et al. 2012, A&A, 537, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haskell, B., & Antonopoulou, D. 2014, MNRAS, 438, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Haskell, B., & Melatos, A. 2015, Int. J. Mod. Phys. D, 24, 30008 [Google Scholar]
- Haskell, B., Pizzochero, P. M., & Sidery, T. 2012, MNRAS, 420, 658 [NASA ADS] [CrossRef] [Google Scholar]
- in ’t Zand, J. J. M., Strohmayer, T. E., & Baykal, A. 1997, ApJ, 479, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Inam, S. Ç., Şahiner, Ş., & Baykal, A. 2009, MNRAS, 395, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Jenke, P. A., Finger, M. H., Wilson-Hodge, C. A., & Camero-Arranz, A. 2012, ApJ, 759, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, P. B. 1990, MNRAS, 246, 315 [NASA ADS] [Google Scholar]
- Kaspi, V. M., Lackey, J. R., & Chakrabarty, D. 2000, ApJ, 537, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Klochkov, D., Staubert, R., Postnov, K., Shakura, N., & Santangelo, A. 2009, A&A, 506, 1261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lyne, A. G., Shemar, S. L., & Smith, F. G. 2000, MNRAS, 315, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. W., Bildsten, L., Chakrabarty, D., et al. 1997, ApJ, 488, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Pandharipande, V. R., Pines, D., & Smith, R. A. 1976, ApJ, 208, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Pines, D., Shaham, J., Alpar, M. A., & Anderson, P. W. 1980, Prog. Theoret. Phys. Suppl., 69, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Pizzochero, P. M. 2011, ApJ, 743, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Pringle, J. E., & Rees, M. J. 1972, A&A, 21, 1 [NASA ADS] [Google Scholar]
- Rappaport, S., & Joss, P. C. 1977, Nature, 266, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Şaşmaz Muş, S., & Göğüş, E. 2013, ApJ, 778, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Seveso, S., Pizzochero, P. M., & Haskell, B. 2012, MNRAS, 427, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M. 1981, A&A, 102, 36 [NASA ADS] [Google Scholar]
- Yu, M., Manchester, R. N., Hobbs, G., et al. 2013, MNRAS, 429, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Zdunik, J. L., Bejger, M., & Haensel, P. 2008, A&A, 491, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Z., & Li, X.-D. 2010, A&A, 518, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zuo, W., Li, Z. H., Lu, G. C., et al. 2004, Phys. Lett. B, 595, 44 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Rotational parameters and luminosities of four accreting pulsars showing among the largest and stable spin-down rates (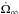 ) in XRBs.
) in XRBs.
All Figures
 |
Fig. 1 Schematic representation of the cylindrical geometry assumed in Sect. 2.3. The z-axis is parallel to the spin-axis of the NS. The dotted line shows a vortex line with half length |
| In the text | |
 |
Fig. 2 Δtgl − t∞ diagram of 13 accreting pulsars. Black refers to spin-down, blue to spin-up. Pulsars with horizontal arrows experience a “random walk” of the spin period, and so the value Δtgl reported in the diagram is a lower-limit. Pulsars with vertical arrows have ongoing spin-up or spin-down. We obtained t∞ and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.