| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201425557 | |
| Published online | 01 June 2015 | |
Variation in sunspot properties between 1999 and 2014
1
Kiepenheuer-Institut für Sonnenphysik,
Schöneckstr. 6,
79104
Freiburg,
Germany
e-mail:
rrezaei@kis.uni-freiburg.de
2
National Solar Observatory (NSO), 3010 Coronal Loop, Sunspot, NM
88349,
USA
3
Max-Planck Institute for Solar System Research,
37077
Göttingen,
Germany
4
Instituto de Astrofísica de Canarias (IAC),
vía Láctea, 38200,
La Laguna, Tenerife,
Spain
5
Departamento de Astrofísica, Universidad de La
Laguna, 38205, La
Laguna, Tenerife,
Spain
Received: 19 December 2014
Accepted: 24 April 2015
Aims. We study the variation in the magnetic field strength, area, and continuum intensity of umbrae in solar cycles 23 and 24.
Methods. We analyzed a sample of 374 sunspots observed from 1999 until 2014 with the Tenerife Infrared Polarimeter at the German Vacuum Tower Telescope and the Facility InfRared Spectropolarimeter at the Dunn Solar Telescope. The sample of field strength, area, and intensities was used to trace any long-term or cyclic trend of umbral properties in the last 15 years.
Results. Sunspots are systematically weaker, that is, have a weaker field strength and stronger continuum intensity, toward the end of cycle 23 than they had at the maximum of cycle 23. The linear trend reverses with the onset of cycle 24. We find that the field strength decreases in the declining phase of cycle 23 by about 112 (± 16) G yr-1, while it increases in the rising phase of cycle 24 by about 138 (± 72) G yr-1. The umbral intensity shows the opposite trend: the intensity increases with a rate of 0.7 (± 0.3)% of Ic yr-1 toward the end of cycle 23 and decreases with a rate of 3.8 (± 1.5)% of Ic yr-1 toward the maximum of cycle 24. The distribution of the umbral maximum field strength in cycle 24 is similar to that of cycle 23, but is slightly shifted toward lower values by about 80 G, corresponding to a possible long-term gradient in umbral field strength of about 7 ± 4 G yr-1. If instead of the maximum umbral field we consider the average value over the entire umbra, the distribution shifts by about 44 Gauss.
Conclusions. The umbral brightness decreases in the rising stage of a solar cycle, but increases from maximum toward the end of the cycle. Our results do not indicate a drastic change of the solar cycle toward a grand minimum in the near future.
Key words: sunspots / Sun: photosphere / Sun: evolution / Sun: magnetic fields
© ESO, 2015
1. Introduction
Sunspots are the largest magnetic flux concentrations in the solar photosphere. The magnetic energy density inside sunspots is higher than the kinetic energy density, resulting in a partial suppression of the convection. Larger umbrae are darker and show a higher magnetic field strength (Bray & Loughhead 1964). Sunspot properties have been summarized in several review papers (Solanki 2003; Thomas & Weiss 2004; Moradi et al. 2010; Rempel & Schlichenmaier 2011; Borrero & Ichimoto 2011).
Biermann (1941) proposed that sunspots are cooler than their surroundings because the convective energy transport is suppressed by the strong magnetic fields. Later studies show that the convection is not fully suppressed (Jahn 1989). Since the mainly vertical field lines in umbra partially quench the convection, several authors searched for a relation between umbral intensity and umbral field strength. Kopp & Rabin (1992), Penn et al. (2002), Schad & Penn (2010), and Rezaei et al. (2012) presented this relation for different samples of sunspots in the near-infrared wavelength range, while among others, Norton & Gilman (2004), Leonard & Choudhary (2008), Pevtsov et al. (2011), Watson et al. (2014), Kiess et al. (2014), and Schad (2014) made similar analyses in the visible wavelength range.
A similar trend was found for the local relation between the magnetic field strength and intensity within a single sunspot: the umbral intensity is inversely dependent on the magnetic field strength in a nonlinear way, as shown, for example, by von Klüber (1948), Lites et al. (1993), Martinez Pillet & Vazquez (1993), Balthasar & Schmidt (1993), Stanchfield et al. (1997), Westendorp Plaza et al. (2001), and Penn et al. (2003). Theoretical considerations (e.g., Nordlund & Stein 1990) also predict such a relationship. Hot rising material (like umbral dots) partially expels field lines, which results in a weaker magnetic field strength in umbral dots than in the dark umbra, as seen in the magnetoconvection simulations of Schüssler & Vögler (2006).
Norton et al. (2013) compared the relation of the intensity to the field strength in individual spots and in a small sample of sunspots and found a strong correlation between intensity and field strength in both cases. Norton & Gilman (2004) found that the umbral intensity is a good tracer of the magnetic field strength because the umbral contrast in the visible is higher than in the infrared (see also Kiess et al. 2014). Determining the relation of the intensity to the field strength based solely on MDI or HMI data is difficult, however, because for high field strengths, the spectral line splits beyond the spectral range sampled by the five or six sparsely spaced filter measurements.
Several authors found evidence that the minimum continuum intensity is a function of umbral area (or radius). The high umbral contrast in the visible wavelengths allowed Mathew et al. (2007), Schad (2014), and Kiess et al. (2014), among others, to study the variation of umbral continuum intensity as a function of size. These authors reported a nonlinear decrease of the intensity with umbral radius. Schad & Penn (2010) and Rezaei et al. (2012) used 0.87 and 1.56 μm continuum intensities and reported nonlinear and linear relations between minimum intensity and umbral size, respectively.
There are contradictory reports about temporal variation of the umbral intensity. Albregtsen et al. (1984), for instance, found that umbrae are brighter at the end of a cycle than at its beginning. This linear trend was challenged by Norton & Gilman (2004), who found a cyclic variation such that the intensity decreases from the early phase to the maximum of a cycle and then increases after the cycle maximum. Yet another group of authors, among them, Mathew et al. (2007), found no temporal variation in umbral intensity as a function of solar cycle. These incompatible results are discussed in Sect. 5.3.
The relation between umbral intensity and field strength implies that the temporal variation of the umbral intensity might be linked with a temporal variation in the field strength. This was observed by several groups using different telescopes and spectral lines (Watson et al. 2011; Pevtsov et al. 2011; Rezaei et al. 2012). The variation in the field strength of sunspots in the last two cycles has been the subject of several studies (Livingston 2002; Penn et al. 2003; Norton & Gilman 2004; Penn & MacDonald 2007; Leonard & Choudhary 2008; Schad & Penn 2010). Livingston (2002) found that cycle 23 was weaker than cycle 22. Livingston et al. (2006) and Penn & Livingston (2011) found that the field strength of sunspots was stronger at the beginning of cycle 22 than at its end. Rezaei et al. (2012), Pevtsov et al. (2014), and Schad (2014) reported a cyclic variation of the field strength, but found no significant trace of a long-term variation in their data. Livingston et al. (2012) predicted a monotonic decrease of sunspot field strength that should lead to the disappearance of sunspots in cycle 25.
Rezaei et al. (2012, hereafter Paper I) studied 185 sunspots observed by the Tenerife Infrared Polarimeter (TIP-I and TIP-II, respectively; Martínez Pillet et al. 1999; Collados et al. 2007) between 1999 and 2011. This work is an extension of our previous work (Paper I) with almost twice as many spots and extending toward the maximum phase of cycle 24. We use the same technique as in Paper I, that is, spectropolarimetric observations of sunspots at infrared wavelengths, to study the variation of umbral properties and estimate an upper limit for any long-term variation.
2. Observations
We analyzed a sample of 374 sunspots observed from 1999 to 2014. Each sunspot was scanned by moving the solar image across a spectrograph slit, resulting in a two-dimensional map. Among them, 317 spots have been observed with TIP at the German Vacuum Tower Telescope (VTT, Schröter et al. 1985). Using the service-mode observations1 at the Dunn Solar Telescope, we also gathered 57 sunspot maps observed with the Facility InfRared Spectropolarimeter (FIRS, Jaeggli et al. 2006, 2010). FIRS operates at a wavelength range similar to TIP. A list of spectral lines and the number of maps observed in each wavelength are shown in Table 1. Only one new spectral line was introduced in this analysis. The new line, Fe i 1078.3 nm, has an effective Landé factor of 1.5 and is similar to the Fe i 1089.6 nm line (see, e.g., Balthasar & Collados 2005). Thanks to the DST service mode observations, there is a better temporal coverage in 2013−2014.
Atomic parameters of the spectral lines (Nave et al. 1994; Radziemski, Jr. & Andrew 1965).
Our analysis used only sunspots with a limb distance of at least 60 arcsec (θ< 72°, i.e., μ> 0.3). Beyond θ> 72°, the magnetic neutral line passes through the umbra. In addition, there is no reliable umbral center-to-limb correction curve for the intensity at the very limb. Avoiding spots that were close to the limb allowed us to reliably estimate the heliocentric angle from full-disk images of the Michelson Doppler Imager (MDI, Scherrer et al. 1995) onboard the SOHO spacecraft or the Helioseismic and Magnetic Imager (HMI, Scherrer et al. 2012; Schou et al. 2012) onboard the Solar Dynamics Observatory (SDO, Pesnell et al. 2012). We used the measured heliocentric angles to correct for the center-to-limb variation of umbral parameters (Sects. 3.2 and 3.3). In addition, the umbral and penumbral area of each spot was also measured in the full-disk images of MDI (till end of 2009) and HMI (from 2010 onward). The full-disk images of continuum intensity were corrected for center-to-limb effects using the same method as in Kiess et al. (2014). A fixed threshold of 0.6 and 0.9 Ic was used to select the umbra and penumbra, respectively. The measured areas were corrected for projection effects.
3. Data reduction
3.1. Field strength measurement
For each sunspot map, we first created an average quiet Sun profile that was used to estimate the spectral dispersion and the continuum intensity. Similar to Paper I, we counted the number of lobes for each Stokes-V profile above 4σ noise level and discarded all abnormal profiles, that is, profiles showing large Stokes-V asymmetries or multiple lobes. The distance of the two σ-components was then used to estimate the magnetic field strength (Eq. (1), Paper I) assuming the strong-field approximation (Stix 2002; Landi degl’Innocenti & Landolfi 2004). This assumption is fulfilled in the near-infrared wavelength range in which the lobe separation is significantly larger than the Doppler width of the line (e.g., Rezaei et al. 2006).
3.2. Center-to-limb variation of umbral intensity
Profiles in every map were normalized to the continuum intensity of average quiet Sun in the same map. This is possible since we have a two-dimensional scan for each sunspot and each map covers some granulation area outside the sunspot. We used the limb-darkening measurements of Albregtsen et al. (1984) to correct the measured intensities for the given heliocentric angle in each wavelength band.
3.3. Center-to-limb variation of field strength
To account for the variation of sunspot field strength with distance from the center of the solar disk, we have created separate CLV curves for each spectral line. To this end, each spectral line was synthesized at 20 heliocentric angles and the corresponding profiles were analyzed like observations. The measured field strength then resulted in CLV curves for the field strength estimated from each line. As expected, the field strength did not show a large CLV variation for all lines except for the Si i 1082.7 nm line, which is the strongest line in the list. Values of magnetic field strength and continuum intensities were then corrected for the given heliocentric angles. This resulted in a data set in which all spots appear as if observed at disk center.
Summary of the temporal gradients of the continuum intensity, the magnetic field strength, and the umbral area in different time intervals.
3.4. Scaling field strength and intensity to the Fe I 1.56 μm line
To have all continuum intensities scaled to a fixed wavelength range, namely 1.56 μm, we used the SIR code (Ruiz Cobo & del Toro Iniesta 1992; Bellot Rubio 2003) to synthesize a set of standard umbral models (at disk center). This includes the three models of Maltby et al. (1986) and models of Collados et al. (1994) and Socas-Navarro (2007) for each wavelength range. Then we made a linear fit to the ratio of continuum intensit ies between 1.08 and 1.56 μm. This resulted in the following equation: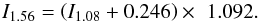 (1)To have a uniform sample of umbral intensities, we applied this correction to all observations.
(1)To have a uniform sample of umbral intensities, we applied this correction to all observations.
There is a systematic offset in the estimated field strengths since different spectral lines form at different heights in the atmosphere, resulting in slightly different atmospheric parameters (e.g., Cabrera Solana et al. 2005). In absence of information about the gradient of the magnetic field strength in each sunspot at a given heliocentric angle, we synthesized all lines for a few umbral model atmospheres (e.g., Collados et al. 1994; Socas-Navarro 2007). The synthesized profiles were analyzed the same way as observed ones. The systematic offsets between different lines were then corrected such that all measured values are adjusted to the one from the Fe i 1564.8 nm line.
3.5. Error estimate
Error estimates for the magnetic field strength usually result in small errors since they only relate to uncertainties in the separation of the σ-lobes in Stokes-V. This uncertainty introduces a random error with a σB about 20 to 60 G, depending on the wavelength range and the dispersion of the spectra. The value is comparable to the formal error attributed to field strength in inversions of the Fe i line at 1564.8 nm (e.g., Beck et al. 2007). The systematic error due to the different sensitivity of spectral lines to the solar atmosphere was accounted for in Sect. 3.4.
 |
Fig. 1 Scatter plot of corrected sunspot intensity and field strength for all observed sunspots. Different symbols denote different observed wavelengths. |
 |
Fig. 2 Continuum intensity at 1.56 μm as a function of umbral radius. The black line shows a linear fit and the gray line 3σ margins. For a description of different symbols, see caption of Fig. 1. |
 |
Fig. 3 Variation of the maximum field strength (left) and the minimum continuum intensity (right) as a function of time. The vertical dotted lines at 2001 and 2009 indicate the maximum and minimum of cycle 23, respectively. The lines at 2012 and 2013 mark the possible maximum of cycle 24. The solid line shows a least-squares, the dashed line a Bayesian fit to the data between the corresponding vertical lines. The green line in both panels shows a linear fit to all data points. A summary of the fit parameters is presented in Table 2. Arrows indicate the temporal extent of the two cycles. For a description of different symbols, see Fig. 1. |
The amount of the field strength gradient in sunspot atmospheres is variable from one spot to another as well as from one model to another. We have adopted the cool model of Collados et al. (1994) to estimate the offsets between magnetic field strength values retrieved from different spectral lines. To estimate the uncertainty due to the assumed field strength gradient, we repeated the computations with the hot model of Collados et al. (1994). The differences between the offsets from these two models amount to 50−130 G. Hence, a more realistic error for the maximum field strength in each sunspot is approximately 80−140 G (taking 60 G as the random error). As discussed in Sect. 5, we can use the mean umbral field strength instead of the maximum field strength to trace cyclic and long-term variations. The advantage of using the mean value is that the random noise is smoothed out since each umbra contains several hundred to several thousand pixels.
4. Results
4.1. Relation of field strength to intensity
Our homogenized sample shows the well-known empirical relations between the minimum umbral intensity vs. the maximum field strength, Bmax (Fig. 1), in agreement with earlier observations (Kopp & Rabin 1992; Penn et al. 2002). Since all intensities and magnetic field strength values were scaled to the Fe i 1564.8 nm line, the slope is only comparable to other works when observations have been performed in this spectral line.
4.2. Relation of intensity to radius
From measurements of the minimum umbral continuum intensity from spectropolarimetric data and the umbral area derived from solar full-disk images (Sect. 2), we can investigate the relation of intensity to radius of sunspot umbrae. Figure 2 shows the variation of the minimum umbral intensity at 1.56 μm vs. umbral radius along with a linear fit. The slope of the linear fit is 1.6 ± 0.2% of Ic Mm-1. The trend is clear and has less scatter than Fig. 4 of Rezaei et al. (2012): the present results do not suffer from incomplete areas since we used full-disk continuum maps to measure the umbral areas, while Rezaei et al. (2012) used the umbral area in each observed map.
4.3. Temporal evolution
Temporal evolution of the sunspot magnetic field strength and continuum intensity are shown in Fig. 2. Compared to our results in Paper I, we have better statistics, in particular for the years around the cycle minimum (2005−2009). The best-fit lines in Fig. 2 are a least-squares and a Bayesian fit (Patil et al. 2010; Hogg et al. 2010) with similar results.
In the declining phase of cycle 23 (2001−2009), the field strength monotonically decreases with a rate of 112 ± 16 G yr-1. The onset of the new cycle reverses the trend: the field strength monotonically increases annually from 2009 toward the maximum of cycle 24. This means that the magnetic field strength shows a cyclic variation in phase with the solar cycle. Adopting the beginning of 2012 as the maximum of cycle 24, we find a temporal gradient of the field strength of about 138 ± 72 G yr-1. If we assume that the maximum was at the beginning of 2013, then the rate reduces to 108 ± 38 G yr-1. As discussed in Kiess et al. (2014), the first active region of opposite polarity appeared early in 2008 on the disk, but the Sun remained very quiet during 2008. Hence we adopted 2009 as beginning of the new cycle (see also McIntosh et al. 2013). As seen in Fig. 1 of Kiess et al. (2014), cycle 24 has a weak and broad maximum. It is therefore possible that the rise time takes much longer than the typical value of 40−60 month, if cycle 24 stays in the same weak activity level (the Waldmeier effect). However, there is a large scatter in the plot of the time a solar cycle needs to progress from minimum to its maximum, in other words, in the rise time, versus the cycle amplitude (see Fig. 26 of Hathaway 2010).
The umbral intensity also shows a cyclic trend in antiphase with the solar cycle: at first it increases with a rate of 0.7 ± 0.3% of Ic yr-1 in the declining phase of cycle 23. The trend switches to a negative slope of −3.8 ± 1.5% of Ic yr-1 between 2009 and 2012. Adopting 2013 instead of 2012 as the maximum of cycle 24, we find a similar value for the temporal gradient of the intensity of −3.0 ± 0.9% of Ic yr-1. The onset of cycle 24 reverses the linear trend of the umbral intensity, as seen in the right panel of Fig. 3, in contrast to the finding of Livingston et al. (2012). This figure shows that the umbral intensity has a cyclic variation: it starts to increase again from 2012 onward, and at the same time, the field strength decreases. This indicates that taking 2012 as the maximum of cycle 24 was perhaps a correct selection. As discussed by Norton & Gallagher (2010), for instance, the recent solar cycles showed a double maximum because the maximum activity on the two hemispheres occurs with a time gap of about a year. The latest sunspot numbers indicate a second maximum in 2014 for the current cycle, but since the presented data do not fully cover 2014, we retain 2012 as the most probable maximum.
Table 2 shows that the temporal gradients of the umbral intensity and the field strength significantly change between the end of 2012 and the end of 2013. This might indicate that the maximum was somewhere in 2012. More investigations are required to clearly answer this question.
The variation in the umbral intensity during a solar cycle means that on average, umbrae at cycle maximum are darker than those close to minimum. The intensity difference of about 4% of Ic between the maximum and minimum amounts to some 150 K difference in the brightness temperature of the umbra, taking into account the HSRA brightness temperature of the quiet Sun at 1.56 μm of ≈6700 K (Gingerich et al. 1971).
We also present a linear fit to the whole data (1999−2014) to study a possible (monotonic) long-term trend in umbral properties. The fit shows that there is a weak long-term trend in the magnetic field strength of −13 ± 4 G yr-1. The trend in continuum intensity is 0.2 ± 0.1% of Ic yr-1. The results of this and all other linear fits are shown in Table 2.
While the maximum umbral field strength was discussed in literature (as well as in this paper), we would like to investigate the average field strength of sunspot umbrae as well. This is motivated by the observation that the average field strength does not suffer from the random errors that exist in individual measurements. Reporting a mean field strength is therefore recommended, but is available only to authors who have two-dimensional maps of sunspots. Repeating the same monotonic linear fit for the average field strength of umbrae rather than their maximum, we would obtain a temporal gradient of about −6 ± 3 G yr-1. In Sect. 5.6, we compare the temporal gradient of the field strength with an independent measurement based on the distribution of the field strength in cycles 23 and 24.
5. Discussion
5.1. Continuum intensity as a function of umbral size
It is known from previous observations that larger umbrae are darker. This was first attributed to stray light by Zwaan (1965), but later studies found a real relation between the size and intensity in sunspot umbrae (McIntosh 1981; Stellmacher & Wiehr 1988; Martinez Pillet & Vazquez 1993). Mathew et al. (2007), Wesolowski et al. (2008), Leonard & Choudhary (2008), de Toma et al. (2013), Schad (2014), and Kiess et al. (2014) studied the variation of the umbral intensity in the visible wavelength range. Schad & Penn (2010) used the Fe i 868.8 nm line in their investigation. All of these authors found a nonlinear relation between the minimum umbral intensity and the umbral area, fitted either with a quadratic, a logarithmic, or a power-law function. In contrast, Rezaei et al. (2012) presented a linear relation of the infrared intensity to radius and did not find a nonlinear trend as in the visible wavelength range. Our present results agree with those of Rezaei et al. (2012), although the trend has less scatter in our data than was reported by Rezaei et al. (2012) because we here used an independent measurement of the umbral area that does not suffer from incomplete spatial coverage of the sunspots in the maps. The slope of the intensity-radius variation is shallower in infrared measurements than in visible observations because the Planck function has a steeper gradient at 0.6 μm than at 1.56 μm.
As shown by Kiess et al. (2014, Fig. 7), the umbral radius has a tight correlation with the total magnetic flux of the sunspot. In this context, it can be understood why larger umbrae are darker: the horizontal pressure balance with the surrounding granulation implies an increasing magnetic field strength toward the center of the umbra for larger umbrae. The higher field strength then further suppresses the umbral mode of magnetoconvection. In addition, the radiative energy transport through the boundary of the umbra and penumbra becomes progressively inefficient with increasing umbral size. As a result, the gas temperature decreases with umbral size.
5.2. Temporal variation of the umbral field strength
Several authors reported an increase of the umbral field strength in the rising phase and a decrease in the declining phase of the solar cycle. We find the same cyclic variation in umbral field strength, in agreement with Pevtsov et al. (2011), who used the old Soviet-era observations in visible wavelengths that cover five solar cycles. These authors found a temporal gradient of the field strength in the declining phase of cycle 23 of about −119 G yr-1. Watson et al. (2011) used a similar wavelength range and found that the field strength decreased by 70 G yr-1 in the declining phase of cycle 23. Unlike these visible measurements, Penn & Livingston (2006) used a sample of 900 intensity profiles of sunspots (each average of five recorded spectrums) between 1998 and 2005 observed in the Fe i 1564.8 nm line and reported a monotonic temporal gradient of −52 G yr-1, while in Paper I, we reported a linear trend of −94 G yr-1 using full Stokes maps of 185 sunspots observed in infrared spectral lines (both reports correspond to the declining phase of cycle 23). The temporal gradient of the field strength in the declining phase of cycle 23 in this contribution (−112 G yr-1) agrees with our previous measurements and with those of Pevtsov et al. (2011) and Watson et al. (2011) within the error margins.
Regardless of whether 2012 or 2013 is adopted as the maximum of cycle 24, we find a positive temporal gradient of the magnetic field strength with time in the rising phase of this cycle that is three times larger than the one-σ error margin. This is inconsistent with Livingston et al. (2012), who claimed a monotonic decrease of the sunspot field strength through the whole cycle.
5.3. Temporal variation of the umbral intensity
As discussed in Sect. 1, there are contradictory reports about the temporal evolution of the umbral brightness during a solar cycle. While some authors reported no temporal variation over several solar cycles, others found linear or cyclic trends.
Linear trend.
Several authors found that umbrae brighten during a solar cycle (in agreement with Albregtsen & Maltby 1978). Albregtsen et al. (1984), for instance, examined 22 mature spots between 1968 and 1983 and stated that umbrae are brighter toward the end of a solar cycle. Maltby et al. (1986) came to the same conclusion: the umbral intensity increases monotonically during a solar cycle, and there is a sharp discontinuity between the umbral brightness at the end of a cycle and the beginning of the next cycle. Penn & Livingston (2006) also reported an increase in umbral continuum intensity of 1.8% per year (at 1.5 μm wavelength) between 2001 and 2006 (declining stage of cycle 23). Watson et al. (2011) used MDI data and found that umbrae brightened during the declining phase of cycle 23. In Paper I, we also found a similar trend using infrared data: the umbral intensity increased in the declining phase of cycle 23.
No trend.
Mathew et al. (2007) analyzed 160 sunspots using SOHO MDI data and did not find any variation in umbral intensity between 1998 and 2004. When spots of all sizes were included, de Toma et al. (2013) did not find any trace of variation in umbral intensities between 1986 and 2012 in full-disk images of the San Fernando telescope. Wesolowski et al. (2008) also found no significant variation in umbral intensity either in the rising or declining phase of cycle 23 (1997−2004). Norton et al. (2013) and Kiess et al. (2014) found no significant temporal variation in the rising phase of cycle 24 using HMI data.
Cyclic trend.
Norton & Gilman (2004) used MDI observations at 676.8 nm and for the first time noted that the umbral intensity decreased in the rising stage of cycle 23 while it increased in the declining stage. This cyclic variation contradicts all studies that reported either a linear or no trend within the cycle. Penn & MacDonald (2007) observed the Sun at 868.8 nm using the KittPeak facilities between 1992−2003 and reported a cyclic oscillation in umbral intensities such that umbrae are darker at cycle maximum and brighter at cycle minimum. In our analysis, we find both an increase in umbral intensity in the declining phase of cycle 23 (as in Paper I) and a decrease in umbral intensity in the rising phase of cycle 24 (Table 2). Hence, we recovered the cyclic variation of the umbral intensity during a solar cycle at 1.56 μm as reported by Norton & Gilman (2004) and Penn & MacDonald (2007) for shorter wavelengths.
 |
Fig. 4 Variation of umbral area as a function of time. For a description of lines and different symbols, see Figs. 1 and 3. |
5.4. Temporal variation of the umbral area
A cyclic variation of the total sunspot area as a function of solar cycle was reported by Watson et al. (2011). The reported temporal gradients of umbral area by Mathew et al. (2007) are within the error margins, while Rezaei et al. (2012) found no significant variation. The results of our study (Fig. 4 and right column of Table 2) also show a cyclic variation: the umbral area increases from cycle minimum toward the maximum, but then decreases from the maximum toward the next minimum. The sign of the temporal gradient of the umbral area in the declining and rising stages of cycles 23 and 24 complies with the temporal variation of field strength since both quantities have a positive correlation. The temporal gradients of umbral area are usually not as reliable as those of the field strength or the intensity. The monotonic linear trend of umbral area for the whole time span (1999−2014) has a different sign: while the field strength decreases, the umbral area shows an increase. This is perhaps due to the fact that up to 2009, we used the MDI continuum with a pixel size of about two arcseconds, a factor four larger than for the HMI full-disk continuum images. The uncertainties in the measured areas are therefore accordingly larger between 1999−2009 than for 2010−2014. Watson et al. (2014) also discussed systematic differences between umbral intensities in MDI and HMI data. Our results agree with those of Kiess et al. (2014), who reported a linear increase of the umbral area in the rising phase of cycle 24.
 |
Fig. 5 Comparison of the distribution of maximum field strength in sunspots observed in cycles 23 and 24. The maximum of the two Gaussians for cycle 23 and 24 is at 2.68 and 2.60 kG, respectively. The dashed curve shows the distribution of the measured magnetic field strength in cycle 23 from 2003 until 2007 reported by Livingston et al. (2012). |
5.5. Cyclic variation of umbrae
The well-known relation between umbral area, intensity, and field strength was reported by many authors (for recent studies see Kiess et al. 2014; Schad 2014). This implies that a cyclic variation in any one of these three umbral parameters are likewise expected to appear in the other two. We presented such cyclic variations in the intensity, area, and the field strength. During a solar cycle, the location of sunspots progressively moves equatorward. Sunspots first appear at about 30−40°, and at the end of a cycle, they appear close to 10°.
The butterfly diagram of magnetic field strength of Schad (2014), based on Hinode data, does not show that throughout a cycle sunspots have a lower magnetic field strength at high latitudes and gradually show higher field strength at lower latitudes or vice versa. In other words, the rise of a flux tube through the convection zone should not disperse sunspots to place weak spots at higher latitudes and strong ones at lower latitudes. This is in contrast to Norton & Gilman (2004), who found that darker or brighter umbrae appear systematically at lower or higher latitudes. More investigations are required to determine whether there is a systematic relation between umbral parameters (intensity, area, field strength) and their location on the solar disk. Each of these parameters has its own cyclic variation, but so far, no strong relation has been established between the latitude and the other three.
5.6. Long-term variation of the umbral field strength and intensity
We find an upper limit for a long-term trend that is overlaid on the cyclic variation of the intensity and field strength of sunspots. Figure 5 shows two Gaussian curves corresponding to the distributions of the magnetic field strength in the last two cycles. We used a Kolmogorov-Smirnov test (Press et al. 1992) to measure the distance of the sample of the magnetic field strengths of sunspots against a given distribution to determine the best distribution for each cycle. The distribution of the umbral field strength is well represented by a Gaussian (same as, e.g., Livingston et al. 2012). The widths of our distributions (Gaussian width =375 and 364 ± 20 G for cycles 23 and 24) are close to the 320 G reported by Livingston et al. (2012). We find that the distribution in cycle 24 is similar to cycle 23, but the curve was shifted toward lower values: the Gaussian distribution of field strength peaks at 2.60 ± 0.02 kG in cycle 24 instead of at 2.68 ± 0.02 kG in cycle 23. These values are significantly different from the 2.20 kG reported by Livingston et al. (2012, for the 2003−2007 time interval, see Fig. 5. In addition to Gaussians, other functions were also used to study the distribution of the umbral magnetic field strength (e.g., Schad 2014). The width of the distribution hence depends on the assumed distribution function.
We attribute the shift of 80 ± 20 G between the peak field strength in cycles 23 and 24 (within 11 ± 1 years) to a long-term trend. Therefore, the temporal gradient of a long-term trend based on the distribution of field strengths is −80 / 11 ≈ −7 ± 4 G yr-1. The long-term gradient estimated in this way is smaller than the value of −13 ± 4 G yr-1 reported using a linear fit to all data points in the sample, but it remains consistent within the error bars. The estimated long-term trend using distributions is also close to the linear fit to the average umbral field strength (−6 ± 3 G yr-1). Since the average field strength is statistically more reliable than the maximum field strength and its result is consistent with the estimation of the long-term trend using the distribution of the field strengths, we also estimated the best-fit Gaussian for the distribution of the average field strength. The average field strength distribution peaks at 2.32 and 2.28 kG for cycles 23 and 24, respectively. The difference (44 ± 16 G) is half of the field strengths measured based on the maximum field strength (80 G). In summary, we find 6 ± 3 G yr-1 as the long-term trend in the average umbral field strength, while the temporal gradient in the maximum field strength is 7 ± 4 G yr-1. An upper limit for the long-term trend in maximum field strength is about 13 ± 4 G yr-1.
Since our sample is not complete, we cannot use the field strength of individual sunspots to compare the highest value in cycle 23 with the highest value in cycle 24. Such a comparison is sensitive to the completeness of the sample. The distribution of the magnetic field strength, however, is not sensitive to the presence or absence of individual spots. We accordingly deem it more reliable to compare the magnetic field distribution of the two cycles to estimate a possible long-term trend. The linear fit to all data points (green lines in Fig. 2) provides a direct comparison to the results reported by Livingston et al. (2012) and Schad (2014). An upper limit for the gradient in the magnetic field strength in our data is at most about 13 ± 4 G yr-1, which is four times lower than the rate of 46 G yr-1 reported by Livingston et al. (2012). Our estimated long-term trend in the field strength is not consistent with Schad (2014), who found no long-term tendency in the field strength of 7530 sunspots observed with Hinode.
The amplitude of the cyclic variation of the magnetic field strength (−112 G yr-1 in the declining phase, +138 or +108 G yr-1 in rising phase) is an order of magnitude larger than the amplitude we estimate as an upper limit for the long-term trend (−13 ± 4 G yr-1), in agreement with our finding in Paper I. Livingston et al. (2012) attributed an annual decrease of the sunspot field strength of 46 G yr-1 (1998−2002) to a long-term trend and concluded that the Sun would cease to generate sunspots in the next cycle. Penn & Livingston (2006) speculated that if the temporal rate of −52 G yr-1 continues monotonically, then the number of spots in cycle 24 will be half of that in cycle 23 and there will be very few spots in cycle 25. Nagovitsyn et al. (2012) studied the same data as Penn & Livingston (2006) and found a cyclic variation in addition to a long-term trend. Watson et al. (2011) studied cycle 23 using SOHO MDI data and reported a long-term trend in the umbral field strength of about −24 G yr-1. Watson et al. (2014) used data of MDI, HMI, and Kitt Peak and found a rate of about −22 G yr-1 between 1996 and 2013, about twice higher than the rate we find.
5.7. Diversity of measurement techniques and results
Stray-light contamination.
Livingston et al. (2012), Penn & Livingston (2006), and other authors who used the McMath-Pierce telescope on Kitt Peak used the intensity profile of the umbra (at Fe i 1564.8 nm line) to measure the magnetic field using the separation of the two σ-components. Position and strength of these σ-components can be modified by stray light. A stray-light profile usually comes from a radius of ≈10′′ (Mattig 1971; Beck et al. 2011) and mostly contains contributions from bright line profiles in the quiet Sun. This contamination not only gives rise to inaccurate magnetic field strength measurements, but also affects the evaluation of the umbral continuum intensity. Unlike Stokes-I, the Stokes-V signal that we used in our analysis is less sensitive to the (mainly unpolarized) stray light. Mathew et al. (2007) performed a stray-light correction for MDI data, while Kiess et al. (2014) argued that the amount of stray light is negligible in the HMI data. Our ground-based observations were not corrected for stray light for two main reasons. All of the data were taken with real-time seeing correction by adaptive optics, or at least with a tip-tilt correction for the VTT data taken before 2004. That provided a spatial resolution of about 1′′ or better for most of the data and should have reduced spatial stray light or smearing to some extent. The second reason is that using polarized Stokes profiles to measure the magnetic field strength instead of intensity profiles is less sensitive to stray light because the polarization signal is strongest in the umbra and weakest in the quiet Sun surrounding a sunspot, exactly opposite to the case for intensity.
Bright spots instead of dark spots.
Livingston et al. (2012) reported many sunspots with a minimum umbral intensity at 1.56 μm of about one (their Fig. 2). If the minimum umbral intensity equals that of the average quiet Sun, then the penumbra should be brighter than the granulation (assuming that the penumbra is brighter than the umbra). Such bright spots have not been observed at any other wavelength or instrument. We would like to stress that between 2011 and 2013, all those bright sunspots should have been recorded with the HMI at 617 nm wavelength range. Since we are not aware of a single example of a bright sunspot in HMI continuum maps, there must be something unaccounted for in their measurements. A possible explanation is an unknown (but large) amount of stray light in their data. One would need to identify all sunspots used by Livingston et al. (2012, after 2010) in the HMI data and to measure their umbral intensity and magnetic field strength, and compare these results with other HMI data like those of Kiess et al. (2014).
Telluric blends.
The intensity profile of Fe i 1564.8 nm line suffers from strong telluric blends in its red wing. An example of a contaminated intensity profile of this line was presented by Mathew et al. (2003, their Fig. 2). As seen in this figure, the high magnetic sensitivity of the Fe i 1564.8 nm line can be unusable due to strong contamination of the telluric blend, making Stokes-I measurements imprecise. Since the telluric blends change with solar elevation and weather conditions, it is difficult to correct for them. Note that the telluric blends are of no concern in an analysis of polarized light like our Stokes-V analysis.
Molecular blends.
Yet another source of contamination of Stokes-I profiles in the umbra are (solar) molecular lines. Some of these lines, such as the OH lines close to the Fe i 1565.2 nm lines, also show strong polarization signals. They modify not only the shape of the intensity profile, but also all Stokes profiles. Dark umbral profiles either in visible or near-infrared wavelengths suffer to some extent from molecular blends, even in well-known spectral lines like the one used on HMI (Wittmann 1972; Boyer et al. 1975). The famous Fe i 1564.8 nm line with its high Zeeman sensitivity (geffλ) also suffers from several solar molecular blends, as listed, for example, by Livingston et al. (2006). Molecular blends always contaminate Stokes-I measurements, but only some of them have a high effective Landé factor and contaminate the polarization signal. It is noteworthy that none of the lines we have used in this study (Table 1) suffers from a significant contamination by strong molecular blends in the Stokes-V signal.
Limited wavelength sampling.
Norton & Gilman (2004), Mathew et al. (2007), Watson et al. (2011, 2014), and Kiess et al. (2014) as well as several other authors used MDI or HMI, that is, space-based two-dimensional spectropolarimeters. These instruments provided and still provide full Stokes measurement of a visible spectral line sampled at five or six filter positions. This restricts the measurements of the highest field strength values since for either MDI or HMI, the spectral lines saturates below about 3000 G. For a magnetic field strength greater than this value, only the distance of the two lobes increases, not their amplitude. This results in a partial coverage of the Stokes-V signal in these filter instruments, which complicates and may even prevent a proper retrieval of the magnetic field complicated. A limited wavelength sampling, however, does not affect measurements of the umbral continuum intensity and area.
Two-dimensional maps vs. single-slit measurements.
Another possible reason for the discrepancies between different authors is the spatial coincidence of the location of the strongest field strength and the lowest continuum intensity. Livingston et al. (2012), for instance, by default assumed that the location of the maximum field strength is identical to the location of the minimum intensity and consequently reported the field strength at the location of the minimum intensity as the maximum field. As shown by Harvey (1986), for instance, the location of the strongest magnetic field strength is not necessarily the location of the minimum intensity. In 20% of the sunspots used for this study, the locations of the minimum intensity and maximum field strength differ by more than 3′′. In these spots the magnetic field strength at the location of minimum intensity is on average 190 G (7%) lower than the maximum field strength. This difference is larger than the total uncertainty estimated in Sect. 3.5, demonstrating the importance of using two-dimensional maps to estimate the minimum intensity and maximum field strength independently.
6. Conclusion
The umbral continuum intensity shows a periodic variation with the phase of the solar cycle: the intensity decreases from the beginning of a cycle up to the maximum, but increases from the maximum of a cycle toward its end. The cyclic variation in umbral properties dominates a possible long-term variation because its amplitude is about an order of magnitude larger. The distribution of the sunspot field strength in the present cycle does not show a significant deviation from the distribution in cycle 23, except for a small shift toward lower values. The Gaussian distribution of the sunspot maximum field strength in cycle 24 peaks at about 2600 G, some 80 G lower than in cycle 23. The relative shift in the average field strength is 44 G. If the weak long-term trend that we observed between 1999 and 2014 persisted, it would take more than a century for sunspots to vanish. Our data in cycle 23 and the first five years of cycle 24 do not show any signature that the next cycle will be qualitatively different from the current cycle 24.
Acknowledgments
The German VTT is operated by the Kiepenheuer-Institut für Sonnenphysik at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias (IAC). The Dunn Solar Telescope at Sacramento Peak/NM is operated by the National Solar Observatory (NSO). NSO is operated by the Association of Universities for Research in Astronomy (AURA), Inc. under cooperative agreement with the National Science Foundation (NSF). This publication makes use of data obtained during Cycle 1 and 2 of DST Service Mode Operations under the proposal ID P115 and P496. We are grateful to Rolf Schlichenmaier for his helpful comments. R.R. acknowledges financial support by the DFG grant RE 3282/1-1. M.C. thanks for the financial support by the Spanish Ministry of Science and Innovation through project AYA2010-18029 (Solar Magnetism and Astrophysical Spectropolarimetry). We acknowledge discussions at the workshops on “Extracting Information from spectropolarimetric observations: comparison of inversion codes” at the ISSI in Bern.
References
- Albregtsen, F., & Maltby, P. 1978, Nature, 274, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Albregtsen, F., Joras, P. B., & Maltby, P. 1984, Sol. Phys., 90, 17 [Google Scholar]
- Balthasar, H., & Collados, M. 2005, A&A, 429, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balthasar, H., & Schmidt, W. 1993, A&A, 279, 243 [NASA ADS] [Google Scholar]
- Beck, C., Bellot Rubio, L. R., Schlichenmaier, R., & Sütterlin, P. 2007, A&A, 472, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Fabbian, D. 2011, A&A, 535, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellot Rubio, L. R. 2003, Inversion of Stokes profiles with SIR (Freiburg: Kiepenheuer Institut für Sonnenphysik) [Google Scholar]
- Biermann, L. 1941, Vierteljahrsschr. Astr. Gesellsch., 76, 194 [Google Scholar]
- Borrero, J. M., & Ichimoto, K. 2011, Liv. Rev. Sol. Phys., 8, 4 [Google Scholar]
- Boyer, R., Sotirovski, P., & Harvey, J. W. 1975, A&AS, 19, 359 [NASA ADS] [Google Scholar]
- Bray, R. J., & Loughhead, R. E. 1964, Sunspots (Chapman Hall) [Google Scholar]
- Cabrera Solana, D., Bellot Rubio, L. R., & del Toro Iniesta, J. C. 2005, A&A, 439, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collados, M., Martinez Pillet, V., Ruiz Cobo, B., del Toro Iniesta, J. C., & Vazquez, M. 1994, A&A, 291, 622 [NASA ADS] [Google Scholar]
- Collados, M., Lagg, A., Díaz Garcí A, J. J., et al. 2007, in The Physics of Chromospheric Plasmas, eds. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf. Ser., 368, 611 [Google Scholar]
- de Toma, G., Chapman, G. A., Cookson, A. M., & Preminger, D. 2013, ApJ, 771, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Gingerich, O., Noyes, R. W., Kalkofen, W., & Cuny, Y. 1971, Sol. Phys., 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, J. 1986, in Small Scale Magnetic Flux Concentrations in the Solar Photosphere, eds. W. Deinzer, M. Knölker, & H. H. Voigt, 25 [Google Scholar]
- Hathaway, D. H. 2010, Liv. Rev. Sol. Phys., 7, 1 [Google Scholar]
- Hogg, D. W., Bovy, J., & Lang, D. 2010, unpublished [arXiv:1008.4686] [Google Scholar]
- Jaeggli, S. A., Habbal, S. R., Kuhn, J. R., & Nayfeh, M. H. 2006, BAAS, 38, 918 [NASA ADS] [Google Scholar]
- Jaeggli, S. A., Lin, H., Mickey, D. L., et al. 2010, Mem. Soc. Astron. Italiana, 81, 763 [NASA ADS] [Google Scholar]
- Jahn, K. 1989, A&A, 222, 264 [NASA ADS] [Google Scholar]
- Kiess, C., Rezaei, R., & Schmidt, W. 2014, A&A, 565, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kopp, G., & Rabin, D. 1992, Sol. Phys., 141, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Landi degl’Innocenti, E., & Landolfi, M. 2004, in Polarization in Spectral Lines (Dordrecht: Kluwer Academic Publishers), Astrophys. Space Sci. Lib., 307 [Google Scholar]
- Leonard, T., & Choudhary, D. P. 2008, Sol. Phys., 252, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Elmore, D. F., Seagraves, P., & Skumanich, A. P. 1993, ApJ, 418, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W. 2002, Sol. Phys., 207, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W., Harvey, J. W., Malanushenko, O. V., & Webster, L. 2006, Sol. Phys., 239, 41 [Google Scholar]
- Livingston, W., Penn, M. J., & Svalgaard, L. 2012, ApJ, 757, L8 [Google Scholar]
- Maltby, P., Avrett, E. H., Carlsson, M., et al. 1986, ApJ, 306, 284 [Google Scholar]
- Martinez Pillet, V., & Vazquez, M. 1993, A&A, 270, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V., Collados, M., Sánchez Almeida, J., et al. 1999, in High Resolution Solar Physics: Theory, Observations, and Techniques, ASP Conf. Ser., 183, 264 [NASA ADS] [Google Scholar]
- Mathew, S. K., Lagg, A., Solanki, S. K., et al. 2003, A&A, 410, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathew, S. K., Martínez Pillet, V., Solanki, S. K., & Krivova, N. A. 2007, A&A, 465, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattig, W. 1971, Sol. Phys., 18, 434 [NASA ADS] [CrossRef] [Google Scholar]
- McIntosh, P. S. 1981, in The Physics of Sunspots, eds. L. E. Cram, & J. H. Thomas, 7 [Google Scholar]
- McIntosh, S. W., Leamon, R. J., Gurman, J. B., et al. 2013, ApJ, 765, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Moradi, H., Baldner, C., Birch, A. C., et al. 2010, Sol. Phys., 267, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Nagovitsyn, Y. A., Pevtsov, A. A., & Livingston, W. C. 2012, ApJ, 758, L20 [Google Scholar]
- Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P., & Brault, J. W. 1994, ApJS, 94, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, Å., & Stein, R. F. 1990, in Solar Photosphere: Structure, Convection, and Magnetic Fields, ed. J. O. Stenflo, IAU Symp., 138, 191 [NASA ADS] [Google Scholar]
- Norton, A. A., & Gallagher, J. C. 2010, Sol. Phys., 261, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. A., & Gilman, P. A. 2004, ApJ, 603, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. A., Jones, E. H., & Liu, Y. 2013, J. Phys. Conf. Ser., 440, 012038 [NASA ADS] [CrossRef] [Google Scholar]
- Patil, A., Huard, D., & Fonnesbeck, C. J. 2010, J. Stat. Soft., 35, 4 [Google Scholar]
- Penn, M. J., & Livingston, W. 2006, ApJ, 649, L45 [Google Scholar]
- Penn, M. J., & Livingston, W. 2011, in The Physics of the Sun and Star Spots, IAU Symp., 273, 126 [NASA ADS] [Google Scholar]
- Penn, M. J., & MacDonald, R. K. D. 2007, ApJ, 662, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Penn, M. J., Ceja, J. A., Bell, E., Frye, G., & Linck, R. 2002, Sol. Phys., 205, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Penn, M. J., Walton, S., Chapman, G., Ceja, J., & Plick, W. 2003, Sol. Phys., 213, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Pevtsov, A. A., Nagovitsyn, Y. A., Tlatov, A. G., & Rybak, A. L. 2011, ApJ, 742, L36 [Google Scholar]
- Pevtsov, A. A., Bertello, L., Tlatov, A. G., et al. 2014, Sol. Phys., 289, 593 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing (Cambridge University Press), 2nd edn. [Google Scholar]
- Radziemski, Jr., L. J., & Andrew, K. L. 1965, J. Opt. Soc. Am., 55, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., & Schlichenmaier, R. 2011, Liv. Rev. Sol. Phys., 8, 3 [Google Scholar]
- Rezaei, R., Schlichenmaier, R., Beck, C., & Bellot Rubio, L. R. 2006, A&A, 454, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rezaei, R., Beck, C., & Schmidt, W. 2012, A&A, 541, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Schad, T. A. 2014, Sol. Phys., 289, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Schad, T. A., & Penn, M. J. 2010, Sol. Phys., 262, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Schröter, E. H., Soltau, D., & Wiehr, E. 1985, Vistas Astron., 28, 519 [Google Scholar]
- Schüssler, M., & Vögler, A. 2006, ApJ, 641, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H. 2007, ApJS, 169, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Stanchfield, II, D. C. H., Thomas, J. H., & Lites, B. W. 1997, ApJ, 477, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Stellmacher, G., & Wiehr, E. 1988, A&A, 191, 149 [NASA ADS] [Google Scholar]
- Stix, M. 2002, The Sun: An Introduction (Berlin: Springer-Verlag), 2nd edn. [Google Scholar]
- Thomas, J. H., & Weiss, N. O. 2004, ARA&A, 42, 517 [NASA ADS] [CrossRef] [Google Scholar]
- von Klüber, H. 1948, ZAp, 24, 121 [NASA ADS] [Google Scholar]
- Watson, F. T., Fletcher, L., & Marshall, S. 2011, A&A, 533, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, F. T., Penn, M. J., & Livingston, W. 2014, ApJ, 787, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Wesolowski, M. J., Walton, S. R., & Chapman, G. A. 2008, Sol. Phys., 248, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Westendorp Plaza, C., del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 2001, ApJ, 547, 1130 [NASA ADS] [CrossRef] [Google Scholar]
- Wittmann, A. 1972, Sol. Phys., 23, 294 [NASA ADS] [CrossRef] [Google Scholar]
- Zwaan, C. 1965, in Stellar and Solar Magnetic Fields, ed. R. Lust, IAU Symp., 22, 277 [Google Scholar]
All Tables
Atomic parameters of the spectral lines (Nave et al. 1994; Radziemski, Jr. & Andrew 1965).
Summary of the temporal gradients of the continuum intensity, the magnetic field strength, and the umbral area in different time intervals.
All Figures
 |
Fig. 1 Scatter plot of corrected sunspot intensity and field strength for all observed sunspots. Different symbols denote different observed wavelengths. |
| In the text | |
 |
Fig. 2 Continuum intensity at 1.56 μm as a function of umbral radius. The black line shows a linear fit and the gray line 3σ margins. For a description of different symbols, see caption of Fig. 1. |
| In the text | |
 |
Fig. 3 Variation of the maximum field strength (left) and the minimum continuum intensity (right) as a function of time. The vertical dotted lines at 2001 and 2009 indicate the maximum and minimum of cycle 23, respectively. The lines at 2012 and 2013 mark the possible maximum of cycle 24. The solid line shows a least-squares, the dashed line a Bayesian fit to the data between the corresponding vertical lines. The green line in both panels shows a linear fit to all data points. A summary of the fit parameters is presented in Table 2. Arrows indicate the temporal extent of the two cycles. For a description of different symbols, see Fig. 1. |
| In the text | |
 |
Fig. 4 Variation of umbral area as a function of time. For a description of lines and different symbols, see Figs. 1 and 3. |
| In the text | |
 |
Fig. 5 Comparison of the distribution of maximum field strength in sunspots observed in cycles 23 and 24. The maximum of the two Gaussians for cycle 23 and 24 is at 2.68 and 2.60 kG, respectively. The dashed curve shows the distribution of the measured magnetic field strength in cycle 23 from 2003 until 2007 reported by Livingston et al. (2012). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


