| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 5 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425470 | |
| Published online | 02 June 2015 | |
Research Note
The evolution of the spatially resolved metal abundance in galaxy clusters up to z = 1.4⋆
1 INAF, Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna Italy
e-mail: stefano.ettori@oabo.inaf.it
2 INFN, Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
3 Physics and Astronomy Dept., Michigan State University, East Lansing, MI 48824, USA
4 INAF, Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34131 Trieste, Italy
5 INAF–IASF, via Bassini 15, 20133 Milan, Italy
6 Department of Physics and Astronomy, University of California at Irvine, 4129 Frederick Reines Hall, Irvine, CA 92697–4575, USA
7 INAF, Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
Received: 5 December 2014
Accepted: 1 April 2015
Context. We present the combined analysis of the metal content of 83 objects in the redshift range 0.09−1.39, and spatially resolved in the three bins (0−0.15, 0.15−0.4, >0.4) R500, as obtained with similar analysis using XMM-Newton data in our previous two papers.
Aims. By combining these two large data sets, we investigate the relations between abundance, temperature, radial position and redshift holding in the intracluster medium.
Methods. We fit functional forms to the combination of the different physical quantities of interest, i.e., intracluster medium (ICM) metal abundance, radius, and redshift. We use the pseudo-entropy ratio to separate the cool core (CC) cluster population, where the central gas density tends to be relatively higher, cooler and more metal rich, from the non-cool core systems.
Results. The average, redshift-independent, metal abundance measured in the three radial bins decreases moving outwards, with a mean metallicity in the core that is even three (two) times higher than the value of 0.16 times the solar abundance in Anders & Grevesse (1989, Geochim. Cosmochim. Acta, 53, 197) estimated at r> 0.4 R500 in CC (NCC) objects. We find that the values of the emission-weighted metallicity are well fitted by the relation Z(z) = Z0 (1 + z)− γ at the given radius. A significant scatter, intrinsic to the observed distribution and of the order of 0.05−0.15, is observed below 0.4 R500. The nominal best-fit value of γ is significantly different from zero (>3σ) in the inner cluster regions (γ = 1.6 ± 0.2) and in CC clusters only. These results are also confirmed with a bootstrap analysis, which provides a still significant negative evolution in the core of CC systems (P> 99.9 per cent, when counting the number of random repetitions, which yields γ> 0). No redshift evolution is observed when regions above the core (r> 0.15 R500) are considered. A reasonable good fit of both the radial and redshift dependence is provided from the functional form Z(r,z) = Z0(1 + (r/ 0.15 R500)2)− β(1 + z)− γ, with (Z0,β,γ) = (0.83 ± 0.13,0.55 ± 0.07,1.7 ± 0.6) in CC clusters and (0.39 ± 0.04,0.37 ± 0.15,0.5 ± 0.5) for NCC systems.
Conclusions. Our results represent the most extensive study of the spatially resolved metal distribution in the cluster plasma as function of redshift. Our study defines the limits that numerical and analytic models describing the metal enrichment in the ICM have to meet.
Key words: galaxies: clusters: intracluster medium / X-rays: galaxies: clusters
The full data set is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/578/A46
© ESO, 2015
1. Introduction
The hot, thin X-ray emitting plasma in galaxy clusters (i.e. the intracluster medium, ICM) is enriched with metals ejected form supernovae (SNe) explosions through subsequent episodes of star formation and subsequent diffusion through several mechanisms, e.g., ram pressure stripping, galactic winds, outflows from active Galactic nuclei, galaxy-galaxy interactions (e.g. Renzini 1997; Schindler & Diaferio 2008).
X-ray observations provide direct measurements of the metal abundance in the ICM, as well as their radial distribution and variation as a function of time. These measures represent the “footprint” of cosmic star formation history and are crucial to tracing the effect of SN feedback on the ICM at different cosmic epochs (e.g. Ettori 2005; Calura et al. 2007; Cora et al. 2008; Fabjan et al. 2010).
Several studies have addressed the radial distributions of metals in the ICM at low redshift (e.g. Finoguenov et al. 2000; De Grandi & Molendi 2001; Irwin & Bregman 2001; Tamura et al. 2004; Baldi et al. 2007; Leccardi & Molendi 2008; Snowden et al. 2008). A few others have constrained the evolution of the metal abundance at z ≳ 0.3 (e.g. Balestra et al. 2007; Maughan et al. 2008; Anderson et al. 2009; a statistical analysis of the combination of these different data sets is presented in Andreon 2012). In Baldi et al. (2012a), we have presented the XMM-Newton analysis of 39 galaxy clusters at 0.4 <z< 1.4, covering a temperature range of 2 ≲ kT ≲ 12.8 keV. We were able to resolve their abundance in three radial bins.
In this work, we combine this data set with that presented in Leccardi & Molendi (2008), which includes 44 objects at z< 0.31, with gas temperatures between 2.9 keV and 11.3 keV. The analysis performed on the XMM-Newton data in the two samples is identical and can be statistically combined to probe the ICM abundance as a function of radial position and redshift.
We adopt a cosmological model with H0=70 km s-1 Mpc-1, Ωm=0.3, and ΩΛ=0.7 throughout. Solar abundance values published in Anders & Grevesse (1989) are adopted for reference. Confidence intervals are quoted at 1σ unless otherwise stated.
2. Data analysis
 |
Fig. 1 Abundance distribution as function of redshift as estimated in three radial bins (0−0.15 R500, 0.15−0.4 R500, and >0.4 R500). Filled points indicate CC clusters. Left: all data are plotted with the best fits done in the given radial bin (dotted line) and including the radial dependence (dashed line); right: the best fits in redshift and radius (dashed lines) are shown with representative data points obtained as a weighted mean, with the relative error (solid bars) and dispersion (dashed bars). |
Details on the X-ray data reduction and analysis are presented in Leccardi & Molendi (2008) and Baldi et al. (2012a), which include a discussion on the systematic effects that could affect our estimates of the ICM metallicity. Most of these measurements, which are for high temperature (kT> 2 keV) systems at medium-high redshifts (z> 0.1), are mainly based on the strength of the iron K line (at the rest-frame energies of 6.6−7.0 keV)1. We briefly mention here that we performed a simultaneous spectral fit on spectra accumulated from the two MOS detectors over the energy range 0.7−8.0 keV, using a Cash statistics applied to the source plus background counts, with a modelled background emission. The free parameters of the thermal model apec in XSPEC (Arnaud 1996) are temperature, abundance, and normalization. Local absorption is fixed to the Galactic neutral hydrogen column density, as obtained from radio data (Kalberla et al. 2005), and the redshift to the value is measured from optical spectroscopy.
Because of the better statistics in lower redshift clusters, the X-ray spectral analysis of most objects in Leccardi & Molendi (2008) was performed using a finer radial binning with respect to Baldi et al. (2012a). Thus, we had to degrade the spatial resolution of Leccardi & Molendi (2008) abundance profiles to match its resolution with Baldi et al. (2012a) and obtain uniform abundance profiles in three radial bins: 0−0.15 R500, 0.15−0.4 R500, and >0.4 R500, where R500 is estimated through a scaling relation (e.g. Vikhlinin et al. 2006; see Baldi et al. 2012 for details) by using a global gas temperature that does not include the core emission (<0.15 R500). We first carried out the spatial degradation by interpolating the abundance profile (and its relative error) over the radial points of the observed surface brightness profile S(r) of each cluster. Then, we used the surface brightness profile as a weighting factor for the interpolated abundance profile, together with the errors on the abundance profile itself, so that – in each resulting bin – regions with higher surface brightness and smaller uncertainties in the measure of the abundance would have a larger weight in the computation of the average abundance. This scheme reproduces an emission–weighted profile of the metal abundance. Hydrodynamical simulations have shown that an emission–weighted metallicity matches the original value in simulations at better than 5% (e.g. Rasia et al. 2008). Following this approach, the average
abundance ⟨ Z ⟩, and the relative error σ⟨ Z ⟩, in the Rmin − Rmax bin was computed as: 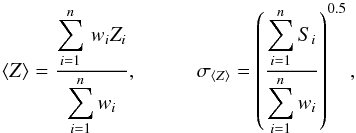 (1)where Zi and σZi are the abundance profile and the error on the abundance profile, respectively,
(1)where Zi and σZi are the abundance profile and the error on the abundance profile, respectively, 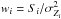 is the weighting factor, and the sum is done over the n radial bins falling in the radial range Rmin − Rmax in the abundance profile of each cluster, as measured in Leccardi & Molendi (2008).
is the weighting factor, and the sum is done over the n radial bins falling in the radial range Rmin − Rmax in the abundance profile of each cluster, as measured in Leccardi & Molendi (2008).
Results of the combined analysis on the redshift and radial distribution of the metal abundance.
3. Results on the spatially resolved abundance evolution
This work presents our final effort to use archived data to constrain the evolution of the spatially resolved ICM abundance. Our analysis separates the central regions, where cool cores (if any) appear, and the rest of the cluster atmosphere. We require that the spectrum from which the metallicity is measured contains at least 300 net counts. We consider a total of 221 data points corresponding to the spatially resolved spectroscopic measurements of the metal abundance distribution in 83 galaxy clusters in the redshift range 0.092−1.393. By estimating the pseudo-entropy ratio σ = (T0/T1) × (EM0/EM1)− 1 / 3, where T0 and T1 are the temperatures measured in the r< 0.15R500 region and in the 0.15 − 0.4 R500 annulus, respectively, and EM0 and EM1 are the corresponding emission measures, we define as non-cool core (NCC) clusters 54 (out of 83) objects that have σ ≥ 0.6 (see e.g. Leccardi et al. 2010; Baldi et al. 2012b). The data points are plotted as function as radius and redshift, separating between CC and NCC systems, in Fig. 1. All the results are presented in Table 1.
In the r< 0.15 R500 radial bin, we have 70 data points over the entire redshift range. The distribution of the metal abundance correlates significantly with the redshift (Spearman’s rank ρz = −0.25, corresponding to a significance of 2.1σ versus the null-hypothesis of no correlation; see Table 2), with the temperature (ρT = −0.3, 2.5σ) and with the pseudo-entropy ratio (ρσ = −0.4, 3.3σ). These correlations point towards a significant effect induced from the cooling activities taking place in these regions, where the ICM at high density radiates more efficiently, lowering its global temperature and increasing its metal budget (see e.g. Leccardi & Molendi 2008). Fitting the data points in this bin with a power law in the form Z ∝ (1 + z)− γ, we obtain γ = 1.60 ± 0.22, which differs from zero at high significance (>6σ). When a bootstrap analysis is done, i.e. the fit is repeated 105 times after a random sampling with replacement and the median, we consider the 1st and 3rd quartiles to estimate location and dispersion of the distribution of the best-fitting parameters. We also find that the central values are recovered, but the relative errors are increased by about a factor of 2, mostly because a more proper sampling of the intrinsic scatter is performed with the bootstrap analysis. The negative evolution (γ> 0) is still detected in >99.9 per cent of the replica. When we consider CC and NCC systems separately, the normalization Z0 is different by a factor of 2.2 in favour of CC systems, where a negative evolution is still detected at very high significance. Instead, no evolution is measured (γ = 0.5 ± 0.4) in NCC objects, although the case for negative evolution is still observed in about 80% of the bootstrapped repetitions.
Eighty-three data points are located in the radial bin 0.15 R500<r< 0.4R500, where a 2.8σ significant correlation between pseudo-entropy ratio and redshift is detected, suggesting an increase of σ (i.e larger incidence of NCC systems) with the redshift. A mild anti-correlation between Z and redshift is also present in this bin (significance of 2.2σ). We measure γ = 0.70 ± 0.32 (1σ range of 0.16−1.31 after bootstrap analysis). The case for negative evolution is still observed in about 91% of the bootstrapped samples. Similar values are measured in the population of NCC clusters, which dominates the sample in this radial bin, with a normalization (and a mean metallicity value) that is lower than the corresponding value measured for CC systems by about 30 per cent.
Finally, we do not find evidence of negative redshift evolution of the metallicity in the last radial bin considered in our analysis (r> 0.4 R500), either. In this case, we constrain a value for γ of 0.26 ± 0.61 (γ> 0 with a probability P ≈ 65% after bootstrap analysis) with 68 data points. Similar results are obtained in the CC and NCC populations, where an average value of Z = 0.16 Z⊙ is estimated.
As the sample is highly heterogeneous and not in any sense representative of the cluster population, it is not expected to weigh properly against the relative incidence of these cool cores clusters. Moving at higher redshift, for instance, lower metal abundance associated with the inner regions suggest that less pronounced cool cores are resolved in our sample (see e.g. Santos et al. 2010; Samuele et al. 2011).
Spearman’s rank correlation coefficients.
4. Summary and conclusions
We present the statistical analysis of the spatially resolved spectroscopic results of the XMM-Newton observations of 83 clusters of galaxies in the redshift range 0.09 <z< 1.39 and with a gas temperature between 2 keV and 12.8 keV. In a consistent and similar way (see details in Leccardi & Molendi 2008; Baldi et al. 2012a), we resolved the cluster emission for all objects in the data set in three different regions: the core region (corresponding to 0 <r< 0.15R500), the region immediately surrounding the core (0.15 R500<r< 0.4 R500), and the outskirts of the cluster (r> 0.4 R500). Using the pseudo-entropy ratio σ, we also distinguish between cool core and non-cool core objects, with CC clusters that represent ~35 per cent of the whole sample. Our results are summarized in Tables 1 and 2.
We find strong (significance at 3σ or higher) correlations between (i) metallicity and pseudo-entropy ratio (in the inner bin) and, in the entire sample; (ii) metallicity and redshift; and (iii) pseudo-entropy ratio and redshift.
By fitting a constant value (under the assumption of no-evolution) to the metal abundance measured in the three radial bins, we confirm a neat decrease moving outwards, with the inner bin being even three (two) times more metal rich than the outermost bin in CC (NCC) systems (0.49 / 0.32, 0.27 / 0.18 and 0.16 / 0.16 for CC/NCC systems in the three radial bins, respectively).
We constrain the parameters of the functional form Z(r,z) = Z0(1 + (r/ 0.15 R500)2)− β(1 + z)− γ. The best-fitting values are Z0 = 0.70 ± 0.03 (0.62−0.79, 1st−3rd quartile from the bootstrap analysis), β = 0.56 ± 0.03(0.48 − 0.65) and γ = 1.3 ± 0.2 (0.95−1.72). The CC and NCC systems behave differently, with (Z0,β,γ) equal to (0.83 ± 0.13,0.55 ± 0.07,1.7 ± 0.6) and (0.39 ± 0.04,0.37 ± 0.15,0.5 ± 0.5), respectively (error bars refer to the bootstrap analysis).
At a given radius, we find a statistically significant negative evolution in the distribution of the metal abundance as a function of redshift in the inner radial bin (>3.5σ; the probability from the bootstrap analysis to measure γ> 0 is larger than 99.9 per cent). We show that this level of evolution with cosmic time is entirely consistent with the same evolution observed in the CC-only population. On average, we measure a mean metallicity in the local systems that is about 3−4.5 (1.4 in NCC clusters) times the value measured at z ≈ 1, which is consistent with the constraints we publish in Baldi et al. (2012a) and, using (mostly) Chandra data, in Balestra et al. (2007). At the same redshift, the metallicity decreases radially, reaching at ~0.5 R500 about 37 (in CC) and 50 (in NCC) per cent of the value estimated at 0.15 R500. By requiring a reduced χ2 of 1 in the performed fit, we estimate an intrinsic scatter in Z of about 0.15,0.05 and 0.05 in the three radial bins, respectively. In the inner bin, the scatter of ~0.15 is also measured only in the CC systems, whereas NCC clusters show a value of 0.05 consistently in the inner two radial bins.
The CC clusters show evidence of negative evolution just in the inner radial bin (<0.15 R500), where the accumulation of the plasma during the cluster formation makes the ICM denser and, as consequence of radiative processes, cooler and more metal rich. Most of the above-mentioned correlations (i.e. ρz, ρT and ρσ in Table 2) can be then interpreted as due to the strong influence of this centrally-located cool gas. The NCC systems do not show any statistically significant deviation from γ = 0 at any radial bin. Both CC and NCC systems present similar average metallicity, and an intrinsic scatter almost consistent with zero, in the outer bin (r> 0.4 R500) only. We conclude that, for what concerns the metal distribution, this cluster volume is the most homogeneous in both CC and NCC systems, and might be considered the most representative of the average cluster environment.
We stress that this work provides the most robust constraints reachable with archived XMM-Newton and Chandra data on the distribution of the metal abundance as a function of radius and redshift in the ICM. Larger samples of high redshift X-ray clusters, together with deeper Chandra and XMM-Newton observations even of the clusters already present in the archive, would be crucial to putting tighter constraints on the evolution of the ICM metal abundance. These samples are also needed to provide a robust modelling of the physical processes responsible for the enrichment of the cluster plasma during its assembly over cosmic time, from the accumulation of the iron mass in the CC cluster cores (e.g. De Grandi et al. 2004; Böhringer et al. 2004) to the history of the processes responsible for the metal release into the ICM through ejections from supernovae Types Ia and II (e.g. Ettori 2005), as well as through galaxy transformation in the cluster volume (e.g. Calura et al. 2007) and their modelling in joint semi-analytic/hydrodynamical numerical simulations (e.g. Cora et al. 2008; Fabjan et al. 2010).
The full data set analysed here is available at http://pico.bo.astro.it/~settori/ abun/xmm.dat and at the CDS.
Acknowledgments
We thank Sabrina De Grandi and Mauro Sereno for their discussion. We acknowledge financial contribution from contracts ASI-INAF I/009/10/0 and Prin-INAF 2012 on “A unique data set to address the most compelling open questions about X-Ray Galaxy Clusters”. We thank the anonymous referee for useful comments that helped to improve the presentation of the results in this paper.
References
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Anderson, M. E., Bregman, J. N., Butler, S. C., & Mullis, C. R. 2009, ApJ, 698, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2012, A&A, 546, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Baldi, A., Ettori, S., Mazzotta, P., Tozzi, P., & Borgani, S. 2007, ApJ, 666, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Baldi, A., Ettori, S., Molendi, S., et al. 2012a, A&A, 537, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldi, A., Ettori, S., Molendi, S., & Gastaldello, F. 2012b, A&A, 545, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balestra, I., Tozzi, P., Ettori, S., et al. 2007, A&A, 462, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Matsushita, K., Churazov, E., Finoguenov, A., & Ikebe, Y. 2004, A&A, 416, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calura, F., Matteucci, F., & Tozzi, P. 2007, MNRAS, 378, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Cora, S. A., Tornatore, L., Tozzi, P., & Dolag, K. 2008, MNRAS, 386, 96 [NASA ADS] [CrossRef] [Google Scholar]
- De Grandi, S., & Molendi, S. 2001, ApJ, 551, 153 [NASA ADS] [CrossRef] [Google Scholar]
- De Grandi, S., Ettori, S., Longhetti, M., & Molendi, S. 2004, A&A, 419, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ettori, S. 2005, MNRAS, 362, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Fabjan, D., Borgani, S., Tornatore, L., et al. 2010, MNRAS, 401, 1670 [NASA ADS] [CrossRef] [Google Scholar]
- Finoguenov, A., David, L. P., & Ponman, T. J. 2000, ApJ, 544, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J. A., & Bregman, J. N. 2001, ApJ, 546, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leccardi, A., & Molendi, S. 2008, A&A, 487, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leccardi, A., Rossetti, M., & Molendi, S. 2010, A&A, 510, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maughan, B. J., Jones, C., Forman, W., & Van Speybroeck, L. 2008, ApJS, 174, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Rasia, E., Mazzotta, P., Bourdin, H., et al. 2008, ApJ, 674, 728 [Google Scholar]
- Renzini, A. 1997, ApJ, 488, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Samuele, R., McNamara, B. R., Vikhlinin, A., & Mullis, C. R. 2011, ApJ, 731, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, J. S., Tozzi, P., Rosati, P., & Böhringer, H. 2010, A&A, 521, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schindler, S., & Diaferio, A. 2008, Space Sci. Rev., 134, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Mushotzky, R. F., Kuntz, K. D., & Davis, D. S. 2008, A&A, 478, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tamura, T., Kaastra, J. S., den Herder, J. W. A., Bleeker, J. A. M., & Peterson, J. R. 2004, A&A, 420, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Results of the combined analysis on the redshift and radial distribution of the metal abundance.
All Figures
 |
Fig. 1 Abundance distribution as function of redshift as estimated in three radial bins (0−0.15 R500, 0.15−0.4 R500, and >0.4 R500). Filled points indicate CC clusters. Left: all data are plotted with the best fits done in the given radial bin (dotted line) and including the radial dependence (dashed line); right: the best fits in redshift and radius (dashed lines) are shown with representative data points obtained as a weighted mean, with the relative error (solid bars) and dispersion (dashed bars). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


