| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 4 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201526054 | |
| Published online | 20 May 2015 | |
Research Note
A graph of dark energy significance on different spatial and mass scales
1
Tuorla ObservatoryDepartment of Physics and Astronomy, University of
Turku,
21500
Piikkiö,
Finland
e-mail:
pekkatee@utu.fi
2
Sternberg Astronomical Institute, Moscow University,
119899
Moscow,
Russia
3
Tartu Observatory, 61602
Tõravere,
Estonia
4
University of Alabama, Tuscaloosa, AL
35487-0324,
USA
Received: 9 March 2015
Accepted: 21 March 2015
Context. The current cosmological paradigm sees the formation and evolution of the cosmic large-scale structure as governed by the gravitational attraction of dark matter (DM) and the repulsion of dark energy (DE).
Aims. We characterize the relative importance of uniform and constant dark energy, as given by the Λ term in the standard ΛCDM cosmology, in galaxy systems of different scales from groups to superclusters.
Methods. An instructive “Λ significance graph” is introduced where the matter-DE density ratio ⟨ ρM ⟩ /ρΛ for different galaxy systems is plotted against the radius R. This presents gravitation- and DE-dominated regions and directly shows the zero velocity radius, the zero-gravity radius, and the Einstein-Straus radius for any fixed value of mass.
Results. Example galaxy groups and clusters from the local universe illustrate the use of the Λ significance graph. These are generally located deep in the gravity-dominated region ⟨ ρM ⟩ /ρΛ> 2, and are virialized. Extended clusters and the main bodies of superclusters can reach down near the borderline between gravity-dominated and DE-dominated regions ⟨ ρM ⟩ /ρΛ = 2. The scale-mass relation from the standard two-point correlation function intersects this balance line near the correlation length.
Conclusions. The log ⟨ ρM ⟩ /ρΛ vs. log R diagram is a useful and versatile way to characterize the dynamical state of systems of galaxies within the Λ-dominated expanding universe.
Key words: galaxies: clusters: general / dark matter / dark energy
© ESO, 2015
1. Introduction
According to the standard Λ cold dark matter (ΛCDM) cosmology, a large majority of the material contents of the universe or about 95 per cent in energy density is made of unknown dark substances called dark matter and dark energy (DE). Dark matter is revealed by its gravitation, while dark energy (represented by Einstein’s cosmological constant Λ in standard cosmology) is an “antigravitating” uniform vacuum-like fluid. The DE background produces antigravity which is stronger than matter gravity in the present universe as a whole, making the universal expansion accelerate. According to the Planck Surveyor results (Planck Collaboration XVI 2014), the global density of the DE is, in round numbers, ρΛ ≈ 6 × 10-30 g cm-3 1.
Because of the non-uniform distribution of gravitating matter, the cosmic antigravity can also be stronger locally than gravity on scales of ~1−10 Mpc (Chernin 2001), which in principle makes it possible to detect the DE in the local galaxy universe, as reviewed by Byrd et al. (2012, 2015). For a recent study about the DE in the vicinity of the Local Group see Saarinen & Teerikorpi (2014).
The presence of DE, along with gravitating matter, influences the formation of the large scale structure on all scales from groups of galaxies to superclusters. In regions where the DE dominates the gravitating matter, new structures do not condense and linear perturbations of density decay (or even non-linear, if sheet-like; Chernin et al. 2003). The antigravity of DE also puts an upper limit on the size of a bound system of a certain mass, and it influences dynamic mass determinations, leading to too low a mass Chernin et al. (2009, 2012).
A useful parameter that characterizes the influence of DE is the energy density ratio ⟨ ρM ⟩ /ρΛ as calculated for the system or scale under inspection. In the present Note, we introduce a graph presenting the ratio ⟨ ρM ⟩ /ρΛ for systems of different sizes and masses. This diagram directly displays a few relevant scales that appear for each fixed mass of a spherical or slightly flattened system in ΛCDM cosmology. The location of a galaxy system in the diagram indicates whether its overall dynamics are dominated by gravity or DE antigravity. This Λ significance graph also has limited use for flattened systems.
2. Zero-gravity radius and Einstein-Straus scale
A natural scale that appears around a mass point (or a spherically symmetric system) embedded in the dark energy background is the zero-gravity radius RZG. In a weak field situation one may write (Chernin et al. 2009) the force affecting a test particle with mass m as the sum of Newton’s gravity force produced by the mass M and Einstein’s antigravity force due to DE: 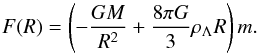 (1)At the zero-gravity distance R = RZG (Chernin 2001),
(1)At the zero-gravity distance R = RZG (Chernin 2001), 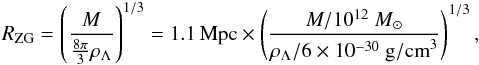 (2)gravity is equal to antigravity.
(2)gravity is equal to antigravity.
Another interesting scale is related to the Einstein-Straus radius RES. This comes from the central mass plus vacuole solution by Einstein & Straus (1945), where the radius of the vacuole is such that the mean density within it is equal to the current density of the Friedmann universe: ![\begin{equation} R_{\mathrm{ ES}} = \left[M /\left(\frac{4 \pi}{3} \rho_{\rm m}\right)\right]^{1/3} = R_{\mathrm{ZG}} \left(2\frac{\rho_{\Lambda}}{\rho_{\rm m}}\right)^{1/3} \simeq 1.7 R_{\mathrm{ZG}} . \end{equation}](/articles/aa/full_html/2015/05/aa26054-15/aa26054-15-eq18.png) (3)This may be imagined as the radius of the spherical volume from which the mass making up the system has been gathered in the past during the gravitational instability process.
(3)This may be imagined as the radius of the spherical volume from which the mass making up the system has been gathered in the past during the gravitational instability process.
Dark energy puts an absolute upper limit on the size of a gravitationally bound system: it must be located within its zero-gravity sphere where gravity dominates.
3. Matter-to-DE ratio vs. scale diagram
It is instructive and useful to construct a diagram where the x-axis is the logarithm of the spatial scale (or the radius of a system) and the y-axis gives the (log) ratio of the average density ⟨ ρM ⟩ of a system and the (constant) DE density equal to the global value ρΛ.
For ρΛ ≈ 6 × 10-30 g cm-3, the ratio ⟨ ρM ⟩ /ρΛ becomes 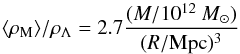 (4)where M is the mass within the radius R. In logarithms:
(4)where M is the mass within the radius R. In logarithms: 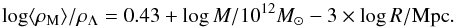 (5)In the log ⟨ ρM ⟩ /ρΛ vs. log R diagram, this relation forms a family of inclined straight lines for each fixed value of mass M. Figure 1 explains the meaning of the different lines and regions in such a diagram. The fraction of the DE density grows when one goes downwards in the diagram. In the upper part of the diagram, the systems are dominated by gravitation. They may be bound, and for sufficiently high ⟨ ρM ⟩ /ρΛ, they can be virialized (Sect. 5).
(5)In the log ⟨ ρM ⟩ /ρΛ vs. log R diagram, this relation forms a family of inclined straight lines for each fixed value of mass M. Figure 1 explains the meaning of the different lines and regions in such a diagram. The fraction of the DE density grows when one goes downwards in the diagram. In the upper part of the diagram, the systems are dominated by gravitation. They may be bound, and for sufficiently high ⟨ ρM ⟩ /ρΛ, they can be virialized (Sect. 5).
We show three horizontal lines in Fig. 1. The uppermost line gives the zero-velocity radius RZV when intersecting the inclined constant mass line. This density ratio is obtained from the classical relation between M and RZV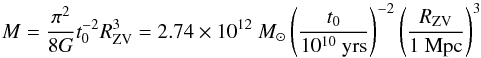 (6)by Lynden-Bell (1981). In addition, the effect of Λ increases RZV by about 1.15 or the inferred mass by about 1.5 (Peirani & de Freitas Pacheco 2006; Saarinen & Teerikorpi 2014; Tully 2015). The calculation leads to
(6)by Lynden-Bell (1981). In addition, the effect of Λ increases RZV by about 1.15 or the inferred mass by about 1.5 (Peirani & de Freitas Pacheco 2006; Saarinen & Teerikorpi 2014; Tully 2015). The calculation leads to 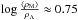 .
.
The middlemost horizontal line is for the ratio ⟨ ρM ⟩ /ρΛ = 2 (gravity = antigravity). The lowest one is for the global matter-to-DE ratio 0.43. Spherical systems below the middlemost line are dynamically dominated by the antigravitating DE background.
When we consider systems of a fixed mass M and go down along the inclined straight line (Eq. (5)), it intersects the middlemost line at the zero-gravity radius RZG(M) (Eq. (2)), which also is the maximal possible size of a bound system. For systems below this line, the radius of the system exceeds the zero-gravity radius. Then the system is not gravitationally bound as a whole; however, this is valid for a spherical system.
Furthermore, the point of intersection with the lowest (“global”) line formally gives the Einstein-Straus radius RES for this same central mass (Eq. (3)). This is also the distance where the Hubble flow around the mass reaches the global Hubble expansion rate (Teerikorpi & Chernin 2010). Below the lowest line, there is matter underdensity.
In a perfectly uniform Friedmann model, only the points of the lowest line exist. Then R refers to the current size of a comoving volume containing the matter mass M2.
In Fig. 1 we have also shown what happens if the mass of a system is M1 as measured within a radius R1, and then increases (e.g., M ∝ R), up to a zero-gravity radius  , the absolute upper limit for the size of a bound system. Chernin et al. (2012) considered such a situation for galaxy groups using different mass-radius laws (density profiles).
, the absolute upper limit for the size of a bound system. Chernin et al. (2012) considered such a situation for galaxy groups using different mass-radius laws (density profiles).
 |
Fig. 1 Log⟨ ρM ⟩ /ρΛ vs. log R for spherical systems. The inclined lines correspond to different mass values. Above the “gravity = antigravity” line, the region is dynamically dominated by gravitation, and below this line by DE. Intersections give the radii RZV, RZG, and RES. Dotted inclined lines illustrate the case where the mass increases with the radius (see the text). |
4. Example systems of galaxies
To illustrate the meaning of the ⟨ ρM ⟩ /ρΛ vs. scale diagram, we calculated the ratio ⟨ ρM ⟩ /ρΛ for several well-known galaxy systems (listed below) and put them in the log ⟨ ρM ⟩ /ρΛ vs. log R diagram of Fig. 2. In some cases, we plot the results for two or more increasingly large radii around the system. The mass and size values are characteristic rather than accurate.
The Local Group. The mass of the LG has notable uncertainty, with values cited from 1.5 to about 4 × 1012M⊙ (e.g., van den Bergh 1999; Chernin et al. 2009; Partridge et al. 2013). Here we use the mass value 2 × 1012M⊙ and the radius R = 1.0 Mpc. Also, we have plotted the zero-gravity region, RZG = 1.4 Mpc, in order to illustrate its location at the intersection of the two lines, as noted above.
The Local Sheet. In addition to the Local Group, this local flattened system comprises other groups and galaxies within about 6 Mpc and seems to form a dynamically separate system, since it is not just an arbitrarily defined part of the plane of the Local Supercluster (McCall 2014). Its mass within the radius of 5 Mpc is about 2 × 1013M⊙, as a sum of the masses of the groups involved (e.g., Table 1 in Chernin et al. 2015).
The Fornax cluster. For an inner part of this cluster (“Fornax1” in our diagram), we use the virial mass 7 × 1013M⊙ (Drinkwater et al. 2001) for Rvir = 1.4 Mpc. Using a Tolman-Bondi infall model (with Λ), Nasonova et al. (2011) derived 2.2 × 1014M⊙ within 4.6 Mpc (“Fornax2”).
 |
Fig. 2 Log ⟨ ρM ⟩ /ρΛ vs. log R/ Mpc for example galaxy systems. The inclined lines are for the mass values indicated in M⊙. Some symbols are slightly shifted in crowded regions. The dotted curve gives the characteristic mass within radius R from the standard 2-point correlation function. “Flat” is the gravity = antigravity line for the limiting case of a flattened system. The region where β1/2tΛ/tcross> 10 is shown. |
Virgo and the Local Supercluster. The centre of the LSC, the Virgo cluster at a distance of 16.5 Mpc (“Vir1”) has a virial mass ≈ 0.7 × 1015M⊙ within 1.8 Mpc. The zone of infall (up to 7 Mpc) may have one fifth of that mass (Karachentsev et al. 2014). The mass further up towards the LG distance is not well known. A Tolman-Bondi mass of about 3.5 × 1015M⊙ (Ekholm et al. 2000) may be an upper limit owing to the sphericity assumed. It is given in Fig. 2 as “Vir2”.
The Coma cluster. Chernin et al. (2013) analysed the observational results on the mass of the Coma cluster at different distances from the centre using different mass profiles and considering the influence of DE. They conclude that at 1.4 Mpc, the mass is 4.4 × 1014M⊙ (Coma1), 2.6 × 1015M⊙ at 4.8 Mpc(Coma2), and 5.4 × 1015M⊙ at 14 Mpc(Coma3). The mass value at 14 Mpc takes DE into account.
The Perseus-Pisces supercluster. For the inner part of the PP supercluster, Hanski et al. (2001) derived the virial mass value of about 1.5 × 1015M⊙ within 2.6 Mpc (PP1). For the larger region within 22 Mpc (PP2), the value 8 × 1015M⊙ was obtained from an analysis based on the Tolman-Bondi model including the Λ term.
The Corona Borealis supercluster. Pearson et al. (2014) find that the central parts of the Corona Borealis supercluster (CB) could have a wide mass range of about 0.6−12 × 1016h-1M⊙ within a radius of 12.5 h-1 Mpc, with the likely value around 1 × 1016h-1M⊙. We used the representative values 1.5 × 1016M⊙ within 19 Mpc.
The Laniakea supercluster. This supercluster (Tully et al. 2014) is the largest well-studied aggregation of matter in the observable universe. According to Tully et al. (2014), the supercluster has a radius of 80 Mpc, if approximated as round, and a mass of about 1017M⊙, which comes from the volume and the mean cosmic density. No independent total mass estimate is available.
Also, the region of dwarf galaxy associations (DGAs) is shown in the log ⟨ ρM ⟩ /ρΛ vs. log R diagram of Fig. 2. They have radii ~0.3 Mpc and virial masses within (0.05−1) × 1012M⊙ (refs. in Chernin & Teerikorpi 2014). We have also marked the location (SDSS groups) around which the galaxy groups (with less than 50 members) extracted from the SDSS-DR10 survey are concentrated (masses from the virial theorem; Tempel et al. 2014).
5. Discussion
The individual objects in Fig. 2 represent a heterogeneous collection of examples from the nearby universe. Nevertheless, it is interesting to note that the systems are generally found above the “gravity = antigravity” ⟨ ρM ⟩ = 2ρΛ line, which defines the absolute upper size for a gravitationally bound spherical system.
Prominent groups and clusters are usually located deep within the gravity-dominated radius (R much less than RZG), which is also required for them to be virialized. The virial theorem in a general form (Chernin et al. 2009) is 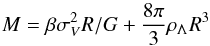 (7)where β is a constant close to unity. By dividing by (4π/ 3)R3ρΛ and inserting the timescale tΛ = (((8π/ 3)GρΛ)− 1/2, one obtains
(7)where β is a constant close to unity. By dividing by (4π/ 3)R3ρΛ and inserting the timescale tΛ = (((8π/ 3)GρΛ)− 1/2, one obtains 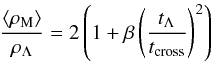 (8)where the crossing time tcross = R/σV should be considerably shorter than tΛ ≈ 17 × 109 yrs for a virialized system. We indicate in Fig. 2 the region where
(8)where the crossing time tcross = R/σV should be considerably shorter than tΛ ≈ 17 × 109 yrs for a virialized system. We indicate in Fig. 2 the region where 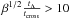 . There R is at least about five times smaller than RZG.
. There R is at least about five times smaller than RZG.
We note that going upwards along a constant-M line makes the influence of the DE on the virial mass determination decrease. It can be shown that the mass derived from Eq. (7) is a factor of (1 + α(R/RZG)3) higher than the classical result (here α ~ 1). The increase is insignificant for well-virialized systems.
In Fig. 2 the systems above the “zero-velocity line” (Sect. 3) are totally within the collapsing region. The outer parts of systems below the line have not been retarded down to zero velocity (e.g., the extended Fornax, Coma, and Virgo systems).
For example, we can read from Fig. 2 that if the mass of the Virgo cluster only controlled the Local Supercluster up to the distance of the LG, then the zero-gravity distance is around 11 Mpc, and we are in the DE-dominated region. However, a higher mass, say 3.5 × 1015M⊙, could keep us within the gravity-dominated region (Vir2 in Fig. 2).
The main body of the Corona Borealis supercluster lies near the zero-velocity line. This is an example where a supercluster made of several rich clusters may be bound, containing much intercluster matter (Pearson et al. 2014).
The Local Sheet is found below the ⟨ ρM ⟩ = 2ρΛ line. However, it is a strongly flattened system (hence in brackets), and the condition ⟨ ρM ⟩ = 2ρΛ for “gravity = antigravity” at the outer border is not valid.
A flattened system, if viewed as a disc, cannot be bound as a whole if the antigravity force between its centre and the edge (one radius away) is greater than the gravity pulling the edge inwards. It is known that a disc exerts a higher gravity force on a particle at its edge than a sphere of the same mass and radius. If the ratio of these forces is α ( > 1), then Eq. (1) leads to the balance condition ⟨ ρM ⟩ = (2 /α)ρΛ. Therefore the “gravity = antigravity” line should be lowered for a flattened system. Here, ⟨ ρM ⟩ is the mean density caused by the mass M within the sphere having the radius R (not the mean density of the disc).
For a flat disc, with the density increasing inwards, the ratio α< 3π/ 4, while the limiting case of constant density gives α = 3π/ 4 = 2.35 (see e.g., Woltjer 1967). In this limiting case, the y coordinate of the balance line in Fig. 2 would be shifted down by 0.37 so that log ⟨ ρM ⟩ /ρΛ = −0.07 in order to roughly take flattened systems into account.
Chernin et al. (2015) conclude that the Local Sheet is expanding with acceleration. This would agree with its possible location even below the “flat” line in Fig. 2. In fact, the zero-gravity spheres around the LG and nearby groups do not appear to intersect, also suggesting accelerating Hubble recession (Byrd et al. 2012).
The location of the Laniakea supercluster near the “global” line simply reflects the way its mass was estimated from the mean cosmic density by Tully et al. (2014). Even without an independent mass estimate, it is clear that as a prominent mass concentration the supercluster can hardly lie below the global line (in the region of voids). On the other hand, if it were to be found near or above the ⟨ ρM ⟩ = 2ρΛ line, its mass had to be very large ≳ 4 × 1017M⊙, which is theoretically unlikely for massive bound objects (e.g., Holz & Perlmutter 2012).
The Λ significance diagram may also throw light on the general galaxy field, as described by the two-point correlation function (without biasing). With the values generally regarded as standard, i.e. the correlation length 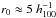 Mpc and the correlation exponent γ ≈ 1.75, we calculated typical mass values within the radius R, as explained in Teerikorpi et al. (2005). These have been plotted in the diagram of Fig. 2 as a dashed curve. As already noted by Teerikorpi et al. (2005), the correlation length r0 is not far from the zero-gravity radius that corresponds to the fluctuation described by the correlation function. Beyond r0, the decreasing fluctuations lie in the DE-dominated region, where the pairwise velocity dispersion of the Hubble flow also starts to diminish.
Mpc and the correlation exponent γ ≈ 1.75, we calculated typical mass values within the radius R, as explained in Teerikorpi et al. (2005). These have been plotted in the diagram of Fig. 2 as a dashed curve. As already noted by Teerikorpi et al. (2005), the correlation length r0 is not far from the zero-gravity radius that corresponds to the fluctuation described by the correlation function. Beyond r0, the decreasing fluctuations lie in the DE-dominated region, where the pairwise velocity dispersion of the Hubble flow also starts to diminish.
6. Concluding remarks
The log ⟨ ρM ⟩ /ρΛ vs. log R diagram is a useful way to characterize systems of galaxies. Different regions in the diagram correspond to the mass and size of a system and its dynamical state within the Λ-dominated expanding universe.
The Λ significance graph will be used in forthcoming separate studies to discuss clusters and superclusters, especially as extracted from the SDSS survey. A preliminary inspection of the distribution of SDSS DR7 superclusters shows a range of ⟨ ρM ⟩ /ρΛ and an interesting dependence on the size and morphology of the system, which also can be studied using simulated systems.
If we calculate RZG around a point in a homogenous world from Eq. (2), this radius will increase directly proportional to the radius of the considered matter sphere. This means that one cannot ascribe physical significance to the zero-gravity radius within a fully uniform universe – every point is as it would be on the surfaces of a great number of zero-gravity spheres of arbitrarily different sizes, not feeling any force.
Acknowledgments
We thank G. Bisnovatyi-Kogan, L. Liivamägi, and E. Saar for useful discussions and the referee for very helpful remarks. ME was supported by the ETAG project IUT26-2 and by the European Structural Funds grant for the Centre of Excellence “Dark Matter in (Astro)particle Physics and Cosmology” TK120.
References
- Byrd, G. G., Chernin, A. D., Teerikorpi, P., & Valtonen, M. J. 2012, Paths to Dark Energy: Theory and Observation (Berlin: De Gruyter) [Google Scholar]
- Byrd, G. G., Chernin, A. D., Teerikorpi, P., & Valtonen, M. J. 2015, Observations of General Relativity at strong and weak limits. in General Relativity: The most beautiful of theories, Applications and trends after 100 years, ed. C. Rovelli (Berlin: De Gruyter) [Google Scholar]
- Chernin, A. D. 2001, Physics-Uspekhi, 44, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Chernin, A. D., & Teerikorpi, P. 2014, Astron. Rep., 58, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chernin, A. D., Nagirner, D. I., & Starikova, S. V. 2003, A&A, 399, 19 [Google Scholar]
- Chernin, A. D., Teerikorpi, P., Valtonen, M. J., et al. 2009, A&A, 507, 1271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chernin, A. D., Teerikorpi, P., Valtonen, M. J., et al. 2012, A&A, 539, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chernin, A. D., Bisnovatyi-Kogan, G. S., Teerikorpi, P., Valtonen, M. J., & Byrd, G. G. 2013, A&A, 553, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chernin, A. D., Emelyanov, N. V., & Karachentsev, I. D. 2015, MNRAS, in press [Google Scholar]
- Drinkwater, M. J., Gregg, M. D., & Colless, M. 2001, ApJ, 548, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Einstein, A., & Straus, E. G. 1945, Rev. Mod. Phys., 17, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Ekholm, T., Lanoix, P., Teerikorpi, P., Fouqué, P., & Paturel, G. 2000, A&A, 355, 835 [NASA ADS] [Google Scholar]
- Hanski, M., Theureau, G., Ekholm, T., & Teerikorpi, P. 2001, A&A, 378, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holz, D. E., & Perlmutter, S. 2012, ApJ, L36 [Google Scholar]
- Karachentsev, I. D., Tully, R. B., Wu, P.-F., Shaya, E. J., & Dolphin, A. E. 2014, ApJ, 782, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1981, Observatory, 101, 111 [NASA ADS] [Google Scholar]
- McCall, M. L. 2014, MNRAS, 440, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Nasonova, O. G., de Freitas Pacheco, J. A., & Karachentsev, I. D. 2011, A&A, 532, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Partridge, C., Lahav, O., & Hoffman, Y. 2013, MNRAS, 436, 45 [Google Scholar]
- Pearson, D. W., Batiste, M., & Batuski, D. J. 2014, MNRAS, 441, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Peirani, S., & de Freitas Pacheco, J. A. 2006, New Astron., 11, 325 [Google Scholar]
- Peirani, S., & de Freitas Pacheco, J. A. 2008, A&A, 488, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saarinen, J., & Teerikorpi, P. 2014, A&A, 568, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teerikorpi, P., & Chernin, A. D. 2010, A&A, 516, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teerikorpi, P., Chernin, A. D., & Baryshev, Yu. V. 2005, A&A, 440, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Tamm, A., Gramann, M., et al. 2014, A&A, 566, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tully, R. B. 2015, AJ, 149, A54 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., Courtois, H., Hoffman, Y., & Pomarède, D. 2014, Nature, 513, 71 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 1999, A&ARv, 9, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Woltjer, L. 1967, in Lectures in Applied Mathematics (American Mathematical Society), 9, 1 [Google Scholar]
All Figures
 |
Fig. 1 Log⟨ ρM ⟩ /ρΛ vs. log R for spherical systems. The inclined lines correspond to different mass values. Above the “gravity = antigravity” line, the region is dynamically dominated by gravitation, and below this line by DE. Intersections give the radii RZV, RZG, and RES. Dotted inclined lines illustrate the case where the mass increases with the radius (see the text). |
| In the text | |
 |
Fig. 2 Log ⟨ ρM ⟩ /ρΛ vs. log R/ Mpc for example galaxy systems. The inclined lines are for the mass values indicated in M⊙. Some symbols are slightly shifted in crowded regions. The dotted curve gives the characteristic mass within radius R from the standard 2-point correlation function. “Flat” is the gravity = antigravity line for the limiting case of a flattened system. The region where β1/2tΛ/tcross> 10 is shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


