| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201525628 | |
| Published online | 05 May 2015 | |
Modeling optical and UV polarization of AGNs
III. From uniform-density to clumpy regions
1
Astronomical Institute of the Academy of Sciences,
Boční II 1401,
14100
Prague,
Czech Republic
e-mail:
frederic.marin@asu.cas.cz
2
Observatoire Astronomique de Strasbourg, Université de Strasbourg,
CNRS, UMR 7550, 11 rue de l’Université, 67000
Strasbourg,
France
3
Department of Astronomy and Astrophysics, University of California
at Santa Cruz, California
95064, USA
Received: 8 January 2015
Accepted: 17 March 2015
Context. A growing body of evidence suggests that some, if not all, scattering regions of active galactic nuclei (AGNs) are clumpy. The inner AGN components cannot be spatially resolved with current instruments and must be studied by numerical simulations of observed spectroscopy and polarization data.
Aims. We run radiative transfer models in the optical/UV for a variety of AGN reprocessing regions with different distributions of clumpy scattering media. We obtain geometry-sensitive polarization spectra and images to improve our previous AGN models and their comparison with the observations.
Methods. We use the latest public version 1.2 of the Monte Carlo code stokes presented in the first two papers of this series to model AGN reprocessing regions of increasing morphological complexity. We replace previously uniform-density media with up to thousands of constant-density clumps. We couple a continuum source to fragmented equatorial scattering regions, polar outflows, and toroidal obscuring dust regions and investigate a wide range of geometries. We also consider different levels of fragmentation in each scattering region to evaluate the importance of fragmentation for the net polarization of the AGN.
Results. In comparison with uniform-density models, equatorial distributions of gas and dust clouds result in grayer spectra and show a decrease in the net polarization percentage at all lines of sight. The resulting polarization position angle depends on the morphology of the clumpy structure, with extended tori favoring parallel polarization while compact tori produce orthogonal polarization position angles. In the case of polar scattering regions, fragmentation increases the net polarization unless the cloud filling factor is small. A complete AGN model constructed from the individual, fragmented regions can produce low polarization percentages (<2%), with a parallel polarization angle for observer inclinations up to 70° for a torus half opening angle of 60°. For type-2 viewing angles the polarization switches to perpendicular and rises to ~50%.
Conclusions. Our modeling shows that the introduction of fragmented dusty tori significantly alters the resulting net polarization of an AGN. Comparison of our models to polarization observations of large AGN samples greatly favors geometrically compact clumpy tori over extended ones.
Key words: galaxies: active / galaxies: Seyfert / polarization / radiative transfer / scattering
© ESO, 2015
1. Introduction
Fragmentation is a ubiquitous phenomenon in astrophysics. Theories exploring the stability of uniform-density, self-gravitating media predict fragmentation if the initial amount of matter is spread over large distances (Jeans 1902; Hunter 1962; Arny 1966). However, observations of fragmented systems in external galaxies are complicated by the small size of the resulting clumps. Current instruments are unable to fully resolve the detailed morphology of distant yet luminous systems such as active galactic nuclei (AGNs).
Optical/UV observations of the narrow-line region (NLR) in NGC 1068, obtained by Evans et al. (1991), and later by Capetti et al. (1995), revealed the presence of several knots of different luminosity in the outflowing gas. These authors identified these clumps with inhomogeneities in the medium. Similar results are found in other studies at the same wavelengths (Capetti et al. 1997) or longer (Packham et al. 1997), strengthening the idea that the outflows of NGC 1068 are not continuous. More recently, Aalto et al. (2012), using the Plateau de Bure millimeter interferometer, found that the large-scale molecular wind of the ultraluminous infrared galaxy Mrk 231 is likely to consist of dense, clumpy gas clouds with high abundances of hydrogen cyanide (HCN). They attribute these HCN properties to shock-driven compression and fragmentation in the outflows.
There is less direct evidence for the well-known “dusty torus”, the supposed bulk circumnuclear medium shielding the inner AGN along the equatorial plane. The torus size invoked by the unified model (Antonucci 1993), typically from 0.1 to 100 parsecs, is inconsistent with self-gravitational stability. Krolik & Begelman (1988) and Pier & Krolik (1992) argued on theoretical grounds that AGN tori are likely to consist of individual, optically thick molecular clumps in collision-free orbits that are sustaining the vertical torus height required by observations. Self-shielded from the full continuum, the gas/dust clouds would survive temperatures of a few hundred degrees Kelvin in the inner toroidal regions (Li 2007). As noted by Nenkova et al. (2002), the 10 μm silicate feature is a consequence of the torus being clumpy.
Fragmented dynamical dust distributions in AGNs have started to be investigated in numerical simulations. Based on the suggestions of Pier & Krolik (1992, 1993) about the nature of the obscuring dust, Nenkova et al. (2002) undertook IR modeling of a distribution of clumps around a central irradiating source. The authors successfully reproduced the inclination-dependent behavior of the 10 μm silicate feature, the width of the far-IR emission peak, and the 0.01–100 μm spectral energy distribution (SED) of both type-1 and type-2 objects. Similar work in the far-IR – UV wavelengths (Nenkova et al. 2008a,b, 2010; Schartmann et al. 2008, 2014; Hönig & Kishimoto 2010; Heymann & Siebenmorgen 2012), and in the X-ray-band (Risaliti et al. 2002; Liu & Li 2014) was conducted to reproduce and/or study the spectroscopic behavior of fragmented tori.
The interferometric observations of the type-2 Circinus galaxy undertaken by Tristram et al. (2007) with the mid-infrared (MIDI) instrument at the Very Large Telescope strongly support the presence of a clumpy toroidal structure. The data are inconsistent with a smooth density distribution and indicate clumpy or filamentary structures. In a fragmented medium, the low-density gaps between the clouds allow radiation to propagate between optically thick clumps so that obscuration along the equatorial plane is less effective. In addition to this, the equilibrium between cloud mergers and tidal shearing keeps the covering factor of the clump distribution close to unity in the equatorial direction (Krolik & Begelman 1988). Since the scattering probability increases with the filling factor of a fragmented region, an impact on the polarization properties of the escaping radiation is expected. Ultraviolet/optical spectropolarimetry thus becomes an ideal counterpart to mid-infrared interferometry to explore the morphology of AGNs.
In this paper, the third of our series (Paper I: Goosmann & Gaskell 2007; Paper II: Marin et al. 2012), we investigate, for the first time, the UV/optical polarization of AGN with fragmented reprocessing regions. We compare uniform-density models of dusty tori, outflowing winds and accretion flows to their fragmented counterparts and build an AGN model made of more than four thousands reprocessing clumps. We also explore different configurations of the clumpy AGN model to test the impact of several morphological parameters and analyze our results with respect to polarimetric observations.
The remainder of the paper is organized as follows: in Sect. 2 we briefly summarize our previous modeling work on AGN with stokes and study polarization signatures of individual, clumpy reprocessing regions. A three-component model approximating the unified scheme of AGN is explored in Sect. 3. In Sect. 4 we discuss our results and relate them to past spectropolarimetric observations before drawing our conclusions in Sect. 5.
2. Polarization signatures from clumpy regions
In the context of multiple reprocessing between a large variety of emitting, scattering and absorbing regions, it is important to first test how an individual fragmented region differs from a uniform-density one. Because polarimetry is sensitive to the geometry of the reprocessing medium, a clumpy distribution of spheres is likely to alter the net polarization degree in a different way than uniform-density regions. We thus reanalyze the individual reprocessing regions presented in Papers I and II after introducing clumpiness.
For the remainder of this paper, we loosely define a type-1 AGN orientation as an inclination where the observer’s line of sight toward the central source that does not intercept the torus boundaries1. In this case, the viewing angle, i, is smaller than the half-opening angle of the toroidal structure, with both angles being measured from the symmetry axis. Otherwise, the object is a type-2 AGN (such as in Fig. 1).
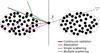 |
Fig. 1 Schematic view of a fragmented region. Clumps are shielding each other from the central source, but gaps between the spheres allow part of radiation to escape from the model, even along equatorial directions where obscuration is most efficient (in the case of circumnuclear dust). |
 |
Fig. 2 Sketches of the different models investigated in this paper. Tori with cylindrical cross-section, either extended or compact, are explored in Sect. 2.3, polar winds in Sect. 2.4, and flared disks in Sect. 2.5. Partially and fully fragmented AGN models are presented in Sect. 3. |
Polarization of light will be described by its polarization degree, P, ranging from 0% (unpolarized) to 100% (fully polarized), and by its polarization position angle γ. If the E-vector of the radiation is aligned with the projected torus axis, the polarization is called parallel (γ = 90°). When γ = 0°, polarization is said to be perpendicular. A convention, already used in Papers I and II, identifies parallel and perpendicular polarization by the sign of P: a negative value of P stands for parallel polarization, a positive P for perpendicular one. Plotting P over inclination thus allows us to easily identify the observed polarization dichotomy in thermal AGNs (type-1 AGNs being generally polarized parallel to the axis of the torus while type-2 AGNs being polarized perpendicularly). Finally, our computations include both linear and circular polarization and the sum of the two is shown when plotting P. However, circular polarization has nearly no impact on the total polarization, being at least a hundred times lower than linear polarization.
2.1. A brief overview of stokes
stokes is a public Monte Carlo code that simulates the radiative transfer between radiatively coupled emitting and reprocessing media and computes the polarization properties as a function of the viewing direction from the near-infrared to the hard X-ray-band. The latest release, stokes 1.2, can be downloaded from Internet2. In Goosmann & Gaskell (2007; Paper I), we presented the first version of the code and investigated how the morphology of individual AGN reprocessing regions influences the resulting polarization. In Marin et al. (2012; Paper II), we upgraded the computational speed of the code and added an imaging routine. We developed an AGN model composed of three different scattering media and explored the parameter space that could reproduce the spectropolarimetric behavior of different AGN types, such as Seyfert galaxies and quasars, but also “naked”, “bare”, FR-I, LINERs. Since then, our code has been used to explore a large range of AGN properties (see Marin & Goosmann 2014, for a list of examples).
The fast performance the code allows us to significantly increase the number of scattering regions. Multiple scattering is a prerequisite in such models since individual clouds are radiatively coupled. The version 1.2 of stokes is able to process a model with more than 10 000 individual scattering clouds and to obtain good-quality spectra by sampling 5 × 108 photons or fewer in a timescale of a day (depending on the presence of absorbers and the required precision).
2.2. Characterizing a fragmented medium
The overall picture of AGN becomes more complicated when replacing uniform-density components by their clumpy counterparts. The radiative transfer calculations take more time as the amount of scattering increases. Complex radiative interactions arise between consecutive clouds and alter the resulting spectra and polarization (see Fig. 1) at a given viewing angle.
To investigate the impact of fragmentation, we first re-compute the polarization of isolated, uniform-density scattering regions presented in Paper II, namely the dusty torus, the polar winds and the hot accretion flow. We conserve the model geometry but replace the region by clumpy distributions of spheres, such as shown in Fig. 2. These spheres are distributed uniformly inside the scattering region without overlapping, leaving gaps between clouds. To characterize such media and evaluate how fragmentation affects the polarization, we rely on the filling factor ℱ, ranging from 0 to 1 (uniform-density region). ℱ is evaluated by summing up the volume of the clumps and dividing the total by the volume of the same, unfragmented reprocessing region.
For the remainder of this paper, several thousand of clumps are modeled as constant density spheres of equal radii. Three filling factors are investigated: 0.06 (highly fragmented region), 0.13 and 0.25 (moderate fragmentation). In comparison, in their X-ray spectral model for clumpy tori, Liu & Li (2014) used a filling factor ≤0.1 for their fragmented models. The total optical depth along the observer’s viewing angle strongly depends on ℱ: for a model with ℱ ~ 0.06, 1 to 3 clumps can pile-up along a line of sight that crosses the cloud distribution, while tens of clumps can hide the irradiating source in the case of ℱ ~ 0.25.
In the following sections, we investigate the spectropolarimetric signature of fragmented dusty tori, polar outflows and hot accretion flows. The results of each clumpy model will be compared with the polarization and flux (normalized to the flux of the central source) of the same, but uniform-density model. The parametrization of those models is based on the set of constraints derived from Papers I and II. For all our models, we define an isotropic, point-like source at the center of the model emitting an unpolarized spectrum with a power-law SED3F∗ ∝ ν−α and α = 1.
2.3. Clumpy torus models
2.3.1. Extended tori
Our first model features an obscuring dusty torus with an elliptical cross-section, centered on the source, symmetric to the equatorial plane. According to the simple unified scheme (Antonucci 1993), its outer boundary can extend up to 100 pc, while the inner radius of tori is probably on the order of half a light year for a 1038 W AGN (Kitchin 2007). We thus use an inner radius of 0.25 pc and an outer radius of 100 pc for our first set of torus models. In Paper II, we concluded that “a wide half-opening angle (~60°) for the torus helps to produce parallel polarization, whereas narrow tori [...] produce polar-scattering-dominated AGNs”. In this paper, we still model circumnuclear dust distributions with half-opening angles 30° ≤ θ0 ≤ 60° to check if clumping can have a positive impact on our previous conclusions about uniform-density tori. Similarly to Paper II, our models have an optical depth in the V-band of τdust = 750 along the radial direction. In the case of fragmented models, the radius of the spherical gas clouds is fixed to 2 pc for all half-opening angles. We vary the number of clouds, from 350 to 3500, in order to preserve ℱ. All the clouds, independently of the model, have an optical thickness τdust = 60, which is in agreement with the value (≥60) used by Nenkova et al. (2008a). Our torus models are considered as optically and Compton4 thick (Kartje 1995). Finally, the clumps and the uniform-density tori are filled with dust grains based upon the Milky Way mixture (Draine & Lee 1984).
 |
Fig. 3 Modeling an optically-thick, elliptically-shaped, extended and fragmented torus with θ0 = 30° measured relative to the symmetry axis. The fraction F/F∗ of the central flux (upper four panels) and the spatially integrated polarization P (lower four panels) are seen at different viewing inclinations, i, from 2000 to 8000 Å. The fluxes and polarizations are shown for a uniform-density model and three fragmented counterparts with filling factors ranging from 0.06 to 0.25. We note the change in scale between the spectra of the four models. |
The fractions F/F∗ of the central flux, F∗, are presented in Figs. 3–5 (top panels), for θ0 = 30°, 45°, and 60°, respectively. In comparison with a uniform-density torus, the model with ℱ ~ 0.06 shows, after renormalization, a similar dependence on inclination. The flux is maximum for unobstructed viewing angles, i.e., close to the polar directions. With the onset of partial obscuration at intermediate inclinations, F/F∗ shows lower fluxes. Maximum attenuation is observed at an equatorial viewing angle (i ~ 81°), independently of the half-opening angle, but models with ℱ ~ 0.06 are found to be unable to efficiently block photons escaping from the central source. The net type-2 fluxes are high in comparison with the flux of the uniform-density model. We also note that the spectral shape is less curved (grayer), since radiation can escape in between the clumps, leading to a lower absorption efficiency. With higher ℱ, the partial covering of the source becomes more important for intermediate and edge-on views. The dependence of opacity with respect on inclination results in lower fluxes at type-2 inclinations. However, even a model with ℱ ~ 0.25 cannot completely cancel the escaping flux because of multiple scatterings between the clumps, leading to a non-null probability of observing the inner AGN regions at extreme orientations (Elitzur 2008). It indicates that, for a clumpy torus with a medium filling factor, some optical AGN flux could be detected at high inclinations, if not diluted by the star light and starburst radiation from the host galaxy. If there is contamination by starlight, then the intrinsic luminosity of the obscured nuclei has to be renormalized for observations.
The impact on the polarimetric signatures of extended clumpy tori, see Figs. 3−5 (bottom panels), is greater. Any model with ℱ ~ 0.06 gives polarization about ten times lower than for a uniform-density torus. In addition, for θ0 = 30° and 45°, the sign of P changes from positive (perpendicular polarization) to negative (parallel polarization) between a uniform-density and a clumpy torus, respectively. In the case of θ0 = 60°, the uniform-density torus already induces negative polarization because of its scattering geometry, where photons scatter off the side walls of the dust structure and naturally yield γ values parallel to the torus axis. It is an effect already predicted by Kartje (1995) and illustrated here. The spectral shape of polarization is similar to our previous results (Papers I and II): the 2000–3000 Å dust feature (specific to the dust prescription, see Draine & Lee 1984 and Goosmann & Gaskell 2007) and the increase in polarization in the red tail of the spectra are properly reproduced by torus models with ℱ ~ 0.06. P is minimum at polar viewing angles, where source photons can directly escape from the torus funnel. At intermediate torus inclinations, the escaping polarization is higher and is maximum toward the edge of the model. There are sufficiently large gaps between the clouds of the fragmented models for the radiation to escape along the equatorial plane, contributing to the net polarization. A similar behavior is seen for the models with ℱ ~ 0.13, where P is inferior to 1% at type-2 inclinations. Finally, when the cloud distributions properly cover the central source (ℱ ≥ 0.25), a large fraction of the photons is absorbed owing to dense obscuration and the few escaping photons carry a larger P (up to 1% for θ0 = 45°). However, coupled to a small F/F∗, the resulting polarized flux from equatorial inclinations is expected to be negligible. In the case of a model with θ0 = 30°, the dust feature vanishes while it is preserved in the 45° and 60° models. The insufficient statistics prevents us to estimate the average polarization degree at a viewing angle i = 81° in the former case.
The reprocessing by extended (outer radius = 100 pc), fragmented tori is thus different from the case of uniform-density regions with smooth boundaries. While some spectroscopic characteristics such as the spectral shape and the graphite peak are conserved (even though the spectra of fragmented tori are grayer), polarization can clearly break a degeneracy of the torus reprocessing. The parallel orientation of the photon position angle is explained by the angular dependence of opacity and by the small number of clouds at the torus maximum height. Because of the oblate geometry of the extended torus, most of the cloudlets are concentrated along the equatorial plane and scattering preferentially produces parallel polarization.
2.3.2. Compact tori
In the previous subsection, we explored the polarimetric signatures of an extended torus. However, the morphology of the dusty material around AGN is still a matter of debate and several authors have preferred more compact models: to fit the SED of the quasar 3C 249.1, also known as PG 1100+772, Heymann & Siebenmorgen (2012) used a compact (external radius: 6 pc) AGN dust torus model composed of more than 5000 optically-thick clouds. Goosmann & Matt (2011) also modeled a compact toroidal structure (external radius: 0.5 pc) to evaluate the expected X-ray polarization emerging from the Seyfert-2 galaxy NGC 1068. The difference in the geometry of the extended and compact tori can be seen in Fig. 2. For similar opening angles (as shown in Fig. 2) and similar filling factors, the main difference between the compact and extended torus is that the inner wall is steeper for the compact torus.
To investigate the impact of a non-extended torus on the resulting polarization, we ran simulations for a more compact model based on the work of Heymann & Siebenmorgen (2012). Following their prescription, we compute a torus model with an inner radius of 0.4 pc and outer radius 6 pc. The half-opening angle of the torus is set to 45° with respect to the symmetry axis of the torus and we compare two realizations. The first model is uniform, with τdust = 200 along the radial direction and the clumpy model is composed of thousands of spheres with Rsphere = 0.2 pc, ℱ ~ 0.25 and optical thickness τdust = 50. The total optical depth along the equatorial plane is thus similar for the two cases.
 |
Fig. 6 Modeling compact tori (left: uniform-density model; right: clumpy torus) with θ0 = 45° measured relative to the symmetry axis. In the case of the fragmented torus, the filling factor is equal to 0.25 and the optical thickness per clump is 50 in the V-band. The fraction F/F∗ of the central flux (upper figures) and the spatially integrated polarization P (lower figures) are seen at different viewing inclinations, i, from 2000 to 8000 Å. We note the change in scale between the polarization spectra of the two models. |
Results are given in Fig. 6. The spectroscopic behavior of a toroidal model does not change between a compact (Fig. 6 top-left) and an extended (Fig. 4 top panel) medium, regardless of its uniformity; pole-on inclinations produce the highest fluxes while F/F∗ is a minimum at the equator. However, the polarization percentages between a compact (Fig. 6 bottom-left) and an extended uniform-density torus (Fig. 4 bottom panel) are quite different: a compact, uniform torus produces about twice as much polarization as its extended counterpart because of the different geometries of their inner walls. The steeper walls of the compact torus favors the production of perpendicular polarization, except along the equatorial direction where scattering of the surface most directly facing the observer and producing parallel polarization prevails. In the case of an extended torus, this surface is more extended as the inner torus walls are shallower, resulting in a canceling mix of parallel and perpendicular polarization, ultimately lowering P. However, in agreement with the work of Kartje (1995) and Paper I, both uniform-density models mainly produce a net perpendicular polarization angle.
More important changes appear for compact clumpy structures seen through the prism of polarization. While an extended, fragmented circumnuclear region only produces parallel polarization with polarization less than ~1% (Fig. 4, bottom panel), a compact model produces perpendicular polarization together with P up to 3.5% (Fig. 6, bottom right figure). It is a purely geometrical effect: the torus being smaller in diameter while sustaining a similar height (scaled with the half-opening angle), the torus has a less oblate morphology. Hence, the angular dependence of opacity provides higher obscuration at intermediate inclinations and radiation does not longer scatter preferentially along the midplane, resulting in polarization position angles orthogonal to the scattering plane.
Thus, we find that while compact and extended clumpy tori produce similar flux levels, their polarization properties are rather different: in the case of an extended torus, P is about three times smaller and its polarization angle is orthogonal to the one produced by a clumpy compact torus. We thus expect a different net polarization signature of AGNs depending on the torus model used. A detailed comparison of different fragmented tori and their impact on polarization will be explored in Sect. 3.
 |
Fig. 7 Modeled images of the polarized flux, PF/F∗, for a clumpy, compact dusty torus of half-opening angle 45° measured relative to the axis of symmetry; PF/F∗ is color-coded and integrated over 2000 to 8000 Å. γ and P are represented by black vectors (a vertical vector indicates a polarization of γ = 90°, and a horizontal vector stands for an angle of γ = 0°). The length of the vector is proportional to P. Top: image at i ∽ 18° (face-on view); middle: i ∽ 45°; bottom: i ∽ 81° (edge-on view). |
2.3.3. Polarization imaging
Using the imaging capabilities of the latest version of stokes (Paper II), we compute the polarization maps of a compact torus model such as presented in Sect. 2.3.2. We sample 109 photons distributed in 104 spatial bins (100 × 100 pixels). Each pixel stores the spectra of the four stokes parameters across a wavelength range of 2000 to 8000 Å. Integrating over this range, the images simultaneously show PF/F∗, P, and γ. The polarization position angle γ is represented by black vectors drawn in the center of each pixel; the length of the vector being proportional to P. The black vectors rotate from a vertical (parallel polarization) to a horizontal position (perpendicular polarization).
Figure 7 presents imaging results at three different inclinations: 18°, 45° and 81°, representative of a type-1 view, a line of sight grazing the torus height, and a type-2 inclination, respectively. The peculiar pole-on and edge-on values we choose reflect the geometric division of our model space, as our results are recorded as a function of cosi, where i is measured from the axis of the torus (see Paper I). The pole-on view of our model (Fig. 7 top figure) allows us to probe the inner funnel of the circumnuclear matter, where most of the polarized flux is concentrated. Because of the clumpy structure of the model, the torus funnel has no smooth, continuous walls; radiation sweeps between the cloudlet distribution and reaches farther portions of the medium. The polarization map clearly shows individual polarized flux knots at radial distances up to 2.5 pc from the full continuum. In comparison with a uniform-density torus model (see Fig. 4 in Paper II) where most of the polarized photons are absorbed at distances inferior to 0.5 pc, a clumpy structure allows the radiation to penetrate farther into the inner structure of the torus. The photon flux decreases at large distances from the central engine, producing polarized signatures up to 5 pc. In Fig. 7 (middle), the inner funnel disappears behind the torus horizon, even if the structure is fragmented. The optical thickness of the clouds prevents a direct view of the inner parts of the AGN, but allows photons to escape at large distances from the source after cumulative scattering events (increasing the resulting P). Along the equatorial plane (Fig. 7 bottom), PF/F∗ sharply decreases as it is heavily obscured by dust particles. The residual fluxes emerge from multiple scattering between the gas clumps and the slightly more polarized flux appearing at the top of the structure is due to the non-orthogonal inclination of the line of sight (81°), resulting in an asymmetric pattern between the top and bottom parts of the torus. Several clouds can be detected as a result of higher PF/F∗ knots but most of the structure is opaque.
2.4. Fragmented polar outflows
Investigating the clumpiness of AGN outflows may lead to the most relevant observational predictions that we can realize, as direct comparisons can be undertaken with past detections from the Hubble Space Telescope (HST), when the COSTAR-corrected Faint Object Camera (FOC) was mounted5. We now look at two different realizations of the winds, the first one using electron-filled spheres to mimic the ionized winds and the second one using dust clouds to represent the more extended NLR.
2.4.1. Ionization cones
Following the numerous observations of AGN ionization cones presented in Wilson (1996), we model a 10 pc-long, hourglass-shaped scattering region filled with electron spheres of radius Rsphere = 0.27 pc and optical depth τelec = 0.3 (in comparison, the uniform-density model has τelec = 1). Since the cloudlets are filled with absorption-free, optically thin material, the effective optical thickness along the radial direction is expected to vary between the different filling factors. We evaluate τtotal to be roughly similar between the uniform-density and the models with ℱ ~ 0.06, while τtotal is closer to unity for the two models with higher filling factors. The half-opening angle of the double cone is again set to 30°. The emitting source is not restricted to radiating along a preferred direction aligned with the cones as for the model described in Paper I, but emits isotropically.
 |
Fig. 8 Modeling an electron-filled, fragmented, scattering double-cone with θ0 = 30° measured relative to the symmetry axis. The fraction F/F∗ of the central flux is integrated from 2000 to 8000 Å (upper panel) and the spatially integrated polarization P is plotted versus inclination i (lower panel). |
We find that the fraction F/F∗ of the central flux (Fig. 8, upper panel) is very similar between a uniform-density and a fragmented model using a low filling factor. Because of obscuration of the nuclei by the cloudlet distribution and subsequent scattering off the observer’s line of sight, less flux is detected at type-1 inclinations. However, because of the Thomson, elastic scattering mechanism, the flux difference between type-1 and type-2 viewing angles is not important as no absorption occurs. When the filling factor increases, multiple scattering is enhanced even when considering optically thin scattering clouds. A larger fraction of the flux is deviated from the polar direction and F/F∗ decreases.
The polarization degree curves (Fig. 8, bottom panel) fit in with this consideration: a model with ℱ ~ 0.06 reproduces the integrated polarization degree that we found for a uniform-density model, with a maximum P at equatorial viewing angles. The shape of P with respect to the system’s inclination is quite similar too. For ℱ > 0.06, as there are more scattering targets and a higher effective optical depth, the resulting polarization percentage increases up to a factor of three. The inclination dependence is preserved but P increases. The polarization position angle is positive for all the models as the spheres are situated mainly along the vertical axis of the model.
A model of fragmented winds is able to reproduce the same degree of positive polarization, as well as the same P-dependency on inclination, as a uniform-density model if the filling factor of the wind is small (<0.1). This threshold is consistent with the radio constraints on the volume filling factors of AGN winds found by Blustin & Fabian (2009). Denser cloud distributions produce higher polarization degrees as a result of the multiplication of scattering targets that ultimately increases the total optical depth. Uniform models are then good approximations for real systems containing only a few gas clouds. It is noteworthy that this result is in contrast to flux-only measurements, where models with higher ℱ resemble uniform-density models (Ashton 2005).
2.4.2. NLR winds
We now consider a fragmented outflow consisting of dusty spheres with Rsphere = 2.7 pc and τdust = 0.1 (previous uniform-density model: τdust = 0.3). The clouds are optically thin in order to represent the NLR clouds detected farther away from the irradiating source, where dust can form and survive (Hönig et al. 2012). We consider that the dusty double-cone sustains the same half-opening angle as the ionized outflows, θ0 = 30°. According to the observations of Hönig et al. (2012) and our simulations in Marin & Goosmann (2012), the inner and outer boundaries of the reprocessing region were fixed to 10 pc and 100 pc above the source, respectively.
 |
Fig. 9 Modeling an optically thin, dusty, fragmented double-cone with θ0 = 30° measured relative to the symmetry axis. The fraction F/F∗ of the central flux (upper panel) and the spatially integrated polarization P (lower panel) are seen at different viewing inclinations, i, from 2000 to 8000 Å. |
The F/F∗ spectra produced by scattering on a small number of spheres (Fig. 9 upper panel) reproduces the expected flux behavior: there is an unabsorbed photon flux along lines of sight that do not cross the NLR, and the flux is slightly absorbed at pole-on directions. The graphite peak signature is marginally detectable when considering a ℱ ~ 0.06 model but when looking at a denser cloud distribution (ℱ ~ 0.13 and 0.25), the 2000−3000 Å dust feature becomes more apparent and the flux of radiation escaping from the model at i ~ 19° is lower. The ℱ ~ 0.13 case is found to be the closest one to the uniform-density model.
The polarization percentage induced by a fragmented wind with a low number of scattering targets is in the same range as for a uniform model (Fig. 9 lower panel). According to the scattering phase function of polarization, a maximum polarization degree is observed for equatorial viewing angles, with the 2000−3000 Å peak also revealed in polarization percentage. For observer’s lines of sight close to the polar direction, P is minimum as absorption by dust grains limits the transmission of photons through the gas. For a ℱ ~ 0.06 model, P is slightly lower than for the uniform-density case, but for a larger number of gas clouds, the models are very similar, as expected from Fig. 9 (upper panel). For a ℱ ~ 0.25 model, P is higher than for a uniform-density regions because of a larger number of scattering targets and an increased probability for scattered radiation to escape from the model in between the cloudlets.
It is interesting to note that a polar distribution of spheres does not strongly affect the resulting polarization degree in comparison with a uniform-density model. Taking into account a low to moderate number of clumps, one can use a continuous outflow model as a good approximation for polarimetric modeling. This result does not apply to equatorial distributions of gas (see Sect. 2.3 and the following section).
2.5. Disrupted accretion flow
The last scattering region to be examined is the accretion flow between the torus and the accretion disk. According to the simulations of Young (2000), Smith et al. (2004), and Paper II, this flow is likely to be a flattened region (half-opening angle of 80°) with a distribution of optically thin matter between 3 × 10-4 pc and 5 × 10-4 pc. We thus model a fragmented equatorial scattering region composed of electron spheres with Rsphere = 1.17 × 10-5 pc and τelec = 0.3 (in the previous uniform-density model, τelec was set to unity).
Equatorial scattering by a distribution of ionized clouds only affects equatorial lines of sight (Fig. 10 upper panel). When radiation passes through the model, it escapes more easily from a fragmented model with a low number of scattering targets than from a uniform-density reprocessing region. Thus, the observed flux is higher along the equator for sparsely populated models. For larger ℱ, the angular dependence of opacity changes, the partial covering of the source is larger, so the flux recorded at i> 75° is minimized. However, because of a higher total optical depth and the gaps between clouds, the number of photons reprocessed along the equator is still higher than for a uniform model, even when considering a large filling factor.
As photons more easily escape from a fragmented model, the fraction of reprocessed radiation is lower, so the polarization degree (Fig. 10 lower panel) decreases. The general tendency is the same in comparison with a continuous accretion flow: the maximum polarization degree is detected at equatorial inclinations, but its percentage is much lower. A fragmented medium also reproduces the parallel orientation of the photon polarization angle, similarly to an extended clumpy dusty torus model. To maximize P, equatorial covering must be higher, and only with ℱ > 0.2 the model can approximatively reproduce the polarization signature of the uniform-density case.
 |
Fig. 10 Modeling of an equatorial, electron-filled, fragmented scattering disk with a half-opening angle θ0 = 80°. The fraction F/F∗ of the central flux (upper panel) and the spatially integrated polarization P (lower panel) are seen at different viewing inclinations, i, integrated over 2000 to 8000 Å. We note the change in scale between the polarizations of the four models. |
3. AGN modeling with clumpy structures
3.1. Comparison with a uniform-density model
Now that we have investigated the isolated reprocessing components separately, our last step is to construct a three-component model to approach a typical unified scheme for AGNs (Antonucci 1993). To do so, we gather three fragmented regions around the central emitting source. First, the equatorial electron-dominated flow is modeled using a ℱ ~ 0.25 model in order to maximize the production of parallel polarization at polar viewing angles (Smith et al. 2004), see Sect. 2.5. Then, at greater distances, a fragmented torus is set to obscure the flux coming from the inner part of the AGN. We opted for another ℱ ~ 0.25 model to enhance the partial covering factor of the source (Hönig & Kishimoto 2010). However, as noted in Sect. 2.3, an extended or a compact, clumpy, circumnuclear medium results in very different polarization signatures. We thus opted for two realizations of our AGN model, one with a compact dusty structure and a second with a large torus recovered from our simulations in Sects. 2.3.1 and 2.3.2, respectively. We now set the fragmented tori to the same half-opening angles: θ0 = 30°. Finally, the tori are set to collimate the ionized outflows. Following observational evidence for polar outflows with low filling factors (e.g., NGC 3516, MR 2251-178, and MCG-6-30-15, Blustin & Fabian 2009) we opt for a wind model with ℱ ~ 0.06, see Sect. 2.4.1.
We present the resulting AGN modeling in Fig. 11, comparing a model made with purely uniform-density reprocessing regions to two clumpy models with different torus sizes (extended torus: middle column, compact torus: right column). The fraction F/F∗ of the central flux is found to be different, in terms of intensity, between a uniform-density model (Fig. 11, top-left) and its fragmented counterparts. The amount of radiation in the polar direction is maximum for all models since the polar winds are optically thin. The flux is seen in transmission and has not suffered many scattering events. When the viewing angle increases, F/F∗ slowly decreases for the clumpy AGN model with an extended torus, but not as fast as in the uniform-density case or the clumpy AGN with a compact circumnuclear structure. Part of the photons previously trapped by the inner walls of the uniform-density dusty torus are now able to escape, thus contributing to the flux. As soon as the line of sight toward the system crosses the torus horizon, the flux decreases sharply, but is still 100 times larger than in the uniform-density case owing to the non-perfect obscuration of the nuclei by the gas clumps. Along the equatorial plane, where a minimum amount of radiation is detected, photons escape from the model by (mostly) orthogonal scattering in the winds, and by direct transmission through the circumnuclear matter. The resulting type-2 F/F∗ is then much higher for a fragmented model with a large toroidal structure than for the other two models. F/F∗ is found to be roughly similar between the uniform-density and the clumpy AGN model with a compact torus. This is in agreement with our conclusions found in Sect. 2.3.2, indicating that a compact dusty structure acts in a similar manner to a uniform-density torus, but producing grayer intensity fluxes because of clumping.
 |
Fig. 11 Modeling the AGN unified scheme by three reprocessing regions (see text). The fraction F/F∗ of the central flux is plotted from 2000 to 8000 Å (upper panel) and the spatially integrated polarization P is plotted versus the observer’s inclination i (lower panel). Left column: an AGN model composed of only uniform-density reprocessing regions, while the middle and right columns: different AGNs (with an extended torus in the middle and a compact torus on the right side sustaining the same, θ0 = 30°, half-opening angle). The clumpy models are composed of the same three reprocessing regions (regarding the smooth-density AGN) which are now fragmented (radiation supported disk: ℱ ~ 0.25, torus: ℱ ~ 0.25, and ionized winds: ℱ ~ 0.06). |
Fragmentation strongly influences the resulting polarization signatures of an AGN model. In the uniform-density case (Fig. 11, bottom-left), parallel (negative) polarization is only detected at viewing angles close to the pole (i ~ 19°), but in the case of a clumpy model with an extended torus (Fig. 11, bottom-middle) parallel polarization is detected up to i ~ 57°. Such an inclination coincides with a viewing angle passing directly through the torus clumps without suffering too much absorption. There is a dual contribution from the accretion flow and from the extended dusty torus that are both producing negative polarization (see Sect. 2.3.1). The levels of P range from 0.1% to 0.6% for type-1 AGN. When the observer’s line of sight crosses the bulk of the dusty torus, where there is a maximum density of spheres, the photon position angle switches from parallel to perpendicular orientation as radiation from the equatorial regions is strongly suppressed. Most of the flux is seen by orthogonal scattering in the ionized winds, only producing 0° (perpendicular) polarization angles. P is much lower for i ~ 70° in the fragmented case (P ~ 7%), where photons reprocessed on the equatorial components are not properly shaded by the torus clumps, than in the case of a uniform-density model (P ~ 60%) where polarization mostly originates from scattering on the winds. Finally, at an extreme type-2 inclination, the polarization degree is maximum, with P ~ 40%. For all the viewing angles, P is found to be approximatively wavelength-independent, which is in agreement with the spectropolarimetric observations of NGC 1068 (Antonucci & Miller 1985), 3C 256 (Dey et al. 1996), or 3C 324 (Cimatti et al. 1996). The case of a fragmented model with a compact torus is less different than a uniform-density AGN since it does not favor the production of parallel polarization. because of the compact scale of the clumpy torus, negative polarization is only detected at i ≤ 30°, with a similar degree of P. However, the level of perpendicular polarization at intermediate and equatorial inclinations is about 1.5 to 2 times lower than for a uniform-density case, since the torus is less effective in producing high degrees of polarization (owing to depolarization induced by multiple scattering on a clumpy distribution of reprocessing regions). At maximum inclinations, P is equal to 50%.
Eventually, we find that there are big discrepancies between the two clumpy AGN models, depending on the morphology of their circumnuclear dust region. For the same half-opening angle (θ0 = 30°), radial opacity (τ ≫ 1) and filling factor (ℱ = 0.24), an AGN with an extended torus produces the smallest P and parallel polarization up to ~70° while a compact torus mimics the polarimetric behavior of a uniform-density AGN model but with reduced polarization degrees. We stress that it is due to the geometry of the tori: an extended torus being more oblate than its compact counterpart, thus favoring the production of parallel polarization.
3.2. Exploring partially fragmented models
Considering that P is wavelength-independent for all the previous AGN models, we integrate the polarization percentages over 2000−8000 Å and compare the uniform-density and fragmented AGN to intermediate models. In Fig. 12, four morphologically-similar cases are plotted versus inclination for two different geometries of the torus (extended and compact). In black is the completely uniform-density AGN model shown in Paper II and Fig. 11 (left column). Red squares represent a model with a uniform-density dusty torus but fragmented accretion flow and ionized outflows. In orange is a model with uniform-density polar winds but fragmented equatorial regions. Finally, indigo triangles stand for an AGN model purely composed of small clouds. Figure 12 (top) presents AGN modeling with extended tori and Fig. 12 (bottom) AGN with compact tori.
As stated in the previous paragraphs, a uniform-density AGN shows low, parallel polarization degrees at type-1 inclinations and high, perpendicular P at type-2s. The transition between the two polarization regimes occurs when the observer’s line of sight crosses the dust horizon and is clearly recognizable as the polarization degree suddenly drops to very low values. This pronounced dip results from the canceling contribution of parallel photons originating from scattering off the equatorial disk (and off the inner torus surfaces in the case of extended dusty tori) and perpendicular polarization emerging from compact tori and polar winds. The resulting polarization drop, already observed in Paper II, is a consequence of the sharp-edge torus simplification. If the torus stays uniform, fragmenting the polar outflows and the accretion flow has virtually no impact, regardless of the torus geometry. Type-1 polarization remains similar while type-2 polarization is marginally lower. However, if the torus is replaced by a cloud distribution but the outflows retain their uniformity, the picture changes drastically.
We study AGN models with extended tori first. The angle at which the polarization dichotomy appears is much larger, close to 60°, since the line of sight toward the inner AGN region is only partially obscured. Type-1 polarization remains lower than 1% and increases at type-2 orientations larger than 65°, up to 50%. When considering a purely clumpy model, such as in Fig. 11 (middle column), parallel polarization up to 2% emerges from the model at type-1 views, up to i ~ 70°, with the consequences described in the beginning of this section. In addition to that, it is interesting to note that the shape of the integrated polarization versus AGN inclination is the same from one model to another, with a polarization hump in the type-1 domain and a fast rise of P when the polarization position angle switches from parallel to perpendicular.
For AGN models with compact tori, the situation is similar to a uniform-density AGN model since obscuration is more effective. When the torus remains uniform-density but the winds and the equatorial scattering disk are clumpy, the resulting inclination-dependent polarization cannot be disentangled from the uniform-density model. To alter the AGN polarization signature, a fragmented torus is necessary, reducing the overall polarization by a factor of 1.5 to 2. However, in contrast to an AGN model with an extended toroidal structure, the onset of the polarization dichotomy does not vary. Finally, a fully-fragmented AGN produces a marginally lower P but conserves the principal characteristics of the uniform-density model.
One of the major conclusion emerging from Fig. 12 is that the impact of a fragmented dusty torus is of utmost importance for AGN modeling if its dimensions along the midplane extend up to hundreds of parsecs. Extended clumpy tori strongly affect the angle at which the polarization dichotomy occurs and help to produce parallel polarization at type-1 angles, even if its half-opening angle is considered to be very small (θ0 = 30°).
 |
Fig. 12 Investigating the impact on P of uniform-density reprocessing regions within a fragmented model. A purely uniform-density model is shown with black dots, a clumpy model with a uniform-density dusty torus with red squares, a clumpy model with uniform-density polar winds with orange diamonds and a purely clumpy model with indigo triangles. A dashed line indicates a polarization position angle γ = 90° (parallel), and a solid line stands for γ = 0° (perpendicular). Top figure: AGN modeling with extended tori; bottom: AGN modeling with compact tori. |
3.3. Impact of the overall opening angle
It is now clearly identified that most of the differences (in terms of polarization) arise when replacing a uniform, dusty toroidal region with a fragmented counterpart. From Paper II, we know that another influential parameter is the total opening angle of the model, defined as the half-opening angle shared by both the torus and the outflows. To investigate the resulting polarization from various opening angles, we now construct three fragmented models. The first one is the clumpy AGN model used in the previous section, with a half-opening angle θ0 of 30° with respect to the symmetry axis of the system (i.e., narrow winds and bulky torus). The second and the third model present larger θ0, respectively 45° and 60° (wide outflows and an oblate torus rather flattened along the equatorial plane). Similarly to Sects. 3.1 and 3.2, those three models are investigated with either an extended or a compact clumpy torus. The filling factors of the equatorial flow, circumnuclear matter and ionized winds are the same as the ones used in Sect. 3.1, namely ℱflow ~ 0.25, ℱtorus ~ 0.25, and ℱwind ~ 0.06.
Figure 13 (top) shows the inclination-dependent integrated polarimetric signature of the three fragmented AGN models with an extended dusty torus. In comparison with the model previously investigated (θ0 = 30°, represented with black dots), a model with θ0 = 45° (red squares) produces fewer instances of parallel polarization at type-1 angles (<1%) since the geometry of the polar winds strengthens the production of diluting, perpendicular polarization. The turning point between the dominance of parallel and perpendicular polarization starts at i ~ 75°, when the inner regions of the model are effectively hidden behind circumnuclear dust. Perpendicular polarization at type-2 viewing angles rises up to 38% at maximum. The third model, with θ0 = 60° (orange diamonds) follows a similar trend. The turning point starts at i ~ 80° and a maximal polarization degree of 16% is obtained along equatorial directions. Depending on the parametrization of the model, it is possible to vary both the polarization degree and the inclination at which perpendicular polarization dominates. Increasing the number of clumps representative of the polar winds will lead to higher perpendicular polarization (see Sect. 2.4.1 and Fig. 8) and thus shift the orientation at which the polarization dichotomy appears toward smaller i. Nevertheless, we find that extended tori are rather incompatible with observations when the medium is purely clumpy (see Sect. 4).
Figure 13 (bottom) presents the same analyzes but for AGN models with compact tori. We find that, depending on the global half-opening angle of the model, the onset inclination of the polarization dichotomy is very similar to the half-opening angle of the fragmented dusty torus. The net polarization is decreasing with flattened tori since their geometry promotes parallel polarization, a behavior already obtained in the case of uniform-density AGN models (Paper II). The amount of polarization at type-1 inclinations does not exceed 1% but for equatorial lines of sight P can be as high as 50% for tori with a small half opening angle, decreasing to 20% for θ0 = 60°. In comparison with AGN models with extended tori, the polarization dichotomy resulting from AGN with compact tori is more likely to fit polarimetric observations (Marin 2014) while reducing the overall polarization degree.
 |
Fig. 13 Investigating the impact of the total opening angle of the system on the spatially integrated polarization P. A model with total opening angle of 30° is shown with black dots, 45° with red squares and 60° with orange diamonds. All the models are made of fragmented reprocessing regions (see text). A dashed line indicates a polarization position angle γ = 90° (parallel), and a solid line stands for γ = 0° (perpendicular). Top figure: AGN modeling with extended, fragmented tori; bottom: AGN modeling with compact, fragmented tori. |
4. Discussion
The goal of this paper has been to investigate for the first time the net polarization emerging from non-smooth density distributions of dust grains, and evaluate the impact of clumping.
We find that clumping produces several major changes in polarimetric signatures, mainly as a result of rather different polarization degrees and polarization position angles emerging from clumpy tori. When coupled to other reprocessing regions, the resulting AGN model shows large deviations from an AGN made of purely uniform-density structures, particularly when extended dusty tori are implemented. It follows that a correct estimation of the morphology, filling factor, covering factor and half-opening angle of the torus is necessary to reproduce observed optical/UV polarization measurements.
In the following, we discuss our modeling results in the framework of past polarimetric observations and recent other numerical simulations.
4.1. Modeling versus observations
Modeled under ideal conditions, our AGNs composed of a variety of clumpy reprocessing regions are expected to produce different results according to the geometry of their obscuring torus. In the case of extended dusty matter, low polarization degrees (<2%) associated with parallel polarization arises at type-1 viewing angles, while the transition between parallel and perpendicular polarization occurs at i> 70°. Perpendicular P up to 40% is produced at edge-on inclinations. Using compact tori, AGN models produce lower parallel polarization at type-1 inclinations (<1%) and slightly higher P at type-2s (~50%) but in our models the transition between type-1 and type-2 classes starts between 24° and 59° (for a clumpy torus half opening angle of 30° and 60°, respectively). Compared with the AGN models investigated in Paper II, consisting of uniformly-filled scattering regions, fragmentation leads to higher polarization along polar directions and lower P along the equator. Moreover, while a uniform-density dusty torus with θ0 = 60° was necessary to produce a transition between parallel and perpendicular polarization at i ~ 60°, we have shown in Sect. 3 that extended fragmented tori tend to shift this value to higher inclinations as a result of less effective obscuration along observer’s viewing angles grazing the torus horizon.
It is interesting to evaluate the relevance of fully fragmented AGN models within the framework of the compendium of inclinations of Seyfert galaxies published by Marin (2014). In this work, 53 estimated AGN inclinations are matched with ultraviolet/optical continuum polarization measurements and constraints for AGN modeling are derived. The transition between type-1 and type-2 inclination is found to occur between 45° and 60°, which is in agreement with our modeling of a clumpy AGN with a compact dusty torus and global half-opening angles of 30° to 60°. The level of parallel polarization at type-1 orientations is correctly reproduced (except for several enigmatic, highly polarized type-1 AGN, see below), as well as the amount of parallel polarization at type-2 inclinations. An AGN model with a compact, but disrupted, dusty torus is thus in agreement with observations and helps to decrease the production of perpendicular polarization at type-2 inclinations. However, AGN models with extended clumpy tori cannot reproduce the observed polarization dichotomy onset (<60°) since their oblate morphology reduces the efficiency of obscuration at intermediate angles for a moderate filling factor. This means that extended tori are incompatible with observations6 and future simulations must focus on compact structures, independently of their fragmentation level.
Several issues remain. Results from Marin (2014) show that P is expected to rise promptly, from 0.7% to 30%, between inclinations of 45° and 60° a behavior that cannot be reproduced by a circumnuclear distribution of dust clouds. In addition to that, the question of highly polarized (P> 4%) type-1 AGN, such as Fairall 51 (Martin et al. 1983), IC 4329A (Brindle et al. 1990) or ESO 323-G077 (Schmid et al. 2003) holds still. Our analysis confirms that clumpy AGNs with compact tori are not the solution to reproduce high parallel or perpendicular polarization at type-1 inclinations and that another solution must be found. It is clear from our series of papers that the unified model of AGN, established from polarimetric observations, is true at zeroth order but detailed radiative transfer calculations point toward a need for adjustments. Theoretical models treating the reprocessing regions of AGN as dynamical structures started to emerge at the end of last millennium with the work of Proga et al. (2000), based on similar studies for cataclysmic variables and OB stars (e.g., Pereyra et al. 1997; Proga et al. 1998, 1999). Soon after, Elvis (2000) suggested a phenomenological model for quasar disk winds. Those models predict that mass-loss from AGN is in the form of radiation-driven outflows, where momentum is extracted from the radiation field near accreting disks by line opacity (Castor et al. 1975). Such winds could be associated with the AGN ionization cones and also be responsible for a failed dusty wind along the equator (Elitzur & Shlosman 2006; Gallagher et al. 2014), where dust can form and survive if shielded from the full continuum by inner highly-ionized disk-born winds (Elvis 2012; Czerny & Hryniewicz 2012; Czerny et al. 2015). Such models are being currently investigated in order to see if they can reproduce the observed spectroscopic and polarimetric signatures of AGNs. Preliminary studies based on the model of Elvis (2000) showed that line-driven accretion disk wind models are good candidates to replace the usual axisymmetric unified model (Marin & Goosmann 2013a,b,c; Marin 2014).
4.2. Clumpy tori and changing look AGN
In the X-ray domain, several intermediate type AGN (1.5, 1.8, 1.9) have been discovered displaying rapid transitions between reflection-dominated (Compton thick, as in our models) to transmission-dominated (Compton-thin) states. Such dramatic X-ray spectral changes are characteristic of a sub-class of Seyfert galaxies called “changing look” AGN (Risaliti et al. 2005). Those variations are attributed to clouds composed of optically thick, cold atomic material transiting in front of the observer’s line of sight, creating X-ray eclipses, rather than to intrinsic emission variability. The rapid timescales of those eclipses, lasting from hours to days (e.g., Elvis et al. 2004), suggest that the absorbers are situated on compact scales close to the low-ionization-line broad line region (LIL BLR, see review by Turner & Miller 2009). Longer eclipses, up to months, have also been detected in 8 objects by Markowitz et al. (2014), indicating a possible location of the obscuring cloud within the inner regions of infrared-emitting dusty tori.
The analogy between changing look AGN and clumpy tori is straightforward. If the molecular clouds composing a fragmented torus are in a dynamical state, as expected by Krolik & Begelman (1988), Seyfert-galaxies within a specific range of inclinations should show variation in their spectroscopic and polarimetric properties. Since the apparent motion of the torus gas clouds is much slower than the clouds from the BLR (Risaliti et al. 2002), long-term monitoring is necessary to investigate these potential phenomena. By extension, our paper shows that we expect differences in terms of polarization between two AGNs with the same inclination and a clumpy distribution of absorbing matter, but with the line of sight of the first model being obscured by a clump while the other model is free of absorption. From Fig. 12, we see that for an inclination of 50° and an extended torus, a perpendicular polarization of about 50% is expected when the central engine is obscured while, if there is no clump along the observer’s view, parallel polarization with P< 2% is more probable. In the case of a compact yet fragmented torus, P would decrease from 25% to 9% for the same inclination. The real change in polarization is likely to be less dramatic since neighboring clumps would also affect the net polarization degree, but one can expect a variation of several percent in the polarization and a possible switch of the position angle. Preliminary spectropolarimetric modeling has been conducted in the X-ray range for a clumpy distribution of gas clouds around the central part of NGC 1365 by Marin et al. (2013) and a switch of the polarization position angle has been predicted between the soft and the hard X-ray-bands.
4.3. An alternative solution to fragmentation
In Papers I and II, we considered smooth dusty tori (i.e., continuous dust distributions that change either slowly or not at all with distance from the AGN engine). In this paper, we have investigated the case of circumnuclear obscuration using a fragmented medium composed of constant density spheres. Both models have failures and successes in reproducing peculiar aspects of AGN observations (see also the discussions in Vollmer et al. 2004; Dullemond & van Bemmel 2005; Feltre et al. 2012).
However, there is a third, lesser-known competitor: bulk tori maintained by nuclear starbursts. In this scenario, supernovae (SNe), from nuclear star-bursts situated within the inner 100 pc of low-luminosity AGNs (LLAGNs, 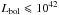 erg s-1), could put out enough energy to keep up the scale height of the dusty torus (Fabian et al. 1998). The bulky torus is essentially supported from the inside by SNe energy boosts and is then neither smooth nor fragmented, but has a Swiss cheese or sponge-like structure. The proposed scenario of Fabian et al. (1998) was investigated in detail by Wada & Norman (2002) using three-dimensional hydrodynamical simulations. The authors assumed a toroidal geometry around the central supermassive black hole (SMBH) in which the energy input from SNe is in equilibrium with the turbulent energy dissipation. Doing so, they infer new constraints on the inclination of LLAGNs as the torus half-opening angle seems to be correlated with the SMBH mass. The polarization signal of such a scenario remains unexplored and could lead to different signatures than the uniform-density and the fragmented tori. However one must keep in mind that, according to Krolik & Begelman (1988), stirring by stellar processes might not be strong enough to compete with energy dissipation in the circumnuclear gas.
erg s-1), could put out enough energy to keep up the scale height of the dusty torus (Fabian et al. 1998). The bulky torus is essentially supported from the inside by SNe energy boosts and is then neither smooth nor fragmented, but has a Swiss cheese or sponge-like structure. The proposed scenario of Fabian et al. (1998) was investigated in detail by Wada & Norman (2002) using three-dimensional hydrodynamical simulations. The authors assumed a toroidal geometry around the central supermassive black hole (SMBH) in which the energy input from SNe is in equilibrium with the turbulent energy dissipation. Doing so, they infer new constraints on the inclination of LLAGNs as the torus half-opening angle seems to be correlated with the SMBH mass. The polarization signal of such a scenario remains unexplored and could lead to different signatures than the uniform-density and the fragmented tori. However one must keep in mind that, according to Krolik & Begelman (1988), stirring by stellar processes might not be strong enough to compete with energy dissipation in the circumnuclear gas.
5. Conclusions and future work
We have modeled a set of isolated clumpy structures and have run Monte Carlo simulations in order to compare their resulting polarization signatures with the uniform models analyzed in Paper II. We have created three different fragmented models using spheres of constant radius and density, corresponding to the respective filling factors: ℱ ~ 0.06, ℱ ~ 0.13 and ℱ ~ 0.25.
We find that equatorial distributions of clumps, either for a dusty torus or an ionized accretion flow, tend to decrease the net polarization percentage, independently of the filling factor. The resulting polarization position angle depends on the half-opening angle and on the morphology of the given region. Extended clumpy configurations with half-opening angles <=45° give rise to parallel polarization for type-1 and type-2 viewing angles, while similar compact yet fragmented tori produce perpendicular polarization. A residual photon flux always manages to escape from the central parts of the model even when considering an observer’s line of sight passing through the highly-covered equatorial region. Because of multiple scattering and thus depolarization, this equatorial flux is carrying a weak polarization degree (<1%) that is likely to be diluted by star-light emission. In the case of scattering regions distributed along the polar directions, the impact of fragmentation is reduced: a small number of clouds is able to properly reproduce the polarization behavior of uniform-density models. Increasing the cloud distribution only results in increasing the net polarization percentage as the total optical depth increases along the observer’s line of sight. As in the uniform-density density case, fragmented outflows solely produce perpendicular polarization angles.
Combining the radiation supported electron region with the dusty torus and the polar outflows, we then modeled AGNs only made of clumpy structures. Such models, with a torus half-opening angle of 30°, produce different results according to the radial size of the clumpy tori. For extended tori (wider than tens of parsecs) a small polarization percentage (up to 2%), associated with parallel polarization, arises at inclinations up to i ~ 70°. When the observer’s line of sight passes through the central part of the equatorial dusty matter, polarization increases and switches from parallel to perpendicular orientation. A large P (~40%) is found at edge-on viewing angles. Active galactic nuclei models with compact tori behave rather similarly to uniform-density models except that they produce significantly lower polarization at intermediate and type-2 orientations. The observed polarization dichotomy is better reproduced by models with compact yet fragmented tori with θ0 ≥ 45°.
It was also shown that fragmented dusty tori have the strongest impact on P. Large, fragmented tori are not viable solutions to replace geometrically flat, uniform-density dust distributions regardless of their half-opening angle; compact circumnuclear structures must be favored. Hence, particular attention should be focused on the circumnuclear region: while unfragmented tori give similar results in terms of intensity fluxes and polarization behavior, cloudlet distributions of absorbing gas that are able to reproduce the observed spectroscopic signatures of nearby Seyfert galaxies might not work when polarization is considered. To check the validity of compact, clumpy AGN tori, multi-wavelength and time-resolved spectropolarimetric modeling are needed. We are planning to undertake this in future work.
This definition assumes a sharp-edge torus in angular direction; it is a basic simplification as real tori are likely to have soft-edges (see, e.g., Alonso-Herrero et al. 2003).
Around 10–18 μm, an apparent optical depth of 0.4 corresponds to an hydrogen column density of nH = 2 × 1022 cm-2 (Levenson 2014). A torus is considered as Compton thick when nH ≥ 1024 cm-2.
This is in agreement with the X-ray results obtained by Gandhi et al. (2015), who shown that the observed Fe Kα emission radii of 9 type-1 AGN are similar to, or smaller than the radius of the BLR, favoring compact tori.
Acknowledgments
We thank the anonymous referee who provided insight and expertise that greatly assisted our paper. This research has been supported by the Academy of Sciences of the Czech Republic, the French PNHE and the grant ANR-11-JS56-013-01 “POLIOPTIX”. Part of this work was supported by the COST Action MP1104 “Polarization as a tool to study the Solar System and beyond”.
References
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2012, A&A, 537, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., Quillen, A. C., Rieke, G. H., Ivanov, V. D., & Efstathiou, A. 2003, AJ, 126, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Arny, T. T. 1966, ApJ, 145, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Ashton, C. E. 2005, Ph.D. Thesis, University of London, University College London (UK) [Google Scholar]
- Blustin, A. J., & Fabian, A. C. 2009, MNRAS, 396, 1732 [NASA ADS] [CrossRef] [Google Scholar]
- Brindle, C., Hough, J. H., Bailey, J. A., et al. 1990, MNRAS, 244, 577 [NASA ADS] [Google Scholar]
- Capetti, A., Axon, D. J., Macchetto, F., Sparks, W. B., & Boksenberg, A. 1995, ApJ, 446, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Capetti, A., Macchetto, F. D., & Lattanzi, M. G. 1997, Ap&SS, 248, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Cimatti, A., Dey, A., van Breugel, W., Antonucci, R., & Spinrad, H. 1996, ApJ, 465, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B., & Hryniewicz, K. 2012, J. Phys. Conf. Ser., 372, 012013 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B., Modzelewska, J., Petrogalli, F., et al. 2015, Adv. Space Res., 55, 1806 [Google Scholar]
- Dey, A., Cimatti, A., van Breugel, W., Antonucci, R., & Spinrad, H. 1996, ApJ, 465, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Dullemond, C. P., & van Bemmel, I. M. 2005, A&A, 436, 47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elitzur, M. 2008, New A Rev., 52, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., & Shlosman, I. 2006, ApJ, 648, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M. 2000, ApJ, 545, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M. 2012, in AGN Winds in Charleston, eds. G. Chartas, F. Hamann, & K. M. Leighly, ASP Conf. Ser., 460, 186 [Google Scholar]
- Elvis, M., Risaliti, G., Nicastro, F., et al. 2004, ApJ, 615, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, I. N., Ford, H. C., Kinney, A. L., et al. 1991, ApJ, 369, L27 [Google Scholar]
- Fabian, A. C., Barcons, X., Almaini, O., & Iwasawa, K. 1998, MNRAS, 297, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Feltre, A., Hatziminaoglou, E., Fritz, J., & Franceschini, A. 2012, MNRAS, 426, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, S. C., Abado, M. M., & Everett, J. E. 2014, IAU Symp., 304, 311 [NASA ADS] [Google Scholar]
- Gandhi, P., Hoenig, S. F., & Kishimoto, M. 2015, Arxiv e-prints [arXiv:1502.02661] [Google Scholar]
- Goosmann, R. W., & Gaskell, C. M. 2007, A&A, 465, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goosmann, R. W., & Matt, G. 2011, MNRAS, 415, 3119 [NASA ADS] [CrossRef] [Google Scholar]
- Heymann, F., & Siebenmorgen, R. 2012, ApJ, 751, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F., & Kishimoto, M. 2010, A&A, 523, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Antonucci, R., et al. 2012, ApJ, 755, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, C. 1962, ApJ, 136, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Jeans, J. H. 1902, Roy. Soc. London Philos. Trans. Ser. A, 199, 1 [Google Scholar]
- Kartje, J. F. 1995, ApJ, 452, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Kitchin, C. 2007, Galaxies in Turmoil: The Active and Starburst Galaxies and the Black Holes That Drive Them, Astronomers’ Universe (Springer) [Google Scholar]
- Krolik, J. H., & Begelman, M. C. 1988, ApJ, 329, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Levenson, N. A. 2014, IAU Symp., 304, 112 [NASA ADS] [Google Scholar]
- Li, A. 2007, in The Central Engine of Active Galactic Nuclei, eds. L. C. Ho, & J.-W. Wang, ASP Conf. Ser., 373, 561 [Google Scholar]
- Liu, Y., & Li, X. 2014, ApJ, 787, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F. 2014, MNRAS, 441, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F., & Goosmann, R. W. 2012, in SF2A-2012: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, eds. S. Boissier, P. de Laverny, N. Nardetto, et al., 587 [Google Scholar]
- Marin, F., & Goosmann, R. W. 2013a, MNRAS, 436, 2522 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F., & Goosmann, R. W. 2013b, in SF2A-2013: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, eds. L. Cambresy, F. Martins, E. Nuss, & A. Palacios, 475 [Google Scholar]
- Marin, F., & Goosmann, R. W. 2013c, in SF2A-2013: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, eds. L. Cambresy, F. Martins, E. Nuss, & A. Palacios, 479 [Google Scholar]
- Marin, F., & Goosmann, R. W. 2014, SF2A-2014: Proc. Annual meeting of the French, Society of Astronomy and Astrophysics, eds. J. Ballet, F. Martins, F. Bournaud, R. Monier, & C. Reylé, 103 [arXiv:1409.7278] [Google Scholar]
- Marin, F., Goosmann, R. W., Gaskell, C. M., Porquet, D., & Dovčiak, M. 2012, A&A, 548, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marin, F., Porquet, D., Goosmann, R. W., et al. 2013, MNRAS, 436, 1615 [NASA ADS] [CrossRef] [Google Scholar]
- Markowitz, A. G., Krumpe, M., & Nikutta, R. 2014, MNRAS, 439, 1403 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P. G., Thompson, I. B., Maza, J., & Angel, J. R. P. 1983, ApJ, 266, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Ivezić, V., & Elitzur, M. 2002, ApJ, 570, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Ivezić, v., & Elitzur, M. 2008a, ApJ, 685, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Nikutta, R., Ivezić, v., & Elitzur, M. 2008b, ApJ, 685, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Nenkova, M., Sirocky, M. M., Nikutta, R., Ivezić, v., & Elitzur, M. 2010, ApJ, 723, 1827 [NASA ADS] [CrossRef] [Google Scholar]
- Packham, C., Young, S., Hough, J. H., Axon, D. J., & Bailey, J. A. 1997, MNRAS, 288, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Pereyra, N. A., Kallman, T. R., & Blondin, J. M. 1997, ApJ, 477, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Pier, E. A., & Krolik, J. H. 1992, ApJ, 399, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Pier, E. A., & Krolik, J. H. 1993, ApJ, 418, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., Stone, J. M., & Drew, J. E. 1998, MNRAS, 295, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., Stone, J. M., & Drew, J. E. 1999, MNRAS, 310, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., Stone, J. M., & Kallman, T. R. 2000, ApJ, 543, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Elvis, M., & Nicastro, F. 2002, ApJ, 571, 234 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Elvis, M., Fabbiano, G., Baldi, A., & Zezas, A. 2005, ApJ, 623, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Schartmann, M., Meisenheimer, K., Camenzind, M., et al. 2008, A&A, 482, 67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schartmann, M., Wada, K., Prieto, M. A., Burkert, A., & Tristram, K. R. W. 2014, MNRAS, 445, 3878 [NASA ADS] [CrossRef] [Google Scholar]
- Schmid, H. M., Appenzeller, I., & Burch, U. 2003, A&A, 404, 505 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, J. E., Robinson, A., Alexander, D. M., et al. 2004, MNRAS, 350, 140 [Google Scholar]
- Tristram, K. R. W., Meisenheimer, K., Jaffe, W., et al. 2007, A&A, 474, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, T. J., & Miller, L. 2009, A&ARv, 17, 47 [Google Scholar]
- Vollmer, B., Beckert, T., & Duschl, W. J. 2004, A&ARv, 413, 949 [Google Scholar]
- Wada, K., & Norman, C. A. 2002, ApJ, 566, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, A. S. 1996, Vis. Astron., 40, 63 [Google Scholar]
- Young, S. 2000, MNRAS, 312, 567 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Schematic view of a fragmented region. Clumps are shielding each other from the central source, but gaps between the spheres allow part of radiation to escape from the model, even along equatorial directions where obscuration is most efficient (in the case of circumnuclear dust). |
| In the text | |
 |
Fig. 2 Sketches of the different models investigated in this paper. Tori with cylindrical cross-section, either extended or compact, are explored in Sect. 2.3, polar winds in Sect. 2.4, and flared disks in Sect. 2.5. Partially and fully fragmented AGN models are presented in Sect. 3. |
| In the text | |
 |
Fig. 3 Modeling an optically-thick, elliptically-shaped, extended and fragmented torus with θ0 = 30° measured relative to the symmetry axis. The fraction F/F∗ of the central flux (upper four panels) and the spatially integrated polarization P (lower four panels) are seen at different viewing inclinations, i, from 2000 to 8000 Å. The fluxes and polarizations are shown for a uniform-density model and three fragmented counterparts with filling factors ranging from 0.06 to 0.25. We note the change in scale between the spectra of the four models. |
| In the text | |
 |
Fig. 4 Same as in Fig. 3 except that the torus has an opening angle of θ0 = 45°. |
| In the text | |
 |
Fig. 5 Same as in Fig. 3 except that the torus has an opening angle of θ0 = 60°. |
| In the text | |
 |
Fig. 6 Modeling compact tori (left: uniform-density model; right: clumpy torus) with θ0 = 45° measured relative to the symmetry axis. In the case of the fragmented torus, the filling factor is equal to 0.25 and the optical thickness per clump is 50 in the V-band. The fraction F/F∗ of the central flux (upper figures) and the spatially integrated polarization P (lower figures) are seen at different viewing inclinations, i, from 2000 to 8000 Å. We note the change in scale between the polarization spectra of the two models. |
| In the text | |
 |
Fig. 7 Modeled images of the polarized flux, PF/F∗, for a clumpy, compact dusty torus of half-opening angle 45° measured relative to the axis of symmetry; PF/F∗ is color-coded and integrated over 2000 to 8000 Å. γ and P are represented by black vectors (a vertical vector indicates a polarization of γ = 90°, and a horizontal vector stands for an angle of γ = 0°). The length of the vector is proportional to P. Top: image at i ∽ 18° (face-on view); middle: i ∽ 45°; bottom: i ∽ 81° (edge-on view). |
| In the text | |
 |
Fig. 8 Modeling an electron-filled, fragmented, scattering double-cone with θ0 = 30° measured relative to the symmetry axis. The fraction F/F∗ of the central flux is integrated from 2000 to 8000 Å (upper panel) and the spatially integrated polarization P is plotted versus inclination i (lower panel). |
| In the text | |
 |
Fig. 9 Modeling an optically thin, dusty, fragmented double-cone with θ0 = 30° measured relative to the symmetry axis. The fraction F/F∗ of the central flux (upper panel) and the spatially integrated polarization P (lower panel) are seen at different viewing inclinations, i, from 2000 to 8000 Å. |
| In the text | |
 |
Fig. 10 Modeling of an equatorial, electron-filled, fragmented scattering disk with a half-opening angle θ0 = 80°. The fraction F/F∗ of the central flux (upper panel) and the spatially integrated polarization P (lower panel) are seen at different viewing inclinations, i, integrated over 2000 to 8000 Å. We note the change in scale between the polarizations of the four models. |
| In the text | |
 |
Fig. 11 Modeling the AGN unified scheme by three reprocessing regions (see text). The fraction F/F∗ of the central flux is plotted from 2000 to 8000 Å (upper panel) and the spatially integrated polarization P is plotted versus the observer’s inclination i (lower panel). Left column: an AGN model composed of only uniform-density reprocessing regions, while the middle and right columns: different AGNs (with an extended torus in the middle and a compact torus on the right side sustaining the same, θ0 = 30°, half-opening angle). The clumpy models are composed of the same three reprocessing regions (regarding the smooth-density AGN) which are now fragmented (radiation supported disk: ℱ ~ 0.25, torus: ℱ ~ 0.25, and ionized winds: ℱ ~ 0.06). |
| In the text | |
 |
Fig. 12 Investigating the impact on P of uniform-density reprocessing regions within a fragmented model. A purely uniform-density model is shown with black dots, a clumpy model with a uniform-density dusty torus with red squares, a clumpy model with uniform-density polar winds with orange diamonds and a purely clumpy model with indigo triangles. A dashed line indicates a polarization position angle γ = 90° (parallel), and a solid line stands for γ = 0° (perpendicular). Top figure: AGN modeling with extended tori; bottom: AGN modeling with compact tori. |
| In the text | |
 |
Fig. 13 Investigating the impact of the total opening angle of the system on the spatially integrated polarization P. A model with total opening angle of 30° is shown with black dots, 45° with red squares and 60° with orange diamonds. All the models are made of fragmented reprocessing regions (see text). A dashed line indicates a polarization position angle γ = 90° (parallel), and a solid line stands for γ = 0° (perpendicular). Top figure: AGN modeling with extended, fragmented tori; bottom: AGN modeling with compact, fragmented tori. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


