| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A137 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201424797 | |
| Published online | 19 May 2015 | |
Particle-in-cell simulation study of the interaction between a relativistically moving leptonic micro-cloud and ambient electrons
1 Department of Science and Technology (ITN), Linkoping University, 60174 Norrkoping, Sweden
e-mail: mark.e.dieckmann@liu.se
2 Centre for Plasma Physics, Queen’s University Belfast, BT7 1NN, Belfast, UK
e-mail: g.sarri@qub.ac.uk & m.zepf@qub.ac.uk
3 Anton Pannekoek Institute for Astronomy/GRAPPA, University of Amsterdam, 1098 Amsterdam, The Netherlands
e-mail: s.b.markoff@uva.nl
Received: 12 August 2014
Accepted: 23 March 2015
Context. The jets of compact accreting objects are composed of electrons and a mixture of positrons and ions. These outflows impinge on the interstellar or intergalactic medium and both plasmas interact via collisionless processes. Filamentation (beam-Weibel) instabilities give rise to the growth of strong electromagnetic fields. These fields thermalize the interpenetrating plasmas.
Aims. Hitherto, the effects imposed by a spatial non-uniformity on filamentation instabilities have remained unexplored. We examine the interaction between spatially uniform background electrons and a minuscule cloud of electrons and positrons. The cloud size is comparable to that created in recent laboratory experiments and such clouds may exist close to internal and external shocks of leptonic jets. The purpose of our study is to determine the prevalent instabilities, their ability to generate electromagnetic fields and the mechanism, by which the lepton micro-cloud transfers energy to the background plasma.
Methods. A square micro-cloud of equally dense electrons and positrons impinges in our particle-in-cell (PIC) simulation on a spatially uniform plasma at rest. The latter consists of electrons with a temperature of 1 keV and immobile ions. The initially charge- and current neutral micro-cloud has a temperature of 100 keV and a side length of 2.5 plasma skin depths of the micro-cloud. The side length is given in the reference frame of the background plasma. The mean speed of the micro-cloud corresponds to a relativistic factor of 15, which is relevant for laboratory experiments and for relativistic astrophysical outflows. The spatial distributions of the leptons and of the electromagnetic fields are examined at several times.
Results. A filamentation instability develops between the magnetic field carried by the micro-cloud and the background electrons. The electromagnetic fields, which grow from noise levels, redistribute the electrons and positrons within the cloud, which boosts the peak magnetic field amplitude. The current density and the moduli of the electromagnetic fields grow aperiodically in time and steadily along the direction that is anti-parallel to the cloud’s velocity vector. The micro-cloud remains conjoined during the simulation. The instability induces an electrostatic wakefield in the background plasma.
Conclusions. Relativistic clouds of leptons can generate and amplify magnetic fields even if they have a microscopic size, which implies that the underlying processes can be studied in the laboratory. The interaction of the localized magnetic field and high-energy leptons will give rise to synchrotron jitter radiation. The wakefield in the background plasma dissipates the kinetic energy of the lepton cloud. Even the fastest lepton micro-clouds can be slowed down by this collisionless mechanism. Moderately fast charge- and current neutralized lepton micro–clouds will deposit their energy close to relativistic shocks and hence they do not constitute an energy loss mechanism for the shock.
Key words: instabilities / magnetic fields / plasmas / methods: numerical / ISM: jets and outflows
© ESO, 2015
1. Introduction
Accreting compact objects (neutron stars and black holes) can emit relativistic plasma jets (e.g. Lovelace 1976; Blandford & Znajek 1977; Blandford & Payne 1982). Some recent examples of such jets are those inferred for gamma-ray bursts (GRBs; Cenko et al. 2010), or now directly observed at near-event horizon scales in active galactic nuclei (AGN; Hada et al. 2011; Doeleman et al. 2012) and X-ray binaries (XRBs; e.g. Mirabel et al. 1992; Fender 2001; Corbel et al. 2002). Energetic processes, which yield a heating and subsequent thermalization of the plasma via the interaction of charged particles with the self-generated electromagnetic fields, can be expected to develop within the jet and at its collision boundary with the ambient interstellar or intergalactic medium. The large mean free path of the particles in the jet and in the ambient medium implies that these processes can not be mediated by binary collisions between particles; rather relativistic beam instabilities and collisionless shocks will thermalize the plasma flow. Such shocks can be external, forming between the jet and the ambient medium, or internal, resulting from strong spatial variations of the plasma’s mean flow velocity within the jet.
The huge energy density carried by a relativistic jet in the form of radiation, electromagnetic fields and kinetic energy can trigger pair-production. It is thus likely that such jets carry a significant fraction of positrons, that can react more easily to electromagnetic fields than heavier ions. We may thus neglect in some cases the ion contribution to the plasma processes close to the external and internal shocks; for example if the processes take place on short spatio-temporal scales. More specifically, the ion reaction is negligible if the instabilities grow and saturate on time scales that are comparable to a few tens of inverse plasma frequencies and if the spatial scales of the plasma structures are of the order of an electron skin depth. These are millisecond- and kilometer scales if the electron number density is ≈1 cm-3.
Accordingly, a wide range of theoretical (Medvedev & Loeb 1999; Brainerd 2000; Bret et al. 2006, 2010; Milosavljevic & Nakar 2006; Tautz & Lerche 2012) and particle-in-cell (PIC) simulation studies (Sakai et al. 2000; Honda et al. 2000; Silva et al. 2003; Jaroschek et al. 2004; Medvedev et al. 2005; Dieckmann et al. 2009a,b; Vieira et al. 2012) have addressed the instabilities of counterstreaming lepton beams and the formation of shocks in pair plasmas (Kazimura et al. 1998; Haruki & Sakai 2003; Sironi & Spitkovsky 2011; Sironi et al. 2013; Bret et al. 2013) that are triggered when plasmas collide at a relativistic speed.
In the meantime, recent advances in laser technology have opened up another means to study the processes expected to take place in relativistic leptonic flows. It is now possible to produce clouds of electrons and positrons in the laboratory that are large and dense enough to initiate their collective (plasma) behavior. High-energy electron/positron clouds have been reported by Chen et al. (2010). However, the small percentage of positrons in the leptonic cloud (10%) and the relatively low density (transverse size smaller than the collisionless skin depth) prevent plasma behavior to occur. Using this experimental approach, these characteristics can be achieved with the 10 PW laser facilities that will be available at the end of this decade (Ridgers et al. 2012). Adopting a different laser-driven scheme first proposed by Sarri et al. (2013a), dense and neutral leptonic clouds have been recently achieved (Sarri et al. 2013b). The small divergence and neutrality of the reported beams allow for the study of the growth of plasma instabilities, that are likely relevant for relativistic astrophysical flows. In the following paragraphs we put forward a scenario motivated in part by recent PIC simulations and experiments, which we here propose to study further with a pointed PIC simulation.
A plasma shock transforms the directed flow energy of the upstream flow into thermal energy of the downstream plasma. If the shock were mediated by binary collisions between particles, it would form a sharp boundary perfectly separating the two plasma populations with different mean flow speeds, temperatures and field energy densities. However, the collisionless nature of the plasma expected for astrophysical jets implies that their internal and external shocks are mediated instead by electromagnetic fields. The self-generated electromagnetic fields are able to sustain the plasma shock and can confine the bulk of the heated plasma in its downstream region. However, unlike the case of collisional shocks, the confinement will not be perfect. Energetic electrons, positrons and ions can leak out from the downstream region and move upstream. PIC simulations of relativistic shocks involving electrons and ions (Martins et al. 2009) or electrons and positrons (Chang et al. 2008) show evidence for such a leakage. The leaking particles will not necessarily have a spatially uniform thermal distribution. Hence micro-clouds of electrons and positrons, with dimensions comparable to the thickness of the transition layer of a leptonic shock, can exist close to sharp boundaries like shocks, that separate plasma populations with vastly different mean kinetic energy densities. For the sake of this work, we neglect escaping ions since their large inertia implies that they can usually not move in unison with the escaping leptons.
Escaping clouds of relativistic electrons introduce a strong net current ahead of the shock. These clouds will either lose their energy to the growth of strong magnetic fields (Sarri et al. 2012) or they will drive a return current in the plasma ahead of the shock. For the latter case, two-stream instabilities will develop and thermalize the electron clouds. If a sufficiently dense population of positrons exists close to the shock, then the escaping electrons can be charge-and current-neutralized by comoving positrons. This overall charge-and current-neutralized beam can drive electromagnetic instabilities ahead of the shock. A foreshock will then develop, which expands upstream along the normal direction of the shock (Chang et al. 2008) until the point where the leaking particles can no longer drive plasma instabilities. In principle, because of the lack of binary collisions, the micro-clouds could propagate indefinitely if they did not drive plasma instabilities, in which case their energy would be lost from the shock. It is thus interesting to determine whether or not a skin depth-scale leptonic cloud will in fact interact with an ambient plasma through collective plasma instabilities or if such clouds constitute an energy loss mechanism for a relativistic shock.
Our PIC simulation study presented here is thus motivated by this need to better understand the physics of localized relativistic lepton clouds. Using a two-dimensional PIC simulation, we examine the impact of a small electron-positron cloud on an ambient plasma consisting of electrons and immobile ions. The number density and the average speed of the initially thermal electrons and positrons is equal and spatially uniform within the cloud. Consequently, the lepton cloud is free of any net charge and net current at the start of the simulation. The relative speed between the cloud and the ambient plasma corresponds to a Lorentz factor of 15, which is likely somewhat higher than that of the jets of XRBs, but typical for AGN (e.g. Lister et al. 2013). Only lepton clouds that move faster than the jet and the shock can move from the region behind the shock into the upstream region of the shock.
The temperature of the ambient electrons is 1 keV and that of the cloud leptons is 100 keV, typical values inferred from pair Comptonization models in, e.g., XRBs (see, e.g. Sunyaev & Titarchuk 1980; Esin et al. 1997; Merloni & Fabian 2002), or shock-heated ambient gas (e.g. Lanz et al. 2015) in order to explore a physical scale that is both feasible to simulate, and also potentially relevant for real systems. The pair cloud is launched initially in a vacuum and then collides with the ambient electron plasma that is spatially bounded and uniform. We consider a normal incidence of the pair cloud with respect to the boundary that separates the ambient plasma from the vacuum. The slow growth of the instability implies that all plasma processes develop in a region that is well-separated from this boundary and the latter is thus not important for the plasma dynamics.
This paper is structured as follows. Section 2 discusses the simulation code and the initial conditions. Section 3 presents the simulation results. Section 4 is the discussion.
2. The simulation code and the initial conditions
PIC codes employ a mixed Lagrangian-Eulerian scheme (Dupree 1963) to solve the following set of equations. Ampère’s law and Faraday’s law: 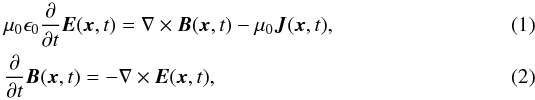 are solved on a numerical (Eulerian) grid. The EPOCH code (Ridgers et al. 2013), which we use here, solves Gauss’ law as a constraint and ∇·B = 0 to round-off precision.
are solved on a numerical (Eulerian) grid. The EPOCH code (Ridgers et al. 2013), which we use here, solves Gauss’ law as a constraint and ∇·B = 0 to round-off precision.
Coulomb collisions between particles are negligible for processes within and close to the transition layers of leptonic shocks if they develop on time scales that are comparable to the inverse plasma frequency ωp,i = (nie2/ϵ0me)1 / 2, where ni is the number density of the leptons of species i, e is the elementary charge and me is the electron mass. The absence of collisions implies that the plasma is not automatically in a thermal equilibrium, which would be characterized by a Maxwellian velocity distribution.
A more appropriate description of a collisionless plasma is thus given by the phase space density distribution fi(x,v,t), for which the position x and the velocity v are independent variables. Each plasma species i is represented by a separate phase space density distribution fi(x,v,t). The number density and the average speed are derived from this distribution as 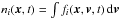 and
and 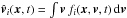 , respectively. The charge density in Gauss’ law is obtained from the number density, and the current density in Ampère’s law is computed using the average speed.
, respectively. The charge density in Gauss’ law is obtained from the number density, and the current density in Ampère’s law is computed using the average speed.
A PIC code approximates the phase space density distribution fi(x,v,t) of each plasma species i by an ensemble of Lagrangian- or computational particles (CPs). These CPs correspond to phase space blocks with a charge-to-mass ratio that equals that of the plasma particles they stand for. The force imposed on charged particles by electromagnetic fields is proportional to their charge q, while their inertia is determined by their mass m. The acceleration is thus proportional to q/m and the plasma evolution does not depend on any other quantity. The numerical values of the charge qi and mass mi of a CP that represents particles of the species i can thus be different from that of individual particles of this species as long as their ratio is the same. The relativistic momentum pj = miΓjvj of each CP with index j of the species i is evolved in time by a numerical approximation of the Lorentz force equation 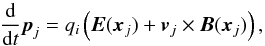 (3)and its position xj is updated through
(3)and its position xj is updated through 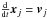 .
.
The algorithm on which explicit PIC codes are based can be summarized as follows. The current carried by each CP is interpolated to the grid. The summation over all current contributions gives the macroscopic current J(x,t), which is defined on the grid. The electromagnetic fields are updated per time step with this macroscopic current, and then interpolated back to the position xj of each CP and the particle momentum is then updated using the new electromagnetic fields. Each cycle advances the plasma and the field distribution by a finite time step Δt. A more detailed description of the PIC method can be found elsewhere (e.g. Dawson 1983).
Our simulation resolves the x–y plane and all three momentum components. The boundary conditions are periodic along y and open along x. We introduce three different species and we label their respective parameters by the subscripts b, e and p. Background electrons (labeled b) with the charge −e and mass me, the number density nb = n0, the plasma frequency ωp = (n0e2/ϵ0me)1 / 2 and the skin depth λe = c/ωp are introduced into the simulation box. The total box size is given by −1.8 λe ≤ x ≤ 117 λe and −13.4 λe ≤ y ≤ 13.4 λe. All electric and magnetic field components are set to zero at the simulation’s start. The electromagnetic fields are thereafter computed from the plasma currents.
The background electrons are placed into the interval 0 ≤ x ≤ 115 λe. The ambipolar electric field, which develops after some time at the boundary between the electrons and the vacuum bands at large and low x, reduces the number of electrons that can escape through the open boundary. The background electrons are at rest in the simulation frame and they have a Maxwellian velocity distribution with a temperature Tb = 1 keV. The ions form an immobile background of positive charges, which compensates the negative charge of the electrons. Immobile ions are introduced implicitly into PIC simulations if we introduce mobile electrons and set the electric field to zero. The background electrons and the immobile ions correspond to the ambient plasma. The ambient plasma in laboratory experiments is residual gas, which has been ionized by secondary x-ray radiation from the solid target, which is used for pair production. The ambient plasma could correspond to, e.g., shock-heated interstellar medium ahead of astrophysical jets or a surrounding accretion flow.
A square lepton cloud, which consists of electrons (label e) and positrons (label p) with equal number densities ne = np = n0, is placed in the (vacuum) interval −0.9 λe ≤ y ≤ 0.9 λe and −1.8 λe ≤ x ≤ 0. The side length of the cloud is 1.8 λe or 2.5 in units of the total leptonic skin depth 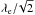 of the e+e− cloud. The mean speed vc of the cloud is aligned with the x-direction and yields the relativistic factor
of the e+e− cloud. The mean speed vc of the cloud is aligned with the x-direction and yields the relativistic factor 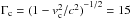 . Its momentum distribution in the cloud’s frame of reference is a relativistic Maxwellian with the temperature Tc = 100 keV.
. Its momentum distribution in the cloud’s frame of reference is a relativistic Maxwellian with the temperature Tc = 100 keV.
As mentioned before, the temperatures for the ambient electrons and the lepton clouds are representative of some selected systems, but would be too high to represent the typical interstellar medium or jet plasma far from the base, respectively. The high value is chosen for numerical reasons; a high temperature increases the Debye length λD = (ϵ0kBTb/n0e2)1 / 2 of the background electrons. This Debye length, which is the smallest scale over which collective plasma interactions are more important than Coulomb collisions, sets the cell size in the PIC simulation and it is proportional to the time step. A high temperature Tb speeds up the simulation and hence it allows us to resolve a larger spatial domain. The thermal noise levels in the plasma increase with the plasma temperature. These fluctuations set the initial amplitude of the unstable waves. The growth and saturation of the waves is thus accelerated by a high temperature, which decreases further the computational cost of the simulation. A temperature of 100 keV corresponds to a thermal spread of the electrons, which is only a minor fraction of the relative speed between the lepton cloud and the ambient plasma. Thermal effects on the beam instabilities are thus negligible and the actual value of the plasma temperature is not important. The rapid growth of the instability that we observe implies that it must develop close to the transition layer of the external shock of the jet, where the interstellar medium and the jet plasma are hot and closer to our initial values for the temperature.
The simulation box is resolved by 8000 × 1600 grid cells along x and y respectively. The cells have a uniform spacing Δx = 0.015 λe along both directions. The background electrons are represented by a total of 1.4 × 109 CPs and the electrons and positrons of the cloud by a total of 6.1 × 107 CPs, respectively. The cloud will travel along the x-direction, which is the vertical direction in all figures.
In what follows, we normalize the electric field as eE/ωpmec, the magnetic field as eB/ωpme, particle speeds as v/c, the macroscopic current (on the grid) as J/enoc and the densities as nb,e,p(x,y) /n0. Space and time are normalized as x/ λe, y/ λe and ωpt. The Maxwell-Lorentz set of equations can be normalized with these substitutions and our results can be scaled to any density that results in a weakly correlated plasma.
3. Simulation results
An unmagnetized relativistic leptonic beam of infinite extent, that interacts with a uniform background plasma, can be unstable to the two-stream mode, to the oblique mode and to the filamentation mode (see the review by Bret et al. 2010 and references therein). However, the two-stream and oblique mode instabilities are suppressed in our simulation by the tiny size of the lepton cloud. The resonance condition implies that the longitudinal component ku of the wave vector of two-stream and oblique modes, which is aligned with the mean velocity vector of the cloud vc ∥ x, is ωp/ku ≈ vc. This wave vector component corresponds with vc ≈ c to the wavelength λu = 2π λe in the simulation frame. This resonance condition states that a perturbation, which is moving at almost the speed of light in the simulation frame, has to interact resonantly with the background electrons that are at rest in this frame. The only resonance frequency of unmagnetized electrons is the plasma frequency. The value of λu exceeds the cloud’s thickness of 1.8 λe by a factor of 3. The resonant instabilities can, however, only grow if the cloud can accommodate an integer number of wave periods along the flow velocity vector and these instabilities are thus suppressed. The same limitation holds for laser-plasma experiments, where the longitudinal dimension of the beam is smaller than λe.
In contrast, the filamentation instability is a non-resonant instability and obeys other constraints than the resonant two-stream and oblique modes. The wave vector of the filamentation modes is oriented almost perpendicularly to vc. The wavelength of the filamentation modes can be much smaller than λu if the thermal speed of the leptons is small compared to the relative speed between the ambient plasma and the cloud plasma, which is the case considered here. The limited longitudinal extent of the cloud does not constrain the growth of the filamentation instability, because there is no condition on the wavelength along this direction. Our simulation is thus designed to test if and to what extent the filamentation instability can grow.
3.1. Time t = 27.5
The number density distributions of the background electrons and of the cloud’s electrons and positrons are shown in Fig. 1 at the simulation time 27.5. The fastest particles of the lepton cloud with the speed v ≲ c have propagated for a distance of ≈27 during this time. The lateral density distribution resembles a Maxwellian, which is a consequence of the finite evolution time and the Maxwellian momentum distribution. The relativistic mean speed of the lepton bullet along x implies that thermal diffusion is less pronounced along this direction.
 |
Fig. 1 Lepton density distribution at the time t = 27.5. Panel a): normalized density nb(x,y) + ne(x,y) of the background electrons and the cloud’s electrons. Panel b): normalized density nb(x,y) + np(x,y) of the background electrons and the cloud’s positrons. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
The spatial distributions ne(x,y) and np(x,y) of the cloud’s electrons and positrons are practically identical. The cloud should be almost charge- and current neutral and the electromagnetic fields weak. The number density distribution nb(x,y) of the background electrons appears to be unaffected.
The normalized number density difference nd(x,y) = np(x,y)−ne(x,y) yields a more accurate measure of the charge and current density distributions of the lepton cloud. Figure 2 reveals a modulation of nd(x,y) on a larger scale.
 |
Fig. 2 Net charge density of the cloud at the time t = 27.5. The net charge is calculated as np(x,y)−ne(x,y) (normalization to n0e) and the color scale is linear. |
The modulations are most pronounced at the back of the cloud at x ≈ 25.5. A minimum of nd(x,y) is observed at y ≈ 0, which is flanked by two maxima at y ± 0.7. The interaction of the electrons and positrons of the cloud with the background electrons is mediated by the micro-currents of the particles. The direction of the micro-current vectors of the cloud particles, measured in the reference frame of the background electrons, depends on the particle charge. The same holds for the direction of the force between background electrons and the electrons and positrons of the cloud. Consequently the latter are redistributed differently within the cloud by their interaction with the background electrons. The space charge associated with this modulation will result in an electric field. This electric field will be almost parallel to the y-axis; it will have a weak Ex-component, since the oscillations get weaker with increasing x. The space charge and the relativistic cloud speed will furthermore result in a magnetic Bz component in the laboratory frame.
Figure 3 confirms that a magnetowave is growing in the lepton cloud. The wave length of the oscillations at the rear side of the lepton cloud is comparable to an electron skin depth. The wave vector forms a right angle with the cloud velocity vector, which is typical for the waves that are driven by the filamentation instability (Bret et al. 2005).
 |
Fig. 3 Normalized magnetic amplitude Bz(x,y) at the time t = 27.5. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
Additional waves with a much shorter wave length are present within and outside of the cloud. These waves arise from a finite grid instability and they are thus a numerical artifact. Their frequency exceeds by far the plasma frequency, which allows them to leave the lepton cloud. A second consequence of their high frequency ω ≫ ωp is that their interaction with the plasma is weak. The loss of energy of the cloud to these waves is negligible in our simulation. This instability and some of its consequences are described elsewhere (Dieckmann et al. 2006; Godfrey & Vay 2013, 2014).
The in-plane electric field is displayed in Fig. 4.
 |
Fig. 4 Normalized in-plane electric field components at the time t = 27.5. Panel a): Ex(x,y) and panel b): Ey(x,y). The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
The Ex field remains at noise levels. The spatial distribution of the electric Ey-component shows the same oscillations with a short wave length, which we have already observed in Fig. 3. Strong electric field oscillations of Ey inside the lepton cloud and along the y-direction follow those of the Bz-component in Fig. 3.
The direct comparison of the distributions of Bz in Fig. 3 and Ey in Fig. 4b reveals the source of the electric field. The electric field distribution resembles the magnetic one, both qualitatively and quantitatively. Their amplitudes match and this implies with our normalization that Ey(x0,y0) /Bz(x0,y0) ≈ c at the positions (x0,y0) inside the region with the strong magnetic field. The magnetic structure is confined to the lepton cloud and its relativistic motion gives rise to a convective electric field in the reference frame of the simulation box.
Figure 4b shows electric field striations that are aligned with the x-axis and trail the lepton cloud. The modulus of the electric field amplitude of these striations is lower than that of the convective electric field in the cloud and the phases of both fields are shifted by π. These oscillations are tied to the return current in the background electrons, which is induced by the convective electric field in the cloud. This claim is supported by the following estimate:
The amplitude modulus | Bz | in Fig. 3 reaches a peak value of Bmax ≈ 4.5 × 10-4 and the thermal velocity of the background electrons with a temperature Tb = 1 keV is vth = 0.045. The thermal gyroradius of the background electrons would be ≈1000, which exceeds the maximum extent of the simulation box by an order of magnitude. The effect of the magnetic field on the background electrons is thus negligible. The background electrons are, however, exposed to the strong convective electric field during a time interval δt = δx/c, where δx ≈ λe is the distance along x where the convective electric field is strong. This time interval is thus 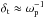 , which is long enough to enforce an electron reaction. Ions with their much larger inertia would see the convective electric field as a short impulse.
, which is long enough to enforce an electron reaction. Ions with their much larger inertia would see the convective electric field as a short impulse.
This bulk acceleration of the background electrons by the cloud’s convective electric field generates a current, which induces an electric field in the background plasma. The convective and the induced electric field have opposite polarities, since the induced electric field tries to diminish the electric field of the driver. Once the cloud’s convective electric field has left the perturbed plasma, the electrons will undergo high frequency oscillations at the plasma frequency ωp. High-frequency electrostatic oscillations in an unmagnetized plasma are known as Langmuir waves and they are only weakly damped; the oscillation will persist long after the cloud set it in motion. The electric field of the Langmuir oscillations will be polarized along the y-direction, since they were driven by the convective electric field with the same polarization direction.
The motion along x of the spatially localized electric field driver, which is confined to the cloud, together with the oscillation in time of the electric field that has been induced in the background plasma, imply that the latter should be phase-modulated along x. The induced electric field oscillates once during 2π/ωp and the cloud propagates for a distance 2πc/ωp during this time. The spatial period of the modulation along x should thus equal 2π λe. We use the term wakefield to describe the two-dimensional electric field distribution in the background plasma. We next verify that a wakefield is present in the simulation data.
The wave length of the oscillations along the x-direction, which are trailing the lepton cloud in Fig. 3b, is λL ≈ 2π λe or 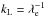 . These waves fullfill the resonance condition ωp/kL ≈ c thus we can identify them as Langmuir waves driven by the convective electric field of the cloud.
. These waves fullfill the resonance condition ωp/kL ≈ c thus we can identify them as Langmuir waves driven by the convective electric field of the cloud.
We can summarize our findings as follows: a magnetic field grows in the reference frame of the lepton cloud, however the plasma instability responsible for the wave growth is not the filamentation instability in its most basic form. The classic filamentation instability is driven by a magnetic deflection of two counter-streaming electron beams moving in opposite directions, which is only possible if both beams move relativistically in the rest frame of the magneto-wave and provide the strong spatially alternating current that is necessary to sustain the oscillatory magnetic field. The mean speed of the cloud’s electrons and positrons with respect to the magnetic field vanishes, because the latter does not propagate in the cloud frame. The current contribution of these two species is thus negligible, implying that they can not participate in a magnetic instability that is driven by strong currents.
The instability is instead triggered by an interaction of the magneto-wave, stationary in the reference frame of the cloud, and the background plasma. Let us consider the background plasma in the rest frame of the cloud. The fast motion of the background electrons and the ions, which form a positive and immobile charge density distribution in the reference frame of the background plasma, implies that their partial currents are strong in the reference frame of the cloud. Initially, they cancel out each other. A magnetic perturbation caused by the ever-present electromagnetic noise in PIC simulations, which is stationary in the cloud’s reference frame, deflects the relativistically moving background electrons. The deflected electrons do no longer move in unison with the positive charge background and a net current develops in the cloud frame. This net current re-inforces the magnetic perturbation, which leads to an instability. The magnetic deflection of the electrons in the cloud frame is equivalent to their electric deflection in the simulation frame, which is the source of the wakefield in Fig. 4b.
The spatial separation of the background electrons from the positive charge background also introduces a spatial charge in the cloud frame, which gives rise to a net electric field. The growing magnetic field yields via Ampère’s law a rotational electric field. Both electric field components add up to a net electric field in the cloud frame, which will separate its electrons and positrons. Figure 2 is evidence of the separation of both species.
3.2. Time t = 45
Figure 5 shows the number density distributions of the background electrons and the cloud’s leptons at the time t = 45.
 |
Fig. 5 Lepton density distribution at the time t = 45. Panel a): normalized density nb(x,y) + ne(x,y) of the background electrons and the cloud’s electrons. Panel b): normalized density nb(x,y) + np(x,y) of the background electrons and the cloud’s positrons. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
The fastest leptons of the cloud have reached the position x ≈ 44. The lateral width of the cloud has increased further due to the thermal motion of its electrons and positrons and the peak densities have been reduced to a value of about ≈0.6. The electron and positron distributions look similar.
The number density difference nd(x,y) shown in Fig. 6 demonstrates that the spatial separation between the cloud’s electrons and positrons has progressed, which implies that the instability is still growing.
 |
Fig. 6 Net charge density of the cloud at the time t = 45. The net charge is calculated as np(x,y)−ne(x,y) (normalization to n0e) and the color scale is linear. |
A pronounced minimum is observed at y ≈ 0 and x ≈ 42.7, which is surrounded by two maxima. The amplitude of the oscillations along the y-axis has more than doubled compared to those in Fig. 2, while the peak number density of the cloud has decreased. The amplitude of the oscillations exceeds by far that of the fluctuations.
 |
Fig. 7 Normalized magnetic amplitude Bz(x,y) at the time t = 45. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
The amplitude of the magneto-wave in Fig. 7 has increased by almost 50 percent compared to that in Fig. 3. Its wave length along the y-direction has increased due to the thermal dispersion of the lepton cloud. The instability appears to be robust against changes of the cloud distribution; the reason being the briefness of the interaction between the cloud and the background plasma. The steady stream of unperturbed background electrons into the lepton cloud implies that there are no memory effects in the plasma; the incoming electrons simply adapt to the existing magnetic field structure and amplify it with their current. This scenario is not the case for the filamentation instability in an unbounded plasma. The particles are heated up by the non-linear saturation of the latter, which results in a destruction of its magnetic field structures. One reason is that hot particles can no longer be confined magnetically to the current channels that sustain the magnetic field. The current channels and the magnetic fields they generate are dispersed by the thermal motion of particles. The magnetic field in Fig. 7 is strong only inside the lepton cloud. No magnetic field is present in the background electrons behind the cloud.
The larger magnetic field amplitude leads to a larger convective electric field. Figure 8 reveals that this field is now strong enough to induce visible wave oscillations in both in-plane electric field components.
 |
Fig. 8 Normalized in-plane electric field components at the time t = 45. Panel a): Ex(x,y) and panel b): Ey(x,y). The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
The wavelength of the oscillations of Ex and Ey are correlated, shifted by π/ 2 in both in-plane directions. The wavelength of the oscillations along the x-direction is 2π, while the wavelength along the y-direction matches that of the electric field distribution inside the cloud. The trailing waves have thus been driven resonantly by the convective electric field. No corresponding structures are visible in the magnetic field, which implies that the velocities of the background electrons are non-relativistic. The convective electric field is not strong enough to drive relativistic currents.
3.3. Time t = 110
Figure 9 shows the density distribution of the background electrons and the distributions of the cloud’s electrons and positrons.
 |
Fig. 9 Lepton density distribution at the time t = 110. Panel a): normalized density nb(x,y) + ne(x,y) of the background electrons and the cloud’s electrons. Panel b): normalized density nb(x,y) + np(x,y) of the background electrons and the cloud’s positrons. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
The front of the cloud has reached the position ≈108 and its longitudinal width has remained almost unchanged. The lateral width of the cloud is now about 12, which exceeds its initial value by a factor ≈6.5. The consequence of this spread is that the peak of the unmodulated cloud density at the front of the cloud has decreased by a factor four compared to its initial value. The density modulation at the rear end of the lepton cloud is now clearly visible. The density of the background electrons is also modulated and the oscillation amplitude is a few percent of nb.
The number density difference nd(x,y), displayed in Fig. 10, now has a minimum value at x ≈ 0.5 and y ≈ 106.75 that is comparable to the cloud’s number density at the front end.
 |
Fig. 10 Net charge density of the cloud at the time t = 110. The net charge is calculated as np(x,y)−ne(x,y) (normalization to n0e) and the color scale is linear. |
The instability has reached its peak. From now on the thermal dissipation of the cloud is likely to decrease the amplitude of the density oscillation, at least in absolute terms.
Figure 11 shows that the magnetic field resulting from the relativistically moving net charge of the cloud is substantial. The peak value in Fig. 11a is ≈0.06, which exceeds that at t = 27.5 by more than an order of magnitude.
 |
Fig. 11 Normalized magnetic amplitude Bz(x,y) at the time t = 110. Panel a): magnetic field distribution within the lepton cloud. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. Panel b): magnetic field distribution behind the cloud. The color scale is linear. |
A weak magnetic wakefield is revealed by Fig. 11. The in-plane currents, which drive the electric field, also yield a weak magnetic out-of-plane component. Its amplitude is, however, a factor of 60 weaker than the magnetic field within the lepton cloud.
Figure 12 reveals a strong electrostatic wakefield trailing the cloud.
 |
Fig. 12 Normalized in-plane electric field components at the time t = 110. Panel a): Ex(x,y) and panel b): Ey(x,y). The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
The peak amplitude value of these wakefield oscillations is about 0.03. The strength of this electrostatic wakefield becomes more evident when scaled to physical units. This electric field amplitude would be about 3 V/m in a plasma with an electron number density of 1 cm-3, which is typical for the interstellar medium. The energy density Ke = ϵ0E2/ 2 corresponding to an electric field amplitude of 3 V/m, equals 104 times the gas pressure Kp = ngkBTg of a gas with the density ng = 1 cm-3 and temperature Tg = 300 K. The latter is representative for the interstellar medium far upstream of the jet’s external shock. The peak value of the electric field would be 100 MV/m in a laboratory plasma with density 1015 cm-3. In spite of the observed large electric field amplitudes, the lepton cloud fails to magnetize the background plasma. A magnetic field is induced when the current ∝v/c becomes more important than space charge, with respect to the generation of electromagnetic fields. The energy density distribution of the background electrons can provide insight into how far the background electrons are from reaching the relativistic speeds that will make the current strong. The latter are necessary to make the plasma dynamics magnetically dominated. Figure 13 shows the electric Ey component and the kinetic energy density of the electrons over a wide spatial interval.
 |
Fig. 13 Panel a): normalized electric Ey component at the time t = 110 over a long x-interval. Panel b): normalized energy density of the background electrons at the time t = 110. The energy is expressed in units of their initial thermal energy density. The color scale is linear in both plots. |
The electric wakefield in Fig. 13a shows an amplitude that increases with x. Langmuir waves have a group velocity that is comparable to the electron’s thermal speed at best. The group velocity of Langmuir waves decreases with increasing wavelengths and we can thus neglect wave propagation effects. The wakefield oscillations remain localized and the electric field profile thus reflects the temporal growth of the convective electric field that is moving with the lepton cloud. The electric field becomes strong enough in the interval x> 65 to visibly enhance the kinetic energy density of the electrons. However, the enhancement is limited to about 1.4 times the initial value. The initial temperature of the background electrons has been Tb = 1 keV and the peak kinetic energy is thus far from being relativistic.
4. Discussion
We have examined here the interaction of a tiny cloud of electrons and positrons with a background plasma, via a particle-in-cell simulation. The density of the cloud’s electrons and positrons and their mean speeds were set to be equal, thus the cloud was free of any net charge and net current at the onset of the simulation. The lepton cloud moved relative to a background plasma at a speed corresponding to a Lorentz factor of 15. The background plasma consisted of mobile electrons and a positive immobile charge background, and the density of the background electrons matched the density of the cloud’s electrons in the simulation frame. All initial field components were set to zero.
In our simulations we have seen an instability forming inside the cloud, that in some ways is analogous to the filamentation instability frequently invoked to explain the magnetic fields generation in the jets of GRB’s (Medvedev & Loeb 1999; Brainerd 2000). The canonical filamentation instability is driven by counterstreaming lepton beams deflected into opposite directions by a magnetic perturbation. This deflection groups leptons sharing the same direction of micro-current vectors into channels; thus electrons flowing in the same direction are grouped together, as are electrons and positrons flowing in opposite directions. The net current of these flow channels amplifies the magnetic field. This classical form of the filamentation instability could not develop in our case study. The convection speed of the magnetic field and the mean speed of the electrons and positrons of the cloud all vanished in the reference frame of the cloud. The instability we observe has thus been solely driven by the interaction between the cloud magnetic field and the background electrons, which are relativistic in the cloud frame. This instability is thus similar to the case of the magnetic barrier considered by Smolsky & Usov (1996). It can also be interpreted as an extreme form of a filamentation instability between asymmetric lepton beams (Tzoufras et al. 2007).
The amplitude of the magnetic field inside the lepton cloud grew to a value equivalent to 100 μG in an interstellar medium with an electron number density of 1 cm-3 or to about 6000 G in a laboratory plasma with electron number density 1015 cm-3. The relativistic speed of the lepton cloud and the magnetic field it carried created a strong convective electric field in the reference frame of the background plasma. This field would be 108 V/m in a laboratory plasma of density 1015 cm-3 and 3 V/m in an interstellar medium with the density 1 cm-3. The energy density of this electric field would exceed the pressure of the interstellar medium by several orders of magnitude.
These electric fields were not strong enough to accelerate the background electrons to a speed that could induce significant magnetic fields in the background plasma, thus the magnetic field remained confined to the cloud. The electric field did however induce an electrostatic wakefield in the plasma. This wakefield constitutes an energy loss mechanism for relativistically moving pairs, able to slow down even the fastest pair flows, such as those emitted by AGNs. The simulation has shown that the magnetic fields remained high even though the thermal dispersion of the lepton cloud implied that its shape and number density underwent substantial changes. The lepton cloud can thus lose energy to the wakefield over a long time, which leads to a substantial cumulative energy loss.
In this sense, the type of instability we observed in our simulation could in principle also become important for the generation of radiation by the jets of, e.g., GRBs, AGN, and XRBs. For instance, it has been suggested that some of the electromagnetic radiation of relativistic jets is generated by the synchrotron jitter mechanism (Medvedev 2000; Keenan & Medvedev 2013), where energetic leptons interact with a small-scale magnetic field. The plasma close to collision-less shocks is non-thermal, which in a collision-less plasma can lead to phase space density distributions that are not uniform in space and that can have energetic beams. An accumulation of leptons that is spatially localized and confined to a small velocity interval could be interpreted as a spatially localized beam or a micro-cloud. In real systems, we expect non-thermal plasma throughout the jets where shocks are present. Compact lepton clouds escaping from the shocks could move independently and at moderately relativistic relative speeds through upstream plasma. Head-on collisions between the upstream particles and a relativistically moving cloud that are mediated by the collective magnetic field may generate more energetic electromagnetic radiation than if these particles were to interact with a magnetic field that is stationary in the jet frame.
Yet another important consequence of the filamentation-type instability we have observed here is that even microscopic lepton clouds, which are charge- and current neutralized, undergo collective interactions with the surrounding plasma. If this instability did not develop, then the absence of binary collisions between plasma particles would imply that these clouds could leave the vicinity of the relativistic shock. The clouds would carry away energy and constitute an energy loss mechanism. If this instability occurs in real jets, it would ensure that these clouds cannot travel far and hence they would deposit their mean flow energy into electromagnetic fields and collisionless heating of the foreshock plasma. The shock transition layer remains in this case spatially localized and its width does not increase steadily in time. The magnetic instability would contribute to a rapid plasma thermalization, which would make the shock behave like a fluid shock even if binary collisions between particles are negligible.
Our numerical results also serve as a motivation for further laboratory experiments. The cloud size, the growth time of the instability and the peak electric field are such that the instability could be observed in a laboratory experiment. These realizable scales thus allow us to study plasma processes potentially giving rise to some of the most violent outbreaks of electromagnetic radiation in a controlled laboratory experiment. Until now these could ony be approached theoretically and by means of numerical simulations.
Acknowledgments
M.E.D. wants to thank Vetenskapsrdet for financial support through the grant 2010-4063. G.S. and M.B. wish to thank the EPSRC for supporting this work through the grants EP/L013975/1 and EP/I029206/I. The Swedish High Performance Computing Center North (HPC2N) has provided the computer time and support. SM is grateful to the University of Texas in Austin for its support, through a Beatrice Tinsley Centennial Visiting Professorship.
References
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Brainerd, J. J. 2000, ApJ, 538, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Bret, A., Firpo, M. C., & Deutsch, C. 2005, Phys. Rev. Lett., 94, 115002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bret, A., Firpo, M. C., & Deutsch, C. 2006, Laser Part. Beams, 24, 27 [Google Scholar]
- Bret, A., Gremillet, L., & Dieckmann, M. E. 2010, Phys. Plasmas, 17, 120501 [NASA ADS] [CrossRef] [Google Scholar]
- Bret, A., Stockem, A., Fiuza, F., et al. 2013, Phys. Plasmas, 20, 042102 [NASA ADS] [CrossRef] [Google Scholar]
- Cenko, S. B., Frail, D. A., Harrison, F. A., et al. 2010, ApJ, 711, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, P., Spitkovsky, A., & Arons, J. 2008, ApJ, 674, 378 [Google Scholar]
- Chen, H., Wilks, S. C., Meyerhofer, D. D., et al. 2010, Phys. Rev. Lett., 105, 015003 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Corbel, S., Fender, R. P., Tzioumis, A. K., et al. 2002, Science, 298, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, J. M. 1983, Rev. Mod. Phys., 55, 403 [Google Scholar]
- Dieckmann, M. E., Frederiksen, J. T., Bret, A., & Shukla, P. K. 2006, Phys. Plasmas, 13, 112110 [NASA ADS] [CrossRef] [Google Scholar]
- Dieckmann, M. E., Kourakis, I., Borghesi, M., & Rowlands, G. 2009a, Phys. Plasmas, 16, 074502 [NASA ADS] [CrossRef] [Google Scholar]
- Dieckmann, M. E., Shukla, P. K., & Stenflo, L. 2009b, Plasma Phys. Controll. Fusion, 51, 065015 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Fish, V. L., Schenck, D. E., et al. 2012, Science, 338, 355 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dupree, T. H. 1963, Phys. Fluids, 6, 1714 [NASA ADS] [CrossRef] [Google Scholar]
- Esin, A. A., McClintock, J. E., & Narayan, R. 1997, 489, 865 [Google Scholar]
- Fender, R. 2001, MNRAS, 322, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Godfrey, B. B., & Vay, J. L. 2013, J. Comp. Phys., 248, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Godfrey, B. B., & Vay, J.-L. 2014, J. Comp. Phys., 267, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hada, K., Doi, A., Kino, M., et al. 2011, Nature, 477, 185 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Haruki, T., & Sakai, J. I. 2003, Phys. Plasmas, 10, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Honda, M., Meyer-ter Vehn, J., & Pukhov, A. 2000, Phys. Plasmas, 7, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Jaroschek, C. H., Lesch, H., & Treumann, R. A. 2004, ApJ, 616, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Kazimura, Y., Sakai, J. I., Neubert, T., & Bulanov, S. V. 1998, ApJ, 498, L183 [Google Scholar]
- Keenan, B. D., & Medvedev, M. V. 2013, Phys. Rev. E, 88, 013103 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, L., Ogle, P. M., Evans, D., et al. 2015, ApJ, 801, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2013, AJ, 146, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Lovelace, R. V. E. 1976, Nature, 262, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, S. F., Fonseca, R. A., Silva, L. O., & Mori, W. B. 2009, ApJ, 695, L189 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, M. V. 2000, ApJ, 540, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, M. V., & Loeb, A. 1999, ApJ, 526, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, M. V., Fiore, M., Fonseca, R. A., Silva, L. O., & Mori, W. B. 2005, ApJ, 618, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., & Fabian, A. C. 2002, MNRAS, 332, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Milosavljevic, M., & Nakar, E. 2006, ApJ, 641, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F., Rodríguez, L. F., Cordier, B., Paul, J., & Lebrun, F. 1992, Nature, 358, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Ridgers, C. P., Brady, C. S., Duclous, R., et al. 2012, Phys. Rev. Lett., 108, 165006 [Google Scholar]
- Ridgers, C. P., Brady, C. S., Ducious, R., et al. 2013, Phys. Plasmas, 20, 056701 [NASA ADS] [CrossRef] [Google Scholar]
- Sakai, J., Nakayama, T., Kazimura, Y., & Bulanov, S. 2000, J. Phys. Soc. Jpn., 69, 2503 [NASA ADS] [CrossRef] [Google Scholar]
- Sarri, G., Macchi, A., Cecchetti, C. A., et al. 2012, Phys. Rev. Lett., 109, 205002 [NASA ADS] [CrossRef] [Google Scholar]
- Sarri, G., Schumaker, W., Di Piazza, A., et al. 2013a, Plasma Phys. Controll. Fusion, 55, 40th Conference of the European-Physical-Society on Plasma Physics, VTT Tech Res Ctr Finland, Espoo, FINLAND, JUL 01−05 [Google Scholar]
- Sarri, G., Schumaker, W., Di Piazza, A., et al. 2013b, Phys. Rev. Lett., 110, 255002 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Silva, L. O., Fonseca, R. A., Tonge, J. W., et al. 2003, ApJ, 596, L121 [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2011, ApJ, 741, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Sironi, L., Spitkovsky, A., & Arons, J. 2013, ApJ, 771, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Smolsky, M. V., & Usov, V. V. 1996, ApJ, 461, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Titarchuk, L. G. 1980, A&A, 86, 121 [NASA ADS] [Google Scholar]
- Tautz, R. C., & Lerche, I. 2012, Phys. Rep., 520, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Tzoufras, M., Ren, C., Tsung, F. S., Tonge, J. W., & Mori, W. B. 2007, Phys. Plasmas, 14, 062108 [NASA ADS] [CrossRef] [Google Scholar]
- Vieira, J., Fang, Y., Mori, W. B., Silva, L. O., & Muggli, P. 2012, Phys. Plasmas, 19, 063105 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Lepton density distribution at the time t = 27.5. Panel a): normalized density nb(x,y) + ne(x,y) of the background electrons and the cloud’s electrons. Panel b): normalized density nb(x,y) + np(x,y) of the background electrons and the cloud’s positrons. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
| In the text | |
 |
Fig. 2 Net charge density of the cloud at the time t = 27.5. The net charge is calculated as np(x,y)−ne(x,y) (normalization to n0e) and the color scale is linear. |
| In the text | |
 |
Fig. 3 Normalized magnetic amplitude Bz(x,y) at the time t = 27.5. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
| In the text | |
 |
Fig. 4 Normalized in-plane electric field components at the time t = 27.5. Panel a): Ex(x,y) and panel b): Ey(x,y). The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
| In the text | |
 |
Fig. 5 Lepton density distribution at the time t = 45. Panel a): normalized density nb(x,y) + ne(x,y) of the background electrons and the cloud’s electrons. Panel b): normalized density nb(x,y) + np(x,y) of the background electrons and the cloud’s positrons. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
| In the text | |
 |
Fig. 6 Net charge density of the cloud at the time t = 45. The net charge is calculated as np(x,y)−ne(x,y) (normalization to n0e) and the color scale is linear. |
| In the text | |
 |
Fig. 7 Normalized magnetic amplitude Bz(x,y) at the time t = 45. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
| In the text | |
 |
Fig. 8 Normalized in-plane electric field components at the time t = 45. Panel a): Ex(x,y) and panel b): Ey(x,y). The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
| In the text | |
 |
Fig. 9 Lepton density distribution at the time t = 110. Panel a): normalized density nb(x,y) + ne(x,y) of the background electrons and the cloud’s electrons. Panel b): normalized density nb(x,y) + np(x,y) of the background electrons and the cloud’s positrons. The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
| In the text | |
 |
Fig. 10 Net charge density of the cloud at the time t = 110. The net charge is calculated as np(x,y)−ne(x,y) (normalization to n0e) and the color scale is linear. |
| In the text | |
 |
Fig. 11 Normalized magnetic amplitude Bz(x,y) at the time t = 110. Panel a): magnetic field distribution within the lepton cloud. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. Panel b): magnetic field distribution behind the cloud. The color scale is linear. |
| In the text | |
 |
Fig. 12 Normalized in-plane electric field components at the time t = 110. Panel a): Ex(x,y) and panel b): Ey(x,y). The color scale is linear. The black curve outlines the contour where the lepton cloud’s number density is 0.06 n0. |
| In the text | |
 |
Fig. 13 Panel a): normalized electric Ey component at the time t = 110 over a long x-interval. Panel b): normalized energy density of the background electrons at the time t = 110. The energy is expressed in units of their initial thermal energy density. The color scale is linear in both plots. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


