Periodicity in some light curves of the solar analogue V352 Canis Majoris

P. Kajatkari; L. Jetsu; E. Cole; T. Hackman; G. W. Henry; S.-L. Joutsiniemi; J. Lehtinen; V. Mäkelä; S. Porceddu; K. Ryynänen; V. Solea

doi:10.1051/0004-6361/201322847

Home

All issues

Volume 577 (May 2015)

A&A, 577 (2015) A84

Full HTML

Free Access

Issue		A&A Volume 577, May 2015


Article Number		A84
Number of page(s)		5
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/201322847
Published online		07 May 2015

A&A 577, A84 (2015)

Research Note

Periodicity in some light curves of the solar analogue V352 Canis Majoris^⋆

P. Kajatkari¹, L. Jetsu¹, E. Cole¹, T. Hackman¹^,2, G. W. Henry³, S.-L. Joutsiniemi¹, J. Lehtinen¹^,4, V. Mäkelä¹, S. Porceddu¹, K. Ryynänen¹ and V. Solea¹

¹ Department of Physics, Gustaf Hällströmin katu 2a (PO Box 64), University of Helsinki, 00014 Helsinki, Finland
e-mail: lauri.jetsu@helsinki.fi
² Finnish Centre for Astronomy with ESO, University of Turku, Väisäläntie 20, 21500 Piikkiö, Finland
³ Center of Excellence in Information Systems, Tennessee State University, 3500 John A. Merritt Blvd., Box 9501, Nashville, TN 37209, USA
⁴ Nordic Optical Telescope, 38700 Santa Cruz de la Palma, Spain

Received: 14 October 2013
Accepted: 24 March 2015

Abstract

Aims. We applied the Continuous Period Search (CPS) method to 14 yr of V-band photometry of the active G6.5 solar analog V352 CMa. Our aim was to show that CPS can successfully model the presence or absence of periodicity in low-amplitude light curves.

Methods. CPS computes values for the mean brightness, photometric period, amplitude and minimum of selected datasets. We also applied the Power Spectrum Method (PSM) to these datasets and compared the performance of this frequently applied method to that of CPS.

Results. We found an apparent 11.7 ± 0.5 yr cycle in the mean brightness. The mean of the individual photometric rotation periods is 7.24 ± 0.22 days. The lower limit for the differential rotation coefficient is |k| > 0.12, assuming that period changes in V352 CMa follow the solar pattern. The Kuiper method detected stable, active longitudes rotating with a period of 7.157 ± 0.002 days, from the epochs of light minimum, but these structures vanished after the year 2009. CPS performed better than the traditional PSM, because the latter assumes a sinusoidal model for the data even when this was not correct.

Key words: methods: data analysis / stars: activity / starspots / stars: individual: V352 CMa

^⋆

The analysed photometry and numerical results of the analysis are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/577/A84

© ESO, 2015

1. Introduction

V352 CMa (HD 43162) was among the first 384 bright, extreme-ultraviolet sources detected by the ROSAT satellite (Shara et al. 1993). Its metallicity and space motion indicate that it belongs to the young disk population (Eggen 1995). It was included in a list of 38 nearby, young, single solar analogs having ages between 0.2 and 0.8 Gyr (Gaidos 1998). We collected values for some of its physical parameters from the literature and list them in Table 1. Strong Ca H&K emission (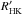 $R_{HK}^{'}$ $\hbox{$R'_{\mathrm{HK}}$}$ ), high X-ray luminosity (R_X), and rapid rotation (vsini) all indicate that HD 43162 is a young star. Its high lithium abundance also supports a young age (Gaidos 1998; Santos et al. 2004a). However, the metallicity ([Fe/H]) estimates are inconsistent with HD 43162’s youth (Table 1). Except for Gaidos et al. (2000) and Gaidos & Gonzalez (2002), the effective surface temperature (T_eff) and gravity (log g) estimates agree and support the spectral type G6.5 V (Gray et al. 2006).

V352 CMa was classified as a member of a stellar kinematical group (hereafter SKG) of 19 stars by Jeffries & Jewell (1993). It was later identified as a member of the kinematic group IC 2391, a more recently identified SKG containing 29 stars. The estimated age of IC 2391 is 45 Myr (Nakajima et al. 2010; Maldonado et al. 2010; Nakajima & Morino 2012). However, only two stars in IC 2391 are among the 19 members of the original SKG defined by Jeffries & Jewell (1993): V352 CMa and LQ Hya. This demonstrates how difficult it is to confirm the membership in any particular SKG.

Table 1

Physical parameters of V352 CMa.

Christian et al. (2003) observed an extreme ultraviolet flare in an M3.5 V star (EUVE J0613–23.9B) located just 2.́5 away from V352 CMa (EUVE J0613–23.9). This M3.5 V star was identified as a binary companion of V352 CMa (Raghavan et al. 2010). About 90% of the ROSAT source positions are accurate to 1′ or better, while 100% are within 2.́1 of their catalogued positions (Shara et al. 1993). The distance between V352 CMa and its M3.5 companion is 2.́5, close to the ROSAT 2′1 limit. This companion was excluded from our photometric measurements of V352 CMa by the 55′′ focal-plane diaphragm of the photometer. The orbital plane of the companion must be nearly perpendicular to the line of sight because v_rad appears to be constant (Table 1). If the rotation axis of V352 CMa is perpendicular to this orbital plane, the light curve amplitudes would be supressed by our high-inclination viewing angle. V352 CMa is one of 11 stars with debris disks detected with the Spitzer Space Telescope (Kóspál et al. 2009). However, it is the only star in this sample without a known planet.

Cutispoto et al. (1999) determined the photometric rotation period of V352 CMa, 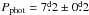$P_{phot} = 7 \overset{d}{.} 2 \pm 0 \overset{d}{.} 2$ $\hbox{$P_{\mathrm{phot}}=7\fd2 \pm 0\fd2$}$ , from a light curve with a low 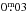$0 \overset{m}{.} 03$ $\hbox{${0\fm03}$}$ peak-to-peak amplitude. Gaidos et al. (2000) found no periodicity in their photometry, which were the same data as our Season 1 of this paper. Hipparcos photometry also failed to detect any periodicity (Koen & Eyer 2002, n = 228 observations). Wright et al. (2004) derived P_phot ≈ 8^d from observed B − V and $R_{HK}^{'}$ $\hbox{$R'_{\rm HK}$}$ values. In this paper, we analyse long-term photometry of V352 CMa with Continuous Period Search (CPS) method (Lehtinen et al. 2011). The previous studies have indicated that periodicity may be present or absent in any particular observing season. We show that CPS is an ideal method for analysing this type of challenging data. We also compare CPS to Power Spectrum Method (PSM) formulated by Horne & Baliunas (1986).

2. Observations

The photometry of our target star S = V352 CMa was obtained with the T3 0.4 m automated photoelectric telescope (APT) at Fairborn Observatory in Arizona. The observations were made during 14 observing seasons between December 23rd, 1998 (HJD = 2 451 170.8) and March 17th, 2012 (HJD = 2 456 003.6). 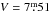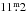The comparison star was C=HD 43879 (F5V, $V = 7 \overset{m}{.} 51$ $\hbox{${V=7\fm51}$}$ ), which is a visual double with $V = 7 \overset{m}{.} 3$ $\hbox{${V=7\fm3}$}$ and $11 \overset{m}{.} 2$ $\hbox{${11\fm2}$}$ components. The angular separation of the two components is 6.̋7, so both fall easily within in the 55′′ focal-plane diaphragm of the photometer. The check star was K=HD 43429 (K1 III, $V = 5 \overset{m}{.} 99$ $\hbox{${V=5\fm99}$}$ ). The standard Johnson differential magnitudes, ΔV_{S − C}, are plotted in Fig. 1a. The mean (m) and the standard deviation (s) of these n = 1257 observations are $m \pm s = - 1 \overset{m}{.} 0929 \pm 0 \overset{m}{.} 0096$ $\hbox{${m \pm s = -1\fm0929 \pm 0\fm0096}$}$ . The lower panel displays the ΔV_{K − C} differential magnitudes. The standard deviation of these ΔV_{K − C} observations (n = 1025) is $0 \overset{m}{.} 0079$ $\hbox{${0\fm0079}$}$ , which we take as an estimate of the precision of a single observation. We used this estimate to test the constant brightness hypothesis for ΔV_{S − C}. The result, χ² = 1854, for these ΔV_{S − C} observations (n = 1257) indicates that the variability implied by the V352 CMa observations is real. There are also clear trends in the n = 14 seasonal ΔV_{S − C} means having $s = 0 \overset{m}{.} 0036$ $\hbox{${s=0\fm0036}$}$ (Fig. 1a: filled circles). 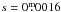The respective seasonal ΔV_{K − C} means are more stable with $s = 0 \overset{m}{.} 0016$ $\hbox{${s=0\fm0016}$}$ (Fig. 1b: filled circles). More detailed information of the operation of the T3 0.4 m APT and the data reduction procedures can be found, e.g., in Henry (1999) and Fekel & Henry (2005).

Fig. 1

Differential photometry of V352 CMa. a) All ΔV_{S − C} data (crosses), their mean level (continuous line) and the seasonal ΔV_{S − C} means (filled circles) connected with dashed lines. b) All ΔV_{K − C} data. The magnitude scale and the notations are as in a).

Fig. 2

Light curves of all independent datasets (IND(τ) = 1). All notations are explained in the 3rd paragraph of Sect. 4.1

3. CPS method

CPS was formulated by Lehtinen et al. (2011), where it is described in detail. Here, we only briefly describe CPS, because we have already applied it to the photometry of several stars (Hackman et al. 2011, 2013; Lehtinen et al. 2012; Kajatkari et al. 2014). CPS divides the data into segments (SEG) and datasets (SET). The maximum length for a dataset is ΔT_max = 30^d. Each dataset has to contain at least n ≥ n_min = 12 observations y_i = ΔV_{S − C}(t_i). This division gives 14 segments (i.e., observing seasons). Our notation for the mean of the n observing times t_i of a dataset is τ.

CPS model is a Kth order Fourier series $\begin{matrix} ŷ (t_{i}) = ŷ (t_{i}, β̅) = M + \sum_{k = 1}^{K} [B_{k} \cos (k 2 πf t_{i}) + C_{k} \sin (k 2 πf t_{i})] . \end{matrix}$ $\begin{eqnarray} \hat{y}(t_i) = \hat{y}(t_i,\bar{\beta}) = M + \sum_{k=1}^K{\left[B_k\cos{(k2\pi ft_i)} + C_k\sin{(k2\pi ft_i)}\right]}. \nonumber \label{model} \end{eqnarray}$ Of the free parameters $\hbox{$\bar{\beta}=[M,B_1,...,B_K,C_1,...,C_K,f]$}$ , the physically meaningful ones are the mean, M(τ) and the period, P(τ) = f^-1(τ). The other free parameters B₁,...,B_K,C₁,...,C_K give the total amplitude of the model, A(τ), as well as the epochs of the primary and secondary minima in time, t_min,1(τ) and t_min,2(τ).

CPS uses a Bayesian information criterion to choose the best modelling order K for each dataset (Lehtinen et al. 2011, Eq. (6)). We tested orders 0 ≤ K ≤ 2.

CPS results correlate for temporally overlapping subsets because they contain common data. To eliminate such correlation, we selected a sequence of independent datasets with no common data. The notations IND(τ) = 1 and 0 are used for independent and not independent (i.e. overlapping) datasets, respectively.

The error estimates for M(τ), A(τ), P(τ), t_min,1(τ) and t_min,2(τ) were determined with the bootstrap method. This bootstrap was also used to identify the reliable and unreliable light curve parameters. Our notations are R(τ) = 0 for reliable estimates and R(τ) = 1 for unreliable estimates.

For reliable datasets, CPS also gives the time scale of change of the light curve, T_C(τ), i.e., the time that the light curve model is valid for the subsequent datasets.

4. Results

The CPS results are published electronically at the CDS. We use the same format specified by Lehtinen et al. (2011, Appendix A).

4.1. General results

The total number of modelled datasets is 485. Of these, no periodicity was detected in 178 datasets (K = 0), where the best model was constant brightness ŷ(t_i) = M(τ). Periodicity was detected in 307 datasets. The best orders were K = 1 for 170 datasets and K = 2 for 137 datasets.

The light curves of all independent datasets are shown in Fig. 2. The continuous lines display the periodic curves (K ≥ 1). The phases were first computed from φ₁ = FRAC [(t − t_min,1(τ)) /P(τ)], where FRAC [x] removes the integer part of its argument x. Then the phases φ_al,1 of the t_min,1(τ) epochs were computed from the constant period ephemeris HJD 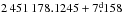$2 451 178.1245 + 7 \overset{d}{.} 158$ $\hbox{$2\,451\,178.1245+7\fd158$}$ E (see Sect. 4.4). Finally, the data and the light curves were plotted as a function of φ = φ₁ + φ_al,1. The dashed lines display the aperiodic curves (K = 0), where the “phases” are φ_i = (t_i − t₁)/(t_n − t₁). The SEG, SET, τ and R(τ) values are also given in each panel.

The results for M(τ), A(τ), P(τ), t_min,1(τ) and t_min,2(τ) are summarised below.

	IND(τ) = 1	IND(τ) = 1	IND(τ) = 0	IND(τ) = 0
	R(τ) = 0	R(τ) = 1	R(τ) = 0	R(τ) = 1

M(τ)	n = 39 [■]	n = 14 [Λ]	n = 331 [×]	n = 101 [×]
A(τ)	n = 20 [■]	n = 14 [Λ]	n = 172 [×]	n = 101 [×]
P(τ)	n = 20 [■]	n = 14 [Λ]	n = 172 [×]	n = 101 [×]
t_min,1(τ)	n = 20 [■]	n = 14 [Λ]	n = 172 [×]	n = 101 [×]
t_min,2(τ)	n = 5 [▴]	n = 8 [△]	n = 65 [×]	n = 47 [×]

The symbols given in parenthesis are used in Figs. 3a–d, where error bars are displayed only for IND(τ) = 1 datasets.

The light curve shape of V352 CMa evolved significantly only within 37 datasets, where the T_C mean was 51 days. This mean exceeded 65 days in the other 333 datasets, where the light curve did not change within the segment. These values, T_C = 51 and 65 days, indicate that the chosen length of the datasets, ΔT_max = 30^d, should give reliable CPS results.

4.2. Activity cycles

Fig. 3

a) Mean M(τ), b) amplitude A(τ), c) period P(τ) and d) phases of the primary t_min,1(τ) and secondary t_min,2(τ) minima. The symbols are explained in the 3rd paragraph of Sect. 4.1. The horizontal lines in c) represent the P_w ± 3ΔP_w levels. The phases in d) were calculated from HJD $2 451 178.1245 + 7 \overset{d}{.} 158$ $\hbox{$2\,451\,178.1245+7\fd158$}$ E.

The long-term M(τ) and A(τ) changes of V352 CMa are shown in Fig. 3, panels a) and b).

PSM has been applied to search for activity cycles in chromospheric Ca II H&K emission line data (e.g., Baliunas et al. 1995). Rodonò et al. (2000) applied this method to the following light curve parameters: M(τ) (axisymmetric part of spot distribution), A(τ) (non-axisymmetric part of spot distribution), M(τ) − A(τ)/2 (minimum spotted area) or M(τ) + A(τ)/2 (maximum spotted area). We applied PSM to the same independent and reliable estimates of V352 CMa. The false alarm probability of the best cycle, P_C = 11.7 ± 0.5 yr for the n = 39 values of M(τ), is F = 0.01. This cycle probability is 1 − F = 0.99. The cycles for the n = 20 values of A(τ), M(τ) − A(τ)/2 and M(τ) + A(τ)/2 reached only F ≥ 0.26.

4.3. Differential rotation

The weighted mean of the independent and reliable P(τ)(n = 20) estimates is 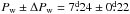$P_{w} \pm Δ P_{w} = 7 \overset{d}{.} 24 \pm 0 \overset{d}{.} 22$ $\hbox{$P_{\mathrm{w}} \pm \Delta P_{\mathrm{w}} = 7\fd24 \pm 0\fd22$}$ . This range of period changes, P_w ± 3ΔP_w, (Fig. 3c: dotted lines) gave Z = 6ΔP_w/P_w = 0.19 ≡ 19% (Lehtinen et al. 2011, Eq. (14)). The average of the light curve half amplitude A(τ)/2 in these datasets was only $0 \overset{m}{.} 011$ $\hbox{${0\fm011}$}$ . The precision of the photometry, $σ_{N} = 0 \overset{m}{.} 07$ $\hbox{$\sigma_{\mathrm{N}}=0\fm07$}$ , gives an amplitude to noise ratio of A/N ≲ 2. 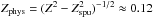Even if the spurious period changes were Z_spu ≥ 0.15, the estimated real physical changes could be $Z_{phys} = (Z^{2} - Z_{spu}^{2})^{- 1 / 2} \approx 0.12$ $\hbox{$Z_{\mathrm{phys}}=(Z^2 - Z_{\mathrm{spu}}^2)^{-1/2} \approx 0.12$}$ (Lehtinen et al. 2011, Table 3 and Eq. (15)). Here, we assume that the solar law of surface differential rotation can be applied to V352 CMa and that the period P(τ) changes can be used as reliable tracer surface differential rotation. We used k ≈ Z_phys/h, where the minimum and maximum latitudes of spot activity were b_min and b_max, and h = sin²b_max − sin²b_min (Jetsu et al. 2000). The maximum value, h = 1, would be reached if spots formed at all latitudes between the equator and pole of V352 CMa. All other alternatives give h< 1 ⇒ | k | >Z_phys ≈ 0.12. This result is comparable to the solar value k = 0.20, where sunspots typically form at latitudes −30° ≤ b ≤ 30° (i.e., h = 0.25).

4.4. Active longitudes

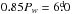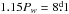We applied the non-weighted Kuiper test (Jetsu & Pelt 1996) to the reliable primary minima t_min,1(τ) of 20 independent datasets. The test range was between $0.85 P_{w} = 6 \overset{d}{.} 0$ $\hbox{$0.85 P_w = 6\fd0$}$ and $1.15 P_{w} = 8 \overset{d}{.} 1$ $\hbox{$1.15 P_w = 8\fd1$}$ . The critical level for the best period $P_{al, 1} = 7 \overset{d}{.} 158 \pm 0 \overset{d}{.} 002$ $\hbox{$P_{\mathrm{al,1}}=7\fd158 \pm 0\fd002$}$ was Q = 0.004. The test for the reliable t_min,1(τ) and t_min,2(τ)(n = 25) of all independent datasets gave the same result, $P_{al, 1, 2} = 7 \overset{d}{.} 158 \pm 0 \overset{d}{.} 002$ $\hbox{$P_{\mathrm{al,1,2}}=7\fd158 \pm 0\fd002$}$ , but the critical level for this period had lower significance, Q = 0.056. The phases of all primary and secondary minima are shown in Fig. 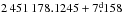3d, computed from the ephemeris HJD $2 451 178.1245 + 7 \overset{d}{.} 158$ $\hbox{$2\,451\,178.1245+7\fd158$}$ E. The phases of t_min,1 were very stable between 1998 and 2009 (Fig. 3d: filled squares). However, this long–lived structure vanished after 2009 when the light curve amplitudes A(τ) decreased.

4.5. Comparison of CPS and PSM

We also applied PSM to all datasets analysed with CPS. Our aim was to check how often these two methods detected the same periodicity. We use the abbreviation “C₀” for the case $\begin{matrix} P_{CPS} - σ_{P_{CPS}} \leq P_{PSM} \leq P_{CPS} + σ_{P_{CPS}}, \end{matrix}$ $\begin{eqnarray*} P_{\mathrm{CPS}} - \sigma_{P_{\mathrm{CPS}}} \le P_{\mathrm{PSM}} \le P_{\mathrm{CPS}} + \sigma_{P_{\mathrm{CPS}}}, \end{eqnarray*}$ where P_CPS ± σ_{P_CPS} and P_PSM were the periods detected with CPS and PSM, respectively. For six different criteria, we checked the number of cases where C₀ was true

Criterion	K = 1 or 2 [%]	K = 1 [%]	K = 2 [%]

A(τ) > 0	173/307 ≡ 56	141/170 ≡ 83	32/137 ≡ 23
A(τ) > 0.015	129/240 ≡ 54	97/112 ≡ 87	32/128 ≡ 25
A(τ) > 0.030	15/40 ≡ 38	3/3 ≡ 100	12/37 ≡ 32

F< 0.5	152/258 ≡ 59	126/149 ≡ 85	26/109 ≡ 24
F< 0.1	52/86 ≡ 60	41/42 ≡ 98	11/44 ≡ 25
F< 0.05	25/36 ≡ 69	18/18 ≡ 100	7/18 ≡ 39

Case C₀ was true only in 56% cases for all periodicity detections (n = 307:K = 1 or 2, A(τ) > 0.00). This occurred more often for K = 1 (83%) than for K = 2 (23%) models. These fractions increased for larger amplitudes, A(τ) > 0.015. For the highest amplitudes, A(τ) > 0.030, case C₀ was true for all K = 1 models (100%) but not for all K = 2 models (32%).

As expected, the probability for case C₀ being true also increased when the false alarm probability F decreased. For F< 0.05, case C₀ was true for all K = 1 models (100%), but again not for all K = 2 models (39%).

In conclusion, PSM did not always detect the correct period for the K = 2 light curves. This was true also for high amplitudes A(τ) and for small false-alarm probabilities F.

4.6. Periodicities of V352 CMa

We discovered the following periodicities

P_w = 7.24 ± 0.22 days = Mean of rotation period
P_al,1 = 7.158 ± 0.002 days = Period of active longitudes
P_C = 11.7 ± 0.5 yr = Activity cycle in M(τ)

in the long–term photometry of V352 CMa. The scatter of the published age estimates is large (Table 1: between 33 and 6500 Myr). Combining P_w = 7.24 days to the colour index B − V = 0.705 (Gaidos 1998; Cutispoto et al. 1999) gives a gyrochronological age of 295 ± 36 Myr for V352 CMa (Barnes 2007, Eqs. (3) and (16)). Gyrochronology can provide theoretical age estimates (e.g. Barnes 2010; Barnes & Kim 2010), while the CoRot (do Nascimento et al. 2013) and the Kepler (do Nascimento et al. 2014) space missions provide the required accurate rotation measurements for solar analogs or “solar twins”.

5. Conclusions

We wanted to test the performance of CPS by applying it to low-amplitude light curves of V352 CMa. This was challenging because the dispersions of the ΔV_{V − C} and ΔV_{K − C} magnitudes were comparable (Figs. 1a, b). From a total of 485 datasets, CPS failed to detect any periodicity in 178 ≡ 37% of the datasets.

Comparison of CPS and PSM revealed that both methods gave the same best periods for high amplitude to noise ratio light curves, but only if the correct model for the data was a sinusoid (K = 1). The periods detected were usually different for the K = 2 models – even for the higher A/N light curves. We conclude that incorrect periods P(τ) or model orders K often lead to incorrect values for M(τ), A(τ), t_min,1 and t_min,2.

We detected signs of an activity cycle, P_C = 11.7 ± 0.5 yr(F = 0.010), in the mean magnitudes M(τ) (n = 39). However, this cycle is only 1.3 yr shorter than the time span of the data, ΔT = 13.0 yr.

The P(τ) period changes could be mostly spurious (Z_spu > 0.15) due to low A/N ratio (Lehtinen et al. 2011, Table 3). If the law of solar differential rotation were valid in V352 CMa, and these P(τ) changes traced this phenomenon, the surface differential rotation coefficient would be | k | > Z_phys ≈ 0.12.

The Kuiper method detected an active longitude rotating with a period of 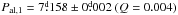$P_{al, 1} = 7 \overset{d}{.} 158 \pm 0 \overset{d}{.} 002 (Q = 0.004)$ $\hbox{$P_{\mathrm{al,1}}=7\fd158 \pm 0\fd002 ~(Q=0.004)$}$ . This long-lived structure was present between 1998 and 2009, but it vanished when the amplitudes of the light curves fell to near zero in 2010.

Acknowledgments

This research at the Department of Physics (University of Helsinki) was performed in collaboration with the participants of the course “Variable stars”, which was lectured in spring 2012. This work has made use of the SIMBAD database at CDS, Strasbourg, France and NASA’s Astrophysics Data System (ADS) bibliographic services. The work by PK and JL was supported by the Vilho, Yrjö and Kalle Väisälä Foundation. The automated astronomy program at Tennessee State University has been supported by NASA, NSF, TSU and the State of Tennessee through its Centers of Excellence program.

References

Abt, H. A., & Willmarth, D. 2006, ApJS, 162, 207 [NASA ADS] [CrossRef] [Google Scholar]
Andersen, J., Nordstrom, B., Ardeberg, A., et al. 1985, A&AS, 59, 15 [NASA ADS] [Google Scholar]
Árnadóttir, A. S., Feltzing, S., & Lundström, I. 2010, A&A, 521, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
Barnes, S. A. 2007, ApJ, 669, 1167 [NASA ADS] [CrossRef] [Google Scholar]
Barnes, S. A. 2010, ApJ, 722, 222 [NASA ADS] [CrossRef] [Google Scholar]
Barnes, S. A., & Kim, Y.-C. 2010, ApJ, 721, 675 [NASA ADS] [CrossRef] [Google Scholar]
Beavers, W. I., & Eitter, J. J. 1981, PASP, 93, 765 [NASA ADS] [CrossRef] [Google Scholar]
Beavers, W. I., & Eitter, J. J. 1986, ApJS, 62, 147 [NASA ADS] [CrossRef] [Google Scholar]
Brugamyer, E., Dodson-Robinson, S. E., Cochran, W. D., & Sneden, C. 2011, ApJ, 738, 97 [NASA ADS] [CrossRef] [Google Scholar]
Christian, D. J., Mathioudakis, M., Jevremovic, D., et al. 2003, Inform. Bull. Variable Stars, 5447, 1 [NASA ADS] [Google Scholar]
Cutispoto, G., Pastori, L., Tagliaferri, G., Messina, S., & Pallavicini, R. 1999, A&AS, 138, 87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Decin, G., Dominik, C., Malfait, K., Mayor, M., & Waelkens, C. 2000, A&A, 357, 533 [NASA ADS] [Google Scholar]
do Nascimento, Jr., J.-D., Takeda, Y., Meléndez, J., et al. 2013, ApJ, 771, L31 [NASA ADS] [CrossRef] [Google Scholar]
do Nascimento, Jr., J.-D., García, R. A., Mathur, S., et al. 2014, ApJ, 790, L23 [NASA ADS] [CrossRef] [Google Scholar]
Eggen, O. J. 1995, AJ, 109, 1327 [NASA ADS] [CrossRef] [Google Scholar]
Fekel, F. C., & Henry, G. W. 2005, AJ, 129, 1669 [NASA ADS] [CrossRef] [Google Scholar]
Fernandes, J. M., Vaz, A. I. F., & Vicente, L. N. 2011, A&A, 532, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gaidos, E. J. 1998, PASP, 110, 1259 [NASA ADS] [CrossRef] [Google Scholar]
Gaidos, E. J., & Gonzalez, G. 2002, New A, 7, 211 [Google Scholar]
Gaidos, E. J., Henry, G. W., & Henry, S. M. 2000, AJ, 120, 1006 [NASA ADS] [CrossRef] [Google Scholar]
Gontcharov, G. A. 2006, Astron. Lett., 32, 759 [NASA ADS] [CrossRef] [Google Scholar]
Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [NASA ADS] [CrossRef] [Google Scholar]
Hackman, T., Mantere, M. J., Jetsu, L., et al. 2011, Astron. Nachr., 332, 859 [NASA ADS] [CrossRef] [Google Scholar]
Hackman, T., Pelt, J., Mantere, M. J., et al. 2013, A&A, 553, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Haywood, M. 2001, MNRAS, 325, 1365 [NASA ADS] [CrossRef] [Google Scholar]
Henry, G. W. 1999, PASP, 111, 845 [NASA ADS] [CrossRef] [Google Scholar]
Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
Jeffries, R. D., & Jewell, S. J. 1993, MNRAS, 264, 106 [NASA ADS] [CrossRef] [Google Scholar]
Jetsu, L., & Pelt, J. 1996, A&AS, 118, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Jetsu, L., Hackman, T., Hall, D. S., et al. 2000, A&A, 362, 223 [NASA ADS] [Google Scholar]
Kajatkari, P., Hackman, T., Jetsu, L., Lehtinen, J., & Henry, G. W. 2014, A&A, 562, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Koen, C., & Eyer, L. 2002, MNRAS, 331, 45 [NASA ADS] [CrossRef] [Google Scholar]
Kóspál, Á., Ardila, D. R., Moór, A., & Ábrahám, P. 2009, ApJ, 700, L73 [NASA ADS] [CrossRef] [Google Scholar]
Lehtinen, J., Jetsu, L., Hackman, T., Kajatkari, P., & Henry, G. W. 2011, A&A, 527, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lehtinen, J., Jetsu, L., Hackman, T., Kajatkari, P., & Henry, G. W. 2012, A&A, 542, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Maldonado, J., Martínez-Arnáiz, R. M., Eiroa, C., Montes, D., & Montesinos, B. 2010, A&A, 521, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Martínez-Arnáiz, R., Maldonado, J., Montes, D., Eiroa, C., & Montesinos, B. 2010, A&A, 520, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Nakajima, T., & Morino, J.-I. 2012, AJ, 143, 2 [NASA ADS] [CrossRef] [Google Scholar]
Nakajima, T., Morino, J.-I., & Fukagawa, M. 2010, AJ, 140, 713 [NASA ADS] [CrossRef] [Google Scholar]
Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rodonò, M., Messina, S., Lanza, A. F., Cutispoto, G., & Teriaca, L. 2000, A&A, 358, 624 [NASA ADS] [Google Scholar]
Santos, N. C., Israelian, G., & Mayor, M. 2001, A&A, 373, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Santos, N. C., Israelian, G., García López, R. J., et al. 2004a, A&A, 427, 1085 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Santos, N. C., Israelian, G., Randich, S., García López, R. J., & Rebolo, R. 2004b, A&A, 425, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Shara, M. M., Shara, D. J., & McLean, B. 1993, PASP, 105, 387 [NASA ADS] [CrossRef] [Google Scholar]
Wright, J. T., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2004, ApJS, 152, 261 [NASA ADS] [CrossRef] [Google Scholar]

All Tables