| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201424485 | |
| Published online | 09 April 2015 | |
Entropy generation at multi-fluid magnetohydrodynamic shocks with emphasis to the solar wind termination shock
Argelander Institut für Astronomie der Universität Bonn, Abteilung f. Astrophysik und Extraterrestrische
Forschung,
Auf dem Huegel 71,
53121
Bonn,
Germany
e-mail:
msiewert@astro.uni-bonn.de
Received: 27 June 2014
Accepted: 16 December 2014
In a series of earlier papers, we developed expressions for ion and electron velocity distribution functions and their velocity moments at the passage over the solar wind termination shock. As we have shown there, with the introduction of appropriate particle invariants and the use of Liouville’s theorem one can get explicit solutions for the resulting total downstream pressure by adding up from partial pressure contributions of solar wind protons, solar wind electrons and pick-up protons. These expressions are the first step toward delivering the main contributions to the total plasma pressure in the downstream plasma flow and consistently determine the shock compression ratio. Here we start from these individual fluid pressures downstream of the shock and thereafter evaluate for the first time the shock-induced entropy production of the different fluids, when they are passing over the shock to the downstream side. As shown here, the resulting ion entropy production substantially deviates from earlier calculations using a pseudo-polytropic reaction of the ions to the shock compression, with polytropies selected to describe fluid-specific reactions at the shock passage similar to those seen by the Voyagers. From these latter models, ion entropy jumps are derived that depend on the pick-up ion abundance, while our calculations deliver an abundance-independent ion entropy production that only depends on the shock compression ratio and the tilt angle between the upstream magnetic field and the normal to the shock surface. We also show here that the thermodynamically permitted upper limit in the entropy production is only reached when strongly heated electrons are included in the entropy balance.
Key words: shock waves / plasmas / solar wind / Sun: heliosphere
© ESO, 2015
1. Introduction
The plasma physics of shocks in the literature was essentially reduced to the consideration of flux conservation requirements well known as Rankine-Hugoniot relations (see e.g. Serrin 1959; Landau & Lifshitz 1977; Gombosi 1998) Usually, in these relations the internal microphysics of the shock transition is not formulated in an explicit way; instead it is an attempt to describe the main shock features with the help of conservation equations requiring the conservation of the fluxes of the mass, the momentum, and the energy at the plasma passage from upstream to downstream side of the shock. Even though this is naturally the main physical request, this procedure nevertheless has the drawback that these conservation relations do not allow for a unique solution, since the fluid-like conservation requests do not establish a closed system of equations, thus not allowing for one unique solution. To arrive at specific, discrete solutions one has to make an assumption in addition to the fluid-like conservation requirements. Often this is done assuming a polytropic relation between the pressure and density, prescribing for example the rate of entropy generation at the shock passage.
Things become much more complicated, if anisotropic plasma pressures and magnetic field stresses are taken into account. In that case, the system of conservation equations is substantially enlarged (see Hudson 1970; Baumjohann & Treumann 1996; Gombosi 1998; Erkaev et al. 2000; Diver 2001) and can only be solved by adding additional information, such as e.g. two adiabatic equations requiring the conservation of two Chew-Goldberger-Low (CGL)-invariants (Chew et al. 1956) as suggested by e.g. Neubauer (1970). This approach is in agreement with the work by Sarris & van Allen (1974), who already proposed that magnetic invariants are conserved at the shock. These authors could theoretically represent data on shock-processed ions obtained by Explorer 33 and 35 well, when assuming that these particles are multiply reflected at their magnetic mirror points and finally move downstream under conservation of their magnetic moments. The same conclusion was reached by Terasawa (1979) when comparing ion spectra of magnetohydrodynamic (MHD) shock-reflected ions calculated by two different approaches: the “adiabatic approach” applicable at extended shocks and conserving magnetic moments and the so-called “kink-treatment” applicable at thin shocks. The results are nearly identical concerning the spectra obtained, showing that even under conditions where moment conservation is not evidently fulfilled, particles nevertheless behave as if their moments are conserved. Leroy & Mangeney (1984) also confirmed this, showing that test particle electrons at the Earth‘s bow shock are energized according to the conservation of their magnetic moments.
Concerning the conservation of the particle’s magnetic moment at the transition over the solar wind termination shock, we have carried out dedicated investigations in recent papers by Fahr & Siewert (2010, 2013). In Fahr & Siewert (2010) we investigated different cases of perpendicular shocks with shock thicknesses D that were either smaller or larger than the particle’s gyroradius; in both cases we found that the magnetic moment is conserved. In a more recent paper by Fahr & Siewert (2013), we have studied the general phase space transport equation and identified therein a term (i.e. transport operator for focused particle motions) that describes the particle’s tendency to conserve its magnetic moment and that under many favourable conditions, magnetic moment conservation is guaranteed.
Furthermore, Siewert & Fahr (2008, 2009, 2010) have thereafter studied the action of shock-generated unstable anisotropic distribution functions that drive magneto-acoustic and Alfvénic turbulences. This was identified as a specific microphysical relaxation process, which effectively operates downstream of the shock especially working in terms of efficient entropy generation.
Furthermore, the system is substantially more complicated even on the fluid level if more than one plasma fluid is considered. If instead of a monofluid, for instance a multi-fluid plasma has to be consistently described at its shock passage, then a number of additional complications have to be faced to arrive at appropriate solutions (see Zank et al. 1993; Le Roux & Fichtner 1997, 1999), with Chalov & Fahr (1994, 1995, 1996) providing descriptions for two- and three-fluid plasmas passing over the solar wind termination shock. The three fluids treated in these studies as being subject to the bulk motion of the solar wind are normal solar wind protons (SW, i.e. eV-energetic), pick-up protons (PUIs, i.e. KeV-energetic) and anomalous cosmic ray protons (ACRs, i.e. MeV-energetic). A consistent solution of the shock passage of this three-fluid plasma is only possible if some additional prescriptions are made about how these fluids thermodynamically interact with each other when undergoing a shock.
Chalov & Fahr (1996), find that, according to the pickup proton pressure Ppui, a specific percentage η of these ions is Fermi-1 accelerated at the shock and injected to the MeV-energetic ACR fluid regime with an average energy of Einj, where both η and Einj are unknown parameters that need to be fixed by numbers. This, however, has the interesting consequence that PUI‘s do not react adiabatically to the shock, but rather in a quasi-isothermal mode with an effective polytropic index γpui given by 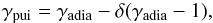 (1)where γadia = 5 / 3 is the adiabatic index and δ is given by
(1)where γadia = 5 / 3 is the adiabatic index and δ is given by 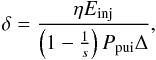 (2)with s being the compression ratio of the shock.
(2)with s being the compression ratio of the shock.
Thus one can see that the entropy production occuring at the shock passage in this case is specifically different for the different fluids and is regulated by specific assumptions for values of η and Einj (see Fig. 8 of Chalov & Fahr 1996).
In the following, we now study in detail the entropy generation in the different fluids when they are passing over the shock, including electrons as an independent separate fluid. Hereby we try to avoid the above mentioned ad-hoc assumptions, instead introducing kinetic information on the single particle behaviour at the shock passage. For that purpose we first derive the expressions for the downstream pressures of these separate fluids after taking a short look into general aspects of the entropy generation at the shock under Boltzmann kinetic auspices.
2. The Boltzmann entropic view
To study the entropy of multi-component systems, we first need to understand the entropy of a single fluid that is described by an arbitrary physical velocity distribution function f(v). Therefore, we need to establish the basic equations required to calculate the entropy of f first. Therefore, we may profit in our understanding by first establishing the basic equations required for this simplified mono-fluid view. Let us assume that at some distance upstream and downstream of the shock transition, due to rapid relaxation processes, we may find quasi-equilibrium distribution functions. Then one can express the upstream and the downstream particle entropy with the help of these distribution functions.
According to e.g. Landau & Lifshitz (1977), for a state of a system close to a thermodynamic equilibrium, assumed to prevail at some distance upstream and downstream of the shock, the kinetic ensemble entropy per particle can be given by the expression (see also Weizel 1958; Cercignani 1988; Brey & Santos 1992; Treumann 2001) 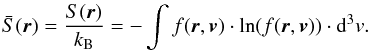 (3)This equation is valid only in the rest frame of the system, i.e. a reference frame where the plasma does not possess a bulk flow speed (U = 0), as defined by
(3)This equation is valid only in the rest frame of the system, i.e. a reference frame where the plasma does not possess a bulk flow speed (U = 0), as defined by 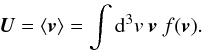 (4)For a system in motion, the definition of the entropy has to be modified to account for the so-called bulk particle flow speed U,
(4)For a system in motion, the definition of the entropy has to be modified to account for the so-called bulk particle flow speed U, 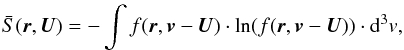 (5)since otherwise, and for an arbitrary distribution function f, the definition of the entropy would not be unique. This configuration is commonly found in systems where the plasma flow is accelerated or decelerated, and where a “natural” reference frame for the system cannot be easily found. One classical example for such a system is an MHD shock wave, where, depending on the problems under investigation, one could select the rest frame of the upstream plasma, the downstream plasma, or the shock front itself.
(5)since otherwise, and for an arbitrary distribution function f, the definition of the entropy would not be unique. This configuration is commonly found in systems where the plasma flow is accelerated or decelerated, and where a “natural” reference frame for the system cannot be easily found. One classical example for such a system is an MHD shock wave, where, depending on the problems under investigation, one could select the rest frame of the upstream plasma, the downstream plasma, or the shock front itself.
We are mainly interested in entropy jumps at MHD shock waves, where the actual distribution function f(v) is not known or readily available in their inner transition region and where classical MHD does not provide a good approximation. Thus we shall assume here that, far enough upstream and downstream of the shock, one may have a sufficiently relaxed distribution function allowing us to calculate the associated entropy according to expression 3. This then allows us to express the total entropy jump ΔS over the shock imputing a smooth change from the upstream to the downstream quasi-equilibrium distribution function. Then one should be able to express the entropy change ΔS over the shock by the following expression: 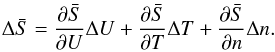 (6)This expression can be simplified by noting that the kinetic expression for the Boltzmann entropy is only applicable for quasi-LTE conditions, i.e. sufficiently relaxed plasma states. Connected with the shock influence through shock-associated electric and magnetic fields, the plasma properties may have temporarily attained non-relaxed intermediate features like asymmetric, anisotropic distributions. This is the case when using anisotropic MHD jump conditions, see e.g. Erkaev et al. (2000), Fahr & Siewert (2006), Siewert & Fahr (2007), or jet-like velocity structures, e.g. due to a possible overshooting of electrons or heavy ions, as discussed by Fahr et al. (2012). Thus, the standard definition of the Boltzmann entropy can evidently not be applied as long as these intermediate, perturbed, non-relaxed conditions have not yet reached a quasi-LTE with the help of instabilities driving isotropisation and relaxation processes. Nevertheless, Eq. (6) may provide a valuable first-order estimate of the final permitted entropy jump.
(6)This expression can be simplified by noting that the kinetic expression for the Boltzmann entropy is only applicable for quasi-LTE conditions, i.e. sufficiently relaxed plasma states. Connected with the shock influence through shock-associated electric and magnetic fields, the plasma properties may have temporarily attained non-relaxed intermediate features like asymmetric, anisotropic distributions. This is the case when using anisotropic MHD jump conditions, see e.g. Erkaev et al. (2000), Fahr & Siewert (2006), Siewert & Fahr (2007), or jet-like velocity structures, e.g. due to a possible overshooting of electrons or heavy ions, as discussed by Fahr et al. (2012). Thus, the standard definition of the Boltzmann entropy can evidently not be applied as long as these intermediate, perturbed, non-relaxed conditions have not yet reached a quasi-LTE with the help of instabilities driving isotropisation and relaxation processes. Nevertheless, Eq. (6) may provide a valuable first-order estimate of the final permitted entropy jump.
Following the line of Boltzmann’s understanding, in the above expression the distribution function should be applied as a normalized one, i.e. as a velocity-space probability distribution, so that no explicit dependence of 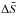 on the density jump Δn appears in the expression for
on the density jump Δn appears in the expression for 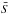 . However, there will be an implicit dependence on n because the temperature is directly related to the density, allowing us to rewrite Eq. (6) in the form
. However, there will be an implicit dependence on n because the temperature is directly related to the density, allowing us to rewrite Eq. (6) in the form 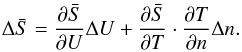 (7)This result clearly shows the “kinetic” (first term on the right) and the “thermal” (second term on the right) contributions to the total entropy jump, while at the same time replacing the temperature jump ΔT with the density jump Δn, allowing us to express the entropy jump as a function of parameters appearing directly in the jump conditions.
(7)This result clearly shows the “kinetic” (first term on the right) and the “thermal” (second term on the right) contributions to the total entropy jump, while at the same time replacing the temperature jump ΔT with the density jump Δn, allowing us to express the entropy jump as a function of parameters appearing directly in the jump conditions.
2.1. The entropy jump for a Maxwell-Boltzmann distribution at the termination shock
In the following, we make explicit use of two relaxed model distribution functions to describe the plasma on the upstream and downstream sides of the solar wind termination shock (TS) in the shock frame. When introducing shock parameters, the subscripts 1 and 2 are used to denote quantities on the upstream and downstream sides of the shock.
First, we assume that the thermal upstream plasma is well described by a shifted Maxwell-Boltzmann distribution function, i.e. 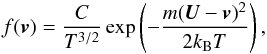 (8)with a normalisation factor C = n(m/ 2πkB)3 / 2. For an MHD shock, this is the standard kinetic description that is implicitly assumed to persist on the upstream side, and, after some relaxation, also on the downstream side of the shock.
(8)with a normalisation factor C = n(m/ 2πkB)3 / 2. For an MHD shock, this is the standard kinetic description that is implicitly assumed to persist on the upstream side, and, after some relaxation, also on the downstream side of the shock.
To simplify the following calculations, we introduce the shorthand notation 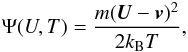 (9)which allows us to write down the entropy in the more compact form
(9)which allows us to write down the entropy in the more compact form ![\begin{eqnarray} \bar{S} &=& -\frac{C}{T^{3/2}} \int \exp \left( -\Psi \right) \cdot \left[ \ln \frac{C}{T^{3/2}} - \Psi \right] {\rm d}^3v \nonumber\\ \label{eq-s-maxwell-0} &=& - \ln \frac{C}{T^{3/2}} + \frac{C}{T^{3/2}} \int \exp ( -\Psi) \Psi {\rm d}^3v. \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq30.png) (10)After evaluating the integrals, one simply obtains
(10)After evaluating the integrals, one simply obtains 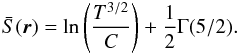 (11)Considering that thermodynamics is only interested in entropy jumps, but not in absolute values, the constant second term in this sum can be interpreted as a normalisation constant (see e.g. Collier 1995).
(11)Considering that thermodynamics is only interested in entropy jumps, but not in absolute values, the constant second term in this sum can be interpreted as a normalisation constant (see e.g. Collier 1995).
This expression in principle allows us to derive the entropy jump 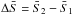 between both sides of the shock, assuming that we have solved the MHD jump conditions. However, it is also possible to derive a more explicit expression for the entropy jump that does not depend on explicit values for the shock parameters. Using Eq. (10), it is possible to evaluate the partial derivatives in Eq. (7). After some elementary operations, we obtain the relations
between both sides of the shock, assuming that we have solved the MHD jump conditions. However, it is also possible to derive a more explicit expression for the entropy jump that does not depend on explicit values for the shock parameters. Using Eq. (10), it is possible to evaluate the partial derivatives in Eq. (7). After some elementary operations, we obtain the relations 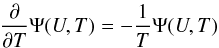 (12)and
(12)and 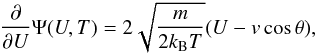 (13)where θ = ∠(U,v). Using these relations, we obtain
(13)where θ = ∠(U,v). Using these relations, we obtain 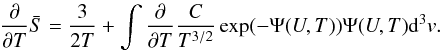 (14)Evaluating the partial derivatives and collecting terms, we further obtain
(14)Evaluating the partial derivatives and collecting terms, we further obtain 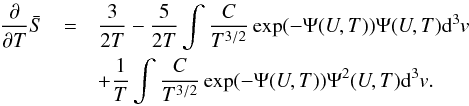 (15)With some some elementary substitutions, this allows us to solve the integrals, and we obtain
(15)With some some elementary substitutions, this allows us to solve the integrals, and we obtain 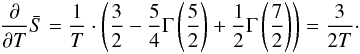 (16)Analogously for the remaining partial derivative, we obtain
(16)Analogously for the remaining partial derivative, we obtain 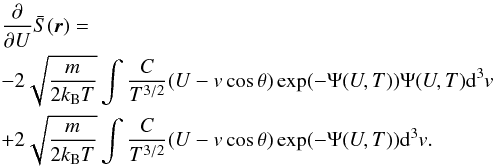 (17)After introducing spherical coordinates and substituting w = U − vcosθ, this expression becomes
(17)After introducing spherical coordinates and substituting w = U − vcosθ, this expression becomes 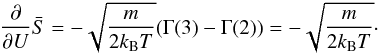 (18)Therefore, we obtain an entropy jump calculated on the basis of a shifted Maxwell-Boltzmann distribution given by
(18)Therefore, we obtain an entropy jump calculated on the basis of a shifted Maxwell-Boltzmann distribution given by 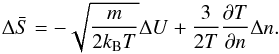 (19)The only unknown parameter entering this expression is the thermodynamic relation between temperature and density, which reflects the entire microphysics inside the shock transition layer that is inaccessible to MHD.
(19)The only unknown parameter entering this expression is the thermodynamic relation between temperature and density, which reflects the entire microphysics inside the shock transition layer that is inaccessible to MHD.
Depending on the behaviour of 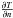 , the entropy jump may be negative, suggesting that the shock transition is physically impossible. However, one also has to consider that the partial derivative essentially represents an average of the entire microphysics of the shock transition to which the single fluid approximation may be an overly strong simplification, and the presence of plasma-wave interactions or heavy ions in principle even allow a decrease in the entropy in a single part of the entire system (see also Eq. (2)).
, the entropy jump may be negative, suggesting that the shock transition is physically impossible. However, one also has to consider that the partial derivative essentially represents an average of the entire microphysics of the shock transition to which the single fluid approximation may be an overly strong simplification, and the presence of plasma-wave interactions or heavy ions in principle even allow a decrease in the entropy in a single part of the entire system (see also Eq. (2)).
In the limit of a single component shock, one can request the entropy change to be positive (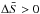 ), and obtain
), and obtain 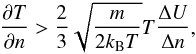 (20)which can be simplified further by introducing the MHD compression ratio s = U1/U2 = n2/n1, resulting in
(20)which can be simplified further by introducing the MHD compression ratio s = U1/U2 = n2/n1, resulting in 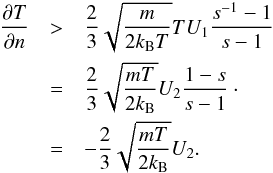 (21)This equation provides an easy approach to the question whether a physical, entropy-increasing shock is possible without having to introduce additional non-trivial thermodynamic degrees of freedom to the shock transition.
(21)This equation provides an easy approach to the question whether a physical, entropy-increasing shock is possible without having to introduce additional non-trivial thermodynamic degrees of freedom to the shock transition.
2.2. The entropy of a κ function
The shock passage very likely provokes non-thermal equilibrum conditions, and therefore, a distribution function f(v) that differs from the classical thermodynamic Maxwellian (Eq. (8)) is required. Following theoretical arguments studied by e.g. Treumann (1999), Treumann et al. (2004), or Livadiotis & McComas (2012) we adopt a non-thermal κ function to describe the quasi-stable non-thermal downstream equilibrum state that likely develops on the near downstream side of the shock. Therefore, we need to understand the entropy stored in a κ-function, which allows us to compare it to the entropy gain using a conventional Maxwellian distribution (Eq. (19)).
Taking the standard definition of an isotropic κ distribution, ![\begin{eqnarray} f_\kappa(\vec{v}) = \frac{n}{(\pi \sqrt{\kappa} \Theta^{2})^{3/2}} \frac{\Gamma(\kappa+1)}{\Gamma (\kappa-3/2)}\left[1+\frac{v^{2}}{\kappa\Theta^{2}}\right]^{-(\kappa+1)} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq50.png) (22)with
(22)with 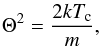 (23)we are able to calculate the κ-entropy using the same Boltzmann formalism as used above for the Maxwell-Boltzmann distribution, as long as one assumes that the κ-function reflects an equilibrum state between classical elastic scattering and energy diffucion (see e.g. Collier 1995). Under these conditions, the entropy of a κ distribution function is given by
(23)we are able to calculate the κ-entropy using the same Boltzmann formalism as used above for the Maxwell-Boltzmann distribution, as long as one assumes that the κ-function reflects an equilibrum state between classical elastic scattering and energy diffucion (see e.g. Collier 1995). Under these conditions, the entropy of a κ distribution function is given by ![\begin{eqnarray} \bar{S}^{\kappa} &=& \ln \Bigg\{\frac{(\Theta ^{2}\pi \kappa )^{3/2}\Gamma (\kappa -1/2)}{\Gamma (\kappa +1)}\nonumber\\ && \times \exp \left[(\kappa +1)(\digamma (\kappa +1)-\digamma (\kappa -1/2))\right]\Bigg\}, \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq52.png) (24)where the digamma function z is defined by:
(24)where the digamma function z is defined by: 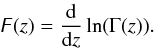 (25)Using elementary properties of the gamma function (see e.g. Abramowitz & Stegun), the somewhat unwieldy expression can be simplified by first eliminating the z symbols, leading to
(25)Using elementary properties of the gamma function (see e.g. Abramowitz & Stegun), the somewhat unwieldy expression can be simplified by first eliminating the z symbols, leading to ![\begin{eqnarray} \bar{S}^{\kappa } &=& \ln \left\{\frac{(\Theta ^{2}\pi \kappa )^{3/2}\Gamma (\kappa-1/2)}{\Gamma (\kappa +1)}\right.\nonumber\\ && \left. \times \exp \left[(\kappa +1) \left(\frac{\kappa \Gamma (\kappa )}{\Gamma (\kappa +1)}-\frac{(\kappa -3/2)\Gamma (\kappa -3/2)}{\Gamma (\kappa-1/2)}\right)\right]\right\}\cdot \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq55.png) (26)After further evaluation the γ functions in the exponent cancel out, leaving only
(26)After further evaluation the γ functions in the exponent cancel out, leaving only 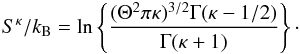 (27)One specifically interesting property of this expression is the limit for κ → ∞, which should reproduce the classical Maxwellian limit (Eq. (11)). Using Stirlings formula (see e.g. Abramowitz & Stegun), one easily sees that
(27)One specifically interesting property of this expression is the limit for κ → ∞, which should reproduce the classical Maxwellian limit (Eq. (11)). Using Stirlings formula (see e.g. Abramowitz & Stegun), one easily sees that 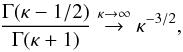 (28)and the entropy becomes
(28)and the entropy becomes 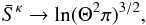 (29)which (with the exception of a different normalisation, see Collier 1995) is just the entropy for a Maxwellian distribution function.
(29)which (with the exception of a different normalisation, see Collier 1995) is just the entropy for a Maxwellian distribution function.
2.3. The classical MHD shock entropy gain and the polytropic index γ
For completeness, we also briefly mention the entropy gain found in most MHD textbooks, as is derived from classical shock relations, and without paying much attention to the kinetic origin of the entropy (see e.g. Serrin 1959; Landau & Lifshitz 1977). This jump in entropy per unit mass at the shock, judged in the respective frames of the bulk plasma flow, is given by ![\begin{eqnarray} \Delta \bar{S}_{\rm MHD} = \ln \left[\frac{P_{2}}{P_{1}} \left(\frac{\rho _{1}}{\rho _{2}}\right)^{\gamma_{\rm adia}}\right], \label{eq-delta-s-mhd} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq61.png) (30)where γadia = 5 / 3 is the so-called adiabatic index. For this specific choice of γadia, it immediately follows that a gas, reacting strictly adiabatically at the shock compression, will not increase its thermal entropy at all when judged in the bulk frame, which strongly suggests that the shock transition most probably may not be purely adiabatic. Judged in an absolute rest frame, however, there will be an entropy increase due to the change in the bulk velocity even under adiabatic conditions, as evident from Eq. (19).
(30)where γadia = 5 / 3 is the so-called adiabatic index. For this specific choice of γadia, it immediately follows that a gas, reacting strictly adiabatically at the shock compression, will not increase its thermal entropy at all when judged in the bulk frame, which strongly suggests that the shock transition most probably may not be purely adiabatic. Judged in an absolute rest frame, however, there will be an entropy increase due to the change in the bulk velocity even under adiabatic conditions, as evident from Eq. (19).
However, the adiabatic index γadia is just a special case of the more general polytropic relation, which for the system studied here can be represented in the form 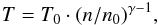 (31)where γ is the more general polytropic index, for which γ = γadia is just one special value. In addition to the obvious impact on the MHD entropy jump (Eq. (30)), this equation also allows us to quantify the previously unknown parameter in Eq. (19), i.e. the partial derivative
(31)where γ is the more general polytropic index, for which γ = γadia is just one special value. In addition to the obvious impact on the MHD entropy jump (Eq. (30)), this equation also allows us to quantify the previously unknown parameter in Eq. (19), i.e. the partial derivative 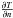 , which for the general polytropic relation becomes
, which for the general polytropic relation becomes 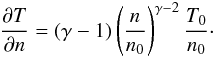 (32)Observational data studies usually treat the polytropic index γ as a free fit parameter, while theoretical studies often apply this relation as an “ad-hoc” boundary condition; in principle, for arbitrary shocked systems, the T-n relation could be of a form that differs from this model approach. However, at an MHD shockwave, this approach can be justified by the fact that the microphysics of the shock can not be modelled by a fluid theory, and therefore, a polytropic index can be interpreted as an averaged description of the microphysical plasma-wave interactions in the shock transition layer. Applying Eqs. (32) to Eq. (21), one easily sees that the monofluid polytropic approach to the MHD shock always increases the entropy in the system for γ> 1, which covers pretty much all polytropic indices found in the literature (where, usually, γ = 1...2).
(32)Observational data studies usually treat the polytropic index γ as a free fit parameter, while theoretical studies often apply this relation as an “ad-hoc” boundary condition; in principle, for arbitrary shocked systems, the T-n relation could be of a form that differs from this model approach. However, at an MHD shockwave, this approach can be justified by the fact that the microphysics of the shock can not be modelled by a fluid theory, and therefore, a polytropic index can be interpreted as an averaged description of the microphysical plasma-wave interactions in the shock transition layer. Applying Eqs. (32) to Eq. (21), one easily sees that the monofluid polytropic approach to the MHD shock always increases the entropy in the system for γ> 1, which covers pretty much all polytropic indices found in the literature (where, usually, γ = 1...2).
We present one possible way of connecting an effective polytropic index with a multi-fluid MHD shock wave, thus introducing theoretical concepts to the ad-hoc boundary condition, and compare the result with the best-fitting effective polytropic index found by Wu et al. (2009) at the solar wind termination shock.
3. The multi-fluid plasma at the termination shock
3.1. Pressures in a multi-fluid system
As suggested by Eq. (30), the upstream and downstream pressures of the shocked plasma provide an important quantity for the entropy problem. For an MHD approach, the upstream and downstream pressures directly enter Eq. (30), while for the kinetic approach (Eq. (7)), we need to convert between pressures (that appear in the jump conditions) and temperatures (that appear in the kinetic distribution function). Because the immediate downstream side of the shock may represent a thermal nonequilibrum, this conversion can be difficult; we assume that the downstream side is defined as the region where a new (possibly non-thermal) equilibrum has been reached so that we can ignore more details of the shock transition. However, we do not ignore the multi-fluid characteristics of the shock, for which we adopt an overshooting description, i.e. a description where particles possessing different electric charges and masses will react differently to the global electric ramp of the shock potential. While thermal and PUI protons do not require this additional detail, it becomes important when we study the entropy gain of the electron component in Sect. 4.3.
We consider MHD shocks in a one-dimensional approach with the shock normal n assumed to be parallel to the upstream bulk flow velocity U1 and an upstream magnetic field vector tilted by an angle α with respect to n. We consider three different fluids, namely solar wind protons, solar wind electrons, and pick-up ions. For an explicit description of the downstream pressure P2,p of the thermal SW proton component, we adopt the relations given by Fahr et al. (2012) and Fahr & Siewert (2013), 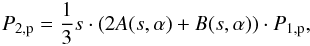 (33)where the indices 1, 2 denote upstream and downstream quantities, respectively, s = U1/U2 denotes the shock compression ratio, and the functions A(s,α) and B(s,α) are given by
(33)where the indices 1, 2 denote upstream and downstream quantities, respectively, s = U1/U2 denotes the shock compression ratio, and the functions A(s,α) and B(s,α) are given by 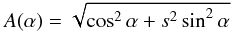 (34)and
(34)and 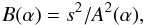 (35)where the angle α defines the inclination between the shock surface normal n and the upstream magnetic field B1 (i.e. for a perpendicular shock this means α = π/ 2).
(35)where the angle α defines the inclination between the shock surface normal n and the upstream magnetic field B1 (i.e. for a perpendicular shock this means α = π/ 2).
In our multi-fluid description, the downstream PUI pressure P2,pui is derived in the same way as the downstream proton pressure P2,p, i.e. the main difference between both pressures is a factor Γ1 = P1,pui/P1,p, and therefore is simply given by the following analogous formula ![\begin{eqnarray} \label{eq-p2p-pui} P_{\rm 2,pui} &=& \frac{1}{3}s\left[2A(\alpha )+\frac{s^{2}}{A^{2}(\alpha )}\right]\cdot P_{\rm 1,pui}\nonumber\\ &=& \frac{1}{3}s\left[2A(\alpha )+\frac{s^{2}}{A^{2}(\alpha )}\right]\cdot \Gamma_1 P_{\rm 1,p}. \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq84.png) (36)This approach turns out to be justified because a pick-up proton cannot be physically differentiated from a solar wind proton as a different ion species, for several reasons. The main complication when dealing with an initial distribution of PUIs at a shock is the reflection of a certain fraction of the energetic ions from the electric shock potential. Considering the total velocity u of an individual ion in the shock frame, i.e. u = v + U, it becomes obvious that some ions may possess a velocity vector that does not enable them to cross the shock potential at the first attempt. Instead, these ions are reflected into the shock precursor region where they induce local two-stream instabilities. Following this, they do gain energy and momentum from interactions with just these instabilities, until they finally get transported across the shock. In many MHD shock simulations, a different (i.e. purely numerical) approach to this situation has been studied, but the answer concerning the resulting final downstream plasma mixture has not yet been conclusively given (see Scholer 1993; Liewer et al. 1993; Kucharek & Scholer 1995; Lembege et al. 2004; Kucharek et al. 2006; Zank et al. 2010; Matsukiyo & Scholer 2011; Wu et al. 2010). Results obtained in these simulations strongly depend on the shock compression ratio and especially on the upstream PUI velocity distribution used by the authors at the start of their simulations, e.g. cooled or heated shell distributions. Nevertheless, these simulations clearly demonstrate that a coupling between PUIs and thermal ions is involved at the shock in a natural way.
(36)This approach turns out to be justified because a pick-up proton cannot be physically differentiated from a solar wind proton as a different ion species, for several reasons. The main complication when dealing with an initial distribution of PUIs at a shock is the reflection of a certain fraction of the energetic ions from the electric shock potential. Considering the total velocity u of an individual ion in the shock frame, i.e. u = v + U, it becomes obvious that some ions may possess a velocity vector that does not enable them to cross the shock potential at the first attempt. Instead, these ions are reflected into the shock precursor region where they induce local two-stream instabilities. Following this, they do gain energy and momentum from interactions with just these instabilities, until they finally get transported across the shock. In many MHD shock simulations, a different (i.e. purely numerical) approach to this situation has been studied, but the answer concerning the resulting final downstream plasma mixture has not yet been conclusively given (see Scholer 1993; Liewer et al. 1993; Kucharek & Scholer 1995; Lembege et al. 2004; Kucharek et al. 2006; Zank et al. 2010; Matsukiyo & Scholer 2011; Wu et al. 2010). Results obtained in these simulations strongly depend on the shock compression ratio and especially on the upstream PUI velocity distribution used by the authors at the start of their simulations, e.g. cooled or heated shell distributions. Nevertheless, these simulations clearly demonstrate that a coupling between PUIs and thermal ions is involved at the shock in a natural way.
To get a reliable answer to this problem for our purposes, we look at the work of Chalov & Fahr (1996), who studied the kinetic transport of a statistical sample of PUIs as they pass over the electric and magnetic shock structure. Thir treatment starts from a realistic upstream PUI distribution function taking the cooling of PUIs into account before they enter the shock according to most up-to-date theories (see Chalov & Fahr 1995). Following the method by Decker (1988) involving a de Hoffmann-Teller frame and the conservation of the magnetic moment, they found that (Chalov & Fahr 1996, Figs. 6 and 7), for realistic upstream PUI distributions, the fraction of reflected (second order PUIs) over directly transmitted (first order PUIs) is less than 10-2 and is especially low for perpendicular shocks (α = π/ 2). Taking this result as solid, it is thus possible to assume that PUIs behave practically the same way as SW ions, and that they are all transmitted through the shock, with just a negligibly small number of reflected PUIs not taken into account in our present consideration. We study the entropy gain in this approximation of the multi-component shock in Sect. 4.1.
3.2. The joint downstream ion distribution
In addition to this straightforward approach, we will also apply a different description of the downstream plasma, motivated by the coupling between thermal and non-thermal ions that is naturally introduced at the shock. Since both downstream ion populations (i.e. thermal protons and PUIs) are located at overlapping regions in phase space, it is possible to describe them as one joint downstream pick-up ion and solar wind proton distribution. As demonstrated by Fahr & Siewert (2013), the main features of this combined ion distribution can be represented surprisingly well by a joint Kappa distribution, ![\begin{eqnarray} f_{2}(v)=\frac{n_{2}}{(\pi \kappa _{2}\Theta _{2}^{2})^{3/2}}\frac{\Gamma (\kappa _{2}+1)}{\Gamma (\kappa _{2}-3/2)} \left[1+\frac{v^{2}}{\kappa _{2}\Theta _{2}^{2}}\right]^{-(\kappa _{2}+1)}, \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq88.png) (37)with a Gaussian core velocity spread Θ2 and a net Kappa index κ2 as characteristic parameters. We interprete the downstream solar wind proton population as constituting the so-called Gaussian core Θ2 of the Kappa distribution (following Collier 1995; Heerikhuisen et al. 2008; Livadiotis & McComas 2009) and thus fix the needed Kappa function parameters as done by Fahr & Siewert (2013). The downstream thermal width Θ2 of the Gaussian core then becomes
(37)with a Gaussian core velocity spread Θ2 and a net Kappa index κ2 as characteristic parameters. We interprete the downstream solar wind proton population as constituting the so-called Gaussian core Θ2 of the Kappa distribution (following Collier 1995; Heerikhuisen et al. 2008; Livadiotis & McComas 2009) and thus fix the needed Kappa function parameters as done by Fahr & Siewert (2013). The downstream thermal width Θ2 of the Gaussian core then becomes 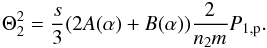 (38)The joint Kappa index κ2 follows from the requirement of the pressure identity
(38)The joint Kappa index κ2 follows from the requirement of the pressure identity 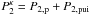 , resulting in
, resulting in ![\begin{eqnarray} \kappa _{2}=\frac{3[1+\zeta K]}{2\zeta \lbrack K-1]} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq93.png) (39)with the parameter K given by
(39)with the parameter K given by 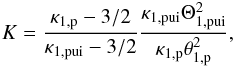 (40)where the upstream PUI abundance is given by ζ = n1,pui/n1,p. We assume separate Kappa distribution functions on the upstream side of the TS, one for the thermal ions (using the parameters Θ1,p and κ1,p), and another separate function for the PUIs (using the parameters Θ1,pui and κ1,pui). This allows for a greater flexibility in upstream configurations, with κ → ∞ for a pure Maxwellian distribution (i.e. the thermal component), and κ → 3 / 2 for a pure v-5 power law (i.e. the PUI component). In the following, we will adopt the same parameters as Fahr & Siewert (2013), resulting in the parameter K = 119.
(40)where the upstream PUI abundance is given by ζ = n1,pui/n1,p. We assume separate Kappa distribution functions on the upstream side of the TS, one for the thermal ions (using the parameters Θ1,p and κ1,p), and another separate function for the PUIs (using the parameters Θ1,pui and κ1,pui). This allows for a greater flexibility in upstream configurations, with κ → ∞ for a pure Maxwellian distribution (i.e. the thermal component), and κ → 3 / 2 for a pure v-5 power law (i.e. the PUI component). In the following, we will adopt the same parameters as Fahr & Siewert (2013), resulting in the parameter K = 119.
We study the entropy gain at the multi-component shock in this approach in greater detail in Sect. 4.4.
3.3. Downstream pressures in magneto-adiabatic or pseudo-polytropic approaches
Before calculating actual entropy gains, we study the alternate approach by Wu et al. (2009), where the relation between downstream and upstream PUI pressures is obtained as a pseudo-adiabatic reaction of the PUIs to the shock compression given by 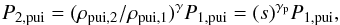 (41)where instead of a joint κ index or a kinetically derived enhancement factor, a PUI-specific polytropic index γp ≥ γadia = 5 / 3 is used to describe an additional heating of PUIs at the shock passage, which is needed to make the simulation results better fit the Voyager-2 shock data (see Richardson et al. 2008). We can now compare their approach with our kinetic model by deriving the adequate polytropic index γp that would give equivalent PUI pressure transformations as derived from our model. This requirement leads to the following expression:
(41)where instead of a joint κ index or a kinetically derived enhancement factor, a PUI-specific polytropic index γp ≥ γadia = 5 / 3 is used to describe an additional heating of PUIs at the shock passage, which is needed to make the simulation results better fit the Voyager-2 shock data (see Richardson et al. 2008). We can now compare their approach with our kinetic model by deriving the adequate polytropic index γp that would give equivalent PUI pressure transformations as derived from our model. This requirement leads to the following expression: ![\begin{eqnarray} \Pi (\alpha ,s) = \frac{1}{3}s \left[2A(\alpha )+\frac{s^{2}}{A^{2}(\alpha )}\right] = (\rho_{\rm pui,2}/\rho _{\rm pui,1})^{\gamma_{\rm p}} = s^{\gamma_{\rm p}}, \label{eq-pi-gamma} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq107.png) (42)or, for the resulting polytropic index
(42)or, for the resulting polytropic index 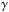 ,
, 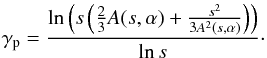 (43)For a quasi-perpendicular shock as encountered by the Voyager-2 spacecraft, we need to adopt α = 90°, where
(43)For a quasi-perpendicular shock as encountered by the Voyager-2 spacecraft, we need to adopt α = 90°, where 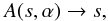 (44)and Eq. (43) reduces to
(44)and Eq. (43) reduces to 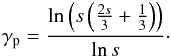 (45)For a compression ratio of s = 3, we simply obtain
(45)For a compression ratio of s = 3, we simply obtain 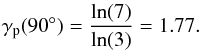 (46)Evaluating the same equation for a more parallel shock, e.g. with α = 20°, we instead obtain γp(20°) = 1.82. Global results for all angles and various compression ratios are presented in Fig. 1, which demonstrates that, for most magnetic field orientations, our kinetic model for the shock transition results in an over-adiabatic behaviour. As demonstrated by Fig. 1, this overadiabatic behaviour with γp>γadia = 5 / 3, dominates the parameter region for angles α< 30° and α> 40°. However, for angles between 30°<α< 40°, the effective polytropic indices are unexpectedly close to the classical adiabatic value of γp ≃ γadia). The reason for this is not directly evident from the calculations presented here, but can be understood with the help of the results published earlier by Fahr & Siewert (2010). This earlier paper demonstrates that the range of tilt angles between 30° and 40° is characterized by the absence of downstream ion temperature anisotropies (i.e. T⊥ ≃ T∥), which can be easily seen in Fig. 3 of that study. This means that, on this narrow intervall the two degrees of freedom parallel and perpendicular to B are equally heated, which is the same behaviour as the one found in the case of an unmagnetized gas. In addition, the changes of the temperature from upwind to downwind behave the same as in the adiabatic shock compression, i.e. P2/P1 = (n2/n1)γadia.
(46)Evaluating the same equation for a more parallel shock, e.g. with α = 20°, we instead obtain γp(20°) = 1.82. Global results for all angles and various compression ratios are presented in Fig. 1, which demonstrates that, for most magnetic field orientations, our kinetic model for the shock transition results in an over-adiabatic behaviour. As demonstrated by Fig. 1, this overadiabatic behaviour with γp>γadia = 5 / 3, dominates the parameter region for angles α< 30° and α> 40°. However, for angles between 30°<α< 40°, the effective polytropic indices are unexpectedly close to the classical adiabatic value of γp ≃ γadia). The reason for this is not directly evident from the calculations presented here, but can be understood with the help of the results published earlier by Fahr & Siewert (2010). This earlier paper demonstrates that the range of tilt angles between 30° and 40° is characterized by the absence of downstream ion temperature anisotropies (i.e. T⊥ ≃ T∥), which can be easily seen in Fig. 3 of that study. This means that, on this narrow intervall the two degrees of freedom parallel and perpendicular to B are equally heated, which is the same behaviour as the one found in the case of an unmagnetized gas. In addition, the changes of the temperature from upwind to downwind behave the same as in the adiabatic shock compression, i.e. P2/P1 = (n2/n1)γadia.
 |
Fig. 1 Polytropic indices obtained from our kinetic shock model according to Eq. (43) for different magnetic field orientations and MHD compression ratios. |
These values display the same behaviour found by Wu et al. (2009), who found a general over-adiabatic behaviour when trying to best fit the Voyager-2 shock observations. They obviously needed a preferential heating of the PUI-fluid compared to the SW fluid, and in their case obtain it by a fluid-specifically increased polytropic index.
While this may suggest that the two theoretical approaches can both deliver similar results, it must, however, be recognized that the selected γp-value invokes an unexplained ad-hoc process for PUIs. This follows from the fact that this approach treats the PUI protons and their thermodynamic reaction to a shock compression in a substantially different way from that of the normal solar wind protons. The justification for this approach may be that some of the PUI protons are reflected by the shock and later get transmitted after experiencing some energy gain. On the other hand, seen from physical grounds and argued on the basis of results presented by Chalov & Fahr (1996), who found that PUI reflection is fairly unlikely, that protons should react like protons, and disregarded whether they are of the PUI or of the solar-wind type. In our approach, this results in PUIs being heated more efficiently than solar wind protons because of the simple fact that PUIs are already hotter upstream of the shock. This means that protons of both fluids in fact do react completely alike, and the resulting pressure conversion simply is derived under conservation of kinetic particle invariants. This difference in the shock reaction also leads to different entropy production rates, as we shall demonstrate in the remaining sections. Especially the entropy generated in the pseudo-polytropic multi-ion shock turns out to be much different from corresponding results that we obtain when using our “magneto-adiabatic” approach. We present explicit values for the entropy generated in a pseudo-polytropic, multi-ion shock in Sect. 4.2.
4. The entropy production at the multi-fluid shock
4.1. The entropy jump in the “magneto-adiabatic” approach
Using our “magneto-adiabatic” formulae for the downstream ion pressures (Eq. (33)), we are now able to calculate the following entropy jump in the MHD limit (Eq. (30)): ![\begin{eqnarray} \Delta \bar{S} = \ln \left[\frac{s}{3(1+\zeta K)}(2A+B)(1+\zeta K) \left(\frac{\rho _{1}}{\rho _{2}}\right)^{\gamma_{\rm adia}}\right], \label{eq-deltas-magnet-0} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq127.png) (47)where ζ = npui/np is the PUI abundance, and K is a parameter reflecting the upstream thermal and non-thermal proton configuration (see Sect. 3.2 for a more detailed explanation). Interestingly enough, this equation simplifies to an expression independent from the PUI abundance ζ and the upstream parameter K, simply given by:
(47)where ζ = npui/np is the PUI abundance, and K is a parameter reflecting the upstream thermal and non-thermal proton configuration (see Sect. 3.2 for a more detailed explanation). Interestingly enough, this equation simplifies to an expression independent from the PUI abundance ζ and the upstream parameter K, simply given by: ![\begin{eqnarray} \Delta \bar{S} = \ln \left[\frac{s}{3}(2A+B)s^{-\gamma_{\rm adia}}\right]\cdot \label{eq-deltas-magnet} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq130.png) (48)This expresses the expected fact that the entropy production in our case does not depend on the abundance ζ of upstream pick-up ions, which trivially follows from the concept that PUI protons at the TS should behave exactly like solar wind protons, i.e. depending only on the compression ratio s and the magnetic tilt angle α. A graphical representation of the entropy gain for this pressure model is given in Fig. 2.
(48)This expresses the expected fact that the entropy production in our case does not depend on the abundance ζ of upstream pick-up ions, which trivially follows from the concept that PUI protons at the TS should behave exactly like solar wind protons, i.e. depending only on the compression ratio s and the magnetic tilt angle α. A graphical representation of the entropy gain for this pressure model is given in Fig. 2.
We can also compare this result with the effective polytropic indices γp presented in Fig. 1. Adopting a description using polytropic indices, we obtain ![\begin{eqnarray} \Delta \bar{S} = \ln \left[s^{\gamma_{\rm p}-\gamma_{\rm adia}}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq131.png) (49)This relation easily proves that, for γp< 8 / 3, the normalized entropy increase is of the order of lns, i.e. between 0 and 1.38, which agrees with the numerical results given in Fig. 2.
(49)This relation easily proves that, for γp< 8 / 3, the normalized entropy increase is of the order of lns, i.e. between 0 and 1.38, which agrees with the numerical results given in Fig. 2.
4.2. The entropy jump for non-adiabatic PUIs
 |
Fig. 2 Normalized ion entropy gain as a function of the magnetic field tilt angle α and the compression ratio s for the magnetio-adiabatic approach. |
In the description by Wu et al. (2009), however, the entropy jump explicitly depends on the pick-up ion abundance ζ as we will demonstrate now. Following these authors, solar wind protons and pick-up ions do react to the shock compression in different polytropic forms, the first characterized by a polytropic index γp, the latter by a larger pseudo-polytropic index γpui. Thus, when looking for the related proton entropy jump of the joint ion population, one finds the following result that is valid for these multi-polytropic conditions: ![\begin{eqnarray} \Delta \bar{S}^{\rm p} = \ln \left[\frac{P_{\rm p1}s^{\gamma _{\rm p}}+P_{\rm pui,1}s^{\gamma _{\rm pui}}}{P_{\rm p1}+P_{\rm pui,1}}\left(s^{-\gamma _{\rm adia}}\right)\right]\cdot \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq134.png) (50)Now, introducing the same representation of the upstream pressures Ppui,1 and Pp,1, as used in our approach, and again introducing the PUI abundance ζ, we obtain an entropy jump given by
(50)Now, introducing the same representation of the upstream pressures Ppui,1 and Pp,1, as used in our approach, and again introducing the PUI abundance ζ, we obtain an entropy jump given by ![\begin{eqnarray} \Delta \bar{S}^{\rm p} = \ln \left[\frac{s^{\gamma _{\rm p}}+\zeta Ks^{\gamma _{\rm pui}}}{1+\zeta K} s^{-\gamma _{\rm adia}}\right]. \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq137.png) (51)We now assume that solar wind protons are reacting adiabatically at the shock, so we can select γp = γadia, and obtain an entropy jump of
(51)We now assume that solar wind protons are reacting adiabatically at the shock, so we can select γp = γadia, and obtain an entropy jump of ![\begin{eqnarray} \Delta S^{\rm p} = k_{\rm B}\ln \left[\frac{1+\zeta Ks^{\gamma _{\rm p}-\gamma _{\rm adia}}}{1+\zeta K}\right], \label{eq-deltas-wu} \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq139.png) (52)making it evident that their expression inherently depends on the PUI abundance ζ.
(52)making it evident that their expression inherently depends on the PUI abundance ζ.
A graphical representation of the entropy gain in this model is presented in Fig. 3, where one easily sees that 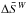 is about one order of magnitude smaller than the magneto-adiabatic entropy gains presented in the previous section. This can be understood easily, as the entropy gain in the non-adiabatic PUI desciption is exclusively related to the non-adiabatic PUI behaviour, which only make a fraction of the entire entropy of the system. Thermal ions, behaving adiabatically, do not increase their entropy at all in this representation.
is about one order of magnitude smaller than the magneto-adiabatic entropy gains presented in the previous section. This can be understood easily, as the entropy gain in the non-adiabatic PUI desciption is exclusively related to the non-adiabatic PUI behaviour, which only make a fraction of the entire entropy of the system. Thermal ions, behaving adiabatically, do not increase their entropy at all in this representation.
 |
Fig. 3 Normalized ion entropy gain as a function of the PUI abundance ζ and the PUI polytropic index γ for a shock where thermal protons behave adiabatically, and the PUIs behave non-adiabatically. The compression ratio is s = 3. |
The selection of this assumption was based on a best-fit approach to the Voyager data, which does not allow us to assess the behaviour of the thermal solar wind plasma component. Therefore, any theoretical modelling must take great care when making model assumptions concerning the behaviour of the thermal protons. However, our results suggest that the thermal protons do most likely not behave adiabatically at the shock (unless average tilt angles of α ≃ 40° are assumed, see Fig. 1), as this behaviour obviously results in a strong suppression of entropy production.
4.3. The entropy jump for a multi-fluid system including electrons
Finally, we also include the downstream electron pressure that we have derived in Fahr & Siewert (2013), combine it with the ion pressure and derive a more consistent description of the total particle entropy increase. In this earlier description, we found that the electron downstream pressure is substantially increased as a reaction of the negatively charged electrons to the electric shock potential. Therefore, one can expect that the electron entropy will be increased as well, and we can start with Eq. (47), add the electron pressure as found in the earlier study, and obtain ![\begin{eqnarray} \Delta \bar{S}^{\rm e} &=& \ln \left[\frac{P_{2,tot}}{P_{1}}\left(\frac{\rho _{1}}{\rho _{2}}\right)^{\gamma _{\rm adia}}\right]\nonumber\\ &=& \ln \left[\frac{P_{\rm 2,p}+P_{2,{\rm pui}}+P_{\rm 2,e}}{P_{\rm 1,p}+P_{\rm 1,{\rm pui}}+P_{\rm 1,e}} \left(\frac{\rho _{1}}{\rho _{2}}\right)^{\gamma _{\rm adia}}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq142.png) (53)Now, keeping in mind that P1,p ≃ P1,e, we can adopt P1,p + P1,pui + P1,e = P1,p(2 + ζK) and obtain to the expression
(53)Now, keeping in mind that P1,p ≃ P1,e, we can adopt P1,p + P1,pui + P1,e = P1,p(2 + ζK) and obtain to the expression ![\begin{eqnarray} \Delta \bar{S}^{\rm e} &=& \ln \left[\frac{s^{-\gamma _{\rm adia}}}{2+\zeta K} \left(\frac{s}{3}(2A(\alpha)+B(\alpha )\right)(1+\zeta K) \right. \nonumber\\ && \left. +\frac{s^{2}-1}{s}\frac{U_{1}^{2}}{c_{\rm 1,p}^{2}}\left[\sin ^{2}\alpha A(\alpha )+\cos ^{2}\alpha B(\alpha )\right] \right], \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq145.png) (54)where the final identity follows from Fahr & Siewert (2013). Here, U1/c1,p is the ratio of the upstream plasma flow speed and the thermal proton sound speed (i.e. a sonic Mach number).
(54)where the final identity follows from Fahr & Siewert (2013). Here, U1/c1,p is the ratio of the upstream plasma flow speed and the thermal proton sound speed (i.e. a sonic Mach number).
As one can see in this expression for the total entropy jump related to the particles, the dependence on the PUI abundance ζ now reappears, since not all particles, i.e. electrons and ions, react alike when passing over the shock. However, as it turns out, the term with the resulting ζ-dependence is negligible compared to the electron term; in fact, assuming that ζK ≫ 1, the dependence on these parameters drops out completely. In contrast to ions, electrons experience strong overshooting at the shock, resulting in strong heating by thermalisation of this kinetic overshoot energy. However, the magnitude of the entropy jump now has increased significantly because of the large downstream electron pressure as shown in Fig. 4, where we demonstrate that electrons in fact provide the strongest contribution to the entropy increase, and that the Mach number M = U1/c1,p provides the strongest influence on the overall entropy jump. In addition to this, we also have studied the dependence on the MHD compression ratio s, where one easily sees that the influence of this parameter is also strong (Fig. 5).
Unfortunately, there is neither data available to check on this point, nor is there any running mission dedicated to TS electrons, so it is impossible to verify this result observationally in the forseeable future. Nevertheless, our results suggest that the electron component possesses a strong dependence on various parameters of the shock that can be difficult to observe otherwise, so any future mission to the solar wind TS would greatly benefit from a dedicated electron instrument.
 |
Fig. 4 Normalized entropy gain as a function of the magnetic field tilt angle α and the Mach number M for a shock where electron overshooting is taken into account. The compression ratio is s = 3. |
 |
Fig. 5 Normalized entropy gain as a function of the magnetic field tilt angle α and the compression ratio s for a shock where electron overshooting is taken into account. The mach number is M = 5. |
4.4. The entropy jump using a downstream κ function for a combined proton component
Finally, we study the impact of using a downstream κ function to represent the joint thermal and PUI proton populations. In Sect. 3.2, we introduced joint downstream proton distribution function describing both a thermal core and non-thermal tail of PUI protons. Since the parameters of the κ-function were set up in a way that the pressure is identical to the magneto-adiabatic entropy (see Sect. 4.1), we can not expect new results from this side. Instead, we now present some selected, more general aspects of entropy jumps with κ functions at the shock.
First, we find that κ-functions originate in a model function for data fits (Vasyliunas 1968), and even after all of the progress that has been made with understanding κ-functions, one still commonly finds modelling approaches where this function and its parameters are not strongly supported by theoretical arguments. Therefore, we now close our study of the multi-component TS with a brief overview of entropy jumps in κ-functions.
Considering Eq. (27) and the discussion following it, we can find the following relation between the Maxwellian and the κ-entropy: 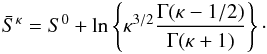 (55)This equation easily proves an important point. As long as the upstream and downstream κ-values remain the same, the contribution to the entropy jump cancels out, and the entropy increase simplifies to the classical Maxwellian expression S0. When there are different κ-indices on both sides of the termination shock, one obtains an additional contribution to the power indices:
(55)This equation easily proves an important point. As long as the upstream and downstream κ-values remain the same, the contribution to the entropy jump cancels out, and the entropy increase simplifies to the classical Maxwellian expression S0. When there are different κ-indices on both sides of the termination shock, one obtains an additional contribution to the power indices: ![\begin{eqnarray} \label{eq-deltas-kappa} \Delta \bar{S}^\kappa &=& \Delta \bar{S}^0 + \ln \left[ \left( \frac{\kappa_2}{\kappa_1} \right)^{3/2} \frac{\Gamma\left(\kappa_2-\frac{1}{2}\right)}{\Gamma\left(\kappa_1-\frac{1}{2}\right)} \frac{\Gamma\left(\kappa_1+1\right)}{\Gamma\left(\kappa_2+1\right)} \right] \nonumber\\ &=& \Delta \bar{S}^0 + \ln \left[ \sqrt{ \frac{\kappa_2}{\kappa_1} } \frac{\Gamma\left(\kappa_2-\frac{1}{2}\right)}{\Gamma\left(\kappa_1-\frac{1}{2}\right)} \frac{\Gamma(\kappa_1)}{\Gamma(\kappa_2)} \right]\cdot \end{eqnarray}](/articles/aa/full_html/2015/04/aa24485-14/aa24485-14-eq153.png) (56)This relation holds true for arbitrary physical values of κ and clearly demonstrates that the additional contribution to
(56)This relation holds true for arbitrary physical values of κ and clearly demonstrates that the additional contribution to 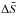 depends only on the κ-parameters on both sides of the shock. In addition, Eq. (56) is only applicable to systems where the number of individual shock components does not change between both sides, i.e. it is not applicable to the joint downstream model adopted in Sect. 3.2.
depends only on the κ-parameters on both sides of the shock. In addition, Eq. (56) is only applicable to systems where the number of individual shock components does not change between both sides, i.e. it is not applicable to the joint downstream model adopted in Sect. 3.2.
4.5. An eye-guide estimate of the thermodynamically permitted total entropy jump
The total entropy jump resulting from the thermodynamically permitted conversion of the free kinetic energy of the upstream flow can now be compared with the above considerations. For a monofluid plasma, i.e. taking protons and pick-up protons together as one joined ion fluid, this entropy generation can simply be estimated with the following procedure: The normalized maximum entropy jump per particle, 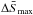 , is given by the following classical thermodynamic expression
, is given by the following classical thermodynamic expression 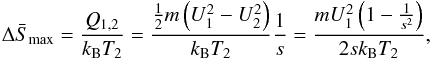 (57)where T2 denotes the effective downstream temperature of the plasma mixture that absorbs the converted kinetic energy. Taking Voyager-2 shock crossing data for solar wind protons taken as the thermodynamically relevant fluid, i.e. T2 = 2 × 105 K; s = 2.5; U1 = 4 × 107 cm/s, one then would find
(57)where T2 denotes the effective downstream temperature of the plasma mixture that absorbs the converted kinetic energy. Taking Voyager-2 shock crossing data for solar wind protons taken as the thermodynamically relevant fluid, i.e. T2 = 2 × 105 K; s = 2.5; U1 = 4 × 107 cm/s, one then would find 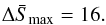 (58)Comparing this with the values
(58)Comparing this with the values 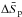 and
and 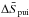 , which we have displayed in our Figs. 2–5, one could easily allow an increase of the effective downstream temperature by a factor of 80 to 100. Thus one could allow for an increase in the downstream pressure by about this factor without violating any fundamental thermodynamic law. If, for instance, the downstream thermal ensemble is characterized by a temperature of the order of T2 = 2 × 107 K (instead as for normal solar wind protons of 2 × 105 K) still everything would be in complete thermodynamic order without violating fundamental principles. Hence the strongly heated downstream electrons, which in our approach (Fahr & Siewert 2013) attain temperatures of the order of Te,2 ≥ 107 K, are in excellent agreement with thermodynamically allowed values, and they also support the maximum entropy principle much better than a pure proton plasma.
, which we have displayed in our Figs. 2–5, one could easily allow an increase of the effective downstream temperature by a factor of 80 to 100. Thus one could allow for an increase in the downstream pressure by about this factor without violating any fundamental thermodynamic law. If, for instance, the downstream thermal ensemble is characterized by a temperature of the order of T2 = 2 × 107 K (instead as for normal solar wind protons of 2 × 105 K) still everything would be in complete thermodynamic order without violating fundamental principles. Hence the strongly heated downstream electrons, which in our approach (Fahr & Siewert 2013) attain temperatures of the order of Te,2 ≥ 107 K, are in excellent agreement with thermodynamically allowed values, and they also support the maximum entropy principle much better than a pure proton plasma.
If, instead of T2 = 2 × 105 K, one would assume the effective thermal downstream plasma mixture, due to the strongly heated electrons, to be of the order of T2 = 2 × 107 K (instead of just the electron temperature Te,2), it then would bring the maximum entropy jump just down to the achieved level 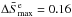 (see Figs. 2 and 3).
(see Figs. 2 and 3).
5. Conclusions
We have investigated how much particle-specific entropy is produced at the passage of the multi-fluid solar wind plasma over the MHD termination shock. Hereby, we have started from a consistent solution of the multi-fluid MHD Rankine-Hugoniot shock relations to first find the consistent value of the resulting compression ratio s. With the additional help of kinetic information on the behaviour of the particle velocity components at the shock passage and with the use of the Liouville theorem, we then obtain expressions for the downstream distribution functions and the pressures of the different fluids like solar wind protons, pick-up protons, and electrons. Using standard thermodynamic expressions, we can calculate fluid-specific entropy productions from the individual fluid pressures. The calculated entropy productions per particle, both of solar wind protons and pick-up protons, then amount to much lower values than allowed by thermodynamically maximal values of ΔSmax/kb = 16. Only when we include the electron fluid as the downstream fluid with by far the highest temperature, can we then calculate for the first time a reasonably high value for the joint entropy production of the shocked multi-fluid plasma. Not only do the shocked electrons represent the most important part of the whole entropy production, they also are shown to be the plasma fluid with the highest thermal pressure. This fact allows for many interesting new conclusions concerning the dynamics of the downstream heliosheath plasma flow.
Similar results are also obtained by shock simulations carried out by Lembège et al. (2003). While most of the other shock simulations treat the electrons as a background fluid with an electron temperature reacting adiabatically to the density increase, i.e. 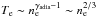 , Lembège et al. (2003) treat electrons kinetically and allow them to be heated according to two-stream or viscous friction mechanisms. The result hereby is that Lembège et al. (2003) obtain electron temperature increases by factors of about 50, while in case of the Voyager-shock (Richardson et al. 2008) the adiabatic heating only leads to a temperature increase of about a factor of 2. We conclude that Lembège et al. (2003) obtain about the same electron heating as we, namely the heating corresponding to the full thermalisation of the electron overshoot velocities.
, Lembège et al. (2003) treat electrons kinetically and allow them to be heated according to two-stream or viscous friction mechanisms. The result hereby is that Lembège et al. (2003) obtain electron temperature increases by factors of about 50, while in case of the Voyager-shock (Richardson et al. 2008) the adiabatic heating only leads to a temperature increase of about a factor of 2. We conclude that Lembège et al. (2003) obtain about the same electron heating as we, namely the heating corresponding to the full thermalisation of the electron overshoot velocities.
The preceeding points out the difference between the approaches presented here or by Lembège et al. (2003) and those of many other shock-related papers. The former approaches treat collisionless shocks in which electrons at the shock transition preserve their complete degree of thermodynamical freedom, i.e. they are not tied to ions, so that quasi-neutrality and identical ion and electron bulk velocities are enforced everywhere (see e.g. Leroy et al. 1981, 1982). Over distances of electron relaxation lengths, electrons are allowed to react freely to the shock electric field, while thereafter relaxing to the joint downstream plasma system by which the frozen-in downstream magnetic field is also transported. This thermodynamic degree of freedom is absolutely important for the conversion of upstream kinetic energy into downstream thermal energy, whereas when ions and electrons are considered to be dynamically coupled to each other this channel of entropy generation is blocked. In a simplified approach for the case of a parallel shock this has quantitatively been demonstrated in Verscharen & Fahr (2008).
Furthermore not only do shocked electrons represent the most important part of the whole entropy production, in contrast to earlier representations, they are also shown to be the plasma fluid component with the highest thermal pressure. This fact allows for many interesting new conclusions concerning the dynamics of the downstream heliosheath plasma flow, which under these conditions may be nearly incompressible (see Fahr & Siewert 2013, and below in this section).
On question, however, with respect to these predicted suprathermal electrons, is why these electrons have not been obviously detected in the heliosheath by the Faraday cup instrumentations onboard of Voyager-1/-2. Our answer is presently the following: The predicted suprathermal electrons downstream of the shock do in fact heavily charge up every spacecraft in the heliosheath to negative potentials of about –30 V, which then as a consequence screen off most of the electrons from the detectors (see paper by Fahr & Richardson, in prep.).
Even though the main outcome here can be seen in the fact that the decisive part of the entropy production at the plasma passage over the shock is represented by the strongly heated downstream electrons, we also want to emphasize the related earlier result from Fahr & Siewert (2013) who found that these latter, nearly massless particles do also represent the dominant contribution to the total downstream plasma pressure (and thus, the entropy, as seen from Eq. (30)). This eminent feature has some important consequences for the form, how the downstream plasma flow organizes itself, as we shall demonstrate below.
As is well known from the equation of motion of the multi-fluid plasma mixture, one can construct a typical streamline-constant for the downstream plasma flow, called the Bernoulli constant CB, with the property (U·gradCB) = 0. In case of the multi-fluid plasma, which we have considered, we find CB as given by (see Landau & Lifshitz 1977) 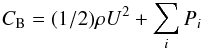 (59)where ρ = ∑ iρi denotes the total mass density of the plasma, and Pi denote the different downstream pressures of SW protons, PUI protons, and electrons. Taking into account that amongst the downstream pressures the electron pressure Pe,2 is by far dominant, one can write for the stagnation streamline, i.e approaching from downstream of the termination shock the stagnation point of the heliosheath flow at the heliopause, the following relation
(59)where ρ = ∑ iρi denotes the total mass density of the plasma, and Pi denote the different downstream pressures of SW protons, PUI protons, and electrons. Taking into account that amongst the downstream pressures the electron pressure Pe,2 is by far dominant, one can write for the stagnation streamline, i.e approaching from downstream of the termination shock the stagnation point of the heliosheath flow at the heliopause, the following relation 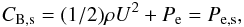 (60)where Pe,s is the electron pressure at the stagnation point. This relation can easily be rearranged to
(60)where Pe,s is the electron pressure at the stagnation point. This relation can easily be rearranged to 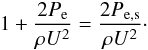 (61)We introduce the effective sound velocity cs and the effective Mach number in the heliosheath flow by
(61)We introduce the effective sound velocity cs and the effective Mach number in the heliosheath flow by 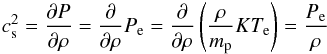 (62)and
(62)and 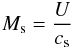 (63)then brings the above relation into the following form
(63)then brings the above relation into the following form 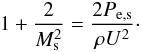 (64)Finally, we point out that
(64)Finally, we point out that 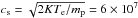 cm/s then shows that
cm/s then shows that 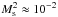 and that hence in the above relation the first term on the left side, i.e. “1”, can be neglected, then leads to the simple requirement
and that hence in the above relation the first term on the left side, i.e. “1”, can be neglected, then leads to the simple requirement 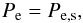 (65)and with a polytropic relation of gas and density like Cp = P/ργ then simply states that ρ/ρs = 1− γ = 1, i.e. that the density along the stagnation streamline, to be generalized to other streamlines, is constant, and that the plasma consequently behaves as an incompressible fluid, which then for instance allows a flow potential Φ to be used as Fahr & Fichtner (1991) have done to describe the heliosheath streamlines through ρU = − gradΦ.
(65)and with a polytropic relation of gas and density like Cp = P/ργ then simply states that ρ/ρs = 1− γ = 1, i.e. that the density along the stagnation streamline, to be generalized to other streamlines, is constant, and that the plasma consequently behaves as an incompressible fluid, which then for instance allows a flow potential Φ to be used as Fahr & Fichtner (1991) have done to describe the heliosheath streamlines through ρU = − gradΦ.
Acknowledgments
M. Siewert is grateful to the Deutsche Forschungsgemeinschaft for financial support granted to him in the frame of the project Si-1550/2-2.
References
- Baumjohann, W., & Treumann, R. A. 1996, Basic space plasma physics (London: Imperial College Press) [Google Scholar]
- Brey, J. J., &Santos, A. 1992, Phys. Rev. A, 45, 8566 [NASA ADS] [CrossRef] [Google Scholar]
- Cercignani, C. 1988, The Boltzmann Equation and Its Applications (New York: Springer-Verlag) [Google Scholar]
- Chalov, S. V., &Fahr, H.-J. 1994, A&A, 288, 973 [NASA ADS] [Google Scholar]
- Chalov, S. V., &Fahr, H.-J. 1995, Planet. Space Sci., 43, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Chalov, S. V., &Fahr, H. J. 1996, Sol. Phys., 168, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Chew, G. F.,Goldberger, M. L., &Low, F. E. 1956, Proc. R. Soc. London A, 236, 112 [Google Scholar]
- Collier, M. R. 1995, Geophys. Res. Lett., 22, 2673 [NASA ADS] [CrossRef] [Google Scholar]
- Decker, R. B. 1988, Space Sci. Rev., 48, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Diver, D. A. 2001, A Plasma Formulary for Physics, Technology and Astrophysics (Hoboken, New Jersey: John Wiley) [Google Scholar]
- Erkaev, N. V.,Vogl, D. F., &Biernat, H. K. 2000, J. Plasma Phys., 64, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H.-J., &Fichtner, H. 1991, Space Sci. Rev., 58, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H.-J., &Siewert, M. 2006, A&A, 458, 13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H.-J., &Siewert, M. 2010, Astrophys. Space Sci. Trans., 6, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Fahr, H.-J., &Siewert, M. 2013, A&A, 558, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fahr, H.-J.,Siewert, M., &Chashei, I. 2012, Ap&SS, 341, 265 [Google Scholar]
- Gombosi, T. I. 1998, Physics of the Space Environment (New York: Cambridge University Press) [Google Scholar]
- Heerikhuisen, J., Pogorelov, N. V., Florinski, V., Zank, G. P., & Le Roux, J. A. 2008, ApJ, 682, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, P. D. 1970, Planet. Space Sci., 18, 1611 [NASA ADS] [CrossRef] [Google Scholar]
- Kucharek, H., &Scholer, M. 1995, J. Geophys. Res., 100, 1745 [NASA ADS] [CrossRef] [Google Scholar]
- Kucharek, H., Möbius, E., & Scholer, M. 2006, in Physics of the Inner Heliosheath, eds. J. Heerikhuisen, V. Florinski, G. P. Zank, & N. V. Pogorelov, AIP Conf. Ser., 858, 196 [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1977, Lehrbuch der theoretischen Physik (Berlin: Akademiker-Verlag) [Google Scholar]
- Le Roux, J. A., &Fichtner, H. 1997, ApJ, 477, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Le Roux, J. A., &Fichtner, H. 1999, J. Geophys. Res., 104, 4709 [NASA ADS] [CrossRef] [Google Scholar]
- Lembège, B.,Savoini, P.,Balikhin, M.,Walker, S., &Krasnoselskikh, V. 2003, J. Geophys. Res., 108, 1256 [CrossRef] [Google Scholar]
- Lembege, B.,Giacalone, J.,Scholer, M., et al. 2004, Space Sci. Rev., 110, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, M. M., &Mangeney, A. 1984, Ann. Geo., 2, 449 [Google Scholar]
- Leroy, M. M.,Goodrich, C. C.,Winske, D.,Wu, C. S., &Papadopoulos, K. 1981, Geophys. Res. Lett., 8, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, M. M.,Winske, D.,Goodrich, C. C.,Wu, C. S., &Papadopoulos, K. 1982, J. Geophys. Res., 87, 5081 [NASA ADS] [CrossRef] [Google Scholar]
- Liewer, P. C.,Goldstein, B. E., &Omidi, N. 1993, J. Geophys. Res., 98, 15211 [NASA ADS] [CrossRef] [Google Scholar]
- Livadiotis, G., &McComas, D. J. 2009, J. Geophys. Res., 114, 11105 [Google Scholar]
- Livadiotis, G., &McComas, D. J. 2012, ApJ, 749, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Matsukiyo, S., &Scholer, M. 2011, J. Geophys. Res., 116, 8106 [CrossRef] [Google Scholar]
- Neubauer, F. M. 1970, Z. Phys., 237, 205 [Google Scholar]
- Richardson, J. D.,Kasper, J. C.,Wang, C.,Belcher, J. W., &Lazarus, A. J. 2008, Nature, 454, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sarris, E. T., & van Allen, J. A. 1974, J. Geophys. Res., 79, 4157 [NASA ADS] [CrossRef] [Google Scholar]
- Scholer, M. 1993, J. Geophys. Res., 98, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Serrin, J. 1959, Handbuch der Physik, Vol. VIII, Mathematical principles of classical fluid mechanics (Berlin: Springer Verlag) [Google Scholar]
- Siewert, M., &Fahr, H.-J. 2007, A&A, 463, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siewert, M., &Fahr, H.-J. 2008, A&A, 485, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siewert, M., &Fahr, H.-J. 2009, A&A, 501, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terasawa, T. 1979, Planet. Space Sci., 27, 193 [Google Scholar]
- Treumann, R. A. 1999, Phys. Scr., 59, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Treumann, R. A. 2001, Ap&SS, 277, 81 [Google Scholar]
- Treumann, R. A.,Jaroschek, C. H., &Scholer, M. 2004, Phys. Plasmas, 11, 1317 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyliunas, V. M. 1968, J. Geophys. Res., 73, 2839 [NASA ADS] [CrossRef] [Google Scholar]
- Verscharen, D., &Fahr, H.-J. 2008, A&A, 487, 723 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weizel, W. 1958, Das Boltzmannsche H-Theorem (Springer Verlag), 1516 [Google Scholar]
- Wu, P.,Winske, D.,Gary, S. P.,Schwadron, N. A., &Lee, M. A. 2009, J. Geophys. Res., 114, 8103 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, P.,Liu, K.,Winske, D., et al. 2010, J. Geophys. Res., 115, 11105 [CrossRef] [Google Scholar]
- Zank, G. P.,Webb, G. M., &Donohue, D. J. 1993, ApJ, 406, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P.,Heerikhuisen, J.,Pogorelov, N. V.,Burrows, R., &McComas, D. 2010, ApJ, 708, 1092 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Polytropic indices obtained from our kinetic shock model according to Eq. (43) for different magnetic field orientations and MHD compression ratios. |
| In the text | |
 |
Fig. 2 Normalized ion entropy gain as a function of the magnetic field tilt angle α and the compression ratio s for the magnetio-adiabatic approach. |
| In the text | |
 |
Fig. 3 Normalized ion entropy gain as a function of the PUI abundance ζ and the PUI polytropic index γ for a shock where thermal protons behave adiabatically, and the PUIs behave non-adiabatically. The compression ratio is s = 3. |
| In the text | |
 |
Fig. 4 Normalized entropy gain as a function of the magnetic field tilt angle α and the Mach number M for a shock where electron overshooting is taken into account. The compression ratio is s = 3. |
| In the text | |
 |
Fig. 5 Normalized entropy gain as a function of the magnetic field tilt angle α and the compression ratio s for a shock where electron overshooting is taken into account. The mach number is M = 5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


