| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 8 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201425056 | |
| Published online | 26 February 2015 | |
MIARMA: A minimal-loss information method for filling gaps in time series
Application to CoRoT light curves⋆
Instituto de Astrofísica de Andalucía – CSIC,
18008
Granada,
Spain
e-mail: javier@iaa.es; garrido@iaa.es; jcsuarez@iaa.es
Received: 25 September 2014
Accepted: 11 December 2014
Context. Gaps in time series cause spurious frequencies in the power spectra. In light curves of pulsating stars, this hampers identifying the theoretical oscillation modes. When these gaps are smaller than the total time span, the commonly used approach to overcome these difficulties involves linear interpolation. The original frequency content of the pulsating stars is not preserved in the resulting time series.
Aims. The method presented here intends to minimize the effect of the gaps in the power spectra by gap-filling that preserves at best the original information, that is, the stellar oscillation frequency content for asteroseismology.
Methods. We used a forward-backward predictor based on autoregressive moving-average modelling (ARMA) in the time domain. The algorithm MIARMA is particularly suitable for replacing invalid data such as those present in the light curves of the CoRoT satellite due to the pass through the South Atlantic Anomaly, and eventually for the data gathered by the NASA planet hunter Kepler. We selected a sample of stars from the ultra-precise photometry collected by the asteroseismic camera on board the CoRoT satellite: the δ Scuti star HD 174966, showing periodic variations of the same order as the CoRoT observational window, the Be star HD 51193, showing longer time variations, and the solar-like HD 49933, with rapid time variations.
Results. We show that in some cases linear interpolations are less reliable than previously believed. The ARMA interpolation method provides a cleaner power spectrum, that is, less contaminated by spurious frequencies. In summary, MIARMA appears to be a suitable method for filling gaps in the light curves of pulsating stars observed by CoRoT since the method aims to preserve their frequency content, which is a necessary condition for asteroseismic studies.
Key words: asteroseismology / methods: data analysis / stars: oscillations
© ESO, 2015
1. Introduction
As pointed out by Deeming (1975), gaps change the original frequency content of any sampled signal because the observed power spectrum is the result of a convolution of the original signal with the observational window. When the gaps are smaller than the total time span, techniques based on gap-filling have commonly been used (Fahlman & Ulrych, 1982; Brown & Christensen-Dalsgaard, 1990; Fossat et al., 1999; Roques et al., 2000; García et al., 2014). For larger gaps, the pre-whitening techniques become unavoidable (Breger et al., 1993). Most of the popular gap-filling algorithms do not guarantee the preservation of the original frequency content, which is crucial for asteroseismology to be reliable. The most widely used technique, as is the case for CoRoT data, is the linear interpolation because of its simplicity.
Space missions such as CoRoT (Baglin et al., 2006) or Kepler (Gilliland et al., 2010) have observed a large sample of stars with two main objectives: first the detection of transits to search for planets orbiting other stars, and second, to characterize the stars through asteroseismology. Asteroseismology enables determining global properties of the stars such as radius or age and also allows inferring the internal structure and internal rotation profile. For this objective a long and uninterrupted observation is required to obtain reliable results. To detect transits, more precise measurements and a better time sampling is required. The requisites for both these objectives are fulfilled by the space missions, which are observing continuously and with an unprecedented resolution. Nevertheless, a photometric time series without gaps is an ideal case that is never reached. In practice, there are always some invalid flux measurements as a result of operational procedures such as the change of mask, reorientation, data downloading, or environmental effects such as the impact of energetic particles, as is the case when CoRoT passes through the South Atlantic Anomaly (SAA). These produce invalid data or interruptions in the time series that affect the analyses in the frequency domain.
We introduce here a new gap-filling algorithm (MIARMA) that is based on an non-closed form and can represent any kind of function, even non-analytic functions, thus preserving at best the original frequency content of the signal. This method uses a forward-backward predictor based on autoregressive moving average (ARMA) models to fill the gaps in astronomical time series. By applying this method to time series of stars with different pulsational characteristics observed by CoRoT satellite, new properties of the light curves are revealed.
We first review in Sect. 2 some of the problems found when analysing gapped time series, which are reduced when appropriate interpolation methods are used, and we show that some of the usual interpolation methods are inappropriate, proving that an adequate gap-filling method can significantly improve the frequency determination of the oscillations in time series. In Sect. 3 we describe the method for gap-filling based on modelling valid data segments as ARMA processes. Then, in Sect. 4 we apply the method to three different cases: the δ Scuti star HD 174966, the Be star HD 51193, and the solar-like HD 49933. We discuss the consequences of our results in Sect. 5, and the conclusions are presented in Sect. 6.
2. Gaps in time series
To consider the effects of the gaps (meaning not only the lack of measurements, but also invalid flux measurements) in the estimation of the power spectra, one must consider (Deeming, 1975) 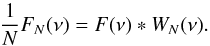 (1)That is, the discrete Fourier transform (DFT) FN(ν) of a gapped time series is the convolution of the Fourier transform of the original function F(ν) with the spectral window WN(ν), which is defined as the DFT of the function describing the observational time. All problems related to gaps in time series derive from this simple formula. First of all, the spectral window always contains a sinc function related to the length of the observation. This reduces the amplitudes of the peaks caused by harmonic components because the power is spread in sidelobes. For long observations, as is the case with space satellites, this effect is insignificant. However, when there are gaps in the time series, and when these gaps are regularly distributed, another sinc function appears in the spectral window related to the length of the gaps that spreads much more power of the central peak in sidelobes – spectral leakage. As a consequence, the signal-to-noise ratio is reduced, leading to a less reliable frequency detection that affects parameter estimation.
(1)That is, the discrete Fourier transform (DFT) FN(ν) of a gapped time series is the convolution of the Fourier transform of the original function F(ν) with the spectral window WN(ν), which is defined as the DFT of the function describing the observational time. All problems related to gaps in time series derive from this simple formula. First of all, the spectral window always contains a sinc function related to the length of the observation. This reduces the amplitudes of the peaks caused by harmonic components because the power is spread in sidelobes. For long observations, as is the case with space satellites, this effect is insignificant. However, when there are gaps in the time series, and when these gaps are regularly distributed, another sinc function appears in the spectral window related to the length of the gaps that spreads much more power of the central peak in sidelobes – spectral leakage. As a consequence, the signal-to-noise ratio is reduced, leading to a less reliable frequency detection that affects parameter estimation.
The spectral window can also cause spurious frequencies to appear far from the central peak, which can be confused with other peaks and mislead the frequency detection and identification.
On the other hand, WN(ν) is a complex function, which means that it introduces a deviation in the original phases of the signal. This deviation is difficult to determine when the gaps are irregularly distributed. This hinders determining the phases, which is crucial for resonance studies in high-amplitude pulsating stars (Garrido & Rodríguez, 1996) or for determining phase differences between different wavelengths for mode identification (Garrido, 2000).
Another problem concerns the normalisation of the periodogram to give a consistent estimate of the power spectrum. This problem was solved by Scargle (1982) with a proper normalisation of the real and imaginary part that preserves the statistical properties of the regular sampling when the sampling is irregular. However, the Lomb-Scargle periodogram gives the same result as filling with zeros the gaps to obtain a regular sampling and then calculating the periodogram through a fast Fourier transform (FFT). It can be shown that the convolution of the data with the spectral window introduces correlations between Fourier frequencies (Stahn & Gizon, 2008). In this way, as the Lomb-Scargle periodogram does not remove the effect of the spectral window, correlations between frequencies due to the gaps are maintained.
These effects have a lower impact in the case of CoRoT and Kepler than in ground-based observations since the duty cycle is always higher than 80% and the gaps are not as regularly distributed as the diurnal cycle. However, it is still crucial to reduce them to obtain a consistent estimate of the power spectra. This is especially relevant in the case of CoRoT observations because the invalid data measurements introduced by the SAA are quasiperiodic (Auvergne et al., 2009).
To obtain the power spectrum of a gapped time series, many approaches have been used in the past. The most simple one is filling the gaps with zeros and then computing the periodogram of the evenly sampled time series with an FFT. This technique has the same pathologies that are found when using unequally spaced data. Replacing the gaps with zeros does not avoid the spectral window contribution at all.
A second approach more commonly used is a simple linear interpolation between valid segments. This might be a good approach when the gaps and the variance of the time series are small, but in other cases this solution is insufficient to remove the aliases, as can be seen in Fig. 1.
Other more sophisticated gap-filling techniques (e.g. Fossat et al. 1999) used an approach based on the autocorrelation of the oscillation signals.
More recently, the inpainting technique, based on a sparse representation of a dictionary of multi-scale cosine functions, is being used for filling gaps in CoRoT (Sato et al., 2010; Mathur et al., 2010, 2013) and Kepler data (Pires et al., 2015; García et al., 2014).
We adopted a signal-identification method based on an non-closed form expression that allows any type of function to be modelled, regardless of whether it is analytic or not. We used a forward-backward predictor for filling gaps that takes data before and after the gaps and interpolates by means of autoregressive moving-average models. This method does not require choosing any a priori closed-form representation, and for this reason, the information loss can be minimized using a statistical criterion. In this sense, the method aims to preserve the original frequency content of the signal.
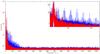 |
Fig. 1 Periodogram of the δ Scuti star HD 172189 calculated using an FFT of the linearly interpolated time series (blue), and as interpolated by MIARMA (red). The frequencies in the δ Scuti instability range in the inset are affected by the spectral window. |
3. MIARMA
3.1. Autoregressive and moving-average methods
The aim of these methods is to determine a parametric representation of a time series assuming that the correlation between data can be expressed in a recursive formula like this: 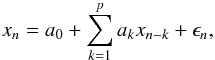 (2)where xn is the time series, ak are the p parameters of the autoregressive model AR(p) of order p, ϵn is the error, and usually, a0 = 0 when the time series has zero mean. This representation can be used to model any type of variability, regardless of whether it is analytic or not. For example, Yule (1927) showed that the solution of the differential equation of the damped harmonic oscillator can be expressed as an AR(2) process, that is,
(2)where xn is the time series, ak are the p parameters of the autoregressive model AR(p) of order p, ϵn is the error, and usually, a0 = 0 when the time series has zero mean. This representation can be used to model any type of variability, regardless of whether it is analytic or not. For example, Yule (1927) showed that the solution of the differential equation of the damped harmonic oscillator can be expressed as an AR(2) process, that is, 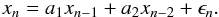 Then, for time series caused by multi-periodic pulsating stars with M harmonic components, it is reasonable to assume an AR representation with 2*M coefficients.
Then, for time series caused by multi-periodic pulsating stars with M harmonic components, it is reasonable to assume an AR representation with 2*M coefficients.
A moving-average process (MA) is defined as 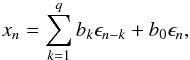 (3)where ϵn is an independent white-noise process, bk are the q parameters of the model MA(q), and b0 is usually normalised to 1. The moving-average model can be identified with a linear filter with coefficients bk and input ϵn giving xn as the output.
(3)where ϵn is an independent white-noise process, bk are the q parameters of the model MA(q), and b0 is usually normalised to 1. The moving-average model can be identified with a linear filter with coefficients bk and input ϵn giving xn as the output.
These two representations are directly related: the MA representation is based on correlations between the inputs ϵn , while the AR representation is based on correlations between the outputs xn. It can be demonstrated that an AR representation can be determined from an MA and vice versa.
On the other hand, a mixed autoregressive moving-average process ARMA(p,q) can be expressed as 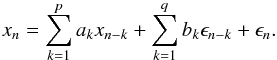 (4)Note that with the notation used above, the AR(p) process represented in Eq. (2) can also be ARMA(p,0), and the MA(q) process represented in Eq. (3) can be also ARMA(0,q). Thus the ARMA representation is a generalisation of AR and MA. Furthermore, some processes can be represented with a finite number of parameters in the ARMA representation while they require infinite parameters in a pure AR or MA. In these cases, an ARMA model can exactly represent a signal while the others cannot, and it is computationally more efficient. For a comprehensive discussion of these methods see Scargle (1981).
(4)Note that with the notation used above, the AR(p) process represented in Eq. (2) can also be ARMA(p,0), and the MA(q) process represented in Eq. (3) can be also ARMA(0,q). Thus the ARMA representation is a generalisation of AR and MA. Furthermore, some processes can be represented with a finite number of parameters in the ARMA representation while they require infinite parameters in a pure AR or MA. In these cases, an ARMA model can exactly represent a signal while the others cannot, and it is computationally more efficient. For a comprehensive discussion of these methods see Scargle (1981).
Autoregressive methods have been used in the past in the context of pulsating stars for filling gaps. Fahlman & Ulrych (1982) used them for the first time with pure AR processes and global modelling. However, it can be easily seen that this method fails when the time series is non-stationary since the coefficients change during the observation. Roques et al. (2000) used an AR local model. This allows reproducing seasonal changes in the time series and a certain non-stationarity is permitted, but the order is fixed by an arbitrary criterion, that is, the average length of the data segments.
Roth & Zhugzhda (2010) used a second-order AR process whose parameters are determined through the expectation maximization algorithm. In that case, the amplitudes of the estimates depend on the duration of the time series and the computational cost is high because they have to model the whole time series globally as well.
As far as we know, these have been the only non-analytic approaches for filling gaps used in the field of asteroseismology.
We can state that the ARMA representation is as general as Wold’s theorem (Wold, 1938) permits, namely that any stationary signal can be represented as the sum of a deterministic (AR) plus a stochastic process (MA). In this way, these models are robust since an exact representation of the signal can be found independently of its properties: periodic or aperiodic, deterministic or stochastic, analytic or non-analytic, chaotic or not. As explained in the following subsection, non-stationarity in the signal is overcome by the algorithm because of the locality of the interpolation method.
3.2. Algorithm
The algorithm MIARMA (method of interpolation by autoregressive and moving average) is similar to the original algorithm introduced by Fahlman & Ulrych (1982), but instead of AR models, ARMA models are used. In addition, MIARMA implements local models instead of a global model for the whole data set.
The models are selected by using a statistical criterion that guarantees minimal-loss information. This is possible because the models have an non-closed form expression, that is, no hypothesis about the form of the signal is introduced.
The algorithm basically consists of three steps: first, a criterion based on physical principles for selecting the optimal order of the ARMA model; secondly, the data segments before and after a given gap are fitted using an ARMA model of the order selected in the first step; next, the gap is interpolated using a weighted function of a forward and a backward prediction based on the models of the selected data segments. The second and third steps are repeated for each gap contained in the entire time series.
In the next sections we describe each of these steps thoroughly.
3.2.1. Criterion for selecting the order
The criterion for selecting the order is a crucial step in this process. The order of the ARMA model defines the complexity of the signal that is susceptible to be modelled (i.e. the number of harmonic components that can be modelled, that is, the frequency content). In this sense: too low values lead to models with insufficient spectral resolution, too high values lead to overfitting and instability. We follow a statistical treatment for selecting the order based on the Akaike information criterion (Akaike, 1974). This criterion is based on the maximization of the likelihood of the model parameters, that is, the quadratic mean error of the prediction (Ulrych & Ooe, 1979). The AIC parameter is defined as 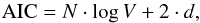 (5)where V is the sum of the squares of the residuals for a given model, d is the number of parameters (for ARMA d = p + q), and N the number of data to be modelled. The quantity V is obtained by fitting an ARMA(p,q) model each time. The first term of AIC formula quantifies the entropy rate or prediction error of the model. The second term penalizes the number of free parameters used by the model. According to Akaike’s theory, the optimal ARMA model is the one with the lowest AIC value. The Akaike criterion derives from purely physical considerations, indeed, it was called originally the principle of maximum entropy. Therefore, this criterion is objectively self-consistent because it guarantees that the model found is the best approximation to the physical process observed using the available information.
(5)where V is the sum of the squares of the residuals for a given model, d is the number of parameters (for ARMA d = p + q), and N the number of data to be modelled. The quantity V is obtained by fitting an ARMA(p,q) model each time. The first term of AIC formula quantifies the entropy rate or prediction error of the model. The second term penalizes the number of free parameters used by the model. According to Akaike’s theory, the optimal ARMA model is the one with the lowest AIC value. The Akaike criterion derives from purely physical considerations, indeed, it was called originally the principle of maximum entropy. Therefore, this criterion is objectively self-consistent because it guarantees that the model found is the best approximation to the physical process observed using the available information.
The procedure used here for selecting the order iterates from a set of models with different orders (p,q) and selects the one with the lowest AIC value. In this way, the optimal ARMA model for the data segment is always guaranteed regardless of the range of the orders (p,q) explored. Note that to obtain a robust estimation of the order (i.e. valid for the entire time series), the longest uninterrupted data segment is selected to calculate the AIC coefficients.
3.2.2. Gap-filling
After the orders are selected using AIC, an ARMA model is locally fitted to the data segment located before and after every gap. To do this, the coefficients ak and bk in Eq. (4) have to be determined for each data segment. For an AR model the parameters can be determined using minimum least squares, the moment method, or MCMC methods, but for an ARMA model, it is necessary to use an iterative procedure to obtain the coefficients of the MA part. MIARMA calculates the coefficients using an iterative algorithm that minimizes the sum of the quadratic errors by checking the convergence after a number of iterations.
The ARMA interpolation in the gaps is based on the following equations: 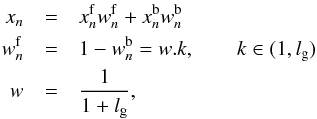 (6)where
(6)where 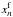 and
and 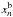 are forward and backward predictions inside the gaps,
are forward and backward predictions inside the gaps, 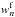 and
and 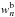 are the weights normalizing those predictions, and lg is the length of the gap.
are the weights normalizing those predictions, and lg is the length of the gap.
Commonly used algorithms for fitting ARMA models are insensitive to the arrow of time, that is, they cannot make backward predictions. We solve this problem by mirroring the data segment after the gap, performing a forward prediction and subsequently mirroring the result again. Although Roques et al. (2000) used a backward prediction, as far as we know, our technique is a novel solution in the field.
The whole gap-filling algorithm here described is carried out through each gap contained in the time series analysed, and the procedure is iterated until no gap is left or a predefined limit is reached.
Predictions lose coherence rapidly when the gaps are much larger than the data segments modelled. In this way, the method is self-consistent because it can decide whether a prediction is no longer feasible from attending the coherence loss. Unlike common gap-filling techniques, which are based on analytic methods assuming that the pattern modelled in the data segments is stable and repeats until infinite, the method introduced here takes into account the natural prediction limits. It is possible to decide when a given prediction is unreliable (e.g. a possible result when applying this algorithm is that no interpolation is reliable). That is, in contrast to analytic methods, this algorithm guarantees that the predictions are reliable. In this sense, MIARMA is optimised to preserve the frequency content of the time series, meaning that it guarantees that the conditions for Parseval’s theorem to be valid are fulfilled.
 |
Fig. 2 Example of comparison between ARMA gap-filling (red) and the linear interpolation (blue) for two gaps in the light curve of the δ Scuti star HD 174966 observed by CoRoT. |
This algorithm is particularly suited to process time series such as those observed by CoRoT, with gaps smaller than the data segments between them. Sometimes it might occur that a data segment modelled is small and the large-scale information of the signal is loss, but in this case, only a much smaller gap can be filled, where the large-scale components of the signal are not relevant. As far as we know, this would be the first time that a gap-filling algorithm presents this self-consistent property.
4. Results: CoRoT data
The pass through the SAA introduces most of the invalid data (gaps) that are present in CoRoT observations (Auvergne et al., 2009). As described in Samadi et al. (2007), two sets are available in CoRoT level 2 data: the gapped data, and a regularly sampled dataset obtained by using linear interpolation to patch the invalid data.
As an example, Fig. 1 shows the periodogram of the CoRoT level 2 data for the star HD 172189. Note that when interpolating linearly the gaps the spurious peaks due to the spectral window appears clearly, but they are almost removed when MIARMA is used.
Here we compare the regularly sampled light curves obtained by using MIARMA with the original CoRoT level 2 data (linearly interpolated) in three cases of stars showing different pulsational characteristics: the δ Scuti HD 174966, showing periodic variations of the same order as the CoRoT observational window, the Be star HD 51193, showing longer time-variations, and the solar-like HD 49933, with rapid time variations. The data we use in the next sections were all gathered by the ultra-high precision CCD cameras on board the CoRoT satellite with the primary objective of studying stellar pulsations (seismofield camera).
4.1. HD 174966
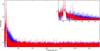 |
Fig. 3 Periodogram of the light curve of HD 174966 observed by CoRoT after the ARMA interpolation (red) and after the linear interpolation (blue). In the inset we show the range where δ Scuti pulsations are excited. |
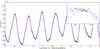 |
Fig. 4 Comparison between ARMA gap-filling (red) and the linear interpolation (blue) for the light curve of the Be star HD 51193 observed by CoRoT. In the inset we show a short segment of 1.44 h of duration. Note that the size of gaps is about 0.014 d, which is two orders of magnitude smaller than the pulsation period of the star (~days). |
The case of A-F main-sequence stars is particularly critical because they show pulsation frequencies close to the orbital frequency of the satellite. In particular, the δ Scuti star HD 174966 might be considered as a prototype for investigating the impact in this type of variable stars.
For this star it is clear that the linear interpolation does not preserve the signal (see Fig. 2), in contrast to the ARMA interpolation.
The power spectrum of the linearly interpolated time series is seriously affected by the spectral window of CoRoT (see Fig. 3), in contrast with the ARMA interpolation, where the window is eliminated. The impact of the linear interpolation in the power spectrum is as strong as the gapped data.
The linear interpolation does definitively not improve the original power spectrum, which is biased by orbital aliases in this type of pulsating stars.
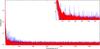 |
Fig. 5 Periodogram of HD 51193 obtained after ARMA interpolation (red) and after linear interpolation (blue). In the inset we show the range from 0 to 130 d-1. |
 |
Fig. 6 Comparison between ARMA interpolation (upper panel in red) and linear interpolation (lower panel in green) for the light curve of HD 49933 observed by the CoRoT satellite. Valid data are depicted in blue (both panels). |
4.2. HD 51193
When the variation period is much longer than the size of the gaps, which is the case of Be stars, the filling provided by linear and ARMA interpolation looks similar (see Fig. 4). However, this is only a matter of scale, as can be seen in the inset of Fig. 4 for the Be star HD 51193. It is commonly assumed that gaps this small in the light curve have no effect on the power spectrum, but we show here that for HD 51193 the spectrum obtained from the linear interpolation provided by the CoRoT pipeline is clearly biased by the spectral window of the orbital frequency (13.97 cd-1), in contrast to the ARMA interpolation, in which this effect has been removed (see Fig. 5).
On the other hand, because of the ultra-high sensitivity of the instrument detectors, even the very small temperature variations within the technical specifications are sufficient to make the instrument response a function of the orbit. This produces a modulation of the signal, which is more significant for the frequencies with the highest amplitudes. Such a modulation appears in both spectra as a peak at 13.97 cd-1, which is the orbital period of the satellite (inset of Fig. 5).
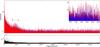 |
Fig. 7 Periodogram of HD 49933 coming from data linearly interpolated (blue), and ARMA interpolation (red). The plotting order is inverted in the inset because the peaks in the p-mode region are higher for the periodogram of ARMA-interpolated data. Lower panel: absolute differences in amplitude between the two methods. |
4.3. HD 49933
The solar-like star HD 49933 was chosen to test MIARMA with a star showing rapid variations; here the CoRoT gaps contain several stellar pulsation cycles. In this case, the optimal ARMA model for the longest segment without invalid data (640 datapoints of a total length of 369 601 datapoints) is ARMA (37, 0), which is a purely autoregressive model with 37 terms.
Although the most frequent gap length is 9 min (Appourchaux et al., 2008), some gaps last up to 0.2 days. Furthermore, this time series has a very high noise level. All these make the linear interpolation quite erratic (see Fig. 6). However, in the interpolated segment between 1.0 and 1.2 days, ARMA predicts a signal with some fine structure. We do not know the origin of this structure, but we are confident that ARMA prediction does not correspond to a white-noise process because the method is based on signal identification assuming white noise.
The comparison of power spectra obtained with the two interpolation methods (Fig. 7) looks quite similar with slightly higher amplitudes for the ARMA interpolation (see inset of the figure). However, a detailed study of their difference using the absolute value of the amplitudes (ΔA = | A(ARMA) − A(LIN) |) shows non-negligible and non-systematic differences (Fig. 7, lower panel).
5. Discussion
Using a method of interpolation that aims to preserve the original frequency content, like MIARMA, may be decisive to perform seismic studies of A-F stars, for example the determination of periodicities in the pulsational spectrum of δ Scuti stars (García Hernández et al., 2009). It has been shown (Pascual-Granado, 2014) that the amplitudes of the periodicities between frequencies are about 20% lower when linear interpolation is used to fill the gaps instead of ARMA interpolation.
We have shown that linear interpolation is insufficient to eliminate the effects of the spectral window in the power spectrum of classical pulsating stars observed by CoRoT. On the other hand, the effects of the linear interpolation on the spectral window are insignificant in the case of solar-like stars. Nevertheless, the contribution of the signal found by ARMA is not included when a linear interpolation is made, so changing the original frequency content. To fulfill the necessary condition for asteroseismology, it is definitively necessary to use a gap-filling that aims to preserve the original frequency content of the signal regardless of the range of the excited pulsational frequencies.
At the same time, the Akaike criterion proves to be relevant to distinguish between white noise and signal. Hence, the fine-scale structure interpolated by using MIARMA clearly is no white-noise process (Akaike, 1998). These are novel features with unknown origin. We can speculate that the origin might be connected with the non-analyticity in A-F stars revealed in previous work of the authors (Pascual-Granado et al., 2014). This has to be examined more deeply in future studies.
6. Conclusions
Small and periodic gaps in time series of pulsating stars released by the space photometric mission CoRoT produce aliases of the satellite orbital period in the power spectra. Because of the very high duty cycle of the instrument, the amplitudes of these aliases are very small. Linear interpolation is commonly used to fill these gaps to remove the aliasing effect. Here we demonstrated that while this approach works for high-frequency pulsators (e.g. solar-like stars), this is not the case for longer period variables (e.g. A-F, Be stars, etc.), for which the aliases remain in the power spectra.
We presented here MIARMA, a new method for filling gaps based on ARMA processes that preserve at best the original information contained in the time series. This method proves to be very suitable for eliminating the aliases on CoRoT light curves, regardless of the type of variability considered.
When the gaps of the CoRoT light curves are filled using this algorithm, all the aliases are eliminated, regardless of the type of variability considered, provided that enough information is available for the solution to be exact. This is the reason why the method has been accepted by the CoRoT Scientific Committee to be implemented in the next correction of the data gathered.
We found that the power spectrum of HD 174966 is clearly aliased when linear interpolation is used to fill the gaps; the light curve of HD 51193 presents a much more aliased spectrum than expected for a low-frequency harmonic signal; and finally, although the linear interpolation does not noticeably affect the power spectrum of the CoRoT light curve of the solar-like star HD 49933, the ARMA interpolation showed rapid variations that were previously not identified and which MIARMA interprets as a signal.
Acknowledgments
The authors acknowledge support from the “Plan Nacional de Investigación” under project AYA2012-39346-C02-01, and from the “Junta de Andalucía” local government under project 2012-P12-TIC-2469.
References
- Akaike, H. 1974, IEEE Trans. Automatic Control, AC-19, 716 [Google Scholar]
- Akaike, H. 1998, in Selected Papers of Hirotugu Akaike (Springer), 275 [Google Scholar]
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baglin, A., Auvergne, M., Barge, P., et al. 2006, in ESA SP, 1306, 33 [Google Scholar]
- Breger, M., Stich, J., & Garrido, R. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Brown, T. M., & Christensen-Dalsgaard, J. 1990, ApJ, 349, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Deeming, T. J. 1975, ApSS, 36, 137 [NASA ADS] [Google Scholar]
- Fahlman, G. G., & Ulrych, T. J. 1982, MNRAS, 199, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Fossat, E., Kholikov, S., Gelly, B., et al. 1999, A&A, 343, 608 [NASA ADS] [Google Scholar]
- García Hernández, A., Moya, A., Michel, E., et al. 2009, A&A, 506, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, R. A., Mathur, S., Pires, S., et al. 2014, A&A, 568, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garrido, R. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 67 [Google Scholar]
- Garrido, R., & Rodrí-guez, E. 1996, MNRAS, 281, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Gilliland, R. L., Brown, T. M., Christensen-Dalsgaard, J., et al. 2010, PASP, 122, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Mathur, S., García, R. A., Catala, C., et al. 2010, A&A, 518, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Bruntt, H., Catala, C., et al. 2013, A&A, 549, A12 [CrossRef] [EDP Sciences] [Google Scholar]
- Pascual-Granado, J. 2014, Ph.D. Thesis, Universidad de Granada [Google Scholar]
- Pascual-Granado, J., Garrido, R., & Suárez, J. C. 2014, in IAU Symp. 301, eds. J. A. Guzik, W. J. Chaplin, G. Handler, & A. Pigulski, 85 [Google Scholar]
- Pires, S., Mathur, S., Garcia, R. A., et al. 2015, A&A, 574, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roques, S., Schwarzenberg-Czerny, A., & Dolez, N. 2000, Baltic Astron., 9, 463 [NASA ADS] [Google Scholar]
- Roth, M., & Zhugzhda, Y. D. 2010, Astron. Lett., 36, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Samadi, R., Fialho, F., Costa, J. E. S., et al. 2007 [arXiv:astro-ph/0703354] [Google Scholar]
- Sato, K. H., García, R. A., Pires, S., et al. 2010 [arXiv:1003.5178] [Google Scholar]
- Scargle, J. D. 1981, ApJSS, 45, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Stahn, T., & Gizon, L. 2008, Sol. Phys., 251, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrych, T. J., & Ooe, M. 1979, in Nonlinear Methods of Spectral Analysis, ed. S. Haykin, 73 [Google Scholar]
- Wold, H. 1938, A study in the analysis of stationary time series 2nd edn. (Almqvist and Wiksell) [Google Scholar]
- Yule, G. U. 1927, Roy. Soc. London Philos. Trans. Ser. A, 226, 267 [Google Scholar]
All Figures
 |
Fig. 1 Periodogram of the δ Scuti star HD 172189 calculated using an FFT of the linearly interpolated time series (blue), and as interpolated by MIARMA (red). The frequencies in the δ Scuti instability range in the inset are affected by the spectral window. |
| In the text | |
 |
Fig. 2 Example of comparison between ARMA gap-filling (red) and the linear interpolation (blue) for two gaps in the light curve of the δ Scuti star HD 174966 observed by CoRoT. |
| In the text | |
 |
Fig. 3 Periodogram of the light curve of HD 174966 observed by CoRoT after the ARMA interpolation (red) and after the linear interpolation (blue). In the inset we show the range where δ Scuti pulsations are excited. |
| In the text | |
 |
Fig. 4 Comparison between ARMA gap-filling (red) and the linear interpolation (blue) for the light curve of the Be star HD 51193 observed by CoRoT. In the inset we show a short segment of 1.44 h of duration. Note that the size of gaps is about 0.014 d, which is two orders of magnitude smaller than the pulsation period of the star (~days). |
| In the text | |
 |
Fig. 5 Periodogram of HD 51193 obtained after ARMA interpolation (red) and after linear interpolation (blue). In the inset we show the range from 0 to 130 d-1. |
| In the text | |
 |
Fig. 6 Comparison between ARMA interpolation (upper panel in red) and linear interpolation (lower panel in green) for the light curve of HD 49933 observed by the CoRoT satellite. Valid data are depicted in blue (both panels). |
| In the text | |
 |
Fig. 7 Periodogram of HD 49933 coming from data linearly interpolated (blue), and ARMA interpolation (red). The plotting order is inverted in the inset because the peaks in the p-mode region are higher for the periodogram of ARMA-interpolated data. Lower panel: absolute differences in amplitude between the two methods. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


