| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 13 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201424713 | |
| Published online | 05 March 2015 | |
Gamma-ray binaries beyond one-zone models: an application to LS 5039⋆
1 Instituto Argentino de Radioastronomía (CCT La Plata, CONICET), C.C.5, (1894) Villa Elisa, Buenos Aires, Argentina
e-mail: sdelpalacio@iar-conicet.gov.ar; romero@iar-conicet.gov.ar
2 Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque, B1900FWA La Plata, Argentina
3 Departament d’Astronomia i Meteorologia, Institut de Ciències del Cosmos (ICC), Universitat de Barcelona (IEEC-UB), Martí i Franquès 1, 08028 Barcelona, Spain
e-mail: vbosch@am.ub.es
Received: 30 July 2014
Accepted: 25 December 2014
Context. Several binary systems hosting massive stars present gamma-ray emission. In most of these systems, despite detailed observational information being available, the nature and the structure of the emitter are still poorly known.
Aims. We investigate the validity of the so-called one-zone approximation for the high-energy emitter in binary systems hosting a massive star. In particular, the case of LS 5039 is considered.
Methods. Assuming a point-like emitter at rest, the presence of a nearby massive star, and the observed MeV and GeV fluxes as a reference, a non-thermal leptonic model is systematically applied for different locations, magnetic fields, and non-radiative losses. This allows us to identify both the emitter configurations that are most compatible with observations and inconsistencies between model predictions and the available data.
Results. In the case of LS 5039, the best parameter combination is fast non-radiative cooling and a low magnetic field. However, discrepancies appear when comparing the model results at the MeV and GeV energy ranges with the observed fluxes. Predictions fail when the orbital motion is included in the analysis, because emitters and energy budgets that are too large are required. Values of X-ray and TeV fluxes that are too high are predicted in such a case, along half of the orbit.
Conclusions. We show that the radiation in LS 5039 does not come from only one electron population, and the emitter is likely extended and inhomogeneous with a low magnetic field. We suggest that the emitter moves at relativistic velocities with Doppler boosting playing a significant role.
Key words: radiation mechanisms: non-thermal / relativistic processes / stars: massive / X-rays: binaries
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Some galactic gamma-ray sources are high-mass binary systems in which one of the components is an early-type star of spectral type OB. Some of these binary systems have been detected from radio to high energies (HE; E> 100 MeV) and/or very high energies (VHE; E> 100 GeV) (Paredes et al. 2013; Dubus 2013). Depending on the nature of the companion (Cn), the systems can be classified as a compact binary (either a microquasar or a binary hosting a young pulsar) or a massive star binary. In a microquasar, the Cn is a stellar-mass black hole (BH) or a neutron star (NS) with a weak magnetic field, which is capable of accreting material coming from the star and generating relativistic jets (e.g., Mirabel & Rodríguez 1999; Bosch-Ramon et al. 2006; Massi & Kaufman 2008; Bosch-Ramon & Khangulyan 2009). In a binary with pulsar, the Cn is a young NS with a strong magnetic field that powers an intense relativistic wind (e.g., Maraschi & Treves 1981; Tavani & Arons 1997; Khangulyan et al. 2007; Romero et al. 2007). Finally, in a massive star binary, the Cn is another massive star with a strong stellar wind (e.g., Eichler & Usov 1993; Benaglia & Romero 2003; Reimer et al. 2006). The non-thermal gamma-ray emission from all these types of systems present the signature of the Cn orbital motion around the massive star in the form of modulation and correlation of the radiation at different energy bands. This has led to the conclusion that the massive star plays a crucial role in determining the high-energy phenomenology (e.g., Bednarek 2007; Khangulyan et al. 2008; Dubus et al. 2008).
The non-thermal emission from high-mass binaries is generated by ultra-relativistic particles, likely accelerated in strong shock-waves in plasma flows. The non-thermal energy could be supplied by accretion and transported by jets in microquasars, or carried by supersonic winds of massive stars or the relativistic wind of a pulsar. Most of the accelerated particles cool down locally through interactions with ambient matter, magnetic fields, and radiation fields. The result at high energies of these interactions depends strongly on the massive star, as it provides targets (mostly ultraviolet -UV- photons) for inverse Compton (IC) scattering and baryons for proton-proton (pp) collisions among other radiation processes. We note, however, that leptons cool down and radiate more efficiently than hadrons under typical conditions. Additionally, the VHE radiation coming from the inner regions of a high-mass binary is likely to undergo absorption due to pair creation in the stellar radiation field (see, e.g., Bosch-Ramon & Khangulyan 2009, for an assessment of the importance of the different processes).
The study of gamma-ray binaries allows us to gain knowledge on physical processes occurring in extreme astrophysical environments. However, there are still many unknown features about the particle acceleration mechanism, the structure of the emitter, and even the nature of the Cn in several cases. These uncertainties manifest themselves in the simplicity of the models adopted and in the departure of their predictions from an accurate representation of the phenomenology of the sources. In this work, we take advantage of the few assumptions required by a simple, one-zone model to carry out a robust exploration of the model validity, which can be useful to sketch physical properties of the objects whose treatment is formally beyond this kind of models.
The structure of this paper is as follows: in Sect. 2, we present a simple and robust tool based on an one-zone model to thoroughly investigate the effects of the emitter-star-observer geometry and different energy losses on the resulting radiation. In Sect. 3, we apply this tool to the system LS 5039 to perform a more detailed analysis, and finally, in Sect. 4, we discuss our results in the context of the current observational data of LS 5039 and summarize the main conclusions of this work.
2. Limitations of one-zone models: informative analysis
2.1. Description of the approach
A one-zone model describes an emitting region in which particles are injected homogeneously and evolve under homogeneous conditions. This is a very simple model, yet capable of incorporating the most relevant physical processes of a given system and of reproducing the main features of its observable quantities. Regardless of its simplicity, the one-zone leptonic model has proven to be a robust tool for studying the high-energy phenomenology in high-mass binary systems (e.g. Kaufman et al. 2002; Bosch-Ramon et al. 2006; Khangulyan et al. 2008; Dubus et al. 2008; Takahashi et al. 2009; Araudo et al. 2009; Zabalza et al. 2011a).
High-mass binary systems can be characterized by the presence of a massive star and an accelerator of relativistic particles, which is a shock between colliding winds or a mechanism associated with a microquasar jet. We consider both the massive star and the accelerator, regardless of its nature, as point-like and, thus, homogeneous objects here. In addition, the accelerator and the emitter are assumed steady and co-spatial, as electrons cannot travel long distances while emitting because of the short-cooling timescales. A sketch of the model is shown in Fig. 1.
 |
Fig. 1 Sketch of the one-zone model considered in this work. |
The injection of relativistic electrons in the emitter is taken to follow an energy distribution Q(E) ∝ E-2exp( − E/Emax) for energies above 1 MeV, which is consistent with a Fermi I acceleration process and also compatible with the observational features of the X-ray emission (e.g., Takahashi et al. 2009; Zabalza et al. 2011a). The relativistic electrons interact with the emitter magnetic and ambient stellar photon field producing a broad radiation spectrum. The electron maximum energy (the cutoff energy Emax above) can be obtained by equating the cooling time to their acceleration time plus the constraint derived from comparing the accelerator/emitter size and the particle gyroradius: R>rg = Emax/qB. For simplicity, however, we take here Emax = 30 TeV, as this is the expected maximum electron energy in LS 5039, the source studied below (Khangulyan et al. 2008, such an energy requires a highly efficient accelerator).
Particles can lose energy through non-radiative losses, which can be through adiabatic cooling or particle escape. Their characteristic timescale is characterized as tad = d/v (see, e.g. Takahashi et al. 2009), where d is the distance from the emitter to the star (a loose upper limit for the emitter size) and v the velocity of the emitting flow. The radiative processes dominant here are IC scattering and synchrotron emission, whereas VHE gamma-ray absorption takes place through pair production in the stellar photon field (Gould & Schréder 1967; Blumenthal & Gould 1970; Aharonian & Atoyan 1981). We notice that the IC scattering takes place in the Klein-Nishina (KN) regime at such high energies and, therefore, has to be computed under such formalism.
We have not considered radiation reprocessing, although an electromagnetic (EM) IC cascade can develop for weak enough magnetic fields, increasing the effective transparency to VHE photons, while the secondary pair radiation can overcome the X-rays from the primary electron distribution in the emitter for stronger magnetic fields (Bosch-Ramon et al. 2008a). We have also assumed that the emitting flow is at most mildly relativistic, as it would be the case for a standing shock in a jet or a wind-colliding region, and, thus, we have not accounted for Doppler boosting, which would significantly increase the model geometrical parameters. A thorough, albeit qualitative, discussion of the impact of these assumptions is worthy and is presented in Sect. 4.
With all these considerations, only two parameters remain free in our model: the escape velocity, v, and the magnetic field to stellar photon energy density ratio, ξ = umag/urad. The value of v is expected to be in the range ~108–3 × 1010 cm s-1, as it seems reasonable that the flow speed is between the stellar wind velocity and close to the speed of light (c); in particular, we adopt the values v = 108 cm s-1 and v = c. As for ξ, a reasonable range to study is ξ = 10-4–1, as it goes from virtually no synchrotron cooling to a case when it becomes dominant. We have explored the parameter values ξ = 10-4, 10-2 and 1.
2.1.1. SEDs and maps: fluxes, spectra and other emitter properties
The spectral energy distribution (SED) is a measure of the amount of energy emitted per time and area units in a certain energy region. As both the IC scattering emission and the pair-production absorption strongly depend on the interaction angle, the emitter-star-observer geometry plays a crucial role in the resulting SEDs. Nonetheless, the study of individual SEDs may not be clear enough to explore these geometrical aspects when the emitter structure and location within the system are not known. Alternatively, one can make use of maps to display all the emitter spatial possibilities at once. First, one computes the particle population and the (absorbed) emission from an emitter placed in all the possible locations of the star-emitter-observer plane. Once this is done, one can extract any relevant quantity for each location and display it in the form of a two-dimensional map (see, e.g., Dubus 2006; Khangulyan et al. 2008; Bosch-Ramon et al. 2008b; Romero et al. 2010, for similar maps of gamma-ray absorption and particle acceleration).
We focus here on the total energy flux in the ranges of 0.3–10 keV (FX), 1–30 MeV (FMeV), 0.1–10 GeV (FGeV), and 0.1–10 TeV (FTeV); the luminosity injected in the relativistic particles (Linj); and the minimum emitter radius normalized to the stellar distance (R/d). We derive R assuming a balance between the ram pressure of the stellar wind and the non-thermal electron pressure, which gives a lower limit for the emitter pressure.
The energy fluxes, even without accounting for spectral features, already inform us if the model reproduces the observations by comparing the predicted and the observed values at different bands. This comparison may suggest the presence of different populations of particles, or the occurrence (presence) of more processes (emitting sites) than those just assumed, for a particular source. Furthermore, the non-detection of sources with certain flux levels, or different-band flux combinations, can rule out the existence of objects with certain properties.
The quantities Linj and R/d hint indirectly at major flaws of the model because either the luminosity budget is too high when we account for our background knowledge on the sources, or the point-like assumption (R ≳ 0.5 d) is violated. The former may suggest radiation beaming as a form of relaxing the energetic constraints, and the latter is probably pointing at a structured and extended emitter, although parameters/locations yielding R ≫ d are probably ruled out.
We have chosen FMeV and FGeV as the most relevant quantities for LS 5039, the source studied below. The observed values of FMeV and FGeV are very high, and trying to reconcile them with a broadband simple model, or studying their energetic and size requirements, might be very informative. Therefore, in what follows, the model fluxes in the MeV and GeV bands have been fixed to the observed values (although not simultaneously).
2.2. An application to LS 5039
The system LS 5039 is a well-studied high-mass binary located at 2.9 kpc (Moldón et al. 2012a), which is proposed as a gamma-ray source by Paredes et al. (2000) and confirmed by Aharonian et al. (2005). The effective temperature of the star is T = 3.9 × 104 K; its radius, R∗ = 9.3 R⊙ (Casares et al. 2005); and the wind velocity, vw(d) = 2400 (1−R∗/d) km s-1 (Kudritzki & Puls 2000). The Cn nature is still unclear; its mass is estimated to be M = 3.7 M⊙, but this value is highly dependent on the poorly known inclination of the orbit (for discussions on the nature of the Cn, see Casares et al. 2005; and Bosch-Ramon & Khangulyan 2009; Dubus 2013 and references therein)1. The orbit of LS 5039 is mildly eccentric, e = 0.24−0.35 (Casares et al. 2005; Aragona et al. 2009; Sarty et al. 2011), with a semi-major axis a ≈ 3.5 R∗. We adopt the value of a as the binary spatial scale here.
As mentioned, we normalize the results of the calculations to the detected MeV and GeV fluxes. In particular, the injection luminosity is set to reproduce the observed MeV and GeV energy fluxes: FGeV = 2.8 × 10-10 erg cm-2 s-1 in the range 0.1–10 GeV (Hadasch et al. 2012) and FMeV = 2.6 × 10-9 erg cm-2 s-1 in the range 1–30 MeV (Collmar & Zhang 2014). We note that the fluxes in these energy bands in LS 5039 vary along one orbit by a factor of a few, so we have taken intermediate values. The observed fluxes in the X-ray and TeV energy bands are: FX ≈ (0.5 − 1.3) × 10-11 erg cm-2 s-1 (Takahashi et al. 2009) and FTeV ≈ (1.9 − 7.4) × 10-12 erg cm-2 s-1 (Aharonian et al. 2006), depending on the orbital phase.
Accounting for the system and stellar parameters of LS 5039, the GeV and MeV fluxes, and the magnetic field and emitter velocity ranges introduced in Sect. 2.1, we have computed several broadband SEDs and maps of the quantities listed in Sect. 2.1.1.
We adopt an upper-limit for the non-thermal injection luminosity of ~1037 erg s-1, which is roughly what is required to explain the inferred MeV luminosities (Collmar & Zhang 2014). Higher values would be in conflict with the two possible scenarios of LS 5039: for the accretion-jet scenario, such a powerful non-thermal emitter is in conflict with the lack of accretion features in the X-ray spectrum and present models of jet formation (Bosch-Ramon et al. 2007; Rea et al. 2011; Barkov & Khangulyan 2012). For the pulsar scenario, the lack of thermal X-ray evidence points to spin-down luminosities below 1037 erg s-1 (Zabalza et al. 2011b).
3. Results
Several SEDs and a set of maps have been obtained for LS 5039. The results presented in this section are just a subset of those obtained and are chosen as the most useful to provide an insight into the physics of LS 5039. They also illustrate the approach described in the previous section. In Appendix A, maps for the extreme parameter cases are shown to provide a wider context to the maps presented here.
3.1. Spectral energy distributions
Just to give a qualitative idea of how the different factors considered here (magnetic field intensity, importance of non-radiative losses and emitter location) affect the resulting spectra, we show SEDs for emitters with different locations and properties in Figs. 2–9. We present some extreme cases of fast/slow non-radiative losses (v = c and v = 108 cm s-1, respectively), high/low magnetic fields (ξ = 1 and ξ = 10-4, respectively, with ξ = umag/urad, which translates into B-fields of ~10–102 G and ~0.1–1 G, respectively, depending on location), and less extreme configurations of the emitter-star-observer. We choose the emitter positions (−a,a) and (a,a), which correspond to an emitter located roughly behind/in front of the star with respect to the observer and at a distance on the order of the system size. In all cases, the normalization was set to FGeV = 2.8 × 10-10 erg cm-2 s-1. We also show the various levels of observed emission in the four energy bands considered (X-rays, MeV, GeV, TeV), so the reader can easily judge the quality of the match.
 |
Fig. 2 Spectral energy distribution for an emitter with fast non-radiative losses and a weak magnetic field located at x = −a and y = a. The massive star is at (0,0), and the observer in the positive x-axis direction. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. Observational constraints in X-rays, MeV, GeV, and TeV energies are also presented. |
 |
Fig. 6 Spectral energy distribution for an emitter with fast non-radiative losses and a weak magnetic field located at x = a and y = a. The massive star is at (0, 0), and the observer in the positive x-axis direction. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. Observational constraints in X-rays, MeV, GeV, and TeV energies are also presented. |
These figures show the typical behavior for a synchrotron/IC one-zone emitter with different IC and absorption geometries under different cooling regimes (see, e.g. Khangulyan et al. 2008; Dubus et al. 2008; Takahashi et al. 2009; Zabalza et al. 2011a).
Regardless of the dominant cooling mechanism, gamma-ray absorption is weaker (stronger) and its maximum occurs at higher (lower) energies when the emitter is in front of (behind) the star. The IC component becomes harder (softer) and, as well as the absorption due to pair creation, also weaker (stronger) when the emitter is in front of (behind) the star. Furthermore, the pair-creation threshold shifts to higher energies when the emitter is in front of the star. All these variations are related to the different electron-photon and photon-photon interaction angles as seen from the observer such that smaller (larger) angles correspond to an emitter in front of (behind) the star. On the other hand, synchrotron radiation is not affected by changes in the geometry (at the same distance to the star, which translates in the same value of the magnetic field). This is clear in the figures, as no spectral changes are seen in the synchrotron component between both geometries for the same cooling setup.
Concerning the dominant cooling process, both synchrotron and IC emission under IC dominance become harder at the energies in which the KN effect is relevant, as the KN IC cross section strongly drops with energy. As this drop is actually faster than in synchrotron, it implies that synchrotron cooling easily overcomes IC as the main cooling channel at the highest energies. On the other hand, synchrotron and IC in Thomson regime both soften the radiation spectra, yielding flat SEDs right above the energies in which non-radiative losses are relevant. Finally, the impact of non-radiative losses is to harden (unless it had to compete with KN IC cooling) the synchrotron and IC spectra below a given energy, which is higher when these losses are faster. Given the fixed normalization, it is not possible to directly compare the levels of emission between plots with different parameter choices.
In Sect. 3.3, we show a method for finding a rough approximation of the best fit parameters, emitter position, and normalization.
3.2. Maps
Figures 10–19 show the maps with intermediate non-radiative losses (v = 109 cm s-1) and an intermediate magnetic field (ξ = 10-2) for both FMeV and FGeV normalizations. The color scale of all the maps has been chosen such that the color of areas with values about ten times above and below the established limits for each quantity are intense red and blue, respectively.
The calculation results displayed as maps of Linj, R/d, FX, FMeV (FGeV), and FTeV tend to give values for Linj, R/d, FX, FTeV, and FGeV when fixing FMeV, that are too large for half or more of the possible emitter locations. This occurs because of the very high energetic needs to explain the (MeV) GeV fluxes when the emitter is in front (x> 0) of the star. The maps presented in this section, which are obtained by fixing v and ξ to intermediate values, already show the general trends and allow us to investigate the disparities between fixing FMeV or FGeV. These disparities are basically stronger energetic requirements, a larger emitter, and a larger departure from the observed fluxes at other bands when fixing FMeV.
When looking at extreme parameter choices in Appendix A, we find that the larger qualitative changes in the represented quantities come from magnetic field variations, whereas those produced by modifying the non-radiation timescale are quantitative and rather moderate in most of the cases. This happens because a different synchrotron-to-IC cooling ratio severely modifies the energy distribution of the radiation, unlike non-radiative cooling, which affects both the synchrotron and the IC components in a more uniform manner. As seen from the SEDs above, the GeV fluxes for x = −a are dominated by IC radiation in most of the cases, whereas synchrotron (IC) dominates for high (low) B-values for x = a. On the other hand, the MeV fluxes are mostly of synchrotron origin for x = a, whereas IC becomes dominant for low B-values for x = −a. The slopes of the spectra for each component also vary more under radiative losses than under non-radiative ones. All this explains the strong changes in the color maps when going from low to high B cases.
3.3. Identification of the best model
We are interested in finding the parameters, emitter position, and normalization that best reproduce observations. At this stage, we focus only on flux levels of different energy bands, ignoring orbital phase information. We find that it is still possible to estimate how close the model and the set of parameters adopted from matching the observations are. Using a minimum deviation method for this task, a quantitative assessment can be made to illustrate which emitter conditions are closer to the observational values. To provide such an estimate, we first search in the literature observations of LS 5039 along its orbit, and then we calculate the average, minimum, and maximum energy flux in the X, MeV, GeV, and TeV energy band. The average energy fluxes can be considered as observational points with 1σ errors given by the respective maximum and minimum energy flux. Then, we calculate the SED for a given scenario and emitter location and compare the theoretical energy fluxes with the observational data. We estimate the deviation of this fit by doing a simple χ2 test with four observational points (actually three, as one is fixed by the normalization). We repeat this procedure for every possible emitter location for each magnetic field and escape velocity values considered. Then we identify the parameters and emitter location that yielded the best fit (i.e. the lowest χ2 value). Using this procedure, we find that the minimum deviation (χ2 = 7.5) is achieved for an emitter with a low magnetic field (B = 0.5 G), fast adiabatic losses (v = c), a position of (x,y) = ( − 1.2a,0.8a), and normalization according to the GeV energy flux. The corresponding SED is shown in Fig. 21, along with the observational fluxes in the different energy ranges.
The escape velocity found is similar to the values one would expect for the jet or the shocked pulsar wind in both the microquasar and the pulsar binary scenarios. The magnetic field is consistent with values found by previous studies (e.g., Khangulyan et al. 2008; Dubus et al. 2008; Takahashi et al. 2009; Zabalza et al. 2013). In particular, a direct comparison can be made with Dubus et al. (2008) and Takahashi et al. (2009), as they adopted one-zone models to explain the non-thermal emission from LS 5039 and derived magnetic fields of ≈1 and 3 G, respectively. Regarding the location of the emitter, our results are consistent with an emitter off the orbital plane (Khangulyan et al. 2008; Takahashi et al. 2009), and they also seem to point to a more natural explanation for the X-ray, GeV, and TeV fluxes in the context of a one-zone model than when the MeV data are included. We note that our calculations do account for different emitter locations, which allows for more detailed comparisons with the observed fluxes, although we neglect orbital phase specific information in the likelihood analysis described above. In any case, even simply adopting the observed orbital variations of the fluxes in different bands as statistical errors, large regions of the source are much worse at reproducing this coarse data presentation than the results from the best fit.
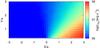 |
Fig. 10 Injection luminosity of relativistic particles in the emitter in the case of intermediate non-radiative losses and magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
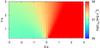 |
Fig. 15 Injection luminosity of relativistic particles in the emitter in the case of intermediate non-radiative losses and magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
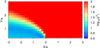 |
Fig. 20 χ2 map for an emitter with fast non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
 |
Fig. 21 Spectral energy distribution for the best fit scenario (χ2 = 7.5), which consists of an emitter with fast non-radiative losses and a weak (B = 0.5 G) magnetic field that is located at x = −1.2a and y = 0.8a. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. Observational constraints in X-rays, MeV, GeV, and TeV energies are also presented. |
4. Discussion
The failure of the one-zone model to globally explain the X-ray, MeV (GeV), and TeV fluxes fixing the GeV (MeV) flux to its observed value implies that some of the assumptions adopted for LS 5039 are incorrect: (i) adopting a pure leptonic radiation model in a dilute magnetized medium with just synchrotron and IC losses and non-radiative cooling that is independent of energy; (ii) accounting for gamma-ray absorption in the stellar photon field but neglecting the role of electromagnetic IC cascading or the synchrotron emission from the produced pairs; (iii) assuming one population of particles follows a power-law and an exponential cutoff in energy under homogeneous conditions in a point-like accelerator/emitter; and (iv) neglecting Doppler boosting. Some of these assumptions appear more robust than others when looking at the known physical or phenomenological properties of the source. These include the following:
(i): Radiation from hadronic interactions, such as pp interac-tions (Romero et al. 2003),cannot be discarded. However, as noted in Bosch-Ramon& Khangulyan (2009), they are not likely tobe important for relativistic protons/nuclei in the environ-ment of LS 5039 with relatively low matter(for pp), X-ray photon (for photomeson production andphotodisintegration) densities, and very long proton syn-chrotron timescales. Pulsar wind comptonization or pulsarmagnetospheric radiation have been discussed as poten-tial sources of GeV-TeV emission in LS 5039(e.g., Sierpowska-Bartosiket al. 2008; Ceruttiet al. 2008; Takataet al. 2014). Consideringthese components would imply a multi-population, non-homogeneous, non-point-like model (see iii) and the presence ofa powerful non-accreting pulsar in the system.
(ii): As discussed by Bosch-Ramon et al. (2008b), the magnetic field in the stellar surroundings could be low, ≲1 G. This would allow the emitter to be located close to the companion, as the effective opacity to TeV photons would be much lower for an emitter behind the star due to electromagnetic IC cascading. Otherwise, the emitter could not be located deep within the system and close to the companion, as the production of the required TeV fluxes, and therefore, the injection luminosity, would be very high and imply secondary synchrotron X-rays above the observed fluxes. However, Fermi data seem to rule out effective electromagnetic IC cascading in LS 5039, as the predicted emission around 1–100 GeV, according to leptonic models, is too high with respect to the observed values (e.g., Cerutti et al. 2010; Yamaguchi & Takahara 2010; Takata et al. 2014). This implies again an emitter far from the star and the companion (see Bosch-Ramon et al. 2007; Szostek et al. 2011, for a similar conclusion when studying X-rays). This is a model independent fact, as the 10–100 GeV range is just around the pair-creation threshold in an UV photon field, and most of the cascade radiation should be released there. A low-energy cutoff in the emitting electron distribution above several hundred GeV may alleviate this constraint on cascading, but then the GeV and TeV components would have to come from different emitting populations (see iii).
(iii): The cooling timescales of electrons are short in LS 5039, if they are accelerated within the binary, ~10 − 104 s (see Fig. 5 in Takahashi et al. 2009), so the one-zone assumption may seem quite natural. However, different populations and a very structured accelerator/emitter are physically well motivated (Vila et al. 2012). As simulations show (see, e.g. Perucho & Bosch-Ramon 2012; Bosch-Ramon et al. 2012, and references therein), both the microquasar and the pulsar scenario present dissipation regions in the periphery of the system and beyond: powerful flows interact in the system and produce a large variety of hydrodynamical phenomena, potentially generating large amounts of non-thermal energy that is carried away outside of the binary (e.g., Zabalza et al. 2013). In addition, as noted, emitting sites other than those of pure hydrodynamical origin, as the cold pulsar wind or the magnetosphere of the pulsar, could be also relevant (see Dubus 2013, for a review on different proposals behind the GeV emission in LS 5039). Therefore, the one-zone assumption is possibly quite inaccurate.
(iv): Doppler boosting in both the microquasar and the pulsar scenario cannot be neglected in general, as relativistic flows are involved in both cases (Mirabel & Rodríguez 1994, 1999; Bogovalov et al. 2008). Simulations show that the interaction between the microquasar jet or the pulsar wind with the stellar wind can lead to slower regions containing non-thermal particles (Perucho & Bosch-Ramon 2012; Bosch-Ramon et al. 2012), but the shocked flow is expected to be mildly relativistic. Reacceleration in the postshock region is expected (Bogovalov et al. 2008). Therefore, even when standing shocks can form, Doppler boosting may be important at some distance from the shock. The energy flux in the observer frame transforms as F ~ δ4F′ for one emitting region, where δ = 1/Γ(1 − βcosθ), Γ is the Lorentz factor, β = v/c (v is the velocity of the flow), and θ the angle between the emitter motion and the line of sight. When most of the injected energy is radiated, one can relate the observed luminosity to the injected one as L ~ δ4Linj/ Γ2, so L ~ (1 + β)4Γ2Linj for an emitter pointing to the observer (θ = 0). This means that even a modest Lorentz factor ≲2 can already enhance the radiation by more than an order of magnitude. At least under some specific source geometries, this shows that adopting δ = 1 is far from realistic.
5. Conclusions
The tool presented in this paper consists of an exhaustive application of the one-zone model that includes non-radiative cooling to non-thermal emitting high-mass binaries. This procedure allows the determination of significant departures from a simple model for any source. This may suggest more complex physical schemes, including relativistic motions, unaccounted radiation components, or a non-uniform emitter. As a test and because of its interesting potential implications, we have exhaustively applied our model to LS 5039, possibly the best known and most intriguing gamma-ray (high-mass) binary. For simplicity, this application has been carried out without a detailed account of the spectral and orbital behavior of the source but has focused on the energy fluxes at different bands. Our results, as noted in Sect. 4, are already suggestive of different extensions of the one-zone model and are also compatible with previous works that had already proposed possible improvements beyond that model. Two additional advantages of the present approach are that it is both robust and slightly model dependent, as it relies on basic source information and physics.
In particular, if the MeV (GeV) data are to be explained with our model (one-zone leptonic model without secondary pair radiation nor Doppler boosting), our study of LS 5039 shows that this tends to over-predict in most of the configurations the X-ray and TeV fluxes. The model also underpredicts (overpredicts) the MeV (GeV) fluxes and requires an emitter of size incompatible with the point-like assumption, with very demanding energetic requirements.
Low magnetic fields and high non-radiative losses still yield relatively good results when the emitter is behind the star. Otherwise, when the emitter is in front of the star, the energetic requirements are too high when trying to explain the MeV and GeV fluxes. This is the case for any combination of the magnetic field and the velocity of the flow values.
Large magnetic fields (regardless of the value of the flow velocity) can be also discarded for almost all configurations, as they yield injection luminosities, emitters, and X-ray fluxes that are too large. We note that the disparities between predictions and observations are already very apparent without accounting for spectral and orbital behavior, which would just narrow even more the applicability of the one-zone model.
Our results strongly favor several emitting populations, as the fluxes in different energy bands are incompatible with just one population. The large predicted emitter also suggests that this should be extended and inhomogeneous. The large energetic requirements when the emitter is in front of the star hints at Doppler boosting as a way to overcome the low radiation efficiencies in the corresponding orbital phases. Finally, the large relativistic pressures derived for the non-thermal particles may also hint to relativistic plasma motions. All this indicates that assumptions (iii) and (iv) should be ruled out and goes in favor of an emitter with characteristic locations at some distance from the star and the companion, as discussed when considering (ii). The assumption of a leptonic model still seems appropriate, but additional components, as the mentioned cold pulsar wind or the pulsar magnetosphere, cannot be discarded.
The maps presented in this paper can be applied, after a simple re-scaling, to the study of other binary systems. With the increase in the number of known binaries, this simple yet powerful analytical tool may become a guide toward better understanding the mechanisms that operate in gamma-ray binaries.
Online material
Appendix A
Appendix A.1: Maps normalizing through FGeV
In Sect. 3.2, we presented the maps for intermediate adiabatic losses (v = 109 cm s-1) and intermediate magnetic fields (ξ = 10-2, which yields B fields of ~10 G close to the massive star to ~1 G far from it). In this section, we present the maps for the normalization set to reproduce the observed GeV flux for four extreme scenarios, varying between fast/slow adiabatic losses (v = c and v = 108 cm s-1, respectively) and high/low magnetic fields (ξ = 1 – B between 10–102 G – and ξ = 10-4 – B between 0.1–1 G – respectively). The results are shown in Figs. A.1–A.20.
Appendix A.2: Maps normalizing through FMeV
In Sect. 3.2, we presented the maps for intermediate adiabatic losses (v = 109 cm s-1) and intermediate magnetic fields (ξ = 10-2, which yields B fields of ~10 G close to the massive star to ~1 G far from it). In this section, we present the maps for the normalization set to reproduce the observed MeV flux for four extreme scenarios, varying between fast/slow adiabatic losses (v = c and v = 108 cm s-1, respectively) and high/low magnetic fields (ξ = 1 – B between 10–102 G – and ξ = 10-4 – B between 0.1–1 G – respectively). The results are shown in Figs. A.21–A.40.
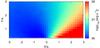 |
Fig. A.1 Injection luminosity of relativistic particles in the emitter in the case of fast non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
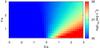 |
Fig. A.6 Injection luminosity of relativistic particles in the emitter in the case of slow non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
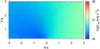 |
Fig. A.11 Injection luminosity of relativistic particles in the emitter in the case of fast non-radiative losses and a strong magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
 |
Fig. A.16 Injection luminosity of relativistic particles in the emitter in the case of slow non-radiative losses and a strong magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
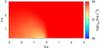 |
Fig. A.21 Injection luminosity of relativistic particles in the emitter in the case of fast non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
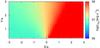 |
Fig. A.26 Injection luminosity of relativistic particles in the emitter in the case of slow non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
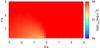 |
Fig. A.31 Injection luminosity of relativistic particles in the emitter in the case of fast non-radiative losses and a strong magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
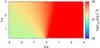 |
Fig. A.36 Injection luminosity of relativistic particles in the emitter in the case of slow non-radiative losses and a strong magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
In addition, note that the radio structures detected in LS 5039 might be consistent with the presence of a non-accreting pulsar (Moldón et al. 2012b).
Acknowledgments
We want to thank the referee for his/her useful and constructive comments. This work is supported by ANPCyT (PICT 2012-00878). V.B-R. acknowledges financial support from MICINN and European Social Funds through a Ramón y Cajal fellowship. This research has been supported by the Marie Curie Career Integration Grant 321520. V.B-R. and G.E.R. acknowledge support by the Spanish Ministerio de Economía y Competitividad (MINECO) under grant AYA2013-47447-C3-1-P.
References
- Aharonian, F. A., & Atoyan, A. M. 1981, Ap&SS, 79, 321 [NASA ADS] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Aye, K.-M., et al. 2005, Science, 309, 746 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2006, A&A, 460, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aragona, C., McSwain, M. V., & Grundstrom, E. D. 2009, ApJ, 698, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Araudo, A. T., Bosch-Ramon, V., & Romero, G. E. 2009, A&A, 503, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barkov, M. V., & Khangulyan, D. V. 2012, MNRAS, 421, 1351 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W. 2007, A&A, 464, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benaglia, P., & Romero, G. E. 2003, A&A, 399, 1221 [Google Scholar]
- Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Bogovalov, S. V., Khangulyan, D. V., Koldoba, A. V., Ustyugova, G. V., & Aharonian, F. A. 2008, MNRAS, 387, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., & Khangulyan, D. 2009, Int. J. Mod. Phys. D, 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch-Ramon, V., Romero, G. E., & Paredes, J. M. 2006, A&A, 447, 263 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., Motch, C., Ribó, M., et al. 2007, A&A, 473, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., Khangulyan, D., & Aharonian, F. A. 2008a, A&A, 482, 397 [Google Scholar]
- Bosch-Ramon, V., Khangulyan, D., & Aharonian, F. A. 2008b, A&A, 489, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosch-Ramon, V., Barkov, M. V., Khangulyan, D., & Perucho, M. 2012, A&A, 544, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casares, J., Ribó, M., Ribas, I., et al. 2005, MNRAS, 364, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Cerutti, B., Dubus, G., & Henri, G. 2008, A&A, 488, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cerutti, B., Malzac, J., Dubus, G., & Henri, G. 2010, A&A, 519, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collmar, W., & Zhang, S. 2014, A&A, 565, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubus, G. 2006, A&A, 451, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubus, G. 2013, A&ARv, 21, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G., Cerutti, B., & Henri, G. 2008, A&A, 477, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eichler, D., & Usov, V. V. 1993, ApJ, 402, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, R. J., & Schréder, G. P. 1967, Phys. Rev., 155, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Hadasch, D., Torres, D. F., Tanaka, T., et al. 2012 ApJ, 749, 54 [Google Scholar]
- Kaufman Bernadó, M. M., Romero, G. E., & Mirabel, I. F. 2002, A&A, 385, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Khangulyan, D., Hnatic, S., Aharonian, F., & Bogovalov, S. 2007, MNRAS, 380, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Khangulyan, D., Aharonian, F., & Bosch-Ramon, V. 2008, MNRAS, 383, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R., & Puls, J. 2000, ARA&A, 38, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., & Treves, A. 1981, MNRAS, 194, 1 [Google Scholar]
- Massi, M., & Kaufman Bernadó, M. 2008, A&A, 477, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mirabel, I. F., & Rodríguez, L. F. 1994, Nature, 371, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Mirabel, I. F., & Rodríguez, L. F. 1999, ARA&A, 37, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Moldón, J., Ribó, M., & Paredes, J. M. 2012a, AIP Conf. Proc., 1505, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Moldón, J., Ribó, M., & Paredes, J. M. 2012b, A&A, 548, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paredes, J. M. 2013, Astropart. Phys., 43, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Paredes, J. M., Martí, J., Ribó, M., & Massi, M. 2000, Science, 288, 2340 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Perucho, M., & Bosch-Ramon, V. 2012, A&A, 539, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rea, N., Torres, D. F., Caliandro, G. A., et al. 2011, MNRAS, 416, 1514 [NASA ADS] [CrossRef] [Google Scholar]
- Reimer, A., Pohl, M., & Reimer, O. 2006, ApJ, 644, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, G. E., Torres, D. F., Kaufman Bernadó, M. M., & Mirabel, I. F., 2003, A&A, 410, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero, G. E., Okazaki, A. T., Orellana, M., & Owocki, S. P. 2007, A&A, 474, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero, G. E., Del Valle, M. V., & Orellana, M. 2010, 518, 12 [Google Scholar]
- Sarty, G. E., Szalai, T., Kiss, L. L., et al. 2011, MNRAS, 411, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Sierpowska-Bartosik, A., & Torres, D. F. 2008, Astropart. Phys., 30, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Szostek, A., & Dubus, G. 2011, MNRAS, 411, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, T., Kishishita, T., Uchiyama, Y., et al. 2009, ApJ, 697, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Takata, J., Leung, G. C. K., & Tam, P. H. T. 2014, ApJ, 790, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Tavani, M., & Arons, J. 1997, ApJ, 477, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Vila, G. S., Romero, G. E., & Casco, N. A. 2012, A&A, 538, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yamaguchi, M. S., & Takahara, F. 2010, ApJ, 717, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V., Paredes, J. M., & Bosch-Ramon, V. 2011a, A&A, 527, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zabalza, V., Bosch-Ramon, V., & Paredes, J. M. 2011b, ApJ, 743, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V., Bosch-Ramon, V., Aharonian, F., & Khangulyan, D. 2013, A&A, 551, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Sketch of the one-zone model considered in this work. |
| In the text | |
 |
Fig. 2 Spectral energy distribution for an emitter with fast non-radiative losses and a weak magnetic field located at x = −a and y = a. The massive star is at (0,0), and the observer in the positive x-axis direction. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. Observational constraints in X-rays, MeV, GeV, and TeV energies are also presented. |
| In the text | |
 |
Fig. 3 As in Fig. 2 but for an emitter with fast non-radiative losses and a strong magnetic field. |
| In the text | |
 |
Fig. 4 As in Fig. 2 but for an emitter with slow non-radiative losses and a weak magnetic field. |
| In the text | |
 |
Fig. 5 As in Fig. 2 but for an emitter with slow non-radiative losses and a strong magnetic field. |
| In the text | |
 |
Fig. 6 Spectral energy distribution for an emitter with fast non-radiative losses and a weak magnetic field located at x = a and y = a. The massive star is at (0, 0), and the observer in the positive x-axis direction. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. Observational constraints in X-rays, MeV, GeV, and TeV energies are also presented. |
| In the text | |
 |
Fig. 7 As in Fig. 6 but for an emitter with fast non-radiative losses and a strong magnetic field. |
| In the text | |
 |
Fig. 8 As in Fig. 6 but for an emitter with slow non-radiative losses and a weak magnetic field. |
| In the text | |
 |
Fig. 9 As in Fig. 6 but for an emitter with slow non-radiative losses and a strong magnetic field. |
| In the text | |
 |
Fig. 10 Injection luminosity of relativistic particles in the emitter in the case of intermediate non-radiative losses and magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
| In the text | |
 |
Fig. 11 As in Fig. 10 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
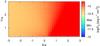 |
Fig. 12 As in Fig. 10 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
 |
Fig. 13 As in Fig. 10 but showing the integrated energy flux in the 1–30 MeV energy band. |
| In the text | |
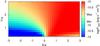 |
Fig. 14 As in Fig. 10 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
 |
Fig. 15 Injection luminosity of relativistic particles in the emitter in the case of intermediate non-radiative losses and magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
| In the text | |
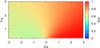 |
Fig. 16 As in Fig. 15 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
 |
Fig. 17 As in Fig. 15 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
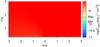 |
Fig. 18 As in Fig. 15 but showing the integrated energy flux in the 0.1–10 GeV energy band. |
| In the text | |
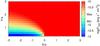 |
Fig. 19 As in Fig. 15 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
 |
Fig. 20 χ2 map for an emitter with fast non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
| In the text | |
 |
Fig. 21 Spectral energy distribution for the best fit scenario (χ2 = 7.5), which consists of an emitter with fast non-radiative losses and a weak (B = 0.5 G) magnetic field that is located at x = −1.2a and y = 0.8a. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. Observational constraints in X-rays, MeV, GeV, and TeV energies are also presented. |
| In the text | |
 |
Fig. A.1 Injection luminosity of relativistic particles in the emitter in the case of fast non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
| In the text | |
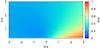 |
Fig. A.2 As in Fig. A.1 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
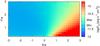 |
Fig. A.3 As in Fig. A.1 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
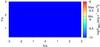 |
Fig. A.4 As in Fig. A.1 but showing the integrated energy flux in the 1–30 MeV energy band. |
| In the text | |
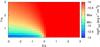 |
Fig. A.5 As in Fig. A.1 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
 |
Fig. A.6 Injection luminosity of relativistic particles in the emitter in the case of slow non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
| In the text | |
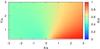 |
Fig. A.7 As in Fig. A.6 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
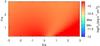 |
Fig. A.8 As in Fig. A.6 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
 |
Fig. A.9 As in Fig. A.6 but showing the integrated energy flux in the 1–30 MeV energy band. |
| In the text | |
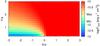 |
Fig. A.10 As in Fig. A.6 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
 |
Fig. A.11 Injection luminosity of relativistic particles in the emitter in the case of fast non-radiative losses and a strong magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
| In the text | |
 |
Fig. A.12 As in Fig. A.11 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
 |
Fig. A.13 As in Fig. A.11 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
 |
Fig. A.14 As in Fig. A.11 but showing the integrated energy flux in the 1–30 MeV energy band. |
| In the text | |
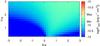 |
Fig. A.15 As in Fig. A.11 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
 |
Fig. A.16 Injection luminosity of relativistic particles in the emitter in the case of slow non-radiative losses and a strong magnetic field. The normalization was set to reproduce an energy flux in the 0.1–10 GeV range equal to 2.8 × 10-10 erg cm-2 s-1. |
| In the text | |
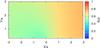 |
Fig. A.17 As in Fig. A.16 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
 |
Fig. A.18 As in Fig. A.16 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
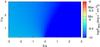 |
Fig. A.19 As in Fig. A.16 but showing the integrated energy flux in the 1–30 MeV energy band. |
| In the text | |
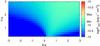 |
Fig. A.20 As in Fig. A.16 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
 |
Fig. A.21 Injection luminosity of relativistic particles in the emitter in the case of fast non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
| In the text | |
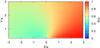 |
Fig. A.22 As in Fig. A.21 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
 |
Fig. A.23 As in Fig. A.21 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
 |
Fig. A.24 As in Fig. A.21 but showing the integrated energy flux in the 0.1–10 GeV energy band. |
| In the text | |
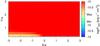 |
Fig. A.25 As in Fig. A.21 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
 |
Fig. A.26 Injection luminosity of relativistic particles in the emitter in the case of slow non-radiative losses and a weak magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
| In the text | |
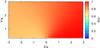 |
Fig. A.27 As in Fig. A.26 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
 |
Fig. A.28 As in Fig. A.26 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
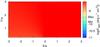 |
Fig. A.29 As in Fig. A.26 but showing the integrated energy flux in the 0.1–10 GeV energy band. |
| In the text | |
 |
Fig. A.30 As in Fig. A.26 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
 |
Fig. A.31 Injection luminosity of relativistic particles in the emitter in the case of fast non-radiative losses and a strong magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
| In the text | |
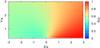 |
Fig. A.32 As in Fig. A.31 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
 |
Fig. A.33 As in Fig. A.31 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
 |
Fig. A.34 As in Fig. A.31 but showing the integrated energy flux in the 0.1–10 GeV energy band. |
| In the text | |
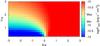 |
Fig. A.35 As in Fig. A.31 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
 |
Fig. A.36 Injection luminosity of relativistic particles in the emitter in the case of slow non-radiative losses and a strong magnetic field. The normalization was set to reproduce an energy flux in the 1–30 MeV range equal to 2.6 × 10-9 erg cm-2 s-1. |
| In the text | |
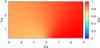 |
Fig. A.37 As in Fig. A.36 but showing the emitter’s size divided by its distance to the star. |
| In the text | |
 |
Fig. A.38 As in Fig. A.36 but showing the integrated energy flux in the 0.3–10 keV energy band. |
| In the text | |
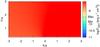 |
Fig. A.39 As in Fig. A.36 but showing the integrated energy flux in the 0.1–10 GeV energy band. |
| In the text | |
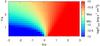 |
Fig. A.40 As in Fig. A.36 but showing the integrated energy flux in the 0.1–10 TeV energy band. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


