| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 8 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201425310 | |
| Published online | 04 February 2015 | |
The Tycho-Gaia astrometric solution
How to get 2.5 million parallaxes with less than one year of Gaia data
Lund ObservatoryDepartment of Astronomy and Theoretical Physics, Lund
University,
Box 43,
22100
Lund,
Sweden
e-mail: daniel.michalikastro.lu.se; lennartastro.lu.se; david@astro.lu.se
Received: 10 November 2014
Accepted: 24 December 2014
Context. The first release of astrometric data from Gaia will contain the mean stellar positions and magnitudes from the first year of observations, and proper motions from the combination of Gaia data with Hipparcos prior information (HTPM).
Aims. We study the potential of using the positions from the Tycho-2 Catalogue as additional information for a joint solution with early Gaia data. We call this the Tycho-Gaia astrometric solution (TGAS).
Methods. We adapt Gaia’s Astrometric Global Iterative Solution (AGIS) to incorporate Tycho information, and use simulated Gaia observations to demonstrate the feasibility of TGAS and to estimate its performance.
Results. Using six to twelve months of Gaia data, TGAS could deliver positions, parallaxes, and annual proper motions for the 2.5 million Tycho-2 stars, with sub-milliarcsecond accuracy. TGAS overcomes some of the limitations of the HTPM project and allows its execution half a year earlier. Furthermore, if the parallaxes from Hipparcos are not incorporated in the solution, they can be used as a consistency check of the TGAS/HTPM results.
Key words: astrometry / methods: data analysis / methods: numerical / space vehicles: instruments / parallaxes / proper motions
© ESO, 2015
1. Introduction
The ESA astrometry satellite Gaia was launched in December 2013 with the aim of mapping more than a billion stars (V ≲ 20) in our Galaxy (Perryman et al. 2001; de Bruijne 2012). For stars brighter than V = 15 mag, it is expected to yield positions, parallaxes and annual proper motions at an accuracy level of 5–25 μas. This accuracy can only be achieved after a global reduction of observations collected over an extended period of time (nominally five years), during which each star is seen crossing the focal plane of Gaia on average about 70 times. The multiple observations of a given star over several years are crucial for a successful disentanglement of the effects of stellar parallax and proper motion. A certain redundancy of observations is also required to estimate the additional parameters for the spacecraft attitude and calibration.
While the final Gaia results are thus expected post-2020, intermediate (provisional and less accurate) releases of astrometric data will be made; the first one is expected in mid-2016. Being based on a much shorter stretch of observations, it is envisaged that this first release will only give the mean positions of the stars, as the remaining parameters may not be reliably resolved. In previous work (Michalik et al. 2014, hereafter the HTPM paper) we have shown that the inclusion of Hipparcos data permits us to compute an astrometric solution for all five astrometric parameters of the Hipparcos stars, based on only one year of Gaia observations. This Hundred Thousand Proper Motions (HTPM, Mignard 2009) project benefits from the ~24 yr time difference between Hipparcos and Gaia to improve the proper motions and, for example, detect long-period astrometric binaries. However, a serious limitation of HTPM is that the Hipparcos stars are not numerous enough to perform an adequate calibration and attitude determination of Gaia. As described in the HTPM paper, additional “auxiliary stars” must therefore be employed. Potentially this could bias the HTPM solution if the Gaia data alone do not allow all five astrometric parameters to be determined for the auxiliary stars.
In the present paper we show that some problems with the HTPM solution can be overcome if the auxiliary stars are replaced by stars from the Tycho-2 Catalogue (Høg et al. 2000b), using their positions at the Hipparcos epoch to constrain the proper motions1. This allows us to solve the full set of astrometric parameters for the Tycho stars as well as for the Hipparcos stars, thus avoiding the potential bias from auxiliary stars. Moreover, we find that such a solution is possible with even less Gaia data than required for HTPM. The resulting Tycho-Gaia astrometric solution (TGAS) could become the first full-sky astrometric solution using Gaia data, providing an important early validation of the instrument, calibration, and data processing, at the sub-mas level. Clearly the resulting parallaxes and proper motions of a few million Tycho stars are extremely interesting also from a scientific viewpoint, e.g. for local Galactic dynamics and cluster studies.
Tycho refers to the star catalogues derived from the star mapper instrument of the Hipparcos satellite. The original Tycho-1 Catalogue (Perryman & ESA 1997) gave positions and magnitudes for about 1 million stars. The later reduction, Tycho-2 (Høg et al. 2000b), extended this to about 2.5 million stars, almost complete to V ≲ 11.5, and with uncertainties of 5–70 mas at the mean epoch of observation (~1991.25). Tycho-2 also gives proper motions, derived from a comparison with old photographic catalogues. These proper motions have uncertainties of a few mas yr-1, but as they may contain systematic errors from the old data, they are not used in the TGAS solution.
 |
Fig. 1 Fractions of the celestial sphere covered by 1, 2, ..., 20 distinct observations according to the nominal scanning law of Gaia, as functions of duration. No dead time is assumed. |
2. Prerequisites for a Tycho-Gaia solution
2.1. How much Gaia data are needed?
A good astrometric solution for (apparently) single stars requires that five astrometric parameters (α,δ,ϖ,μα ∗,μδ) are determined for each star (e.g., Lindegren et al. 2012). A sixth parameter (μr) representing the radial motion (along the line of sight) is formally required for a complete representation of the space motion. In the present context it can be ignored, except for a limited number of nearby, fast-moving stars with significant perspective acceleration, for which it is assumed to be known. Thus, at least five distinct measurements are needed for every star, where “distinct” means that the measurements differ significantly either in time or direction. The scanning law of Gaia causes the direction of its spin axis to change by 4° day-1 (de Bruijne 2012), so that any two scans of the same star separated by at least 5 days may count as distinct. Figure 1 shows that after 0.5 yr, more than 90% of the sky is covered by at least three distinct scans, which together with the two measurements (in α and δ) from Tycho should in principle suffice to determine the five astrometric parameters. The scans are not purely one-dimensional, but contain some across-scan information (Sect. 3), which is crucial for the determination of the satellite’s attitude and calibration parameters.
The real data are affected by significant dead time, increasing the time needed for sufficient sky coverage (Sect. 4.2). Considering that another half year of scanning in principle adds full redundancy to the whole sky, we estimate that the actual amount of Gaia data required for TGAS corresponds to between 0.5 and 1.0 yr including dead time.
2.2. Incorporating the Tycho and HIPPARCOS information
TGAS uses the “joint solution” method described in the HTPM paper (Michalik et al. 2014). That is, the prior information taken from the Hipparcos or Tycho Catalogue is cast in the form of normal equations Nprix = bpri for the astrometric parameters represented by the vector x. These equations are then added to the normal equations Nobsx = bobs derived from the Gaia observations before calculating the solution 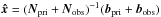 . The main difference compared with HTPM concerns the setting up of the prior information for the non-Hipparcos stars in the Tycho Catalogue, which is described below. For the subset of Hipparcos stars, the prior information is taken from van Leeuwen (2007) and set up exactly as for the HTPM solution (see Sect. 2.6 in the HTPM paper). In addition to this nominal scenario, we show in Sect. 4.3 that a solution can be made without the Hipparcos parallaxes.
. The main difference compared with HTPM concerns the setting up of the prior information for the non-Hipparcos stars in the Tycho Catalogue, which is described below. For the subset of Hipparcos stars, the prior information is taken from van Leeuwen (2007) and set up exactly as for the HTPM solution (see Sect. 2.6 in the HTPM paper). In addition to this nominal scenario, we show in Sect. 4.3 that a solution can be made without the Hipparcos parallaxes.
 |
Fig. 2 All-sky maps in equatorial Hammer-Aitoff projection (pixel size 0.85 deg2). Left: stellar distribution on the sky. Right: number of field of view transits per star. The cyan line denotes the ecliptic. |
For a Tycho-only star the prior information in the Tycho Catalogue consists of the position α, δ at the epoch J1991.25 together with its uncertainties σα ∗, σδ and correlation coefficient ρ. Remaining parameters should be treated as essentially unknown, which means that they can be set to some arbitrary values with very large uncertainties. For the simulated solutions in Sect. 3 they are set to zero with uncertainties σϖ = 1000 mas, σμα ∗ = σμδ = 1000 mas yr-1, and σμr = σvrσϖ/A, where σvr = 100 km s-1 is the prior radial velocity uncertainty and A the astronomical unit (HTPM paper, Eq. (17)). The prior astrometric parameters at J1991.25 are thus taken to be (α,δ,0,0,0,0) with covariance 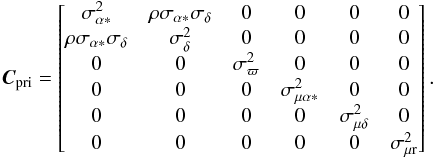 (1)The prior information including the covariance is subsequently propagated to the Gaia reference epoch (~2015) and Npri is calculated as the inverse of the propagated covariance matrix. bpri is calculated from the difference between the prior astrometric parameters and the current best estimate in the solution, as described in the HTPM paper, Eq. (18).
(1)The prior information including the covariance is subsequently propagated to the Gaia reference epoch (~2015) and Npri is calculated as the inverse of the propagated covariance matrix. bpri is calculated from the difference between the prior astrometric parameters and the current best estimate in the solution, as described in the HTPM paper, Eq. (18).
3. Simulations
In order to study the feasibility of TGAS and its potential performance we have made numerical simulations of joint Tycho-Gaia solutions using the AGISLab (Holl et al. 2012) software package. AGISLab was created at Lund Observatory to develop and test Gaia astrometric data processing strategies. While employing the same solution algorithms as the AGIS software used to process the real Gaia data (Lindegren et al. 2012), it runs in a much simplified framework which also allows us to generate simulated input data (CCD transits). The present experiments are made in a similar manner as described in the HTPM paper, to which we refer for details. A main difference is that the auxiliary stars in HTPM are replaced by Tycho stars, for which prior positions are used as described in the previous section.
Another difference is that we make the more conservative assumption that calibration errors contribute a constant RMS noise of 300 μas and 1000 μas per individual CCD observation, in the along-scan and across-scan direction, respectively. Finally, we use a (more realistic) dynamical attitude model (DAM; Risquez et al. 2013). DAM includes a detailed modelling of the attitude perturbations caused by a number of effects such as micro-propulsion thruster noise and micro-meteoroid hits. The observations are simulated using the so-called “astrometric attitude” (Risquez et al. 2013), which is the physical attitude averaged over the time required for a source to cross a CCD. Most of the stars are bright which implies that observations are gated (Kohley et al. 2012) and use a shorter integration time, resulting in a less smoothed attitude. However, we use the attitude computed for the full CCD integration time of 4.4 s, since the additional noise contribution of shorter integration times is less than 12.7 μas, see Table 1 in Risquez et al. (2013), and therefore negligible in the present context.
The real TGAS must cope with a number of complications which are ignored in the present experiments aiming to demonstrate the basic feasibility of the concept. The simplifying assumptions include (i) that there are no data gaps in the observations; (ii) that all stars are assumed to be single, and their motions thus consistent with the astrometric model represented by the five (or six) astrometric parameters; and (iii) that it is possible to adequately calibrate the gates used to observe the bright stars. In Sect. 5.1 we briefly discuss the consequences of these simplifications.
The main steps of the simulations are as follows:
-
1.
Astrometric parameters and uncertainties are read from the Tycho and Hipparcos Catalogues and used to set up the prior information as described in Sect. 2.2 and in the HTPM paper, Sects. 2.6 and 2.7. These parameters are also used as initial values from which the iterative astrometric solution is started.
-
2.
An artificial sky (Fig. 2, left) is created, representing the simulated “true” catalogue (see below). This is required in order to generate Gaia observations of the stars, and as a comparison point to evaluate the quality of the astrometric solution.
-
3.
The Gaia observations (Fig. 2, right) of the Hipparcos and Tycho stars are generated according to the nominal scanning law, including the perturbations from DAM, and observation noise. For the latter we conservatively assume that all Hipparcos and Tycho stars are measured with the same accuracies, per CCD observation, as a star of magnitude G = 13, independent of the actual magnitude (σAL = 94 μas, σAC = 489 μas in the astrometric field).
-
4.
The prior data and simulated observations are processed through the astrometric solution which effectively computes a least-squares estimate of all astrometric parameters together with the parameters describing the instrument attitude as a function of time. The components of the attitude quaternion are represented by cubic splines with a knot interval of 30 s. No special provision is made to handle the rate and angle discontinuities introduced by the use of DAM. The astrometric solution is made for the observation interval 2014.5–2015.0 (0.5 yr), with the reference epoch centred on the observations, i.e., at J2014.75. The reference frame is effectively determined by the positions and proper motions in the Hipparcos subset.
-
5.
The resulting astrometric catalogue is compared with the “true” catalogue and the statistics of the differences are used to characterize the uncertainties of the solution.
The generation of the simulated “true” catalogue is done slightly differently for the Hipparcos stars and the Tycho-only stars (those that are not in the Hipparcos Catalogue). For the Hipparcos subset, “true” astrometric parameters are simulated by perturbing the prior data (i.e., the Hipparcos Catalogue) by amounts that are consistent with the prior covariances. This subset is further described in Sect. 3.2.1 of the HTPM paper. For the Tycho-only stars, the “true” positions are similarly obtained by perturbing the prior values according to their assigned uncertainties and correlations. For the proper motions we regard the values given in Tycho-2 as “true” for the present purpose; this is acceptable as they are not used anywhere in the solution, not even as priors. As the Tycho-2 Catalogue does not contain parallaxes, we simulate their true values based on the apparent magnitudes, neglecting extinction and assuming that the absolute magnitudes have a normal distribution with mean value + 5 mag and standard deviation 3 mag (see HTPM paper, footnote 4). Although it would have been possible to make the parallax distribution dependent on the proper motion of the individual star, we do not consider the added complication worthwhile, as the results are rather insensitive to the assumed distribution. Radial velocities are simulated assuming a centred normal distribution with a conservatively chosen σvr = 100 km s-1.
Uncertainties of the astrometric parameters when processing 0.5 yr of simulated Gaia data jointly with Tycho and Hipparcos priors, nominal scenario.
4. Results
4.1. Nominal scenario
Table 1 summarizes the results obtained in the nominal scenario, i.e., using the full prior information from Hipparcos and assuming no dead time. The upper part of the table gives statistics for the Tycho-only stars, the lower part for the Hipparcos stars. As the priors are very different for the two subsets, they are separately discussed in the following.
4.1.1. Tycho-only stars
Any attempt to solve five parameters with 0.5 yr of Gaia data without a prior utterly fails. Remarkably, however, the inclusion of the Tycho positions allows us to solve not only the proper motions, but also the parallaxes for the 2.5 million Tycho stars with sub-mas precision. Here the proper motions rely entirely on the Tycho positions, as shown by the strong variation of the uncertainty with magnitude, mainly reflecting the variation of positional uncertainty in the Tycho Catalogue. In spite of the fact that the prior parallaxes are set to zero, the posterior estimates have very little bias (the median parallax error is − 0.7 μas).
4.1.2. H ipparcos stars
It is interesting to compare the Hipparcos subset of this solution with the (conservative) HTPM case B, where only the positions were solved for the auxiliary non-Hipparcos stars (see Sect. 4.1 in the HTPM paper). The TGAS simulation is based on half as much Gaia data as HTPM-B, uses more conservative assumptions for attitude and calibration noise, but still provides improvements in all respects: the positions are at least a factor two better and the proper motions improved by about 16%. More importantly, the resulting parallax errors are 26% smaller and centred on zero (median error − 0.03μas), while HTPM-B gave systematically underestimated parallaxes for the Hipparcos stars (median error − 591 μas). This clearly demonstrates that the additional prior provided by the Tycho positions also benefits the Hipparcos subset.
4.1.3. Spatial characteristics of the solution
 |
Fig. 3 All-sky maps characterizing the astrometric performance of the nominal TGAS solution (pixel size 3.4 deg2). The cyan line denotes the ecliptic. a) Actual errors in parallax (TGAS solution minus simulated true values), median per pixel to show that the solution is unbiased. b) Same as before, but RSE per pixel to characterize the size of the actual errors. c) Formal standard errors in parallax as computed in the astrometric solution. d) RSE values of the normalized errors in parallax. |
The quality of the TGAS results for a particular star depends on the number and temporal distribution of its Gaia observations, which in turn depends on the position in the sky. Figure 2 (right) shows the number of field-of-view transits per star as set by the scanning law, yielding relatively few transits in areas within 45° of the ecliptic. Figure 3 shows the error characteristics for the Tycho-only subset. Panel a displays the median of the actual parallax errors (TGAS solution minus the simulated true values). In the well observed areas these are centred on zero, showing that the parallaxes are unbiased. The statistical scatter is larger in areas with few observations and unfavourable temporal distributions. There the errors could also be correlated over several degrees. The overall median of the actual parallax errors is − 0.6 μas. The error maps for the other astrometric parameters have similar characteristics. The size of the actual errors is shown in panel b, displaying the RSE per pixel.
In an astrometric solution of real data the errors cannot be assessed by comparing the solution with the true values. Error estimates must instead come from the formal standard errors (uncertainties), computed as the square-roots of the diagonal elements of the covariance matrix (possibly adjusted depending on the size of the residuals in the solution). It is important that the formal standard errors (panel c) correctly characterize the actual errors. In the ideal case, the normalized error, i.e., the ratio of the actual error to the formal standard error, should follow a normal distribution with zero mean and unit standard deviation all over the sky. It was already shown (by the maps of the actual errors) that the mean values are close to zero. Panel d then shows the RSE values of the normalized parallax errors. These are around 1.0 everywhere2, with a relatively small scatter in the Galactic plane, where there are more stars per pixel. A larger scatter is seen in the more sparsely populated areas of the sky, where the statistical uncertainty of the calculated RSE values is higher. The global RSE value is 1.03, the global RMS value 1.09. This shows that TGAS, under the given assumptions, provides formal standard errors that essentially correctly characterize the actual errors.
4.2. Simulation including data gaps
 |
Fig. 4 All-sky maps for a TGAS simulation with simulated data gaps (see Sect. 4.2). Left: number of field of view transits per star. Right: formal standard errors (uncertainties) in parallax as computed in the astrometric solution. |
The results presented so far and in Table 1 are based on a simulation which includes all observations according to the nominal scanning law over the assumed period of 0.5 yr. The real mission has numerous data gaps of varying lengths, caused for example by orbit maintenance manoeuvres, eclipses by the moon, and solar activity. With no observations acquired at these times, the attitude modelling cannot take advantage of the physical continuity of the attitude across the gaps. The result is a globally weakened astrometric solution, which potentially could make the TGAS solution infeasible for a dataset as short as 0.5 yr. We investigate this in a separate simulation including data gaps.
 |
Fig. 5 Comparison of the parallaxes in TGAS and the Hipparcos Catalogue (nominal TGAS run, i.e., using the Hipparcos parallaxes as prior). Left: the normalized parallax errors (calculated minus the simulated true values, divided by their formal standard errors) are correlated. Right: the differences of the actual parallax values (normalized by their combined standard errors) follow a Gaussian distribution with standard deviation 0.91, less than 1.0 because of the correlation. The solid red line is a Gaussian distribution with unit width. |
 |
Fig. 6 Same as Fig. 5, but for the TGAS run without parallax prior (Sect. 4.3). Left: the normalized parallax errors are uncorrelated. Right: the normalized differences of the actual parallax values have unit standard deviation. |
The acquisition dead time for Gaia (the fraction of time during which no observations are acquired) is estimated to be ≃6%. Additionally, individual observations may be lost due to cosmic rays, CCD defects, charge injection, telemetry losses, etc. Such losses are less damaging to the astrometric solution as they do not create gaps in the attitude determination and sky coverage, although they do affect the results in a statistical way. For bright stars the additional observation dead time is estimated to be about 5%, resulting in a total dead time of 11%.
To explore the robustness of the TGAS solution to acquisition dead time we apply the actual time sequence of data gaps obtained during six months of the early Gaia operations3 to the nominal simulation described in Sect. 3. While most of the applied gaps are shorter than 10 min, the two longest ones are 5.0 and 2.6 days. The total length of the gaps is 15.6 days, corresponding to 8.5% of acquisition dead time. Compared to the nominal value (6%) this simulation is therefore conservative, although we ignore the additional observation dead time.
Removing all observations corresponding to these gaps we find that a stable solution is still possible. Compared with the solution without gaps some stars are observed less, resulting in larger formal errors. About 1000 stars are not observed at all, and were removed from the solution and subsequent statistics. As shown in Fig. 4, the gaps cause considerable inhomogeneity in the sky coverage and formal errors. The white lines and wedges in the left panel show the areas most affected by the data gaps. As expected, stars in those areas also have large formal errors, as seen in the right panel. The formal errors are plotted on the same scale as Fig. 3, panel c, to show that only the areas affected by dead time suffer from larger errors. 441 pixels are saturated, all of these corresponding to areas affected by dead time. For 3.5% of the sky the formal errors are larger than 3 mas. Globally, the parallax and position errors are about 16% higher than in the solution without data gaps. The proper motion errors, which are dominated by the errors in the Tycho positions, are less affected.
4.3. Solution without HIPPARCOS parallax prior
For validation purposes it is desirable to compare the parallax values of the TGAS solution with Hipparcos. This is problematic when using the nominal TGAS since it already incorporates the Hipparcos parallaxes as a prior. As shown in Fig. 5 (left panel) this leads to a statistical correlation between the two datasets (correlation coefficient + 0.23). As a result the differences between the parallaxes have a smaller spread than expected from their combined standard errors (right panel of Fig. 5).
To derive independent parallaxes, we propose a TGAS solution incorporating only the position and proper motion information from the Hipparcos Catalogue. This is achieved by setting the prior parallax value and the corresponding row and column in the Hipparcos prior normal matrix to zero before adding the information arrays. As shown in Fig. 6 this removes the correlation entirely (correlation coefficient − 0.0043) at the expense of a moderate increase in astrometric uncertainties of the Hipparcos subset (Table 2). The results for the Tycho subset are not shown since the values found are virtually identical to the nominal scenario in Table 1.
5. Discussion
5.1. Consequences of the simplifying assumptions
Data gaps:
our simulations show that TGAS is robust to data gaps according to a realistic distribution of acquisition dead time. The data gaps result in an inhomogeneous sky distribution of actual and formal errors, but do not significantly degrade the performance in well-observed regions. Affected areas can be recovered through additional observations after the first half year. The actual length of Gaia observations necessary for a good solution over the whole sky is difficult to estimate without detailed knowledge about the actual distribution of gaps. However, since the whole sky is nominally covered by multiple scans every half year (cf. Fig. 1), it is reasonable to conclude that the required time is less than 1 yr.
Non-single stars:
a large fraction of the TGAS stars are in reality binaries or multiple stars, but not recognised as such in the Tycho Catalogue and thus treated as single in TGAS. Some of them will be resolved by Gaia thanks to its higher resolution, which makes it possible to discard these objects or treat them appropriately.
For systems which are unresolved also by Gaia the space motions of their photocentres will deviate from the linear uniform model represented by the astrometric parameters. In the later astrometric solutions of Gaia data, objects that do not fit the single-star astrometric model will be detected and filtered out for special treatment, but this mechanism is not effective in TGAS due to the small redundancy of observations. TGAS will contain some fraction of such systems with significant deviations from the adopted five-parameter model, which will remain unrecognised in the solution. Their actual astrometric errors will be underestimated by the formal uncertainties. This may be a common characteristic of the early data releases, typically based on datasets with low redundancy and imperfect calibrations.
The impact of astrometric binaries on the derived proper motions should nevertheless be small thanks to the 24 yr baseline of TGAS. The same is true for the TGAS parallaxes as they are dominated by the Gaia observations and at most only a fraction of the error in the annual proper motion contributes to the parallax error. Comparing the proper motions from TGAS and those in Tycho-2 (which incorporate century-old ground-based observations) could reveal not only systematic errors in the Tycho-2 proper motions but also some long-period astrometric binaries.
Bright-star performance and calibration issues:
like any other AGIS solution, TGAS will use the generic calibration model described in Lindegren et al. (2012), Sects. 3.4 and 3.5, which takes into account the actual geometry of the optics and detectors as well as calibrations linked to chromatic image displacements, basic-angle variations, and radiation-induced image displacements. However, a specific complication of TGAS is that it almost exclusively uses stars brighter than magnitude ~12, for which Gaia employs CCD gates (Kohley et al. 2012) to avoid saturation. The gated observations need a separate calibration for each gate, but with the limited amount of Gaia data in a TGAS solution there may not be sufficient observations of bright stars to do so. Gate 4 is used for the brightest stars with magnitudes G ≲ 8.84. If it turns out that this gate cannot be reliably calibrated with half a year of Gaia data, we would in the worst case lose all stars brighter than G ≃ 8.84 in the TGAS solution, or about 2.3% of the Tycho stars. The reduced number of stars degrades the solution somewhat (for example because the attitude is less accurately determined), but we have verified that TGAS works with as few as one million Tycho stars. The bright-star performance is a more serious issue for the HTPM solution, as more than half of the Hipparcos stars are brighter than 8.84 mag.
5.2. Systematics in the Tycho-2 data
The present TGAS experiments assume that the Tycho positions give the barycentric directions to the stars at the standard Hipparcos epoch J1991.25. In reality the Tycho-2 positions refer to slightly different epochs, which could even be different in α and δ. The actual TGAS solution should use the mean effective epoch (tα + tδ) / 2 of each star rather than J1991.25.
A potentially more serious complication is that the Tycho positions do not strictly represent the barycentric directions at the given epochs of observation. The positions were derived from the stacked star mapper photon count records accumulated over the whole Hipparcos mission (Høg et al. 2000a). Parallaxes were typically not taken into account in this process, and the resulting positions are therefore offset by a fraction of the parallax. Both the fraction and direction of the offset depend in a complex way on the distribution, geometry, and weights of the photon count records. There is no simple way to correct for this effect in TGAS, nor was it included in our simulations. However, we argue that its impact on the TGAS results should be very small. The Tycho positions are mainly used to derive the proper motions on a baseline of 24 years. Since the parallax of a given star is typically of similar size as its annual proper motion, and the position offset is just a fraction of the parallax, it follows that the resulting annual proper motion is typically only offset by a few per cent of the parallax. This, in turn, should have an almost negligible impact on the parallax, which is mainly derived from the Gaia observations relative to the extrapolated linear motion.
5.3. Reference frame of TGAS
The Tycho positions around 1991 and the Gaia observations around 2015 are by themselves not sufficient to determine the spin of the reference frame for TGAS, only its orientation at the Tycho epoch. By incorporating positions and proper motions from Hipparcos in TGAS, in the same way as described in the HTPM paper, the TGAS results are effectively on the Hipparcos reference frame.
6. Conclusions
The currently foreseen contents of the first Gaia data release include positions from a two-parameter solution of the early (≲1 yr) data, because a full five-parameter solution will not be feasible, or reliable enough, based on these data alone. Incorporating prior information into the solution makes it possible to solve all five astrometric parameters (i.e., including parallax and proper motion) with significantly less Gaia data. The HTPM project incorporates the Hipparcos Catalogue, resulting in greatly improved astrometry for the ~105 Hipparcos stars. However, as shown in Michalik et al. (2014), such a solution should be based on at least one year of continuous Gaia data, as otherwise the results will be biased by the use of auxiliary stars for which the full set of parameters cannot be resolved.
TGAS extends the original HTPM proposal and takes the idea of a joint solution one step further by combining, in a single global astrometric solution, measurements from the early Gaia mission with data from the Tycho and Hipparcos Catalogues. In this paper we have shown that the approximate positions at the earlier epoch provided by Tycho are sufficient to disentangle the ambiguity between parallax and proper motion in a short stretch of Gaia observations. Therefore TGAS allows us to derive positions, parallaxes, and proper motions for up to 2.5 million stars half a year earlier than the proposed first Gaia data release containing only two parameters, and one year earlier than the proposed second Gaia data release containing the first five parameter solution. Using the five parameter solutions of the Tycho stars for HTPM avoids the risk of biasing the HTPM parallaxes and improves the resulting astrometry for the Hipparcos stars. This is true even when the prior parallaxes from Hipparcos are not used at all in the TGAS/HTPM solution, which provides a stringent test of its consistency with the Hipparcos parallaxes (see Sect. 4.3). The moderate increase in astrometric uncertainties of such a solution compared to the nominal scenario seems to be a price worth paying for the benefit of a catalogue of independent parallaxes. We therefore propose that the solution not using the Hipparcos parallaxes should be the baseline for TGAS/HTPM.
Our simulations of TGAS suggest that the accuracy of the resulting astrometry for the Tycho stars will be similar to the Hipparcos Catalogue, and possibly significantly better depending on the exact scenario of the number of Gaia observations available, dead time intervals, calibration, etc. Moreover, the dataset would be almost complete to V ≃ 11.5, or 3–4 mag fainter than the survey part of the Hipparcos Catalogue. Although the scientific lifetime of the data would be limited, in view of the expected later releases from Gaia, the potential applications cover many areas of stellar and galactic astronomy. Perhaps even more importantly, TGAS offers the opportunity to perform a full-sky scientific validation of the Gaia instrument, calibration, and data processing at sub-mas level much earlier than previously anticipated. For this reason alone, we believe TGAS should be attempted as soon as Gaia has collected sufficient data for such a solution, which could be in early 2015.
Acknowledgments
TGAS originated from discussions with Thierry Forveille and Claus Fabricius during the review phase of the HTPM paper. We are grateful to Ulrich Bastian, Anthony Brown, Jos de Bruijne, José Hernández, Sergei Klioner, Uwe Lammers, Paul McMillan, and the referee Floor van Leeuwen, for providing many supportive comments, questions, and feedback on the manuscript. The DAM data were kindly provided by Daniel Risquez. We gratefully acknowledge support from the Swedish National Space Board and the Royal Physiographic Society in Lund.
References
- de Bruijne, J. H. J. 2012, Ap&SS, 341, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000a, A&A, 357, 367 [NASA ADS] [Google Scholar]
- Høg, E., Fabricius, C., Makarov, V. V., et al. 2000b, A&A, 355, L27 [NASA ADS] [Google Scholar]
- Holl, B., Lindegren, L., & Hobbs, D. 2012, A&A, 543, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kohley, R., Garé, P., Vétel, C., Marchais, D., & Chassat, F. 2012, in SPIE Conf. Ser., 8442 [Google Scholar]
- Lindegren, L., Lammers, U., Hobbs, D., et al. 2012, A&A, 538, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michalik, D., Lindegren, L., Hobbs, D., & Lammers, U. 2014, A&A, 571, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignard, F. 2009, The Hundred Thousand Proper Motions Project, Gaia Data Processing and Analysis Consortium (DPAC) Technical Note GAIA-C3-TN-OCA-FM-040, http://www.cosmos.esa.int/web/gaia/public-dpac-documents [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The Hipparcos and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Risquez, D., van Leeuwen, F., & Brown, A. G. A. 2013, A&A, 551, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, The New Reduction of the Raw Data, Astrophys. Space Sci. Lib. (Springer), 350 [Google Scholar]
All Tables
Uncertainties of the astrometric parameters when processing 0.5 yr of simulated Gaia data jointly with Tycho and Hipparcos priors, nominal scenario.
All Figures
 |
Fig. 1 Fractions of the celestial sphere covered by 1, 2, ..., 20 distinct observations according to the nominal scanning law of Gaia, as functions of duration. No dead time is assumed. |
| In the text | |
 |
Fig. 2 All-sky maps in equatorial Hammer-Aitoff projection (pixel size 0.85 deg2). Left: stellar distribution on the sky. Right: number of field of view transits per star. The cyan line denotes the ecliptic. |
| In the text | |
 |
Fig. 3 All-sky maps characterizing the astrometric performance of the nominal TGAS solution (pixel size 3.4 deg2). The cyan line denotes the ecliptic. a) Actual errors in parallax (TGAS solution minus simulated true values), median per pixel to show that the solution is unbiased. b) Same as before, but RSE per pixel to characterize the size of the actual errors. c) Formal standard errors in parallax as computed in the astrometric solution. d) RSE values of the normalized errors in parallax. |
| In the text | |
 |
Fig. 4 All-sky maps for a TGAS simulation with simulated data gaps (see Sect. 4.2). Left: number of field of view transits per star. Right: formal standard errors (uncertainties) in parallax as computed in the astrometric solution. |
| In the text | |
 |
Fig. 5 Comparison of the parallaxes in TGAS and the Hipparcos Catalogue (nominal TGAS run, i.e., using the Hipparcos parallaxes as prior). Left: the normalized parallax errors (calculated minus the simulated true values, divided by their formal standard errors) are correlated. Right: the differences of the actual parallax values (normalized by their combined standard errors) follow a Gaussian distribution with standard deviation 0.91, less than 1.0 because of the correlation. The solid red line is a Gaussian distribution with unit width. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, but for the TGAS run without parallax prior (Sect. 4.3). Left: the normalized parallax errors are uncorrelated. Right: the normalized differences of the actual parallax values have unit standard deviation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


