| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 5 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425114 | |
| Published online | 29 January 2015 | |
On the gamma-ray emission from 3C 120
1 ICRANet, Piazza della Repubblica 10, 65122 Pescara, Italy
e-mail: narek@icra.it
2 ICRANet-Yerevan, Marshall Baghramian Avenue 24a, 0019 Yerevan, Republic of Armenia
Received: 6 October 2014
Accepted: 11 December 2014
We report the analysis of Fermi Large Area Telescope data from five years of observations of the broad line radio galaxy 3C 120. The accumulation of a larger data set results in the detection of high energy γ-rays up to 10 GeV, with a detection significance of about 8.7σ. A power law spectrum with a photon index of 2.72 ± 0.1 and an integrated flux of Fγ = (2.35 ± 0.5) × 10-8photoncm-2 s-1 above 100 MeV well describe the data averaged over five years of observations. The variability analysis of the light curve with 180, and 365 day bins reveals flux increase (nearly twice its average level) during the last year of observation. This variability on month timescales indicates the compactness of the emitting region. The γ-ray spectrum can be described as synchrotron self-Compton emission from the electron population producing the radio-to-X-ray emission in the jet. The required electron energy density exceeds the magnetic field energy density only by a factor of 2, meaning there is no significant deviation from equipartition.
Key words: galaxies: individual: 3C 120 / gamma rays: galaxies / radiation mechanisms: non-thermal
© ESO, 2015
1. Introduction
The γ-ray detection by Fermi Large Area Telescope (Fermi-LAT) from non blazar active galactic nuclei (e.g., Centaurus A, Abdo et al. 2010b; M 87, Abdo et al. 2009a; NGC 1275, Abdo et al. 2009b) shows that these are different and potentially very interesting classes of γ-ray emitters. This provides an alternative approach for studying high energy emission processes compared to blazars where the emission is strongly Doppler boosted.
At the red shift z = 0.033, 3C 120 is a nearby Seyfert 1 radio galaxy that is an active and powerful emitter of radiation at all the observed wavebands. With bright continuum and broad optical emission lines 3C 120 is usually classified as a broad line radio galaxy (BLRG). Hosting a black hole with a mass 5.5 × 107M⊙, well constrained from the reverberation mapping (Peterson et al. 2004), 3C 120 has a radio morphology more similar to the Fanaroff-Riley class I radio sources (Fanaroff & Riley 1974). The source has a powerful one-sided radio jet extending from a sub-pc up to 100 kpc scales (Walker et al. 1987). Observations with the Very Long Baseline Array at frequencies (22, 43, and 86 GHz) reveal a very rich inner jet structure containing several superluminal components with apparent speed up to 4−6 c (Homan et al. 2001; Gómez et al. 1998, 1999) that can be investigated with better resolution than most other extragalactic superluminal sources because of the relatively low redshift. The jet inclination angle to the line of sight is constrained to be 14° by the measured apparent motion (Eracleous & Halpern 1998). Recently, using X-ray and radio observations, Marscher et al. (2002) found that dips in the X-ray emission are followed by ejections of bright superluminal knots in the radio jet, which clearly establishes an accretion-disk-jet connection.
In X-rays, 3C 120 is a bright (≈ 5 × 10-11ergcm-2 s-1 at 2−10 keV) and variable source on time scales from days to months (Halpern 1985). The ASCA observation shows a broad iron line Kα that can be fitted by Gaussian with σ = 0.8 keV and equivalent width of 400 eV. The knots in the jet of 3C 120 observed in radio and optical bands have also been detected later in the X-ray band with the ROSAT and Chandra (Harris et al. 2004), which indicates the existence of high energy nonthermal particles in these knots. The origin of X-ray emission is highly debated especially when the extrapolation of synchrotron emission fails to take this emission into account. In these cases it can be explained by the inverse-Compton scattering of cosmic microwave background (CMB) photons or by proton synchrotron emission; If so, this component can be extended up to MeV/TeV range (Zhang et al. 2010; Aharonian 2002).
At high energies (HE; > 100 MeV) the source was not detected with the energetic gamma-ray experiment telescope on board the Compton Gamma Ray Observatory, despite several pointing observations (Lin et al. 1993). The 2σ upper limit on the source flux above 100 MeV was set to 9 × 10-8 cm-2 s-1. Afterward, the source was detected with the Fermi-LAT using 15 months of all-sky exposures (Abdo et al. 2010c). The averaged HE spectrum between 100 MeV and 1 GeV can be described by the power law with photon index Γ = 2.71 ± 0.35 and an integral flux F(E> 100 MeV) = (2.9 ± 1.7stat) × 10-8 cm-2 s-1 with the detection significance of 5.6σ. However the source is not included in the Fermi-LAT second source catalog (Nolan et al. 2012, 2FGL) since the averaged signal appeared to be below the required 5σ threshold. This might be evidence of the long-term variability of the flux, since for a steady γ-ray signal the accumulation of longer data set (24 versus 15 months) should result in an increase of the detection significance 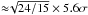 .
.
Abdo et al. (2010c) and Kataoka et al. (2011) investigated the temporal variations of the γ-ray flux (above 100 MeV) over short timescales. The light curve binned in three-month-long periods shows only a few episodes when the flux increased on a level more than 3σ. One such episode occurred during the 15-month data set (Abdo et al. 2010c) and two occurred during the 24-month data set (Kataoka et al. 2011). The rest of the time, the source was undetectable by Fermi-LAT. This was interpreted as a GeV flux variation on 90 day scales. However considering only two periods out of eight have been detected and taking trials into account, post-trial significance probably is even lower than 3σ. Therefore, these conclusions were inconclusive considering the limited statistics of the detected signal.
The peculiar structure of 3C 120 implies different sites (sources) as the origin of the detected GeV γ-rays. Clearly, analogous with blazars, the non thermal beamed radiation can be produced in the innermost part of the jet on scales less than a kilo-parsec (but not strongly boosted because of the larger jet inclination angle compared to blazars). In fact, a powerful jet observed at an inclination angle θ ≤ 14°, producing radio to X-ray flux (with the luminosity ~ 1045ergs-1) via synchrotron emission can produce Doppler boosted γ-ray flux via inverse Compton scattering. This sort of emission would appear as variable on week timescales or shorter with the luminosity Lγ ~ Urad/UBLsyn, which in principle can be detected by Fermi-LAT, depending on the magnetic field and emitting region size. On the other hand, the nonvariable γ-ray emission from the extended structures (e.g., extended lobes, large scale jet, and knots) can extend up to the GeV energies and contribute (at least at some level) the total observed γ-ray flux. For example, a γ-ray emission from the extended lobes of nearby Centaurus A radio galaxy contributes greater than one-half of the total source emission (Abdo et al. 2010a; Yang et al. 2012). Moreover, steady γ-ray emission from 3C 120 on the level of Fermi-LAT sensitivity has already been predicted from the jet knots within both proton synchrotron (Aharonian 2002) and beamed CMB inverse Compton scenarios (Zhang et al. 2010). Therefore the compact and extended structures both remain possible sites for production of the observed γ-rays.
In general the absence of statistically significant indication of variability introduces uncertainties to distinguish between different emission mechanisms. In particular for 3C 120, given the presence of many prominent sites for γ-ray production, the possible variability (or nonvariability) is crucial for understanding the origin of HE emission. Moreover, the spectrum only extends up to 1 GeV that does not provide any possibility to distinguish between the mechanisms using the predicted different spectral shapes. Now the larger data set allows us to study the spectrum with better statistics above 1 GeV, and to investigate the variability in detail. This motivated us to have a new look at the γ-ray emission based on the five years of Fermi-LAT data.
The paper is structured as follows. The results of spectral analysis are presented in Sect. 2. The temporal analysis is presented in Sect. 3. Implications of different emission mechanisms are discussed in Sect. 4, and conclusions are presented in Sect. 5.
2. Fermi-LAT data analysis
2.1. Data extraction
Fermi-LAT on board the Fermi satellite is a pair-conversion telescope, operating since August 4, 2008, and is designed to detect HE γ-rays in the energy range 20 MeV−300 GeV (Atwood et al. 2009). It constantly scans the entire sky every three hours and by default is always in the survey mode. Details about the LAT instrument can be found in Atwood et al. (2009).
For the present analysis, we use publicly available Fermi-LAT ~ 5.3 yr data from 4th August 2008 to 4th December 2013 (MET 239557417–407808003). We use the Pass 7 data and analyze them using the Fermi Science Tools v9r33p0 software package. We select events with zenith angle < 100° and with energy between 100 MeV and 100 GeV. We only used the data when the rocking angle of the satellite was < 52°, to reduce the contamination from the Earth limb γ-rays, which are produced by cosmic rays interacting with the atmosphere. We downloaded photons from a 10° region centered on VLBI radio position of 3C 120 (RA, Dec) = (68.296, 5.354) and worked with a 14° × 14° square region of interest (ROI). We bin photons with gtbin tool with a stereographic projection into pixels of 0.1° × 0.1° and into 30 equal logarithmically-spaced energy bins. Then with the help of gtlike tool, we perform a standard binned maximum likelihood analysis. The fitting model includes diffuse emission components and γ-ray sources within ROI (the model file is created based on 2FGL) and since 3C 120 is not included in 2FGL, we added a pointlike source on the known location of 3C 120 (RA, Dec) = (68.296, 5.354), (Ma et al. 1998). The Galactic background component is modeled using the LAT standard diffuse background model gll_ iem _ v05_ rev1 and iso_source_v05 for the isotropic γ-ray background. The normalization of background models as well as fluxes and spectral indices of sources within 10° are left as free parameters in the analysis.
2.2. Spectral analysis
We assume that the γ-ray emission from 3C 120 is described by the power law and normalization and power law index are considered free parameters, then the binned likelihood analysis is performed. From a binned gtlike analysis, the best-fit power law parameters for 3C 120 are 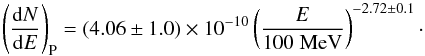 (1)This corresponds to an integral flux of
(1)This corresponds to an integral flux of 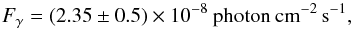 (2)with only statistical errors taken into account. The test statistic (defined as TS = 2(log L − log L0), where L and L0 are the likelihoods when the source is included or not) is TS = 76.3 above 100 MeV, corresponding to a ≈ 8.7σ detection significance. The results are consistent with the parameters found in (Abdo et al. 2010c), namely photon index Γ = 2.71 ± 0.35 and integral flux (2.9 ± 1.7) × 10-8 ph cm-2 s-1 above 100 MeV. The value TS = 76.3 is above the threshold value TS = 25 and 3C 120 should be included in the upcoming Fermi-LAT source catalogs.
(2)with only statistical errors taken into account. The test statistic (defined as TS = 2(log L − log L0), where L and L0 are the likelihoods when the source is included or not) is TS = 76.3 above 100 MeV, corresponding to a ≈ 8.7σ detection significance. The results are consistent with the parameters found in (Abdo et al. 2010c), namely photon index Γ = 2.71 ± 0.35 and integral flux (2.9 ± 1.7) × 10-8 ph cm-2 s-1 above 100 MeV. The value TS = 76.3 is above the threshold value TS = 25 and 3C 120 should be included in the upcoming Fermi-LAT source catalogs.
Figure 1 shows the spectrum of 3C 120 obtained by separately running gtlike for 5 energy bands, where the dashed line shows the best-fit power law function for the data given in Eq. (1). In comparison, results from the previous study of 3C 120 (Abdo et al. 2010c) are presented as blue data points. The highest energy bin (10−100 GeV), is shown as an upper limit.
Since we used the exposure almost 2.5 times longer than in 2 FGL, this can result in additional faint sources in the data that are not properly accounted for in the model file. In order to check if any additional sources were present, the gttsmap tool is used with the best-fit model of 0.1−100 GeV events to create a TS significance map of the 6° × 6° region. Nevertheless, no significant excess hot spots (TS > 25) are found. Therefore, the model file used in the analysis gives a good representation of the data. Next, we obtained the source localization with gtfindsrc, yielding RA = 68.205, Dec = 5.38 with a 95% confidence error circle radius of r95 = 0.05. These localizations are offset by 0.09° from the VLBI radio position of 3C 120 (RA = 68.296, Dec = 5.354) (Ma et al. 1998).
3. Temporal variability
The variability of the observed γ-ray flux could provide important constraints on the emitting region(s). The timescale of the observed flux variation τ would limit the (intrinsic) size of the γ-ray production region to 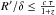 where δ is the Doppler factor and z is the red shift. During the previous variability study, using the accumulation of 90- day Fermi-LAT all-sky survey exposures, the source shows two time intervals when TS > 10 whereas it was mostly being undetectable by Fermi-LAT. This could be interpreted as a possible variability at GeV energies (Kataoka et al. 2011).
where δ is the Doppler factor and z is the red shift. During the previous variability study, using the accumulation of 90- day Fermi-LAT all-sky survey exposures, the source shows two time intervals when TS > 10 whereas it was mostly being undetectable by Fermi-LAT. This could be interpreted as a possible variability at GeV energies (Kataoka et al. 2011).
More observational data set (increased photon statistics) can provide more detail in this regard. Accordingly, the total observational time (from August 4th, 2008 to December 4th, 2013) is divided into different timescales and light curves are generated using the unbinned likelihood analysis with gtlike. To minimize uncertainties in the flux estimation, the photon indices of all sources are fixed to the values obtained in 100 MeV−100 GeV energy range for the whole time period. Instead, the normalization of 3C 120 and background point sources are treated as free parameters. Since no variability is expected from the underlying background diffuse emission, the normalization of both background components is fixed to the values that were obtained for the whole time period.
 |
Fig. 1 Averaged differential spectrum of 3C 120 (above 100 MeV) red points as compared with that based on the initial 15 month data set (Abdo et al. 2010c). The dashed black line shows the power law function determined from the gtlike. |
Figure 2 illustrates the γ-ray flux variation above 100 MeV for 180- and 365-days sampling with red and blue data points, respectively. It is noticeable that up to ≈ 55 400 MJD, γ-rays from 3C 120 are below Fermi-LAT sensitivity (detection significance TS < 10). Afterward a cycle with faint γ-ray emission changes and then the produced flux is sufficient to be detected by Fermi-LAT. For example, the averaged flux in a year sampling is more than twice higher than its average level (see Fig. 2) with highest test statistics corresponding to TS = 63.8 (similar to 180-day sampling TS = 38.92). This is probably caused by the changes in emission states, e.g., the source moves in a state that is characterized by more effective production of γ-rays resulting a flux increase. This flux increase gives proof of flux variability on month timescales.
In addition to reported month timescale variability, flux variation for shorter time periods e.g., a month or sub-month time-scales has been performed over the time interval where the increase of flux was detected. Accordingly, the unibinned likelihood analysis is performed using shorter time sampling (7 and 15 days) for the time period > 56 000 MJD. A γ-ray signal from the source is detected above threshold TS > 10 using a sampling of only seven days. The required condition was fulfilled only in three time intervals with the maximum detection significance 4.8σ reached in the last week of September 2013. The corresponding flux is (2.15 ± 0.6) × 10-7photoncm-2 s-1 nearly an order of magnitude higher than average flux level presented in Eq. (2). Because of limited statistics, however, no definite conclusions about shorter time scale variability can be drawn.
 |
Fig. 2 Gamma-ray light curve from August 4th 2008 to December 4th 2013. The bin size corresponds to 180- (red) and 365-days (blue). The galactic and extragalactic background emission is fixed to the best-fit parameters obtained for the overall time fit. |
4. Discussion and interpretation
The monthly timescale variability of 3C 120 (tvar ~ 6 month) denotes the compactness of the emitting region. Under any reasonable assumption for Doppler boosting, δ = 3 − 5, the emitting region cannot be larger than R<δctvar ~ 1018(δ/ 4) cm. This immediately allows us to exclude jet knots as the main sites where the observed γ-rays are produced. Most likely, the γ-rays are produced in a compact region of the jet, e.g., the blob moving with relativistic velocities. Generally, the broad band spectrum of blazars, as well as those from radio galaxies, which have jets oriented at systematically larger angles to our line of sight, are successfully described by the synchrotron/synchrotron self-Compton (SSC) model (Ghisellini et al. 1985; Celotti et al. 1991; Bloom & Marscher 1996). In this modeling the low energy emission (radio through optical) is represented as a synchrotron emission from leptons in the homogeneous, randomly oriented magnetic field (B) while the HE component (from X-ray to HE γ-ray) is an inverse Compton scattering of the same synchrotron photons. This kind of interpretation for 3C 120 is the first choice considering the results of the modeling of the other Fermi-LAT observed radio galaxies (Abdo et al. 2010b, 2009a,b). Here we apply the SSC mechanism to model the overall SED of 3C 120, particularly in the 0.1−100 GeV energy range. The multifrequency data (sub MeV/GeV energies) are from the simultaneous (quasi-simultaneous) observations of the 3C 120 (Giommi et al. 2012).
We suppose that the emission is coming from a spherical region with the radius Rb moving with Lorentz factor Γ = (1 − β)− 1/2. The emission is boosted by δ = 1/ [Γ(1 − βcos(θ))] where θ is the angle between the bulk velocity and the line of sight. The electron distribution follows N(γ) ∝ γ− αExp [ − γ/γc] with γ>γmin naturally expected from the shock acceleration theories and the electron energy density (Ue) scales with the one of the magnetic fields (UB). Then, several independent parameters used in the modeling can be constrained from the observations. In particular, the superluminal speed puts an upper limit to the jet’s inclination angle at 14° (Eracleous & Halpern 1998). Thus, the flux would be modestly boosted with the Doppler factor δ = 4 if the emitting region moves with the bulk Lorentz factor Γ = 8 at the inclination angle of 12.5°. Next, the monthly timescale variability (180 days) implies that the emitting region is confined to a volume whose radius is determined from the relation Rb/δ< 4.6 × 1017 cm. The Doppler factor of δ ~ (3 − 4) requires an emitting region of ~ 1018 cm.
We assume that HE emission has a pure SSC origin. As a first step, the radio data are included in the modeling, which means that the same electron population is responsible for both synchrotron and inverse-Compton emissions. The best guess values of electron energy distribution, which allows us to properly reproduce the low and HE data, corresponds to α = 2.8, γmin = 800, and γc = 9.8 × 103 (dashed line in Fig. 3). Other model parameters are presented in Table 1. The ratio of nonthermal electron and magnetic field energy densities is equal to Ue/UB ≈ 16 (for magnetic field B = 25 mG). In this case, the jet power in the form of the magnetic field and electron kinetic energy, given by 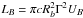 and
and 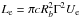 , respectively, are LB = 1.49 × 1044ergs-1 and Le = 2.42 × 1045ergs-1. The total jet power Ljet, defined as Ljet = LB + Le, corresponds to Ljet ≈ 2.57 × 1045ergs-1, which is noticeable high. This interpretation is unlikely since the necessary jet power is of the same order as Eddington accretion power LEdd = 6.8 × 1045 ergs-1 for the 5.5 × 107M⊙ black hole mass in 3C 120. This is not a strong argument considering that some blazars might operate in the super-Eddington regime as follows from observations (Bonnoli et al. 2011).
, respectively, are LB = 1.49 × 1044ergs-1 and Le = 2.42 × 1045ergs-1. The total jet power Ljet, defined as Ljet = LB + Le, corresponds to Ljet ≈ 2.57 × 1045ergs-1, which is noticeable high. This interpretation is unlikely since the necessary jet power is of the same order as Eddington accretion power LEdd = 6.8 × 1045 ergs-1 for the 5.5 × 107M⊙ black hole mass in 3C 120. This is not a strong argument considering that some blazars might operate in the super-Eddington regime as follows from observations (Bonnoli et al. 2011).
 |
Fig. 3 SED of 3C 120 modeled with one-zone SSC component. Black points refers to the simultaneous (quasi-simultaneous) data from (Giommi et al. 2012) and red points from Fermi-LAT data analysis. The solid, dashed, and dot dashed lines corresponds to α = 2.4,2.8, and 2, respectively. The SSC emission is calculated using a simulator developed by Andrea Tramacere (Tramacere et al. 2011, 2009; Massaro et al. 2006) available at http://www.isdc.unige.ch/sedtool/. |
However, this is not the case since the jet power can be relaxed, assuming the hard X-ray emission originates from the thermal Comptonization near the disk. Thus, the predicted flux from the SSC component falls below the hard X-ray limit in Fig. 3 (solid line). Indeed, a reasonable modeling of both radio and HE data gives an electron distribution with the index α = 2.4 between γmin = 700 and γcut = 1.7 × 104. The jet energy carried out by particles (electrons) and magnetic field corresponds to Lj = 6.27 × 1044 ergs-1, which is still high but not dramatic. Moreover, unlike the other case, the electron nonthermal and magnetic field energy densities are close to equipartition Ue/UB ≈ 2 (for B = 30 mG). Even though the ratio Ue/UB ≈ 16 cannot be rejected, recalling other blazars where the jet is massively out of equipartition, the later modeling has an advantage considering the required total jet power.
In principle, the radio to X-ray and γ-ray emissions can be produced in different sites (blobs). Supposing the radio flux does not exceed that presented in Giommi et al. (2012), the electron distribution with a typical power law index α = 2 predicted from strong shock acceleration theories can reproduce HE γ-ray data (dot dashed line in Fig. 3). The modeling requires a relatively high low energy cutoff, γmin = 2500, and energy equipartition between nonthermal electrons and the magnetic field Ue/UB = 1.3 (for B = 25 mG). Moreover, the total jet kinetic power is Ljet ≈ 3.4 × 1044ergs-1 approximately half that in the previous modeling. From the point of view of the necessary lower energy, this model has an advantage over previous model. Nevertheless, this modeling is very sensitive to the choice of the γmin, which can be constrained only with simultaneous data. Although the radio data presented in Fig. 3 are not synchronous, they can be treated as an upper limit. Consequently, the expected luminosity should not be higher than the above obtained value.
In Fig. 3, SSC mechanism provides a good fit to all data except those in the optical/UV band (1015−1016) Hz. This UV excess is likely caused by direct thermal emission from the accretion disk. Indeed, a thermal component with a blackbody temperature > 15 000 K and a luminosity ≥ 2 × 1044ergs-1 can explain detected UV flux. This lower limit to the temperature and luminosity corresponds to minimal UV flux reported in Giommi et al. (2012) and presented in Fig. 3, but a hotter and luminous disk is expected to explain observed data. Thus, SSC radiation plus thermal component (contribution of the accretion disk) can satisfactorily reproduce the entire SED (including UV data). However detailed modeling of the thermal component goes beyond the scope of this paper.
5. Conclusion
We report on the recent observations of 3C 120 with Fermi-LAT. The source is detected up to 10 GeV with statistically significant 8.7σ significance as a result of the accumulation of data from a longer all-sky exposure. The photon index corresponds to Γ = 2.7, which is similar to the nearby FR1 class radio source Centaurus A with a comparable black hole mass (Abdo et al. 2010b) and Fγ = (2.35 ± 0.5) × 10-8photoncm-2 s-1 photon flux above 100 MeV. Adapting the dL = 139.3 Mpc distance, this equals Lγ = 2.1 × 1043 erg s-1, which lies in the typical isotropic γ-ray luminosity range of FR I sources detected by Fermi-LAT (Abdo et al. 2010c). Albeit, the observed γ-ray flux is relatively faint compared with other Fermi-LAT detected radio galaxies (≈ 10-7 photoncm-2 s-1), the isotropic γ-ray luminosity is quite impressive when compared with the Eddington luminosity LEdd = 6.8 × 1045 ergs-1 .
We also report an interesting modification of the γ-ray flux in time. Initially, the source described by the γ-ray flux mostly below than the Fermi-LAT sensitivity threshold appears to be frequently detected afterward. The flux is almost twice more than its average level in the last year of the selected time period (from 2008 to late 2013, see Fig. 2). This increase of flux shows monthly timescale variability of 3C 120, indicating that the γ-rays are produced in sup-parsec regions. A common behavior of the light curves in any day sampling (a month or more) is that the source is mostly undetectable by Fermi-LAT prior to March 2012 then it becomes mostly γ-ray production duty cycles. Moreover, the long lasting source activity that probably continues after December 2013 (nearly two years) indicates a change in the γ-ray production state (from low to high) rather than flaring activity as seen in many blazars (generally in short timescales). In principle this change can have different physical origins. First, the change in the central engine, where possible jets obtain much of their energy from the infall of matter into a supermassive black hole, can at least have some influence. The change in the jet power, hence higher intensity γ-ray, is expected in the case when the additional matter is fueling the accretion disk. In theory, the observations of the region closer to the black hole with sensitive X-ray instruments (e.g., Chandra, XMM-Newton) can prove such a possibility. On the other hand, the environmental influence on the changes in γ-ray emission states cannot be rejected considering the large scale powerful jet up to 100 kpc (e.g., target interacting with the jet). Any of the above mentioned possibilities would be supported by multiwavelength observations. This is beyond the scope of this paper and will be investigated in the future works.
One zone SSC model is used to fit broadband emission from 3C 120. Assuming γ-rays are produced in a compact region (~ 1018 cm), this modeling gives an adequate fit to the SED with modest Doppler boosting δ ~ 4 and no significant bias from equipartition Ue/UB ≈ 2. The necessary jet kinetic power is ≈ 6 × 1044ergs-1, which corresponds to 10 % of Eddington power.
Acknowledgments
We warmly thank Felix Aharonian for detailed and constructive comments that improved the manuscript. We thank the anonymous referee for the useful comments.
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009a, ApJ, 707, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009b, ApJ, 699, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, Science, 328, 725 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 719, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, ApJ, 720, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A. 2002, MNRAS, 332, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, S. D., & Marscher, A. P. 1996, ApJ, 461, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnoli, G., Ghisellini, G., Foschini, L., Tavecchio, F., & Ghirlanda, G. 2011, MNRAS, 410, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti, A., Maraschi, L., & Treves, A. 1991, ApJ, 377, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Eracleous, M., & Halpern, J. P. 1998, ApJ, 505, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Fanaroff, B. L., & Riley, J. M. 1974, MNRAS, 167, 31P [Google Scholar]
- Ghisellini, G., Maraschi, L., & Treves, A. 1985, A&A, 146, 204 [NASA ADS] [Google Scholar]
- Giommi, P., Polenta, G., Lähteenmäki, A., et al. 2012, A&A, 541, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez, J.-L., Marscher, A. P., Alberdi, A., Martí, J. M., & Ibáñez, J. M. 1998, ApJ, 499, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, J.-L., Marscher, A. P., & Alberdi, A. 1999, ApJ, 521, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Halpern, J. P. 1985, ApJ, 290, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. E., Mossman, A. E., & Walker, R. C. 2004, ApJ, 615, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, D. C., Ojha, R., Wardle, J. F. C., et al. 2001, ApJ, 549, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, J., Stawarz, Ł., Takahashi, Y., et al. 2011, ApJ, 740, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y. C., Bertsch, D. L., Dingus, B. L., et al. 1993, ApJ, 416, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C., Arias, E. F., Eubanks, T. M., et al. 1998, AJ, 116, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., Jorstad, S. G., Gómez, J.-L., et al. 2002, Nature, 417, 625 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Massaro, E., Tramacere, A., Perri, M., Giommi, P., & Tosti, G. 2006, A&A, 448, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Tramacere, A., Giommi, P., Perri, M., Verrecchia, F., & Tosti, G. 2009, A&A, 501, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tramacere, A., Massaro, E., & Taylor, A. M. 2011, ApJ, 739, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, R. C., Benson, J. M., & Unwin, S. C. 1987, ApJ, 316, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, R.-Z., Sahakyan, N., de Ona Wilhelmi, E., Aharonian, F., & Rieger, F. 2012, A&A, 542, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, J., Bai, J. M., Chen, L., & Liang, E. 2010, ApJ, 710, 1017 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Averaged differential spectrum of 3C 120 (above 100 MeV) red points as compared with that based on the initial 15 month data set (Abdo et al. 2010c). The dashed black line shows the power law function determined from the gtlike. |
| In the text | |
 |
Fig. 2 Gamma-ray light curve from August 4th 2008 to December 4th 2013. The bin size corresponds to 180- (red) and 365-days (blue). The galactic and extragalactic background emission is fixed to the best-fit parameters obtained for the overall time fit. |
| In the text | |
 |
Fig. 3 SED of 3C 120 modeled with one-zone SSC component. Black points refers to the simultaneous (quasi-simultaneous) data from (Giommi et al. 2012) and red points from Fermi-LAT data analysis. The solid, dashed, and dot dashed lines corresponds to α = 2.4,2.8, and 2, respectively. The SSC emission is calculated using a simulator developed by Andrea Tramacere (Tramacere et al. 2011, 2009; Massaro et al. 2006) available at http://www.isdc.unige.ch/sedtool/. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


