EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 574 (February 2015) A&A, 574 (2015) A63 Full HTML
Free Access
Issue
A&A
Volume 574, February 2015
Article Number A63
Number of page(s) 5
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201424524
Published online 27 January 2015

© ESO, 2015

1. Introduction

According to the recycling scenario (Bhattacharya & van den Heuvel 1991) the population of radio millisecond pulsars and low mass X-ray binaries (LMXBs) share a common evolutionary link. A young, magnetized, slowly rotating neutron star in a binary system can accrete the gas stripped by the donor star spinning up until an old radio millisecond pulsar is formed. Accreting pulsars in LMXBs generally have spin periods lower than 10 ms, but a small number of sources with longer periods has also been found. The recently discovered pulsar IGR J17480-2446 (J17480 in the following) with the spin period 90.6 ms belongs to this small group (Papitto et al. 2011). During the time spanned by the observations, its bolometric luminosity varied within the range (1.7−6.8) × 1037 erg s-1, which implies an accretion rate on the order of (1−4) × 10-9 M⊙ yr-1. The presence of pulsations throughout the observations allowed the authors to estimate the magnetic field at the neutron star surface as ~7 × 108 G, a very low value for an accreting pulsar with such a long period and high luminosity.

In the standard model of evolution in a binary system (Pringle & Rees 1972; Illarionov & Sunyaev 1975), the neutron star during the accretion phase initially spins up until it approaches the so-called spin-up line corresponding to the accretion rate. The spin-up line in the magnetic field – spin period (B-P) diagram is determined by corotation at the Alfven radius. During the further evolution, a balance between spin-up and the rate of field decay is reached, so that the neutron star slides down the corresponding spin-up line with a rate that is determined by field decay (Bhattacharya & Srinivasan 1991). In accordance with this model, measurements of the spin period and accretion rate determine the position of an accreting pulsar in the B-P diagram and can provide an estimate of the magnetic field. In the case of J17480, the spin period 90.6 ms and the accretion rate ~10-9 M⊙ yr-1 imply that the magnetic field should be ~1010 G. The field estimated by Papitto et al. (2011) is much lower and most likely the accreting pulsar in this system does not slide down on the corresponding spin-up line. To the best of our knowledge, J17480 is the first clear example of accreting pulsars with a significant departure from the spin-up line.

In this paper, we demonstrate that pulsars with long spin periods and low magnetic fields (like J17480) can be the natural products of evolution of the neutron star in LMXBs and millisecond pulsars. We show that field decay in a neutron star during the accretion phase can be faster than spin-up, and a significant departure from the spin-up line can be expected during the accretion phase. This mechanism can be the central issue in understanding the origin of a particular class of slowly rotating accreting pulsars in LMXB.

2. Evolutionary model

We consider the magnetic and spin evolution of a neutron star in a binary system with a low-mass companion. We do not specify the mechanism responsible for the origin of the magnetic field in a neutron star. We only assume that the field is maintained by electric currents in the crust. This type of magnetic configuration can be generated, for example, by turbulent dynamo at the beginning of a neutron star life (Bonanno et al. 2005, 2006).

The binary is assumed to be relatively close, thus the companion can fill the Roche lobe at the end of its main-sequence life. During its main-sequence evolution (which lasts ~109−1010 yrs), the secondary loses mass because of the stellar wind and some fraction of the wind plasma can generally be captured and accreted by the neutron star at a certain stage. Both the magnetic and spin evolution may be affected by this accretion and, as a result, the neutron star passes through different evolutionary stages. After the secondary leaves the main sequence and fills its Roche lobe, the rate of mass loss and, hence, the accretion rate can be drastically enhanced. Detailed discussion of evolutionary transformations of the neutron star in a binary system is given by Urpin et al. (1998a) and we follow this scenario. We note that the developed evolutionary model successfully explains the origin of millisecond pulsars (Urpin et al. 1998b), the magneto-rotational evolution of the pulsars in high mass binary systems (Urpin et al. 1998c), and the Her X-1 like pulsars (Konenkov & Urpin 1998).

The most important point in understanding the neutron star evolution is the behavior of the crustal magnetic field. This is determined mainly by the conductive properties of the crust and the material motion throughout it. In a very strong magnetic field, the ohmic dissipation can be accompanied by non-dissipative Hall currents which affect the field decay indirectly, coupling different modes and redistributing the energy among modes. We note that because of the nonlinear nature of the Hall currents, they can generate magnetic features with a smaller length-scale than the background magnetic field (Naito & Kojima 1994). However, these currents are important only at the very early stage of evolution and only if the initial field is very strong. We are interested in the long term evolution and we will neglect the Hall currents. Then, the induction equation in the crust reads 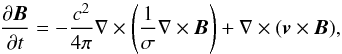(1)where σ is the conductivity and v is the velocity of crustal matter. The velocity v is caused by the flux of the accreted matter and it is nonzero only during the accretion phases. Assuming the spherical symmetry of a flow, the velocity in the negative radial direction can be estimated as v = Ṁ/ 4πr2ρ, where Ṁ is the accretion rate and ρ is the density.

We consider the evolution of an axisymmetric field. Following Wendell et al. (1987) we introduce the vector potential A = (0,0,Aϕ), where Aϕ = S(r,θ,t) /r and (r,θ,ϕ) are the spherical coordinates. In the case of a dipole field, S can be represented as S = s(r,t)sinθ. Then, we have 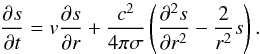(2)The function s(r,t) is related to the surface magnetic field at the pole, Bp(t), by Bp(t) = 2s(R,t) /R2 (Urpin et al. 1994). We normalize s in such a way that s(R,0) = 1. Then, the ratio Bp(t) /Bp(0) is given by s(R,t). Continuity of B at the surface r = R yields the boundary condition ∂s/∂r + s/R = 0. Since σ depends on the temperature T, accretion can influence the field decay by changing the temperature T. Therefore, the magnetic evolution of a neutron star is coupled essentially to its thermal history. This is in contrast to the widely accepted prescription of the magnetic field decay stating that the decay is proportional to the amount of accreted material (Shibazaki et al. 1989). However, such a simple model is obviously insufficient from a theoretical point of view because the decay is determined not only by the duration of accretion (or, equivalently, by the total amount of accreted mass), but also by the conductivity of the crust. The latter depends on the temperature, which is also dependent on the accretion rate.

Therefore, a consistent description of the field decay must take into account both the duration of accretion (or total amount of accreted mass) and accretion rate. In particular, a simple model with a field decay proportional to the amount of accreted material is not in agreement with some observational data. This point is discussed in detail by Wijers (1997). In the model developed in this paper, the magnetic field decay is determined by both the accretion rate and duration of accretion.

During its evolution, the neutron star can be processed in four main evolutionary phases:

Phase (i). During the initial phase, the neutron star is not affected by its companion because the pressure of magnetodipole waves emitted by a rapidly rotating neutron star is very high and prevents the wind plasma of the companion from interaction with the magnetosphere. Thus, the magnetic, thermal, and spin evolution follow those of an isolated star. The magnetic field is governed by Eq. (2) with v = 0. Since the wind plasma does not interact with the neutron star magnetosphere, the spin evolution is determined by magnetodipole radiation, 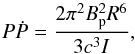(3)where P is the spin period and I is the moment of inertia. Phase (i) lasts as long as the wind plasma is stopped by the pressure of magnetodipole radiation behind the radius of gravitational capture. The stopping radius, Rs, is determined by the balance between the dynamical pressure of the wind and the pressure of magnetodipole waves. The pressure of the wind is 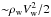, where ρw and Vw are the density and velocity of the wind plasma, respectively. The density of the wind at the distance r from the secondary may be estimated as ρw ~ Ṁ0/ 4πr2Vw with Ṁ0 being the rate of mass loss of the secondary. The pressure of the magnetodipole radiation at the distance Rs from the neutron star is 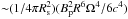, where Ω is the angular velocity of a neutron star. Equating these pressures, we obtain (4)where a is the separation between stars. If Rs is greater than the radius of gravitational capture 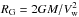(Bondi 1952), being M the neutron star mass, the wind matter is not captured by the neutron star and it cannot interact with the magnetosphere. The condition Rs = RG thus determines the end of phase (i).

Phase (ii). If RG>Rs, a fraction of the wind plasma starts to be captured by the neutron star. The rate of gravitational capture of the wind plasma, Ṁ, is approximately equal to Ṁ = Ṁ0(RG/ 2a)2 if a>RG. Only this fraction of the wind can directly interact with the magnetosphere. Rotation of the neutron star and its magnetosphere is rather fast at this phase, and the magnetosphere acts as a propeller, ejecting the wind plasma (Illarionov & Sunyaev 1975). Since accretion is forbidden during this phase, the thermal and magnetic evolution does not differ from that of an isolated neutron star. The spin evolution can be different, however, because a fraction of the stellar angular momentum is transferred to the wind plasma which penetrates into the magnetosphere. It is usually assumed that the wind plasma interacts with the magnetosphere at the Alfven radius, RA, which is determined by a balance of the Lorentz force and the dynamical pressure of plasma, 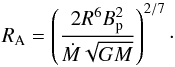(5)If the angular velocity of the neutron star is larger than the Keplerian angular velocity at the Alfven radius, 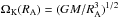, then the wind plasma penetrating to the Alfven radius can extract some portion of the angular momentum from the rapidly rotating magnetosphere. The rate of the angular momentum loss by the neutron star, 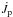, can be estimated as 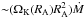. Then, the corresponding spin-down rate of the neutron star during the propeller phase is 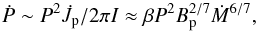(6)where β = (GMR2/ 4)3 / 7/πI. Rotation slows down until the angular velocity of the neutron star becomes comparable to ΩK(RA). This condition determines the critical period, Peq, at which the propeller phase ends, 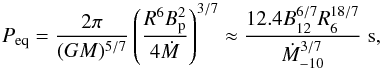(7)where B12 = Bp/ 1012 G, Ṁ-10 = Ṁ/ 10-10 M⊙ yr-1, and R6 = R/ 10 km. This equation determines the spin-up line in the B − P plane.

Phase (iii). This phase begins when Ω becomes smaller than the Keplerian angular velocity at the Alfven radius. The neutron star can no longer work as a propeller, and the accretion from the wind is allowed. Nuclear burning of the accreted material heats the crust, decreases the crustal conductivity, and can induce a significant accretion-driven field decay. Therefore, the magnetic evolution during phase (iii) is driven by Eq. (2) with v ≠ 0. The thermal evolution is determined mainly by pycnonuclear fusion in the crust. The thermal structure of the star with pycnonuclear reactions has been studied by a number of authors (Haensel & Zdunik 1990; Zdunik et al. 1992).

The rotational evolution differs from that during phases (i) and (ii). The accreting matter very likely carries some amount of the angular momentum and transfers it to the neutron star. The angular momentum carried by the wind plasma can be characterized by its Keplerian value, 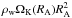, multiplied by an efficiency factor, ξ< 1. This factor depends very strongly on the accretion flow. For example, if the accreted matter forms an accretion disk around the neutron star then ξ ~ 1. If the disk is not formed (which is more typical for wind accretion), the factor ξ is much smaller (~0.1−0.01). The rate of the angular momentum transfer from the wind to the neutron star is 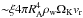. Then, the corresponding spin up rate is 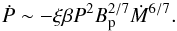(8)As a result of this angular momentum transfer, the neutron star can spin up to a shorter period, which is always larger that the Keplerian period at the Alfven radius, otherwise the star would work as a propeller. Bhattacharya & Srinivasan (1991) argued that the neutron star slides down the corresponding spin-up line with a rate determined by field decay. This evolution can last either until the accretion regime is changed (for instance, because the companion fills its Roche lobe and an enhanced accretion phase starts) or until the magnetic field becomes too weak to maintain a balance in spin up and the rate of the field decay. In the latter case, the neutron star leaves the spin up line and evolves in a very particular way. In our calculations, we assume that the spin period of a neutron star follows Eq. (8) if P ≥ Peq. However, according to the model above discussed, if Eq. (8) leads to P<Peq, we then suppose P = Peq.

Phase (iv). After the end of the main-sequence evolution, the secondary star fills the Roche lobe and the accretion is substantially enhanced. The neutron star is heated to much higher temperatures and the field decay is substantially faster than in the previous phase. In LMXBs, accretion due to Roche-lobe overflow lasts as long as 106−107 yrs, and the magnetic field can be drastically reduced The field decay is still governed by Eq. (2) with v ≠ 0. The thermal structure of accreting neutron stars has been studied by many authors (Fujimoto et al. 1984; Miralda-Escude et al. 1990; Brown & Bildsten 1998). The accreted matter probably forms the Keplerian disk during phase (iv). Therefore, spin up is driven by Eq. (8) with ξ ≈ 1. The neutron star spins up in accordance with Eq. (8) until it reaches the spin-up line corresponding to an enhanced accretion rate. During the further evolution, a balance has to be reached between spin up and the rate of the field decay as during phase (iii), and the neutron star slides down the spin up line with a rate that is determined by the new, much faster, field decay. The star can leave the spin-up line if the field becomes too weak to maintain a balance between spin up and field decay.

When accretion is exhausted, we do not follow the evolution further. Usually, the magnetic field of a pulsar turns out to be rather weak after all these evolutionary transformations and its final location in B-P plane does not change significantly.

3. Numerical results

In our calculations we made use of the public code developed by Dany Page, NSCool1 in which the magnetothermal evolution has been taken into account by coupling the induction equation with the thermal equation via the Joule heating as discussed in Bonanno et al. (2014). In particular, the induction equation was solved via an implicit scheme and the electron conductivity was calculated with the approach described in Potekhin (1999)2. Actual calculations were performed for a neutron star of M = 1.4 M⊙ based on the APR EOS (Akmal et al. 1998) within the minimal cooling framework (Page et al. 2004). The radius and the thickness of the crust for this star are 11.5 km and 1.0 km, respectively. For the crustal composition, we use the so-called accreted matter model by Haensel & Zdunik (2008).

The impurity parameter, Q, is assumed to be constant throughout the crust and equal to 0.001. The initial spin period is assumed to be P0 = 0.01 s, but the results are not sensitive to this value. On the contrary, the evolution is strongly dependent on the original magnetic configuration. The initial magnetic field is assumed to be confined to the outer layers of the crust with densities ρ ≤ ρ0. The calculations presented here are performed for ρ0 = 1013 g/cm3. The initial field strength at the magnetic pole, Bp(0), is 6 × 1012 and 2 × 1013 G. The main-sequence lifetime of the companion is as long as 2 × 109 or 6 × 109 years. In calculations, we suppose Ṁ = 10-14−10-15 M⊙ yr-1 during both the propeller and wind accretion phases: Vw = 500 km s-1; a = 5 × 1012 cm. After the secondary fills its Roche lobe, accretion has to be strongly enhanced and Ṁ can reach the value 5 × 10-9 M⊙ yr-1.

thumbnail Fig. 1

Solid line: evolutionary tracks of pulsars in LMXBs with a relatively low accretion rate during phase IV, Ṁ = 10-11 M⊙ yr-1, a wind accretion rate during phase III of Ṁ = 10-15 M⊙ yr-1, and an initial magnetic field of 3 × 1013 G. The end of phase I is marked with a diamond. The main-sequence phase ends at point (F) after 4.5 × 109 years and marks (A) to (C) represent intervals of 10 Myr after the end of the main sequence. The total duration of the fast accretion phase is 4.62 × 107 years. Dashed line: same as dotted line but for an initial magnetic field of 6 × 1012 G and a wind accretion rate of Ṁ = 10-14 M⊙ yr-1. Dot-dashed line: same as solid line but with a wind accretion rate of Ṁ = 10-10 M⊙ yr-1. The vertical line (in orange) is the observational constraint on the magnetic field and period.
Open with DEXTER

In Fig. 1, we plot the evolutionary tracks for models with a relatively low accretion rate during phase (iv), 10-10 ≥ Ṁ ≥ 10-11 M⊙ yr-1. We choose such a low accretion rate because IGR J17489-2445 is a transient X-ray source. During the several bursts, the accretion rate estimated from the luminosity observations is quite high and can reach ~10-9 M⊙ yr-1. The accretion rate between the bursts is essentially lower. Since the magnetic evolution of a neutron star is relatively slow, it is determined by the average accretion rate rather than its variations, which is why we assume in our calculations that Ṁ is lower than the peak value. In the case of the solid lines, phase (i) lasts 5.3 × 107 yrs when the neutron star is not influenced by the companion. During this phase the field does not decay significantly, thus its surface strength is ≈1012 G when the star enters the propeller stage (phase (ii)). The duration of this stage is ~7 × 107 yrs, but the field does not decay much either because the star is rather cool and the crustal conductivity is high. The wind accretion can last sufficiently long, depending on the duration of the main-sequence life. Accretion heats the neutron star decreasing the conductivity and slightly accelerating field decay. During phase (iv), accretion is greatly enhanced compared to phase (iii) and the field decay is much faster. At some stage, the accreted matter cannot provide a sufficient amount of angular momentum to the neutron star to maintain a balance on the spin-up line. Therefore, the neutron star departs from the spin-up line for the considered accretion rates and becomes a long-period accreting pulsar. The magnetic field of such a pulsar should be rather low because of a fast decay and comparable to the field of millisecond pulsars. For instance, the magnetic field of the models considered in Fig. 1 reaches the value ~108 G after ≈1.5 × 107 yrs of enhanced accretion. However, the periods turn out essentially different for the models with the accretion rates 10-10 and 10-11 M⊙ yr-1 with a longer period corresponding to a low accretion rate. Therefore, long-period low magnetized pulsars seem to be a natural product of the evolution of neutron stars in LMXBs if the accretion rate during the Roche-lobe overflow is not very high.

thumbnail Fig. 2

Same as Fig. 1 but with an accretion rate during phase IV of Ṁ = 2 × 10-9 M⊙ yr-1. The marks (A) to (C) represent intervals of 1 Myr after the end of the main sequence.

Open with DEXTER

In Fig. 2, we plot tracks of the neutron star processed in all transformations in LMXBs with a higher accretion rate due to Roche-lobe overflow, Ṁ = 2 × 10-9 M⊙ yr-1. The evolution is qualitatively the same until the enhanced accretion starts. The further evolution differs, however, although the essential changes are experienced by the neutron star during phase (iv), as in the previous case. Accretion with the rate 2 × 10-9 M⊙ yr-1 heats the neutron star to a temperature ~3 × 108 K and decreases the crustal conductivity substantially. Because of this, the field is reduced by a factor of ~103 after 2.5 × 106 yrs of enhanced accretion. The neutron star can maintain a balance on the spin-up line much longer than in the case of a weaker accretion. However, if accretion lasts sufficiently long, the neutron star leaves the spin-up line since the field decay is fast at the end of phase (iv) in comparison with spin-up. Transfer of the angular momentum becomes too slow in a weak magnetic field for the following reason. If the accretion flow forms the Keplerian disk around a neutron star, the rate of angular momentum transfer can be estimated as 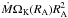, where RA is the Alfven radius that represents the inner boundary of the disk. We note that this estimate is valid only if RA ≫ R. For the considered accretion rate, this condition is satisfied if the magnetic field of a neutron star is greater than ~107 G. If the magnetic field is very weak (Bp< 107 G) then RA ≤ R and the rate of angular momentum transfer is on the order of ṀΩK(R)R2. Since ΩK ∝ r− 3 / 2, the angular momentum transport slows down with a decrease of the magnetic field and becomes very slow in the case of a weak magnetic field. In this paper, we do not consider the evolution of neutron stars with such a weak field. We note that the late evolution in all the other cases in Fig. 2 is basically the same. As a result, the neutron star after the enhanced accretion can have parameters close to those of millisecond pulsars. It turns out that the only difference between the neutron stars shown in Figs. 1 and 2 is the accretion rate during phase (iv).

4. Conclusion

We have considered the evolution of neutron stars in binary systems with a low-mass companion. During the course of this evolution, the neutron star passes through several different evolutionary phases. It is generally believed that the population of millisecond pulsars with P ~ 1−10 ms and B ~ 108−109 G is formed as a result of evolutionary transformations in LMXBs. Our calculations show that, apart from millisecond pulsars, one more class of pulsars can be formed in LMXBs with a period longer than that of millisecond pulsars and with a comparable magnetic field. The only difference between these two classes of objects is that the progenitors of millisecond pulsars experience accretion with a higher accretion rate during the Roche-lobe overflow, whereas accretion onto the progenitors of long-period pulsars occurs with a smaller Ṁ. At a smaller accretion rate, the neutron star leaves the spin-up line and evolves into the region of low magnetic fields and long periods in the B-P diagram. As a result, it has a relatively long period, P> 10 ms, when accretion is exhausted. We note that the period of sources, formed by the considered mechanism, can generally be rather long and can reach ~1 s, but the magnetic field should be weak (~108−1010 G) compared to the typical pulsar field. The recently discovered accreting pulsar IGR J17480-2446 with P = 90.6 ms and estimated magnetic field ~7 × 108 G (Papitto et al. 2011) can be representative of this class of sources. The period of pulsars in this class should satisfy the condition P>Peq for the corresponding accretion rate and can vary within a wide range. Perhaps other known long-period accreting pulsars, GRO J1744–28 (P = 467 ms and B ≈ 2.4 × 1011 G; Cui 1997) and 2A 1822-371 (P = 590 ms and B ≈ 1011 G; Jonker & van der Klis 2001), also belong to this class.

Our conclusion regarding a possibility of IGR J17480-2446 to be a representative of the new class of accreting pulsars is essentially based on the estimate of the magnetic field B ~ 7 × 108 G made by Papitto et al. (2011). This estimate is provided by means of an additional constraint, the observations of a 815 Hz quasiperiodic oscillations (Altamirano et al. 2010). In this case a model of quasiperiod oscillations is then used to obtain the innermost disk edge radius and also the magnetic field strength. Therefore, the estimated value of the magnetic field is model dependent. For instance, using the presence of pulsations throughout the considered observation, Papitto et al. (2011) estimate the magnetic field range as ~2 × 108−2.4 × 1010 G. If

instead of 7 × 108 G, one assumes a value of B ≤ 1010 G from the allowed field range, then IGR J17480-2446 can be a normal mildly recycled pulsar. Therefore, more accurate measurements of the magnetic field are required to confirm that IGR J17480-2446 belongs to the new class. We note, however, that our theoretical modeling clearly predicts that there must exist accreting pulsars in LMXB that exhibit remarkable departures from the spin-up line in their evolution. Even if future measurements indicate that the magnetic field of IGR J17480-2446 is sufficiently high, it will be possible to detect representatives of this new class among other accreting pulsars in future observations.

References

  1. Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
  2. Altamirano, D., Homan, J., Linares, M., et al. 2010, The Astronomer’s Telegram, 2952, 1 [NASA ADS] [Google Scholar]
  3. Bhattacharya, D., & Srinivasan, G. 1991, in Neutron Stars: Theory and Observations, eds. J. Ventura, & D. Pines (Dordrecht: Kluwer Academic Publisher) [Google Scholar]
  4. Bhattacharya, D., & van den Heuvel, E. P. J. 1991, Phys. Rep., 203, 1 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bonanno, A., Urpin, V., & Belvedere, G. 2005, A&A, 440, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bonanno, A., Urpin, V., & Belvedere, G. 2006, A&A, 451, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bonanno, A., Baldo, M., Burgio, G. F., & Urpin, V. 2014, A&A, 561, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  9. Brown, E. F., & Bildsten, L. 1998, ApJ, 496, 915 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cui, W. 1997, ApJ, 482, L163 [NASA ADS] [CrossRef] [Google Scholar]
  11. Fujimoto, M. Y., Hanawa, T., Iben, Jr., I., & Richardson, M. B. 1984, ApJ, 278, 813 [NASA ADS] [CrossRef] [Google Scholar]
  12. Haensel, P., & Zdunik, J. L. 1990, A&A, 227, 431 [NASA ADS] [Google Scholar]
  13. Haensel, P., & Zdunik, J. L. 2008, A&A, 480, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
  15. Jonker, P. G., & van der Klis, M. 2001, ApJ, 553, L43 [NASA ADS] [CrossRef] [Google Scholar]
  16. Konenkov, D., & Urpin, V. 1998, MNRAS, 301, 175 [NASA ADS] [CrossRef] [Google Scholar]
  17. Miralda-Escude, J., Paczynski, B., & Haensel, P. 1990, ApJ, 362, 572 [NASA ADS] [CrossRef] [Google Scholar]
  18. Naito, T., & Kojima, Y. 1994, MNRAS, 266, 597 [NASA ADS] [CrossRef] [Google Scholar]
  19. Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W. 2004, ApJS, 155, 623 [NASA ADS] [CrossRef] [Google Scholar]
  20. Papitto, A., D’Aì, A., Motta, S., et al. 2011, A&A, 526, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Potekhin, A. Y. 1999, A&A, 351, 787 [NASA ADS] [Google Scholar]
  22. Pringle, J. E., & Rees, M. J. 1972, A&A, 21, 1 [NASA ADS] [Google Scholar]
  23. Shibazaki, N., Murakami, T., Shaham, J., & Nomoto, K. 1989, Nature, 342, 656 [NASA ADS] [CrossRef] [Google Scholar]
  24. Urpin, V. A., Chanmugam, G., & Sang, Y. 1994, ApJ, 433, 780 [NASA ADS] [CrossRef] [Google Scholar]
  25. Urpin, V., Geppert, U., & Konenkov, D. 1998a, MNRAS, 295, 907 [NASA ADS] [CrossRef] [Google Scholar]
  26. Urpin, V., Geppert, U., & Konenkov, D. 1998b, A&A, 331, 244 [NASA ADS] [Google Scholar]
  27. Urpin, V., Konenkov, D., & Geppert, U. 1998c, MNRAS, 299, 73 [NASA ADS] [CrossRef] [Google Scholar]
  28. Wendell, C. E., van Horn, H. M., & Sargent, D. 1987, ApJ, 313, 284 [NASA ADS] [CrossRef] [Google Scholar]
  29. Wijers, R. A. M. J. 1997, MNRAS, 287, 607 [NASA ADS] [Google Scholar]
  30. Zdunik, J. L., Haensel, P., Paczynski, B., & Miralda-Escude, J. 1992, ApJ, 384, 129 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Solid line: evolutionary tracks of pulsars in LMXBs with a relatively low accretion rate during phase IV, Ṁ = 10-11 M⊙ yr-1, a wind accretion rate during phase III of Ṁ = 10-15 M⊙ yr-1, and an initial magnetic field of 3 × 1013 G. The end of phase I is marked with a diamond. The main-sequence phase ends at point (F) after 4.5 × 109 years and marks (A) to (C) represent intervals of 10 Myr after the end of the main sequence. The total duration of the fast accretion phase is 4.62 × 107 years. Dashed line: same as dotted line but for an initial magnetic field of 6 × 1012 G and a wind accretion rate of Ṁ = 10-14 M⊙ yr-1. Dot-dashed line: same as solid line but with a wind accretion rate of Ṁ = 10-10 M⊙ yr-1. The vertical line (in orange) is the observational constraint on the magnetic field and period.
Open with DEXTER
In the text
thumbnail Fig. 2

Same as Fig. 1 but with an accretion rate during phase IV of Ṁ = 2 × 10-9 M⊙ yr-1. The marks (A) to (C) represent intervals of 1 Myr after the end of the main sequence.

Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.