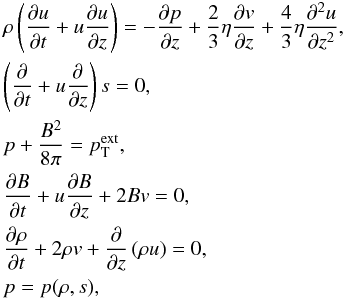| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201424516 | |
| Published online | 10 December 2014 | |
Nonlinear slow magnetoacoustic waves in coronal plasma structures
1 Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, CV4 7AL, UK
e-mail: V.Nakariakov@warwick.ac.uk
2 Institute of Solar-Terrestrial Physics SB RAS, PO Box 291, Lermontov St. 126A, 664033 Irkutsk, Russia
e-mail: afa@iszf.irk.ru
3 School of Space Research, Kyung Hee University, 446-701 Yongin, Gyeonggi, Korea
4 Central Astronomical Observatory at Pulkovo of the Russian Academy of Sciences, 196140 St Petersburg, Russia
Received: 2 July 2014
Accepted: 22 October 2014
Context. There is abundant observational evidence of longitudinal waves in the plasma structures of the solar corona. These essentially compressive waves are confidently interpreted as slow magnetoacoustic waves. The use of the slow waves in plasma diagnostics and estimating their possible contribution to plasma heating and acceleration require detailed theoretical modelling.
Aims. We investigate the role of obliqueness and magnetic effects in the evolution of slow magnetoacoustic waves, also called tube waves, in field-aligned plasma structures. Special attention is paid to the wave damping caused by nonlinear steepening.
Methods. We considered an untwisted straight axisymmetric field-aligned plasma cylinder and analysed the behaviour of the slow magnetoacoustic waves that are guided by this plasma structure. We adopted a thin flux tube approximation. We took into account dissipation caused by viscosity, resistivity and thermal conduction, and nonlinearity. Effects of stratification and dispersion caused by the finite radius of the flux tube were neglected.
Results. We derive the Burgers-type evolutionary equation for tube waves in a uniform plasma cylinder. Compared with a plane acoustic wave, the formation of shock fronts in tube waves is found to occur at a larger distance from the source. In addition, tube waves experience stronger damping. These effects are most pronounced in plasmas with the parameter β at about or greater than unity. In a low-β plasma, the evolution of tube waves can satisfactorily be described with the Burgers equation for plane acoustic waves.
Conclusions.
Key words: magnetohydrodynamics (MHD) / Sun: corona / waves / methods: analytical
© ESO, 2014
1. Introduction
The magnetised plasma of the solar atmosphere is an elastic and compressible medium that can support propagation of magnetohydrodynamic (MHD) waves. Observational data collected during the past two decades show that MHD waves exist everywhere on the Sun. Investigating MHD wave behaviour in the solar atmosphere contributes to our understanding of the coronal heating and solar wind acceleration problems, and also provides us with valuable seismological information about the solar plasma parameters that are difficult or impossible to measure directly.
Of special interest are slow magnetoacoustic waves that are observed in various plasma structures of the solar atmosphere, such as coronal plumes and loops (see Nakariakov 2006; De Moortel 2009; Banerjee et al. 2011; De Moortel & Nakariakov 2012, for reviews of recent findings). The observed rapid damping of coronal slow waves has been the key problem for theoretical investigations since they first were discovered observationally (see, e.g. Roberts 2006; De Moortel 2006). The first interpretation of quasi-periodic propagating EUV intensity disturbances observed in polar plumes and in coronal plasma fans as slow magnetoacoustic waves was presented by Ofman et al. (1999, 2000) and Nakariakov et al. (2000b). These one-dimensional analytical models were based on plane acoustic waves and accounted for effects of weak nonlinearity, dissipations and gravitational stratification of the solar corona. The analytical studies presented in these papers demonstrated that for relative amplitude lower than several percent, nonlinear effects in the wave damping could be neglected. Therefore, further modelling of propagating slow magnetoacoustic waves in 1 MK coronal loops by De Moortel & Hood (2003, 2004) and De Moortel et al. (2004) focused attention on the linear regime alone. It was concluded that thermal conduction was the dominant dissipation mechanism determining the damping rate.
On the other hand, numerical modelling of SUMER/SOHO observations of standing slow magnetoacoustic waves in hot coronal loops with temperatures of up to 10 MK demonstrated the importance of nonlinear effects (Nakariakov et al. 2004; Tsiklauri et al. 2004, see also Wang 2011, for a comprehensive review). Very recently, Ruderman (2013) studied a similar problem analytically and also found reduction of the damping time owing to nonlinear steepening of the wave profile.
Apart from nonlinear effects, there are other factors that can modify the damping rate of slow magnetoacoustic waves guided by plasma non-uniformities. Such factors can also change (strengthen or weaken) the influence of the nonlinearity on the wave evolution. Most analytical studies and numerical simulations of slow magnetoacoustic waves in the corona were focused on the degenerate case of the wave propagation strictly along the magnetic field (e.g. Nakariakov et al. 2000b; Ofman & Wang 2002; De Moortel & Hood 2003; Nakariakov et al. 2004; Tsiklauri et al. 2004; De Moortel & Hood 2004; Ruderman 2013). In this case, the magnetic field is not perturbed and gives only the wave-guiding effect for propagating essentially acoustic waves. However, for a finite-β plasma and non-parallel propagation, the non-zero magnetic field fluctuations interact with the density and velocity perturbations and therefore affect the wave propagation speed as well as the wave evolution. Numerical full-MHD simulations by Ofman et al. (2000), which incorporated the two-dimensional (2D) plume structure, dissipation, nonlinearity, and the gravitational stratification, showed that 2D effects may increase the damping rate. Verwichte et al. (2008) found that SUMER oscillations have a clear tendency for larger amplitude disturbances to have shorter damping times, and studied numerically a nonlinear damping problem for standing slow waves in a 2D model. It was demonstrated that the nonlinearity considerably reduced the damping time due to the significant energy dissipation in the shock front. Recently, the importance of the magnetic component for oblique slow-mode waves has been demonstrated by Nakariakov & Zimovets (2011) and Gruszecki & Nakariakov (2011) in numerical simulations of slow waves in coronal plasma arcades.
Thus, modelling coronal slow magnetoacoustic waves requires assessing whether it is important to take into account the wave-guiding effect. In particular, coronal plumes and loops are regions of the decreased Alfvén speed and act as wave-guides for MHD waves. Recently, Vasheghani Farahani et al. (2011, 2012) have found that the wave-guiding effect modifies the nonlinear evolution of torsional Alfvén waves quite significantly. Likewise, plasma structuring results in the transformation of slow magnetoacoustic waves into the so-called tube mode. This modification is essentially connected with the oblique nature of the waves in the wave-guide (Roberts 2006). It leads to the propagation of the slow magnetoacoustic disturbances along plasma non-uniformities at the tube speed (Defouw 1976; Edwin & Roberts 1983). The tube speed is subsonic and sub-Alfvénic and depends on the magnetic field strength. Therefore, oblique slow waves can be used for the seismological diagnostics of the magnetic field (Roberts 2006; Wang et al. 2007, 2009). However, the role of the slow wave obliqueness in its nonlinear damping has not been revealed.
In this paper we develop the weakly nonlinear analytical model designed in Ofman et al. (2000), Nakariakov et al. (2000b) and Tsiklauri & Nakariakov (2001) for propagating slow magnetoacoustic waves in plasma non-uniformities, taking into account the oblique nature of the perturbations in addition to nonlinearity and dissipation. To simplify the problem, we focus on the wave propagation in a straight plasma cylinder, neglecting effects of the magnetic field curvature, the increase in the flux tube cross-section, the solar wind, and gravitational stratification. In addition, we consider waves with lengths much greater than the diameter of the wave-guiding plasma cylinder. This assumption allows using the thin flux tube approximation (Roberts & Webb 1978; Zhugzhda 1996). This approximation reduces the two-dimensional to a one-dimensional problem that can be treated analytically. The paper is organised as follows: In Sect. 2 we derive the evolutionary equation of Burgers type for weakly nonlinear tube waves. In Sect. 3 we analyse the wave evolution. Section 4 contains the discussion of results and concluding remarks.
2. Burgers equation for tube waves
We consider symmetric (∂/∂ϕ ≡ 0) weakly nonlinear quasi-longitudinal waves in an untwisted and non-rotating straight axisymmetric thin magnetic flux tube in the cylindrical coordinates (r,ϕ,z). We applied the traditional thin flux tube approximation, neglecting dispersive corrections (e.g. Roberts & Webb 1978, see also Zhugzhda 1996), which formally corresponds to the first order of the Taylor expansion of the MHD variables with respect to the radial coordinate. The dispersion of waves in thin flux tubes is due to the finite radius of the flux tube (e.g. Zhugzhda 1996) and to the finite scale of the wave localisation outside the flux tube (e.g. Roberts 1985; Molotovshchikov & Ruderman 1987; Zhugzhda & Goossens 2001; Zhugzhda 2005). More specifically, because the dispersion grows with decreasing wavelength, we considered waves that are sufficiently long for the dispersion to be negligible. The governing set of equations is
where B is the longitudinal component of the magnetic field, v is the radial derivative of the radial component of the plasma velocity, u is the longitudinal component of the plasma velocity, ρ, p and s are the plasma density, pressure, and specific entropy, respectively. The external total pressure 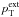 was assumed to be constant and therefore we did not consider disturbances in the external medium, concentrating on waves inside the flux tube. This assumption is justified if the tube speed inside the flux tube is lower than the propagation speeds of waves in the external medium (see Roberts & Webb 1979; Zhugzhda 1996). Equations (1) are different from the equations that describe plane acoustic waves that were used in Nakariakov et al. (2000b), Ofman & Wang (2002), De Moortel & Hood (2003), Nakariakov et al. (2004), Tsiklauri et al. (2004), De Moortel & Hood (2004) and Ruderman (2013), because they contain the magnetic field. Moreover, Eqs. (1) account for the oblique effects (e.g. the radial derivative of the radial component of the plasma flow velocity, v).
was assumed to be constant and therefore we did not consider disturbances in the external medium, concentrating on waves inside the flux tube. This assumption is justified if the tube speed inside the flux tube is lower than the propagation speeds of waves in the external medium (see Roberts & Webb 1979; Zhugzhda 1996). Equations (1) are different from the equations that describe plane acoustic waves that were used in Nakariakov et al. (2000b), Ofman & Wang (2002), De Moortel & Hood (2003), Nakariakov et al. (2004), Tsiklauri et al. (2004), De Moortel & Hood (2004) and Ruderman (2013), because they contain the magnetic field. Moreover, Eqs. (1) account for the oblique effects (e.g. the radial derivative of the radial component of the plasma flow velocity, v).
We took into account viscous dissipation, introducing the first viscosity coefficient η. According to the classical expressions derived in Braginskii (1965), the solar coronal plasma is a highly magnetised plasma with anisotropic transport coefficients. However, Braginskii (1965) pointed out that plasma instabilities could significantly increase the magnitude of the transport coefficients across the magnetic field as a result of micro-turbulence. Thus, we assume η to be isotropic. The thermal conductivity coefficient is known to appear in equations of Burgers type as a part of the dissipation coefficient along with viscosity (Rudenko & Soluyan 1977; Nakariakov et al. 2000b; Ruderman 2013). Likewise, the finite resistivity that becomes important when the wave contains magnetic field perturbations, can also be included in this dissipation coefficient. Keeping this in mind, we omitted the thermal conductivity term from the entropy equation and the resistive term from the induction equation, for simplicity. Note also that the first equation in Eqs. (1) contains the term depending on v since we analysed oblique motions in the flux tube, which is different from pure acoustic waves that propagate strictly along the magnetic field. The last equation in Eqs. (1) is the equation of state.
In the following analysis we assume that the effects of nonlinearity and dissipation are both weak and of the same order of magnitude. A flux tube that is uniform in the z-direction (including the temperature and entropy of the plasma) is considered. Small but finite perturbations of the equilibrium (indicated by the subscript 0) without steady flows (u0 = 0) are introduced as follows: 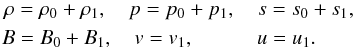 (2)Perturbations of the azimuthal components of the plasma velocity and magnetic field are assigned to be zero since we did not consider the torsional mode in this study. Note that the quantities with the subscript 1 describe full perturbations and include both linear and nonlinear contributions. We will omit this subscript for the velocity components in the remainder of the paper.
(2)Perturbations of the azimuthal components of the plasma velocity and magnetic field are assigned to be zero since we did not consider the torsional mode in this study. Note that the quantities with the subscript 1 describe full perturbations and include both linear and nonlinear contributions. We will omit this subscript for the velocity components in the remainder of the paper.
By substituting Eqs. (2) into Eqs. (1) and restricting our attention to quadratically nonlinear terms only, we obtain
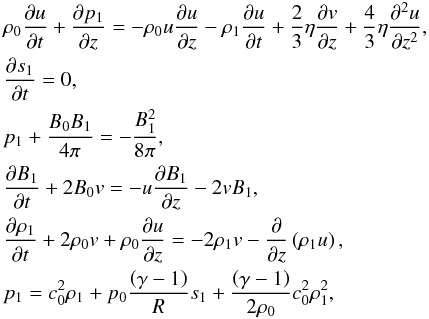 (3)where
(3)where 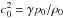 is the equilibrium sound speed and γ is the adiabatic index. In contrast with the plane acoustic wave case, Eqs. (3) account for the effects of the wave obliqueness, and the described perturbations include the radial velocity and the absolute value of the magnetic field. The first-order terms are collected on the left-hand sides of the equations (except for the equation of state) and the second-order terms are collected on the right-hand side. Note that in the entropy equation we neglect the nonlinear term u∂s1/∂z because the entropy perturbations are due to dissipative processes in the plasma and therefore are small in the problem considered. On the other hand, since we investigate quadratically nonlinear processes, we should take into account the term of the order of
is the equilibrium sound speed and γ is the adiabatic index. In contrast with the plane acoustic wave case, Eqs. (3) account for the effects of the wave obliqueness, and the described perturbations include the radial velocity and the absolute value of the magnetic field. The first-order terms are collected on the left-hand sides of the equations (except for the equation of state) and the second-order terms are collected on the right-hand side. Note that in the entropy equation we neglect the nonlinear term u∂s1/∂z because the entropy perturbations are due to dissipative processes in the plasma and therefore are small in the problem considered. On the other hand, since we investigate quadratically nonlinear processes, we should take into account the term of the order of 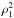 in the equation of state.
in the equation of state.
Considering only the left-hand sides of Eqs. (3), and therefore analysing the propagation of linear waves without dissipation, we can obtain the classical wave equation for the tube waves with the constant characteristic propagation speed 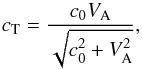 (4)where VA = B0/
(4)where VA = B0/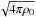 is the equilibrium Alfvén speed. Note that these waves are highly oblique because their longitudinal wavelength is much greater than their transverse spatial scale determined by the radius of the flux tube. It is the applicability condition of the thin flux tube approximation. Accounting for the obliqueness of the long-wavelength waves guided by the magnetic flux tube causes the wave speed to depend on the absolute value of the magnetic field. In the following, we refer to the long-wavelength slow magnetoacoustic waves guided by field-aligned plasma non-uniformities as tube waves.
is the equilibrium Alfvén speed. Note that these waves are highly oblique because their longitudinal wavelength is much greater than their transverse spatial scale determined by the radius of the flux tube. It is the applicability condition of the thin flux tube approximation. Accounting for the obliqueness of the long-wavelength waves guided by the magnetic flux tube causes the wave speed to depend on the absolute value of the magnetic field. In the following, we refer to the long-wavelength slow magnetoacoustic waves guided by field-aligned plasma non-uniformities as tube waves.
Following the procedure described in detail in Ofman et al. (2000) and Nakariakov et al. (2000b), we applied the method of slowly varying amplitudes to derive the evolutionary equation for weakly nonlinear tube waves. By passing to the frame of reference moving at the tube speed cT, and transforming Eqs. (3) in terms of the independent variables ξ = z − cTt and x = εz, where ε is a small parameter characterising the slow rate of wave evolution, we obtain the Burgers equation for the perturbation of the magnetic field B1, 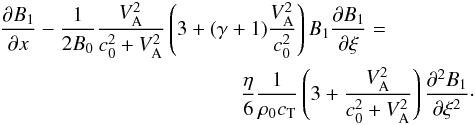 (5)A similar evolutionary equation can be written for the perturbation of the longitudinal component u of the plasma velocity
(5)A similar evolutionary equation can be written for the perturbation of the longitudinal component u of the plasma velocity 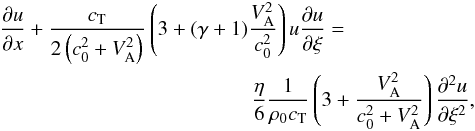 (6)where we substituted linear relations for the wave perturbations into the second-order terms to exclude other dependent variables from the equations. We also neglected the third-order terms in the equations. Note that the nonlinear terms in the derived equations agree exactly with those obtained by Roberts (1985) and Zhugzhda & Nakariakov (1997). The perturbations of other physical quantities in the linear approximation are linked with the longitudinal velocity as
(6)where we substituted linear relations for the wave perturbations into the second-order terms to exclude other dependent variables from the equations. We also neglected the third-order terms in the equations. Note that the nonlinear terms in the derived equations agree exactly with those obtained by Roberts (1985) and Zhugzhda & Nakariakov (1997). The perturbations of other physical quantities in the linear approximation are linked with the longitudinal velocity as 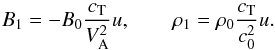 (7)Equations (5) and (6) are Burgers equations that describe the evolution of weakly nonlinear, weakly dissipative tube waves in a thin magnetic flux tube. In the infinite magnetic field limit, (VA/c0 → ∞), the tube speed cT becomes equal to the sound speed c0. In this case, plasma motions in tube waves become exactly longitudinal, and the waves degenerate into pure acoustic waves. Thus, in this limit the effect of the plasma structuring vanishes and Eq. (6) transforms to the well-known Burgers equation for acoustic waves
(7)Equations (5) and (6) are Burgers equations that describe the evolution of weakly nonlinear, weakly dissipative tube waves in a thin magnetic flux tube. In the infinite magnetic field limit, (VA/c0 → ∞), the tube speed cT becomes equal to the sound speed c0. In this case, plasma motions in tube waves become exactly longitudinal, and the waves degenerate into pure acoustic waves. Thus, in this limit the effect of the plasma structuring vanishes and Eq. (6) transforms to the well-known Burgers equation for acoustic waves 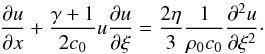 (8)
(8)
3. Tube wave evolution
Because our primary aim is to determine the role of the wave obliqueness in the nonlinear wave evolution, we considered both the Burgers equation for tube waves (Eq. (6)) and the Burgers equation for plane acoustic waves (Eq. (8)), and compared their solutions. For a uniform medium the Cole-Hopf substitution can provide an exact analytical solution to the Burgers equation, reducing it to the linear diffusion equation (Rudenko & Soluyan 1977). However, anticipating the more complex cases of non-uniform equilibria in follow-up investigations, we analysed Eqs. (6) and (8) numerically. We used the NDSolve function of Wolfram Mathematica 8.0 that implements the method of lines for solving initial value problems for partial differential equations.
First of all, we set the initial and boundary conditions for the equations. The solution is determined by the initial condition 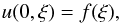 (9)where f represents the initial, sufficiently smooth wave profile, and by the boundary conditions
(9)where f represents the initial, sufficiently smooth wave profile, and by the boundary conditions  (10)where φ1 and φ2 describe the evolution of the chosen edges of the wave profile with x. According to EUV observational data (e.g. Nakariakov 2006; De Moortel & Nakariakov 2012), slow magnetoacoustic disturbances in coronal plumes and plasma fans are registered as trains of harmonic waves. The typical duration of the train is several wavelengths or periods. Accordingly, we assign f(ξ) = umsin(kξ), where um is the amplitude value, k = 2π/λ is the wavenumber, λ = cTP is the wavelength, and P is the wave period. We consider the wave train of two wavelengths long, ξ2 = −ξ1 = λ. In the moving frame of reference we have φ1 = φ2 = 0.
(10)where φ1 and φ2 describe the evolution of the chosen edges of the wave profile with x. According to EUV observational data (e.g. Nakariakov 2006; De Moortel & Nakariakov 2012), slow magnetoacoustic disturbances in coronal plumes and plasma fans are registered as trains of harmonic waves. The typical duration of the train is several wavelengths or periods. Accordingly, we assign f(ξ) = umsin(kξ), where um is the amplitude value, k = 2π/λ is the wavenumber, λ = cTP is the wavelength, and P is the wave period. We consider the wave train of two wavelengths long, ξ2 = −ξ1 = λ. In the moving frame of reference we have φ1 = φ2 = 0.
Secondly, we have to assign plasma parameters inside the tube as well as wave characteristics. Taking typical values from observations of slow waves in polar plumes (e.g. Nakariakov 2006), we have P = 600 s, um = 20 km s-1. The latter value corresponds roughly to the 10% perturbation of the background density. The plasma temperature is assumed to be 1.4 × 106 K and the number density 5.0 × 108 cm-3, γ = 5/3. The dissipation coefficient η is set to (0.04 − 2.12) g cm-1 s-1. In particular, the value η = 0.25 g cm-1 s-1 corresponds to the kinematic viscosity 2.4 × 1014 cm2 s-1 and can be calculated from the classical expressions by Braginskii (1965). Note that in the literature there are also different values for the kinematic viscosity, for instance the so-called traditional value for the coronal viscosity 4.0 × 1013 cm2 s-1 (Aschwanden 2006). We chose the higher values for the effective viscosity because in our formalism the dissipation coefficient also includes thermal conductivity and viscosity, and also keeping in mind that the dissipative coefficient is enhanced by micro-turbulence (see the discussion in Sect. 2). In the following, this combined dissipation coefficient is referred to as effective viscosity. The magnetic field strength is set to 0.5 − 10 G to analyse cases with various plasma β values.
Finally, for numerical simulations, we should normalise the variables. Let the variables in Eqs. (6) and (8) be of the form 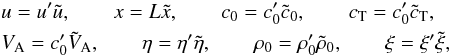 where the tilded variables are the non-dimensional normalised quantities, and u′, L,
where the tilded variables are the non-dimensional normalised quantities, and u′, L, 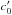 , ξ′, η′, ρ′ are the normalising constants. By setting relations for the scaling constants as
, ξ′, η′, ρ′ are the normalising constants. By setting relations for the scaling constants as 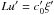 and
and 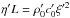 , we obtain for the (tilded) normalised variables the same equations as Eqs. (6) and (8). In particular, for tube waves in polar plumes, the normalising constants are u′ = 106 cm s-1,
, we obtain for the (tilded) normalised variables the same equations as Eqs. (6) and (8). In particular, for tube waves in polar plumes, the normalising constants are u′ = 106 cm s-1, 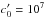 cm s-1, η′ = 10-1 g cm-1 s-1, ρ′ = 10-15 g cm-3, L = 109 cm, and ξ′ = 108 cm.
cm s-1, η′ = 10-1 g cm-1 s-1, ρ′ = 10-15 g cm-3, L = 109 cm, and ξ′ = 108 cm.
 |
Fig. 1 Evolution of the tube wave profile in a co-moving frame of reference, with the distance |
In Figs. 1–3, we present results of numerical simulations of the nonlinear tube wave evolution in a polar plume. Before we discuss the results in detail, we briefly describe the nonlinear wave evolution and formation of shock waves. Nonlinear waves are disturbances of a finite amplitude. In contrast with the linear waves that, strictly speaking, have infinitely small amplitudes, properties of nonlinear waves depend on the value of the amplitude. In nonlinear waves the energy is transferred to smaller spatial scales – the effect of nonlinear cascade. A nonlinear cascade causes a distortion (e.g. steepening) of the wave profile. This in turn develops sharp gradients of various hydrodynamic variables. In the spectral language the steepening corresponds to the transfer of the energy towards larger wave numbers. On the other hand, the efficiency of wave damping by viscosity, thermal conduction, and resistivity is proportional to the wave number squared. Hence, in a nonlinear wave there is the continuous transfer of the energy towards the spectral domain where the dissipative processes are strongest. Thus, the nonlinearity (i.e. finite amplitude of the wave) amplifies the wave damping by dissipation. This effect is usually referred to as nonlinear damping of waves, which is much more efficient than the dissipation of linear waves. For a weak dissipation the nonlinear steepening can lead to the formation of a shock wave. Its width is independent of the dissipation and is determined by the balance between the nonlinear cascade and dissipation. In particular, in Fig. 2 the change in the gradient of the solid curve at x ≈ 20 indicates the formation of the shock and onset of nonlinear damping.
Figure 1 shows the distortion of the tube wave profile with distance from the initial excitation (that is, with height). The wave profile is shown in the co-moving frame of reference, i.e. with respect to the running coordinate. Different curves denote the wave profiles at different values of the spatial coordinate 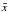 measured along the direction of the wave propagation along the plume. The wave profile steepens and shock fronts form at its descending parts. After the shock formation, the wave decays very rapidly. For the parameters (B0 = 10 G and effective viscosity η = 2.4 × 1014 cm2 s-1), the shocks appear at
measured along the direction of the wave propagation along the plume. The wave profile steepens and shock fronts form at its descending parts. After the shock formation, the wave decays very rapidly. For the parameters (B0 = 10 G and effective viscosity η = 2.4 × 1014 cm2 s-1), the shocks appear at 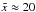 normalised units, or in the physical units at 200 Mm. This value does not contradict the observed evolution of longitudinal waves in polar plumes.
normalised units, or in the physical units at 200 Mm. This value does not contradict the observed evolution of longitudinal waves in polar plumes.
 |
Fig. 2 Evolution of the tube wave amplitude with distance |
Figure 2 shows the evolution of the wave amplitude for different values of the magnetic field strength, that is, for different values of plasma β. The parameter β is here defined as the squared ratio of the sound speed to the Alfvén speed, 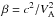 . Note that this definition of β is slightly different from the traditional one. In our definition it is exactly equal to the ratio of the characteristic speeds, which determines the behaviour of the solutions. According to Fig. 2, with the growth of plasma β for a fixed value of the sound speed, the time interval required for the formation of shock fronts increases. This effect is strongly pronounced in a β ≳ 1 plasma and is suppressed in a low-β plasma. On the other hand, damping of the tube wave due to dissipation in a plasma also demonstrates its dependence on β. The amplitude decrease occurring before the shock front has formed increases with the increase in the plasma β. For β> 1, the enhanced dissipation caused by the wave obliqueness can result in very rapid wave damping, so that the shock front does not form.
. Note that this definition of β is slightly different from the traditional one. In our definition it is exactly equal to the ratio of the characteristic speeds, which determines the behaviour of the solutions. According to Fig. 2, with the growth of plasma β for a fixed value of the sound speed, the time interval required for the formation of shock fronts increases. This effect is strongly pronounced in a β ≳ 1 plasma and is suppressed in a low-β plasma. On the other hand, damping of the tube wave due to dissipation in a plasma also demonstrates its dependence on β. The amplitude decrease occurring before the shock front has formed increases with the increase in the plasma β. For β> 1, the enhanced dissipation caused by the wave obliqueness can result in very rapid wave damping, so that the shock front does not form.
 |
Fig. 3 Evolution of the tube wave amplitude with the distance |
Figure 3 demonstrates the evolution of the tube wave amplitude for different values of the effective viscosity. For the classical values of viscosity, the wave damping is less intense for magnetic (tube) waves than for sound waves, which is due to the delayed formation of shock fronts in the wave. However, it should be noted that the effect of the enhanced dissipation on tube waves in a β ≈ 1 plasma can cause significant damping for higher values of viscosity. In this case, the overall decrease in amplitude is more rapid for tube waves, but as seen in the figure, nonlinear effects become negligible.
The results obtained in simulations can be verified by analysing Eq. (6). We rewrite Eq. (6) in terms of the plasma β, 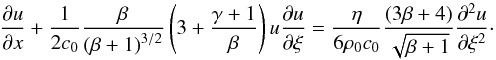 (11)For β ≪ 1, we have the ordinary Burgers equation for plane acoustic waves, Eq. (8). For β ≫ 1, the nonlinear term in Eq. (11) drops to zero as
(11)For β ≪ 1, we have the ordinary Burgers equation for plane acoustic waves, Eq. (8). For β ≫ 1, the nonlinear term in Eq. (11) drops to zero as 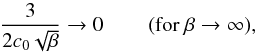 (12)which results in the delay in the formation of shock fronts at the tube wave profile. The high-β case formally corresponds to the incompressible limit. In this limit γ → ∞ and hence c0 → ∞, and for a finite Alfvén speed β → ∞. In the incompressible limit the restoring force for slow-mode waves has a magnetic nature, and they propagate essentially as Alfvén waves. Thus, the quadratically nonlinear term disappears from the equation, and cubic nonlinear effects have to be considered (cf. Nakariakov et al. 2000a). In turn, the dissipative term in Eq. (11) grows as
(12)which results in the delay in the formation of shock fronts at the tube wave profile. The high-β case formally corresponds to the incompressible limit. In this limit γ → ∞ and hence c0 → ∞, and for a finite Alfvén speed β → ∞. In the incompressible limit the restoring force for slow-mode waves has a magnetic nature, and they propagate essentially as Alfvén waves. Thus, the quadratically nonlinear term disappears from the equation, and cubic nonlinear effects have to be considered (cf. Nakariakov et al. 2000a). In turn, the dissipative term in Eq. (11) grows as 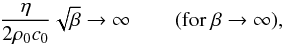 (13)which explains the enhanced dissipation of tube waves.
(13)which explains the enhanced dissipation of tube waves.
It is also useful to investigate the dependence of solutions to Eq. (6) on the wave parameters. Figure 4 shows the evolution of the wave amplitude for different values of the wave period. The shorter the wave is, the more rapidly the nonlinear steepening of its profile occurs. Indeed, this property is common for nonlinear waves. In addition, shorter tube waves are seen to decay faster, even before the shock fronts have formed. We also analysed the tube wave propagation for different initial amplitudes. The effect of nonlinear damping increases with the nonlinearity, that is, with the wave amplitude. According to this expectation, the nonlinear distortion of the wave profile is seen to be more pronounced for waves with higher amplitudes.
 |
Fig. 4 Evolution of the tube wave amplitude with distance |
4. Discussion and conclusions
We have studied the propagation of weakly-nonlinear long wavelength slow magnetoacoustic waves in magnetic flux tubes. Our study was based on the thin flux tube approximation. The waves were considered to be sufficiently long to neglect the wave dispersion. Another assumption made was the small magnitude of the wave nonlinearity and dissipation in the plasma. Indeed, it is known from observations that density perturbations, for example in coronal plumes and magnetic fans, which are identified as slow-mode MHD waves, can be as strong as 10% of the background density. These disturbances are satisfactorily described with the weakly nonlinear approach. Formally, the low dissipation condition requires 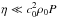 , where P is the wave period (see, e.g. Rudenko & Soluyan 1977), and the relation between the nonlinear and dissipative terms in the final equation can be arbitrary. However, in practice, the best criterion is that the deformation of the wave profile due to dissipation and nonlinearity has to be small on one wavelength scale. In our modelling, the used values of viscosity were appropriate and satisfied this criterion or, at least, were within the margin of the approach scope.
, where P is the wave period (see, e.g. Rudenko & Soluyan 1977), and the relation between the nonlinear and dissipative terms in the final equation can be arbitrary. However, in practice, the best criterion is that the deformation of the wave profile due to dissipation and nonlinearity has to be small on one wavelength scale. In our modelling, the used values of viscosity were appropriate and satisfied this criterion or, at least, were within the margin of the approach scope.
The simplifications described above have allowed us to derive the Burgers-type evolutionary equation, Eq. (6), for tube waves, in which we have combined i) nonlinear wave evolution similar to that described by the Riemann simple-wave solution; ii) wave damping due to dissipation caused by viscosity and also thermal conduction and resistivity; and iii) the wave obliqueness and hence the effects of the finite magnetic field. Because the effects of stratification and magnetic flux tube divergence were neglected, our study may be considered as a local approximation.
The analysis of the evolutionary equation has shown that in comparison with the acoustic case, the formation of shock fronts in tube waves occurs at larger distances from the wave source. Mathematically, this effect is associated with the reduction of the coefficient in the nonlinear term in the equation. Indeed, Eqs. (8) and (11) taken in the case of dissipationless media allow one to determine the characteristic shock formation distances as 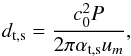 (14)where um is the initial amplitude of the waves, the subscripts t and s show the parameters corresponding to tube and sound waves, and
(14)where um is the initial amplitude of the waves, the subscripts t and s show the parameters corresponding to tube and sound waves, and 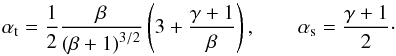 (15)In the dissipationless limit, the shock formation distance is determined as the distance at which the wave develops an infinite gradient. The ratio ds/dt starting with unity at β → 0 monotonically decreases to zero with the growth of plasma β. Thus, in the finite-β regime, accounting for the obliqueness increases the shock formation distance and hence postpones the onset of considerable nonlinear damping, and must not be ignored in coronal wave modelling.
(15)In the dissipationless limit, the shock formation distance is determined as the distance at which the wave develops an infinite gradient. The ratio ds/dt starting with unity at β → 0 monotonically decreases to zero with the growth of plasma β. Thus, in the finite-β regime, accounting for the obliqueness increases the shock formation distance and hence postpones the onset of considerable nonlinear damping, and must not be ignored in coronal wave modelling.
The dissipation coefficient increases with the increase in the parameter β, causing additional damping before the shock front has formed. Note that nonlinear damping that occurs after the shock formation is unaffected by β because it is independent of the dissipation coefficient provided it is small (see, e.g. Rudenko & Soluyan 1977).
The obtained delay in the shock formation and enhanced wave damping before the onset of nonlinear damping are considerable for β ≳ 1, while in a low-β plasma, the evolution of tube waves differs very slightly from that of plane acoustic waves. This finding justifies the applicability of the results previously obtained for propagating longitudinal waves in magnetic fans filled in with the plasma of a moderate temperature (e.g. about 1 MK, see Nakariakov et al. 2000b) and in the lower parts of polar plumes (Ofman et al. 2000). On the other hand, the effects connected with the wave obliqueness appear in the dynamics of longitudinal waves in finite-β plasma wave-guides, such as hot flaring loops (e.g. Shibasaki 2001), magnetic fans filled in with dense hot plasma (Sakao et al. 2007), and in the higher corona (Ofman & Wang 2002). Because in the hot plasma structures of the corona the density scale height is large, effects of stratification can be neglected and the theory developed in this paper can be applied directly. Moreover, the suppression of the nonlinear effects on the longitudinal wave propagation in a finite-β plasma allows focusing on linear effects alone. But, in this case, the effects of obliqueness should be taken into account. The obliqueness effects may also be important for longitudinal waves detected in chromospheric waveguides. Future analysis of waves in these structures requires accounting for the effects of stratification, radiation, and partial ionisation, and is beyond the scope of this paper.
Acknowledgments
The work is supported by the Marie Curie PIRSES–GA–2011–295272 RadioSun project and the Federal Agency for Scientific Organisations base project II.16.1.6 No. 01201281652 (ANA), and the European Research Council under the SeismoSun Research Project No. 321141, STFC consolidated grant ST/L000733/1, the BK21 plus program through the National Research Foundation funded by the Ministry of Education of Korea, and the Russian Foundation of Basic Research under grant 13-02-00044 (VMN).
References
- Aschwanden, M. 2006, Physics of the Solar Corona: An Introduction with Problems and Solutions, Springer Praxis Books/Astronomy and Planetary Sciences (Chichester: Praxis Publishing Limited, UK) [Google Scholar]
- Banerjee, D., Gupta, G. R., & Teriaca, L. 2011, Space Sci. Rev., 158, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Braginskii, S. I. 1965, Rev. Plasma Phys., 1, 205 [NASA ADS] [Google Scholar]
- De Moortel, I. 2006, Roy. Soc. London Philos. Trans. Ser. A, 364, 461 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I. 2009, Space Sci. Rev., 149, 65 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Hood, A. W. 2003, A&A, 408, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Hood, A. W. 2004, A&A, 415, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 3193 [Google Scholar]
- De Moortel, I., Hood, A. W., Gerrard, C. L., & Brooks, S. J. 2004, A&A, 425, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Defouw, R. J. 1976, ApJ, 209, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Gruszecki, M., & Nakariakov, V. M. 2011, A&A, 536, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molotovshchikov, A. L., & Ruderman, M. S. 1987, Sol. Phys., 109, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M. 2006, Roy. Soc. London Philos. Trans. Ser. A, 364, 473 [Google Scholar]
- Nakariakov, V. M., & Zimovets, I. V. 2011, ApJ, 730, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Ofman, L., & Arber, T. D. 2000a, A&A, 353, 741 [NASA ADS] [Google Scholar]
- Nakariakov, V. M., Verwichte, E., Berghmans, D., & Robbrecht, E. 2000b, A&A, 362, 1151 [NASA ADS] [Google Scholar]
- Nakariakov, V. M., Tsiklauri, D., Kelly, A., Arber, T. D., & Aschwanden, M. J. 2004, A&A, 414, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., & Wang, T. 2002, ApJ, 580, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Nakariakov, V. M., & DeForest, C. E. 1999, ApJ, 514, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., Nakariakov, V. M., & Sehgal, N. 2000, ApJ, 533, 1071 [Google Scholar]
- Roberts, B. 1985, Phys. Fluids, 28, 3280 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B. 2006, Phil. Trans. R. Soc. A, 364, 447 [CrossRef] [Google Scholar]
- Roberts, B., & Webb, A. R. 1978, Sol. Phys., 56, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B., & Webb, A. R. 1979, Sol. Phys., 64, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Rudenko, O. V., & Soluyan, S. I. 1977, Theoretical Foundations of Nonlinear Acoustics (New York and London: Plenum Publishing Corporation, Consultants Bureau) [Google Scholar]
- Ruderman, M. S. 2013, A&A, 553, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakao, T., Kano, R., Narukage, N., et al. 2007, Science, 318, 1585 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Shibasaki, K. 2001, ApJ, 557, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiklauri, D., & Nakariakov, V. M. 2001, A&A, 379, 1106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsiklauri, D., Nakariakov, V. M., Arber, T. D., & Aschwanden, M. J. 2004, A&A, 422, 351 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasheghani Farahani, S., Nakariakov, V. M., Van Doorsselaere, T., & Verwichte, E. 2011, A&A, 526, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasheghani Farahani, S., Nakariakov, V. M., Verwichte, E., & Van Doorsselaere, T. 2012, A&A, 544, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verwichte, E., Haynes, M., Arber, T. D., & Brady, C. S. 2008, ApJ, 685, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. 2011, Space Sci. Rev., 158, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Innes, D. E., & Qiu, J. 2007, ApJ, 656, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T. J., Ofman, L., & Davila, J. M. 2009, ApJ, 696, 1448 [NASA ADS] [CrossRef] [Google Scholar]
- Zhugzhda, Y. D. 1996, Phys. Plasmas, 3, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Zhugzhda, Y. D. 2005, Plasma Phys. Rep., 31, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Zhugzhda, Y. D., & Goossens, M. 2001, A&A, 377, 330 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhugzhda, Y. D., & Nakariakov, V. M. 1997, Phys. Lett. A, 233, 413 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Evolution of the tube wave profile in a co-moving frame of reference, with the distance |
| In the text | |
 |
Fig. 2 Evolution of the tube wave amplitude with distance |
| In the text | |
 |
Fig. 3 Evolution of the tube wave amplitude with the distance |
| In the text | |
 |
Fig. 4 Evolution of the tube wave amplitude with distance |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.