EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 573 (January 2015) A&A, 573 (2015) A36 Full HTML
Free Access
Issue
A&A
Volume 573, January 2015
Article Number A36
Number of page(s) 11
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201424399
Published online 12 December 2014

© ESO, 2014

1. Introduction

Since Nicolaus Copernicus (Copernicus 1543) proposed for the first time the model of the solar system, it has taken nearly 450 yr to detect the first planet around stars other than the Sun (Wolszczan & Frail 1992; Mayor & Queloz 1995; Marcy & Butler 1996). The progress has been much faster since, and the first multiple planetary system orbiting a main-sequence (MS) star was found only a few years later by Butler et al. (1999).

Today, the focus of most planet searches is on MS stars with planets in stable habitable zones (HZ). From a list of almost 1800 exoplanet candidates1, 20 are potentially habitable2, including the first Earth-like planet (Gliese 581 d – Udry et al. 2007). We have also found extrasolar systems as complex as our own (e.g., 55 Cnc – Fischer et al. 2008; HD 10180 – Lovis et al. 2011; Kepler 11 – Lissauer et al. 2011).

Stars beyond the MS are frequently avoided in planet searches because they are known to exhibit various types of variability: RV variations of unknown origin were pointed out to be common in red giants (RGs) by Walker et al. (1989), and multiple pulsation modes are often present (Hatzes & Cochran 1993; Wood et al. 1999; De Ridder et al. 2009; Kallinger et al. 2010; Mosser et al. 2013). In addition, the rotation of starspots across the stellar disk can affect the spectral line profiles of these stars (Vogt et al. 1987; Walker et al. 1992; Saar & Donahue 1997).

Several authors have collected precise data to understand the origin of RV variations in RGs. Some of these RG stars with RV variations (β Gem – Hatzes & Cochran 1993; Reffert et al. 2006; Reffert & Quirrenbach 2011; γ Cep – Campbell et al. 1988; Endl et al. 2011; Reffert & Quirrenbach 2011) are now recognized as having planetary-mass companions (Hatzes et al. 2003, 2006). HD 177830 (Vogt et al. 2000) and ϵ Ret (Butler et al. 2001) are interesting cases to illustrate the problems with this type of systems given that both were reported to host a planetary companion as “evolved subgiants” and were only much later recognized to be bona fide giants by Mortier et al. (2013). As a consequence, ι Dra b (Frink et al. 2002) is usually considered the first deliberate discovery of a planet around a RG star.

Searches for planets around stars beyond the MS have, soon after the first discovery, become recognized as important in building a complete picture of planet formation and evolution for several reasons. First, they allow extending the reach of the most versatile RV technique, which is not applicable on the MS because of the high effective temperature of the stars and their fast rotation rates, to objects with masses significantly higher than solar (e.g., o UMa, a 3 M⊙ giant with a planet – Sato et al. 2012). Second, the planetary systems around evolved stars are much older than those around MS stars, and therefore they are suitable for long-term dynamical stability considerations (Debes & Sigurdsson 2002; Veras & Mustill 2013; Mustill et al. 2014). Planetary systems around giants are also subject to changes induced by stellar evolution (Villaver & Livio 2007, 2009; Villaver et al. 2014), and therefore are suitable for studies of star – planet interactions (e.g., Adamów et al. 2012), and last but not least, evolved planetary systems carry information on the initial population of planetary systems to be found around white dwarfs (Farihi et al. 2010).

It is no surprise then that several projects devoted to searches for RV planets that orbit RGs were launched: the McDonald Observatory Planet Search (Cochran & Hatzes 1993; Hatzes & Cochran 1993), the Okayama Planet Search (Sato et al. 2003), the Tautenberg Planet Search (Hatzes et al. 2005), the Lick K-giant Survey (Frink et al. 2002), the ESO Ferros planet search (Setiawan et al. 2003a,b), Retired A Stars and Their Companions (Johnson et al. 2007), the Coralie and HARPS searches (Lovis & Mayor 2007), the Boyunsen Planet Search (Lee et al. 2011), and one of the largest, the PennState – Toruń Centre for Astronomy Planet Search (PTPS, Niedzielski et al. 2007; Niedzielski & Wolszczan 2008a,b).

Within PTPS we monitored over 1000 stars for RV variations with the Hobby-Eberly Telescope (HET) and its High-Resolution Spectrograph since 2004. As part of this effort, about 300 planetary or brown dwarf (BD) candidates were identified that merit more intense precise RV follow-up. The program Tracking Advanced Planetary Systems (TAPAS) with HARPS-N is the result of intensifying the monitoring of a selected number of PTPS-identified targets, that is, those with potentially multiple and/or low-mass companions, with expected p-mode oscillations of a few m s-1, and systems with evidence of recent or future star-planet interactions (Li-rich giants, low-orbit companions, etc.).

TYC 1422-614-1 is a red clump giant star selected as a TAPAS target because the HET observations showed that it was a relatively inactive giant with expected p-mode oscillations of only 4 m s-1 showing a complex RV variation pattern that required more epochs of precise data. After several years of PTPS observations, our continuously updated model for the rare multiplanetary system around this giant was still not consistent, and because the very important and rare RV minimum was expected during a period in which HET was not operational because of an upgrade, we chose to add this star to the TAPAS target list.

In this paper we report the discovery of a multiple planetary system orbiting the giant star TYC 1422-614-1, the first planetary-system result of TAPAS, our intensive monitoring with HARPS-N of some of the PTPS selected targets. The paper is organized as follows: in Sect. 2 we present the observations obtained for this target and outline the reduction and measurement procedures, Sect. 3 shows the results of the Keplerian and Newtonian data modeling, in Sect. 4 we extensively discuss the influence of the stellar activity on the RV variation measurements; and in Sects. 5 and 6, we discuss the results of our analysis and present the conclusions.

2. Observations and data reduction

TYC 1422-614-1 (2MASS J10170667+1933304) is a V = 10.21 and B − V = 0.95 mag (Høg et al. 2000) star in the constellation of Leo. Since a trigonometric parallax is not available for this star, its mass, age, and radius were estimated on the basis of spectroscopically determined atmospheric parameters by Zieliński et al. (2012). To provide a better constraint to the stellar parameters, we have constructed a probability distribution function using the algorithm of da Silva et al. (2006), a modified version of the Bayesian estimation method idealized by Jørgensen & Lindegren (2005) and Nordström et al. (2004), and stellar isochrones from PARSEC (Padova and Trieste stellar evolution code, Bressan et al. 2012). Even though our results agree very well with those of Zieliński et al. (2012) , without a trigonometric parallax they are rather uncertain and model dependent. The amplitude of p-mode oscillations Vosc was estimated from the scaling relation by Kjeldsen & Bedding (1995). The vrotCCF\hbox{$v_{\rm rot}^{\rm CCF}$}sini⋆ was obtained by Nowak (2012) from a cross-correlation function (CCF) analysis of about 200 spectral lines following the prescription of Carlberg et al. (2011). Adamów et al. (2014), based on abundance calculations via Spectroscopy Made Easy package (Valenti & Piskunov 1996) modeling of 27 spectral lines for six elements, found no chemical anomalies for TYC 1422-614-1 with respect to a full sample of RG stars. A summary of all the available data for TYC 1422-614-1 is given in Table 1.

Table 1

Summary of the available data on TYC 1422-614-1.

The spectroscopic observations presented in this paper were made with the 9.2 m effective aperture (11.1 × 9.8 m) HET (Ramsey et al. 1998) and its High-Resolution Spectrograph (HRS, Tull 1998) in the queue scheduled mode (Shetrone et al. 2007), and with the 3.58 m Telescopio Nazionale Galileo (TNG) and its High Accuracy Radial velocity Planet Searcher in the North hemisphere (HARPS-N, Cosentino et al. 2012). Time-series of photometric data were obtained from the All Sky Automated Survey (ASAS, Pojmanski 2002).

2.1. Hobby-Eberly Telescope data

The HET and HRS spectra were gathered with the HRS fed with a 2 arcsec fiber, working in the R = 60 000 mode with a gas cell (I2) inserted into the optical path. The spectra consisted of 46 echelle orders recorded on the blue charge-coupled device (CCD) chip (407.6–592 nm) and 24 orders on the red chip (602–783.8 nm). Details of our survey, the observing procedure, and data analysis have been described in detail elsewhere (Niedzielski et al. 2007; Nowak et al. 2013). The configuration and observing procedure employed in our program were, in practice, identical to those described by Cochran et al. (2004). The basic data reduction was performed using standard IRAF3 tasks and scripts developed for PTPS. With the precision reached, we used the Stumpff (1980) algorithm to refer the measured RVs to the solar system barycenter.

Since HRS is a general-purpose spectrograph, neither temperature nor pressure controlled, the precise RV measurements with this instrument are best accomplished with the I2 cell technique. We use a combined gas-cell (Marcy & Butler 1992; Butler et al. 1996), and cross-correlation (Queloz 1995; Pepe et al. 2002) method for this purpose. The implementation of this technique to our data is described in Nowak (2012) and Nowak et al. (2013). The precision of RV and line bisector velocity span (BS), as well as the long-term stability of our measurements, has been verified by the analysis of data obtained from monitoring stars that do not exhibit detectable RV variations and stars with well-described RV or BS variations. The results for the K0 giant BD+70 1068 presented in Niedzielski et al. (2009b) show a σ = 12 m s-1, to which contributed an intrinsic RV uncertainty of 7 m s-1 and, the approximately 10 m s-1 amplitude of solar-type oscillations (Kjeldsen & Bedding 1995). In Nowak et al. (2013) we performed a more detailed analysis of our RV precision and stability using our own RVs to fit orbital solutions for HD 209458 and HD 88133, while our BS precision was demonstrated for HD 166435. In general, we find that our observing procedure with HET and HRS results in RV precisions of about 5–8 m s-1 depending on the signal-to-noise ratio (S/N) of the spectra, and the effective temperature of the star, for BS measurements the precision is 2–3 times lower.

This instrumental setup, observing, and reduction techniques and data modeling tools have allowed us to report the discovery of 19 planetary-mass companions, mostly to evolved stars (Niedzielski et al. 2007, 2009a,b; Gettel et al. 2012a,b; Adamów et al. 2012; Nowak 2012; Nowak et al. 2013; Niedzielski et al., in prep.)

2.2. HARPS-N data

HARPS-N, a near-twin of the HARPS instrument mounted at the ESO 3.6 m telescope in La Silla (Mayor et al. 2003), is an echelle spectrograph covering the visible wavelength range between 383 nm and 693 nm with a resolving power of R ~ 115 000. The spectra are re-imaged on a 4k × 4k CCD, where echelle spectra of 69 orders are formed for each fiber.

The instrument is located in a thermally controlled environment within a vacuum-controlled enclosure to ensure the required stability and is fed by two octagonal fibres at the Nasmyth B focus of the TNG (with an aperture on the sky of 1 arcsec). Both fibers are equipped with an image scrambler to provide a uniform spectrograph pupil illumination, independent of pointing decentering. This instrument is expected to deliver measurements of radial velocities with the highest accuracy currently available, with 1 m s-1 achievable from S/N = 100 spectra.

Radial velocity measurements and their uncertainties as well as BS were obtained with the standard user pipeline, which is based on the weighted CCF method (Fellgett 1955; Griffin 1967; Baranne et al. 1979; Queloz 1995; Baranne et al. 1996; Pepe et al. 2002). To obtain highest precision RV, we used the simultaneous Th–Ar calibration mode of the spectrograph. TYC 1422-614-1 RVs were obtained with the K5 cross-correlation mask.

The instrument has been successfully used to detect exoplanets by Covino et al. (2013); Desidera et al. (2013); Hébrard et al. (2013) and Pepe et al. (2013).

3. Modeling of RV data

TYC 1422-614-1 was observed over 3651 days between modified Julian day, MJD 53 034 and 56 685. In total, we collected 86 epochs of precise RV and BS, 69 with HET and 17 with HARPS-N.

The data obtained with HET and HRS cover 69 epochs of observations over 3410 days between MJD 53 034 and MJD 56 445 with a typical S/N of 150–250 at 569 nm. The best-quality template with an S/N of 316 was used for the RV measurements. The resulting RVs show a peak-to-peak amplitude of 621.1 m s-1 and uncertainties of 7.7 m s-1 on average. The BS peak-to-peak amplitude is 145 m s-1, with a mean value of 14.1 m s-1 and a precision of 21.3 m s-1 on average (see Table 2). The observed RV variations are ~4 times higher than the BS variations and are not correlated (r = 0.005), hence they are most likely due to Doppler shifts.

We also collected 17 epochs of RV with HARPS-N over 408 days between MJD 56 277 and MJD 56 685 with an average uncertainty of 1.6 m s-1 (see Table 3). HARPS-N RV measurements show a peak-to-peak amplitude of 568.5 m s-1. The BS shows a mean value of 82.5 m s-1 and a peak-to-peak amplitude of 40.1 m s-1, which is 15 times lower than the RV. The RV and BS show a correlation of r = 0.63, which is marginally significant because the critical value is r15,0.01 = 0.61. A more detailed inspection of the BS data shows that this is likely a random effect due to small statistics, and we assume that at least in the first approximation the RV signal is indeed due to Doppler shifts (we discuss this question in Sect. 4).

3.1. Keplerian analysis

We modeled Keplerian orbits to the observed RV variations using the hybrid approach proposed by Goździewski et al. (2003); Goździewski & Migaszewski (2006), and Goździewski et al. (2007). The global search for orbital parameters was made with a genetic algorithm (GA). After the range of plausible orbital parameters was narrowed, a nonlinear least-squares fit to the data quickly converge to the final solution. In particular, with a set of periodic signals in RV time-series identified in its Lomb-Scargle (LS) periodogram (Lomb 1976; Scargle 1982), we searched for possible orbital solutions over a wide range of parameters with PIKAIA (Charbonneau 1995). We present the LS periodogram of TYC 1422-614-1 RV in Fig. 1 (top panel). The GA semi-global search identified a narrow parameter range in the search space, which was then explored using the MPFIT algorithm (Markwardt 2009) to locate the best-fit Keplerian solution delivered by RVLIN (Wright & Howard 2009) modified after Ford & Gregory (2007) and Johnson et al. (2011a) to allow the stellar jitter to be fitted as a free parameter.

We scrambled the residuals, which is also called bootstrapping (Murdoch et al. 1993; Kuerster et al. 1997; Marcy et al. 2005; Wright et al. 2007), to assess the uncertainties of the best-fit orbital parameters. The width of the resulting distribution of 105 trials between the 15.87th and 84.13th percentile was adopted as a parameter uncertainty.

The results of the Keplerian analysis are presented in Fig. 2 and Table 4. As an example, the bootstrapping analysis of orbital parameters for component c is presented in Fig. 3, where we present a 2D period-eccentricity distribution.

The false-alarm probability FAP < 0.0005 of the final orbital solution was estimated by repeating the whole hybrid Keplerian analysis on 20 000 sets of scrambled data.

thumbnail Fig. 1

From top to bottom: lomb-Scarge periodograms for the a) original HET RV data of TYC 1422-614-1; b) RV residua (HET and TNG) without planet c; and c) RV residua (HET and TNG) after the best Keplerian two-planetary fit. See also Fig. 5.

thumbnail Fig. 2

Keplerian best fit of the two-planetary model to the observed RV of TYC 1422-614-1. HET and HRS data are presented in red and TNG and HARPS-N data in green. The estimated jitter due to p-mode oscillations has been added to the uncertainties.

The resulting jitter is larger than our estimate of unresolved p-mode oscillations of 4 m s-1 and points to an additional source of RV scatter of unknown nature, to an additional component, or to stellar activity.

The Keplerian two-planet best fit results in a marginally significant period of 2.9 days and a weaker one of ~2280 days in RV residua (Fig. 1). The short period is probably an artifact because the fundamental radial pulsational period that we estimated according to the formalism of Cox et al. (1972) is expected to be much shorter, 0.52 days. The longer period is very uncertain and comparable with the time span of our observations; if it is confirmed by future observations, it may even be due to another as yet unresolved companion or long-term stellar variability.

Table 4

Keplerian orbital parameters of TYC 1422-614-1 b and c.

thumbnail Fig. 3

Illustration of the bootstrapping analysis (105 realizations) of the Keplerian parameters of TYC 1422-614-1 c uncertainties, a 2D histogram of orbital period and eccentricity. Both 1D histograms are plotted with the 15.87 and 83.13 percentile (i.e., 1σ) ranges shown.

3.2. Newtonian analysis

The ratio between the orbital periods of the two planets is Pc/Pb = 0.355, close to a 7:20 commensurability, which suggests that the system might be in a mean motion resonance. A Newtonian model of the system was obtained with the software Systemic 2.16 (Meschiari et al. 2009). The Keplerian orbital solution provided the initial parameters for the Bulirsch–Stoer integrator, running with a precision parameter of 10-16. The planetary system was assumed to be co-planar. The differential evolution algorithm with 5000 steps and Levenberg-Marquardt minimization were used to find the best-fit model. The bootstrap method with 105 trials was used to estimate parameter uncertainties, calculated as median absolute deviations. The parameters of the best-fit dynamical model are given in Table 5. In most cases, they agree with the Keplerian model well within 1σ. The only exception is Pc, for which the dynamical solution gives a value greater by ~10 days. The goodness of the fit was found to be similar to that of the Keplerian approach.

The planetary system was found to be stable on a timescale of 106 yr. The Swift regularized mixed variable symplectic (RMVS) integrator was used to trace the behavior of the orbital parameters. The simulation shows that ab may vary between 0.685 and 0.693 AU and eb may oscillate between 0.0 and 0.1 with a period of 190 yr. At the same time, ac and ec may range from 1.368 to 1.393 AU and from 0.03 to 0.06, respectively. The period ratio based on the Newtonian model is Pc/Pb = 0.349, which is even closer to the 7:20 commensurability. The eccentricity-type resonant angles, defined as a linear combination of mean longitudes and arguments of periastron, show no libration. The difference between arguments of periastron, defined as Δω = ωc − ωb, demonstrates a lack of apsidal alignment and oscillations. Thus, the system is not in a dynamical resonance. Variations in eccentricities in the first thousand years are shown in Fig. 4.

Table 5

Dynamical orbital parameters of TYC 1422-614-1 b and c.

thumbnail Fig. 4

Evolution of planetary eccentricities in the first thousand years, calculated for the orbital solution given in Table 5.

4. Stellar activity

Giants are well-known to exhibit all sorts of variations; stellar activity, pulsations, and rotation-induced effects should be considered before a companion hypothesis is formulated.

4.1. Ca II H and K lines

The flux at the cores of the Ca II H and K lines is a good tracer of chromospheric activity (e.g., Noyes et al. 1984; Duncan et al. 1991), and therefore the Ca II H and K line profiles are widely accepted as stellar activity indicators. The Ca II H and K lines as well as the infrared Ca II triplet lines at 849.8–854.2 nm lie outside the HET and HRS wavelength range, but the Ca II H and K lines are available from the TNG HARPS-N spectra. The S/N in the blue spectrum of our red giant star is low, (~10–20), but no trace of a reversal as typical for active stars (Eberhard & Schwarzschild 1913) is present, and thus no obvious chromospheric activity can be deduced.

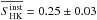To quantify possible activity-induced line profile variations, we calculated an instrumental SHKinst\hbox{$S_{\rm HK}^{\rm inst}$} index according to the prescription of Duncan et al. (1991) for all 17 epochs of HARPS-N observations and correlated them with RV and BS. The mean value of SHKinst=0.25±0.03\hbox{$\overline {S_{\rm HK}^{\rm inst}}=0.25 \pm 0.03$}, which places TYC 1422-614-1 among inactive subgiants according to Isaacson & Fischer (2010). The correlation coefficient r = 0.56 is below the critical value (r15,0.01 = 0.61) and no correlation between SHKinst\hbox{$S_{\rm HK}^{\rm inst}$} and RV can be inferred from our data. There is also no relation between SHKinst\hbox{$S_{\rm HK}^{\rm inst}$} and BS (r = 0.52). A much better relation exists between our SHKinst\hbox{$S_{\rm HK}^{\rm inst}$} index and the RV uncertainty (r = −0.65), which suggests that the observed SHKinst\hbox{$S_{\rm HK}^{\rm inst}$} scatter in our data is only noise and that no measurable chromospheric activity is present in TYC 1422-614-1.

4.2. Hα analysis

thumbnail Fig. 5

From top to bottom: Lomb-Scargle periodograms of a) IHα activity index; b) IFe index; c) ASAS photometry; and d) HET and HRS BS. See also Fig. 1.

In addition to the Ca II H and K lines, we used the HET and HRS Hα (656.2808 nm) line data as a chromospheric activity indicator because, as Cincunegui et al. (2007) showed, the calcium and hydrogen line indices do not always correlate and cannot be used interchangeably as activity indicators.

Following the procedure described in detail in Maciejewski et al. (2013), which is based on the approach presented by Gomes da Silva et al. (2012) and Robertson et al. (2013, and references therein), we measured the Hα index (IHα) for the 69 HET and HRS spectra. To take possible instrumental effects into account, we also measured the index of the Fe I 654.6239 nm control line (IFe), which is insensitive to stellar activity. Moreover, as the wavelength regime relevant to Hα and Fe I line indices may still contain weak I2 lines, we also measured Hα and Fe I indices for the iodine flat-field spectra (II2,Hα and II2,Fe).

The marginal rms variations of the II2Hα = 0.11% and II2,Fe = 0.32% in comparison to the relative scatter of the IHα = 2.19% and the IFe = 1.1% index indicate that the contribution of the weak iodine lines to the Hα and Fe line indices in TYC 1422-614-1 is negligible. The significant relative scatter variation of the Fe line equal to half of the Hα rms variation is driven by two outliers exceeding the ±3σ level from the mean value; this decreases to 0.64% when the outliers are excluded.

There are no significant signals present in the LS periodograms of the IFe index (Fig. 5b), in contrast to the IHα periodogram, where a significant signal with a period of ~2550 days (almost seven years), similar to that observed in the RV residuals, is clearly visible (Fig. 5a). Therefore we put forward the hypothesis that this periodicity is driven by long-term chromospheric activity of TYC 1422-614-1 analogously to the eleven-year solar cycle.

No excess fluctuation power in the LS periodogram of the IHα index is present at the 198.44 and 569.2 day periods detected in the RV data. We therefore conclude that none of the signals present in the RV data is driven by chromospheric activity of the parent star.

4.3. Photometric variability

From ASAS (Pojmanski 1997, 2002) we have 367 epochs of TYC 1422-614-1 observations covering HJD 2 452 622 and 2 454 989, which means that they are partly contemporaneous with our HET observations. The photometric observations were compiled from four different fields, two of which contain enough data for an independent analysis with 135 (field 1) and 185 (field 2) epochs. After iterative 3σ filtering, 355 epochs were used to analyze the photometric variability. These data show a mean brightness of mASAS = 10.186 ± 0.011 mag (rms). The scatter in brightness of TYC 1422-614-1 is much larger than the p-mode oscillations amplitude predicted from the scaling relations of Kjeldsen & Bedding (1995), 0.13 mmag (the reason obviously being the limited precision of ASAS photometry for this star). The star was not classified as a variable in ASAS-3.

The field 1 data show no significant periodic signal, but both field 2 and all combined data show a weak periodic signal of 473 days (see Fig. 5c). To determine whether this periodic signal was real, we performed a bootstrap analysis, and after 10 000 trials we found a FAP10 000 = 0.02, which means that although it is weak, it cannot be ignored. A formal sine fit to the combined data with a period of 473 days results in an amplitude of 0.011 ± 0.002 mag, that is, at the level of the mean brightness uncertainty.

What might be the origin of that periodic signal? It is much longer than the p-mode oscillations (~3 h) or the radial pulsations (0.52d). It is also well outside the uncertainties of the two Keplerian periods found in Sects. 3.1 and 3.2.

The only source of this photometric periodicity (if it is indeed real) may be a spot or a group of spots rotating with the star; therefore it might represent the true stellar rotation period. Using the stellar radius from Table 1, we obtain a vrot = 0.7 km s-1, suggesting a very slow rotation rate.

The projected rotation velocity obtained by Nowak (2012) (see Table 1) is lower than the average K giant projected rotational velocity of 3 km s-1 (Fekel 1997). This suggests that this is a very slow rotator, and as such its measured rotational speed value is expected to be uncertain because the projected rotation velocity is ~3 times lower than the instrumental PSF. If we assume that the 473 day photometric period is the stellar rotational period, then we find a good agrement, within uncertainties, between the photometric rotation period and the value obtained by Nowak (2012) from spectral analysis, vrotCCFsini⋆=1.4±0.7\hbox{$v_{\rm rot}^{\rm CCF} \sin i_{\star}= 1.4\pm0.7$} km s-1. A slow rotational velocity for TYC 1422-614-1 is also consistent with the low chromospheric stellar activity (see e.g., do Nascimento et al. 2003). We therefore assume that the rotation period of TYC 1422-614-1 is 473 days.

We used the ASAS data on TYC 1422-614-1 to estimate an upper limit to the stellar surface covered by hypothetic spots. Under the assumption that the only source of the observed brightness scatter are spots rotating on the surface of TYC 1422-614-1, the fraction, f, of the star covered is then determined from the mean brightness change (mean brightness uncertainty), and we obtain f ≈ 1.5%. With this and the rotational period derived from ASAS photometry, we considered the impact of such spots on the RV and BS because they can alter the spectral line profiles and mimic Doppler shifts (Walker et al. 1992). Using the results of the extensive simulations of Hatzes (2002), we estimate that spots of f ≈ 1.5% will result in RV and BS variations with an amplitude of 20 m s-1 and 27 m s-1 at maximum.

The observed RV variations in TYC 1422-614-1 are 15 times larger, so they cannot originate from spectral line deformations due to spots. Furthermore, any contribution to the observed RV variations from stellar spots is expected to be very small, at the level of ~7%. Our assumption that the observed RV variations are due to Doppler shifts is therefore fully justified. We note, however, that the ASAS photometric data show a trace of a long period similar to that present in RV residua and IHα.

The observed BS variations show a similar (HARPS-N) or even larger (HET) amplitude than the estimated one, it is therefore particularly important to study the BS in more detail.

4.4. Line bisector analysis

The HET and HRS and HARPS-N BS were calculated from different instruments and sets of spectral lines. They are not directly comparable, and so we considered them separately.

The HET and HRS BS LS periodogram shows no significant periodic signal (Fig. 1). Although the observed BS variations are larger than the values estimated from photometry, there is no correlation between RV and BS. Altogether, there is no observational evidence of spectral line deformation influence on RV in the HET data. The observed HET BS scatter may reflect either additional stellar activity that we do not resolve in time with our observations, such as p-mode oscillations, or it might be the effect of underestimated uncertainties.

The TNG HARPS-N data are more precise than the HET and HRS data, but we do not have enough epochs of observations for a conclusive periodogram analysis. The HARPS-N BS amplitude is comparable to the HET and HRS BS standard deviation. The RV and BS show a correlation of r = 0.63, which is marginally significant because the critical value is r15,0.01 = 0.61. A closer examination of the BS data shows, however, that the correlation may very well be a random effect due to small statistics because variations of ~16 m s-1 were observed during one night. Nevertheless, the amplitude of observed BS variation is consistent with the upper limit estimated from the available photometry.

Fortunately, the HARPS-N data cover the full observed RV amplitude, and the amplitude of BS variations supports our conclusion from Sect. 4.3 that the spectral line deformation due to a hypothetical spot, if real, may contribute only to a minor fraction of the observed RV variations.

We conclude, therefore, that although the HET and HRS BS data show no evidence of a stellar activity influence on the measured RV, the HARPS-N BS data prove a lack of chromospheric activity, but suggests an additional RV signal from a spectral line distortion of an as yet unknown period. The RV scatter present in post-fit residua is too large for unresolved p-mode oscillations, but it is consistent with our estimates of the RV contamination due to spots.

5. Discussion

thumbnail Fig. 6

Hertzsprung-Russel diagram for the complete PTPS sample with TYC 1422-614-1 position indicated and 1.1 M⊙, z = 0.008 stellar evolutionary track from Bertelli et al. (2008) and, in green, the path of the star with planet c within the optimistic HZ of Kopparapu et al. (2013). The orange and red rectangles indicate the phase of planet b and c ingestion.

The stellar spectroscopic parameters and the stellar luminosity converge to locate TYC 1422-614-1 in the track of a K2 giant that quickly evolves up the red giant branch (RGB). The star is already undergoing the first dredge-up but, within uncertainties, it is most likely located before the luminosity jump (see Fig. 6). The radius of the star is estimated to be 6.85 ± 1.38 R⊙.

Considering angular momentum conservation alone, the innermost planet located at 0.69 AU (and with a/R∗ = 22) is not expected to have experienced orbital decay caused by the stellar tides nor orbital expansion due to mass-loss (see Villaver & Livio 2009 and Villaver et al. 2014). The planet, however, is expected to be engulfed by the star as it ascends to the tip of the RGB. Using the approximate location of TYC 1422-614-1 following a path of a M = 1.1 M⊙z = 0.008 star from Bertelli et al. (2008), we calculated the evolution of the planet orbit and found that it is expected to be engulfed in all the possible scenarios considered under several mass-loss prescriptions. Our orbital evolution calculations show that planet b is expected to enter the stellar envelope as the planetary orbit decays as a result of tidal forces when the star reaches a radius of ≈43 R⊙. An estimated upper limit for the time left for the planet before entering the stellar envelope is ≈120 mln yr (computed assuming the star follows the Bertelli et al. 2008 track), during its ascent on the RGB.

The outermost planet is expected to reach the stellar surface as well, but slightly later, when the stellar radius reaches a value of ≈75 R⊙ in about 130 mln yr. While the innermost planet will be most likely destroyed inside the stellar envelope (see Villaver & Livio 2007), the outcome for the outermost planet is more uncertain as, given its high mass, might provide enough angular momentum at the stellar surface to trigger the partial ejection of the envelope (García-Segura et al. 2014) and/or become partially eroded and a close companion to the star (Bear & Soker 2011, 2012).

The evolution of the stellar radius over the past 100 Myr along the RGB phase is shown in Fig. 7 together with the expected orbital evolution of the planets in the TYC 1422-614-1 system. We have assumed the lowest planet mass for the calculation and show a star that undergoes the Reimers mass-loss prescription with an η = 0.6 (for more details see Villaver & Livio 2009; Villaver et al. 2014).

thumbnail Fig. 7

Solid line: the past 100 Myr in the evolution of the stellar radius as the star evolves to the tip of the RGB. The star is evolving under the Reimers mass-loss prescription with η = 0.6. The evolution of the initial orbits of planets TYC 14221614-1 b and c are shown as dashed lines asuming their Mpsini lowest masses.

If we consider the evolutionary status of the star in terms of the stellar surface gravity, TYC 1422-614-1 with log  g = 2.85 is the second-most evolved multiple planetary system found to date around a giant star (the record holder is BD+20 2457 with its log  g = 1.77). In this regard, BD+20 2457 and TYC 1422-614-1 are very similar and interesting systems: both host a multiple planetary system around a very evolved star (R/R⊙ = 33 and 6.85) with mass close to solar and including a massive planet/BD Mp ≥ 10 MJ.

Assuming its current orbital separation, planet c was within the optimistic habitable zone (HZ) defined by Kopparapu et al. (2013) for about four billion years after the star reached the ZAMS. We have then a solar-mass star with a long MS evolution and a giant planet/BD that stayed in the HZ for a reasonable time.

As a result of the evolution of the location of the HZ as the star leaves the MS, currently neither planet b nor c reside within HZ (see e.g., Lopez et al. 2005; Danchi & Lopez 2013).

TYC 1422-614-1 belongs to the very small sample4 of known multiple planetary systems around giants (i.e., stars with log  g< 3.5). Multiple systems around giants include BD+20 2457 b, c (Niedzielski et al. 2009b), 24 Sex b,c and HD 200694 b, c (Johnson et al. 2011b), HD 4732 b, c (Sato et al. 2013), Kepler 391 b, c (Rowe et al. 2014), and Kepler 56 b, c, d (Huber et al. 2013). They represent ≈16% of all the planets orbiting giant stars (including TYC 1422-614-1). This fraction is slightly smaller, but consistent, with that on the MS considering that about ≈20% planets orbiting MS stars are in multiple systems.

The two companions orbiting TYC 1422-614-1 have semi-major axes of 0.69 and 1.37 AU and minimum masses of 2.5 and 10.0 MJ. The outer companion has a mass that is suspiciously close to the upper mass limit for planets, and as such, its plausible formation mechanism merits a more detailed discussion.

There are only five other multiple systems known that contain a candidate BD-mass companion: HD 168443 b, c – Marcy et al. (2001), HD 38529 b, c – Fischer et al. (2003), HD 202206 b, c – Correia et al. (2005), HAT-P-13 b, c – Bakos et al. (2009), and BD+20 2457 b, c (Niedzielski et al. 2009b). All of them, with the exception of BD+20 2457 and HD 202206, have the more massive component in the outermost orbit. Apparently, such systems exist very rarely around solar-mass stars of various metallicity and evolutionary stage, but it is important to note that two out of the six known systems revolve around giants. Furthermore, the system of TYC 1422-614-1 presents almost circular orbits, while in other systems of this group, huge eccentricities of up to 0.662 (HAT-P-13 c) are common.

The detection of an object with a minimum mass close to the BD limit in a relatively close orbit to a solar-mass star may offer additional clues to the as yet unknown most likely formation mechanism of BD and its relation with stellar and planetary formation. The BD desert (Marcy & Butler 2000; Grether & Lineweaver 2006), the observed paucity of BD companions to solar-mass stars within 3 AU, has been put forward as possible evidence of a differentiation in the formation mechanism according to object mass.

In TYC 1422-614-1, as in four out of the six systems of the class, the planet with the lower mass is in an innermost orbit. Because the outer planet is clearly more massive, it is unlikely that the inner planet scattered the outer planet to its current orbit. Furthermore, if we assume that the outer planet in these systems formed in the stellar protoplanetary disk, it is reasonable to assume that the inner planet also formed there. In fact, theoretically, “planets” with masses >10 MJ can in principle be formed by core-accretion in protoplanetary disks (Mordasini et al. 2009). However, it is interesting to note that the metallicity distribution of BD companions seems to be inconsistent with the predictions of the core-accretion formation mechanism (Ma & Ge 2014) and that TYC 1422-614-1 has indeed subsolar metallicity.

On the other hand, we can consider that the largest planet or BD in these systems is formed by the alternative mecanism: disk fragmentation (see e.g., Stamatellos & Whitworth 2009). Most of the BD formed by this mechanism are expected to be either ejected from the system or stay bound to the central star at relatively wide orbits. Thus, a closely bound system such as TYC 1422-614-1 is a very unlikely outcome of this process. Furthermore, the formation and location of the innermost planet raises even more questions on the possibility of disk fragmentation than the formation mechanism for the massive companion.

Two other multiple systems with a massive planet or BD orbiting close to the star, HD 202206 (Correia et al. 2005) and BD+20 2457 (Niedzielski et al. 2009b), have architectures in which the innermost companion is the more massive one, suggesting that if it formed as a BD by disk instability, the second outermost planet might have formed in the circumbinary disk composed of the main star and the BD (see e.g., Correia et al. 2005).

Altogether, the rare class of objects to which TYC 1422-614-1 belongs might provide important clues for the planet or BD formation mechanism and places constraints on the lowest mass clump that the disk fragmentation mechanism allows or the highest mass that core-accretion is capable of. While disk fragmentation seems to be the most likely mechanism for BD formation in general, the presence of an innermost planet and the close orbit of the massive companion raises some important questions on the viability of this mechanism for the formation of systems like TYC 1422-614-1. The core-accretion model, given the low metallicity of the star, could be problematic as well unless a much more massive disk than usual is assumed to increase the efficiency of the process.

6. Conclusions

Our combined set of observations of TYC 1422-614-1 obtained with HET and HRS and TNG and HARPS-N show high precision RV variations that can be attributed with a high level of confidence to Doppler shifts. Our analysis of the data combined with photometric time-series from ASAS led us to propose the discovery of two low-mass components orbiting that K2 giant. We found an additional weak long-term component in the post-fit RV residue IHα and ASAS photometry, which we argue is most likely due to stellar activity or yet another companion. A stellar rotation period of 473 days was determined from ASAS photometry, which agrees with the results of spectroscopic determination.

The planetary system orbiting TYC 1422-614-1 is one of a very special kind because the star is a solar-mass giant with multiple planets (only five other such systems are known), the star is in an advanced evolutionary stage up the RGB, and it is hosting a planet with a minimum mass close to the BD limit in a 1.37 AU orbit. The existence of such a massive planet so close to the star can offer important constraints to the planet or BD formation mechanism and limits because the star has subsolar abundances and another relative massive planet is orbiting the star in an innermost location. Furthermore, although the HZ is expected to have moved outward as the star left the MS, it is also interesting to note that TYC 1422-614-1 b could have remained in the HZ for about four billion years. Finally, following orbital evolution, both planets are expected to reach the stellar surface long before the star has completed its ascent up the RGB as a result of orbital decay caused by tidal interaction.

Online material

Table 2

HET and HRS RV and BS measurements of TYC 1422-614-1.

Table 3

TNG and HARPS-N RV and BS measurements of TYC 1422-614-1.

3

IRAF is distributed by the National Optical Astronomy Observatories, which are operated by the Association of Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.

Acknowledgments

We thank the HET and TNG resident astronomers and telescope operators for support. A.N., Mo.A., K.K., G.N., B.D., and Mi.A. were supported in part by the Polish Ministry of Science and Higher Education grant N N203 510938 and by the Polish National Science Centre grant UMO-2012/07/B/ST9/04415. MoA was also supported by the Polish National Science Centre grant no. UMO-2012/05/N/ST9/03836. E.V. work was supported by the Spanish Ministerio de Ciencia e Innovacion (MICINN), Plan Nacional de Astronomia y Astrofisica, under grant AYA2010-20630 and by the Marie Curie grant FP7-People-RG268111. A.W. was supported by the NASA grant NNX09AB36G. G.M. acknowledges the financial support from the Polish Ministry of Science and Higher Education through the Iuventus Plus grant IP2011 031971. D.A.G.H. acknowledges support for this work provided by the Spanish Ministry of Economy and Competitiveness under grant AYA-2011-29060. The HET is a joint project of the University of Texas at Austin, the Pennsylvania State University, Stanford University, Ludwig-Maximilians-Universität München, and Georg-August-Universität Göttingen. The HET is named in honor of its principal benefactors, William P. Hobby and Robert E. Eberly. The Center for Exoplanets and Habitable Worlds is supported by the Pennsylvania State University, the Eberly College of Science, and the Pennsylvania Space Grant Consortium. This research has made use of the SIMBAD database, operated at CDS (Strasbourg, France) and NASA’s Astrophysics Data System Bibliographic Services. This research has made use of the Exoplanet Orbit Database and the Exoplanet Data Explorer at http://exoplanets.org.

References

  1. Adamów, M., Niedzielski, A., Villaver, E., Nowak, G., & Wolszczan, A. 2012, ApJ, 754, L15 [NASA ADS] [CrossRef] [Google Scholar]
  2. Adamów, M., Niedzielski, A., Villaver, E., Wolszczan, A., & Nowak, G. 2014, A&A, 569, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bakos, G. Á., Howard, A. W., Noyes, R. W., et al. 2009, ApJ, 707, 446 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baranne, A., Mayor, M., & Poncet, J. L. 1979, Vistas Astron., 23, 279 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bear, E., & Soker, N. 2011, MNRAS, 411, 1792 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bear, E., & Soker, N. 2012, ApJ, 749, L14 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bertelli, G., Girardi, L., Marigo, P., & Nasi, E. 2008, A&A, 484, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
  10. Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
  11. Butler, R. P., Marcy, G. W., Fischer, D. A., et al. 1999, ApJ, 526, 916 [NASA ADS] [CrossRef] [Google Scholar]
  12. Butler, R. P., Tinney, C. G., Marcy, G. W., et al. 2001, ApJ, 555, 410 [NASA ADS] [CrossRef] [Google Scholar]
  13. Campbell, B., Walker, G. A. H., & Yang, S. 1988, ApJ, 331, 902 [NASA ADS] [CrossRef] [Google Scholar]
  14. Carlberg, J. K., Majewski, S. R., Patterson, R. J., et al. 2011, ApJ, 732, 39 [Google Scholar]
  15. Charbonneau, P. 1995, ApJS, 101, 309 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cincunegui, C., Díaz, R. F., & Mauas, P. J. D. 2007, A&A, 469, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Cochran, W. D., & Hatzes, A. P. 1993, in Planets Around Pulsars, eds. J. A. Phillips, S. E. Thorsett, & S. R. Kulkarni, ASP Conf. Ser., 36, 267 [Google Scholar]
  18. Cochran, W. D., Endl, M., McArthur, B., et al. 2004, ApJ, 611, L133 [NASA ADS] [CrossRef] [Google Scholar]
  19. Copernicus, N. 1543, D revolutionibus orbium coelestium (Norimbergae, Apud J. Detrim 1543, Bruxelles: Culture et civilisation, 1966) [Google Scholar]
  20. Correia, A. C. M., Udry, S., Mayor, M., et al. 2005, A&A, 440, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in SPIE Conf. Ser., 8446 [Google Scholar]
  22. Covino, E., Esposito, M., Barbieri, M., et al. 2013, A&A, 554, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Cox, J. P., King, D. S., & Stellingwerf, R. F. 1972, ApJ, 171, 93 [NASA ADS] [CrossRef] [Google Scholar]
  24. da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Danchi, W. C., & Lopez, B. 2013, ApJ, 769, 27 [NASA ADS] [CrossRef] [Google Scholar]
  26. De Ridder, J., Barban, C., Baudin, F., et al. 2009, Nature, 459, 398 [Google Scholar]
  27. Debes, J. H., & Sigurdsson, S. 2002, ApJ, 572, 556 [NASA ADS] [CrossRef] [Google Scholar]
  28. Desidera, S., Sozzetti, A., Bonomo, A. S., et al. 2013, A&A, 554, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. do Nascimento, Jr., J. D., Canto Martins, B. L., Melo, C. H. F., Porto de Mello, G., & De Medeiros, J. R. 2003, A&A, 405, 723 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Duncan, D. K., Vaughan, A. H., Wilson, O. C., et al. 1991, ApJS, 76, 383 [NASA ADS] [CrossRef] [Google Scholar]
  31. Eberhard, G., & Schwarzschild, K. 1913, ApJ, 38, 292 [NASA ADS] [CrossRef] [Google Scholar]
  32. Endl, M., Cochran, W. D., Hatzes, A. P., & Wittenmyer, R. A. 2011, in AIP Conf. Ser., eds. S. Schuh, H. Drechsel, & U. Heber, 1331, 88 [Google Scholar]
  33. Farihi, J., Hoard, D. W., & Wachter, S. 2010, ApJS, 190, 275 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fekel, F. C. 1997, PASP, 109, 514 [NASA ADS] [CrossRef] [Google Scholar]
  35. Fellgett, P. 1955, Optica Acta, 2, 9 [Google Scholar]
  36. Fischer, D. A., Marcy, G. W., Butler, R. P., et al. 2003, ApJ, 586, 1394 [NASA ADS] [CrossRef] [Google Scholar]
  37. Fischer, D. A., Marcy, G. W., Butler, R. P., et al. 2008, ApJ, 675, 790 [NASA ADS] [CrossRef] [Google Scholar]
  38. Ford, E. B., & Gregory, P. C. 2007, in Astronomical Society of the Pacific Conference Series, Vol. 371, Statistical Challenges in Modern Astronomy IV, ed. G. J. Babu & E. D. Feigelson, 189 [Google Scholar]
  39. Frink, S., Mitchell, D. S., Quirrenbach, A., et al. 2002, ApJ, 576, 478 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  40. García-Segura, G., Villaver, E., Langer, N., Yoon, S.-C., & Manchado, A. 2014, ApJ, 783, 74 [NASA ADS] [CrossRef] [Google Scholar]
  41. Gettel, S., Wolszczan, A., Niedzielski, A., et al. 2012a, ApJ, 756, 53 [Google Scholar]
  42. Gettel, S., Wolszczan, A., Niedzielski, A., et al. 2012b, ApJ, 745, 28 [NASA ADS] [CrossRef] [Google Scholar]
  43. Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2012, A&A, 541, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Goździewski, K., & Migaszewski, C. 2006, A&A, 449, 1219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Goździewski, K., Konacki, M., & Maciejewski, A. J. 2003, ApJ, 594, 1019 [NASA ADS] [CrossRef] [Google Scholar]
  46. Goździewski, K., Maciejewski, A. J., & Migaszewski, C. 2007, ApJ, 657, 546 [NASA ADS] [CrossRef] [Google Scholar]
  47. Grether, D., & Lineweaver, C. H. 2006, ApJ, 640, 1051 [NASA ADS] [CrossRef] [Google Scholar]
  48. Griffin, R. F. 1967, ApJ, 148, 465 [NASA ADS] [CrossRef] [Google Scholar]
  49. Hatzes, A. P. 2002, Astron. Nachr., 323, 392 [NASA ADS] [CrossRef] [Google Scholar]
  50. Hatzes, A. P., & Cochran, W. D. 1993, ApJ, 413, 339 [NASA ADS] [CrossRef] [Google Scholar]
  51. Hatzes, A. P., Cochran, W. D., Endl, M., et al. 2003, ApJ, 599, 1383 [NASA ADS] [CrossRef] [Google Scholar]
  52. Hatzes, A. P., Guenther, E. W., Endl, M., et al. 2005, A&A, 437, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Hatzes, A. P., Cochran, W. D., Endl, M., et al. 2006, A&A, 457, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Hébrard, G., Almenara, J.-M., Santerne, A., et al. 2013, A&A, 554, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, A&A, 355, L27 [NASA ADS] [Google Scholar]
  56. Huber, D., Carter, J. A., Barbieri, M., et al. 2013, Science, 342, 331 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  57. Isaacson, H., & Fischer, D. 2010, ApJ, 725, 875 [NASA ADS] [CrossRef] [Google Scholar]
  58. Johnson, J. A., Fischer, D. A., Marcy, G. W., et al. 2007, ApJ, 665, 785 [NASA ADS] [CrossRef] [Google Scholar]
  59. Johnson, J. A., Clanton, C., Howard, A. W., et al. 2011a, ApJS, 197, 26 [NASA ADS] [CrossRef] [Google Scholar]
  60. Johnson, J. A., Payne, M., Howard, A. W., et al. 2011b, AJ, 141, 16 [NASA ADS] [CrossRef] [Google Scholar]
  61. Jørgensen, B. R., & Lindegren, L. 2005, A&A, 436, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. Kallinger, T., Mosser, B., Hekker, S., et al. 2010, A&A, 522, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
  64. Kopparapu, R. K., Ramirez, R., Kasting, J. F., et al. 2013, ApJ, 765, 131 [NASA ADS] [CrossRef] [Google Scholar]
  65. Kuerster, M., Schmitt, J. H. M. M., Cutispoto, G., & Dennerl, K. 1997, A&A, 320, 831 [NASA ADS] [Google Scholar]
  66. Lee, B.-C., Mkrtichian, D. E., Han, I., Kim, K.-M., & Park, M.-G. 2011, A&A, 529, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Lissauer, J. J., Fabrycky, D. C., Ford, E. B., et al. 2011, Nature, 470, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  68. Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
  69. Lopez, B., Schneider, J., & Danchi, W. C. 2005, ApJ, 627, 974 [NASA ADS] [CrossRef] [Google Scholar]
  70. Lovis, C., & Mayor, M. 2007, A&A, 472, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Lovis, C., Ségransan, D., Mayor, M., et al. 2011, A&A, 528, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Ma, B., & Ge, J. 2014, MNRAS, 439, 2781 [NASA ADS] [CrossRef] [Google Scholar]
  73. Maciejewski, G., Niedzielski, A., Wolszczan, A., et al. 2013, AJ, 146, 147 [NASA ADS] [CrossRef] [Google Scholar]
  74. Marcy, G. W., & Butler, R. P. 1992, PASP, 104, 270 [NASA ADS] [CrossRef] [Google Scholar]
  75. Marcy, G. W., & Butler, R. P. 1996, ApJ, 464, L147 [NASA ADS] [CrossRef] [Google Scholar]
  76. Marcy, G. W., & Butler, R. P. 2000, PASP, 112, 137 [NASA ADS] [CrossRef] [Google Scholar]
  77. Marcy, G. W., Butler, R. P., Vogt, S. S., et al. 2001, ApJ, 555, 418 [NASA ADS] [CrossRef] [Google Scholar]
  78. Marcy, G. W., Butler, R. P., Vogt, S. S., et al. 2005, ApJ, 619, 570 [NASA ADS] [CrossRef] [Google Scholar]
  79. Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
  80. Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
  81. Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
  82. Meschiari, S., Wolf, A. S., Rivera, E., et al. 2009, PASP, 121, 1016 [NASA ADS] [CrossRef] [Google Scholar]
  83. Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Mortier, A., Santos, N. C., Sousa, S. G., et al. 2013, A&A, 557, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Mosser, B., Dziembowski, W. A., Belkacem, K., et al. 2013, A&A, 559, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Murdoch, K. A., Hearnshaw, J. B., & Clark, M. 1993, ApJ, 413, 349 [NASA ADS] [CrossRef] [Google Scholar]
  87. Mustill, A. J., Veras, D., & Villaver, E. 2014, MNRAS, 437, 1404 [NASA ADS] [CrossRef] [Google Scholar]
  88. Niedzielski, A., & Wolszczan, A. 2008a, in IAU Symp., eds. Y.-S. Sun, S. Ferraz-Mello, & J.-L. Zhou, 249, 43 [Google Scholar]
  89. Niedzielski, A., & Wolszczan, A. 2008b, in Extreme Solar Systems, eds. D. Fischer, F. A. Rasio, S. E. Thorsett, & A. Wolszczan, ASP Conf. Ser., 398, 71 [Google Scholar]
  90. Niedzielski, A., Konacki, M., Wolszczan, A., et al. 2007, ApJ, 669, 1354 [NASA ADS] [CrossRef] [Google Scholar]
  91. Niedzielski, A., Goździewski, K., Wolszczan, A., et al. 2009a, ApJ, 693, 276 [NASA ADS] [CrossRef] [Google Scholar]
  92. Niedzielski, A., Nowak, G., Adamów, M., & Wolszczan, A. 2009b, ApJ, 707, 768 [NASA ADS] [CrossRef] [Google Scholar]
  93. Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Nowak, G. 2012, Ph.D. Thesis, Nicolaus Copernicus Univ., Toruń, Poland [Google Scholar]
  95. Nowak, G., Niedzielski, A., Wolszczan, A., Adamów, M., & Maciejewski, G. 2013, ApJ, 770, 53 [Google Scholar]
  96. Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
  97. Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Pepe, F., Cameron, A. C., Latham, D. W., et al. 2013, Nature, 503, 377 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  99. Perryman, M. A. C., & ESA 1997, The Hipparcos and Tycho catalogues. Astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
  100. Pojmanski, G. 1997, Acta Astron., 47, 467 [NASA ADS] [Google Scholar]
  101. Pojmanski, G. 2002, Acta Astron., 52, 397 [NASA ADS] [Google Scholar]
  102. Queloz, D. 1995, in New Developments in Array Technology and Applications, eds. A. G. D. Philip, K. Janes, & A. R. Upgren, IAU Symp., 167, 221 [Google Scholar]
  103. Ramsey, L. W., Adams, M. T., Barnes, T. G., et al. 1998, in SPIE Conf. Ser. 3352, ed. L. M. Stepp, 34 [Google Scholar]
  104. Reffert, S., & Quirrenbach, A. 2011, A&A, 527, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Reffert, S., Quirrenbach, A., Mitchell, D. S., et al. 2006, ApJ, 652, 661 [NASA ADS] [CrossRef] [Google Scholar]
  106. Robertson, P., Endl, M., Cochran, W. D., & Dodson-Robinson, S. E. 2013, ApJ, 764, 3 [NASA ADS] [CrossRef] [Google Scholar]
  107. Rowe, J. F., Bryson, S. T., Marcy, G. W., et al. 2014, ApJ, 784, 45 [NASA ADS] [CrossRef] [Google Scholar]
  108. Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
  109. Sato, B., Ando, H., Kambe, E., et al. 2003, ApJ, 597, L157 [NASA ADS] [CrossRef] [Google Scholar]
  110. Sato, B., Omiya, M., Harakawa, H., et al. 2012, PASJ, 64, 135 [NASA ADS] [CrossRef] [Google Scholar]
  111. Sato, B., Omiya, M., Wittenmyer, R. A., et al. 2013, ApJ, 762, 9 [NASA ADS] [CrossRef] [Google Scholar]
  112. Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
  113. Setiawan, J., Hatzes, A. P., von der Lühe, O., et al. 2003a, A&A, 398, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  114. Setiawan, J., Pasquini, L., da Silva, L., von der Lühe, O., & Hatzes, A. 2003b, A&A, 397, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  115. Shetrone, M., Cornell, M. E., Fowler, J. R., et al. 2007, PASP, 119, 556 [NASA ADS] [CrossRef] [Google Scholar]
  116. Stamatellos, D., & Whitworth, A. P. 2009, MNRAS, 392, 413 [Google Scholar]
  117. Stumpff, P. 1980, A&AS, 41, 1 [NASA ADS] [Google Scholar]
  118. Tull, R. G. 1998, in SPIE Conf. Ser. 3355, ed. S. D’Odorico, 387 [Google Scholar]
  119. Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  120. Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  121. Veras, D., & Mustill, A. J. 2013, MNRAS, 434, L11 [NASA ADS] [CrossRef] [Google Scholar]
  122. Villaver, E., & Livio, M. 2007, ApJ, 661, 1192 [NASA ADS] [CrossRef] [Google Scholar]
  123. Villaver, E., & Livio, M. 2009, ApJ, 705, L81 [NASA ADS] [CrossRef] [Google Scholar]
  124. Villaver, E., Livio, M., Mustill, A. J., & Siess, L. 2014, ApJ, 794, 3 [NASA ADS] [CrossRef] [Google Scholar]
  125. Vogt, S. S., Penrod, G. D., & Hatzes, A. P. 1987, ApJ, 321, 496 [NASA ADS] [CrossRef] [Google Scholar]
  126. Vogt, S. S., Marcy, G. W., Butler, R. P., & Apps, K. 2000, ApJ, 536, 902 [NASA ADS] [CrossRef] [Google Scholar]
  127. Walker, G. A. H., Yang, S., Campbell, B., & Irwin, A. W. 1989, ApJ, 343, L21 [NASA ADS] [CrossRef] [Google Scholar]
  128. Walker, G. A. H., Bohlender, D. A., Walker, A. R., et al. 1992, ApJ, 396, L91 [NASA ADS] [CrossRef] [Google Scholar]
  129. Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
  130. Wood, P. R., Alcock, C., Allsman, R. A., et al. 1999, in Asymptotic Giant Branch Stars, eds. T. Le Bertre, A. Lebre, & C. Waelkens, IAU Symp., 191, 151 [Google Scholar]
  131. Wright, J. T., & Howard, A. W. 2009, ApJS, 182, 205 [NASA ADS] [CrossRef] [Google Scholar]
  132. Wright, J. T., Marcy, G. W., Fischer, D. A., et al. 2007, ApJ, 657, 533 [NASA ADS] [CrossRef] [Google Scholar]
  133. Zieliński, P., Niedzielski, A., Wolszczan, A., Adamów, M., & Nowak, G. 2012, A&A, 547, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1

Summary of the available data on TYC 1422-614-1.

In the text
Table 4

Keplerian orbital parameters of TYC 1422-614-1 b and c.

In the text
Table 5

Dynamical orbital parameters of TYC 1422-614-1 b and c.

In the text
Table 2

HET and HRS RV and BS measurements of TYC 1422-614-1.

In the text
Table 3

TNG and HARPS-N RV and BS measurements of TYC 1422-614-1.

In the text

All Figures

thumbnail Fig. 1

From top to bottom: lomb-Scarge periodograms for the a) original HET RV data of TYC 1422-614-1; b) RV residua (HET and TNG) without planet c; and c) RV residua (HET and TNG) after the best Keplerian two-planetary fit. See also Fig. 5.
In the text
thumbnail Fig. 2

Keplerian best fit of the two-planetary model to the observed RV of TYC 1422-614-1. HET and HRS data are presented in red and TNG and HARPS-N data in green. The estimated jitter due to p-mode oscillations has been added to the uncertainties.

In the text
thumbnail Fig. 3

Illustration of the bootstrapping analysis (105 realizations) of the Keplerian parameters of TYC 1422-614-1 c uncertainties, a 2D histogram of orbital period and eccentricity. Both 1D histograms are plotted with the 15.87 and 83.13 percentile (i.e., 1σ) ranges shown.

In the text
thumbnail Fig. 4

Evolution of planetary eccentricities in the first thousand years, calculated for the orbital solution given in Table 5.
In the text
thumbnail Fig. 5

From top to bottom: Lomb-Scargle periodograms of a) IHα activity index; b) IFe index; c) ASAS photometry; and d) HET and HRS BS. See also Fig. 1.
In the text
thumbnail Fig. 6

Hertzsprung-Russel diagram for the complete PTPS sample with TYC 1422-614-1 position indicated and 1.1 M⊙, z = 0.008 stellar evolutionary track from Bertelli et al. (2008) and, in green, the path of the star with planet c within the optimistic HZ of Kopparapu et al. (2013). The orange and red rectangles indicate the phase of planet b and c ingestion.
In the text
thumbnail Fig. 7

Solid line: the past 100 Myr in the evolution of the stellar radius as the star evolves to the tip of the RGB. The star is evolving under the Reimers mass-loss prescription with η = 0.6. The evolution of the initial orbits of planets TYC 14221614-1 b and c are shown as dashed lines asuming their Mpsini lowest masses.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.