| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424276 | |
| Published online | 10 December 2014 | |
Absorption of crystalline water ice in the far infrared at different temperatures
Astrophysikalisches Institut und Universitätssternwarte, Friedrich-Schiller-Universität Jena, Schillergäßchen 2–3, 07745 Jena, Germany
e-mail: caroline.reinert@uni-jena.de
Received: 26 May 2014
Accepted: 16 September 2014
The optical properties of ice in the far infrared are important for models of protoplanetary and debris disks. In this report, we derive a new set of data for the absorption (represented by the imaginary part of the refractive index κ) of crystalline water ice in this spectral range. The study includes a detailed inspection of the temperature dependence, which has not been conducted in such detail before. We measured the transmission of three ice layers with different thicknesses at temperatures ϑ = 10...250 K and present data at wavelengths λ = 80...625 μm. We found a change in the spectral dependence of κ at a wavelength of 175 ± 6 μm. At shorter wavelengths, κ exhibits a constant flat slope and no significant temperature dependence. Long-ward of that wavelength, the slope gets steeper and has a clear, approximately linear temperature dependence. This change in behaviour is probably caused by a characteristic absorption band of water ice. The measured data were fitted by a power-law model that analytically describes the absorption behaviour at an arbitrary temperature. This model can readily be applied to any object of interest, for instance a protoplanetary or debris disk. To illustrate how the model works, we simulated the spectral energy distribution (SED) of the resolved, large debris disk around the nearby solar-type star HD 207129. Replacing our ice model by another, commonly used data set for water ice results in a different SED slope at longer wavelengths. This leads to changes in the characteristic model parameters of the disk, such as the inferred particle size distribution, and affects the interpretation of the underlying collisional physics of the disk.
Key words: methods: laboratory: solid state / techniques: spectroscopic / circumstellar matter / stars: individual: HD 207129
© ESO, 2014
1. Introduction
Water in its different forms is ubiquitous in star- and planet-forming regions (van Dishoeck et al. 2014, and references therein) as well as in actual planetary systems like the solar system (Encrenaz 2008). Water vapour was observed in 24% of gas-rich disks around T Tauri stars (Riviere-Marichalar et al. 2012) and in protoplanetary disks such as TW Hydrae (Hogerheijde et al. 2011). Water ice can be observed in all these disks (e.g. Waters et al. 1996). On the other hand, liquid water is only assumed to exist in certain objects within the solar system (e.g. Tobie et al. 2008; Kalousová et al. 2014), but is generally hard to detect remotely. Especially when a disk gets older, i.e. it transforms into a debris disk, we expect only solid state forms to survive the sublimation and dissociation caused by stellar radiation.
There are two basic types of water ice: crystalline and amorphous. Which of the two ice types occurs depends on the temperature at which it has formed. Ice formed at temperatures below 110 K acquires a totally amorphous structure, while at higher temperatures it becomes crystalline (Smith et al. 1994; Moore & Hudson 1992). If amorphous ice is warmed above 110 K, it will also become crystalline. But the transformation occurs not at this single temperature, but over a range up to 130 K (e.g. Schmitt et al. 1989). Crystallization is an irreversible process, which leads to the suggestion that water ice in a crystalline form dominates even in cold regions of protolanetary systems. Because of radial mixing, the crystalline water ice, which has possibly formed in the warmer regions of the disk near the star, could have been spread over the whole disk. A similar scenario is used to explain the existence of crystalline silicates in colder regions of protoplanetary disks (e.g. van Boekel et al. 2004). On any account, crystalline water ice was found in several protoplanetary disks around young stars (e.g. Terada & Tokunaga 2012; McClure et al. 2012).
As successors of the described protoplanetary disks, debris disks must contain crystalline water ice as well because the dust in them is produced by collisions between small bodies, which have initially formed in the protoplanetary stage of the system. Some crystalline minerals have already been found, notably crystalline silicates in the environment of β Pictoris (e.g. de Vries et al. 2012). Yet no clear observational evidence for water ice in debris disks has been found so far. However, including crystalline water ice into the assumed composition for debris dust has been shown to improve models of debris disks in many cases, resulting in a better fit to the observations (e.g. Chen et al. 2008; Reidemeister et al. 2011; Lebreton et al. 2012; Donaldson et al. 2013).
Therefore, the optical properties of ice are important for understanding of the physics of planetary and protoplanetary systems. The far-infrared spectral range (λ> 50 μm) is especially interesting since the thermal radiation emitted by such cold objects peaks at these wavelengths. There have been many experimental campaigns to measure optical data (for absorption in particular) of water ice in the infrared. Most of these campaigns cover the near-infrared range (e.g. Grenfell & Perovich 1981; Kou et al. 1993) and the region of the strong absorption bands of water ice around 44 and 63 μm (Moore & Hudson 1992; Smith et al. 1994; Johnson & Atreya 1996; Schmitt et al. 1998). The shapes of the features at 44 and 63 μm has been found to differ for amorphous and crystalline ice. In the latter, two sharp peaks at both positions are clearly seen, whereas in amorphous ice there is one smaller and broader peak at around 44 μm with only a shoulder at the longer wavelength end. While the feature region is well explored, there were only a few investigations of wavelengths beyond them (λ ≥ 100 μm).
In this paper, we measure the absorption of crystalline water ice at 45 μm <λ< 1000 μm for six different temperatures between 10 K and 250 K. We approximate the behaviour by power-law models and take particular care of the temperature dependence of the absorption index κ and a previously noted water ice feature at about 166 μm generated by intermolecular bending modes (Wozniak & Dera 2007), because this feature is not yet discussed in the astronomical literature.
Section 2 gives a short overview of the previous measurements on ice in the far infrared. The measurement techniques and the treatment of the data are described in Sect. 3. The results are presented in Sect. 4. In Sect. 5, we compare our results to previous data sets and discuss possible future measurements. To illustrate how our results can be applied to specific objects, in Sect. 6 we use them to simulate the debris disk of HD 207129. Section 7 lists our conclusions.
2. Previous work
Investigations on the absorption of water ice for wavelengths beyond 100 μm are rare and differ substantially in quality. Some of these data sets comprise very few data points (see Irvine & Pollack 1968; Bertie et al. 1969), some spread over more than an order of a magnitude (see Hudgins et al. 1993), and some only give relative values (see Bertie & Whalley 1967). Accordingly, for further inspection we only selected three data sets free of these shortcomings:
-
Curtis et al. (2005) condensedwater vapour on a cooled substrate to produce an ice layer. Theymeasured at the temperature at which the ice had formed. Thesetemperatures ranged from 106 K to 176 K where between the measurements at 126 K and 136 K the ice transforms from amorphous to crystalline state. Additionally, they adjusted the layer thickness to the wavelength region of the measurement. For the far-infrared region the thickest layers were used to obtain an appropriate absorption signal. Altogether, their data cover the range from 15 μm to 192 μm.
-
Whalley & Labbé (1969) froze distilled water in their experiments and measured in a wavelength region of λ = 235...455 μm. This technique always resulted in polycrystalline water ice, independent from the temperature.
-
Mishima et al. (1983) performed their measurements with monocrystalline ice cubes at wavelengths from 400 μm to 1.25 mm. The technique used to produce monocrystalline ice is not described in their study.
These three data sets are visualized in Fig. 1 for temperatures near 100 K and crystalline ice only. The figure plots the imaginary part κ of the refractive index N = n + iκ depending on the wavelength. We have chosen κ because it is a material parameter independent of the geometry of the sample.
 |
Fig. 1 Data for the imaginary part κ of the refractive index N = n + iκ. Shown are data from Curtis et al. (2005), Mishima et al. (1983) and Whalley & Labbé (1969) for crystalline water ice near 100 K. |
Most of these data are for crystalline ice. Only Hudgins et al. (1993) and Curtis et al. (2005) measured both ice types beyond the feature area. The Curtis et al. data reveal no significant difference between the two ice types, except for the features (Fig. 2). The data of Hudgins et al. show a huge scatter for λ> 100 μm, but also no particular difference between the amorphous and crystalline ice type. In this case, there is not even a difference in the feature region to be seen. This might lead to the suggestion that Hudgins et al. measured amorphous ice only, despite the temperature of 140 K. For λ> 200 μm, no measurements of both ice types have been performed. As a result, a comprehensive comparison of amorphous and crystalline ice is hard to make.
 |
Fig. 2 Imaginary part κ of the refractive index N for different temperatures and ice types from Curtis et al. (2005) and Hudgins et al. (1993). |
To overcome the problems of the measurements and to alleviate applications of the laboratory data to astronomical objects, there have been some attempts to create an artificial model to describe the optical properties of ice.
Warren (1984) combined multiple data sets for crystalline water ice into one, ranging from the ultraviolet to the radio wave region (44.3 nm to 8.6 m). To obtain a data set for a temperature of ϑ = 213 K(− 60 °C) he used the difference in absorption between the 100 K and 200 K measurements from the data of Mishima et al. (1983) and Whalley & Labbé (1969) to extrapolate linearly to 213 K. He also used the extrapolation to fill the gap at λ ≈ 170...235 μm where no data were available.
Except for the treatment of the temperature dependence in Warren (1984), only Irvine & Pollack (1968) discussed the change in the absorption. However, their study only covers the λ ≤ 100 μm range.
A revised version of the data from Warren (1984) was published by Warren & Brandt (2008), who included more recent data, for example from Curtis et al. (2005). They used three measurements of Curtis et al. (2005) at the highest temperatures (156 K, 166 K and 176 K) and extrapolated their temperature dependence linearly to 266 K. Unfortunately, the new data set offers no improvement at wavelengths λ> 100 μm, because of the lack of data in this region (see Fig. 6 in their publication).
Li & Greenberg (1998) used a simpler way to create a new data set for amorphous water ice. They took the 10 K measurement from Hudgins et al. (1993) for amorphous water ice up to λ = 100 μm and extrapolated them with the aid of a simple power law (κ ∝ λ-0.5) up to λ = 10 mm. Although their model disagrees with some other measurements (e.g. Whalley & Labbé 1969; Mishima et al. 1983), it remains the most commonly used data set for models of diverse astronomical objects, especially debris disks (e.g. Su et al. 2005; Löhne et al. 2012).
All three models for ice in a range of λ = 50...1000 μm are shown in Fig. 3.
 |
Fig. 3 Data for the imaginary part κ of the refractive index N. Shown are the models from Warren (1984), Li & Greenberg (1998), and Warren & Brandt (2008). |
3. Methods
3.1. Experimental methods
3.1.1. Sample production
The best controlable way to produce a layer of water ice is to deposit water vapour on a cooled substrate (e.g. Smith et al. 1994; Moore & Hudson 1992; Hudgins et al. 1993; Curtis et al. 2005). In the far infrared, where κ drops to ~10-3 at ~500 μm (see Fig. 1), the absorption coefficient δ = 4πκλ-1 is as small as 0.025 mm-1. Therefore, we need relatively thick ice layers to measure significant absorption. In this case, the depositing method is hard to use because it requires a very long deposition time.
Thicker ice layers can be obtained by freezing a certain amount of distilled water (Whalley & Labbé 1969) or by producing a big single crystal of water ice (Mishima et al. 1983). Either way, this always results in ice of crystalline type.
Our experiments are similar to those of Whalley & Labbé (1969). The samples were produced by putting double distilled water between two windows of polyethylene (see Fig. 4) in a continuous flow helium cryostat (CryoVac KONTI Spektro B) and freezing it by cooling the cryostat down to 250 K. One of the windows had an extra rim of height d0. In this way, we obtained an ice layer of hexagonal (Ih) polycrystalline water ice with an approximate, nominal thickness d0 for our measurements.
The windows were made from polyethylene powder that was pressed with a specially manufactured die at a pressure of 10 t cm-2. Afterwards the powder was fused at a temperature of 140 °C. The resulting windows had a thickness of D1,2 = 0.91...1.78 mm at room temperature.
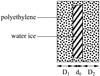 |
Fig. 4 Construction of the sample (details in the text). |
3.1.2. Measurements
All the measurements were taken in a Fourier transformation infrared spectrometer (BRUKER 113v) with the cryostat inserted into the sample chamber. We measured directly in the cryostat through four polyethylene windows in the walls of the cryostat. The inner board of the cryostat was cooled by liquid helium. With a contact gas (also helium) the sample was then cooled to 250 K, 200 K, 150 K, 100 K, 50 K, and 10 K. At each temperature we investigated the transmission T by first taking a reference spectrum with an empty sample holder in the cryostat and then measuring the sample itself. By doing this we eliminated the influence of the optical devices on the spectrum of the sample.
We measured in three different wavelength regions and used two different detectors (one of deuterated triglycine sulfate and a LHe-cooled bolometer). The wavelength regions are mostly determined by the thickness of the mylar foil in the beam splitter. We used three different beam splitters with foils of 12 μm, 23 μm, or 125 μm where the thickest was used for the longest wavelengths.
Depending on the wavelength region, we varied d0 from 100 μm to 3 mm. To probe the shorter wavelengths with λ = 45...200 μm, a thin layer of d0 ≈ 100 μm was used (measurement 1, M1). For λ = 100...500 μm, we used a layer of about 500 μm thickness (measurement 2, M2). For the longest wavelengths, λ = 200...1000 μm, we chose d0 ≈ 3000 μm (measurement 3, M3). The reason for this approach is the steepness of the absorption spectrum. Towards shorter wavelengths, the ice gets opaque, for longer wavelengths, the absorption drops below detectable values. How rapidly the drop turns out depends on the temperature ϑ. Therefore, we chose the layer thickness in such a way that for representative wavelengths (100 μm, 200 μm and 350 μm) of the corresponding spectral ranges the absorption does not drop below 20% for all temperatures, but is still thin enough to be not opaque at these wavelengths. The range where reliable measurements are possible shifts to shorter wavelengths with decreasing thickness of the ice layer.
3.2. The background spectrum
As mentioned above, the sample consists not only of an ice layer, but also of two additional polyethylene windows. To isolate data describing only the ice, we needed to divide the measured transmission T by a background spectrum T0 that only derives from the absorption in the polyethylene windows.
When measuring such a background spectrum of the two polyethylene windows separated by a vacuum layer, the result is influenced by interference effects due to multiple reflection in the interlayer. These interferences almost disappear when the vacuum is replaced by ice later on, because the amplitude of the intereferences A is proportional to Δn2, where Δn is the difference between the real parts of the reflective indices of polyethylene, nPE, and the interlayer, nvac/ice. The difference Δn shrinks from Δn ≈ 1.5 with vacuum to Δn ≈ 0.3 with ice in between. Because of these effects we had to remove the interferences in the background itself by taking only the polyethylene windows into account.
To do this, we used the commercial thin-layer optics program SCOUT 21 to fit an oscillator model to the measured background spectrum. The model describes a three-layer system that consists of a polyethylene layer D1, a vacuum layer dvac, and another polyethylene layer D2. The thickness of the vacuum interlayer dvac was considered unknown.
To describe the wavelength-dependent complex refractive index 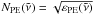 (with
(with 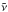 being the wavenumber and ε the dielectric function) of polyethylene in this model we used two Lorentz oscillators, a and b. Oscillator b describes the absorption band of polyethylene near 130 μm. The refractive index is then given by
being the wavenumber and ε the dielectric function) of polyethylene in this model we used two Lorentz oscillators, a and b. Oscillator b describes the absorption band of polyethylene near 130 μm. The refractive index is then given by 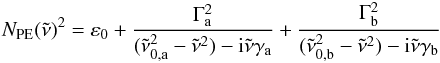 (1)where
(1)where 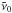 is the resonance position, Γ is the strength, γ is the damping of an oscillator, and ε0 was set to 2.25 (
is the resonance position, Γ is the strength, γ is the damping of an oscillator, and ε0 was set to 2.25 (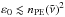 ). For the vacuum layer,
). For the vacuum layer, 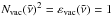 applies.
applies.
Varying the parameters 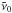 , Γ, and γ for each of the two oscillators as well as the thickness of the vacuum layer dvac, the transmission calculated from the oscillator model was fitted to the measured background spectrum. Figure 5 demonstrates that the model reproduces the data quite well. There is only a slight discrepancy at the shorter wavelengths. It traces back to the divergence of the beam of the spectrometer that limits its coherence at short wavelengths. This effect was not considered in the model.
, Γ, and γ for each of the two oscillators as well as the thickness of the vacuum layer dvac, the transmission calculated from the oscillator model was fitted to the measured background spectrum. Figure 5 demonstrates that the model reproduces the data quite well. There is only a slight discrepancy at the shorter wavelengths. It traces back to the divergence of the beam of the spectrometer that limits its coherence at short wavelengths. This effect was not considered in the model.
 |
Fig. 5 Examples for the transmission T0 of the background measurement and the corresponding oscillator fit. For the background measurement the sample only consisted of the two polyethylene windows with D1 and D2 (here: D1 = 1.68 mm and D2 = 1.65 mm) and a vacuum interlayer of thickness dvac (best-fit here: dvac = 143 μm). |
Once all oscillator parameters for polyethylene and the (best fitting) thickness of the vacuum interlayer are known, the vacuum layer can be removed from of the model. Then, with the found 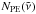 , we were able to calculate a transmission spectrum for two polyethylene windows, even with variable thicknesses D1 and D2. This way we got a modelled background spectrum T0 for each sample configuration and temperature. For exemplary thicknesses D1 and D2, the resulting background spectra T0 for different temperatures ϑ between 10 K and 250 K are shown in Fig. 6.
, we were able to calculate a transmission spectrum for two polyethylene windows, even with variable thicknesses D1 and D2. This way we got a modelled background spectrum T0 for each sample configuration and temperature. For exemplary thicknesses D1 and D2, the resulting background spectra T0 for different temperatures ϑ between 10 K and 250 K are shown in Fig. 6.
 |
Fig. 6 Calculated background spectra T0 for a system of two polyethylene windows with D1 = 1.68 mm and D2 = 1.65 mm at temperatures between 10 K and 250 K. On the right is a close up on the region of the feature and the temperature dependence therein. |
Clearly, the background spectrum is temperature dependent. There is a shift to longer wavelengths and a broadening of the 130 μm feature of polyethylene. Accordingly, the parameters for oscillator b had to be calculated for all temperatures used in the measurements. In contrast, oscillator a, which causes the continuum absorption, showed no significant temperature dependence after all, having a constant γ over the entire temperature range. All calculated parameters for a and b are listed in Table 1. Note that the resonance position 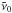 is almost constant, while the actual feature position in the spectra
is almost constant, while the actual feature position in the spectra 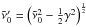 is temperature dependent, since γ = γ(ϑ).
is temperature dependent, since γ = γ(ϑ).
Best-fit oscillator parameters Γ, 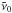 (or
(or 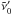 ) and γ for the modelled background spectra at all measuring temperatures.
) and γ for the modelled background spectra at all measuring temperatures.
 |
Fig. 7 Coefficient κ for the measurements M1 to M3 at the temperatures 10 K, 50 K, 100 K, 150 K, 200 K and 250 K for λ ≳ 100 μm. |
3.3. Correction of data
In each of the three wavelength ranges measured, the transmission of the respective ice layer (100 μm, 500 μm, or 3 mm) varied between very low values and almost complete transparency. The strong overlap of the wavelength ranges allowed us to use only those measured values where the absorption was detected with the highest sensitivity and accuracy, i.e. in the range of transmission values between 10% and 90% of the maximum value. The wavelength ranges resulting from this constraint are listed in Table 2.
The comparison with M1 and M3 showed that M2 suffered from a relatively strong additional intensity loss caused by scattering effects and deflection of the beam. This can be caused by inhomogeneities of the ice layer or impurities in the ice itself. Since for the thinner ice layers the layer thickness is also more uncertain, we decided to normalize M1 and M2 to the values of M3. The latter showed almost no additional losses and the layer thickness should be accurate to about 10%. The only correction done for M3 was to include the reflection losses at the two polyethylene-ice boundaries of the sample, which were not considered in the model of the background spectra by raising the transmission by about 1.8%.
Intensity loss, on the one hand, and the uncertainty in the thickness, on the other hand, suggest using two normalization factors. First, the transmission is corrected by a factor fcorr giving a higher transmission Tcorr,j = (Tj/T0,j) × fcorr, with Tj = T(λj) being the original measured data points and T0,j = T0(λj) the background transmission at the same wavelengths λj. Second, we varied the nominal thickness d0 to a corrected value of dcorr. We determined the values for the correction by minimizing the difference of the measured transmissions in the overlapping wavelength regions first of M3 and M2, and second of the corrected version of M2 and the original M1. The correction factors were determined for each temperature and then averaged to get a single set for all temperatures.
As a result, the nominal thickness d0 = 100 μm for M1 turned out to require a stronger correction to dcorr = 202 ± 33 μm, whereas the measured transmission of M1, in principle, needed no correction. For M2 the opposite was found: the nominal thickness d0 = 500 μm was accurate to 10%, whereas the transmission had to be corrected by a factor of fcorr = 1.6 ± 0.1.
3.4. Describing the absorption
To describe the absorption, we chose the imaginary part κ (many other terms are used in the literature) of the complex refractive index N. As explained before, this is most appropriate, because κ is a constant of the material itself and therefore independent of the geometry of the sample.
To gain κ(λj) from the transmission measurements at each wavelength λj, we applied the equation 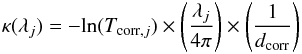 (2)to all points of the transmission measurement Tj.
(2)to all points of the transmission measurement Tj.
4. Results
In Fig. 7 the resulting data are displayed for the three measurements M1 to M3 at all six temperatures from 10 K to 250 K. The measurement M1 yields a smooth curve with only a bit of noise at the longer wavelength end of its domain. In some cases some artefacts appear that are caused by incomplete reduction of the 130 μm feature of polyethylene in the background spectrum. The data from M2 are much noisier, especially at higher temperatures and at longer wavelengths, whereas those from M3 are very smooth again, with only slight interference effects (fringe pattern) at wavelengths beyond 500 μm. Besides, a low beam intensity around 447 μm caused by the optical properties of the beam splitter (125 μm polyethylene foil) forced us to leave out the wavelengths from 416.7 μm to 476.2 μm in M3.
4.1. Temperature dependence
The behaviour of κ obviously changes at around λ = 200 μm. Short-ward of that wavelength, the slope stays nearly constant. At longer wavelengths, κ decreases with increasing λ, and there is a clear temperature dependence of the slope. To quantify these visual impressions, we fitted the data with power laws of the form 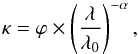 (3)where ϕ and α are constant for all temperatures in each of the three measurements M1 to M3. The parameter of interest is α because it basically describes the slope of κ. The constant λ0 is used for normalization and was set to 200 μm as a typical wavelength.
(3)where ϕ and α are constant for all temperatures in each of the three measurements M1 to M3. The parameter of interest is α because it basically describes the slope of κ. The constant λ0 is used for normalization and was set to 200 μm as a typical wavelength.
We fitted the power law at the three measurements 1 to 3, which lead us to the fits κ(M1) to κ(M3). The fitting was done in the central 50% of the ranges listed in Table 2. The resulting α depending on the temperature is plotted in Fig. 8.
Used wavelength ranges for the measurements M1 to M3.
 |
Fig. 8 Slopes α of κ(M1) to κ(M3) depending on the temperature ϑ. The lines indicate the linear interpolation. |
The slope of κ(M1) is flat, α1 = 0.1...0.5, over the entire temperature range, whereas that of κ(M2) and κ(M3) is much steeper. For κ(M2), α is decreasing with temperature from α2 ≃ 5 (ϑ = 10 K) to α2 ≃ 2.5 (ϑ = 250 K). An even stronger temperature dependence occurs for κ(M3), with α ranging from more than 4 at 10 K to about only 0.5 at 250 K. A linear fitting with αi(ϑ) = mi × ϑ + ni (i = 1,2,3) results in 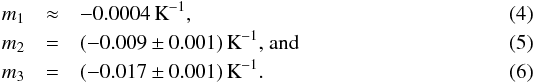 To determine more accurately the wavelength where the behaviour of the slope is changing, we searched for the intersection of the three power law fits at each temperature ϑ (see Fig. 9).
To determine more accurately the wavelength where the behaviour of the slope is changing, we searched for the intersection of the three power law fits at each temperature ϑ (see Fig. 9).
 |
Fig. 9 Wavelength of intersection between κ(M1) and κ(M2), and κ(M2) and κ(M3) at different temperatures ϑ. The lines indicate the linear interpolation. |
The intersection point between κ(M1) and κ(M2) is nearly independent of temperature, λintersec.1 - 2 = (175 ± 2) μm. In contrast, the intersection between κ(M2) and κ(M3) depends on temperature linearly: 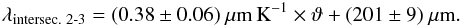 (7)Such a behaviour can be explained by a spectral feature that is broadening with temperature, and therefore the slope α is decreasing with temperature in the region of the long wavelength wing of the feature. In fact, Wozniak & Dera (2007) reported an absorption band at around 166 μm caused by an intermolecular bending mode that can be associated with the intersection value of κ(M1) and κ(M2).
(7)Such a behaviour can be explained by a spectral feature that is broadening with temperature, and therefore the slope α is decreasing with temperature in the region of the long wavelength wing of the feature. In fact, Wozniak & Dera (2007) reported an absorption band at around 166 μm caused by an intermolecular bending mode that can be associated with the intersection value of κ(M1) and κ(M2).
4.2. Analytic model
Having determined the temperature dependence, we now create a simple analytic model that can be applied to the actual temperature of any object of interest. For this purpose, we assume three power laws 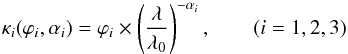 (8)to account for the three distinct regions with different behaviour of the absorption. Region 1 starts at λ = 94 μm right after the strong absorption features of water ice at around 44 μm and 63 μm. The other two regions are separated by the intersection wavelengths λintersec.1 - 2 and λintersec.2 - 3 found above. The longest wavelength λmax covered by the model is the maximum wavelength probed in measurement 3 (see Table 2). It increases linearly with temperature:
(8)to account for the three distinct regions with different behaviour of the absorption. Region 1 starts at λ = 94 μm right after the strong absorption features of water ice at around 44 μm and 63 μm. The other two regions are separated by the intersection wavelengths λintersec.1 - 2 and λintersec.2 - 3 found above. The longest wavelength λmax covered by the model is the maximum wavelength probed in measurement 3 (see Table 2). It increases linearly with temperature: 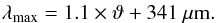 (9)The slopes αi are those from the linear fits αi(ϑ) described above (Eqs. (4) to (6)):
(9)The slopes αi are those from the linear fits αi(ϑ) described above (Eqs. (4) to (6)): 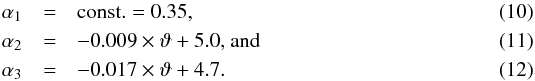 The factors ϕi were determined by finding the best possible fitting at the region boundaries. The result was a nearly constant value for ϕ1 and a linear dependence for ϕ2 and ϕ3:
The factors ϕi were determined by finding the best possible fitting at the region boundaries. The result was a nearly constant value for ϕ1 and a linear dependence for ϕ2 and ϕ3: 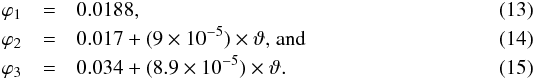 Note that the value for ϕ1 is somehow artificial and due to the fitting at the region boundaries. There is no clear temperature dependence like this seen in the measurements. However, the resulting model from Eqs. (8)–(15) is visualised in Fig. 10 for three exemplary temperatures.
Note that the value for ϕ1 is somehow artificial and due to the fitting at the region boundaries. There is no clear temperature dependence like this seen in the measurements. However, the resulting model from Eqs. (8)–(15) is visualised in Fig. 10 for three exemplary temperatures.
 |
Fig. 10 Analytic model for κ calculated for the temperatures 10 K, 150 K, and 250 K (formulas are given in the text). |
Further, to make the model usable, we had to extend the data set to λ< 94 μm and λ>λmax. We did this by applying the λ = 15...94 μm measurements from Curtis et al. (2005) for crystalline ice at a temperature of 136 K. At λ< 15 μm we used data from Li & Greenberg (1998). Finally, at λmax<λ< 10 mm the absorption was computed by an extrapolation of κ3(ϕ3,α3).
For most applications, the real part n of the complex refractive index N is also needed. The Kramers-Kronig relation links n and κ, which means that a similarity in κ of two data sets implies a similarity in n of the two. But contrary to κ, n does not spread over a wide range in the far infrared in the data sets discussed above. In case of crystalline water ice n always stays in a narrow range of n = 1.75...1.85 with no strong temperature dependence, for λ ≥ 100 μm (see Fig. 11). Amorphous ice has a slightly reduced refractive index (see data of Li & Greenberg or Curtis at 106 K). Minor temperature related variations seem to be linked to the change of the 44 and 63 μm features in the absorption. Therefore, we just used temperature independent data of Warren (1984) for n in our model in the wavelength range λ> 94 μm. This compilation used, amongst others, the data of Mishima et al. (1983) and Whalley & Labbé (1969), which have good agreement with our data in terms of κ (see Sect. 5.1). At shorter wavelengths (λ< 94 μm) we used data from Curtis et al. (2005) and Li & Greenberg (1998) for n in the same wavelength ranges as for κ.
 |
Fig. 11 Real part n of the complex refractive index N for different data sets. |
5. Discussion
5.1. Comparison with literature
We compared both our measured data and our model with literature data for the two temperatures 100 K and 200 K. We chose the data sets of Curtis et al. (2005), Mishima et al. (1983), and Whalley & Labbé (1969) for this comparison and generally found good agreement with our data (see Fig. 12), with a few exceptions reviewed below. Also, our model reproduces our measured data with good accuracy.
There is a slight disagreement between our measurements and those by Curtis et al. (2005) at 106 K, which could be caused by the fact that their data at this temperature are for amorphous ice, since amorphous ice seems to have a higher absorption in the region right after the strong feature (see Fig. 2). In addition, a small peak in their 176 K measurement at about 100 μm is not seen in our data. Note, however, that this peak was not found in any other measurement from the literature either. At 100 K, the data of Mishima et al. (1983) suggest a slightly higher absorption compared to our results. This may possibly be caused by extrapolating κ3(ϕ3,α3) to λ>λmax, where it is not supported by measurements.
 |
Fig. 12 Comparison of literature data for κ and our measurements at temperatures of 100 K (top) and 200 K (bottom). Literature for 100 K: Curtis et al. (2005) at 106 K, Whalley & Labbé (1969) at 100 K, Mishima et al. (1983) at 100 K. For 200 K: Curtis et al. (2005) at 176 K, Whalley & Labbé (1969) at 200 K, Mishima et al. (1983) at 200 K. All literature data are for crystalline ice, except for the 106 K-measurement of Curtis et al. (2005), which is for amorphous ice. |
The feature that we found at 175 ± 6 μm can also be seen in the compilation data of Warren (1984) with the caveat that the underlying data have a gap surrounding this wavelength. Yet, Warren (1984) noticed that the data sets at different temperatures converge at a wavelength of around 166 μm. Although he offered no explanation, why this is happening, he based his interpolation in this wavelength range on this fact. As a result, he obtained a slight bend in the absorption index κ (see Fig. 13). Later, Wozniak & Dera (2007) associated this bend with an absorption band of crystalline water ice. They argued that the feature is caused by intermolecular bending modes. In the revised publication of Warren’s data (Warren & Brandt 2008), the feature is not seen at all because of the scarcity of data points in this area (see Fig. 13).
 |
Fig. 13 Coefficient κ in the region around the 175 μm feature in the data sets of Warren (1984) and Warren & Brandt (2008) compared to our model at the same temperatures. |
5.2. Outlook
What still remains largely unexplored are the possible fine differences in optical properties of different types of ice. Although Fig. 2 suggests that most of the differences between amorphous and crystalline ice are in the regions of spectral features, this is only valid at λ ≤ 200 μm. We do not know the behaviour of amorphous ice at longer wavelengths. For silicates, there is an immense rise in the absorption for the amorphous structure at long wavelengths (Fabian et al. 2000). This is because of the disorder of the solid that allows for absorption by vibration modes that cannot be excited in an ordered crystal. The same effect could possibly occur for water ice. To verify this, it would be straightforward to carry out measurements similar to those described here, but with amorphous ice. However, we cannot produce amorphous ice by freezing distilled water. We would have to use the depositing method, which is not easy, as sufficiently thick layers are required for reliable measurements.
Besides possible differences between amorphous and crystalline ice there might be differences in the crystalline ice itself, since two possible types (hexagonal ice Ih and cubic ice Ic) exist in astronomical environments. Also, the knowledge about differences in polycrystalline and monocrystalline ice needs significant improvement. Future measurements should address these uncertainties as well.
6. Application on the debris disk HD 207129
Of many possible applications of our model, we have selected here one specific object to illustrate how our model works and which kind of implications replacing one model of ice with another might have.
The object in question is the debris disk around the G2V star HD 207129 at a distance of 15.6 pc (Rhee et al. 2007). The disk has been observed by many instruments at wavelengths from mid-infrared through submillimetre wavelengths, resulting in a densely sampled spectral energy distribution (SED) and resolved images at several wavelengths. Accordingly, detailed models of the disks have been developed. For more information about the object, the observational data, and models that describe the disk, see Marshall et al. (2011); Löhne et al. (2012) and references therein.
It is not our intention to create a more accurate model of the debris disk than was done previously. We merely aim to show the principal impact of the ice data on the disk’s SED. Therefore, we chose a very simple model consisting of one dust ring and one material component. The disk was described by a power law model of the form 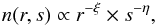 (16)which gives the number density n(r,s) at each radius r ∈ [rmin,rmax] and particle size s ∈ [smin,smax]. Both ξ and η were assumed to be constant over the entire disk. The values for all the parameters were taken from the modelling paper of Löhne et al. (2012):
(16)which gives the number density n(r,s) at each radius r ∈ [rmin,rmax] and particle size s ∈ [smin,smax]. Both ξ and η were assumed to be constant over the entire disk. The values for all the parameters were taken from the modelling paper of Löhne et al. (2012): 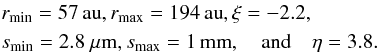 These values were found for a dust composition with 50% water ice (data from Li & Greenberg 1998) and 50% astro-silicate (data from Draine 2003). In our simulations of the SED2, we assumed a dust composition with different fractions of ice ranging from 40% to 80% with the optical data given by our own model (at a temperature of 55 K). For comparison, we did the same with the data given by Li & Greenberg (1998). Similar to Löhne et al. (2012), we mixed the optical constants of ice and astronomical silicate (Draine 2003) by means of the Bruggeman (1935) mixing rule. The absorption index κ for the two (pure) ices and two exemplary mixtures is shown in Fig. 14. One can see a clear dominance of the astronomical silicate on the optical properties of the ice-silicate mixture, because the difference of a mixture with 40% and 80% ice is relatively small compared with 80% ice to 100% ice. Note that the optical properties of the astronomical silicate are also uncertain because the material was first introduced to describe the observations in the interstellar medium (ISM; Draine & Lee 1984). Since the ISM is a completely different environment than the neighbourhood of a star, the optical properties of the silicate dust might be different here.
These values were found for a dust composition with 50% water ice (data from Li & Greenberg 1998) and 50% astro-silicate (data from Draine 2003). In our simulations of the SED2, we assumed a dust composition with different fractions of ice ranging from 40% to 80% with the optical data given by our own model (at a temperature of 55 K). For comparison, we did the same with the data given by Li & Greenberg (1998). Similar to Löhne et al. (2012), we mixed the optical constants of ice and astronomical silicate (Draine 2003) by means of the Bruggeman (1935) mixing rule. The absorption index κ for the two (pure) ices and two exemplary mixtures is shown in Fig. 14. One can see a clear dominance of the astronomical silicate on the optical properties of the ice-silicate mixture, because the difference of a mixture with 40% and 80% ice is relatively small compared with 80% ice to 100% ice. Note that the optical properties of the astronomical silicate are also uncertain because the material was first introduced to describe the observations in the interstellar medium (ISM; Draine & Lee 1984). Since the ISM is a completely different environment than the neighbourhood of a star, the optical properties of the silicate dust might be different here.
 |
Fig. 14 Coefficient κ in our model (at ϑ = 55 K) and in the data of Li & Greenberg (1998) for pure ice (top), a mixture of 80% ice and 20% astronomical silicate (middle), and 60% ice and 40% astronomical silicate (bottom). |
Strictly speaking, we are not allowed to use the parameters from Löhne et al. (2012) for ice fractions other than 50%. In principle, we would need to vary all of the parameters simultaneously, trying to find the best fit (with a least χ2-test) to the observational data (given in Table 3) for each of the mixtures and each of the ice models. However, for illustrative purposes we decided to use a simpler approach and varied only one parameter, η, being aware that a change of η implies a change in other disk parameters, too.
Photometry data of HD 207129 for λ> 20 μm.
For the photosphere of the star we used a model from the Phoenix NextGen grid of Hauschildt et al. (1999) that corresponds to the temperature, metallicity, and surface gravity of the star. According to Rhee et al. (2007), the disk has a black-body temperature of 55 K, which we used as ϑ in our ice model.
The resulting SEDs of the simulations for three amounts of ice are shown in Fig. 15. The best-fit η values for five ice-silicate mixtures and each of the two ice data sets are listed in Table 4.
 |
Fig. 15 Modelled SED of the debris disk around HD 207129. From left to right: with 40%, 60%, and 80% of water ice in the dust material (the rest is astronomical silicate from Draine 2003). Compared are two models for the optical data of water ice: our model (at ϑ = 55 K) and the model of Li & Greenberg (1998). |
In the simulations done with our model η is always smaller, compared to those done with the Li & Greenberg model, to counteract the steeper slope of κ at longer wavelengths in our data set. The difference of η between the two models grows with the amount of ice in the mixture. That is expected because the higher the amount of ice the stronger the influence of the ice data themselves on the SED. The differences are rather subtle, but not negligible. For moderate ice fractions (<70%), they are less than 0.05 in terms of η, despite the big gap in κ between our model and that from Li & Greenberg (1998) at wavelengths greater than 200 μm. This is due to the dominant influence of the astronomical silicate on the slope of κ (see Fig. 14) and therefore the SED.
Comparison of the observational data with the model SED produced from our optical data reveals a discrepancy at longer wavelengths that increases with the fraction of ice. This discrepancy, which is caused by the 175 μm feature and the resulting break in the absorption and emission efficiency, is also reflected by an increased 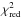 , as seen in Table 4. The SEDs modelled with data of Li & Greenberg (1998) do not exhibit that break.
, as seen in Table 4. The SEDs modelled with data of Li & Greenberg (1998) do not exhibit that break.
The slope η is known to be closely related to the physics in the underlying collisional cascade from which the size distribution results. For example, a well-known relation exists between η in a steady state and the slope of the size-dependent critical specific energy for disruption, b (O’Brien & Greenberg 2003): 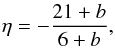 (17)with b = 0... − 0.4 (e.g. Benz & Asphaug 1999; Wada et al. 2013). Assuming that a power-law size distribution is realistic, we can use the new data to rule out ice fractions above 60%. With higher fractions of ice, the index η of the size distribution alone can no longer be used to fit the observational data properly. While a flatter size distribution, corresponding to a lower η, would be needed to compensate the steeper fall-off in the sub-millimetre, it would also reduce the emission at shorter wavelengths, introducing a discrepancy with the IRAS and the PACS 70 μm data.
(17)with b = 0... − 0.4 (e.g. Benz & Asphaug 1999; Wada et al. 2013). Assuming that a power-law size distribution is realistic, we can use the new data to rule out ice fractions above 60%. With higher fractions of ice, the index η of the size distribution alone can no longer be used to fit the observational data properly. While a flatter size distribution, corresponding to a lower η, would be needed to compensate the steeper fall-off in the sub-millimetre, it would also reduce the emission at shorter wavelengths, introducing a discrepancy with the IRAS and the PACS 70 μm data.
A more general fitting approach could still yield good agreement for ice-dominated models. An overall flatter size distribution with an additional peak of micron-sized grains would reproduce both the short- and long-wavelength observations. Such a wavy deviation from a power law might be explained readily by a collisional cascade with a lower cut-off due to radiation pressure blow-out (Thébault et al. 2003; Krivov et al. 2006), potentially shaped further by drag processes (Reidemeister et al. 2011; Wyatt et al. 2011) as well as collisional spreading and damping (Thébault 2009; Pan & Schlichting 2012). In that case, the additional constraints on the chemical composition would instead be transformed to constraints on the collisional physics. Thus, an accurate determination of η, or the shape of the size distribution in general, is important for understanding the material properties and variety of physical processes operating in debris disks.
The best-fit η, the dust mass mdust, and corresponding reduced χ2 for each fraction of water ice.
With the new model, we can also give more accurate values for the modelling parameters, shown here exemplarily for η. Because evidence exists that in some cases up to 90% of water ice is assumed to be realistic (e.g. the Kuiper belt in the solar system, Vitense et al. 2010), this would lead to significant changes in η. Besides, the colder the disk (e.g. cold debris disks in Krivov et al. 2013), the greater the difference, because at longer wavelengths α grows with decreasing temperature (see Fig. 8). Whereas Li & Greenberg (1998) has a constant αLi + Greenberg = 0.5 over the entire wavelength range, our α is markedly higher.
Besides η, we calculated the total dust mass mdust of the disk by fitting the model to the available observations for λ> 20 μm (Table 3). Like η, the inferred mass depends on the ice fraction and the ice data. The mass is always a bit higher for our ice model, ranging from 1.01 × 10-2M⊕ to 1.68 × 10-2M⊕, and the difference to the model with the Li & Greenberg (1998) data increases with the ice fraction.
At this point, however, we refrain from deeper analysis for that object.
7. Conclusions
In this paper, we presented a new data set for the imaginary part of the refractive index κ (describing the absorption) of crystalline water ice. The new data cover a wavelength range of λ = 81...625 μm and a temperature range of ϑ = 10...250 K. With this, our data extend across most of the far-infrared region, including the previous gap in the data from about 200 μm to 235 μm. Additionally, a complete temperature coverage is now achieved for that wavelength range. To check our results, we compared them to the previous measurements at temperatures and wavelengths, at which the latter were available, and found very good agreement with our data.
We find that for λ ≲ 200 μm the slope of κ stays flat and shows no change with temperature. At longer wavelengths, κ falls off with increasing λ. In this wavelength range, the slope of κ sensitively depends on the temperature, getting steeper at lower temperatures. This behaviour persists over the whole temperature range. The temperature dependence of κ starts at a wavelength of 175 ± 6 μm. This can be associated with an absorption feature caused by intermolecular bending modes (Wozniak & Dera 2007) at a wavelength of around 166 μm. This can be noted in the data compilation of Warren (1984), but not in later data sets. We can now confirm these data with a direct measurement.
We approximated the data by a simple power-law based model. The model can be conveniently applied to compute absorption values for water ice at any temperature of interest.
Applying the new model to the debris disk HD 207129 with a temperature of 55 K results in a noticeable difference from a similar model, but with ice data from Li & Greenberg (1998). The derived size distribution of dust becomes flatter, while the dust mass slightly increases. The larger the assumed ice fraction in the dust composition, the greater the differences. A comparison with the observational data also gave a clue about the possible ice content in the disk, which can most probably not be higher than 70% in the case of HD 207129. In general, we argue that replacing the previously used ice data sets with the set presented here may result in appreciable changes of the parameters of many debris and protoplanetary disks inferred from their modelling.
For the simulation we used to the program “SEDUCE” (short for “SED Utility For Circumstellar Environments”) from Müller (2010).
Acknowledgments
We thank the referee, Bernard Schmitt, for constructive remarks, which helped to improve our paper. Also we want to acknowledge Gabriele Born for her help in the laboratory and the Deutsche Forschungsgemeinschaft for funding our work (grants MU1164/8-1and MU1164/7-2).
References
- Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Bertie, J. E., & Whalley, E. 1967, J. Chem. Phys., 46, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Bertie, J. E., Labbé, H. J., & Whalley, E. 1969, J. Chem. Phys., 50, 4501 [NASA ADS] [CrossRef] [Google Scholar]
- Bruggeman, D. A. G. 1935, Ann. Phys., 24, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C. H., Fitzgerald, M. P., & Smith, P. S. 2008, ApJ, 689, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Curtis, D. B., Rajaram, B., Toon, O. B., & Tolbert, M. A. 2005, Appl. Opt., 44, 4102 [NASA ADS] [CrossRef] [Google Scholar]
- de Vries, B. L., Acke, B., Blommaert, J. A. D. L., et al. 2012, Nature, 490, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Donaldson, J. K., Lebreton, J., Roberge, A., Augereau, J.-C., & Krivov, A. V. 2013, ApJ, 772, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ARA&A., 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Encrenaz, T. 2008, ARA&A, 46, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, D., Jäger, C., Henning, T., Dorschner, J., & Mutschke, H. 2000, in ISO Beyond the Peaks: The 2nd ISO Workshop on Analytical Spectroscopy, eds. A. Salama, M. F. Kessler, K. Leech, & B. Schulz, ESA SP, 456, 347 [Google Scholar]
- Grenfell, T. C., & Perovich, D. K. 1981, J. Geophys. Res., 86, 7447 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Hogerheijde, M. R., Bergin, E. A., Brinch, C., et al. 2011, Science, 334, 338 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hudgins, D. M., Sandford, S. A., Allamandola, L. J., & Tielens, A. G. G. M. 1993, ApJS, 86, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Irvine, W. M., & Pollack, J. B. 1968, Icarus, 8, 324 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, B. R., & Atreya, S. K. 1996, Icarus, 119, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Jourdain de Muizon, M., Laureijs, R. J., Dominik, C., et al. 1999, A&A, 350, 875 [NASA ADS] [Google Scholar]
- Kalousová, K., Souček, O., Tobie, G., Choblet, G., & Čadek, O. 2014, J. Geophys. Res., 119, 532 [CrossRef] [Google Scholar]
- Kou, L., Labrie, D., & Chylek, P. 1993, Appl. Opt., 32, 3531 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Krist, J. E., Stapelfeldt, K. R., Bryden, G., et al. 2010, ApJ, 140, 1051 [Google Scholar]
- Krivov, A. V., Löhne, T., & Sremčević, M. 2006, A&A, 455, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivov, A. V., Eiroa, C., Löhne, T., et al. 2013, ApJ, 772, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, J., Augereau, J.-C., Thi, W.-F., et al. 2012, A&A, 539, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, A., & Greenberg, J. M. 1998, A&A, 331, 291 [NASA ADS] [Google Scholar]
- Löhne, T., Augereau, J.-C., Ertel, S., et al. 2012, A&A, 537, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marshall, J. P., Löhne, T., Montesinos, B., et al. 2011, A&A, 529, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClure, M. K., Manoj, P., Calvet, N., et al. 2012, ApJ, 759, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Mishima, O., Klug, D. D., & Whalley, E. 1983, J. Chem. Phys., 78, 6399 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, M. H., & Hudson, R. L. 1992, ApJ, 401, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, S. 2010, Ph.D. Thesis, Friedrich-Schiller-Universität Jena [Google Scholar]
- Nilsson, R., Liseau, R., Brandeker, A., et al. 2010, A&A, 518, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Brien, D. P., & Greenberg, R. 2003, Icarus, 164, 334 [CrossRef] [Google Scholar]
- Pan, M., & Schlichting, H. E. 2012, ApJ, 747, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Reidemeister, M., Krivov, A. V., Stark, C. C., et al. 2011, A&A, 527, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rhee, J. H., Song, I., Zuckerman, B., & McElwain, M. 2007, ApJ, 660, 1556 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Riviere-Marichalar, P., Ménard, F., Thi, W. F., et al. 2012, A&A, 538, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmitt, B., Grim, R., & Greenberg, M. 1989, in Infrared Spectroscopy in Astronomy, ed. E. Böhm-Vitense, ESA SP, 290, 213 [NASA ADS] [Google Scholar]
- Schmitt, B., Quirico, E., Trotta, F., & Grundy, W. M. 1998, Optical properties of ices from UV to infrared, eds. B. Schmitt, C. de Bergh, & M. Festou (Kluwer Academic Publishers), 227, 199 [Google Scholar]
- Smith, R. G., Robinson, G., Hyland, A. R., & Carpenter, G. L. 1994, MNRAS, 271, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Su, K. Y. L., Rieke, G. H., Misselt, K. A., et al. 2005, ApJ, 628, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Tanner, A., Beichman, C., Bryden, G., Lisse, C., & Lawler, S. 2009, ApJ, 704, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Terada, H., & Tokunaga, A. T. 2012, ApJ, 753, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P. 2009, A&A, 505, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., Augereau, J. C., & Beust, H. 2003, A&A, 408, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tobie, G., Cadek, O., & Sotin, C. 2008, Icarus, 196, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Trilling, D. E., Bryden, G., Beichman, C. A., et al. 2008, ApJ, 674, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- van Boekel, R., Min, M., Leinert, C., et al. 2004, Nature, 432, 479 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Dishoeck, E. F., Bergin, E. A., Lis, D. C., & Lunine, J. I. 2014, in Protostars and Planets VI, eds. H. Beuther, R. Klessen, C. Dullemond, & T. Henning (University of Arizona Press), accepted [arXiv:1401.8103] [Google Scholar]
- Vitense, C., Krivov, A. V., & Löhne, T. 2010, A&A, 520, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wada, K., Tanaka, H., Okuzumi, S., et al. 2013, A&A, 559, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Warren, S. G. 1984, Appl. Opt., 23, 1206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Warren, S. G., & Brandt, R. E. 2008, J. Geophys. Res., 113, 14220 [Google Scholar]
- Waters, L. B. F. M., Molster, F. J., de Jong, T., et al. 1996, A&A, 315, L361 [NASA ADS] [Google Scholar]
- Whalley, E., & Labbé, H. J. 1969, J. Chem. Phys., 51, 3120 [NASA ADS] [CrossRef] [Google Scholar]
- Wozniak, B., & Dera, J. 2007, Light Absorption by Water Molecules and Inorganic Substances Dissolved in Sea Water (New York: Springer), 33, 11 [Google Scholar]
- Wyatt, M. C., Clarke, C. J., & Booth, M. 2011, Celest. Mech. Dyn. Astron., 111, 1 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Best-fit oscillator parameters Γ, 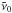 (or
(or 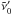 ) and γ for the modelled background spectra at all measuring temperatures.
) and γ for the modelled background spectra at all measuring temperatures.
The best-fit η, the dust mass mdust, and corresponding reduced χ2 for each fraction of water ice.
All Figures
 |
Fig. 1 Data for the imaginary part κ of the refractive index N = n + iκ. Shown are data from Curtis et al. (2005), Mishima et al. (1983) and Whalley & Labbé (1969) for crystalline water ice near 100 K. |
| In the text | |
 |
Fig. 2 Imaginary part κ of the refractive index N for different temperatures and ice types from Curtis et al. (2005) and Hudgins et al. (1993). |
| In the text | |
 |
Fig. 3 Data for the imaginary part κ of the refractive index N. Shown are the models from Warren (1984), Li & Greenberg (1998), and Warren & Brandt (2008). |
| In the text | |
 |
Fig. 4 Construction of the sample (details in the text). |
| In the text | |
 |
Fig. 5 Examples for the transmission T0 of the background measurement and the corresponding oscillator fit. For the background measurement the sample only consisted of the two polyethylene windows with D1 and D2 (here: D1 = 1.68 mm and D2 = 1.65 mm) and a vacuum interlayer of thickness dvac (best-fit here: dvac = 143 μm). |
| In the text | |
 |
Fig. 6 Calculated background spectra T0 for a system of two polyethylene windows with D1 = 1.68 mm and D2 = 1.65 mm at temperatures between 10 K and 250 K. On the right is a close up on the region of the feature and the temperature dependence therein. |
| In the text | |
 |
Fig. 7 Coefficient κ for the measurements M1 to M3 at the temperatures 10 K, 50 K, 100 K, 150 K, 200 K and 250 K for λ ≳ 100 μm. |
| In the text | |
 |
Fig. 8 Slopes α of κ(M1) to κ(M3) depending on the temperature ϑ. The lines indicate the linear interpolation. |
| In the text | |
 |
Fig. 9 Wavelength of intersection between κ(M1) and κ(M2), and κ(M2) and κ(M3) at different temperatures ϑ. The lines indicate the linear interpolation. |
| In the text | |
 |
Fig. 10 Analytic model for κ calculated for the temperatures 10 K, 150 K, and 250 K (formulas are given in the text). |
| In the text | |
 |
Fig. 11 Real part n of the complex refractive index N for different data sets. |
| In the text | |
 |
Fig. 12 Comparison of literature data for κ and our measurements at temperatures of 100 K (top) and 200 K (bottom). Literature for 100 K: Curtis et al. (2005) at 106 K, Whalley & Labbé (1969) at 100 K, Mishima et al. (1983) at 100 K. For 200 K: Curtis et al. (2005) at 176 K, Whalley & Labbé (1969) at 200 K, Mishima et al. (1983) at 200 K. All literature data are for crystalline ice, except for the 106 K-measurement of Curtis et al. (2005), which is for amorphous ice. |
| In the text | |
 |
Fig. 13 Coefficient κ in the region around the 175 μm feature in the data sets of Warren (1984) and Warren & Brandt (2008) compared to our model at the same temperatures. |
| In the text | |
 |
Fig. 14 Coefficient κ in our model (at ϑ = 55 K) and in the data of Li & Greenberg (1998) for pure ice (top), a mixture of 80% ice and 20% astronomical silicate (middle), and 60% ice and 40% astronomical silicate (bottom). |
| In the text | |
 |
Fig. 15 Modelled SED of the debris disk around HD 207129. From left to right: with 40%, 60%, and 80% of water ice in the dust material (the rest is astronomical silicate from Draine 2003). Compared are two models for the optical data of water ice: our model (at ϑ = 55 K) and the model of Li & Greenberg (1998). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


