| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 13 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201424749 | |
| Published online | 05 December 2014 | |
On the consistency of magnetic field measurements of Ap stars: lessons learned from the FORS1 archive
1 Armagh Observatory, College Hill, Armagh BT61 9DG, UK
e-mail: jls@arm.ac.uk; sba@arm.ac.uk
2 Physics & Astronomy Department, The University of Western Ontario, London, Ontario, Canada N6A 3K7
3 Argelander Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: lfossati@astro.uni-bonn.de
Received: 4 August 2014
Accepted: 14 October 2014
Context. The ESO archive of FORS1 spectropolarimetric observations may be used to create a homogeneous database of magnetic field measurements. However, no systematic comparison of FORS field measurements to those obtained with other instruments has been undertaken so far.
Aims. We exploit the FORS archive of circular spectropolarimetric data to examine in a general way how reliable and accurate field detections obtained with FORS are.
Methods. We examine the observations of Ap and Bp stars, on the grounds that almost all of the unambiguous detections of magnetic fields in the FORS1 archive are in these kinds of stars. We assess the overall quality of the FORS1 magnetic data by examining the consistency of field detections with what is known from previous measurements obtained with other instruments, and we look at patterns of internal consistency.
Results. FORS1 magnetic measurements are fully consistent with those made with other instruments, and the internal consistency of the data is excellent. However, it is important to recognise that each choice of grism and wavelength window constitutes a distinct instrumental measuring system, and that simultaneous field measurements in different instrumental systems may produce field strength values that differ up to 20%, or more. Furthermore, we found that field measurements using hydrogen lines only yield results that meaningfully reflect the field strength as sampled specifically by lines of hydrogen for stars with effective temperatures above about 9000 K.
Conclusions. In general the magnetic field measurements of Ap and Bp stars obtained with FORS1 are of excellent quality, accuracy and precision, and FORS1 provides an extremely useful example that offers valuable lessons for field measurements with other low-resolution Cassegrain spectropolarimeters.
Key words: catalogs / stars: magnetic field / polarization / techniques: polarimetric
© ESO, 2014
1. Introduction
During a full decade of operations, between 1999 and 2009, the FORS1 instrument on the ESO Very Large Telescope collected a large number of magnetic field measurements of various kinds of stars. Together with the ESPaDOnS instrument of the Canada-France-Hawaii Telescope (CFHT), and the MuSiCoS and NARVAL instruments of the 2 m Telescope Bernard Lyot of the Pic-du-Midi Observatory, FORS1 has been one of the most important instruments worldwide for observational studies of stellar magnetism.
Using the FORS1 instrument, magnetic fields have been detected in a large number of previously unmeasured peculiar A and B (Ap and Bp) stars (Bagnulo et al. 2006; Kochukhov & Bagnulo 2006; Hubrig et al. 2006), a class of stars long known to harbour fields of typically kG strength. In addition, fields have been securely discovered in a small number of other types of stars such as the early B type β Cep variable HD 46328 = ξ1 CMa (Hubrig et al. 2006), the O6.5f?p star HD 148937 (Hubrig et al. 2008), and several weak-field white dwarfs (Aznar Cuadrado et al. 2004; Landstreet et al. 2012). In contrast, a large number of rather marginal magnetic field discoveries reported in non-Ap stars on the basis of FORS1 measurements have been shown to be spurious (Bagnulo et al. 2012). These are probably due to small instabilities in the instrument, to image motion caused by atmospheric and seeing variations, and to errors in the data reduction (Bagnulo et al. 2012, 2013). This situation makes clear the importance of careful study of instrumental behaviour as an adjunct to scientific measurements.
A first assessment of the capabilities of the instrument for measuring fields in non-degenerate stars was made by Bagnulo et al. (2002). This was followed by development of methods to treat large numbers of measurements in a consistent way (Bagnulo et al. 2006), and a careful study of the general principles on which observing strategies should be based (Bagnulo et al. 2009). Most recently, we have re-reduced the full sample of circular spectropolarimetric data of stars with FORS1 in a uniform way, and used the resulting large database to explore the reproducibility and precision of those FORS field measurements used to claim detection of weak magnetic fields (Bagnulo et al. 2012). Although all of these studies have been focussed on FORS1, they are expected to be generally relevant to field measurements with similar low-resolution Cassegrain spectropolarimeters, and to apply in particular to FORS2, which has inherited the polarimetric optics of FORS1.
However, no similar study has been undertaken of the quality and behaviour of the magnetic field measurements in cases where the detection of the field is not in question. This is the focus of the present paper.
During the period when FORS1 was in use, over 1400 polarimetric spectra were acquired of several hundred stars. Of the stars observed, about 175 are known, at least provisionally, to have been classified as magnetic Ap or Bp stars. More than 300 spectra of such stars were obtained in polarimetric mode with FORS1. Such stars, if correctly identified by classification, are known to possess magnetic fields that can almost always be detected at the level of ⟨ Bz ⟩ ~ 102 G or more (Aurière et al. 2007). ⟨ Bz ⟩, often called the mean longitudinal field, is the mean value of the line-of-sight component of the magnetic field, averaged over the visible stellar hemisphere, and is the signature of a magnetic field to which a low-resolution spectropolarimeter is sensitive.
Thus it should be possible to study the characteristics of field measurements with FORS1 in the strong-field limit (when detection of a field is clear) by studying the internal consistency and systematic behaviour of ⟨ Bz ⟩ measurements of single stars, and by comparing observations of known magnetic Ap stars taken with FORS1 with similar measurements obtained with other spectropolarimeters.
The following questions suggest themselves as ones that should be examined:
-
Are measurements of ⟨Bz⟩ made with FORS consistent with comparable measurements made with other spectropolarimeters?
-
FORS can be used with several different grisms and wavelength regions. To what extent are ⟨Bz⟩ measurements obtained with these different instrumental configurations similar or different?
-
It has become normal to report ⟨Bz⟩ values obtained with FORS from spectral lines of hydrogen and from metal lines separately. To what extent is this division meaningful, and what is the relationship between the two kinds of measurement?
-
The basic approximation made in the deduction of ⟨Bz⟩ values from FORS circular polarisation spectra is the so-called weak-field approximation, which is expected to break down at large fields. Is there evidence of such breakdown, either from comparison of ⟨Bz⟩ values derived separately from lines of hydrogen and of metals, or from comparisons with field measurements with other instruments?
The next section of the paper describes the relevant features of the data and the reductions. The third and fourth sections answer the questions posed above as far as possible, and a final section summarises our conclusions.
2. Instrument settings and data reduction
2.1. Basic data reduction procedure
The first experiments using FORS1 to measure fields in non-degenerate stars (Bagnulo et al. 2002) showed an obvious Zeeman polarisation signal in the Balmer lines of the magnetic Ap star HD 94660, and revealed that the forest of blended metal lines also produces a complex signal in Stokes V/I. The corresponding value of the mean longitudinal field ⟨ Bz ⟩ is obtained by using the weak-field approximation (the approximation that the line splitting is small compared to the width of the line): 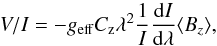 (1)where geff is the effective Landé factor (which is 1.0 for H lines and set to 1.25 for metal lines), Cz = 4.67 × 10-13 Å-1, I(λ) and V(λ) are the Stokes intensity and circular polarisation components from the stellar polarisation spectrum, and λ is wavelength (Landstreet 1982). This equation is applied to each pixel in the V(λ) /I(λ) spectrum, with the required slope dI/ dλ estimated from the two adjacent pixels. The resulting ensemble of values of V/I are plotted as a function of λ2(1 /I)(dI/ dλ), a straight line is fitted, and the mean value of ⟨ Bz ⟩ derived from the slope of the correlation diagram. The uncertainty in ⟨ Bz ⟩ is obtained from the uncertainty of the slope of the correlation (Bagnulo et al. 2012).
(1)where geff is the effective Landé factor (which is 1.0 for H lines and set to 1.25 for metal lines), Cz = 4.67 × 10-13 Å-1, I(λ) and V(λ) are the Stokes intensity and circular polarisation components from the stellar polarisation spectrum, and λ is wavelength (Landstreet 1982). This equation is applied to each pixel in the V(λ) /I(λ) spectrum, with the required slope dI/ dλ estimated from the two adjacent pixels. The resulting ensemble of values of V/I are plotted as a function of λ2(1 /I)(dI/ dλ), a straight line is fitted, and the mean value of ⟨ Bz ⟩ derived from the slope of the correlation diagram. The uncertainty in ⟨ Bz ⟩ is obtained from the uncertainty of the slope of the correlation (Bagnulo et al. 2012).
This process is illustrated in Fig. 1. The strong Zeeman signatures that coincide with the higher Balmer lines are quite obvious in this figure, as is the fact that the V/I spectrum is considerably “noisier” between the Balmer lines (in fact with small Zeeman signatures from individual and blended metal lines) than the expected photon noise, shown as a blue band below the V/I spectrum. The figure also shows for comparison a “null spectrum”, computed by co-adding individual polarisation sub-exposures with signs changed in such a way as to cause the real polarisation signal to cancel out. The null spectrum is a sort of “check spectrum” that is expected to show about as much scatter as arises from photon noise, and indeed this is what is seen (e.g. Bagnulo et al. 2012).
This basic scheme has been used by virtually all observers to obtain ⟨ Bz ⟩ values from FORS1 circular polarisation spectra. A number of large surveys of various classes of stars have been published, several of which have produced numerous marginal (3 to 5σ) detections of magnetic fields (Hubrig et al. 2006, 2009a,b), particularly in classical Be stars and pulsating early-type B stars. Combinations that have been used on FORS1 for magnetic measurements of Ap stars are listed in Table 1.
Grism-wavelength range choices used on FORS1 to study Ap stars.
 |
Fig. 1 Top panel: part of the intensity spectrum of HD 94660, arbitrarily normalised (black); circular polarisation spectrum V(λ) /I(λ) (red); null (verification) spectrum), shifted vertically by −0.5 for clarity (blue); uncertainties of V/I and null spectra, shifted vertically by −0.5 for clarity (light blue band). The green stripes above and below the spectrum show regions included in ⟨ Bz ⟩ measurement in the H lines; pink stripes show regions included in the metal line measurement. Lower left panels: correlation diagrams for determination of field strength from V/I and I using H lines (upper box) and using metal lines (lower box). Lower right panels: the same with the null spectrum. |
2.2. Error estimation
Several of the weak field detection published by FORS users were in conflict with clear non-detections with other instruments such as ESPaDOnS at the CFHT (Shultz et al. 2012). This problem, together with concerns about which of several possible reduction algorithms would produce the most robust results, led us to build a mostly automated reduction system around the ESO FORS pipeline (Izzo et al. 2010). Thanks to this suite of software tools, almost the entire archive of FORS1 magnetic measurements could easily be repeatedly re-reduced to experiment with various algorithms and error estimates. This in turn made it possible to identify the most nearly optimal methods of reducing the FORS1 magnetic measurements and estimating realistic measurement uncertainties.
We found that many surveys had underestimated the measurement uncertainties of FORS1 data, and had not taken into account the occurrence of small instrumental shifts due to flexures, and small apparent radial velocity changes caused by seeing variations during very short exposures (Bagnulo et al. 2012, 2013). In general we found that our error estimates were higher than those published in previous works. We also identified the occurrence of “occasional outliers”, i.e., field measurements which appear significant at the 3 or 4σ level but which are mainly due to small observational velocity shifts rather than real Zeeman polarisation. Such outliers also appear occasionally in the “null fields”, field measurements obtained from the null profiles, although the fields determined from the null spectrum should be always found consistent with zero. The occurrence of outliers led to the recommendation that field discoveries with FORS should only be considered secure if they are above about the 5σ level and are observed at least twice (Bagnulo et al. 2012).
A major consequence of this project was to confirm (or at least not to reject) a small number of marginal field detections from the surveys in various classes of stars other than the magnetic Ap/Bp stars, but to show that the large majority were spurious (Bagnulo et al. 2012).
A catalogue of ⟨ Bz ⟩ values for most of the FORS1 spectropolarimetric observations is being made available by Bagnulo et al. (in prep.).
3. Characteristics of FORS1 ⟨ Bz ⟩ values derived from Ap stars
This paper is devoted to understanding and characterising the behaviour of FORS1 when the objective is to measure a magnetic field whose existence is not in question. Because no observatory test or calibration programmes were carried out specifically to address this issue, we turn to the contents of the newly reduced FORS1 magnetic field measurement archive to find data sets that allow us to study the response of FORS1 to stellar spectra containing clear evidence of Zeeman polarisation. As mentioned above, almost all the stars with large enough fields to be easily detected belong to the class of magnetic Ap and Bp stars. Therefore, from this point on, this paper will almost entirely focus on FORS1 measurements of such stars.
3.1. Measurements with various grism and wavelength combinations
The magnetic Ap and Bp stars are characterised by having fossil fields. These are fields which change in structure only on time scales much longer than 102 yr, and which may therefore be considered to have fixed surface magnetic geometries. The field structures are in general not symmetric about the rotation axis, however, and so as a magnetic Ap or Bp star rotates, the measured magnetic field, particularly the component along the line of sight, varies periodically with the stellar rotation.
Measurement of the value of ⟨ Bz ⟩ and its variation as a function of the rotational phase of the underlying magnetic star generally leads to a simple, usually sinusoidal, variation. The dispersion of the individual data points with respect to the mean curve is determined by the uncertainty of each measurement, and a strong test for the correctness of the uncertainties is that the scatter about the mean curve is consistent with them. Such magnetic curves are quite useful for obtaining a simple, approximate model of the surface magnetic field geometry of the star being observed. However, it is well known that field measurements made with different instruments do not lead to the same magnetic curves, or even the same extreme values of ⟨ Bz ⟩ (e.g. Borra & Landstreet 1977; Bychkov et al. 2005). Sometimes there appears to be a modest scale change, or at times a shift of zero point.
This effect is not really surprising. As discussed e.g. by Landstreet (1982), ⟨ Bz ⟩ is in principle a mean over the visible hemisphere of local line of sight fields (or operationally of their polarisation signatures), weighted by the local surface brightness and line strength. Different elements will have different degrees of darkening and line weakening towards the stellar limb, and this effect will depend on the wavelength region used for observation. Thus the upper Balmer lines will have a different weighting of the contribution of various parts of the visible stellar hemisphere from disk centre to limb than the upper Paschen lines, where the limb darkening is weaker and the lines are shallower. Iron lines in the blue will have different surface weighting than hydrogen, and than iron lines in the red. Each specific choice of spectral lines to include in the polarisation spectrum that is collapsed into a single ⟨ Bz ⟩ measurement will lead to a somewhat different instrumental system in which to measure ⟨ Bz ⟩. Furthermore, many magnetic upper main sequence stars are known to exhibit important variations in local abundances of various chemical elements, both horizontally and vertically. This patchiness varies (often quite strongly) from one element to another. Clearly, the sampling of the magnetic field over the visible hemisphere of the star will depend on the distribution of elements whose lines are used for field measurement. This effect is expected to lead to differences in the deduced value of ⟨ Bz ⟩ when this quantity is derived from spectral lines of different elements, even within a single limited spectral region. This effect has been observed: some Ap stars, such as 53 Cam = HD 65339 and α2 CVn = HD 112413, are known to yield ⟨ Bz ⟩ measures that differ strongly depending on the element chosen for the measurement, as shown by Wade et al. (2000, Figs. 4 and 5).
Comparison of ⟨ Bz ⟩ values obtained with different grisms
The implications of this situation are clear: only by employing a single instrumental observing system (grism, wavelength window, resolving power), and by reducing all observations and deducing the values of ⟨ Bz ⟩ with the same procedures, can we be fairly sure that the magnetic curve(s) of a particular star will be simple and not exhibit “excess” scatter. There is no guarantee that observations of a single star that are obtained in different instrumental systems, or reduced by a variety of methods, can be combined to produce magnetic curves that will show the same degree of coherence, such as smooth (even sinusoidal) variation with rotational phase. This is a very important consideration to keep in mind, because it is easy to use FORS (and most similar instruments) in a variety of instrumental configurations by changing the grism, the central wavelength of observation, and the slit width. The ease with which a variety of instrumental systems can be chosen has encouraged observers to experiment with various settings, for example to see which result in the most precise measurements of ⟨ Bz ⟩ per unit time. It is clear from Table 1 that the available choices may well have rather different weightings over the stellar disk, and may also yield different values of ⟨ Bz ⟩ even for simultaneous measurements.
To explore how different are the resulting ⟨ Bz ⟩ values from these different possible grism settings, we can look in the newly reduced archive of measurements for stars with fairly large fields (1 kG or more, to have good signal-to-noise ratio for the field meaurements) and fields that hardly change between measurements of ⟨ Bz ⟩ with different grisms, either because the field measurements are back-to-back, or because the period of field variation period is very long compared to the interval between measurements.
A list of the useful pairs found is shown in Table 2, which provides the modified Julian date (MJD) of each observation, the grism used, the range in wavelength of the spectrum obtained, the resolving power R, the total shutter time tint, and the ⟨ Bz ⟩ value measured. The field values in the table are obtained using (almost) all lines in the spectral window. In each case, the comparison is with the most commonly used configuration, grism 600 B. For the first four stars, the comparison measurements were made immediately one after the other (“back-to-back”). For the last set, taken with HD 201601 = γ Equ, we use the fact that the rotation period is of order 75 yr to make the approximation that all four measurements refer to almost the same rotational phase.
We see from the comparisons that it is indeed important to check how closely the same ⟨ Bz ⟩ values are obtained from simultaneous measurements with different grisms if more than one instrumental configuration is used. We also see that, in our test cases, configurations with similar wavelength coverage as grism 600 B (grism 1200 B and grism 1200 g) yield very similar ⟨ Bz ⟩ values, but that, compared to grism 600 B, grism 600 R seems to yield field values about 10% larger, while grism 600 I (with only one case) appears to provide a considerably smaller ⟨ Bz ⟩ value than is obtained with grism 600 B.
One other useful test we can make is to compare the final uncertainty in ⟨ Bz ⟩ obtained in a given observing time using grism 600 B and either grism 1200 B or 1200 g. We have two back-to-back comparisons between 600 B and 1200 B, one with HD 94660 and one with HD 201601. In both cases for equal integration time the uncertainty σ⟨ Bz ⟩ with the higher dispersion grism is about 2/3 as large as with the lower dispersion grism, suggesting that in this spectral region there may be a substantial advantage to using the higher dispersion grism. Even though grism 1200 B covers a narrower wavelength window than grism 600 B, the amplitude of the V/I signal is larger, as is the slope dI/ dλ, with the higher dispersion grism, leading to more precisely determined values of ⟨ Bz ⟩.
On the other hand, on the basis of a single comparison using HD 94660, there appears to be no advantage to using grism 1200 g (in the wavelength window 4290–5470 Å) rather than grism 600 B (in its usual wavelength window of 3470–5880 Å). With equal integration times the two grisms produce essentially equal uncertainties. This is probably because the setting used for this observation with grism 1200 g lacks all the higher Balmer lines, which in the usual setting for grism 600 B contribute quite a lot to the total signal, at least for HD 94660.
 |
Fig. 2 Portion of a spectrum in I, V/I, and N of the cool roAp star HD 137949. All symbols are the same as in Fig. 1. In contrast to that figure, notice the absence of any systematic saw-tooth pattern in V/I within the Balmer lines. |
3.2. What is the meaning of “hydrogen” and “metal line” ⟨ Bz ⟩ measurements?
The initial impetus to measure magnetic fields using lines of hydrogen rather than those of common metals arose in part from the development of hydrogen line photopolarimeters which were used in searches for fields both in white dwarfs (Angel & Landstreet 1970) and in Ap stars (Landstreet et al. 1975). It was quickly realised that field measurements made using hydrogen lines have two important advantages. First, because hydrogen is overwhelmingly the dominant element in most stellar atmospheres, a field measurement using H lines is unlikely to be affected by significant non-uniformity of the abundance. That is, hydrogen is the one element that probably samples the field quasi-uniformly (except for limb effects) over the visible hemisphere. Secondly, the Balmer lines are generally so broad that sensitivity to a field is almost independent of vsini, so that surveys can be carried out that do not suffer from very strong selection effects favouring low vsini values.
The first experiments carried out on HD 94660 to explore magnetic field detection in non-degenerate stars with FORS1 showed a clear Zeeman polarisation signature in the Balmer lines, as expected. Initially it was anticipated that the low resolution of FORS1 would make field measurements using the heavily blended metal line spectrum impractical, but experiments revealed useful polarisation signals in the metal line spectrum between the Balmer lines (Bagnulo et al. 2002). Ever since these first measurements, it has been normal to report field estimates (made in the same way) separately for the signal within the H lines, and for the (usually lower-amplitude) signal in the continuum between Balmer lines. These are generally called Balmer line and metal line measurements respectively. Frequently a value of ⟨ Bz ⟩ is also reported using (nearly) the full spectrum, including both Balmer lines and metal lines.
It is sometimes found that the Balmer line and metal line ⟨ Bz ⟩ measurements differ from one another, occasionally by a factor of up to about two, while in many stars the two measurements are rather similar. This situation has not been seriously discussed in the literature, and it brings an air of uncertainty to measurements made with FORS. It is certainly worth trying to understand the origin of this effect.
We start by asking if the division during data reduction into H and metal line measurements always has any meaning. Figure 1 shows an example of the frequently used “standard star” HD 94660, in which a field of only about ⟨ Bz ⟩ ≈ 2100 G produces a strong, obvious saw-tooth Zeeman pattern in the higher Balmer lines. In contrast, the amplitude of the (significant) Zeeman polarisation in between the Balmer lines is considerably lower, but of course can be exploited over a larger wavelength window. In this star the division into H and metal line measurements appears to be quite justified. In contrast, the spectrum of the cool roAp star HD 137949 is shown in Fig. 2. In this spectrum, a field of almost exactly the same strength shows no clear Zeeman pattern associated with Balmer lines at all. Instead, the signal in the V/I spectrum, which is clearly much larger in amplitude than the noise spectrum seen in the NV spectrum, does not seem to be much different within the Balmer lines than outside them. In this star, it does not appear that there is a separately detectable Balmer line signal without some very detailed modelling of the spectrum. In HD 137949 the “Balmer line field” is actually simply the field as measured using the metal lines that happen to be blended with H lines.
With this example in mind, it is worthwhile to try to find simple criteria that enable us to know whether there is a meaningful ⟨ Bz ⟩ measurement that is primarily sensitive to the signal in H lines. In stars with fields of a few kG or more, this can be determined by direct inspection of the spectrum, as in the examples shown here. However, for the far commoner case of a field of order 1 kG or less, the polarisation signature is generally too weak in comparsion to the noise to be classified visually.
We have categorised a few stars with large fields as having strong Balmer line signals or not on the basis of visual inspection. A regularity that quickly emerges from this is that the stars with effective temperatures above about 10 000 K all have strong, obvious Balmer line polarisation signals, while several roAp stars with Teff around 7–8000 K and large fields all lack obvious signal in the H lines. In the available FORS1 data, there are almost no strongly magnetic Aps in the intermediate temperature range, but at a minimum we can conclude that it is probably not specifically meaningful to assign ⟨ Bz ⟩ value based on H lines to any roAp star, and probably not to any Ap star with Teff< 9000 K.
3.3. Is there evidence of “saturation” of the metal line signal for large ⟨ Bz ⟩?
One of the reasons that the division of ⟨ Bz ⟩ measurements into H line measures and metal line measureswas made initially was the concern that, because the determination of the value of ⟨ Bz ⟩ using metal lines was based on the weak field approximation, the signal in metal lines might cease to increase linearly with ⟨ Bz ⟩ at a field strength of only 1 or 2 kG: it might “saturate”. In contrast, the polarisation in the very broad H lines was expected to remain linear with ⟨ Bz ⟩ up to 10 kG or more (Bagnulo et al. 2006). With a substantial sample of magnetic Ap stars available, we can try to detect evidence of such saturation.
One straight-forward method of searching for a breakdown in the linear relationship between ⟨ Bz ⟩ as measured by H lines and ⟨ Bz ⟩ as measured using metallic lines is to make use of the fact that the hot star HD 75049 (with Teff ≈ 10 000 K), which has a very strong Balmer line Zeeman pattern visible in the spectrum, has a field strength that varies from about 1 to 10 kG. We can test whether the metal line ⟨ Bz ⟩ values begin to saturate in this field strength interval by plotting ⟨ Bz ⟩(H) versus ⟨ Bz ⟩(metal) and looking for non-linearity. Note that this test is possible because this star has a high enough Teff to have a clear H line Zeeman signature; it could not be carried out with a star like HD 137949.
 |
Fig. 3 Comparison of ⟨ Bz ⟩ measured using Balmer lines (x-axis) with ⟨ Bz ⟩ measured using metal lines (y-axis) in the strongly variable magnetic Ap star HD 75049. Each point is the field measurement pair from a single FORS1 observation. |
 |
Fig. 4 Comparison of ⟨ Bz ⟩ measured using Balmer lines (x-axis) with ⟨ Bz ⟩ measured using metal lines (y-axis) in the full magnetic star sample, for stars with at least 5σ field detections, with both H and metal σ< 250 G, and spectral types of early A or B. In the upper right corner, the two outliers are HD 66318 with ⟨ Bz ⟩ (metal) > ⟨ Bz ⟩ (H), and HD 318107 with ⟨ Bz ⟩ (metal) < ⟨ Bz ⟩ (H). In the negative field region the two most obvious outliers are NGC 2244–334, well above the mean line at ⟨ Bz ⟩ (H) = −9700 G, and NGC 2169–12 at ⟨ Bz ⟩ (H) = −3500 G. All remaining points with ⟨ Bz ⟩ (H) < − 4000 G are measurements of HD 75049. The line represents equality of the two ⟨ Bz ⟩ values. |
The result of the comparison of ⟨ Bz ⟩(H) vs ⟨ Bz ⟩(metal) is shown in Fig. 3. It is clear from the figure that there is a simple offset between the two kinds of ⟨ Bz ⟩ measurements (a situation found from time to time in field measurements using various other methods) but no non-linearity is apparent. It does not appear that the values of ⟨ Bz ⟩ obtained from metal lines behave non-linearly with respect to the values obtained from H lines up to at least 10 000 G.
Another useful test is to select hot stars from the full FORS1 Ap sample that have clearly non-zero ⟨ Bz ⟩ values in both H lines and metal lines, and compare the values. This result is seen in Fig. 4. At first glance, this figure shows a satisfactory level of agreement even up to | ⟨ Bz ⟩ | ~ 10 000 G, but there is less new information, and more disturbing news, than meets the eye. All the points with ⟨ Bz ⟩ (H) < − 4000 G (except for one strongly deviating point from NGC 2244-334) are from one star, HD 75049, already shown in Fig. 3. A few points lying close to (0, 0) also show substantial difference between the two values of ⟨ Bz ⟩. Similarly, the two stars at the far upper right of the figure deviate from the ⟨ Bz ⟩ (H) = ⟨ Bz ⟩(metal) line by a significant amount. However, overall there is no hint of general departure from a linear relationship between ⟨ Bz ⟩(metal) and the field strength as measured by ⟨ Bz ⟩(H).
⟨ Bz ⟩ measures of ESPaDOnS spectra of stars with large ⟨ Bz ⟩(H) – ⟨ Bz ⟩(metal) differences.
Thus, our conclusion is that, within the limits of the available data, there is no indication that the weak-field approximation used in determining field strengths from FORS1 data saturates or becomes non-linear, at least for field strength ≲10 kG.
3.4. Stars in which H line and metal line ⟨ Bz ⟩ values are strongly discordant
Although most of the measurements of ⟨ Bz ⟩(H) and ⟨ Bz ⟩(metal) agree reasonably well (Fig. 4), a few hot stars show quite large differences between these two kinds of measurement. These unusual stars have differences of a factor of 1.5 or even 2 between the two values. Prominent examples of such discrepancies are found in the FORS1 measurements of HD 66318, HD 318107, NGC 2244-334, and NGC 2169-12. It is clear that these differences may well be due to strongly non-uniform distributions of some of the important elements, which then sample the field strength differently over the surface than hydrogen does.
We are able to test this hypothesis a little further because of the availability of high-resolution polarisation spectra of three of these discrepant stars taken with the ESPaDOnS spectropolarimeter on the CFHT. The ESPaDOnS spectra have resolving power R = 65 000, and cover almost the entire wavelength window between 3800 Å and 1.04 μm, and so it is possible to measure the magnetic field using essentially only lines of one element at a time (this is problematic for the FORS1 spectra because nearly all metal lines are blended).
For some of the relevant ESPaDOnS spectra, field strengths of useful precision can be derived from indiviual lines using by measuring the separation of the line centroids in right and left circular polarisation, or by the equivalent method of evaluating the following expression across an isolated spectral line: ![\begin{equation} \bz = 2.14 \times 10^{12} \frac{\int v V(v){\rm d}v}{\lambda g c \int[I_{\rm c} -I(v)] {\rm d}v}, \end{equation}](/articles/aa/full_html/2014/12/aa24749-14/aa24749-14-eq102.png) (2)where v is a velocity coordinate across the line, c is the speed of light in the same velocity units, λ is the unperturbed wavelength of the line in Å units, g is the Landé factor of the line, and I(v) and V(v) are respectively the Stokes intensity and circular polarisation components (Mathys 1989; Donati et al. 1997). Note that this method of evaluating ⟨ Bz ⟩ assumes that the spectral lines are weak, but (unlike Eq. (1)) it makes no assumption about the size of the Zeeman splitting relative to the line widths, so it does not saturate in the presence of large fields.
(2)where v is a velocity coordinate across the line, c is the speed of light in the same velocity units, λ is the unperturbed wavelength of the line in Å units, g is the Landé factor of the line, and I(v) and V(v) are respectively the Stokes intensity and circular polarisation components (Mathys 1989; Donati et al. 1997). Note that this method of evaluating ⟨ Bz ⟩ assumes that the spectral lines are weak, but (unlike Eq. (1)) it makes no assumption about the size of the Zeeman splitting relative to the line widths, so it does not saturate in the presence of large fields.
However, for most of the ESPaDOnS spectra, the signal-to-noise ratio in V is much too small for measurements precise enough to clearly reveal differences in fields as sampled by the spectral lines of different elements. For this reason, values of ⟨ Bz ⟩ are derived for ESPaDOnS polarised spectra by using the least-squares deconvolution method (LSD; Donati et al. 1997). The idea is to create averaged spectral line and polarisation profiles, using the strong similarity of different profiles (except for amplitude) when these are plotted in velocity (v) space (I(v) and V(v)). The contribution of each line is weighted by the line strength, the wavelength and the Landé factor, so that lines strongly sensitive to Zeeman splitting are given most weight. This results in a single equivalent spectral line intensity and polarisation profile which has much higher signal-to-noise ratio than real single lines. The LSD line is assigned an equivalent mean wavelength and Zeeman splitting factors, and it is analysed as if it were a real single line, using Eq. (2).
In the available ESPaDOnS spectra of stars from this discrepant sample (NGC 2169-12, NGC 2244-334, and HD 318107), we are usually able to measure ⟨ Bz ⟩ with useful accuracy using LSD average spectral lines of the elements Si, Ti, Cr, and Fe. The results of this experiment are shown in Table 3. (Note that we cannot directly compare these field measurements to those obtained with FORS1, as the ESPaDOnS spectra are in general from different rotational phases than the available FORS1 spectra.) It is quite clear from this table that in the stars showing a strong difference between ⟨ Bz ⟩(H) and ⟨ Bz ⟩(metals) in the FORS data, there are also large and clearly significant differences between the values of ⟨ Bz ⟩ measured with lines of several individual elements. This certainly is consistent with the idea that the discrepancy in the FORS measurements is due to non-uniform distributions of various elements.
It is also interesting to carry out such an experiment for a star for which the FORS ⟨ Bz ⟩ values measured with H lines and with metal lines are in good agreement. HD 49299 (Teff = 9700 K, log g = 4.3) is such a star, with one measurement in which ⟨ Bz ⟩ (H) = −2773 ± 64 G while ⟨ Bz ⟩ (metal) = −2589 ± 104 G, and is a star for which an ESPaDOnS spectrum is available. The results of measuring ⟨ Bz ⟩ with lines of various elements are also shown in Table 3, where it is seen that even in this star the value of ⟨ Bz ⟩ measured using lines of Si is strongly different from the values obtained using lines of iron peak elements! It appears that patchy distributions of various elements are probably very common in magnetic Ap stars, and that accurate agreement between ⟨ Bz ⟩(H) and ⟨ Bz ⟩(metal) usually depends on the structure of the patches rather than on their absence.
4. Comparisons of measurements of fields of well-studied magnetic Ap stars
The FORS1 archive includes some field measurements of Ap stars that have been observed with other instruments, or that have been observed often enough that internal consistency tests can be carried out.
It is well known that the absolute values of measurements of the same stars obtained with different instruments display noticeable discrepancies. Examples of this effect may be found in Mathys (1991, see particularly Figs. 14, 17 and 38), and in Wade et al. (2000, particularly Figs. 3, 4, 5, 9 and 10), where the extremely high precision of the MuSiCoS observations make the various discrepancies quite clear.
As discussed in Sect. 2.2, such disagreements are due to several causes. The basic problem is that the way that the circular polarisation signal from which ⟨ Bz ⟩ is deduced is sampled over the visible stellar hemisphere depends on the wavelength window and resolving power used, on the varying effects of limb darkening and line weakening on lines of different wavelengths, excitation potentials and strengths, and on possible horizontal and vertical abundance variations of the element(s) whose lines are included in the averaged polarisation signal.
Nevertheless, the ⟨ Bz ⟩ values as measured with FORS1 should be similar in strength (usually within perhaps 20 %) to ⟨ Bz ⟩ values measured at the same phase in the field variation cycle with other methods. Furthermore, the variations of ⟨ Bz ⟩ observed with different methods should generally be similar in amplitude and phase. Thus the comparisons we will make are useful to establish that no major difference exists between the data coming from FORS1 and from other instruments. The new reductions of the FORS1 data can also be used in several cases discussed below to study the internal consistency and repeatability of FORS1 magnetic measurements.
4.1. The “reference star” HD 94660
HD 94660 = HR 4263 is a southern magnetic Bp star of V = 6.11. Its effective temperature Teff, derived from Geneva and Strömgren photometry (Mermilliod et al. 1997) with the FORTRAN codes developed by Napiwotzki et al. (1993) and Künzli et al. (1997) (as described in more detail by Landstreet et al. 2007) is about 11500 K, and log g ≈ 4.1.
The field of HD 94660 was one of the first fields discovered using the Balmer-line magnetograph (Borra & Landstreet 1975; Bohlender et al. 1993). The rotation period is approximately 2800 d, determined from the small variations of the mean field modulus between 6.05 and 6.4 kG (Landstreet & Mathys 2000; Mathys & Hubrig 2006). The longitudinal field, as measured by Mathys & Hubrig (1997) using the CASPEC instrument at ESO La Silla Observatory with polarimetric optics, varies by less than about 400 G full amplitude, between about −1750 and −2100 G, but at present the details of this variations are still not very clear because of the small amplitude of variation relative to the measurement uncertainties (Landstreet & Mathys 2000). Nevertheless, the small variation in ⟨ Bz ⟩ together with a declination of −42°, makes this star a convenient reference for checking polarimetric optics in the southern hemisphere.
HD 94660 was observed with FORS1 17 times between 2002 and 2008, with grisms 600 B, 600 R, 1200 g, and 1200 B. The star was occasionally observed quasi-simultaneously with more than one grism, and these field measurements help us to understand how the ⟨ Bz ⟩ field diagnostic changes using different regions of the optical spectrum, as discussed in Sect. 3.1 above. HD 94660 has strong Zeeman signatures in V/I in each of the Balmer lines, so it is of interest to examine how well the ⟨ Bz ⟩ values obtained using H lines agree with ⟨ Bz ⟩ values from metal lines. From the 14 measurements using the two common grism instrumental systems, 600 B and 1200 B, 13 show reasonable agreement between H line and metal line ⟨ Bz ⟩ values, and do not show any significant trend for one value to be larger than the other. On one night (MJD = 54782.376, grism 1200 B) the ⟨ Bz ⟩ values in the two systems differ by slightly more than 3σ. This may be an example of the “occasional outlier” problem that we have identified in FORS1 data, as discussed in Sect. 2.2 above. On two other nights differences of a little less than 3σ are observed.
 |
Fig. 5 Variation of ⟨ Bz ⟩ for HD 94660 with MJD as measured using Balmer lines (blue error bars with circles), and metallic spectrum (green error bars with x’s), for data obtained using the 600 B and 1200 B grisms. The solid smooth curve is best sine wave fit to ⟨ Bz ⟩ measured using Balmer lines, assuming P = 2800 d. The dashed straight red line is the approximately constant field reported by Bohlender et al. (1993); the dashed orange curve is the sine wave fit to CASPEC ⟨ Bz ⟩ measurements described by Landstreet & Mathys (2000). |
A second useful test is the consistency of repeated observations made during one night with a single grism choice. We have one such double observation using grism 600 B, and two using grism 1200 B. In these three cases, all pairs of Balmer line measurements are completely consistent, as are two of the three metal line measurements. However, the pair of metal line measurements with grism 1200 B from MJD = 54 782.376 differs by almost 4σ, reflecting the same outlier mentioned above.
We next consider the relationships between ⟨ Bz ⟩ values measured in various instrumental systems. The field of HD 94660 was measured simultaneously on one night using both the instrumental system of grism 600 B and that of grism 1200 B (see Table 2 above). There is no significant difference between the ⟨ Bz ⟩ values measured in the two systems, which suggests that – for this star at least – we may be able to combine the data from these two measurement systems to study the field strength variations. ⟨ Bz ⟩ measurements in grism 600 B and grism 1200 g on a single night also agree within the uncertainties, so – again for this star – these two systems appear to be approximately comparable.
In the two measures using grism 600 R, the Balmer line measures are about 25% lower, and the metal line measures about 25% larger, than field values measured on the same night with grism 600 B. For HD 94660, these data can clearly not be combined with those from other instrumental systems without determining the substantial adjustment required.
When we fit a sine wave to the Balmer line ⟨ Bz ⟩ values obtained with the 600 B and 1200 B grisms, we find a clear periodicity with a period of 2800 ± 250 d, and no other acceptable period in the range of 1000 to 5000 d. The variation of ⟨ Bz ⟩ with time as measured separately with Balmer lines and metal lines, in the grism 600 B and 1200 B systems, is shown in Fig. 5, together with the fit to the Balmer line data. The clear detection of the period found independently in the ⟨ B ⟩ data (Mathys & Hubrig 2006) is strong confirmation that the observed variations are stellar rather than instrumental. However, both the mean ⟨ Bz ⟩ value (about −2300 G) and the amplitude of variations (about 800 G peak-to-peak) are somewhat larger than the range of ⟨ Bz ⟩ values shown by Landstreet & Mathys (2000), so that combining the FORS1 data with the earlier CASPEC measurements would require rescaling of one of the two data sets.
The best-fit sine wave to the CASPEC ⟨ Bz ⟩ data discussed by Landstreet & Mathys (2000) is shown in Fig. 5. The CASPEC data are based on polarised spectra typically recorded in the wavelength window 5400–6800 Å, considerably to the red of the window used for most of the FORS1 data, and so we expect some offset in the mean values of ⟨ Bz ⟩, as seen in the Figure. Nevertheless, after modest shifting and re-scaling, the agreement is satisfactory. Note that this star has very sharp spectral lines, so observations with a high-resolution spectropolarimeter, such as ESO’s HARPSpol, should be able to provide an extremely high-precision magnetic curve – in yet another instrumental system.
Our conclusion is that observations of the standard Ap star HD 94660 are consistent with previous data, and are quite similar to the approximately constant value of ⟨ Bz ⟩ ≈ − 2520 G found by Bohlender et al. (1993) using the Balmer-line magnetograph (note sign error in their Table 1), as indicated in Fig. 5. However, there is a substantial scale difference between the FORS1 ⟨ Bz ⟩ measurements and those obtained with CASPEC. The variations observed in the FORS1 ⟨ Bz ⟩ data set are consistent with the known period of variation of the star, and are presumably real. This star remains a very useful standard for testing polarimetric instruments and systems in the southern hemisphere.
4.2. The very strongly magnetic star HD 75049
HD 75049 = CPD–50 1770 is a relatively unknown ninth magnitude southern Ap star. According to Elkin et al. (2010) it has Teff = 9600 K and log g = 4.1. Its distance is unknown.
A magnetic field with ⟨ B ⟩ ~ 30 kG was discovered in the star HD 75049 by Freyhammer et al. (2008). The star has been studied in detail by Elkin et al. (2010), who obtained 13 ⟨ Bz ⟩ magnetic field measurements using FORS1 with the 600 B grism during a period of about 3 months. Using this material, Elkin et al. (2010) concluded that the rotation period of the star is P = 4.04899 ± 0.00008 d, and that both ⟨ Bz ⟩ and ⟨ B ⟩ vary smoothly and approximately sinusoidally with that period. Although ⟨ Bz ⟩ does not change sign, the amplitude of variation is quite large, about 10 kG between extrema.
From our data reduction we estimate that a typical standard error of the field as measured with metal lines is larger by roughly a factor of two relative to the measurements reported by Elkin et al. (2010). Our field measurements are also slightly different from those reported by Elkin et al. (2010), but not by important amounts. This star is hot enough that the polarisation signal due to hydrogen Balmer lines is quite clear, so that measuring the field in Balmer lines has a physical meaning. Accordingly we discuss the metal and Balmer line measurements independently.
We have first re-determined the best period using the re-reduced FORS1 magnetic measurements. Compared to the data used by Elkin et al. (2010), the larger error bars in our data lead to lower values of the reduced chi-square value (χ2/ν) of the best-fit sine wave, around 2.5 to 3.0, compared to a value of about 8 for the ⟨ Bz ⟩ values found by Elkin et al. (2010) for the spectral range 3212–6215 Å. However, our best estimate of the rotation frequency and uncertainty from the re-reduced metal line data is f = 0.2471 ± 0.0002 cycles d-1, or a period of P = 4.047 ± 0.003 d, consistent with but about 30 times less precise than the value reported by Elkin et al. (2010).
We have also examined the ⟨ B ⟩ data reported by Elkin et al. (2010) for Fe ii 5018 Å to try to improve the period we derive. This is the line for which the variations of ⟨ B ⟩ have the largest amplitude and apparently have the least scatter. When these data are fit with a sinusoid, the resulting period is about P = 4.0475 ± 0.0058, even less accurate than the period derived from the FORS1 ⟨ Bz ⟩ data.
 |
Fig. 6 Variation of ⟨ Bz ⟩ with rotational phase for HD 75049 as measured using Balmer lines (lower data set), and metallic spectrum (upper data set), for all FORS1 ⟨ Bz ⟩ data. The smooth curves are sine wave fits to the two ⟨ Bz ⟩ curves, assuming P = 4.0476 d. |
We conclude that the period of this star can only be determined from the published magnetic data to a precision of about P = 4.047 ± 0.003 d.
From the relatively small value of χ2/ν that we find for the fit of a simple sine wave to the FORS1 ⟨ Bz ⟩ measurements, we conclude that our standard errors are not underestimated by very much; in fact, if they are accurate, the small remaining discrepancy between the sine wave and the observations could be due to a very slightly non-sinusoidal variation of ⟨ Bz ⟩.
Both the metal line ⟨ Bz ⟩ data and the H line ⟨ Bz ⟩ values can be fit about equally well with sine waves, with compatible best periods, but the ⟨ Bz ⟩ values found using H lines are systematically about 1000 G more negative than those found using metal lines, as was already found by Elkin et al. (2010). This difference is shown in different ways in Figs. 3 and 6, where the variation of ⟨ Bz ⟩ as measured in the two different instrumental systems is illustrated. The fact that the metal line data are well fit by a simple sine wave, and that the sine wave fits to ⟨ Bz ⟩ measured using metal lines and using H line are essentially the same except for a zero-point shift, give further evidence that the metal line ⟨ Bz ⟩ measurements vary approximately linearly with field strength in this field strength range, up to at least about 10 kG. As discussed by Elkin et al. (2010) and above, the systematic difference between the ⟨ Bz ⟩ values measured using the metal lines and those measured with H lines, which appears to correspond to a vertical shift of about 1100 G, is probably due to the fact that the H lines sample the visible disk differently than the typical metal lines. This systematic difference is typical of measurements made of ⟨ Bz ⟩ using different instrumental systems.
4.3. The roAp star HD 83368
The star HD 83368 = HR 3831 = HIP 47145 is (barely) bright enough to be in the Bright Star Catalogue. It is one of the first Ap stars discovered to show the short-period pulsations characteristic of the rapidly-oscillating Ap (roAp) stars (Kurtz 1982). Using photometry to estimate its basic properties as we did for HD 94660 above, we find Teff ≈ 7500 K and log g ≈ 4.4. This star is cool enough that, although the Zeeman polarisation signature is quite clear in the star, there is no systematic difference between the appearance of this signal in and out of the Balmer lines. We do not think that there is any particular physical meaning that can be attached to ⟨ Bz ⟩ values measured in the Balmer lines, and so we discuss only the ⟨ Bz ⟩ values determined from the full spectrum.
HD 83368 was observed twice on one night, first with grism 600 B over a prolonged period during which more than 120 frames were collected at a rate of roughly one per minute, and later with grism 600 R for a few minutes (Hubrig et al. 2004). Our archive includes only the average results of each of these two data sets.
We notice that the two ⟨ Bz ⟩ values from the full spectrum, ⟨ Bz ⟩ = + 1018 ± 30 G (600 B) and ⟨ Bz ⟩ = + 893 ± 52 G (600 R) are consistent with one another. The small difference may be due to statistical noise, or to the fact that the two grism setting sample different wavelength windows (3480–5900 Å and 5250–7420 Å respectively), and thus sample the field strength over the disk somewhat differently.
To make a comparison with previous field measurements, we use the ephemeris of Mathys & Hubrig (1997). Assuming that the last digit of the period is significant, we find that the measurement with grism 600 B was taken at φ = 0.52 ± 0.01, which corresponds to the positive extremum of the field. According to the magnetic curve of Thompson (1983), the field measured with a Balmer line filter polarimeter would be about + 725 G at this phase. According to the fit to CASPEC spectropolarimetry, the field at this phase should be about + 560 G. Thus the FORS1 ⟨ Bz ⟩ measurement is significantly larger than would be found with either of these other two methods, but the difference is not much larger than the difference present between the two comparison values, and is within the range of variation found between different field value measurement methods.
4.4. The extremely peculiar roAp star HD 101065
HD 101065 = HIP 56709 is Przybilski’s star, the most peculiar of the peculiar A stars known. Its spectrum is dominated by lines of such rare earth elements as Dy and Ho. It is the coolest known magnetic Ap star, with Teff = 6400 K and log g = 4.2 (Shulyak et al. 2010). The star has very sharp lines (vsini = 3.5 ± 0.5 km s-1Cowley et al. 2000), but variations are small and the rotation period is unknown. It has a magnetic field which was discovered by Wolff & Hagen (1976) from three photographic Zeeman measurements. All three measurements were in the range between −2000 and −2500 G. Recent observations by Hubrig et al. (2004) using FORS1 have confirmed the presence of the field, but their measurements (long series of short exposures taken on two different nights to search for field variations with pulsation) yielded ⟨ Bz ⟩ field measurements of about −1000 G. Hubrig et al. remark that the field measured in the Balmer lines is about 500 G larger than in the metal lines, a feature we confirm. However, as discussed above, this star is so cool that the “Balmer line ⟨ Bz ⟩ values” are simply measurements of the field using metal lines which are sampled differently over the spectrum from the usual metal line measurement.
There are altogether 13 observations of HD 101065 in the FORS1 archive. Twelve have been taken with grism 600 B in very similar wavelength windows, so these data form a set taken in an essentially fixed instrumental system. Thus these 12 measurements are directly comparable to one another. The twelve 600 B observations cover about five years with a variety of intervals between measurements, so it is of interest to see if the ⟨ Bz ⟩ data reveal the rotation period of the star. A periodogram was computed for the metal line data for all distinguishable periods between 10 yr and 1 day (assuming longer periods are ruled out by the non-zero vsini value reported by Cowley et al. 2000). The fit spectrum shows that the spread of the ⟨ Bz ⟩ values is not large enough to reliably find a period: the values of χ2/ν for a sinusoidal fit to the data range only between 0.4 and 2.9. The best periods appear to be around 4.30 and 1.79 d, but it is not at all clear that one of these is the actual rotation period, assuming that the rotation period is actually within the range tested.
In fact the dispersion in the ⟨ Bz ⟩ data relative to the overall mean, about 105 G, is only marginally larger than typical standard error of about 70 G, and the reduced chi square value of fit assuming that the field is constant is about 1.35. Thus, these data do not reveal strong evidence that the field of HD 101065 is detectably variable. Possibly the star is observed nearly pole-on, consistent with the small value of vsini, or perhaps the field axis is aligned with the rotation axis. Alternatively, it is possible that the reported value of vsini is actually indistinguishable from zero; the star is a roAp pulsator, and the very small reported vsini is certainly close to the threshold for reliable detection in a pulsating, strongly magnetic star. In this case, HD 101065 might have an extremely long rotation period of decades, like HD 201601, and the decade of field measurements with FORS1 may simply cover only a small fraction of the rotation period.
The mean ⟨ Bz ⟩ value measured with the Balmer line windows is about −1850 G, while that measured in the usual way with with metal lines is about −1250 G. The Balmer line ⟨ Bz ⟩ values correspond more closely to the values observed by Wolff & Hagen (1976) than do the metal line values. In spite of the fact that this star is so cool that H does not make a strong contribution to the spectropolarimetric signal within Balmer lines, this difference between the two measurement values is one of the larger differences found among Ap stars. It probably reflects considerable non-uniformity in the metal lines that dominate the field measurement, or the peculiarity of the atmospheric structure of HD 101065, and illustrates clearly the difficulty in interpreting simple field moment measurements such as ⟨ Bz ⟩.
4.5. The very long period roAp star HD 137949 = 33 Lib
 |
Fig. 7 Variation of mean ⟨ Bz ⟩ values for HD 137949 as a function of MJD between 1957 and 2007. Each point represents the mean field measured by a single observer or team, with the vertical error bar showing the dispersion of individual measures (or an estimate of the uncertainty for the first point), and the horizontal error bar showing the extent in time of the measurement set from that team. |
HD 137949 = HIP 75848 = 33 Lib is a cool SrEuCr magnetic Ap with Teff = 7400 K, log g = 4 and a low mass, probably about 1.7 M⊙ (Netopil et al. 2008; Shulyak et al. 2013). It is also a roAp pulsator (Kurtz 1982). It has very sharp spectral lines with clearly resolved Zeeman splitting visible in Fe ii 6149 Å. The mean longitudinal field ⟨ Bz ⟩ has been measured by a number of investigators since the field was discovered by Babcock (1958), as summarised by Mathys et al. (1997). The value of ⟨ Bz ⟩ appears to have been increasing more or less steadily over the past half century at a rate of the order of 20 G/yr. The mean field modulus ⟨ B ⟩ was measured repeatedly during the 1990s over 4.3 yr (Mathys et al. 1997), and was found to remain absolutely constant (within uncertainties of roughly ± 40 G) at 4660 G.
These facts are consistent with a very long rotation period, of the order of 102 yr, and the secular change of ⟨ Bz ⟩ as measured over the decades (see Fig. 7) certainly suggests such a long period. However, it is important to keep in mind that each of the points in the figure was obtained with a different instrumental system. The first three points, representing the mean value of ⟨ Bz ⟩ observed by respectively Babcock (1958), van den Heuvel (1971) and Wolff (1975), were obtained photographically with three different telescope–polarisation analyser–coudé spectrograph combinations (the Palomar 5 m, the Lick 3 m, and the Mauna Kea 2.2 m). All these observations were made in the blue, typically with Kodak 103a-O plates covering roughly 3800–4900 Å, and so might seem to be on essentially a single instrumental system. Comparison of the Lick and Mauna Kea observations of standard stars suggest that both systems are closely comparable and yield similar ⟨ Bz ⟩ data (Wolff & Bonsack 1972), but it appears that measurements made at Lick or Mauna Kea are roughly 20% larger than Mount Wilson–Palomar measurements (Preston & Pyper 1965). Thus within uncertainties the first three ⟨ Bz ⟩ data points in the figure may well not be significantly different.
The ⟨ Bz ⟩ measures contributing to the fourth point, at about MJD 48 900, were obtained in a different wavelength window, between about 5600 and 6800 Å (Mathys et al. 1997). From our exploration of FORS1 data, we can anticipate that the different mix of elements contributing important spectral lines, and the different limb darkening, could easily lead this point to be shifted by 20 % or so from the scale of the first three points. Thus the reality of the secular trend apparent in the first four data groups is not securely established.
The field of HD 137949 was measured seven times over about 5 yr with FORS1, in all but one case with essentially the same instrumental setup using grism 600 B. Five of the six 600 B measurements were carried out within a period about three months in 2007, while the first measurement with 600 B was made five years earlier, in 2002. (One ⟨ Bz ⟩ measurement with grism 600 R was obtained in 2002 as well, yielding a ⟨ Bz ⟩ value only a little larger than the simultaneous measurement with grism 600 B; see Table 2.) If we measure the standard deviation of the full spectrum measurements using all six 600 B values, the dispersion found is about two times larger than would be predicted for a constant field and accurate uncertainties. The dispersion drops to about the expected value if we omit the 2002 measurement. The dispersion of the five values measured in 2007 supports our estimates of the standard errors; the 2002 FORS1 ⟨ Bz ⟩ value using all lines is roughly 3σ larger than the mean of the other five values.
The simplest interpretation of this result is that the field has actually decreased in strength by roughly 230 G in the five years separating the 2002 FORS1 measurement from the others. Of course, if the old ⟨ Bz ⟩ values are all in compatible measurement systems, so that the earlier measurements really do show an increasing field during the second half of the 20th century, this field may have now reached maximum and be declining again. Alternatively, it is possible that the first ⟨ Bz ⟩ measurement with the 600 B grating is one of the occasional data outliers.
To place the FORS1 data in the context of the long-term changes displayed in Fig. 7, note that the average FORS1 data point was obtained in a wavelength window roughly centred on, but a little wider than, the wavelength windows used for the three points from photographic measurements. We would not expect a large offset of the FORS1 ⟨ Bz ⟩ values relative to those obtained using the photographic instrumental systems. It appears that the FORS data support the reality of the very slow secular change in ⟨ Bz ⟩ over half a century at a rate of the order of 30 G yr-1, and consequently an extremely long rotation period, of many decades.
4.6. The very strongly magnetic, periodically variable roAp star HD 154708
A large field was discovered in the very cool Ap star HD 154708, which has Teff = 6800 K, log g = 4.1, and M = 1.5 M⊙, by Hubrig et al. (2005). There are 17 ⟨ Bz ⟩ measurements of the star in the FORS1 archive. Of these, 14 were taken within an interval of 110 d, all with the 600 B grism and covering the same wavelength interval, so that these 14 measurements are in a single instrumental system. In addition, three earlier measurements are available. Two were taken with the 1200 g grism, covering about half the wavelength interval of the 600 B measurements with about twice the spectral resolution, and one was taken with 600 B in a wavelength window slightly different from that used in the long data series, so that it is in essentially the same instrumental system as the 14 contiguous measurements. All these field measurements have been published, with slightly different ⟨ Bz ⟩ values than in our catalogue for each point, by Hubrig et al. (2009c). They report a rotation period of P = 5.3666 ± 0.0007 d. Note that this star is so cool that H line measurements have no particular meaning, so we discuss ⟨ Bz ⟩ data obtained using all lines.
It is found from the series of measurements taken with the 600 B grism that the value of ⟨ Bz ⟩ varies by a total of about 25% of the mean value of ⟨ Bz ⟩ during rotation. This is small enough that, as discussed above, the relationship of the two ⟨ Bz ⟩ measurements taken with the 1200 g grism relative to the larger sample of data is uncertain by an important fraction of the total. These data cannot be used to refine the period of variation without considering the relationship of the two different instrumental systems.
We have two pieces of information that suggest that it may be possible to safely combine the data from the 1200 g grism with that from the 600 B. First, the one comparison that we have of this grism with the 600 B, two almost simultaneous measurements of ⟨ Bz ⟩ of HD 94660 on MJD 53332.3 (see Table 2), yields essentially identical ⟨ Bz ⟩ values in the two systems. Unfortunately, the wavelength setting used for the 1200 g grism is considerably to the red of the setting used for grism 600 B, so this result may not apply to all Ap stars, especially if their temperatures are very different from HD 94660.
The second piece of circumstantial evidence that the two sets of data can be combined is the fact that the values of the two measurements made with the 1200 g grism by chance coincide with the largest and smallest values of ⟨ Bz ⟩ observed with grism 600 B. This strongly suggests that ⟨ Bz ⟩ values measured with the two grisms cover a very similar range of values, and thus are reasonably comparable.
The most recent 13 FORS1 measurements, using all lines, define clearly the rotation period of this star. A periodogram of these 13 data points yields a unique period of 5.369 ± 0.013 d with a minimum χ2/ν value of about 0.56.
We can try to refine this period using the two remaining measures obtained with grism 600 B. Adding these points makes the minimum value of χ2/ν rise to about 3.2, and two minima suggest two equally possible periods, 5.386 ± 0.004 and 5.362 ± 0.004. These two best periods are near the two extremes of the coarser period defined by the 13 point sample. Thus we cannot improve significantly on the period defined by the 13 most recent contiguous measurements.
We then introduce the two earlier field measurements made with grism 1200 g, and carry out a sine wave fit on all 17 data points. The best value of χ2/ν rises to 3.25, and the best period is between 5.3596 and 5.3671, or P = 3.3634 ± 0.0038 d. Most of the increase in the value of χ2/ν comes from the first (grism 600 B) point in 2007, so we drop this point and fit the remaining 16 points, including the two measurements made with grism 1200 g. The unique best fit, with values of χ2/ν as low as 0.93, is found for periods in the range of 5.3600 to 5.3665. This corresponds to P = 5.363 ± 0.003 d, almost exactly the value found with all 17 points.
 |
Fig. 8 Variation of ⟨ Bz ⟩ with rotational phase for HD 154708 as measured using the full spectrum and data from both grism 600 B and 1200 g. The smooth curve is the best sine wave fit to ⟨ Bz ⟩, assuming P = 5.363 d. |
We note that the period of 5.3666 ± 0.0007 d proposed by Hubrig et al. (2009c) on the basis of all the FORS1 ⟨ Bz ⟩ measurements is consistent with the one derived here. However, we are unable to reproduce from these data the very small uncertainty assigned by Hubrig et al. (2009c). We believe that they have underestimated the uncertainty of the rotation period by about a factor of 4.
The variation as a function of rotational phase of the 15 grism 600 B and the two grism 1200 g ⟨ Bz ⟩ values, determined using all lines, is shown in Fig. 8. The smooth curve is a sine wave fit to the 16 “good” ⟨ Bz ⟩ values obtained using all lines. In general, the data points fit the best fit curve very well. This overall good fit suggests that our uncertainties are realistic. The exception to the good fit (the deviating data points at φ = 0.84) illustrates yet again the occasional outliers found in FORS data.
4.7. The long-period roAp star HD 210601 = γ Equ
The ⟨ Bz ⟩ field component of this star has been measured frequently over about 60 years. The data are summarised (and supplemented) by Bychkov et al. (2006), who show that (with a dispersion of roughly 500 G, probably due to the variety of measurement methods adopted) the ⟨ Bz ⟩ data are consistent with a period of 80 or 90 yr. This long period has been confirmed (although its value is still quite uncertain) by the slow, regular change of position angle of linear polarisation of the star (Leroy et al. 1994). ⟨ Bz ⟩ appears to have been near negative extremum during the past decade, with a value of about −1000 G.
The FORS1 catalogue includes four different measurements of this star, each one with a different grism, different resolving power, and different wavelength region. The star is sufficiently cool that the H measurement is not meaningful, so we discuss only the ⟨ Bz ⟩ values obtained from all lines. These data are shown in the last entries of Table 2. The measurements scatter over the same range found at this rotational phase with other methods, from about −450 to about −1700 G. The typical value is about −1200 G, also similar to the results of other measurements.
Let us assume that in fact the magnetic field structure on the visible hemisphere of the star changed little during the four year span in which the observations were made, so that the formally defined value of ⟨ Bz ⟩ has hardly changed during that period. What Table 2 really illustrates is the point we have made repeatedly above, namely that the FORS spectropolarimeter (like similar low-resolution spectropolarimeters) is easily used in a variety of different instrumental modes, each with its own sensitivity to chemical abundance, limb darkening, line weakening, and stellar parameters, and each providing a different numerical value of ⟨ Bz ⟩ even when the mathematical definition of this quantity from the data is unchanged. In this star particularly we see that when searching for periodicity or studying the time variation of ⟨ Bz ⟩, it is essential to use only a single instrumental system.
5. Conclusions
-
1.
The overall ⟨ Bz ⟩ scale used for FORS1 isrealistic, similar to (although generally not identical to) the⟨ Bz ⟩ scales resulting from other fieldmeasurement methods.
-
2.
The standard errors of measurement as estimated by our new reductions are realistic. Fields are generally detected in stars where they are already known to exist, or are repeatedly and/or convincingly detected. The dispersion of ⟨ Bz ⟩ values around mean variation curves are generally consistent with the standard errors we find, apart from the problem of “occasional outliers”.
-
3.
The division of ⟨ Bz ⟩ measurements into hydrogen line and metal line measurements is quite meaningful for Ap stars hotter than perhaps 9000 K. Below this temperature, the distinctive Zeeman signatures in the Balmer lines are overwhelmed by metal line polarisation, and hydrogen ⟨ Bz ⟩ values are not meaningfully different from the metal line measurements except for the fact that they sample the overall wavelength window differently. For cool Ap stars, the hydrogen line measurements have no strong connection with the field as sampled by hydrogen.
-
4.
The field strengths measured with FORS1 are no more different from previous measurements than typical differences between various instrumental measurement systems already in wide use. Furthermore, the values of ⟨ Bz ⟩ as measured using Balmer lines, when these are meaningful, are usually reasonably close to those measured using the metallic spectrum. Differences between the hydrogen line and metal line instrumental systems are usually not large even when ⟨ Bz ⟩ approaches 10 kG, or ⟨ B ⟩ reaches 30 kG. Since these field strengths are close to the upper limits observed in any magnetic Ap or Bp stars, it appears that there is no problem with using the weak field approximation of Eq. (1), which is expected to break down at “very large” fields, to derive ⟨ Bz ⟩ from the metallic spectrum of any magnetic main sequence star observed with FORS1. However, we do find a few “occasional outliers” that should agree with others but instead deviate by 3 or even 4σ from the expected values.
-
5.
Each specific grism and wavelength setting used with FORS defines a specific instrumental system for measuring ⟨ Bz ⟩. Because of difference in sensitivity to patchiness, and differences in limb darkening and line weakening, measurements made with these different systems are not directly comparable except for general magnitude. In particular, it will generally not be safe to use measurements in one instrumental system to refine a period derived with another instrumental system, because of possible (usually unknown) ⟨ Bz ⟩ value shifts or scale changes between the systems, until the relevant shifts have been determined with adequate precision.
-
6.
These conclusions are all expected to apply, more or less exactly, to other similar low-resolution, Cassegrain-mounted spectropolarimeters, and specifically to FORS2, but also, for example, to the ISIS spectropolarimeter of the William Herschel Telescope.
-
7.
FORS in polarimetric mode provides a valuable and extremely powerful tool for measuring magnetic fields in stars, provided its characteristics are well understood. In particular, it is important not to underestimate errors, to be aware of the “occasional outlier” problem, to not expect to reach standard errors of 20 or 30 G without a lot of extra care, and to carry out programmes studying time variation with a single instrumental system.
Acknowledgments
We thank the referee, Dr. G. Mathys, for his careful reading and very useful report. The data used in this work have been provided by the ESO Science Archive Facility from the following programmes: 060.A-9203, 068.D-0403, 069.D-0210, 070.D-0352, 072.C-0447, 073.D-0464, 074.C-0442, 074.D-0488, 075.D-0295, 077.D-0556, 079.D-0240, 079.D-0697, 079.D-5023, 080.D-0170, 081.D0670, 082.D-0342. The data used were obtained in part from observations carried out at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council of Canada, the Institut National des Science de l’Universe of the Centre National de la Recherche Scientifique of France and the University of Hawaii. Work on this project by J.D.L. has been supported by the Natural Sciences and Engineering Research Council of Canada. LF acknowledges support from the Alexander von Humboldt Foundation.
References
- Angel, J. R. P., & Landstreet, J. D. 1970, ApJ, 160, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Aurière, M, Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aznar Cuadrado, R., Jordan, S., Napiwotzki, R., et al. 2004, A&A, 423, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babcock, H. W. 1958, ApJS, 3, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., Szeifert, T., Wade, G. A., Landstreet, J. D., & Mathys, G. 2002, A&A, 389, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landstreet, J. D., Mason, E., et al. 2006, A&A, 450, 777 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Landolfi, M., Landstreet, J. D., et al. 2009, PASP, 121, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Bagnulo, S., Landstreet, J. D., Fossati, L., & Kochukhov, O. 2012, A&A, 538, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bagnulo, S., Fossati, L., Kochukhov, O., & Landstreet, J. D. 2013, A&A, 559, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlender, D. A., Landstreet, J. D., & Thompson, I. B. 1993, A&A, 269, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Borra, E. F., & Landstreet, J. D. 1975, PASP, 87, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Borra, E. F., & Landstreet, J. D. 1977, ApJ, 212, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bychkov, V. D., Bychkova, L. V., & Madej, J. 2005, A&A, 430, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bychkov, V. D., Bychkova, L. D., & Madej, J. 2006, MNRAS, 365, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Cowley, C. R., Ryabchikova, T., Kupka, F., et al. 2000, MNRAS, 317, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Semel, M., Carter, B. D., Rees, D. E., & Cameron, A. C. 1997, MNRAS, 291, 658 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Elkin, V. G., Mathys, G., Kurtz, D. W., Hubrig, S., & Freyhammer, L. M. 2010, MNRAS, 402, 1883 [NASA ADS] [CrossRef] [Google Scholar]
- Freyhammer, L. M., Elkin, V. G., Kurtz, D. W., Mathys, G., & Martinez, P. 2008, MNRAS, 389, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Kurtz, D. W., Bagnulo, S., et al. 2004, A&A, 415, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Nesvacil, N., Schoeller, M., et al. 2005, A&A, 440, 37 [Google Scholar]
- Hubrig, S., Briquet, M., Schöller, M., et al. 2006, MNRAS, 369, 61 [Google Scholar]
- Hubrig, S., Schöller, M., Schnerr, R. S., et al. 2008, A&A, 490, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubrig, S., Steltzer, B., Schöller, M., et al. 2009a, Astron. Nachr., 330, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Briquet, M., De Cat, P., et al. 2009b, Astron. Nachr., 330, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Hubrig, S., Mathys, G., Kurtz, D. W., et al. 2009c, MNRAS, 396, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Kochukhov, O., & Bagnulo, S. 2006, A&A, 450, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Künzli, M., North, P., Kurucz, R. L., & Nicolet, B. 1997, A&AS, 122, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurtz, D. W. 1982, MNRAS, 200, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Izzo, C., de Bilbao, L., Larsen, J., et al. 2010, SPIE, 7737, 729 [Google Scholar]
- Landstreet, J. D. 1982, ApJ, 258, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Landstreet, J. D., & Mathys, G. M. 2000, A&A, 359, 213 [NASA ADS] [Google Scholar]
- Landstreet, J. D., Borra, E. F., Angel, J. R. P., & Illing, R. M. E. 1975, ApJ, 201, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Landstreet, J. D., Bagnulo, S., Andretta, V., et al. 2007, A&A, 470, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Landstreet, J. D., Bagnulo, S., Valyavin, G. G., et al. 2012, A&A, 545, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leroy, J.-L., Bagnulo, S., Landolfi, M., & Landi degl’Innocenti, E. 1994, A&A, 284, 174 [NASA ADS] [Google Scholar]
- Mathys, G. 1989, Fund. Cosm. Phys., 13, 143 [Google Scholar]
- Mathys, G. 1991, A&AS, 89, 121 [NASA ADS] [Google Scholar]
- Mathys, G., & Hubrig, S., 1997, A&AS, 124, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathys, G., & Hubrig, S. 2006, A&A, 453, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathys, G., Hubrig, S., Landstreet, J. D., Lanz, T., & Manfroid, J. 1997, A&AS, 123, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J.-C., Mermilliod, M., & Hauck, B. 1997, A&AS, 124, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Napiwotzki, R., Schönberner, D., & Wenske, V. 1993, A&A, 268, 653 [NASA ADS] [Google Scholar]
- Netopil, M., Paunzen, E., Maitzen, H. M., North, P., & Hubrig, S. 2008, A&A, 491, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preston, G. W., & Pyper, D. M. 1965, ApJ, 142, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Shultz, M., Wade, G. A., Grunhut, J., et al. 2012, ApJ, 750, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Shulyak, D., Ryabchikova, T., Kildiyarova, R., & Kochukhov, O. 2010, MNRAS, 520A, 88S [Google Scholar]
- Shulyak, D., Ryabchikova, T., & Kochukhov, O. 2013, A&A, 551, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thompson, I. B. 1983, MNRAS, 205, 43 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J. 1971, A&A, 11, 461 [NASA ADS] [Google Scholar]
- Wade, G. A., Donati, J.-F., Landstreet, J. D., & Shorlin, S. L. S. 2000, MNRAS, 313, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, S. C. 1975, ApJ, 202, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, S. C., & Bonsack, W. K. 1972, ApJ, 176, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, S. C., & Hagen, G. 1976, PASP, 88, 119 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
⟨ Bz ⟩ measures of ESPaDOnS spectra of stars with large ⟨ Bz ⟩(H) – ⟨ Bz ⟩(metal) differences.
All Figures
 |
Fig. 1 Top panel: part of the intensity spectrum of HD 94660, arbitrarily normalised (black); circular polarisation spectrum V(λ) /I(λ) (red); null (verification) spectrum), shifted vertically by −0.5 for clarity (blue); uncertainties of V/I and null spectra, shifted vertically by −0.5 for clarity (light blue band). The green stripes above and below the spectrum show regions included in ⟨ Bz ⟩ measurement in the H lines; pink stripes show regions included in the metal line measurement. Lower left panels: correlation diagrams for determination of field strength from V/I and I using H lines (upper box) and using metal lines (lower box). Lower right panels: the same with the null spectrum. |
| In the text | |
 |
Fig. 2 Portion of a spectrum in I, V/I, and N of the cool roAp star HD 137949. All symbols are the same as in Fig. 1. In contrast to that figure, notice the absence of any systematic saw-tooth pattern in V/I within the Balmer lines. |
| In the text | |
 |
Fig. 3 Comparison of ⟨ Bz ⟩ measured using Balmer lines (x-axis) with ⟨ Bz ⟩ measured using metal lines (y-axis) in the strongly variable magnetic Ap star HD 75049. Each point is the field measurement pair from a single FORS1 observation. |
| In the text | |
 |
Fig. 4 Comparison of ⟨ Bz ⟩ measured using Balmer lines (x-axis) with ⟨ Bz ⟩ measured using metal lines (y-axis) in the full magnetic star sample, for stars with at least 5σ field detections, with both H and metal σ< 250 G, and spectral types of early A or B. In the upper right corner, the two outliers are HD 66318 with ⟨ Bz ⟩ (metal) > ⟨ Bz ⟩ (H), and HD 318107 with ⟨ Bz ⟩ (metal) < ⟨ Bz ⟩ (H). In the negative field region the two most obvious outliers are NGC 2244–334, well above the mean line at ⟨ Bz ⟩ (H) = −9700 G, and NGC 2169–12 at ⟨ Bz ⟩ (H) = −3500 G. All remaining points with ⟨ Bz ⟩ (H) < − 4000 G are measurements of HD 75049. The line represents equality of the two ⟨ Bz ⟩ values. |
| In the text | |
 |
Fig. 5 Variation of ⟨ Bz ⟩ for HD 94660 with MJD as measured using Balmer lines (blue error bars with circles), and metallic spectrum (green error bars with x’s), for data obtained using the 600 B and 1200 B grisms. The solid smooth curve is best sine wave fit to ⟨ Bz ⟩ measured using Balmer lines, assuming P = 2800 d. The dashed straight red line is the approximately constant field reported by Bohlender et al. (1993); the dashed orange curve is the sine wave fit to CASPEC ⟨ Bz ⟩ measurements described by Landstreet & Mathys (2000). |
| In the text | |
 |
Fig. 6 Variation of ⟨ Bz ⟩ with rotational phase for HD 75049 as measured using Balmer lines (lower data set), and metallic spectrum (upper data set), for all FORS1 ⟨ Bz ⟩ data. The smooth curves are sine wave fits to the two ⟨ Bz ⟩ curves, assuming P = 4.0476 d. |
| In the text | |
 |
Fig. 7 Variation of mean ⟨ Bz ⟩ values for HD 137949 as a function of MJD between 1957 and 2007. Each point represents the mean field measured by a single observer or team, with the vertical error bar showing the dispersion of individual measures (or an estimate of the uncertainty for the first point), and the horizontal error bar showing the extent in time of the measurement set from that team. |
| In the text | |
 |
Fig. 8 Variation of ⟨ Bz ⟩ with rotational phase for HD 154708 as measured using the full spectrum and data from both grism 600 B and 1200 g. The smooth curve is the best sine wave fit to ⟨ Bz ⟩, assuming P = 5.363 d. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


