| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201424546 | |
| Published online | 28 November 2014 | |
Fast-sausage oscillations in coronal loops with smooth boundary
1 Ussuriisk astrophysical observatory, Russion Academy of Sciences, 692533 Primorskiy Kray, Russia
e-mail: lopin78@mail.ru
2 Institute of Automation and Control Processes FEB RAS, Vladivostok, Russia Far Eastern Federal University, 690041 Vladivostok, Russia
Received: 7 July 2014
Accepted: 25 September 2014
Aims. The effect of the transition layer (shell) in nonuniform coronal loops with a continuous radial density profile on the properties of fast-sausage modes are studied analytically and numerically.
Methods. We modeled the coronal waveguide as a structured tube consisting of a cord and a transition region (shell) embedded within a magnetic uniform environment. The derived general dispersion relation was investigated analytically and numerically in the context of frequency, cut-off wave number, and the damping rate of fast-sausage oscillations for various values of loop parameters.
Results. The frequency of the global fast-sausage mode in the loops with a diffuse (or smooth) boundary is determined mainly by the external Alfvén speed and longitudinal wave number. The damping rate of such a mode can be relatively low. The model of coronal loop with diffuse boundary can support a comparatively low-frequency, global fast-sausage mode of detectable quality without involving extremely low values of the density contrast. The effect of thin transition layer (corresponds to the loops with steep boundary) is negligible and produces small reductions of oscillation frequency and relative damping rate in comparison with the case of step-function density profile. Seismological application of obtained results gives the estimated Alfvén speed outside the flaring loop about 3.25 Mm/s.
Key words: Sun: helioseismology / Sun: oscillations
© ESO, 2014
1. Introduction
Coronal seismology as a new branch of solar physics has been rapidly progressing in past decades. It became possible owing to the development of the space observation equipment onboard the TRACE, SOHO, and Hinode satellites. The basic aim of coronal seismology is to determine the physical conditions in the solar corona on the basis of observable coronal oscillation characteristics. These oscillations are commonly attributed to coronal waveguide structures known as coronal loops. Methods of coronal seismology first suggested by Uchida (1970), Rosenberg (1970), and Roberts et al. (1984) are an essential tool in solar physics because the direct measurements of coronal plasma parameters are extremely difficult. The results of the first direct spacecraft observations of coronal oscillations were reported by Aschwanden et al. (1999) and Nakariakov et al. (1999). Previously detected pulsations in solar radio bursts are perhaps the first manifestation of coronal oscillations in the observed data (Rosenberg 1970; Achong 1974; Abrami & Coren 1978; Tapping 1978; Trottet et al. 1979, 1981).
Correct interpretation of coronal oscillations needs to develop the appropriate theoretical models. The coronal magnetic loops are usually modeled as cold plasma cylinders with uniform density and longitudinal magnetic field embedded in uniform magnetic environment. It is well known that such magnetic structures can support fast-sausage (axisymmetric), kink (nonaxisimmetric), and torsional Alfvén wave modes (Defouw 1978; Zaitsev & Stepanov 1982; Edwin & Roberts 1983). All of these modes have their unique wave characteristics. The features of kink waves allow to their direct observation because they displace the loop axis (Aschwanden et al. 1999; Nakariakov et al. 1999). On the basis of observed kink oscillation parameters, Nakariakov & Ofman (2001), Andries et al. (2005), and Van Doorsselaere et al. (2007) were able to estimate the magnetic field strength in coronal loops and the scale height in the corona. The fast-sausage waves can be responsible for observed radio pulsations with periods from a fraction of a second up to several tens of seconds (Trottet et al. 1979; Kupriyanova et al. 2010; Su et al. 2012). The MHD wave modulation of electromagnetic emission of flaring loops is the often suggested mechanism for explaining observed oscillations in solar radio bursts (Rosenberg 1970; Zaitsev & Stepanov 1975; Melnikov et al. 2005; Nakariakov & Melnikov 2009). These quasi-periodic pulsations, interpreted in terms of fast-sausage modes, make it possible to determine the density or magnetic field strength in the solar corona (Rosenberg 1970; Nakariakov et al. 2003; Aschwanden et al. 2004; Van Doorsselaere et al. 2011).
The first studies of fast sausage oscillations in coronal waveguides were performed by Zaitsev & Stepanov (1975), Meerson et al. (1978), Edwin & Roberts (1983), and Roberts et al. (1984). They showed that the model of straight uniform magnetic flux tubes with longitudinal magnetic field and density discontinuity at the tube boundary could support two fast-sausage wave regimes. These are trapped and leaky wave regimes. The last one corresponds to wave radiation in the external medium and leads to attenuation of oscillations in such loops, while the trapped modes are undamped in essence in the absence of non-adiabatic effects. The critical wavelength (wave number) separating these two wave regimes is called cut-off wavelength (wave number). Under the typical coronal conditions, the cut-off wavelength is near loop radius. It means that the coronal loops with a length that is much more than their radius, can only support leaky fundamental fast-sausage modes, while the trapped modes only correspond to high values of axial wave numbers. Even for fairly dense and thick flaring loops, the fundamental fast-sausage mode is leaky. The wave damping decrement in the long-wavelength limit is proportional to the density contrast defined as the ratio of the external to internal plasma densities (Zaitsev & Stepanov 1975; Meerson et al. 1978). Therefore, interpreting observed high quality radio pulsations in terms of global fast-sausage modes requires coronal loops with sufficiently low values of density contrast. A period of standing fast-sausage oscillations is defined as the ratio of tube radius to internal Alfvén speed in the long wavelength limit (Zaitsev & Stepanov 1975; Meerson et al. 1978; Kopylova et al. 2007) and so it requires involvement of rather unrealistic values of loop radius or Alfvén speed to interpret the observed long-period pulsations in terms of coronal MHD waves. Thus, the classic model of coronal loops as a magnetic cylinder with discontinuous density at the boundary experiences difficulties in explaining the observed periods and damping time of fast-sausage oscillations. On the other hand, the step-function density profile is a pure mathematical simplification of realistic density profiles in coronal loops. We therefore aim to examine the effect of continuous radial density profile on the properties of fast-sausage modes.
Such a transverse nonuniformity can be introduced as a transition layer, connecting the internal part of a loop with its environment. The equilibrium density monotonically varies in the transition layer (shell) from its internal to external value. The radially structured models of solar waveguides were previously studied in various aspects. Mikhalyaev & Solov’ev (2005) and Erdélyi & Carter (2006) used the model of coronal loops consisting of core and shell regions with fixed values of density and magnetic field strength to study the features of MHD waves in these magnetic structures. Pneuman (1964) and Edwin & Roberts (1988) analyzed the axisymmetric MHD waves in monolithic coronal flux tubes with a specific parabolic density profile. They found that the diffuseness of magnetic flux tubes leads to increasing the cut-off wave number. The numerical consideration of fast-sausage oscillations of coronal loops as density enhancement in the form of Epstein profile in Cartesian geometry was carried out in the works of Cooper et al. (2003) and Pascoe et al. (2007), while Nakariakov et al. (2012) have performed a numerical study of axisymmetric MHD modes for a smooth cylinder of a cold plasma.
The aim of the present paper is an analytic consideration of fast sausage modes in structured coronal loops with a continuous radial density profile in cylindrical geometry. We study the effect of the transition layer on the cut-off wavelength, frequency, and damping rate of fast-sausage oscillations. The analytical results are supported by numerical calculations of the general dispersion relation.
2. Statement of the problem
We consider the model of coronal loop as a cold plasma (β = 0) density enhancement consisting of a central cord with uniform density ρi surrounded by the coaxial transition layer (or shell) with continuous density profile ρ0(r), gradually decreasing to its value in the environment ρe. The radius of the cord is a and the external radius of the shell is R. The longitudinal magnetic field is uniform and the same everywhere, to keep the magnetic pressure balance at the cord-shell and shell-environment interfaces, B = Bez, where ez is a unit longitudinal vector in the cylindrical coordinate system. Specifically, the density profile has a form ![\begin{equation} \rho (r) = \left\{ \begin{array}{l} \displaystyle {\rho _i ,}\, r \le a,\\[2.5mm] \frac{{{\rho_{\rm e}}{R^2} - {\rho _i}{a^2}}}{{{R^2} - {a^2}}} + ({\rho _i} - {\rho_{\rm e}})\frac{{{R^2}{a^2}}}{{({R^2} - {a^2}){r^2}}},\, a \le r \le R,\\[2.5mm] \displaystyle {\rho _{\rm e}} ,\, r \ge R. \end{array} \right. \end{equation}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq9.png) (1)We introduce characteristic radius r0 of the structured loop determined as ρ0 = (ρi + ρe)/2 with the corresponding value
(1)We introduce characteristic radius r0 of the structured loop determined as ρ0 = (ρi + ρe)/2 with the corresponding value 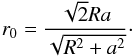 (2)Because it follows from Eq. (2), the characteristic tube radius r0 is equal to a when R ≈ a and tends to constant value
(2)Because it follows from Eq. (2), the characteristic tube radius r0 is equal to a when R ≈ a and tends to constant value 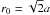 when R ≫ a. Therefore, parameter R can vary in the range a ≤ R< ∞ keeping the physical applicability of the model. The density profile is shown in Fig. 1. We also suppose that the loop ends are anchored in the underlying dense photospheric plasma. It leads to the standing wave pattern in the loop.
when R ≫ a. Therefore, parameter R can vary in the range a ≤ R< ∞ keeping the physical applicability of the model. The density profile is shown in Fig. 1. We also suppose that the loop ends are anchored in the underlying dense photospheric plasma. It leads to the standing wave pattern in the loop.
 |
Fig. 1 Radial profiles of the density in the considered loop model for density contrast χ = 1/9 and different values of the cord-shell radii ratio. The solid, long dashed, dashed, dotted, and dot-dashed curves correspond to the values of a/R = 1, 0.8, 0.5, 0.1, and 0.01, respectively. The vertical axis denotes the value 1 /χ = ρi/ρe. The radial distance is normalized to the cord radius a. |
We then introduce small adiabatic fluctuations of parameters from its equilibrium state, plasma displacements ξ = 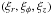 , and magnetic pressure perturbations
, and magnetic pressure perturbations 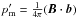 . Since the background parameters are homogeneous along the loop axis (oriented along the z-axis), and axisymmetric perturbations are independent of azimuthal angle φ, we can apply the Fourier transformation in time and longitudinal coordinate z to all variables; i.e.,
. Since the background parameters are homogeneous along the loop axis (oriented along the z-axis), and axisymmetric perturbations are independent of azimuthal angle φ, we can apply the Fourier transformation in time and longitudinal coordinate z to all variables; i.e., 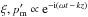 . Then the system of MHD equations can be reduced to two first-order differential equations in terms of radial plasma displacement and total pressure perturbations (Appert et al. 1974; Sakurai et al. 1991). In the particular case of a cold plasma and symmetric sausage wave modes (m = 0), the resulting set of MHD equations has a form
. Then the system of MHD equations can be reduced to two first-order differential equations in terms of radial plasma displacement and total pressure perturbations (Appert et al. 1974; Sakurai et al. 1991). In the particular case of a cold plasma and symmetric sausage wave modes (m = 0), the resulting set of MHD equations has a form
![\begin{eqnarray} && D\frac{{\rm d}}{{{\rm d}r}}\left( {r{\xi _r}} \right) = - Cr{p'_T}, \\[2mm] &&\frac{{{\rm d}{p'_T}}}{{{\rm d}r}} = D{\xi _r}, \end{eqnarray}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq27.png) where
where ![\begin{eqnarray} D &=& \rho \left( {{\omega ^2} - V_{\rm a}^2{k^2}} \right), \\[2mm] C&=&\frac{{{\omega }^{2}}}{V_{\rm a}^{2}}-{{k}^{2}}, \, V_{\rm a}^2 = \frac{{B_z^2}}{{4\pi \rho }}, \end{eqnarray}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq28.png) and Va is the Alfvén speed. Corresponding boundary conditions at the perturbed interfaces are the continuity of radial plasma displacement and Lagrangian magnetic pressure perturbation
and Va is the Alfvén speed. Corresponding boundary conditions at the perturbed interfaces are the continuity of radial plasma displacement and Lagrangian magnetic pressure perturbation
![\begin{eqnarray} &&\left[{{\xi }_{r}} \right]=0, \\[2mm] &&\left[{{{{p}'}}_{\rm m}} \right]=0. \end{eqnarray}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq30.png) The presented boundary conditions by applying to solutions of Eqs. (3) and (4) lead to dispersion relation, determining the features of fast-sausage tube waves. The next stage is to obtain the solutions for ξr and
The presented boundary conditions by applying to solutions of Eqs. (3) and (4) lead to dispersion relation, determining the features of fast-sausage tube waves. The next stage is to obtain the solutions for ξr and 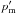 in all regions.
in all regions.
3. Solutions and dispersion relation
The set of first-order differential Eqs. (3) and (4) can be reduced to single second-order differential equation for plasma displacement 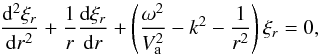 (9)which has the form of Bessel equation. The solution of Eq. (9) in the cord with uniform density must be finite at the tube axis and can be written in terms of Bessel functions of order one:
(9)which has the form of Bessel equation. The solution of Eq. (9) in the cord with uniform density must be finite at the tube axis and can be written in terms of Bessel functions of order one: 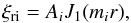 (10)where
(10)where 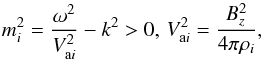 (11)and Ai is an arbitrary constant. Expression for magnetic pressure perturbations according to Eq. (3) is
(11)and Ai is an arbitrary constant. Expression for magnetic pressure perturbations according to Eq. (3) is 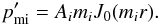 (12)Solutions (10) and (12) corresponds to the body wave regime in the cord since
(12)Solutions (10) and (12) corresponds to the body wave regime in the cord since 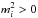 . In the external magnetized medium with uniform density ρe, the solution of Eq. (9) can be expressed in terms of modified Bessel function of the second kind K or Hankel function of the first kind H(1) as
. In the external magnetized medium with uniform density ρe, the solution of Eq. (9) can be expressed in terms of modified Bessel function of the second kind K or Hankel function of the first kind H(1) as ![\begin{equation} \xi_{\rm re}={{A}_{e}}\left\{ \begin{array}{l} \displaystyle {K}_{1} ({n}_{\rm e}r), \, m_{\rm e}^{2}=-n_{\rm e}^{2}<0, \\[3mm] \displaystyle H_{1}^{(1)} ({m}_{\rm e}r), \, m_{\rm e}^{2} >\text{0}\text{,} \end{array}\right. \end{equation}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq41.png) (13)where Ae is arbitrary constant and
(13)where Ae is arbitrary constant and 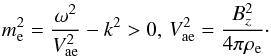 (14)The first solution in Eq. (13) correspond to the evanescent or surface wave regime and vanishes at infinity. The second one describes outwardly propagating waves in the radial direction. From the energy consideration, evanescent solution in the environment leads to the so-called trapped modes in the internal region. Otherwise, the propagating waves in the environment carry the energy away from the interior region, and corresponding wave modes are known as leaky modes. The expression for magnetic pressure perturbations in the environment can be obtained by using Eq. (3).
(14)The first solution in Eq. (13) correspond to the evanescent or surface wave regime and vanishes at infinity. The second one describes outwardly propagating waves in the radial direction. From the energy consideration, evanescent solution in the environment leads to the so-called trapped modes in the internal region. Otherwise, the propagating waves in the environment carry the energy away from the interior region, and corresponding wave modes are known as leaky modes. The expression for magnetic pressure perturbations in the environment can be obtained by using Eq. (3).
In the shell region, the wave Eq. (9) according to Eq. (1) can be rewritten as 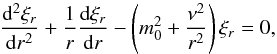 (15)where
(15)where
![\begin{eqnarray} && {{\nu }^{2}}=1-\frac{(1-\chi ){{\omega }^{2}}}{V_{\rm ai}^{2}}\frac{{{R}^{2}}{{a}^{2}}}{{{R}^{2}}-{{a}^{2}}}, \\[2mm] && m_{0}^{2}={{k}^{2}}+\frac{{{\omega }^{2}}}{V_{\rm ai}^{2}}\frac{{{a}^{2}}-\chi {{R}^{2}}}{{{R}^{2}}-{{a}^{2}}}, \,\, \,\, \chi =\frac{{{\rho }_{\rm e}}}{{{\rho }_{i}}}=\frac{V_{\rm ai}^{2}}{V_{\rm ae}^{2}}\cdot \end{eqnarray}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq45.png) The variety of solutions of Eq. (15) depends on the values of
The variety of solutions of Eq. (15) depends on the values of 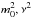 , and
, and 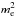 . The first set of solutions is
. The first set of solutions is ![\begin{equation} \xi_{\rm re}\!=\!\left\{ \begin{array}{l} \displaystyle {{A}_{0}}{{K}_{\nu }}({{m}_{0}}r)\text{ }+{{B}_{0}}{{I}_{\nu }}\text{(}{{m}_{0}}r),\, \text{ }m_{0}^{2}>0,\text{ }{{\nu }^{2}}\ge 0, \\[2mm] \displaystyle {{A}_{0}}{{K}_{{\rm i}q}}({{m}_{0}}r)\text{ }+{{B}_{0}}{{L}_{{\rm i}q}}\text{(}{{m}_{0}}r),\,\text{ }m_{0}^{2}\text{ }>\text{0}\text{, }{{\nu }^{2}}=-{{q}^{2}}<0.\text{ } \end{array} \right. \end{equation}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq48.png) (18)For the general case of real non-integer or imaginary order ν, the modified Bessel functions of the first kind Iν and I− ν are linearly independent and solutions of Eq. (15) can be expressed through their relations (Abramowitz & Stegun 1970)
(18)For the general case of real non-integer or imaginary order ν, the modified Bessel functions of the first kind Iν and I− ν are linearly independent and solutions of Eq. (15) can be expressed through their relations (Abramowitz & Stegun 1970)
![\begin{eqnarray} && K_{\nu }({{m}_{0}}r)=\frac{\pi }{2\sin (\pi \nu )} \nonumber \\[2mm] &&\qquad \qquad \; \times~\left( {{I}_{-\nu }}({{m}_{0}}r)-{{I}_{\nu }}({{m}_{0}}r) \right)\text{ for real }\nu \text{ or }\nu ={\rm i}q, \\[4mm] && L_{{\rm i}q}({{m}_{0}}r)=\frac{\pi }{2}\left( {{I}_{-{\rm i}q}}({{m}_{0}}r)+{{I}_{{\rm i}q}}({{m}_{0}}r) \right)\text{. } \end{eqnarray}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq52.png) Both Kiq and Liq are real quantaties for the real m0 according to Eqs. (19) and (20). The set of solutions given by Eq. (18) represents either the pure surface (evanescent) wave regime in the radial direction or hybrid wave regime, describing by the modified Bessel function of imaginary order. Indeed, by using Eqs. (19) and (20), the expansion series of Bessel functions for small argument (Abramowitz & Stegun 1970) we can obtain
Both Kiq and Liq are real quantaties for the real m0 according to Eqs. (19) and (20). The set of solutions given by Eq. (18) represents either the pure surface (evanescent) wave regime in the radial direction or hybrid wave regime, describing by the modified Bessel function of imaginary order. Indeed, by using Eqs. (19) and (20), the expansion series of Bessel functions for small argument (Abramowitz & Stegun 1970) we can obtain ![\begin{eqnarray} && K_{{\rm i}q}({{m}_{0}}r)\approx -\sqrt{\frac{\pi }{q\sin (\pi q)}}\sin \left( q\ln \left( \frac{{{m}_{0}}r}{2} \right)-\delta \right), \\[2mm] && L_{{\rm i}q} ({{m}_{0}}r)\approx \sqrt{\frac{\pi }{q\sin (\pi q)}}\cos \left( q\ln \left( \frac{{{m}_{0}}r}{2} \right)-\delta \right)\cdot \end{eqnarray}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq56.png) Here m0r ≪ 1, δ = argΓ(1 + iq), and Γ is a gamma function. Equations (21) and (22) describe the stationary wave structures at least in the vicinity of the cord-shell interface. While if we consider asymptotic expansions of Bessel functions Iν and I− ν for a large argument, we arrive at (Dunster 1990)
Here m0r ≪ 1, δ = argΓ(1 + iq), and Γ is a gamma function. Equations (21) and (22) describe the stationary wave structures at least in the vicinity of the cord-shell interface. While if we consider asymptotic expansions of Bessel functions Iν and I− ν for a large argument, we arrive at (Dunster 1990) ![\begin{eqnarray} && K_{{\rm i}q}({{m}_{0}}r)\propto {{\rm e}^{-{{m}_{0}}r}}, \,\, \\[2mm] && L_{{\rm i}q}({{m}_{0}}r)\propto {{\rm e}^{{{m}_{0}}r}}, \end{eqnarray}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq61.png) and solutions are evanescent waves far from the interface. Indeed, the waves with phase speed Vph = ω/k in the range Vai ≤ Vph ≤ Vae propagate through the shell up to the critical point, where they are reflected. At this critical point, the local Alfvén speed is equal to the wave phase speed. Thus in this region of the shell,the radially standing wave pattern is formed, while in the far region of the shell, there is the surface wave structure. For this reason we can conclude that pure surface waves in the shell cannot exist in our model. Indeed, as mentioned above, only body modes are possible in the cord with Vph ≥ Vai. As a consequence, they are radially propagating at least in the vicinity of the cord-shell boundary. According to Eq. (17), when a2>χR2, we have
and solutions are evanescent waves far from the interface. Indeed, the waves with phase speed Vph = ω/k in the range Vai ≤ Vph ≤ Vae propagate through the shell up to the critical point, where they are reflected. At this critical point, the local Alfvén speed is equal to the wave phase speed. Thus in this region of the shell,the radially standing wave pattern is formed, while in the far region of the shell, there is the surface wave structure. For this reason we can conclude that pure surface waves in the shell cannot exist in our model. Indeed, as mentioned above, only body modes are possible in the cord with Vph ≥ Vai. As a consequence, they are radially propagating at least in the vicinity of the cord-shell boundary. According to Eq. (17), when a2>χR2, we have 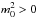 for all values of wave frequency. Then the appropriate solutions of Eq. (15) in the shell are modified Bessel functions of imaginary order and these solutions are valid for any values of
for all values of wave frequency. Then the appropriate solutions of Eq. (15) in the shell are modified Bessel functions of imaginary order and these solutions are valid for any values of 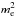 .
.
When 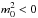 , the set of solutions of Eq. (15) is
, the set of solutions of Eq. (15) is ![\begin{equation} \xi_{\rm re}=\left\{ \begin{array}{l} \displaystyle {{A}_{0}}{{Y}_{\nu }}({{n}_{0}}r)\text{ }+{{B}_{0}}{{J}_{\nu }}\text{(}{{n}_{0}}r) \text{ } ,\text{ }m_{\rm e}^{2}<0, \\[2mm] \displaystyle {{A}_{0}}H_{\nu }^{(2)}({{n}_{0}}r)\text{ }+{{B}_{0}}H_{\nu }^{(1)}\text{(}{{n}_{0}}r),\text{ }m_{\rm e}^{2}>\text{0}\text{. } \\ \end{array} \right. \end{equation}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq68.png) (25)Here
(25)Here 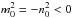 , and ν is real or ν = iq. The first solution in Eq. (25) describes the standing waves in the shell, while the second one is the superposition of outward and inward (reflected) waves. The expression for magnetic pressure perturbations in the shell can be obtained by using Eq. (3).
, and ν is real or ν = iq. The first solution in Eq. (25) describes the standing waves in the shell, while the second one is the superposition of outward and inward (reflected) waves. The expression for magnetic pressure perturbations in the shell can be obtained by using Eq. (3).
Applying the boundary conditions given by Eqs. (7) and (8) to the cord-shell and shell-environment interfaces, we arrive at the desired dispersion relation for fast-sausage waves 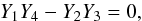 (26)where
(26)where
![\begin{eqnarray} && Y_{1}={{X}_{i}}{{\left( {{m}_{0}}a{{L}_{{\rm i}q}}({{m}_{0}}a) \right)}^{\prime }}-{{L}_{{\rm i}q}}({{m}_{0}}a), \\[2mm] && Y_{2}={{X}_{i}}{{\left( {{m}_{0}}a{{K}_{{\rm i}q}}({{m}_{0}}a) \right)}^{\prime }}-{{K}_{{\rm i}q}}({{m}_{0}}a), \\[2mm] && Y_{3}={{\left( {{m}_{0}}R{{L}_{{\rm i}q}}({{m}_{0}}R) \right)}^{\prime }}-{{X}_{\rm e}}{{L}_{{\rm i}q}}({{m}_{0}}R), \\[2mm] && Y_{4}={{\left( {{m}_{0}}R{{K}_{{\rm i}q}}({{m}_{0}}R) \right)}^{\prime }}-{{X}_{\rm e}}{{K}_{{\rm i}q}}({{m}_{0}}R), \\[2mm] && X_{i}=\frac{{{J}_{1}}({{m}_{i}}a)}{{{m}_{i}}a{{J}_{0}}({{m}_{i}}a)} \\[2mm] && X_{e}=\left\{ \begin{array}{l} \displaystyle -\frac{n{}_{\rm e}R{{K}_{0}}({{n}_{\rm e}}R)}{{{K}_{1}}({{n}_{\rm e}}R)} \text{, }m_{\rm e}^{2}=-n_{\rm e}^{2}<0 \\[6mm] \displaystyle \frac{m{}_{\rm e}RH_{0}^{(1)}({{m}_{\rm e}}R)}{H_{1}^{(1)}({{m}_{\rm e}}R)} \text{, }m_{\rm e}^{2}>0.\\ \end{array} \right. \end{eqnarray}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq72.png) Hereinafter the prime denotes the derivative evaluated at values of the argument m0a and m0R. The dispersion relation given by Eq. (26) is written for ν = iq,
Hereinafter the prime denotes the derivative evaluated at values of the argument m0a and m0R. The dispersion relation given by Eq. (26) is written for ν = iq, 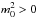 . In other cases the appropriate solutions must be chosen as discussed above. Dispersion Eq. (26) describes the properties of fast-sausage waves in nonuniform structured coronal flux tubes consisting of the central part (cord) and transitional region (shell) with the continuous density profile given by Eq. (1). When R → a, our model reduces to the discontinuous density profile limit. We immediately obtain from Eq. (26)
. In other cases the appropriate solutions must be chosen as discussed above. Dispersion Eq. (26) describes the properties of fast-sausage waves in nonuniform structured coronal flux tubes consisting of the central part (cord) and transitional region (shell) with the continuous density profile given by Eq. (1). When R → a, our model reduces to the discontinuous density profile limit. We immediately obtain from Eq. (26) 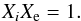 (33)Equation (33) is a well known dispersion relation for fast sausage waves in a cold plasma cylinder with a discontinuity of the density profile at the tube-environment interface (Zaitsev & Stepanov 1975; Edwin & Roberts 1983).
(33)Equation (33) is a well known dispersion relation for fast sausage waves in a cold plasma cylinder with a discontinuity of the density profile at the tube-environment interface (Zaitsev & Stepanov 1975; Edwin & Roberts 1983).
4. Results and discussion
4.1. Cut-off wave number
Cut-off wave number (or wavelength) kc determines the critical point separating the trapped and leaky wave regimes in the loop. It can be obtained if we set Vph = Vae in the dispersion Eq. (26). In this case Xe → 0 and Eqs. (11), (16) and (17) reduce to ![\begin{equation} \begin{array}{l} \displaystyle m_{i}^{2}=k_{}^{2}\frac{1-\chi }{\chi },\text{ }\nu _{}^{2}=1-\frac{(1-\chi )}{\chi }\frac{k_{}^{2}{{R}^{2}}{{a}^{2}}}{{{R}^{2}}-{{a}^{2}}}, \\[3mm] \displaystyle m_{0}^{2}=k_{}^{2}\left( 1+\frac{1}{\chi }\frac{{{a}^{2}}-\chi {{R}^{2}}}{{{R}^{2}}-{{a}^{2}}} \right)\cdot \end{array} \end{equation}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq81.png) (34)The resulting transcendental equation is
(34)The resulting transcendental equation is 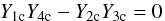 (35)where index c implies that all values in Eq. (35) are evaluated at Vph = Vae. Equation (35) can be solved numerically, but analytical treatment is still possible in the limiting cases. When a → R the thickness of the shell (transition layer) tends to zero. Equation (35) reduces to J0(mica) = 0 and corresponds to the well known solution for cut-off wave number in coronal loops with discontinuous density profiles (Roberts et al. 1984)
(35)where index c implies that all values in Eq. (35) are evaluated at Vph = Vae. Equation (35) can be solved numerically, but analytical treatment is still possible in the limiting cases. When a → R the thickness of the shell (transition layer) tends to zero. Equation (35) reduces to J0(mica) = 0 and corresponds to the well known solution for cut-off wave number in coronal loops with discontinuous density profiles (Roberts et al. 1984) 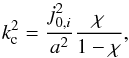 (36)where j0,i are zeros of the Bessel function J0. In the opposite case of a thick shell, when R ≫ a it follows that m0 → 0 and we can substitute the expressions for modified Bessel functions of imaginary order for small argument given by Eqs. (21) and (22) in Eq. (35) to obtain
(36)where j0,i are zeros of the Bessel function J0. In the opposite case of a thick shell, when R ≫ a it follows that m0 → 0 and we can substitute the expressions for modified Bessel functions of imaginary order for small argument given by Eqs. (21) and (22) in Eq. (35) to obtain 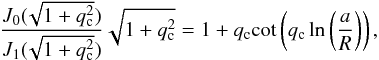 (37)where
(37)where 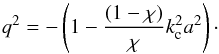 (38)The transcendental Eq. (37) has an infinite number of solutions and can be solved numerically. But we can give a fairly accurate expression for the limiting value of the cut-off wave number of the global fast sausage mode corresponding to the first solution of Eq. (37). Indeed, we can rewrite Eq. (37) in the form
(38)The transcendental Eq. (37) has an infinite number of solutions and can be solved numerically. But we can give a fairly accurate expression for the limiting value of the cut-off wave number of the global fast sausage mode corresponding to the first solution of Eq. (37). Indeed, we can rewrite Eq. (37) in the form ![\begin{equation} q_{\rm c}=-{\rm arccot}\left[\left( 1-\frac{{{J}_{0}}(\sqrt{1+q_{\rm c}^{2}})}{{{J}_{1}}(\sqrt{1+q_{\rm c}^{2}})}\sqrt{1+q_{\rm c}^{2}} \right)q_{\rm c}^{-1} \right]{{\ln }^{-1}}\left( \frac{a}{R} \right)\cdot \end{equation}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq92.png) (39)Since the arccotangent function is bounded on its definition domain and |ln(a/R)| ≫ 1 as R ≫ a, we can conclude that qc ≈ 0 is the approximate solution of Eq. (39) with the corresponding cut-off wave number following from Eqs. (2) and (34)
(39)Since the arccotangent function is bounded on its definition domain and |ln(a/R)| ≫ 1 as R ≫ a, we can conclude that qc ≈ 0 is the approximate solution of Eq. (39) with the corresponding cut-off wave number following from Eqs. (2) and (34) 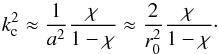 (40)The corresponding cut-off frequency of fundamental fast-sausage mode is
(40)The corresponding cut-off frequency of fundamental fast-sausage mode is ![\hbox{$\omega^{2}=V_{\rm ai}^{2}/\left[{{a}^{2}}\left( 1-\chi \right) \right]$}](/articles/aa/full_html/2014/12/aa24546-14/aa24546-14-eq96.png) . As follows from Eqs. (36) and (40), the cut-off wave numbers differ by a factor j0,1 in two limiting cases. To corroborate these results, we perform numerical calculations of Eq. (37). In Fig. 2 the dependence of the normalized cut-off wave number as a function of cord-shell radii ratio is shown. It is clearly seen that in the limit of discontinuous density profile R → a, the normalized cut-off wave number tends to the value given by Eq. (36), while in the opposite limit its value is determined by Eq. (40). Thus, the effect of the transition layer leads to reduction of cut-off wave number of fundamental mode by a factor j0,1 in diffuse coronal loops.
. As follows from Eqs. (36) and (40), the cut-off wave numbers differ by a factor j0,1 in two limiting cases. To corroborate these results, we perform numerical calculations of Eq. (37). In Fig. 2 the dependence of the normalized cut-off wave number as a function of cord-shell radii ratio is shown. It is clearly seen that in the limit of discontinuous density profile R → a, the normalized cut-off wave number tends to the value given by Eq. (36), while in the opposite limit its value is determined by Eq. (40). Thus, the effect of the transition layer leads to reduction of cut-off wave number of fundamental mode by a factor j0,1 in diffuse coronal loops.
 |
Fig. 2 Dependence of the normalized cut-off wave number kcr0 on the cord-shell radii ratio for density contrast χ = 0.1. The horizontal dashed and dashed-dot lines correspond to the normalized cut-off wave numbers in the limiting cases a/R = 1 and a/R = 0, respectively. |
4.2. The long-wavelength approximation
Let us perform an analytical study of the frequency and damping rate of fast-sausage oscillations in the long-wavelength approximation kr0 ≪ 1 which is equivalent to ka ≪ 1 according to Eq. (2).
4.2.1. The thick shell limit
It is of interest to examine the condition 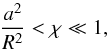 (41)corresponding to a thick transition layer (shell). Nevertheless, according to Eq. (2), the effective loop radius r0 is equal to
(41)corresponding to a thick transition layer (shell). Nevertheless, according to Eq. (2), the effective loop radius r0 is equal to 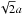 . In this case the expressions for ν and m0 take a form
. In this case the expressions for ν and m0 take a form 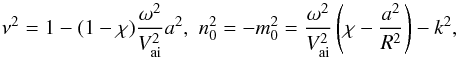 (42)and according to Eq. (24) solution in the shell region is the superposition of Hankel functions. It follows from Eq. (42) that n0a ≪ 1. Then, by using the expansions of Hankel functions for small arguments,the dispersion relation given by Eq. (26) reduces to
(42)and according to Eq. (24) solution in the shell region is the superposition of Hankel functions. It follows from Eq. (42) that n0a ≪ 1. Then, by using the expansions of Hankel functions for small arguments,the dispersion relation given by Eq. (26) reduces to 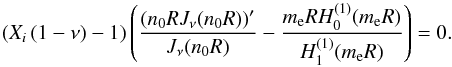 (43)The first factor in Eq. (43) has no roots in the considered domain, while the second one determines the desired dispersion curves. It is straightforward to show from Eq. (42) that
(43)The first factor in Eq. (43) has no roots in the considered domain, while the second one determines the desired dispersion curves. It is straightforward to show from Eq. (42) that 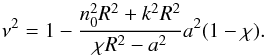 (44)Then, when (a/R)2 ≪ χ, we have ν2 ≈ 1, n0 ≈ me and the dispersion Eq. (43) takes a simple form
(44)Then, when (a/R)2 ≪ χ, we have ν2 ≈ 1, n0 ≈ me and the dispersion Eq. (43) takes a simple form 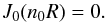 (45)To obtain Eq. (45) we consider that the real part of the second term in Eq. (43) containing the Hankel functions is negligible. Equation (45) immediately gives the dispersion relation
(45)To obtain Eq. (45) we consider that the real part of the second term in Eq. (43) containing the Hankel functions is negligible. Equation (45) immediately gives the dispersion relation 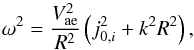 (46)where j0,i are zeros of the Bessel function J0. When kR ≫ j0,i we find
(46)where j0,i are zeros of the Bessel function J0. When kR ≫ j0,i we find 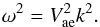 (47)From the derived Eq. (46) we can conclude that the frequency of fast-sausage oscillations in the long-wavelength limit depends on the shell radius, longitudinal wavelength, and external Alfvén speed. In the case kR ≫ j0,i, the frequency is a function of longitudinal wavelength and external Alfvén speed only, and Eq. (47) has the form of the dispersion relation for waves in one-dimensional waveguides. Pascoe et al. (2007) performed the numerical study of fast-sausage oscillations in the loop modeled as a density enhancement in the form of the Epstein profile in Cartesian geometry. They find that in the leaky wave regime the period (or frequency) of fast-sausage oscillations is determined mainly by the external Alfvén speed, which is consistent with our Eqs. (46) and (47). Our case, given by Eq. (41), is similar to the Epstein profile in Cartesian geometry.
(47)From the derived Eq. (46) we can conclude that the frequency of fast-sausage oscillations in the long-wavelength limit depends on the shell radius, longitudinal wavelength, and external Alfvén speed. In the case kR ≫ j0,i, the frequency is a function of longitudinal wavelength and external Alfvén speed only, and Eq. (47) has the form of the dispersion relation for waves in one-dimensional waveguides. Pascoe et al. (2007) performed the numerical study of fast-sausage oscillations in the loop modeled as a density enhancement in the form of the Epstein profile in Cartesian geometry. They find that in the leaky wave regime the period (or frequency) of fast-sausage oscillations is determined mainly by the external Alfvén speed, which is consistent with our Eqs. (46) and (47). Our case, given by Eq. (41), is similar to the Epstein profile in Cartesian geometry.
The attenuation of the loop oscillations due to wave radiation in the external medium leads to complex-valued frequencies. Assuming that ω = ω0 − iγ and γ ≪ ω0, where ω0 is given by either Eq. (46) or Eq. (47), we can derive an expression for damping rate γ through dispersion Eq. (43). We apply the Taylor expansion of Bessel functions on the small quantity γ to the second factor of Eq. (43). Then we separate the real and imaginary parts of resulting complex relation. The real part gives the frequency correction for the damping effect, while the imaginary part leads to the desired damping rate 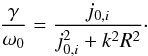 (48)It follows from Eq. (48) the damping rate γ of fundamental fast-sausage mode (corresponds to j0,1) is independent of a low density contrast χ, but is sensitive to the model parameter kR and vanishes when kR ≫ j0,i. Indeed, the last condition corresponds to undamped trapped modes because their phase speed tends to external Alfvén speed Vph → Vae (see Eq. (47)). This effect leads to conservation of the oscillation energy in the core and shell. On the other hand, the damping decrement of modes with high radial wave numbers is approximately
(48)It follows from Eq. (48) the damping rate γ of fundamental fast-sausage mode (corresponds to j0,1) is independent of a low density contrast χ, but is sensitive to the model parameter kR and vanishes when kR ≫ j0,i. Indeed, the last condition corresponds to undamped trapped modes because their phase speed tends to external Alfvén speed Vph → Vae (see Eq. (47)). This effect leads to conservation of the oscillation energy in the core and shell. On the other hand, the damping decrement of modes with high radial wave numbers is approximately 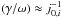 , and it vanishes for large zeros j0,i.
, and it vanishes for large zeros j0,i.
4.2.2. The thin shell limit
The thin transition layer (shell) limit corresponds to the condition l ≪ a, where l = R − a is the thickness of the shell. To further derivation, we rewrite the general dispersion Eq. (26) in more convenient form 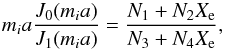 (49)where
(49)where 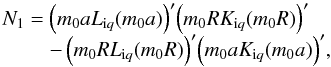 (50)
(50)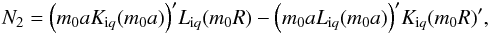 (51)
(51)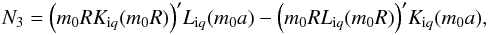 (52)
(52)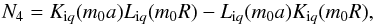 (53)and Xe is given by Eq. (32). Since R = a + l, we can apply the Taylor expansions of Bessel functions on the small quantity l to coefficients given by the above equations. Taking the components up to of order l2 into account we arrive at
(53)and Xe is given by Eq. (32). Since R = a + l, we can apply the Taylor expansions of Bessel functions on the small quantity l to coefficients given by the above equations. Taking the components up to of order l2 into account we arrive at 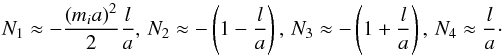 (54)According to Eqs. (54) and (32), dispersion Eq. (49) can be reduced to
(54)According to Eqs. (54) and (32), dispersion Eq. (49) can be reduced to 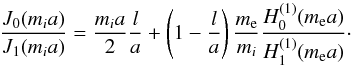 (55)In the case of dense loop, corresponding to condition χ ≪ 1 (or mellmi), dispersion Eq. (55) takes a simple form
(55)In the case of dense loop, corresponding to condition χ ≪ 1 (or mellmi), dispersion Eq. (55) takes a simple form 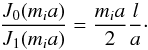 (56)The approximate solution of Eq. (56) can be derived analytically, since l ≪ a. Substituting mia = j0,i + δ into Eq. (56), where δ is a small quantity, and applying the Taylor expansions of Bessel functions on the parameter δ, we immediately obtain δ ≈ − (mia/ 2)(l/a) and desired dispersion relation
(56)The approximate solution of Eq. (56) can be derived analytically, since l ≪ a. Substituting mia = j0,i + δ into Eq. (56), where δ is a small quantity, and applying the Taylor expansions of Bessel functions on the parameter δ, we immediately obtain δ ≈ − (mia/ 2)(l/a) and desired dispersion relation 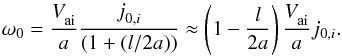 (57)The corresponding damping rate can be obtained by the standard procedure, described above. The result is
(57)The corresponding damping rate can be obtained by the standard procedure, described above. The result is 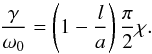 (58)Thus, the effect of the thin transition layer produces small reductions of oscillation frequencies and relative damping decrement, which are linearly proportional to the shell thickness.
(58)Thus, the effect of the thin transition layer produces small reductions of oscillation frequencies and relative damping decrement, which are linearly proportional to the shell thickness.
Condition l → 0 corresponds to the case of a step-function density profile, which was extensively studied in the past. Dispersion Eq. (55) reduces to Eq. (33). In the long-wavelength approximation, Eq. (33) leads to the well-known expression for fast-sausage mode frequency (Zaitsev & Stepanov 1975; Meerson et al. 1978) 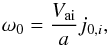 (59)which is valid for low values of density contrast χ ≪ 1. The corresponding damping rate is (Zaitsev & Stepanov 1975; Meerson et al. 1978)
(59)which is valid for low values of density contrast χ ≪ 1. The corresponding damping rate is (Zaitsev & Stepanov 1975; Meerson et al. 1978) 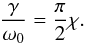 (60)Equation (60) means that only the loops with a low density contrast can support the fast-sausage oscillations of detectable quality.
(60)Equation (60) means that only the loops with a low density contrast can support the fast-sausage oscillations of detectable quality.
 |
Fig. 3 Dependence of the normalized frequency of fast-sausage oscillations on the normalized wave number ka for density contrast χ = 0.1 and different values of the cord-shell radii ratio. The thick solid, thin solid, dashed, dot-dashed and the dotted curves correspond to values of a/R = 1, 0.8, 0.5, 0.1, and 0.02, respectively. |
4.2.3. The short-wavelength limit
The short-wavelength limit corresponds to condition kR>ka ≫ 1. In this case there are only trapped modes. The solutions in the shell region and environment are the modified Bessel functions of imaginary and real order, respectively. Since m0R ≫ 1 and m0a ≫ 1, we can apply the asymptotic expansions of modified Bessel functions for large argument. Dispersion Eq. (26) then reduces to 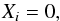 (61)leading to
(61)leading to 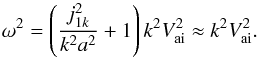 (62)The result given by Eq. (62) is the same as in the classical model of magnetic plasma cylinder with a step-function density profile (Edwin & Roberts 1983).
(62)The result given by Eq. (62) is the same as in the classical model of magnetic plasma cylinder with a step-function density profile (Edwin & Roberts 1983).
4.2.4. Numerical calculations
We performed numerical calculations of general dispersion Eq. (26) in the context of a dependence of the fast-sausage oscillation frequency on the model parameters. We are mainly interested in the leaky wave regime and long-wavelength limit in our calculations. The cord radius and internal Alfvén speed were taken to be unity. Then the frequency of global sausage mode in the case of discontinuous density profile and long-wavelength limit, according to Eq. (59) is simply ωd = j01 ≈ 2.40s-1. In Fig. 3 we have displayed the numerically calculated dispersion curves for global sausage mode as the dependence of frequency on the normalized wave number. The displayed curves correspond to different ratios of cord-shell radii. In the long-wavelength limit (ka ≪ 1), the frequency of global sausage mode strongly depends on the thickness of the shell (or ratio of cord-shell radii). It is evident that for the lower values of cord-shell radii ratio, the frequency becomes lower. This result agrees with analytic calculations in the previous section.
The frequency of fast-sausage mode is mainly determined by the internal Alfvén speed and the radial wave number in the case of thin shell (steep density profile) or discontinuous density profile (see Eq. (49)). In the case of more diffuse loop boundary, the frequency primarily depends on the external Alfvén speed and the longitudinal wave number, as follows from Eqs. (46) and (47). Another important feature is the dependence of frequency upon the longitudinal wave number. In the long-wavelength limit and steep or discontinuous density profile, the frequency is almost independent of the longitudinal wave number in agreement with Eq. (59). In the case of a thick shell, the frequency grows with increasing wave number even when ka ≪ 1. This is evident, since the frequency is a linear function of the longitudinal wave number, according to Eq. (47). For the values of wave number ka> 1, the frequency of global sausage mode increases almost linearly.
 |
Fig. 4 Dependence of the normalized frequency of fast-sausage oscillations on the cord-shell radii ratio for normalized wave number ka = 0.1 and different values of the density contrast χ. The solid, dashed, and dot-dashed curves correspond to values of χ = 0.25, 0.1, and 0.04, respectively. |
The dependence of oscillation frequency on the ratio of cord-shell radii is shown in Fig. 4. We have displayed the curves for different values of density contrast and for normalized wave number ka = 0.1 corresponding to the leaky wave regime. In the long-wavelength limit and thick transitional layer (a/R ≪ 1) the oscillation frequency is determined mainly by the external Alfvén speed. This result is consistent to Eqs. (46) and (47). With a decreasing shell thickness, the frequency increases and tends to the limiting value, which is independent of density (or Alfvén speed) contrast. Indeed, this limiting frequency is given by Eq. (59) and depends on the internal Alfvén speed.
4.2.5. Seismological application
In this section we apply the theoretical results to observed quasi-periodic pulsations of microwave emission in a flare event, where all oscillation characteristics were described. Kupriyanova et al. (2010) reported the results of observation of microwave pulsations associated with the single flaring loop of length L ≈ 25 Mm and approximate cross-section radius a ≈ 2.5 Mm. Several significant spectral components with periods in the range 15–20 s and 8–9 s have been found. The quality of the oscillations varies in the range 12 to 40, with an average value Q ≈ 25. The model of the step-function density profile gives χ ≈ 1/80 (according to Eq. (60)) for the density contrast to explain the observed quality of fundamental oscillations as a leaky mode. Another possibility suggests the existence of principal fast-sausage mode of coronal loop at the cut-off frequency (Nakariakov et al. 2003), which is still trapped mode. In this case the necessary condition for the global sausage mode is 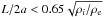 , and we have the estimation χ< 1/60.
, and we have the estimation χ< 1/60.
In all these cases we therefore obtain a rather extreme, but not completely unrealistic estimation of density contrast in flaring coronal loops. We suggest an alternative interpretation. Based on our theoretical results, we identify the observed pulsations with periods in the range 15–20 s as the leaky fundamental fast-sausage mode, excited in flaring loop with diffuse boundary, while the oscillations in the range 8–9 s are possibly the second harmonic. On the basis of Eqs. (46) and (48) we obtain the correct estimation Vae ≈ 3.25 Mm/s for external Alfvén speed for the shell thickness R ≈ 3.4L, without any assumptions about the density contrast. We also emphasize the existence of a broad spectral maxima. We suggest that this effect is due to excitation of harmonics with different radial degrees (or radial wave numbers), but with the same longitudinal wavelength, these harmonics have approximately identical frequency. Indeed, our estimation gives the value k1R ≈ 10.6 for the fundamental mode (k1 = π/L) and according to Eq. (46), we have ω1,1/ω1,2 ≈ 0.91, ω1,2/ω1,3 ≈ 0.88, where the radial degree of the mode is determined by the zeros j0,i of the Bessel function J0. Thus, our model gives an appropriate estimation of Alfvén speed outside the loop and correctly describes the spectral features of observed pulsations, their frequencies, and quality.
5. Conclusions
We have analytically and numerically studied the properties of the fast-sausage oscillations of nonuniform coronal loops. The coronal waveguide is modeled as a low-β plasma cylinder consisting of central cord with uniform density and transition layer (or shell) with continuously varying density in the radial direction. The structured magnetic cylinder is embedded within a magnetic environment with uniform density. Such a model describes the coronal loops with diffuse boundary. We obtained the general dispersion relation governing the properties of fast-sausage waves. The dispersion relation is studied analytically in the long-wavelength limit, which seems to be appropriate for describing the fundamental fast-sausage mode in coronal loops. Analytic expressions of frequency and damping decrement for the case of thick and thin transition layers were derived. The analytic treatment is confirmed by the numerical calculations. The results obtained can be represented as follows:
-
1.
The cut-off wave number slightly decreases with increasingshell thickness. The effect of the thick transition layer leads toreducing the cut-off wave number of the fundamentalfast-sausage mode by a factor j0,1 in comparison to the discontinuous density profile limit.
-
2.
In the case of a steep (thin-shell condition in our model) or discontinuous density profile, which corresponds to a sharp loop boundary, the frequency of fast-sausage modes mainly depends on the internal Alfvén speed and radial wave number (j0,ia-1). The relative damping decrement linearly depends on the density contrast χ for all modes with different radial wave numbers. The effect of the thin transition layer produces small reductions in the oscillation frequencies and relative damping rate of fundamental and high radial wave-number modes. These reductions were found to be linearly proportional to the layer thickness.
-
3.
For a coronal loop with diffuse boundary (thick-shell condition in our model) the frequency of the fundamental fast-sausage mode is determined mainly by the Alfvén speed outside the loop and longitudinal wave number. A similar result has been obtained by Pascoe et al. (2007) and Nakariakov et al. (2012) on the basis of numerical simulations of fast-sausage waves in diffuse coronal loops. The relative damping rate is independent of the low density contrast (χ ≪ 1) but is sensitive to the model parameter kR and radial mode degree (determined by the coefficient j0,i). When kR ≫ j0,i the relative damping decrement of fundamental mode vanishes according to (kR)-2, while for modes with high radial wave numbers, it behaves as
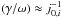 and vanishes for large zeros j0,i.
and vanishes for large zeros j0,i. -
4.
The model of the loop with a diffuse boundary supports comparatively low-frequency and high-quality fundamental fast-sausage oscillations. These oscillations can be responsible for the observed quasi-periodic pulsations with periods up to tens of seconds in flare-associated events.
-
These results have a seismological application. On the basis of observed periods and the damping time of coronal pulsations we can estimate the value of Alfvén speed in the environment of coronal loops by using Eqs. (46) and (48). With our findings, we can interpret the observed quasi-periodic pulsations with periods in the range 10–40 s and rather high quality (Trottet et al. 1979; Kupriyanova et al. 2010) in terms of fundamental fast-sausage oscillations of coronal loops with diffuse boundary. The estimates of external Alfvén speed for the flare event give an appropriate value in the range of 3–4 Mm/s. Our results demonstrate that in the leaky wave regime the period of standing fast-sausage oscillations is determined by the length of the loop with smooth boundary and is comparable to longitudinal external Alfvén transit time. On the other hand, the period of the same mode in the loop with a steep boundary is equal to the transverse internal Alfvén transit time. To develop this problem further we will consider the effect of different density profiles in the shell on the properties of standing fast-sausage modes.
Acknowledgments
The project was supported by the Far Eastern Federal University. The work was supported by the Ministry of Education and Science of the Russian Federation, agreement 14.575.21.0063.
References
- Abramowitz, M., & Stegun, I. A. 1970, Handbookof Mathematical Functions: With Formulas, Graphs, and Mathematical Tables (New York: Dover) [Google Scholar]
- Abrami, A., & Coren, U. 1978, A&AS, 34, 165 [NASA ADS] [Google Scholar]
- Achong, A. 1974, Sol. Phys., 37, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Appert, K., Gruber, R., & Vaclavik, J. 1974, Phys. Fluids, 17, 1471 [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Nakariakov, V. M., & Melnikov, V. F. 2004, ApJ, 600, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, F. C., Nakariakov, V. M., & Williams, D. R. 2003, A&A, 409, 325 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Defouw, R. J. 1976, ApJ, 209, 226 [Google Scholar]
- Dunster, T. M. 1990, Siam. J. Math. Anal., 21, 995 [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys. 88, 179 [Google Scholar]
- Edwin, P. M., & Roberts, B. 1988, A&A, 192, 343 [NASA ADS] [Google Scholar]
- Erdélyi, R., & Carter, B. K. 2006, A&A, 455, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kopylova, Y. G., Melnikov, A. V., Stepanov, A. V., Tsap, Y. T., & Goldvarg, T. B. 2007, Astron. Lett., 33, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Kupriyanova, E. G., Melnikov, V. F., Nakariakov, V. M., & Shibasaki, K. 2010, Sol. Phys., 267, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Meerson, B. I., Sasorov, P. V., & Stepanov, A. V. 1978, Sol. Phys., 58, 165 [Google Scholar]
- Melnikov, V. F., Reznikova, V. E., Shibasaki, K., & Nakariakov, V. M. 2005, A&A, 439, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Sci., 285, 862 [Google Scholar]
- Nakariakov, V. M., Melnikov, V. F., & Reznikova, V. E. 2003, A&A, 412, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mikhalyaev, B. B., & Solov’ev, A. A. 2005, Sol. Phys., 227, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., & Melnikov, V. F. 2009, Space Sci. Rev., 149, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Hornsey, C., & Melnikov, V. F. 2012, ApJ, 761, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Arber, T. D. 2007, A&A, 461, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pneuman, C. W. 1965, Phys. Fluids, 8, 57 [CrossRef] [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenberg, H. 1970, A&A, 9, 159 [NASA ADS] [Google Scholar]
- Sakurai, T., Goossens, M., & Hollweg, J. I. 1991, Sol. Phys., 133, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Su, J. T., Shen, Y. D., Liu, Y., Liu, Y., & Mao, X. J. 2012, ApJ, 755, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Tapping, K. F. 1978, Sol. Phys., 59, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Trottet, G., Pik, M., & Heyvaerts, J. 1979, A&A, 79, 164 [NASA ADS] [Google Scholar]
- Trottet, G., Kerdraon, A., Benz, A. O., & Treumann, R. 1981, A&A, 93, 129 [NASA ADS] [Google Scholar]
- Uchida, Y. 1970, PASJ, 22, 341 [NASA ADS] [Google Scholar]
- Van Doorsselaere, T., De Groof, A., Zender, J., Berghmans, D., & Goossens, M. 2011, ApJ, 740, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2007, A&A, 473, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaitsev, V. V., & Stepanov, A. V. 1975, Issled. Geomagn. Aeron. Fiz. Solntsa, 37, 3 [Google Scholar]
- Zaitsev, V. V., & Stepanov, A.V. 1982, Sov. Astron. Lett., 8, 132 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Radial profiles of the density in the considered loop model for density contrast χ = 1/9 and different values of the cord-shell radii ratio. The solid, long dashed, dashed, dotted, and dot-dashed curves correspond to the values of a/R = 1, 0.8, 0.5, 0.1, and 0.01, respectively. The vertical axis denotes the value 1 /χ = ρi/ρe. The radial distance is normalized to the cord radius a. |
| In the text | |
 |
Fig. 2 Dependence of the normalized cut-off wave number kcr0 on the cord-shell radii ratio for density contrast χ = 0.1. The horizontal dashed and dashed-dot lines correspond to the normalized cut-off wave numbers in the limiting cases a/R = 1 and a/R = 0, respectively. |
| In the text | |
 |
Fig. 3 Dependence of the normalized frequency of fast-sausage oscillations on the normalized wave number ka for density contrast χ = 0.1 and different values of the cord-shell radii ratio. The thick solid, thin solid, dashed, dot-dashed and the dotted curves correspond to values of a/R = 1, 0.8, 0.5, 0.1, and 0.02, respectively. |
| In the text | |
 |
Fig. 4 Dependence of the normalized frequency of fast-sausage oscillations on the cord-shell radii ratio for normalized wave number ka = 0.1 and different values of the density contrast χ. The solid, dashed, and dot-dashed curves correspond to values of χ = 0.25, 0.1, and 0.04, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


