EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 570 (October 2014) A&A, 570 (2014) A46 Full HTML
Free Access
Issue
A&A
Volume 570, October 2014
Article Number A46
Number of page(s) 8
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201424370
Published online 14 October 2014

© ESO, 2014

1. Introduction

Nucleosynthesis of fluorine (19F) is an intriguing and widely debated problem in stellar nucleosynthesis. Several stellar sites have been proposed as 19F factories: core-collapse supernovae (Woosley & Haxton 1988), Wolf-Rayet stars (Meynet & Arnould 2000), and asymptotic giant branch (AGB) stars (Forestini et al. 1992). While some papers have excluded the first two scenarios (Federman et al. 2005; Palacios et al. 2005), more recent studies stressed the importance of both supernovae (Kobayashi et al. 2011) and Wolf-Rayet stars (Jönsson et al. 2014). Among all the proposed scenarios, however, direct proof of fluorine production has only been proved in AGB stars via spectroscopic detections of [F/Fe] enhancements (see Abia et al. 2009 and references therein).

The first systematic search of fluorine enhancements in AGB stars was done by Jorissen et al. (1992), who measured abundances for red giants of type K, Ba, M, MS, S, SC, N, and J of near solar metallicity. This study found very high 19F surface enrichments (up to 30 times solar) in N-type C stars and a clear correlation between the fluorine enhancement and the C/O ratio. The N-type C stars are low-mass stars close to the AGB tip. Although this occurrence was immediately interpreted as clear evidence of the fluorine synthesis by AGB stars, theoretical models failed to reproduce such an extensive surface fluorine enrichment (Forestini et al. 1992; Lugaro et al. 2004; Cristallo et al. 2009). However, re-analysis by Abia et al. (2009, 2010) of the same sample has reconciled theoretical models with observations. A systematic reduction of fluorine abundances by 0.7 dex on average was found, relating this discrepancy to blends with C-bearing molecular lines not properly taken into account in Jorissen et al. (1992). As a matter of fact, at solar-like metallicities, the agreement between theory and observations is rather good. However, existing fluorine observational data may suffer a non negligible reduction due to an error in the adopted HF excitation energies of infrared lines (see Jönsson et al. 2014). This might systematically diminish the spectroscopic 19F estimates by 0.1 dex up to 0.5 dex in the cooler AGB stars.

At low metallicities, the situation is even more complex. Fluorine measurements in three extragalactic low-metallicity (−2 < [Fe/H] < −1) AGB stars (Abia et al. 2011) disagree with theoretical models, which predict fluorine surface abundances that are about an order of magnitude larger (see Cristallo et al. 2009, 2011, and also Figs. 3 and 4 in Abia et al. 2011). On the other hand, these objects are largely enriched in s-process elements with 0.9 < [ ⟨ s ⟩ /Fe ]1< 1.6 (de Laverny et al. 2006; Abia et al. 2008), thus indicating that the s-process nucleosynthesis is connected to the fluorine production in AGB stars. This implies fairly low [F/⟨ s ⟩] values. Lucatello et al. (2011) also find low [F/⟨ s ⟩] in a sample of Galactic s-process, rich, carbon-enhanced, metal-poor stars, thus confirming the results of Abia et al. (2011).

AGB stars are among the most significant polluters of the interstellar medium. In fact, they eject both light (C, N, F, Na) and heavy elements (see Iben & Renzini 1983; Straniero et al. 2006 for a review). This is the result of the combined action of internal nuclear burning and deep convective mixing episodes taking place during the late part of the AGB, the so-called thermally pulsing AGB (TP-AGB) phase. The presence of free neutrons in the He-rich intershell of these stars, which is required for synthesizing elements heavier than iron, also affects the light elements nucleosynthesis and, among others, fluorine.

The major source of neutrons in low-mass AGB stars is the 13C(α,n)16O reaction (Straniero et al. 1995; Gallino et al. 1998), which releases neutrons in the so-called 13C-pocket. It is clear from work done in the 60s that the 13C left in the H-shell ashes is not sufficient to account for the observed s-process abundances (Fowler et al. 1955). Thus, some protons from the convective envelope penetrating the underlying radiative He-intershell are required during third dredge up (TDU) episodes. Later, when the temperature reaches 108 K, those protons are captured by the abundant 12C, leading to the formation of a thin 13C-enriched layer, the so-called 13C pocket. Actually, the mechanism leading to the formation of the 13C pocket is far from completely understood. In the past few decades, many theories have been proposed (e.g., Sackmann et al. 1974; Iben 1982; Iben & Renzini 1983); most recently, mechanisms, such as mechanical overshoot (Herwig et al. 1997), gravity waves (Denissenkov & Tout 2003), opacity-induced overshoot (Straniero et al. 2006, see Sect. 2), and magnetic fields (Trippella et al. 2014) have been proposed.

An additional neutron burst is powered by the 22Ne(α,n)25Mg reaction, which is activated at the base of the convective zone generated by a thermal pulse (TP) when the temperature exceeds 300 MK. Such a condition is typical of more massive AGB stars (4−6 M⊙) (see Karakas & Lattanzio 2014, for a recent review).

The s-process elements are mainly synthesized by the 13C burning in radiative conditions in the 13C-pocket during interpulse periods. Neutron captures activated by the 13C(α,n)16O also lead to synthesizing a suitable amount of 15N, which produces fluorine via the 15N(α,γ)19F reaction (see Sect. 3). During the first TPs, a fraction of the 13C in the 13C pocket may survive up to the interpulse phase. In this case, this 13C is engulfed in the convective shell generated by the subsequent TP and thus burns in a convective environment (Cristallo et al. 2006). Fluorine is also synthesized starting from the 13C left by the H-burning shell. This 19F source requires, however, the presence of quite a large amount of C+N+O in the H-rich envelope.

In this paper we investigate fluorine nucleosynthesis in low-mass AGB stars by evaluating the effects of the variations in the relevant nuclear reaction rates. In particular, we present the results of an analysis based on an AGB stellar model with initial mass M = 2 M⊙ and Z = 10-3. This model is representative of low-mass AGB stars, i.e. the most promising candidates to reproduce the majority of the observed s-process distributions in AGB stars (see, e.g., Abia et al. 2002). Very similar results can be obtained for different metallicities or slightly different masses (in the range 1.5−2.5 M⊙). In this work high initial stellar masses (4−6 M⊙) are not considered since the (eventually) produced fluorine would be efficiently destroyed by α and neutron captures during TPs (see Sect. 3), owing to the higher temperatures attained by these stars. Moreover, the expected surface s-process distributions of intermediate AGB stars are characterized by low or even negative [hs/ls] indexes and high [Rb/Sr] ratios, in striking contrast to the observed spectra (Abia et al. 2002).

The aim of this work is to identify the nuclear processes whose present uncertainties sizeably affect the theoretical predictions and, thus, deserve further experimental investigations. A similar study of fluorine production in AGB stars was presented almost ten years ago by Lugaro et al. (2004). In comparison to that work we extended the study to a larger number of reactions. Moreover, in the past decade, several nuclear cross sections have been measured, or predicted, with improved precision.

In Sect. 2 we briefly present the stellar evolutionary code used to calculate the AGB models. In Sect. 3, the fluorine nucleosynthesis path and the nuclear network we use are illustrated. We also critically discuss the uncertainties affecting all the relevant reaction rates. The results of our analysis are illustrated and discussed in Sect. 4, and our conclusions follow.

Table 1

Sources of the reaction rates relevant for fluorine nucleosynthesis.

2. Stellar models

The stellar models presented in this work were computed with the FUNS (FUll Network Stellar) evolutionary code (see Straniero et al. 2006, and references therein). This code includes a full nuclear network with all the relevant isotopes from H up to Bi, the heaviest element synthesized by the s process, for a total of nearly 500 isotopes linked by more than 1000 nuclear reactions. The coupling of the stellar structure equations with this full network allows some limitations related to the use of simplified assumptions to be overcome so as to describe stellar phases in which the nucleosynthesis is strongly related to the changes in the physical properties of the stellar environment and vice versa. More details on the nuclear network can be found in Straniero et al. (2006) and Cristallo et al. (2009). We made use of low-temperature C-enhanced molecular opacities (Cristallo et al. 2007) to take the modification of the envelope chemical composition determined by the carbon dredge up during the TP-AGB phase into account.

For mass loss, we adopted a Reimers formula with η = 0.4 for the pre-AGB evolution, while for the AGB we fit the Ṁ-Period relation as determined in galactic AGB stars. We followed a procedure similar to the one described by Vassiliadis & Wood (1993), but considering more recent infrared observations of AGB stars (see Straniero et al. 2006 for the references). We find that our mass-loss rate is comparable to a moderate Reimers mass loss rate for the first part of the AGB and then switches to a stronger regime toward the tip of the AGB, but presenting a milder slope with respect to the rate proposed by Vassiliadis & Wood (1993).

In our models, to handle the discontinuity in the radiative gradient arising during TDU episodes, we introduce an exponentially decaying profile of convective velocities at the bottom of the convective envelope. This algorithm efficiently works only during TDU episodes, when the H-rich (opaque) envelope approaches the underlying radiative He-rich layers2. As a net effect, we obtain deeper TDUs and the formation of thin 13C pockets (ΔM < 10-3 M⊙) as a byproduct. The extension in mass of the 13C pocket decreases in mass pulse after pulse, following the natural shrinking of the whole He intershell. Our treatment of the discontinuity in the temperature gradient at the inner border of the convective envelope is based on a free parameter β that has been calibrated in order to maximize the s-process production in low-mass AGB stars (see Cristallo et al. 2009 for details).

Some recent updates are particularly relevant for the present paper. All the neutron capture cross sections were derived from the KADONIS database v 0.3 (Dillmann et al. 2006), except those of Zr isotopes (Tagliente et al. 2010, 2011), Os isotopes (Mosconi et al. 2010), and 197Au (Lederer et al. 2011). For the charged particle reactions involved in the fluorine nucleosynthesis, we have considered available new measurements and, more generally, critically reviewed the available literature (see Sect. 4). The list of reactions relevant for the nucleosynthesis of 19F is reported in Table 1.

3. Nuclear paths involving 19F

The nuclear path leading to fluorine production in low-mass AGB stars is quite complex (Forestini et al. 1992). Within the He intershell, most of the neutrons released by the 13C(α,n)16O reaction during the interpulse period are captured by 14N via the 14N(n,p)14C reaction so that protons are produced. Then, the 14C(α,γ)18O reaction synthesizes 18O, which in turn captures the freshly synthesized protons and leads to producing 15N via the 18O(p,α)15N reaction. This process competes with the main destruction channel of 15N, i.e. the 15N(p,α)12C reaction. Later on, at the development of the following TP, 15N captures an α particle producing 19F. The 15N(α,γ)19F reaction is therefore the major 19F production channel.

A further contribution to 15N production comes from any unburnt 13C in the 13C pocket (Cristallo et al. 2009) and from the 13C left in the H-burning ashes and engulfed in the convective zone generated by a TP, provided there is a large enough C+N+O abundance in the envelope. This 13C is burned rapidly at high temperatures, leading to the synthesis of 15N through the same nuclear chain as is already active in the 13C pocket. In such a case, however, an additional contribution comes from the 14N(α,γ)18F(β+νe)18O nuclear chain. A marginal contribution (less than 10%; see, e.g., Gallino et al. 2010) to fluorine nucleosynthesis is given by the 18O(n,γ)19O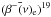F nuclear chain.

The 19F destruction channels are the 19F(p,α)16O, the 19F(α,p)22Ne, and the 19F(n,γ)20F reactions. In low-mass AGB stars, however, the 19F destruction is fairly inefficient, while it could be efficiently activated in higher masses (Lugaro et al. 2004; D’Orazi et al. 2013; Straniero et al. 2014).

4. Reaction rate uncertainties

Thanks to the improvements in experimental methods and novel techniques (e.g., underground nuclear physics, recoil mass separator, trojan horse, etc.), cross sections can be measured at very low energies. This, combined with the refinement of the theoretical tools, allowed determining reaction rates at astrophysically relevant temperatures without doing an extrapolation on a wide energy range. In fact, when direct experimental data are not available, the existence of unknown resonance and/or the correct evaluation of resonance parameters and/or interference pattern between different resonances may dramatically change the cross section extrapolations. A general discussion of techniques that extrapolate the cross sections is beyond the aims of this paper (interested readers may refer to Azuma et al. 2010). Nevertheless, in the cases where the direct experimental data are relatively close to the Gamow peak energies, the experimental uncertainties may represent a fair description of the reaction rate uncertainties also at relevant energies.

The majority of the most relevant proton radiative captures have recently been remeasured with improved precision that extends the data toward and, in some cases well within, the AGB-relevant energy range (see, e.g., the underground measurements of the LUNA collaboration of 14N(p,γ)15O – Imbriani et al. 2005; 15N(p,γ)16O – Leblanc et al. 2010 and 17O(p,γ)18F – Di Leva et al. 2014). The experimental uncertainties are also relatively small at relevant energies, i.e., about 10−15% for most of the processes we have considered.

Also most of the (p,α) reactions involved in the 19F synthesis network have been measured again in the past ten years, reaching a comparable level of experimental precision. For these processes, the uncertainties vary typically between 10% and 30%.

In conclusion, as far as proton-induced processes are concerned, experimental data allow reaction rate calculations at Gamow peak energies without doing large extrapolations of the cross section. In those cases, therefore, the reaction rate uncertainty can be assumed to be robust.

The case of α capture processes is somewhat different. Owing to the much lower penetrability, the experimentally reached investigated energy range is, for most reactions, far from the astrophysically relevant temperatures. Thus, the reaction rates have to be estimated on the basis of cross sections extrapolated to relevant energies by means of models that often include resonance parameters evaluated on the basis of rough estimates. As a consequence, experimental uncertainties are much larger, i.e., about 50% in most of the cases. Moreover, it is likely that new experimental data may produce estimates of α capture reaction rates that are significantly different from the current ones, eventually going beyond the assumed uncertainties.

In this view, we present the results of two different analyses. In the first one, reaction rates are varied within the 2σ uncertainty given by the most recent experiments available in the literature. Then, for a few selected cases, we also present another investigation, conducted by varying the reaction rates by two orders of magnitude.

The experimental status for the key reactions is briefly outlined below, including some details on the sources of the reaction rates used in this work. The quoted uncertainties at the relevant temperature for the fluorine nucleosynthesis represent 2σ standard deviations.

14N(p,γ)15O. In the past ten years there have been several experiments that measured this cross section using both direct and indirect methods. In particular, the experiment performed by the LUNA collaboration (Imbriani et al. 2005; Costantini et al. 2009) has reached the lowest energy, about 70 keV, which corresponds to a stellar temperature of about 50 MK. It is worth noting that a reliable extrapolation of the LUNA data to the solar Gamow peak requires combining low-energy with high-energy data, namely the results of the LENA experiment at TUNL (Runkle et al. 2005). Additional information is provided by experiments that used indirect methods, such as the Doppler shift attenuation method (Bertone et al. 2001; Schürmann et al. 2008), Coulomb excitation (Yamada et al. 2004), and asymptotic normalization coefficients (ANC; Mukhamedzhanov et al. 2003). It is worth noting that the uncertainty on data at high energy affects the low energy extrapolation. For this paper we use the S-factor recommendation of the recent compilation Solar Fusion II (Adelberger et al. 2011). The uncertainty at relevant temperatures is about 10%.

15N(p,γ)16O. The low-energy cross section of this process is determined by the presence of two broad resonances and by their interference. Recent studies that used indirect methods (Mukhamedzhanov et al. 2008; La Cognata et al. 2009) have suggested a significantly lower cross section than previously estimated. A direct experiment (Leblanc et al. 2010; Imbriani et al. 2012), performed in a wide energy window, confirmed that the cross section is about a factor of 2 lower than previously thought. This translates into a significantly lower rate at AGB temperatures. In the present work we use the rate and the corresponding uncertainty presented in Leblanc et al. (2010). The uncertainty at relevant temperatures is about 10%.

17O(p,γ)18F. The cross section of this reaction below Ecm ≃ 400 keV is determined by two narrow resonances, together with the tails of two broad higher energy resonances and the direct capture (DC) component. After the pioneering work of Rolfs (1973) in the seventies, several studies (Fox et al. 2005; Chafa et al. 2007; Newton et al. 2010; Hager et al. 2012; Kontos et al. 2012; Scott et al. 2012) have determined the reaction rate with improving precision in the past decade. Nevertheless, at the temperatures relevant for AGB nucleosynthesis, the reaction rate is dominated by the lowest energy resonance, Ecm = 65 keV, which is too weak to be directly measured with the current experiment possibilities. For the present work, we use the reaction rate determination by Di Leva et al. (2014) based on the measurement of the LUNA collaboration. The uncertainty at relevant temperatures is about 15%.

18O(p,γ)19F. Also in this case the presence of several low energy states influences the determination of the cross section. In particular, the Ecm = 150 keV broad resonance and the direct capture dominate the reaction rate at the astrophysically relevant temperature for AGB nucleosynthesis. Wiescher et al. (1980) and Vogelaar et al. (1990) have directly determined the magnitude of all the relevant states, down to Ecm = 89 keV. For the present work, we adopt the reaction rate given in the recent compilation by Iliadis et al. (2010). The uncertainty at relevant temperatures is about 10%.

15N(p,α)12C. The reaction rate of this process, at the temperatures of interest for this study, is mostly determined by a resonance at Ecm ≃ 100 keV. The cross section was directly determined by Redder et al. (1982). More recently, this reaction has been investigated again using the indirect approach of the trojan horse method (THM; La Cognata et al. 2007), yielding results similar to Redder et al. (1982) for both the central value and the uncertainty. For the present work we use the reaction rate reported in the NACRE compilation Angulo et al. (1999). The uncertainty at relevant temperatures is about 10%.

17O(p,α)14N. Several experiments (Chafa et al. 2007; Newton et al. 2010; Moazen et al. 2007) have determined the magnitude of most of the several resonances that influence the rate of this reaction. As for the 17O(p,γ)18F, the Ecm = 65 keV resonance, directly at the astrophysically relevant energy, makes the reaction rate determination difficult, and the uncertainty is correspondingly large. For the present work we adopt the value suggested by Iliadis et al. (2010). The uncertainty at relevant temperatures is about 20%.

18O(p,α)15N. The low-energy determination of this cross section is complicated by the tail of high-energy broad resonances and by the presence of several low-energy states (Lorenz-Wirzba et al. 1979). Recently, La Cognata et al. (2010) have measured this cross section again with the THM, strongly reducing the corresponding uncertainty. For the present calculations, we use the reaction rate provided by Iliadis et al. (2010). The uncertainty at relevant temperatures is up to 30%.

19F(p,α)16O. The situation is very similar to the previous case. The presence of very low-energy resonances makes direct determination of the cross section very difficult. An indirect experiment using the THM (La Cognata et al. 2011) has observed the presence of resonances not seen before in this process at energies corresponding to typical AGB temperatures, thus implying a significant increase in the reaction rate. Thus, the reaction rate proposed by La Cognata et al. (2011) is used in our calculations. The uncertainty at relevant temperatures is about 30%.

14C(α,γ)18O. Determining this cross section is not easy, because of the difficulty of 14C-target or beam production. Few direct experiments have been performed to determine this cross section (Görres et al. 1992). Recently, the cross section has been determined through indirect techniques by Johnson et al. (2009). Better knowledge of several resonances was achieved with significant improvement in the uncertainty in the reaction rate at temperatures lower than are typical of AGBs. In the temperature window relevant to our study, there is general agreement between the reaction rates provided by Görres et al. (1992) and Johnson et al. (2009). In our calculations we used the reaction rate given by Lugaro et al. (2004), which is based on the Görres et al. (1992) data with the exception of the spectroscopic factor of the 6.2 MeV state, for which they used a higher value. The uncertainty at relevant temperatures is about 50%.

18O(α,γ)22Ne. The determination of this reaction rate is particularly complex, and several experiments have been done to collect all the necessary information. The determination is relatively uncertain at lower energy. We followed the prescriptions by Iliadis et al. (2010). The uncertainty at relevant temperatures is about 50%.

19F(α,p)20Ne. The only available experiment was done by Ugalde et al. (2008). These authors measured this cross section, using an α beam and an F solid target between Ecm = 700 and 1600 keV, still far from the relevant astrophysical energy. The uncertainty at relevant temperatures is up to 50%.

13C(α,n)16O. This reaction is the major neutron source in low-mass AGB stars, and it releases neutrons in radiative conditions during the interpulse period at temperatures T ~ 108K. The 13C(α, n)16O reaction has been studied over a wide energy range, but none of the existing experimental investigations has fully covered the relevant astrophysical energies. The present low-energy limit in a direct experiment is Ecm = 220 keV, while the astrophysical relevant energy is between ~150 and 250 keV. This means that the cross section at the typical AGB temperatures has to be extrapolated from the data through model predictions. For our calculation, we used the reaction rate derived by Heil et al. (2008). The uncertainty at relevant temperatures is up to 50%.

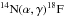. The rate of the 14N(α,γ)18F reaction is dominated by the contribution of a Jπ = 1− resonance at Ecm = 572 keV for temperatures between 0.1 GK and 0.5 GK. For higher temperatures the contributions of resonances at higher energies (Ecm = 883,1088,1189, and 1258 keV) become more important. Below 0.1 GK, additional contributions are possible from the low-energy tail of the 445 keV resonance, the DC component, and the Jπ = 4+ resonance at 237 keV. The lowest directly measured resonance is the one at 445 keV, which has been measured together with the resonance at 1136 keV (Görres et al. 2000).

The strength of the Ecm = 237 keV resonance has never been measured. It has been argued (Görres et al. 2000) that it is extremely small (ωγ ~ 1.5 × 10-18 keV), far below present experimental measurement possibilities.

The DC for this reaction is only theoretically estimated. It is supposed to be ~0.7–0.8 keVb, as calculated from spectroscopic factors using some crude approximations (see comments in Iliadis et al. 2010). The uncertainty at relevant temperatures is up to 20%.

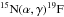. The rate of the 15N(α,γ)19F reaction is dominated by resonance contributions of several low-lying states in 19F. Wilmes et al. (2002) measured all the resonance strengths in the energy window 0.6 MeV to 2.7 MeV. Nevertheless, at astrophysical relevant energies, contributions from the Ecm = 364 keV, 536 keV and 542 keV resonances are important.

thumbnail Fig. 1

Fractional contribution of the different resonances and the DC to the reaction rate.

The strength of the 364 keV resonance has been measured indirectly de Oliveira et al. (1996) using the 15N(7Li,t)19F reaction at 28 MeV, and the uncertainty associated with the model used to derive the results is estimated to be a factor of 2. This resonance directly influences the determination of the reaction rate for temperatures lower than 200 MK. Thus, a direct measurement of its strength is very important. In Fig. 1 we show the contributions of the resonances and the DC to the total rate versus the temperature for the 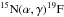. The uncertainty ranges from 15% at 250 MK, up to a factor 2 below 180 MK (see Table 2).

Table 2

2σ percentage cross section upper and lower uncertainties at T = 1 × 108 K and T = 2.5 × 108 K and corresponding percentage fluorine surface variations.

Considering the minor contribution of the 18O(n,γ)19O reaction to 19F production, we exclude this reaction from our analysis. Similarly, we do not take variations in the 19F(n,γ)20F into account, since this reaction is not efficiently activated in low-mass stars.

A list of the studied reaction rates is provided in Table 2 (Col. 1). Upper and lower percentage cross section uncertainties (2σ) are reported at T = 1 × 108 K and T = 2.5 × 108 K (Cols. 2−3 and 4−5). These are the typical temperatures of the nucleosynthesis occurring in the 13C pockets and in the convective shells generated by thermal pulses, respectively.

5. Results

As a first step, we compute a model by using the new set of reaction rates reported in Table 1 (hereinafter the ST case). We select a model with initial mass M = 2 M⊙ and Z = 10-3 ([Fe/H] = −1.15), considered as representative of low-mass AGB stars. The initial He abundance is set to 0.245, and the distribution of metals is assumed to be solar scaled and taken from Lodders (2003). No α-element enhancements are considered. The mixing-length parameter (αm.l.) has been calibrated by computing a standard solar model, and its value is set to 2.1 (Piersanti et al. 2007). The evolution of this model has been stopped after the last TDU, when the core has a mass of 0.686 M⊙ and the mass of the remaining convective envelope is lower than 7 × 10-3 M⊙. During its evolution, this model experiences 20 thermal pulses, 19 of which are followed by TDU. For more details, we refer the interested reader to Cristallo et al. (2009).

With respect to a model computed with the previous version of the network, we obtain a reduction of the surface [F/Fe] of 29% (and a corresponding reduction of the [F/⟨ s ⟩] of 22%). This result is mainly ascribed to the strongly reduced rate (about a factor 1000 at relevant temperatures) of the 14C(α,γ)18O reaction (Lugaro et al. 2004) with respect to the rate adopted in our previous calculations (Caughlan & Fowler 1988). Such a low rate limits the local increase in 18O. Later on, part of this 14C is dredged up to the surface, and it decays to 14N, thus not directly contributing to fluorine nucleosynthesis within the He intershell.

Then, we assume as a reference case the model computed with such a new nuclear network (hereafter the ST case), and we vary one at a time all the reactions reported in Table 2 in both directions (upper and lower limits). For each varied reaction, we compute the evolution of the star from the end of the core He-burning phase up to the tip of the AGB phase.

5.1. 2σ analysis

We first studied the effects on fluorine nucleosynthesis due to variations in the relevant reaction rates by changing them within 2σ values, as derived from the existing literature.

Results are shown in Table 2, where we tabulate the final (i.e., after the last TDU) surface [F/Fe] and [F/⟨ s ⟩] percentage differences with respect to our ST case. For both quantities we provide variations corresponding to upper and lower rates. From the values reported in Table 2, it comes out that the variations in key reaction rates within 2σ have little effect on the final fluorine surface abundances and [F/⟨ s ⟩] ratios. The largest variations are found for the 14N(p, γ)15O, the 19F(α, p)22Ne, and the 13C(α, n)16O reactions. However, such differences in the final surface fluorine abundance are definitely lower than the errors currently affecting spectroscopic observations (at least a factor 2).

Table 3

Scaling factors sf of the computed tests with the corresponding 19F and F/⟨ s ⟩ surface ratios with respect to the reference case.

5.2. Exploration above current experimental uncertainties

To better evaluate the sensitivity of 19F nucleosynthesis to larger variations in selected reaction rates, we ran some additional tests by varying the cross section of α capture processes well beyond the currently quoted uncertainties. The computed tests are listed in Table 3, where we report:

  • scaling factors sf (i.e., the ratio of the modified rate with respect tothe reference case);

  • corresponding final surface 19F ratios with respect to the reference case ();

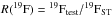  • corresponding final surface F/⟨ s ⟩ ratios with respect to the reference case (R(F/ ⟨ s ⟩ ) = (F/ ⟨ s ⟩ )test/ (F/ ⟨ s ⟩ )ST).

Among the studied rates, the 14C(α,γ)18O and the 18O(α,γ)22Ne show the lowest variations. Large changes in the 14N(α,γ)18F and the 13C(α,n)16O reactions imply small, but appreciable, differences in the final fluorine surface abundances. The remaining two rates, i.e. the 15N(α,γ)19F and the 19F(α,p)22Ne, are able to reduce the surface 19F abundance by a factor of 10 so they deserve a more careful analysis.

5.2.1. The revisited 15N(α,γ)19F

Interestingly enough, the model with a strongly reduced 15N(α,γ)19F roughly matches the observed [F/⟨ s ⟩] ratios found at low metallicity by Abia et al. (2011). As already pointed out, the 15N(α,γ)19F rate is strongly influenced by the presence of the 364 keV resonance, whose intensity is affected by a very large uncertainty. The contribution from the DC component is also difficult to evaluate at the present status of the experimental knowledge. Therefore, although very unlikely, the explored scenario is possible from a nuclear point of view. Nevertheless, a very low value of the 15N(α,γ)19F reaction would not allow AGB stars to synthesize fluorine at solar-like metallicities, contradicting observations (Abia et al. 2010). As already recalled, however, preliminary studies based on a recent reduction of the adopted excitation energies of HF molecular transitions seem to lead to a consistent decrease in the observed fluorine surface abundances in solar-like metalliticy AGB stars (Abia et al., in prep.).

A revision of this reaction rate therefore looks mandatory for minimizing the uncertainty on the 19F nucleosynthesis related to this nuclear process. We will clarify this issue in the near future, when we directly measure the strength of the 364 keV resonance and the intensity of the DC component using the ERNA recoil separator (Schürmann et al. 2005; di Leva et al. 2009; Di Leva et al. 2012).

5.2.2. The revisited 19F(α,p)22Ne

The only other α capture process able to significantly change the surface fluorine abundances in low-mass AGB stars is the 19F(α,p)22Ne. In state-of-the-art modeling, this reaction rate is expected to efficiently work in stars with higher masses (M ≥ 4−5 M⊙3). However, a deep revision of this rate cannot be excluded from first principles. In fact, the 19F(α,p)22Ne cross section is characterized by many broad resonances tailing into the low-energy range. Possible additional resonance contributions in that excitation range were predicted, on the basis of 23Na compound nuclear level structure data. As discussed in Sect. 4, experimental data are still far from the relevant astrophysical energies. The uncertainty is mostly due to the different energy dependence of the cross section predicted by different models. We intend to clarify this point by directly measuring this cross section at an energy lower than Ecm = 660 keV, using a fluorine beam impinging on an α jet gas target surrounded by particle detectors.

6. Conclusions

In this paper we investigated the effects that nuclear reaction rates have on the fluorine production in low mass AGB stars. We found minor variations in the final surface 19F abundance (less than 10%) when varying the rates within 2σ standard deviations. However, some α capture reactions may change well beyond the current accepted uncertainties, owing to the lack of knowledge about the strengths of nuclear resonances at astrophysically relevant energies. Thus, we investigated other possible, although unlikely, scenarios in which we varied some α capture rates by a factor 100. We found that the largest variations are obtained by reducing the 15N(α,γ)19F rate or by increasing the 19F(α,p)22Ne rate. Both reactions have poorly known resonances at astrophysical energies. We plan to experimentally investigate both cross sections in the future by directly measuring the strengths of their resonances.

1

[⟨ s ⟩ /Fe ] = 0.5 ∗ (( [ Sr/Fe ] + [ Y/Fe ] + [ Zr/Fe ] )/3 + ( [ Ba/Fe ] + [ La/Fe ] + [ Nd/Fe ] + [ Sm/Fe ] )/4). The two addends represent the surface enrichment of elements belonging to the first and second peaks of the s-process, respectively.

2

We recall that the local radiative gradient (and thus the convective velocity) is proportional to the opacity.

3

As already highlighted in the Introduction, this class of objects cannot reproduce the observed AGB s-process distributions.

Acknowledgments

This work was supported by Italian Grants RBFR08549F-002 (FIRB 2008 program), PRIN-INAF 2011 project “Multiple populations in Globular Clusters: their role in the Galaxy assembly”, PRIN-MIUR 2012 “Nucleosynthesis in AGB stars: an integrated approach” project (20128PCN59) and from Spanish grants AYA2008-04211-C02-02 and AYA-2011-22460.

References

  1. Abia, C., Domínguez, I., Gallino, R., et al. 2002, ApJ, 579, 817 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abia, C., de Laverny, P., & Wahlin, R. 2008, A&A, 481, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Abia, C., Recio-Blanco, A., de Laverny, P., et al. 2009, ApJ, 694, 971 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abia, C., Cunha, K., Cristallo, S., et al. 2010, ApJ, 715, L94 [NASA ADS] [CrossRef] [Google Scholar]
  5. Abia, C., Cunha, K., Cristallo, S., et al. 2011, ApJ, 737, L8 [NASA ADS] [CrossRef] [Google Scholar]
  6. Adelberger, E. G., García, A., Robertson, R. G. H., et al. 2011, Rev. Mod. Phys., 83, 195 [NASA ADS] [CrossRef] [Google Scholar]
  7. Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
  8. Azuma, R. E., Uberseder, E., Simpson, E. C., et al. 2010, Phys. Rev. C, 81, 5805 [Google Scholar]
  9. Bertone, P. F., Champagne, A. E., Powell, D. C., et al. 2001, Phys. Rev. Lett., 87, 152501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  10. Caughlan, G. R., & Fowler, W. A. 1988, At. Data Nucl. Data Tables, 40, 283 [Google Scholar]
  11. Chafa, A., Tatischeff, V., Aguer, P., et al. 2007, Phys. Rev. C, 75, 5810 [Google Scholar]
  12. Costantini, H., Formicola, A., Imbriani, G., et al. 2009, Rep. Prog. Phys., 72, 086301 [Google Scholar]
  13. Cristallo, S., Gallino, R., Straniero, O., Piersanti, L., & Domınguez, I. 2006, Mem. Soc. Astron. It., 77, 774 [Google Scholar]
  14. Cristallo, S., Straniero, O., Lederer, M. T., & Aringer, B. 2007, ApJ, 667, 489 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
  17. de Laverny, P., Abia, C., Domínguez, I., et al. 2006, A&A, 446, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. de Oliveira, F., Coc, A., Aguer, P., et al. 1996, Nucl. Phys. A, 597, 231 [NASA ADS] [CrossRef] [Google Scholar]
  19. Denissenkov, P. A., & Tout, C. A. 2003, MNRAS, 340, 722 [NASA ADS] [CrossRef] [Google Scholar]
  20. di Leva, A., Gialanella, L., Kunz, R., et al. 2009, Phys. Rev. Lett., 102, 232502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  21. Di Leva, A., Pezzella, A., De Cesare, N., et al. 2012, Nucl. Instrum. Methods Phys. Res. A, 689, 98 [NASA ADS] [CrossRef] [Google Scholar]
  22. Di Leva, A., Scott, D. A., Caciolli, A., et al. 2014, Phys. Rev. C, 89, 5803 [Google Scholar]
  23. Dillmann, I., Heil, M., Käppeler, F., et al. 2006, in Capture Gamma-Ray Spectroscopy and Related Topics, eds. A. Woehr, & A. Aprahamian, AIP Conf. Ser., 819, 123 [Google Scholar]
  24. D’Orazi, V., Lucatello, S., Lugaro, M., et al. 2013, ApJ, 763, 22 [NASA ADS] [CrossRef] [Google Scholar]
  25. Drotleff, H. W., Denker, A., Knee, H., et al. 1993, ApJ, 414, 735 [Google Scholar]
  26. Federman, S. R., Sheffer, Y., Lambert, D. L., & Smith, V. V. 2005, ApJ, 619, 884 [Google Scholar]
  27. Forestini, M., Goriely, S., Jorissen, A., & Arnould, M. 1992, A&A, 261, 157 [NASA ADS] [Google Scholar]
  28. Formicola, A., Imbriani, G., Costantini, H., et al. 2004, Phys. Lett. B, 591, 61 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fowler, W. A., Burbidge, G. R., & Burbidge, E. M. 1955, ApJ, 122, 271 [NASA ADS] [CrossRef] [Google Scholar]
  30. Fox, C., Iliadis, C., Champagne, A. E., et al. 2005, Phys. Rev. C, 71, 5801 [Google Scholar]
  31. Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Gallino, R., Bisterzo, S., Cristallo, S., & Straniero, O. 2010, Mem. Soc. Astron. It., 81, 998 [NASA ADS] [Google Scholar]
  33. Giesen, U., Browne, C. P., Görres, J., et al. 1994, Nucl. Phys. A, 567, 146 [NASA ADS] [CrossRef] [Google Scholar]
  34. Görres, J., Graff, S., Wiescher, M., et al. 1992, Nucl. Phys. A, 548, 414 [NASA ADS] [CrossRef] [Google Scholar]
  35. Görres, J., Arlandini, C., Giesen, U., et al. 2000, Phys. Rev. C, 62, 5801 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hager, U., Buchmann, L., Davids, B., et al. 2012, Phys. Rev. C, 85, 5803 [Google Scholar]
  37. Heil, M., Detwiler, R., Azuma, R. E., et al. 2008, Phys. Rev. C, 78, 025803 [NASA ADS] [CrossRef] [Google Scholar]
  38. Herwig, F., Bloecker, T., Schoenberner, D., & El Eid, M. 1997, A&A, 324, L81 [NASA ADS] [Google Scholar]
  39. Iben, Jr., I. 1982, ApJ, 260, 821 [NASA ADS] [CrossRef] [Google Scholar]
  40. Iben, Jr., I., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] [Google Scholar]
  41. Iliadis, C., Longland, R., Champagne, A. E., Coc, A., & Fitzgerald, R. 2010, Nucl. Phys. A, 841, 31 [NASA ADS] [CrossRef] [Google Scholar]
  42. Imbriani, G., Costantini, H., Formicola, A., et al. 2005, Eur. Phys. J. A, 25, 455 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Imbriani, G., de Boer, R. J., Best, A., et al. 2012, Phys. Rev. C, 85, 5810 [Google Scholar]
  44. Johnson, E. D., Rogachev, G. V., Mitchell, J., Miller, L., & Kemper, K. W. 2009, Phys. Rev. C, 80, 5805 [NASA ADS] [Google Scholar]
  45. Jönsson, H., Ryde, N., Harper, G. M., et al. 2014, A&A, 564, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Jorissen, A., Smith, V. V., & Lambert, D. L. 1992, A&A, 261, 164 [NASA ADS] [Google Scholar]
  47. Karakas, A. I., & Lattanzio, J. C. 2014 [arXiv:1405.0062] [Google Scholar]
  48. Kobayashi, C., Izutani, N., Karakas, A. I., et al. 2011, ApJ, 739, L57 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kontos, A., Görres, J., Best, A., et al. 2012, Phys. Rev. C, 86, 5801 [Google Scholar]
  50. La Cognata, M., Romano, S., Spitaleri, C., et al. 2007, Phys. Rev. C, 76, 5804 [Google Scholar]
  51. La Cognata, M., Goldberg, V. Z., Mukhamedzhanov, A. M., Spitaleri, C., & Tribble, R. E. 2009, Phys. Rev. C, 80, 2801 [Google Scholar]
  52. La Cognata, M., Spitaleri, C., & Mukhamedzhanov, A. M. 2010, ApJ, 723, 1512 [NASA ADS] [CrossRef] [Google Scholar]
  53. La Cognata, M., Mukhamedzhanov, A. M., Spitaleri, C., et al. 2011, ApJ, 739, L54 [Google Scholar]
  54. Leblanc, P. J., Imbriani, G., Görres, J., et al. 2010, Phys. Rev. C, 82, 5804 [Google Scholar]
  55. Lederer, C., Colonna, N., Domingo-Pardo, C., et al. 2011, Phys. Rev. C, 83, 4608 [NASA ADS] [CrossRef] [Google Scholar]
  56. Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
  57. Lorenz-Wirzba, H., Schmalbrock, P., Trautvetter, H. P., et al. 1979, Nucl. Phys. A, 313, 346 [NASA ADS] [CrossRef] [Google Scholar]
  58. Lucatello, S., Masseron, T., Johnson, J. A., Pignatari, M., & Herwig, F. 2011, ApJ, 729, 40 [NASA ADS] [CrossRef] [Google Scholar]
  59. Lugaro, M., Ugalde, C., Karakas, A. I., et al. 2004, ApJ, 615, 934 [NASA ADS] [CrossRef] [Google Scholar]
  60. Meynet, G., & Arnould, M. 2000, A&A, 355, 176 [NASA ADS] [Google Scholar]
  61. Moazen, B. H., Bardayan, D. W., Blackmon, J. C., et al. 2007, Phys. Rev. C, 75, 5801 [Google Scholar]
  62. Mosconi, M., Fujii, K., Mengoni, A., et al. 2010, Phys. Rev. C, 82, 5802 [NASA ADS] [Google Scholar]
  63. Mukhamedzhanov, A. M., Bém, P., Brown, B. A., et al. 2003, Phys. Rev. C, 67, 5804 [Google Scholar]
  64. Mukhamedzhanov, A. M., Bém, P., Burjan, V., et al. 2008, Phys. Rev. C, 78, 5804 [Google Scholar]
  65. Newton, J. R., Iliadis, C., Champagne, A. E., et al. 2010, Phys. Rev. C, 81, 5801 [Google Scholar]
  66. Palacios, A., Arnould, M., & Meynet, G. 2005, A&A, 443, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Piersanti, L., Straniero, O., & Cristallo, S. 2007, A&A, 462, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Redder, A., Becker, H. W., Lorenz-Wirzba, H., et al. 1982, Zeitschrift fur Physik A Hadrons and Nuclei, 305, 325 [Google Scholar]
  69. Rolfs, C. 1973, Nucl. Phys. A, 217, 29 [NASA ADS] [CrossRef] [Google Scholar]
  70. Runkle, R. C., Champagne, A. E., Angulo, C., et al. 2005, Phys. Rev. Lett., 94, 2503 [Google Scholar]
  71. Sackmann, I.-J., Smith, R. L., & Despain, K. H. 1974, ApJ, 187, 555 [NASA ADS] [CrossRef] [Google Scholar]
  72. Schürmann, D., di Leva, A., Gialanella, L., et al. 2005, Eur. Phys. J. A, 26, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Schürmann, D., Kunz, R., Lingner, I., et al. 2008, Phys. Rev. C, 77, 5803 [Google Scholar]
  74. Scott, D. A., Caciolli, A., Di Leva, A., et al. 2012, Phys. Rev. Lett., 109, 202501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  75. Straniero, O., Gallino, R., Busso, M., et al. 1995, ApJ, 440, L85 [NASA ADS] [CrossRef] [Google Scholar]
  76. Straniero, O., Gallino, R., & Cristallo, S. 2006, Nucl. Phys. A, 777, 311 [NASA ADS] [CrossRef] [Google Scholar]
  77. Straniero, O., Cristallo, S., & Piersanti, L. 2014, ApJ, 785, 77 [NASA ADS] [CrossRef] [Google Scholar]
  78. Tagliente, G., Milazzo, P. M., Fujii, K., et al. 2010, Phys. Rev. C, 81, 5801 [NASA ADS] [CrossRef] [Google Scholar]
  79. Tagliente, G., Milazzo, P. M., Fujii, K., et al. 2011, Phys. Rev. C, 84, 5802 [NASA ADS] [Google Scholar]
  80. Trippella, O., Busso, M., Maiorca, E., Käppeler, F., & Palmerini, S. 2014, ApJ, 787, 41 [NASA ADS] [CrossRef] [Google Scholar]
  81. Ugalde, C. 2005, Ph.D. Thesis, University of Notre Dame, USA [Google Scholar]
  82. Ugalde, C., Azuma, R. E., Couture, A., et al. 2008, Phys. Rev. C, 77, 5801 [Google Scholar]
  83. Vassiliadis, E., & Wood, P. R. 1993, ApJ, 413, 641 [NASA ADS] [CrossRef] [Google Scholar]
  84. Vogelaar, R. B., Wang, T. R., Kellogg, S. E., & Kavanagh, R. W. 1990, Phys. Rev. C, 42, 753 [NASA ADS] [CrossRef] [Google Scholar]
  85. Wiescher, M., Becker, H. W., Görres, J., et al. 1980, Nucl. Phys. A, 349, 165 [NASA ADS] [CrossRef] [Google Scholar]
  86. Wilmes, S., Wilmes, V., Staudt, G., Mohr, P., & Hammer, J. W. 2002, Phys. Rev. C, 66, 065802 [NASA ADS] [CrossRef] [Google Scholar]
  87. Woosley, S. E., & Haxton, W. C. 1988, Nature, 334, 45 [NASA ADS] [CrossRef] [Google Scholar]
  88. Yamada, K., Motobayashi, T., Akiyoshi, H., et al. 2004, Phys. Lett. B, 579, 265 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Sources of the reaction rates relevant for fluorine nucleosynthesis.

In the text
Table 2

2σ percentage cross section upper and lower uncertainties at T = 1 × 108 K and T = 2.5 × 108 K and corresponding percentage fluorine surface variations.

In the text
Table 3

Scaling factors sf of the computed tests with the corresponding 19F and F/⟨ s ⟩ surface ratios with respect to the reference case.

In the text

All Figures

thumbnail Fig. 1

Fractional contribution of the different resonances and the DC to the reaction rate.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.