EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 569 (September 2014) A&A, 569 (2014) A88 Full HTML
Free Access
Issue
A&A
Volume 569, September 2014
Article Number A88
Number of page(s) 11
Section Astronomical instrumentation
DOI https://doi.org/10.1051/0004-6361/201423868
Published online 29 September 2014

© ESO, 2014

1. Introduction

The Planck mission (Planck Collaboration I 2014)1 has observed the sky between August 2009 and August 2013 in the frequency range from 30 GHz to 1 THz from its orbital vantage point about the second Sun-Earth Lagrange point (L2). The Planck satellite comprises a telescope, a service module, and two instruments: the High Frequency Instrument (HFI) and the Low Frequency Instrument (LFI). The HFI operates with 52 high-impedance bolometers cooled to 100 mK in a range of frequencies between 100 GHz and 1 THz and shows an unprecedented photon sensitivity within its frequency bands (Planck Collaboration IV 2011). At the same time, however, the HFI detectors exhibit a strong coupling with cosmic-ray radiation that produces transient glitches in the raw time-ordered information (TOI). The data affected by large-amplitude glitches are rendered unusable for science and must be masked in subsequent data processing. The redundancy of Planck’s scanning strategy ensures complete sky coverage even after large-amplitude glitch masking (Planck Collaboration X 2014; Planck Collaboration VI 2011). Smaller-amplitude glitches are flagged and the data are corrected by the subtraction of a parametric fit to an HFI glitch template. Even smaller glitches could remain hidden within the TOI noise, yielding an additional non-Gaussian systematic effect. Therefore, a proper understanding and careful data processing of the glitches are essential to meet the precision cosmology goals of the Planck mission. Uncorrected glitches can influence the estimation of the cosmic microwave background (CMB) angular power spectrum; in particular, there is a potential confusion between glitch residuals and the non-Gaussian features caused by topological defects or inflation processes (Masi et al. 2010).

The impact of cosmic rays on the time-ordered data has also been observed in previous far-infrared space missions that used bolometers. For example, glitches in the COBE-FIRAS data were identified to be caused by cosmic-particle hits on the detectors, because they were not correlated to the position of the mirrors (Boggess et al. 1992; Fixsen et al. 1996). The number of glitches observed for this experiment was sufficiently small and their removal was not a major problem. Glitches have also been identified in the Herschel space observatory, which was injected in a Lissajous orbit around the L2 point together with the Planck satellite. It contains the SPIRE photometer, which uses three bolometer arrays of hexagonally close-packed feedhorn-coupled NTD-detectors operating at 300 mK (43 at 500 μm, 88 at 350 μm, and 139 at 250 μm; Griffin et al. 2010). Glitches caused by cosmic rays have been observed in SPIRE data. Two types of glitches are seen in the SPIRE detector timelines: large events and smaller co-occurring glitches both associated to the impact of cosmic rays on the arrays.

This work, together with a companion article (Planck Collaboration X 2014), provides an improved understanding of the physical origin of the glitches observed in the HFI instrument in-flight data. This paper discusses several ground-based experiments using the collision of protons and α-particles with spare HFI bolometers. These experiments provide better control of the incident particle characteristics (e.g., particle type, energy, impact location) and environmental conditions than the HFI in-flight data.

This article is structured as follows: we first give a short review of the cosmic-ray flux at the second Sun-Earth Lagrange point (L2). In Sect. 3 we describe the geometrical and thermal characteristics of the elements that constitute an HFI bolometer module. In Sect. 4 we summarize the results obtained from the analysis of the glitches in the HFI in-flight data. In Sect. 5 we show the results of the ground characterization of the HFI spare bolometers and describe several radiation tests with protons and α-particles. In conclusion, we discuss the physical interpretation of the glitches seen by HFI in flight and the lessons learnt for future cosmological space missions.

2. Cosmic rays at the second Lagrange point

Cosmic rays (CRs) at L2 are composed of about 89% protons, 10% α-particles, and 1% nuclei of heavier elements; less than 1% are electrons (see, e.g., Mewaldt et al. 2010; Leske et al. 2011). The most important contribution (in terms of both energy and quantity) to the CRs at L2 comes from within our own Galaxy. The incoming charged particles are modulated by the solar wind, which decelerates and partially shields the inner solar system from lower-energy galactic CRs. There is a significant anticorrelation between solar activity and the flux of CRs with energies below 10 GeV.

In addition to deflecting galactic CRs, the Sun is itself a source of CR nuclei and electrons that are accelerated by shock waves that travel through the corona, and by magnetic energy released in solar flares. The typical energy reached in solar particles is in the keV range. On the other hand, during a solar flare, the highest energy reached is typically 10 to 100 MeV, occasionally reaching 1 GeV (roughly once a year) to 10 GeV (roughly once a decade). During the Planck mission, we observed 13 solar flares; each solar flare lasted a few hours and produced a change in temperature of the whole bolometer plate that affected the working point of the bolometers. The data related to these events are flagged and excluded from standard HFI data processing, therefore we did not consider this source of CRs here.

A third population of CRs, referred to as anomalous cosmic rays (ACR), consists primarily of photoionized interstellar hydrogen nuclei that are accelerated at the termination shock in the heliosphere (Stone 2012). Although heavier elements are present in the ACR population, protons with energies from hundreds of keV to 100 MeV represent a marginally important component of the CR flux that affects the Planck HFI.

The flux of CRs is monitored onboard the Planck satellite by the Standard Radiation Environment Monitor (SREM)2 mounted on the exterior of the spacecraft. Solar flares provided a useful test to correlate the signal measured on the outside of the spacecraft with the SREM with signals due to particle impact on HFI. We found that only CRs with energies above 39 MeV can penetrate the focal plane unit (FPU) box (Planck Collaboration X 2014).

thumbnail Fig. 1

Energy distribution of CR protons at L2. The vertical dashed lines represent the range of energies of interest for HFI (from 35 MeV to 10 GeV).

We conclude that the flux of particles that can cause glitches in the HFI data is composed of protons in a range of energies between 39 MeV and 10 GeV. The energy distribution of protons is presented in Fig. 1 (Adriani et al. 2011; Christian et al. 2011; Picozza et al. 2011). Below 39 MeV, protons do not have enough energy to penetrate the FPU box to reach the 100 mK stage. The total flux of CRs peaks around 200 MeV, giving a total proton flux of 3000–4000 particles m-2 sr-1 s-1 GeV-1.

3. HFI bolometers

In this section we describe the different elements that constitute an HFI bolometer module. In general, each element of a bolometer module can interact with CRs and, through the thermal link with the thermistor, it can generate a glitch in the data. One of the goals of this article is to isolate the elements of an HFI bolometer that can have an impact on the HFI data.

The HFI high-impedance bolometers (Holmes et al. 2008) are manufactured using silicon nitride supported metal-mesh absorbers and neutron transmutation doped (NTD) germanium thermistors with a resistance strongly dependent on the temperature. The use of an absorber with a spider-web shape strongly reduces the cross-sectional area (by about 95%) for CR and particle collisions and it was a design consideration for detectors intended for on-orbit and balloon-borne applications. At the same time, the effective in-band cross-sectional surface area is similar to that of a solid absorber; thus, the spider-web absorber technology reduces the CR and out-of band noise produced in the TOI data. For reviews of the theory of high-impedance bolometers see Jones (1953), Mather (1982), Mauskopf (1997), Sudiwala et al. (2000), and Vaillancourt (2005).

The size and grid spacing of the mesh is adapted to operate in six separated frequency bands between 100 and 857 GHz. In flight, four spider-web bolometers (SWBs) in each of the five bands from 143 to 857 GHz measure the total intensity of incident radiation. In addition, eight polarization-sensitive bolometers (PSBs) in each of four bands (100, 143, 217, and 353 GHz) couple only to a single linear polarization and thus measure a linear combination of Stokes parameters I, Q, and U. PSBs are arranged in pairs sensitive to orthogonal polarizations. Bolometer performance strongly depends on the read-out electronics design (Catalano et al. 2010). The electronics chain implemented in the HFI is an evolution of the square-wave-biased AC readout (Rieke et al. 1989; Gaertner et al. 1997), known to improve the low-frequency stability of bolometers.

thumbnail Fig. 2

Top: front perspective mechanical drawing of a polarization-sensitive bolometer (PSB). The illustration shows the forward/upper portion, i.e., PSBa, of the PSBa/b pair. The orientation of the PSBb absorber is orthogonal to the PSBa. Bottom: mechanical drawing of a spider-web bolometer (SWB). In both figures, the printed wiring board (PWB) and cover are not shown. The size of a HFI bolometer module (including the thermometer, the absorber, the silicon die, the housing and the backshort) is between 1.5 and 1.9 cm depending on the working frequency.

The elements of an HFI bolometer module are the following:

  • Thermometer: the bolometer temperature is measured using anNTD germanium semiconducting thermistor. The size of theNTD thermometers is the same in all the SWBs and PSBs; it is 30(thickness) × 100 × 300 μm.

  • Absorber: the millimeter-wave absorber for SWBs and PSBs is a free-standing metallized Si3N4 micromesh supported by Si3N4 beams. The width of the micromesh varies with the HFI band-frequency; it is between 5 and 10 μm. The 1 μm thickness of the Si3N4 structures is the same in all the bolometers. In the PSBs, the grid spacing, always >50 μm, is chosen so that it absorbs millimeter-waves with high efficiency but has a much smaller physical surface area, which significantly reduces the cross-section to CR particles and shorter-wavelength photons.

  • Silicon die: this is a silicon wafer with an initial diameter of 15.2 cm, diced differently for SWBs and PSBs (see Fig. 2). A Si3N4 film of 1 μm was deposited on both sides of the wafer. Gold with a titanium adhesion layer was deposited and patterned on the side of the wafer to define the millimeter-wave absorber, the thermal link to the absorber, and the thermalization bars and contact pads for wire bonding and the indium bump bonds. The bolometer die is located over the backshort (or the housing for the forward PSBs) and glued with epoxy. The silicon die thickness is 350 μm in all the bolometers and the surface area is between 0.4 and 0.8 cm2, depending on the working frequency.

  • Backshort: made of beryllium-copper, it supports the silicon die and permits an optimal absorption of photons by the grid as a result of the λ/ 4 relief machined into it. It is present in SWB bolometers and in the rear PSBs (PSBb).

  • Housing: made of beryllium-copper, it supports the silicon die of the PSBa bolometers.

  • Printed wiring board (PWB): the PWB is mounted in the bolometer module on the opposite side of the backshort from the bolometer and contains surface mount inductors and a ground plane that, with the capacitors and bolometer, forms a filter to attenuate radio-frequency signals before it is rectified at the bolometer.

  • Feed-through: this element is only present in the forward bolometers of a PSB module (PSBa). It electrically links the gold pad of the forward PSB to the module PWB with a very low level of electrical cross-talk with the backward PSB (PSBb). This is achieved by using an aluminium cylinder glued with epoxy in the backshort of the backward PSB. Inside the aluminium the wire is suspended with epoxy.

  • Cover: the cover is made of beryllium-copper. It is installed onto the backshort to protect the PWB and to support a connector.

4. HFI in-flight glitches

The structure and evolution of the in-flight glitches have been discussed in Planck Collaboration VI (2011) and the companion article Planck Collaboration X (2014). In this section we summarize the principal observed characteristics of the in-flight HFI glitches.

We describe the glitches observed by HFI in terms of three characteristics: 1) rate of events and its evolution during the mission; 2) characteristic event profile (glitch template); 3) the absorbed energy distribution.

thumbnail Fig. 3

HFI flight results: average short glitch template (blue), long glitch template (black), and slow glitch template (red) for one PSB in-flight bolometer (Planck Collaboration X 2014).

  • Rate: the evolution of the glitch rate is strongly correlated with theSREM as discussed in Sect. 2. This is evidence thatglitches are produced by CRs and not by local phenomena such asvibrations or read-out electronics noise. The measured in-flightglitch rate was about 20 times higher than expected from the cou-pling between the absorber and the CRs at L2. A phenomenonother than the direct interaction of the CRs with the absorber andNTD has to be invoked to explain this (see PlanckCollaboration X 2014). Two hypotheses havebeen put forward: (1) the NTD thermometer is sensitive to achange in temperature of other (larger) elements; (2) a large por-tion of the glitches come from indirect interaction between CRsand bolometers, for example, protons that interact very close tothe surfaces of materials surrounding the NTD+Grid (in partic-ular copper) produce electron showers able to propagate to theabsorber+NTD.

  • Shape: from data reduction (Planck Collaboration X 2014), we distinguished three families of gltches with different shapes (see Fig. 3): short, long, and slow glitches. We can fit each family with a template that is the sum of first-order low-pass filters: 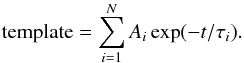(1)Short glitches present a fast decay (between 4 and 10 ms, depending on the bolometer) and a tail with an amplitude of a few percent of the maximum. Long glitches present the same fast decay as the short ones, but have a long (about 10%) relative amplitude tail that shows intermediate to long time-constants of tens of milliseconds and about 1 s. Slow glitches show the same slow time-constants as the long and short glitches, but not the fast decay. The residual glitch signal after template subtraction is significantly reduced. Indeed, the remaining contamination from glitches is below the instrumental noise level, even for channels with the highest glitch rates.

  • Spectrum: the glitch energy distribution was estimated for short, long, and slow glitches. The distributions can be fitted by power-laws with different indices, and different bolometers show very similar results. In Fig. 4, we present the averaged energy spectra of the in-flight PSBs at 217 GHz collected during the full mission. The total number of glitches is dominated by long glitches at low absorbed energies. Short glitches dominate for high absorbed energies. Slow glitches are present only on the PSBa bolometers. Long and slow glitches show the same power law index. The short-glitch distribution shows a double structure with an elevated bump in the high-energy range.

thumbnail Fig. 4

HFI flight results: glitch energy distribution for the three families of glitches with respect to the peak amplitude, in signal-to-noise units, for three different PSB and SWB in-flight bolometers (Planck Collaboration X 2014). The blue line is for the short glitch population, black is for long, red is for slow, and green is for total. Power laws are shown for comparison as dashed lines.

thumbnail Fig. 5

Tandem accelerator test. (A) Histograms of the glitch amplitudes in 2 h of integration time for low amplitudes (0 V – 0.1 mV). (B) Histograms of the glitch amplitudes in 2 h of integration for high amplitudes (greater than 0.1 mV). (C) Glitch template built by stacking all the events of the first family centered at 45 μV (blue) and the family centered at 0.15 mV (red). Both templates show the same fast time-constant τ (4 ms), and the blue template shows a slower time-constant (about 20 ms) with an amplitude relative to the peak of few percent.

Table 1

Summary of the ground-based bolometer tests.

Table 2

Energy absorbed [keV] in the different elements of a bolometer module for normally incident particles.

5. Ground measurements

For an improved understanding of the origins of the glitches seen in HFI flight data, we performed several ground-based tests on spare HFI bolometers between December 2010 and May 2013. The aim of the tests was to obtain a more complete view of the physical origin of the different families of glitches. These tests were performed in different configurations using 23 MeV protons from an ion accelerator and two radioactive α particle sources (241Am and 244Cm). In addition, we used the HFI ground-calibration data to check the impact of the CRs at sea level with HFI bolometers. The sensitivity reached for these tests was about 10 nV Hz1/2, very close to the flight performance. A list of all the tests that were performed is presented in Table 1.

We started by placing spare HFI SWBs in front of an ion accelerator with a proton beam able to cover the full surface of the bolometer module. The results of this test showed that we are able to reproduce short and long glitches observed in flight without any delta-electron3 production process. Because of the limited integration time during the accelerator test, we performed other tests with α sources to investigate the production of long glitches more deeply by using a collimated beam able to interact with small parts of the bolometer module on each test. The results of these tests showed that the silicon die is the origin of long glitches. Two hypotheses were put forward to explain the heat propagation from the silicon die to the NTD thermometer: ballistic phonon propagation and ionization. To distinguish between these two effects we performed a test by breaking the Si 3N 4 legs that support the absorber (65% of the legs were severed) to reduce the ballistic heat transport by a measurable factor.

In the next subsections we give the principal results of each test; this motivates the physical interpretation of glitches in HFI data discussed in Sect. 7.

5.1. Particles on HFI detectors

In the range of energies of interest, the main interaction between particles and materials is ionization. The value ΔE/ Δx versus particle energy is given by the total stopping power curves for silicon, germanium, and copper, and corresponds to the sum of the electronic stopping (inelastic collisions between bound electrons in the solid medium and the ion moving through it) and the nuclear stopping (elastic collisions between the ion and atoms in the sample, almost negligible in the range of energies of interest). In Table 2, we present the energies absorbed in the relevant elements of a bolometer module from α particles and protons at normal incidence.

5.2. Tandem accelerator test

This test was performed in December 2010 at the Institut de Physique Nucléaire (IPN – University of Paris-sud) using the Tandem accelerator4: this accelerates ions by applying an electrostatic field with a feature of supplying high voltage in the middle of the accelerating tube. It can accelerate ions in two steps: first, is accelerates negative ions and second, it accelerates positive ions to higher velocities after transforming negative ions into positive ions in the high-voltage terminal (E = (q + 1)V [MeV]). The Tandem accelerator can produce 23 MeV protons with a beam of about 2.5–3 cm always orthogonal to the detectors. This means that the beam covers the full surface of the bolometer module.

The aim of this test was to obtain a general view of the interaction between protons and the different elements of an HFI bolometer module. We used three spare HFI SWBs. In front of one, at a distance of about 5 mm, we set a 10 μm gold shield to test for possible delta-electron production. The second was placed in front of the Tandem beam without any shield or optics (filters, horns, etc.). The last was used as a reference bolometer.

In Fig. 5, we present the results of the test for the unshielded bolometer. The histogram of the highest glitch amplitude is shown. Two families of events can be isolated. The first family peaks at 45 μV and contains 98.5% of the glitches. The template built by stacking all the glitches of this family (blue curve in Fig. 5C) can be represented by a fit of a two-time-constant model (a faster τ at 4 ms and a slower τ at about 20 ms). This family is similar to the long-glitch family seen within HFI in-flight data. The second family of glitches peaks at about 0.15 mV and contains about 1.5% of the glitches. These glitches agree reasonably well with a template fitting with a single time-constant model with the same 4 ms time-constant as the first glitch family (red curve in Fig. 5C). This family of glitches is similar to the short-glitch family seen in HFI in-flight data. The limited integration time of Tandem experiment did not provide a sufficiently high signal-to-noise ratio to allow a confident fitting of the longer time-constants, as is observed in HFI in-flight data. All the glitches have rising times faster than the sampling of the AC read-out electronics, therefore in most cases the peaks correspond to the first sampled glitch data point.

The bolometer with a gold shield shows the same results as the one without the shield. It seems that we are not able to observe any delta electrons under these conditions.

We can summarize the results of the Tandem accelerator test as follows:

  • We are able to isolate long and short glitches without introducingany delta-electron production process.

  • The two families of glitches show the same rate ratio and the same time-constants as observed in HFI in-flight data.

  • Slow glitches were not observed because we did not use PSB bolometers during this test.

thumbnail Fig. 6

55Fe X-ray calibration run. Event rate versus signal. The distribution is asymmetric and two overlapping peaks are evident.

Table 3

Calibration factors for the 217 GHz SWB, measured under various operating conditions.

5.3. Alpha-particle tests

These tests were performed between June 2011 and April 2013 using the same 100 mK dilution cryostat and read-out electronics as were used in the Tandem test. The aim of these tests was to characterize in detail the long glitches observed in HFI in-flight data. The Tandem accelerator tests have demonstrated that it is possible to have long glitches without involving any delta-electron creation processes. Several tests were conducted, as described in the following subsections.

5.3.1. Calibration run

We used a 55Fe source that produced X-rays at 5.9 keV. A typical spectrum (event rate versus signal) is presented in Fig. 6. The distribution is asymmetric and two overlapping peaks are evident. This distribution can be interpreted as follows: the probability that a 5.9 keV X-ray is absorbed by 1 μm of silicon nitride is about 3.5%. If absorbed in the grid, the 5.9 keV X-ray will ionize the atoms of the silicon nitride. Some of the photoelectrons produced will be absorbed in the silicon nitride itself, which means that this energy will be fully transformed into heat. Nevertheless, as the grid is 1 μm thick, we expect to have a significant rate of photoelectron escape that will produce an asymmetry in the spectrum at lower signals. In addition, at the atomic level, when a core electron is removed and leaves a vacancy, an electron from a higher energy level may fall into the vacancy, which results in a release of energy. This energy can be released in the form of a fluorescence X-ray (for the silicon Kα/β fluorescence X-ray of 1.8 keV) or the energy can be transferred to another electron and ejected via the Auger effect. The Auger electrons will be absorbed very quickly in the silicon nitride, in which case all the 5.9 keV of the 55Fe X-ray will be fully transformed into heat and are then measured by the NTD as a change of temperature. This represents the larger peak in the spectrum at higher energy. If the absorption process produces fluorescence X-rays of 1.8 keV (yield of about 5%), they will be able to escape easily from the silicon nitride, removing 1.8 keV of the energy to be transformed into heat. This represents the second overlapping peak at lower energy. In conformity with this interpretation, we chose to derive the calibration factors in the higher energy peak. Calibration factors (in μV/keV) were calculated for several conditions (see Table 3).

5.3.2. Delta electron test

In this test, the α source was placed in front of the bolometer with a 2.5 mm diaphragm at a distance of about 1 cm. A 10 μm thick copper shield was glued onto the diaphragm. After interacting with the shield, the α particles retain an energy of about 1.1 MeV. In this case, the beam spread permits the α particles to reach both the NTD+absorber and the silicon die. We biased the source and the copper shield with a variable positive voltage from 0 V to 500 V to suppress (or partially suppress) the contribution from delta electrons pulled out of the shield. In Fig. 7, we present the histograms of the number of counts versus absorbed energy for the three applied voltages. The three histograms are centered at about the same value. We conclude that the ground-based tests did not show any measurable production of delta-electrons.

thumbnail Fig. 7

Delta electron test: number of events per hour versus signal, with three different applied voltages.

thumbnail Fig. 8

Silicon die tests. Number of events per hour versus calibrated absorbed energy in the NTD thermometer for two positions of the diaphragm along the silicon die (green and blue) and for the Tandem test (brown). The absorbed energies have been corrected taking into account the differences of the absorbed energy in the silicon die between the tests (1.1 MeV absorbed in the silicon die by α particle in Grenoble tests and 1.6 MeV absorbed in the silicon die from the Tandem accelerator test.)

thumbnail Fig. 9

Silicon die tests. Glitch template built by stacking 466 events caused by impacts in the Si wafer (black curve). The fitted time-constants with exponential models are presented (blue and red curves).

5.3.3. Silicon die tests

In this test, the α source was placed in a variety of positions in front of the silicon die. We used a 1.5 mm diaphragm with 10 μm copper shield at a distance of about 5 mm from the NTD thermometer. In this case, the α particles can interact only with the silicon die. The 1.1 MeV α particle is completely absorbed in the silicon die. We define the attenuation factor Edie/Ebolo as the ratio of the energy absorbed per glitch in the silicon die to the energy absorbed in the NTD thermometer. In this test we checked the variation of the attenuation factor by moving the source between two positions along the silicon die. In Fig. 8 we present the comparison between the energy distribution of the Tandem test (in brown) and the histograms corresponding to the two positions of the diaphragm. The green line corresponds to a little region of the silicon die close to the absorber. The blue line corresponds to larger region close to the gold pad. The attenuation factor can change from about 500 to 1000 between the two positions. For Tandem test, where the silicon die is fully covered by the proton beam, the derived attenuation factor is 650.

In parallel with the tests that used the HFI read-out electronics, we performed several tests dedicated to characterizing the interaction of particles with the silicon die using DC readout electronics operating at ambient temperature without cold JFETs. This electronics chain has been validated by the IAS team for testing scintillating bolometers (Coron et al. 1990). The noise of the readout was about 11 nV Hz1/2, low enough to have a good signal-to-noise ratio on the glitches.

The aim of these tests was to sample fast enough to be able to distinguish different physical processes that might be implicated in the heat propagation from the silicon die to the NTD thermometer. The results of this test agree with the Grenoble and Tandem accelerator tests. In Fig. 9 we present a typical glitch produced from the hit of an α particle on the silicon die, along with the time-constants of an exponential model.

5.3.4. Modified bolometer test

This test was designed to demonstrate the ballistic phonon propagation from the silicon die to the grid + NTD thermistor. To achieve this goal we broke the grid legs (65% of the leg cross-sectional area was severed) to reduce the ballistic heat transport by a measurable factor. The nitride legs were broken using a stainless-steel needle. The break location was made directly at the edge of the Si frame. The breaks were made by placing the needle next to the leg and also with the needle next to the Si frame. The needle was then pushed sideways to break the legs.

We performed an initial reference test with the unmodified bolometer. Then we performed the test with the modified bolometer, using the same setup. The spectrum of the count rate versus the calibrated energy absorbed showed that there was no change in the measured energy or the counts. We did, however, observe a difference in glitch shape between the two runs. We built a template by stacking all the events coming from silicon die hits. We fitted this template with a two-time-constant model (Fig. 10 and Table 4). The amplitude corresponding to the fast time-constant changed by about 20%. This result is consistent with the hypothesis that part of the the heat propagates to the NTD thermometer by ballistic phonons.

thumbnail Fig. 10

Normalized template of the hit on the silicon die. Error bars only show statistical errors.

Table 4

Effect of removing legs from an SWB: two-time-constant model parameters.

5.3.5. Coincidence test

For this test we used a PSB bolometer. The α source was placed in front of the grids of the PSB using a 1.5 mm diaphragm with 10 μm copper shield at a distance of about 5 mm from the NTD thermometer. A PSB bolometer module is surrounded by copper except for a 1.59 mm hole in front of the grids and a small aperture on the silicon die, so in this case, we were completely sure to hit only the grids.

The coincidence of short glitches on PSBa and PSBb seen in flight (Planck Collaboration X 2014) show that approximately 50% of events are seen in both PSBa and PSBb without phase shift and without correlation in amplitude. From modeling the interaction of hundreds of MeV protons with 1 μm silicon nitride with GIANT-45, we found that about ten electrons can be ejected from one grid. This produces a small change in temperature on the other NTD below the detection threshold. The rate of 50% correlation can be explained by geometrical effects such as particles coming from the top or bottom. Glitch PSBa/b coincidences with a strong amplitude correlation, on the other hand, which corresponds to a direct impact of protons on the two grids, were observed to range between 2% and 4%, depending on the bolometer.

These ground-test results give a level of coincidence of about 3% for glitches that are very well correlated in amplitude, when considering only the glitches detected at or above 5σ. This agrees with direct interactions of α particles with the two grids. We observed only few of glitches without a strong amplitude correlation, but the integration time of these tests was insufficient to show the expected 50% level of coincidence due to ejected electrons. We conclude that ground-based coincidence tests did not fully explain the coincidence level between PSB bolometers observed in flight. For a complete analysis of this problem we refer to the companion paper (Planck Collaboration X 2014).

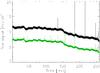thumbnail Fig. 11

HFI ground calibration. Four hours of time-ordered data (TOD) taken under stable environmental conditions. Black: PSBa. Green: PSBb.

5.4. HFI ground calibration

During pre-launch Planck system tests, CRs were seen by HFI, but far fewer than at L2. At sea level, muons are the most numerous charged CR particles, with a mean energy of about 4 GeV (Ramesh et al. 2012). The integral intensity of vertical muons at sea level is about 1 cm-2 min-1 for horizontal detectors. The overall angular distribution of muons at the ground is proportional to cos2δ, where δ is the elevation angle.

During the CSL ground-based tests, the focal plane is almost vertical, therefore we expect to have a few tens of events per hour in the silicon die and a few per day in the absorber + NTD. The absorbed energy in the silicon die is about 150 keV, which means that considering the attenuation factor measured in the Grenoble tests, muons are expected to produce measurable glitches during the pre-launch HFI calibration tests. In addition, these glitches should be seen in coincidence in the PSB bolometers.

To demonstrate the glitch rate observed during the HFI ground-calibration testing, Fig. 11 shows a typical PSB that we observed under stable conditions during the HFI ground-calibration experiments.

We saw about 20 glitches per hour in PSBb (green curve) and fewer in PSBa (black curve). In all the polarized bolometers, the ratio of the PSBa counts to the PSBb counts is the same; almost all the events seen in PSBa coincide with an event seen in PSBb.

6. Discussion

6.1. Short glitches

Short glitches dominate the rate at high energies. This has been confirmed in the ground-based tests (see, e.g., Fig. 5). The thermal response template built from this family agrees well with in-flight HFI bolometer data and ground-based data on the direct interaction of particles with the absorber and NTD thermometer. The energy distribution of the short glitches is similar in all the bolometers and shows a double-peaked structure (Planck Collaboration X 2014). The bump in the short-glitch distribution, centered at about 20 keV, is completely consistent with the interaction between CRs and the NTD thermometer. At low energies, the distribution corresponds to the interaction between the absorber and the CRs.

Another indication that short glitches are produced from direct interaction between CRs and the grid or thermistor can be found in the comparison between the HFI bolometer electronics time-response measured on-sky signal (Planck Collaboration IV 2011) and the transfer function built from the short-glitch template (see Fig. 12). The agreement between the transfer function derived from optical measurements (solid green) and short glitches (black stars) is good, considering that the template is constructed independently of any model. We can conclude that the HFI short glitches are produced by direct interaction of particles with one of the absorber grids (or directly with the NTD thermistor for a small subset of them).

thumbnail Fig. 12

Comparison of the HFI optical transfer function (Planck Collaboration IV 2011; green line), short-glitch template (black stars), and long-glitch template (blue stars).

6.2. Long glitches

By contrast, the long-glitch template (blue stars in Fig. 12) is not consistent with the optical transfer function, indicating a different physical origin for these glitches.

Two hypotheses have been put forward to explain the many long glitches seen in HFI flight data: (1) the NTD thermometer is sensitive to a change in temperature of other (larger) elements; or (2) long glitches are caused by indirect interaction between CRs and bolometers. From the ground-based tests we determined that it is not possible to generate enough delta-electrons to reproduce the energy distribution of HFI in-flight long glitches (Fig. 4). On the other hand, we have shown that the NTD thermometer is sensitive to temperature changes of the silicon die. All the ground-based tests have confirmed this hypothesis. In addition, the HFI ground-based calibration data show a rate of events compatible with the CR flux at sea level over the silicon die surface. Starting from these considerations, we developed a toy model of the impact of CRs with the silicon die in orbit at L2 that can explain the long-glitch spectrum seen by the Planck HFI during flight observations. The details of this model are presented in Planck Collaboration X (2014). These results agree with the results published by the SPIRE collaboration: small co-occurring glitches that are seen simultaneously on many detectors in a given array in the SPIRE detector timelines, are believed to be due to ionizing hits on the silicon substrate that supports all the detectors in an array (Horeau et al. 2012).

The physical interpretation of long glitches can be found in the shape of the long glitches that we have isolated during the ground-based tests. With the improved temporal resolution made possible by the faster DC-based REU readout electronics and sampling, we can clearly see (Fig. 9) the dual time-constant response that results from heat transfer between the silicon die and the NTD thermometers. We identify two possible hypotheses to explain the heat propagation from the silicon die to the NTD thermometer:

Ionization and thermal diffusion:

According to this hypothesis, the faster time-constant is given by ionization within the silicon die. The ionization signal is obtained by the collection of the electron-hole pairs created by interaction of α particles in the silicon crystal via the gold pad. The long tail can still be explained by the heat diffusion between the silicon die and the NTD thermometers. Using the bolometer parameters, we can determine the equivalent bias step amplitude needed to produce a glitch of about 4 keV (the typical energy absorbed in the bolometer from a hit in the silicon die). We obtain ΔIb = 0.2 nA, which is of the same order as the working bias current. If present, an effect as strong as this should be evident through inspection of the raw TOI signals. In fact, before sufficient time has elapsed for heat diffusion within the bolometer, a collected charge must show a peak in the raw signal with a decay-time constant determined only by the RC time-constant of the individual detector read-out circuitry. The sign of this peak should not change with the changing polarity of the detector bias current. Therefore, this effect should be easily distinguished from a thermal glitch. The results of this analysis are presented in Fig. 13: in black we show a template of the typical unperturbed raw signal set during the test. The red and the blue curves represent the difference between a raw signal with a glitch (in the center of the half periods) and the template. There is no evidence of ionization in the raw signals; all the glitches can be fully explained by pure thermal events (i.e., hot and/or cold phonons).

thumbnail Fig. 13

Raw signal analysis of the silicon die tests: unperturbed raw signal (black curve). Difference between a raw signal with a glitch occurred in the center of the half period and the template (blue and red curves).

Ballistic phonon propagation and thermal diffusion:

According to this hypothesis, the faster time-constant, which corresponds to the typical time-constant of the bolometers as measured with optical sources in ground- and flight-calibration testing, can be explained by ballistic phonon heat conduction:6 in our case, ballistic phonons can propagate unhindered from the silicon die and up the grid legs, depending on the geometrical coupling fixed by the size and the number of the legs. The final effect is equivalent to a particle absorbed directly in the grid.

The longer time-constant (tens of milliseconds) represents the non ballistic thermal heat diffusion between the silicon die and the NTD thermometers. This implied time-constant is consistent with the heat capacitance of the silicon die and the thermal conduction of the silicon die to the bolometer itself. A detailed thermal model of the bolometer is presented in a companion article (Spencer et al., in prep.) that describes ground-based tests on flight-spare bolometers conducted in Cardiff. The tests were performed by placing NTD-Ge thermometers and 100 kΩ heaters at various locations on a bolometer module (the silicon die, the PWB, and the module housing). Glitch events were simulated by rapid injection of known quantities of thermal energy through the additional resistors attached to the bolometer module while observing the temperature response of the bolometer and its elements.

The modified bolometer tests of this work have shown that by breaking 8 of the 12 grid-support legs we can reduce the amplitude of the long-glitch fast time-constant amplitude without an accompanying decrease in the glitch long-tail contribution. This implies a reduced effective ballistic cross-sectional area between the silicon die and spider-web absorber/NTD. This completely agrees with the ballistic-conduction hypothesis.

6.3. Slow glitches

Slow glitches are the rarest glitch events we see in the HFI in-flight bolometers. They only affect the PSBa and have a rate of a few per hour in flight. The energy distribution of the slow glitches shows the same power-law index as the energy distribution of long glitches (see Fig. 4). In addition, the slow glitches share the template of the long glitches, but without the component with the shortest time constant. The slow glitches were not reproduced during any of the HFI ground-based tests, both pre-launch with the HFI FPU, and post-launch with flight-spare hardware. In light of this fact, we are limited to proposing a hypothesis for the origin of the slow glitches that is consistent with our current results, but lacks experimental confirmation. The presence of the feed-through (see Sect. 3) connecting the PSBa bolometer to its corresponding silicon die is the only difference between the PSBa bolometers and the other types of bolometers in HFI (PSBb and SWB). The PSBa feed-through elements have a strong thermal coupling with the silicon die and gold pad. A proton hitting a PSBa feed-through can therefore heat the corresponding silicon die to produce heat diffusion from the silicon die to the NTD thermometer. This heating would not have the corresponding ballistic heat conduction associated with a silicon die/CR glitch event, and therefore no fast time-constant would be observed. The differences in the effective surface area of the feed-throughs with respect to the corresponding silicon dies, of a factor of about 100, may explain the differences in the rate between the long and slow glitches.

7. Implications for future space missions

Planck HFI has demonstrated the effectiveness of using a grid absorber instead of a solid/bulk absorber for collecting CMB photons to drastically reduce the number of direct glitches (short glitches). This characteristic allowed HFI to deliver data at the signal-to-noise ratio required for the Planck scientific goals. Nevertheless, we observed more glitches than expected at low energies (long glitches). The ground-based experiments discussed here demonstrated that the silicon die is able to propagate the energy absorbed from CRs to the bolometer absorber and NTD thermometer. In this case, the absorbed energy propagates to the NTD thermometer via ballistic phonons; this is followed by a contribution of thermal diffusion from the silicon die to the absorber and NTD.

The study of the physical processes related to athermal propagation and ionization in a crystal, and more generally, the effects of particles in cryogenic bolometers, have several applications, including new-generation space missions at millimeter and submillimeter wavelengths (e.g., Caserta et al. 1990), high-resolution X-ray spectrometry (e.g., Kelley et al. 2007; Kilbourne et al. 2006; Stahle et al. 2004), and direct detection of dark matter (e.g., Sundqvist 2008; Martineau et al. 2004). In this section we discuss in particular how our results can be used to improve the design of new arrays of millimeter detectors for future space missions such as SPICA-SAFARI (Goicoechea et al. 2011; Spinoglio et al. 2011), PIXIE (Kogut et al. 2011), and CORE (CORE Team 2011).

The goal of improving the noise-equivalent power (NEP) of new experiments by at least one order of magnitude (from 10-17 W Hz −1/2 to 10-18 W Hz −1/2) can be achieved by increasing the focal-plane coverage, using thousands of background-limited instrument performance (BLIP) contiguous pixels7. Each pixel of these arrays must be micromachined starting from a common substrate.

Two new generations of detectors other than classical high-impedance bolometers are in competition in the development of future millimeter space missions. We summarize their principal characteristics and discuss how to minimize the effect of particle impacts.

Transition-edge sensors (TES)

are thermal detectors that use a superconductor thermometer biased at the superconductor transition (Rmean ~ 10 mΩ; e.g., Piat et al. 2002; Hubmayr et al. 2009). The only conceptual difference between the HFI high-impedance bolometers and TES bolometers is the sensitive element used to measure the change in temperature, which is a superconducting element in TES. Direct CRs impacting TES pixels will have the same effect as in the high-impedance bolometers. However, because of the common silicon wafer, the ballistic phonons and thermal heat transport from the wafer to the thermometer will affect several detectors at the same time in TES arrays. This effect could be reduced, for example, by increasing the heat capacity of the substrate and/or directing the ballistic phonon leak toward the housing and not to the pixels.

Kinetic inductance detectors (KIDs)

are superconducting resonant elements electromagnetically coupled to a common read-out transmission line. The absorption of the incoming photons causes a change of the resonance frequency through the breaking of Cooper pairs. The main advantages of KIDs over TES arrays are the straightforward frequency multiplexing readout and a faster time response (always <1 ms). Another conceptual difference is that KIDs are insensitive to a change of base temperature provided that Tbase ≪ Tc (where Tc is the superconductivity critical temperature). Considering an absorber of the same geometry as TES bolometers (suspended grid structure), the effect of particles in KIDs will be reduced by a factor between 10 and 100 due to the (still poorly understood) capability of ballistic phonons to break Cooper pairs. Only phonons with energy exceeding the superconducting gap can break pairs and produce a measurable signal. The presence of such energetic ballistic phonons could be attenuated, as for the TES detectors, by increasing the leak of energy toward the housing. Work is in progress on this subject (Swenson et al. 2010; Moore et al. 2012; Cruciani et al. 2012).

8. Conclusion

We have described several ground-based tests that lead to a physical interpretation of the impact of CR collisions on the Planck HFI bolometers in flight. An analytical model was developed to validate the physical interpretation with both ground-based and in-flight data. Our results are the following:

  • The dominant component of the in-flight long glitches isproduced by the impact of CRs on the silicon wafer that supportsthe absorber and the NTD thermometer. The heat propagates tothe NTD thermometer by ballistic phonons followed by acontribution of thermal diffusion.

  • Short glitches are produced by direct interaction of a particle with either the absorber grid or the NTD-Ge thermistor. In the case of PSB detectors, short glitches may also be the result of secondary electrons from a short glitch induced by a CR in the other PSB detector of the pair.

  • Slow glitches have not been reproduced in the ground-based tests. Their physical origin is consistent with the hypothesis that slow glitches result from the impact of CRs on the feed-through of the PSBa bolometers, but further work is needed to clearly identify their origin.

  • The influence of CR/detector glitches on scientific data quality needs to be included as a design constraint for future-generation detector arrays for space applications. This needs to be included in parallel with all of the other characteristics such as detector NEP and time response. In particular, optical beam-response tests needs to be planned to study irradiation on complete detector arrays (e.g., pixels, substrate, and housing). Starting from the same design conditions (for example, size and shape of the absorber, substrate and thermal contacts), non thermal detectors such as KIDs may present a conceptual advantage.

1

Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA(USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.

2

SREM consists of three detectors (diodes D1, D2, D3) in two detector head configurations (Mohammadzadeh et al. 2003). A total of 15 discriminator levels are available to bin the energy of the detected events.

3

Electrons ejected from matter by ionizing radiation.

6

Ballistic conduction is the unimpeded flow of energy that carries charges over large distances within a material.

7

The sensitivity of bolometers is fundamentally limited by statistical fluctuations of the radiation power from the observed source and the thermal emission from the cryogenic stages of the instrument.

References

  1. Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2011, Science, 332, 69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Boggess, N. W., Mather, J. C., Weiss, R., et al. 1992, ApJ, 397, 420 [NASA ADS] [CrossRef] [Google Scholar]
  3. Caserta, A., Bernardis, P. D., Masi, S., & Mattioli, M. 1990, Nucl. Instrum. Methods Phys. Res. A, 294, 328 [NASA ADS] [CrossRef] [Google Scholar]
  4. Catalano, A., Coulais, A., & Lamarre, J.-M. 2010, Appl. Opt., 49, 5938 [NASA ADS] [CrossRef] [Google Scholar]
  5. Christian, E. R., Bravar, U., de Nolfo, G. A., Ryan, J. M., & Stochaj, S. 2011, AGU Fall Meeting Abstracts, B2017 [Google Scholar]
  6. CORE Team. 2011, http://www.core-mission.org/documents/CoreProposal_Final.pdf [Google Scholar]
  7. Coron, N., Artzner, G., Leblanc, J., Jegoudez, G., & de Marcillac, P. 1990, in 9th Moriond Astrophysics Meeting, eds. J. Audouze, & J. Tran Thanh Van, 275 [Google Scholar]
  8. Cruciani, A., Swenson, L. J., Monfardini, A., et al. 2012, J. Low Temp. Phys., 167, 311 [NASA ADS] [CrossRef] [Google Scholar]
  9. Fixsen, D. J., Cheng, E. S., Gales, J. M., et al. 1996, ApJ, 473, 576 [NASA ADS] [CrossRef] [Google Scholar]
  10. Gaertner, S., Benoit, A., Lamarre, J.-M., et al. 1997, A&AS, 126, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Goicoechea, J. R., Roelfsema, P. R., Jellema, W., & Swinyard, B. M. 2011, in 280th Symposium of the International Astronomical Union, IAU Symp., 280, 179 [NASA ADS] [Google Scholar]
  12. Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
  13. Holmes, W. A., Bock, J. J., Crill, B. P., et al. 2008, Appl. Opt., 47, 5996 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  14. Horeau, B., Boulade, O., Claret, A., et al. 2012 [arXiv:1207.5597] [Google Scholar]
  15. Hubmayr, J., Aubin, F., Bissonnette, E., et al. 2009, submitted [arXiv:0908.1997] [Google Scholar]
  16. Jones, R. C. 1953, J. Opt. Soc. Am., 43, 1917 [Google Scholar]
  17. Kelley, R. L., Mitsuda, K., Allen, C. A., et al. 2007, PASJ, 59, 77 [Google Scholar]
  18. Kilbourne, C. A., Boyce, K. R., Brown, G. V., et al. 2006, Nucl. Instrum. Methods Phys. Res. A, 559, 620 [NASA ADS] [CrossRef] [Google Scholar]
  19. Kogut, A., Fixsen, D. J., Chuss, D. T., et al. 2011, J. Cosmol. Astropart. Phys., 7, 25 [Google Scholar]
  20. Leske, R. A., Cummings, A. C., Mewaldt, R. A., & Stone, E. C. 2011, Space Sci. Rev., 126 [Google Scholar]
  21. Martineau, O., Benoît, A., Bergé, L., et al. 2004, Nucl. Instrum. Meth. Phys. Res. A, 530, 426 [NASA ADS] [CrossRef] [Google Scholar]
  22. Masi, S., Battistelli, E., de Bernardis, P., et al. 2010, A&A, 519, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Mather, J. C. 1982, Appl. Opt., 21, 1125 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  24. Mauskopf, P. D. 1997, Ph.D. Thesis, University of California, Berkeley [Google Scholar]
  25. Mewaldt, R. A., Davis, A. J., Lave, K. A., et al. 2010, ApJ, 723, L1 [NASA ADS] [CrossRef] [Google Scholar]
  26. Mohammadzadeh, A., Evans, H., Nieminen, P., et al. 2003, IEE Trans. Nucl. Sci., 50, 2272 [Google Scholar]
  27. Moore, D. C., Golwala, S. R., Bumble, B., et al. 2012, Appl. Phys. Lett., 100, 232601 [NASA ADS] [CrossRef] [Google Scholar]
  28. Piat, M., Lagache, G., Bernard, J.-P., Giard, M., & Puget, J.-L. 2002, A&A, 393, 359 [Google Scholar]
  29. Picozza, P., Sparvoli, R., Adriani, O., et al. 2011, in Particle Physics at the Year of Astronomy, eds. H. Fritzsch, K. K. Phua, C.-E. B. E. Baaquie, et al., Il Nuovo Cimento, 200 [Google Scholar]
  30. Planck Collaboration IV. 2011, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Planck Collaboration VI. 2011, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Planck Collaboration I. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321529 [Google Scholar]
  33. Planck Collaboration X. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321577 [Google Scholar]
  34. Ramesh, N., Hawron, M., Martin, C., & Bachri, A. 2012 [arXiv:1203.0101] [Google Scholar]
  35. Rieke, F. M., Lange, A. E., Beeman, J. W., & Haller, E. E. 1989, IEE Trans. Nucl. Sci.„ 36, 946 [Google Scholar]
  36. Spinoglio, L., Magliocchetti, M., Gruppioni, C., Franceschini, A., & Isaak, K. 2011, in Galaxy Evolution: Infrared to Millimeter Wavelength Perspective, eds. W. Wang, J. Lu, Z. Luo, et al., ASP Conf. Ser., 446, 11 [Google Scholar]
  37. Stahle, C. K., Boyce, K. R., Brown, G. V., et al. 2004, Nucl. Instrum. Meth. Phys. Res. A, 520, 472 [NASA ADS] [CrossRef] [Google Scholar]
  38. Stone, E. C. 2012, in EGU General Assembly Conference Abstracts, eds. A. Abbasi, & N. Giesen, 14, 3933 [Google Scholar]
  39. Sudiwala, R. V., Maffei, B., Griffin, M. J., et al. 2000, Nucl. Instrum. Meth. Phys. Res. A, 444, 408 [NASA ADS] [CrossRef] [Google Scholar]
  40. Sundqvist, K. 2008, in APS March Meeting, 35015 [Google Scholar]
  41. Swenson, L. J., Cruciani, A., Benoit, A., et al. 2010, Appl. Phys. Lett., 96, 263511 [NASA ADS] [CrossRef] [Google Scholar]
  42. Vaillancourt, J. E. 2005, Rev. Sci. Instrum., 76, 043107 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Summary of the ground-based bolometer tests.

In the text
Table 2

Energy absorbed [keV] in the different elements of a bolometer module for normally incident particles.

In the text
Table 3

Calibration factors for the 217 GHz SWB, measured under various operating conditions.

In the text
Table 4

Effect of removing legs from an SWB: two-time-constant model parameters.

In the text

All Figures

thumbnail Fig. 1

Energy distribution of CR protons at L2. The vertical dashed lines represent the range of energies of interest for HFI (from 35 MeV to 10 GeV).
In the text
thumbnail Fig. 2

Top: front perspective mechanical drawing of a polarization-sensitive bolometer (PSB). The illustration shows the forward/upper portion, i.e., PSBa, of the PSBa/b pair. The orientation of the PSBb absorber is orthogonal to the PSBa. Bottom: mechanical drawing of a spider-web bolometer (SWB). In both figures, the printed wiring board (PWB) and cover are not shown. The size of a HFI bolometer module (including the thermometer, the absorber, the silicon die, the housing and the backshort) is between 1.5 and 1.9 cm depending on the working frequency.
In the text
thumbnail Fig. 3

HFI flight results: average short glitch template (blue), long glitch template (black), and slow glitch template (red) for one PSB in-flight bolometer (Planck Collaboration X 2014).
In the text
thumbnail Fig. 4

HFI flight results: glitch energy distribution for the three families of glitches with respect to the peak amplitude, in signal-to-noise units, for three different PSB and SWB in-flight bolometers (Planck Collaboration X 2014). The blue line is for the short glitch population, black is for long, red is for slow, and green is for total. Power laws are shown for comparison as dashed lines.
In the text
thumbnail Fig. 5

Tandem accelerator test. (A) Histograms of the glitch amplitudes in 2 h of integration time for low amplitudes (0 V – 0.1 mV). (B) Histograms of the glitch amplitudes in 2 h of integration for high amplitudes (greater than 0.1 mV). (C) Glitch template built by stacking all the events of the first family centered at 45 μV (blue) and the family centered at 0.15 mV (red). Both templates show the same fast time-constant τ (4 ms), and the blue template shows a slower time-constant (about 20 ms) with an amplitude relative to the peak of few percent.
In the text
thumbnail Fig. 6

55Fe X-ray calibration run. Event rate versus signal. The distribution is asymmetric and two overlapping peaks are evident.
In the text
thumbnail Fig. 7

Delta electron test: number of events per hour versus signal, with three different applied voltages.

In the text
thumbnail Fig. 8

Silicon die tests. Number of events per hour versus calibrated absorbed energy in the NTD thermometer for two positions of the diaphragm along the silicon die (green and blue) and for the Tandem test (brown). The absorbed energies have been corrected taking into account the differences of the absorbed energy in the silicon die between the tests (1.1 MeV absorbed in the silicon die by α particle in Grenoble tests and 1.6 MeV absorbed in the silicon die from the Tandem accelerator test.)
In the text
thumbnail Fig. 9

Silicon die tests. Glitch template built by stacking 466 events caused by impacts in the Si wafer (black curve). The fitted time-constants with exponential models are presented (blue and red curves).
In the text
thumbnail Fig. 10

Normalized template of the hit on the silicon die. Error bars only show statistical errors.
In the text
thumbnail Fig. 11

HFI ground calibration. Four hours of time-ordered data (TOD) taken under stable environmental conditions. Black: PSBa. Green: PSBb.
In the text
thumbnail Fig. 12

Comparison of the HFI optical transfer function (Planck Collaboration IV 2011; green line), short-glitch template (black stars), and long-glitch template (blue stars).
In the text
thumbnail Fig. 13

Raw signal analysis of the silicon die tests: unperturbed raw signal (black curve). Difference between a raw signal with a glitch occurred in the center of the half period and the template (blue and red curves).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.