| Issue |
A&A
Volume 569, September 2014
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 11 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201322265 | |
| Published online | 24 September 2014 | |
Non-LTE models for synthetic spectra of Type Ia supernovae
IV. A modified Feautrier scheme for opacity-sampled pseudo-continua at high expansion velocities and application to synthetic SN Ia spectra
1
Universitätssternwarte München, Scheinerstr. 1, 81679
München,
Germany
e-mail: hoffmann@usm.lmu.de; uh10107@usm.lmu.de;
pjnh@usm.lmu.de
2
Meteorologisches Institut, Ludwig-Maximilians-Universität
München, Theresienstr.
37, 80333
München,
Germany
e-mail: daniel.sauer@lmu.de
Received:
11
July
2013
Accepted:
22
October
2013
Context. Type Ia supernovae (SN Ia) have become an invaluable cosmological tool because their exceptional brightness makes them observable even at very large distances (up to redshifts around z ≈ 1). To investigate possible systematic differences between local and distant SN Ia requires detailed models whose synthetic spectra can be compared to observations and in which the solution of the radiative transfer is a key ingredient. One commonly employed method is the Feautrier scheme, which is generally very robust but can lead to wrong results under certain conditions that frequently occur when modeling supernova ejecta or even the radiatively driven expanding atmospheres of hot stars.
Aims. We attempt to improve the procedure we have developed for simulating the radiative transfer of metal-rich, intermediate- and low-density, line-dominated atmospheres to allow the method to be applied successfully even under conditions of high expansion velocities.
Methods. We use a sophisticated model atmosphere code that considers the non-LTE effects and large velocity gradients that strongly affect the physics of SN Ia atmospheres at all wavelengths to simulate the formation of SN Ia spectra by the thousands of strong spectral lines that intricately interact with the “pseudo-continuum” formed entirely by these Doppler-shifted lines themselves. We focus on investigating the behavior of the Feautrier scheme under these conditions.
Results. Synthetic spectra of SN Ia, a complex product of computer models replicating numerous physical processes that determine the conditions of matter and radiation in the ejecta, are affected by large spatial jumps of the line-dominated opacities and source functions for which the application of even well established methods may harbor certain pitfalls. We analyse the conditions that can lead to a breakdown of conventional procedures and we derive a modified description that yields more accurate results in the given circumstances for the Feautrier radiative transfer solver.
Key words: radiative transfer / supernovae: general / supernovae: individual: SN 1992A
© ESO, 2014
1. Introduction
Devising a tool that can relate the observed characteristics of SN Ia to specifics of the underlying explosion is fundamental not only for studying the explosion mechanism itself (which is still unclear in many details) but also for investigating possible systematic effects in the evolution of SN Ia from earlier cosmological times to recent ones. The spectra, in particular, offer a wealth of information that may be utilized for this purpose, but owing to the complexity of the problem as a result of back-reactions and the large number of variables involved in forming the spectrum, the interpretation of the spectra must rely on computer models that replicate as closely as possible the physical processes that determine the conditions of matter and radiation in the ejecta. Realistic radiative transfer models thus provide the crucial link between explosion models and observations.
For transfer problems in general, and radiative transfer in particular (see, e.g., Cannon 1970), Feautrier’s (1964) solution of the radiation transfer equation has proved to be enormously successful in many areas of astrophysics. The reasons for its success are that it requires comparatively little computational effort, is numerically stable, and provides good accuracy (cf. Kalkofen & Wehrse 1982).
In our model atmosphere code WM-basic (Pauldrach et al. 1998, 2001, 2012; Pauldrach 2003), we employ the Feautrier method to solve the radiative transfer in the first part of a two-stage iteration procedure. In this first part, we use an approximate, but fast, opacity-sampling method on a comparatively coarse radial grid to account for the influence of spectral lines on the radiation field, while in the second part we use a detailed formal integral on a spatial microgrid that is capable of resolving the details of the line profiles and that correctly treats all multi-line effects. The closer the results of the first, approximate, method are to those of the detailed, exact method, the fewer iterations of the second, numerically much more expensive method are required.
Although this procedure has proven to be very reliable in models for analysing spectra of expanding atmospheres of hot stars (cf. Pauldrach 1987; Pauldrach et al. 1990, 1994, 2001, 2004, 2012; Kaschinski et al. 2012, 2013) and gaseous nebulae (cf. Hoffmann et al. 2012; Weber et al. 2013), the physical conditions in SN Ia constitute a stronger challenge to the method. In SN Ia the dominating source of opacity are lines, while the continuum only plays a minor role (cf. Pauldrach et al. 1996). Here one often encounters the situation that single lines dominate the opacities by several orders of magnitude, and owing to the large velocity gradients in the SN Ia ejecta (homologous expansion, v ∝ r) these lines are strongly Doppler-shifted as well. Because of the usually not very high radial resolution used in the iterations employing the sampling procedure, it frequently happens that at a particular wavelength point the radial dependencies of the opacities and the source functions show large jumps as the line gets Doppler-shifted through the wavelength grid in the observer’s frame. As we show in Sect. 2, the standard Feautrier solution in the form used here fails to correctly describe the radiation field in the presence of large radial opacity jumps, such as those occurring in the metal-rich expansion-dominated ejecta of supernovae. In Sect. 3 we describe an extension that cures this failure and describes the radiation field better without significantly increasing the complexity of the radiative transfer solver. Results of test calculations are presented in Sect. 4, in Sect. 5 we apply our new approach in the actual transport code to calculate improved synthetic spectra for SN Ia, and in Sect. 6 we present the implications of our findings.
2. Concept for realistic atmospheric models of SN Ia
To determine observable physical properties of supernovae via quantitative spectroscopy, the radiative transfer models must be set up in some detail, and therefore, detailed physics must already be implemented to calculate synthetic spectra on the basis of stationary and spherically symmetric envelopes with “photospheres” as lower boundaries. For simulating and understanding the processes involved in SN Ia envelopes, different numerical approaches have been developed to model the radiative transfer and the evolution of the light curves1.
In our approach the description of radiative processes in the supernova ejecta is divided into two parts. First, the deposition of radiative energy via γ-photons resulting from the decay of 56Ni and 56Co, as well as the trapping of photons in the highly opaque, expanding material is treated in a time-dependent simulation using a Monte-Carlo approach (cf. Pauldrach et al. 2014). (It is the interplay between deposition of energy and trapping and escape of photons that leads to the characteristic shape of the light curve.) Second, the actual formation of the spectrum is treated with a detailed non-LTE spectral synthesis code. Since this needs to consider only the outer parts of the ejecta from which radiation actually emerges and where the timescales for interaction of photons with matter become small, this problem can be treated in the form of “snapshots” for a given epoch.
Our focus lies on a sophisticated description of the SN Ia spectra with emphasis on high spectral resolution and detailed modeling of the emission and absorption processes leading to these spectra, in order to quantify the observable physical properties of SN Ia accurately. The spectral synthesis code must therefore provide a consistent solution of the non-LTE occupation numbers of all relevant elements (via a solution of the statistical equilibrium based on accurate atomic models, and including collisional and radiative transition rates for all important ions, low-temperature dielectronic recombination, and Auger ionization due to K-shell absorption of soft X-ray radiation) and of the detailed radiative transfer (taking all significant sources of opacity and emission into account and thereby providing proper treatment of line blocking2 and blanketing3), as well as of the temperature structure (determined via a solution of the microscopic energy equation, which states that the energy – taking the local energy production rates from the radioactive decay chains into account – must be conserved in the atmosphere; cf. Pauldrach et al. 2014). As part of the self-consistent solution of the entire system, one obtains the frequency-resolved radiation field at the outer boundary – the synthetic emergent spectrum – which can, in principle, be directly compared to observations.
Although such spectral synthesis codes are being applied with great success to analysing the spectra of hot stars with winds, reproducing the stellar spectra in great detail, the modeling of SN Ia spectra has not yet reached the same level of realism. It is the complex physical conditions within the expanding SN Ia ejecta compared to those in the atmospheres of hot stars that make it extremely difficult to implement models that allow reliable and quantitative analysis. Despite the underlying microphysics being the same in stellar atmospheres and supernova ejecta, the physical conditions are different enough that approximations that are excellent in stellar atmospheres become invalid in supernovae.
One of these is the commonly applied diffusion approximation as the inner boundary in the radiative transfer modeling, which breaks down because the opacity in SN Ia is dominated by electron scattering over wide wavelength ranges, in contrast to stars that have a strong free-free and bound-free continuum. Electron scattering, however, does not couple the radiation field to the thermal pool, so that the radiation field cannot become Planckian even at depth. We have developed a semi-analytical description that allows us to overcome some of the limiting assumptions in the conventional treatment of the lower boundary in SN Ia radiative transfer models. The improved boundary condition explicitly takes the dominance of scattering processes at the longer wavelengths into account and leads to much better agreement with observed spectra in the near-infrared part (cf. Sauer et al. 2006).
Still, the models tend to predict much more flux in the red and near-infrared parts of the spectrum than is actually observed, and this behavior must be connected to the radiative transfer formalism, which is effectively thwarted by the superposition of thousands of strong metal absorption lines blocking the flux in the UV part of the spectrum within the expanding envelope (cf. Sect. 5). We have identified two severe problems in the radiative transfer related to these extreme conditions. The first one is connected to a hidden form of lambda iteration that is caused by the mutual interaction of strong spectral lines and which is inherently connected to the line blocking effect. Based on this finding we have derived a solution to this problem, such that the formation of these lines results in a correct description of the pseudo-continuum. With the application of this method, the changes obtained in the energy distributions and line spectra lead to much better agreement with the observed spectra than those of previous models (cf. Pauldrach et al. 2014).
The second problem we have encountered in our investigation of the behavior of radiative transfer under the extreme conditions of SN Ia envelopes is related to the standard Feautrier solution, which, in the form it is used, fails to correctly describe the radiation field in the presence of large radial opacity jumps. In our procedure these jumps are a result of spectral lines being Doppler-shifted across the observer’s frame frequencies for which the radiative transfer is being calculated. For the radiative transfer being computed in the comoving frame4 (as described, for example, by Baron et al. 1996), this particular problem is therefore much less likely to arise. But for the purpose of understanding why the radiative transfer scheme behaves this way, the reason for these jumps is not important, and any strong jump in the radial run of the opacities (such as produced, say, by an unresolved (i.e., occurring between two adjacent grid points) large change in the occupation numbers, abundances, or density) may also cause the problem in either reference frame.
2.1. The Feautrier solution to the radiative transfer equation
For the solution of the radiative transfer in the observer’s frame, three similar algorithms are used in our procedure. The initial solution is obtained from a Rybicki method (Rybicki 1971; Mihalas 1978, p. 158) that implicitly solves the transport equation including Thomson scattering. Because this solution does not have very high accuracy, an iteration for the radiation field that enters into the Thomson emissivity is performed. Here, the ray-by-ray solution and the angle-integrated moment equations are iterated. Both systems are solved with a Feautrier scheme (cf. Mihalas 1978, p. 156), and the iteration is performed twice for each frequency point: first for a pure continuum model and afterwards for the full problem with continuum and spectral lines. One crucial limitation of this approach is that, strictly speaking, the Feautrier method is only applicable if the opacities and source functions vary only slowly over radius; i.e., the radial variation of the lines would have to be resolved by the grid. The sampling iteration, however, uses a coarse radial grid consisting of a limited number of depth points. Therefore, at a given frequency point most lines will be present at a single radial grid point only (being Doppler-shifted to different frequency points at the neighboring depth points), and the standard procedure thus has to be modified to be able to use this algorithm (see Sect. 2.3). To understand how the method fails and to determine what modifications are required, the procedure does have to be presented in some detail first.
For the numerical description of the transfer equation, a discretization method that allows sufficient accuracy must be applied, and the solution is then carried out in the usual Cartesian p-z-coordinate system (Fig. 1), in which each p-ray corresponds to a μ-direction in spherical coordinates. The transformation between the r-μ and p-z-coordinates is
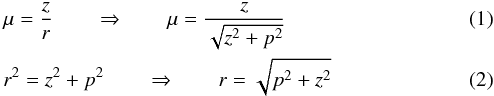 and,
therefore,
and,
therefore, 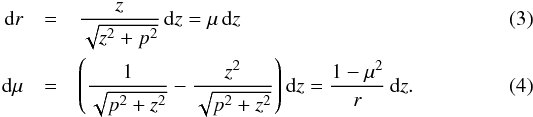 To
solve the transport equation in this p-z geometry, it is useful to convert the radiative
transfer equation dI/
dz = −χI + η, a
first-order differential equation with a single boundary condition, into a second-order
differential equation with a boundary condition for each side (e.g., Mihalas 1978). For this method, introduced by P. Feautrier, the
transfer equation for each p-ray is rewritten for the intensities in positive
and negative z-direction
To
solve the transport equation in this p-z geometry, it is useful to convert the radiative
transfer equation dI/
dz = −χI + η, a
first-order differential equation with a single boundary condition, into a second-order
differential equation with a boundary condition for each side (e.g., Mihalas 1978). For this method, introduced by P. Feautrier, the
transfer equation for each p-ray is rewritten for the intensities in positive
and negative z-direction 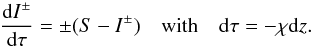 (5)By introducing the new
variables
(5)By introducing the new
variables 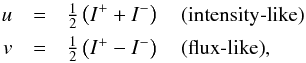 (6)Eq.
(5) can be written as a system of two
coupled differential equations,
(6)Eq.
(5) can be written as a system of two
coupled differential equations, 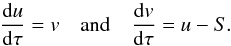 (7)After combining
these two equations by eliminating v, one obtains the single second-order differential
equation for u with the independent variable τ:
(7)After combining
these two equations by eliminating v, one obtains the single second-order differential
equation for u with the independent variable τ: 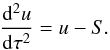 (8)
(8)
 |
Fig. 1 Sketch of the p-z coordinate system that is used for the solution of the radiative transfer. In this geometry, at any given radius r, each p-ray corresponds to a different direction μ. |
In the standard discretized scheme, this equation is represented as a set of difference
equations, one for each radial grid point i along the ray: 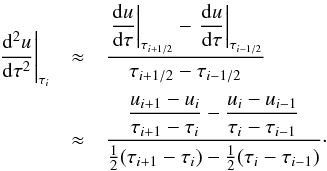 (9)This
represents a linear equation system for ui
(9)This
represents a linear equation system for ui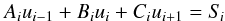 (10)with the
coefficients
(10)with the
coefficients 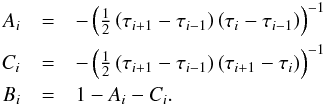 (11)This
tridiagonal matrix system can be solved efficiently by standard linear algebra solvers. In
our non-LTE-models, a Rybicki-type scheme (Rybicki
1971; Mihalas 1978, p. 158) is used that
solves all p-rays simultaneously to implicitly account for the
radiation field J that enters the scattering part of the source
function S
(cf. Appendix A of Pauldrach et al. 2001).
(11)This
tridiagonal matrix system can be solved efficiently by standard linear algebra solvers. In
our non-LTE-models, a Rybicki-type scheme (Rybicki
1971; Mihalas 1978, p. 158) is used that
solves all p-rays simultaneously to implicitly account for the
radiation field J that enters the scattering part of the source
function S
(cf. Appendix A of Pauldrach et al. 2001).
As Eq. (9) contains only differences in
τ that can
be easily derived from the opacities χi at the respective
grid points of the z grid from 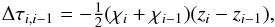 (12)the system behaves well
if opacities and source functions are slowly varying functions of z. Problems can, however,
arise if these conditions cannot be guaranteed, such as when strong ionization edges occur
or a large velocity gradient shifts strong lines in frequency. Such situations can cause
large variations of the opacity from grid point to grid point at a given frequency. One
such problematic situation5 – already discussed by
Pauldrach et al. (2001) – occurs if a point with
a large source function Si and low opacity
χi is adjacent to a
point with high opacity χi + 1 and low or
average source function Si + 1. In reality,
the large source function Si should only have a
weak impact on the radiation field since it occurs in a low-opacity region (and therefore
the emissivity is also low). In the solution of the equation system, however, the emission
computed in this situation is on the order of
(12)the system behaves well
if opacities and source functions are slowly varying functions of z. Problems can, however,
arise if these conditions cannot be guaranteed, such as when strong ionization edges occur
or a large velocity gradient shifts strong lines in frequency. Such situations can cause
large variations of the opacity from grid point to grid point at a given frequency. One
such problematic situation5 – already discussed by
Pauldrach et al. (2001) – occurs if a point with
a large source function Si and low opacity
χi is adjacent to a
point with high opacity χi + 1 and low or
average source function Si + 1. In reality,
the large source function Si should only have a
weak impact on the radiation field since it occurs in a low-opacity region (and therefore
the emissivity is also low). In the solution of the equation system, however, the emission
computed in this situation is on the order of 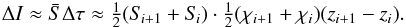 (13)In this expression,
the term Siχi
+ 1 dominates under the assumed conditions, which leads to an
artificially enhanced emission. This happens because physically it does not make sense to
multiply the source function of one point with the opacity of another point. Source
functions, as a matter of principle, are only meaningful quantities relative to the
opacity at the same point. As discussed by Pauldrach et
al. (2001), the method can still be used if the equation system is written in
z instead
of τ (as in
Feautrier’s original paper) because the z-dependence of χ can be treated correctly
only in this formulation. Equation (8) then
becomes
(13)In this expression,
the term Siχi
+ 1 dominates under the assumed conditions, which leads to an
artificially enhanced emission. This happens because physically it does not make sense to
multiply the source function of one point with the opacity of another point. Source
functions, as a matter of principle, are only meaningful quantities relative to the
opacity at the same point. As discussed by Pauldrach et
al. (2001), the method can still be used if the equation system is written in
z instead
of τ (as in
Feautrier’s original paper) because the z-dependence of χ can be treated correctly
only in this formulation. Equation (8) then
becomes 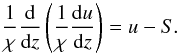 (14)Carrying out the same
discretization as before leads to the new difference system
(14)Carrying out the same
discretization as before leads to the new difference system 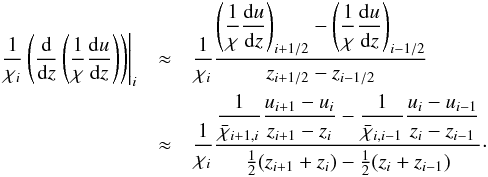 (15)Thus,
the coefficients (cf. Eq. (11)) are now
(15)Thus,
the coefficients (cf. Eq. (11)) are now
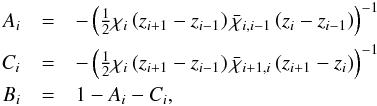 (16)where
the first terms of A and B now contain the local opacity.
For the mean opacity
(16)where
the first terms of A and B now contain the local opacity.
For the mean opacity 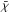 ,
the choice of geometric mean
,
the choice of geometric mean 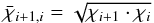 (17)generally
produces reasonable results for stellar atmospheres, where the density increases very
strongly with depth. While this choice puts more weight on the lower of the two opacities,
the arithmetic mean
(17)generally
produces reasonable results for stellar atmospheres, where the density increases very
strongly with depth. While this choice puts more weight on the lower of the two opacities,
the arithmetic mean 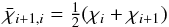 (18)weights the
opacities equally and is more appropriate where the gradients are smaller.
(18)weights the
opacities equally and is more appropriate where the gradients are smaller.
Another caveat in using the Feautrier scheme for solving the radiative transport for conditions where the opacity is not smoothly distributed over radius is that part of the line emissions are incorrectly re-absorbed in the adjacent intervals because the source functions are only defined on the grid points. For a detailed discussion of this issue, see Sect. 2.3.
Boundary conditions.
To close the system in Eq. (9),
appropriate boundary conditions have to be chosen. The respective boundary equations can
be obtained from an expansion of ui in τ at the boundary points
outside (i =
N) and inside (i = 1): 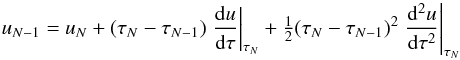 (19)and
(19)and
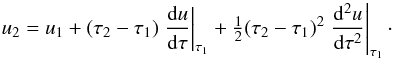 (20)It is assumed
that there is no incident radiation (I− ≡ 0) at the outer boundary6. Thus from Eq. (7), one obtains
(20)It is assumed
that there is no incident radiation (I− ≡ 0) at the outer boundary6. Thus from Eq. (7), one obtains 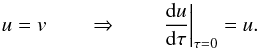 (21)With Eq. (8), this leads to the outer boundary
condition
(21)With Eq. (8), this leads to the outer boundary
condition 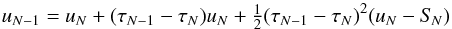 (22)and the
coefficients
(22)and the
coefficients 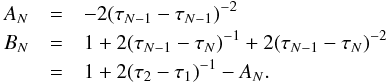 (23)At
the inner boundary, rays that intersect the core (p<R) must be distinguished
from those that do not (p>R). For core rays, the
incident intensity has to be explicitly specified I+ =
Icore, while for non-core rays a
reflecting boundary I+ = I− is
used. Noting that
(23)At
the inner boundary, rays that intersect the core (p<R) must be distinguished
from those that do not (p>R). For core rays, the
incident intensity has to be explicitly specified I+ =
Icore, while for non-core rays a
reflecting boundary I+ = I− is
used. Noting that 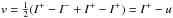 , one
gets in Eq. (7)
, one
gets in Eq. (7) 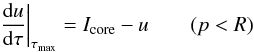 (24)for core-rays and
(24)for core-rays and
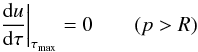 (25)for non-core rays.
Combining Eqs. (19), (8), and (7) one gets
(25)for non-core rays.
Combining Eqs. (19), (8), and (7) one gets 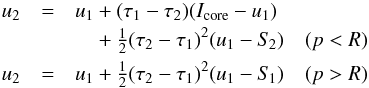 (26)and
the coefficients
(26)and
the coefficients 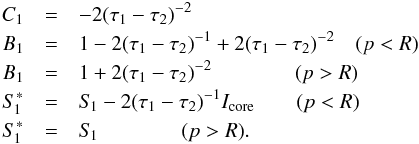 (27)These
boundary conditions can be expressed in terms of the z-variable analogous to
the non-boundary equations. For the issues to be discussed in the present paper, it is
sufficient, at least for the test cases, to assume that the incident intensity
Icore is given. (The much more complex
incident intensity that is actually used in the non-LTE models (cf. Sect. 5) is discussed in detail by Sauer et al. 2006.)
(27)These
boundary conditions can be expressed in terms of the z-variable analogous to
the non-boundary equations. For the issues to be discussed in the present paper, it is
sufficient, at least for the test cases, to assume that the incident intensity
Icore is given. (The much more complex
incident intensity that is actually used in the non-LTE models (cf. Sect. 5) is discussed in detail by Sauer et al. 2006.)
2.2. Solution of the moment equations
A similar system can be employed to solve the moment equations
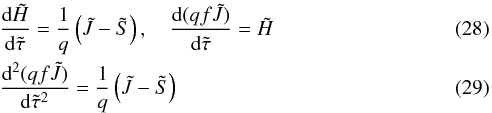 where
all symbols have their usual meanings, and the index ν has again been dropped
for brevity. (q is a “sphericality function”, cf. Auer 1971.) The last equation, Eq. (29), can be written in terms of the radius
r,
where
all symbols have their usual meanings, and the index ν has again been dropped
for brevity. (q is a “sphericality function”, cf. Auer 1971.) The last equation, Eq. (29), can be written in terms of the radius
r,
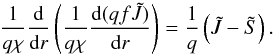 (30)The advantage of
the moment equations is that one can implicitly solve for the contribution of Thomson
scattering to the source function S (assuming full redistribution over angles).
(However, the system still needs the Eddington factors fν =
Kν/Jν
as an external input obtained from the ray-by-ray solution.) By separating the emission
due to true processes and that due to Thomson scattering (ηTh =
χThJ), one can write
(30)The advantage of
the moment equations is that one can implicitly solve for the contribution of Thomson
scattering to the source function S (assuming full redistribution over angles).
(However, the system still needs the Eddington factors fν =
Kν/Jν
as an external input obtained from the ray-by-ray solution.) By separating the emission
due to true processes and that due to Thomson scattering (ηTh =
χThJ), one can write
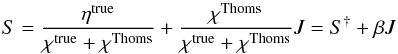 (31)with the definitions
(31)with the definitions
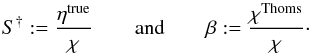 (32)Using this in Eq. (30) gives
(32)Using this in Eq. (30) gives 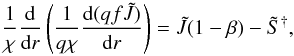 (33)which can be discretized
by
(33)which can be discretized
by 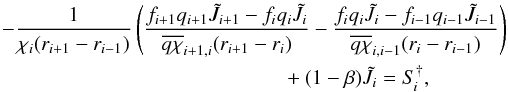 (34)where
(34)where
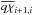 are again appropriate means of the product qχ at adjacent grid points. The coefficients of the
equation system
are again appropriate means of the product qχ at adjacent grid points. The coefficients of the
equation system 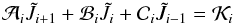 (35)become
(35)become
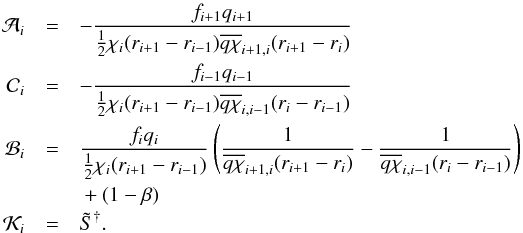 (36)At
the boundaries, the system is closed by employing factors similar to the second Eddington
factor7
(36)At
the boundaries, the system is closed by employing factors similar to the second Eddington
factor7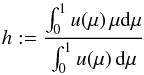 (37)with
u(μ) from the solution of the
ray-by-ray solution. At the outer boundary, since u(τ = 0) ≡
v(τ = 0), this is just
(37)with
u(μ) from the solution of the
ray-by-ray solution. At the outer boundary, since u(τ = 0) ≡
v(τ = 0), this is just
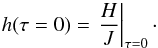 (38)Thus, the outer
boundary equation is
(38)Thus, the outer
boundary equation is 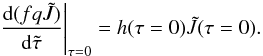 (39)The inner boundary
(r =
R) is treated similarly; however, because
∫uμdμ ≠
H, Icore from the ray-by-ray solution has
to be employed here as well, noting that
(39)The inner boundary
(r =
R) is treated similarly; however, because
∫uμdμ ≠
H, Icore from the ray-by-ray solution has
to be employed here as well, noting that
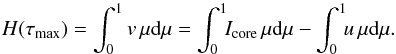 (40)This results in
(40)This results in
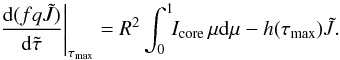 (41)The coefficients at the
outer boundary are
(41)The coefficients at the
outer boundary are 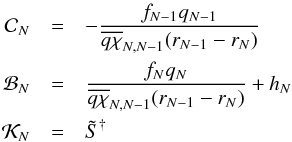 (42)and
at the inner boundary are
(42)and
at the inner boundary are 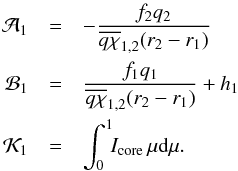 (43)Again,
we assume Icore to be given, and we refer to Sauer et al. (2006) for the details of the
inner-boundary intensity actually used in the models. The solution of this tridiagonal
matrix scheme is again performed by efficient BLAS-functions.
(43)Again,
we assume Icore to be given, and we refer to Sauer et al. (2006) for the details of the
inner-boundary intensity actually used in the models. The solution of this tridiagonal
matrix scheme is again performed by efficient BLAS-functions.
2.3. Self-absorption of lines in the Feautrier scheme
As mentioned in Sect. 2, the Feautrier scheme for the solution of the radiative transfer leads to difficulties if used for physical conditions where the opacities and emissivities have strong variations at adjacent depth points.
In the Feautrier scheme, the total source functions are evaluated on the respective
radial grid points. This effectively sets the entire emission of an interval on that grid
point, while the transport coefficients contain the absorption over an interval between
grid points. Consider the situation where one grid point i has a low opacity
χi (which makes the
source function Si at this point
meaningless), and further assume that the adjacent point i − 1 has a high opacity
χi −
1 and a source function Si −
1 (e.g., by the presence of a strong line). In reality most of
the emission from a line occurs from the region where the line becomes optically thick,
which means that the low-opacity point would “see” the source function of the line at the
point where Δτ ≳
1 is reached. The numerical solution, however, systematically
underestimates the radiation being transported from the point i − 1 into the low-opacity
region i.
This effect can be understood as follows: recall the general structure of the equation
system solved (cf. Sect. 2): 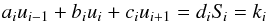 (44)where the
coefficients are such that
(44)where the
coefficients are such that 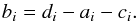 (45)The coefficients
ai and ci relate to the
transport over the intervals [
i,i − 1 ] and [ i,i + 1 ], respectively,
while bi and di describe the local
grid point i.
Thus the former are functions of the “remote” optical depth interval
(45)The coefficients
ai and ci relate to the
transport over the intervals [
i,i − 1 ] and [ i,i + 1 ], respectively,
while bi and di describe the local
grid point i.
Thus the former are functions of the “remote” optical depth interval
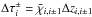 , while
di =
Δτi is a function of
the “local” optical depth interval Δτi =
χiΔzi
+ 1,i − 1:
, while
di =
Δτi is a function of
the “local” optical depth interval Δτi =
χiΔzi
+ 1,i − 1: 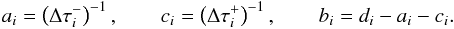 (46)We now consider the
extreme case of a single strong line in a low-opacity environment by setting
χi −
1 ≫ 1, Si − 1 ≠ 0, and
χj ≥
i ≪ 1, Sj ≥
i → 0. For the coefficients in Eq. (44) this means that
(46)We now consider the
extreme case of a single strong line in a low-opacity environment by setting
χi −
1 ≫ 1, Si − 1 ≠ 0, and
χj ≥
i ≪ 1, Sj ≥
i → 0. For the coefficients in Eq. (44) this means that
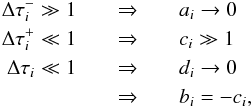 (47)and,
therefore, the equation for ui is
(47)and,
therefore, the equation for ui is
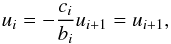 (48)independent of the
value at grid point i −
1. In other words, all points j ≥ i
decouple entirely from the point i − 1, and accordingly, uj in the region
j ≥
i is determined by the emission from that region only.
Figure 2 shows this situation; from the left, an
incident “core” intensity is assumed, whereas the right boundary has no incoming
radiation.
(48)independent of the
value at grid point i −
1. In other words, all points j ≥ i
decouple entirely from the point i − 1, and accordingly, uj in the region
j ≥
i is determined by the emission from that region only.
Figure 2 shows this situation; from the left, an
incident “core” intensity is assumed, whereas the right boundary has no incoming
radiation.
 |
Fig. 2 Toy model to illustrate the problem of self-absorption in the standard Feautrier scheme for a single p-ray (see text). The lower panel shows the opacity distribution for this model. The opacities of the models are chosen such that the same total optical depth over the entire radial interaction zone is reached. The upper panel shows the u function derived from the standard Feautrier solution using an incident intensity I+ = 4 from the left side and I− = 0 on the right side. The black lines denote the run of the source function Sline. |
For this example, two models have been computed: a high-resolution model with a small
grid spacing that resolves the actual line profile, and which we can reasonably assume
yields results very close to the exact solution since it avoids the problems described
above; and a low-resolution model that corresponds more to the conditions present in the
radiative transfer solver used for the sampling method (cf. Sect. 2). The high-resolution model assumes a Gaussian profile for the line,
which in the low-resolution model is represented by a single grid point. The opacity at
that point is chosen such that the optical depth through the radial interaction zone is
the same as for the highly resolved model. The opacity distribution of both models on the
ray is shown in the lower panel. The upper panel shows the u-function derived from the
Feautrier algorithm described above and the adopted source function Sline = 2 in the
line for both models (black dashed line in Fig. 2).
For the left hand boundary, an incident intensity I+ = 4 was
assumed, while the right hand boundary used I− = 0. The red line denotes the
solution of the highly resolved model and follows what one would expect theoretically for
this case: within the optically thick line u approaches Sline, while in
the interval to the right of the line it reaches 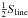 because
because
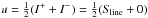 .
Similarly, in the interval to the left of the line where an incident I+ is present,
the result reaches halfway between I+ and Sline
(
.
Similarly, in the interval to the left of the line where an incident I+ is present,
the result reaches halfway between I+ and Sline
(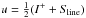 ).
).
The blue line with the bullet points shows the solution for the model on the coarse grid. (The values are only derived on the grid points as indicated; the connecting lines are just for better visibility.) As can be clearly seen, on both sides of the line this solution significantly miscalculates the radiation field compared to the exact solution. In effect, the line emission is not represented in the transport at all because the solutions outside the line are only coupled to the boundary points. Of course an extreme case like the one presented here will rarely occur in real models because the continuous opacity will usually smooth out the profiles and also prevent zero opacity at some points. However, in particular for supernova where the line opacity dominates the total opacity over almost the entire spectrum, cases similar to this are more likely to occur. Here the standard solver will systematically underestimate the radiation field in the (radial) gaps between lines and toward the outer boundary, leading to a loss of total radiative energy that is not represented in the rate equations. (This only affects the solution in our method I for the radiative transport. The detailed solution is derived on a micro-grid that resolves the line profiles in small Δτ-steps (cf. Pauldrach et al. 2001) and therefore does not suffer from this problem.)
 |
Fig. 3 Single-ray models corresponding to Fig. 2 with the ξ-correction applied. While the high-resolution model remains unaffected, the model on the coarse grid now reproduces the analytically expected result much better. |
3. An improved solution method for the Feautrier scheme
As a primary constraint, a proposed correction method should not affect the transport of
radiation through a grid point. Additionally, the solution has to remain unchanged for a
smooth, continuous run of opacities because these cases are correctly represented by the
standard scheme. Furthermore, at high grid resolution, both the new and the old schemes
should agree on the same solution because in the limit of infinitely small intervals the
standard method approaches the exact solution. The first constraint excludes any
modification of the transport terms ai and ci. Therefore, the only
remaining option is to adjust the source terms and the b coefficient. The concept is
to correct the intensity derived at a particular grid point by adding an additional
contribution from the emission of adjacent grid points. The amount of correction has to be a
function of the local Δτi and the respective
remote 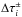 . Thus, we make
the following ansatz for a new coefficient bi and the right hand
side ki of Eq. (44):
. Thus, we make
the following ansatz for a new coefficient bi and the right hand
side ki of Eq. (44): 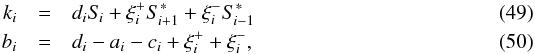 with
correction functions
with
correction functions 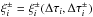 to be determined. The source
functions S∗ are taken to be the (total) line source
functions ηline/χline at
the respective point to ensure that the correction does not affect the continuum transport.
to be determined. The source
functions S∗ are taken to be the (total) line source
functions ηline/χline at
the respective point to ensure that the correction does not affect the continuum transport.
To obtain the original coefficients of Eq. (10) in Sect. 2, the system Eq. (46) has to be divided by di. Thus, coefficients
Ai and Ci in Eq. (16) remain unchanged, while Bi and the right hand side
Ki acquire additional
terms: 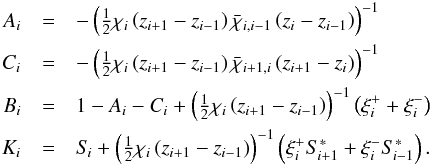 (51)The
coefficients at the boundary conditions have to be adjusted accordingly using the
corresponding adjacent interval.
(51)The
coefficients at the boundary conditions have to be adjusted accordingly using the
corresponding adjacent interval.
3.1. Moment equations
In the solution scheme for the moment Eqs. (35) and (36), a similar method
has to be applied. For consistency with the ray-by-ray solution, the correction terms
ξ±ui
are integrated over μ
dμ introducing a factor
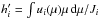 analogous to
h in Eq.
(38). Here, however, the numerical
integration for
analogous to
h in Eq.
(38). Here, however, the numerical
integration for 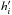 has to be
performed using integration weights on the respective grid point instead of the weights on
the intermesh points used for the flux integration. Eventually, one derives the new
coefficients for the system Eq. (35) to be
has to be
performed using integration weights on the respective grid point instead of the weights on
the intermesh points used for the flux integration. Eventually, one derives the new
coefficients for the system Eq. (35) to be
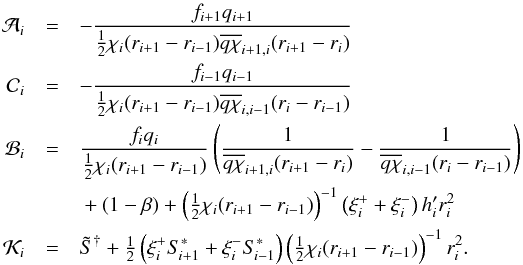 (52)The
first-order boundary conditions for the system remain unchanged because no source
functions enter here.
(52)The
first-order boundary conditions for the system remain unchanged because no source
functions enter here.
3.2. Correction functions ξ±
Now that we know where the correction is to be applied, suitable functions ξ± that depend on the opacities in the “local” and “remote” intervals have to be found. Correction is only needed for the case where the respective remote and the local τ-interval are low. In this case, if the line source function S∗ of the adjacent point is large, the emission of the local point has to be enhanced. In addition, the correction function has to drop to zero for large “remote” Δτ faster than the 1 / Δτ-terms in the transport coefficients.
 |
Fig. 4 Spherically symmetric test models for the corrected Feautrier coefficients. In all models the incident intensity at the core was set to I+ = 4, while at the outer boundary no incoming radiation was assumed. The upper panel shows the uncorrected model, and the lower panel shows the same setup with the correction applied. In this model we assumed an optically thick line (τline = 50), and a low background true opacity and source function. |
A possible choice for the ξ-functions that has been found to provide the
required properties is 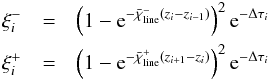 (53)with
the averaged opacities
(53)with
the averaged opacities 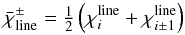 (54)and
(54)and
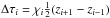 as before. The quadratic term
in Eq. (53) vanishes if the line opacity
in the interval is small, indicating the absence of a significant line at the next grid
point. The power of 2 is necessary to ensure that this term drops to zero faster than the
corresponding transport coefficient ~
as before. The quadratic term
in Eq. (53) vanishes if the line opacity
in the interval is small, indicating the absence of a significant line at the next grid
point. The power of 2 is necessary to ensure that this term drops to zero faster than the
corresponding transport coefficient ~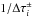 . If a line or
strong continuum is present at the current grid point, the second term becomes zero,
avoiding additional emission in the center of the line.
. If a line or
strong continuum is present at the current grid point, the second term becomes zero,
avoiding additional emission in the center of the line.
 |
Fig. 6 Same setup as in Fig. 4, but including both true opacity and source function, as well as Thomson opacity and emissivity as background. |
 |
Fig. 7 Same situation as in Fig. 6, but for an optically much thinner line (τline = 0.5). Here the old and new methods, as expected, produce very similar results. |
4. Results of test calculations
To test the properties of the new coefficients, we simulated a variety of different situations before applying the method in the actual spectral synthesis code. To estimate the quality of the correction in realistic models, we also investigated situations with continuum opacity (in particular including Thomson scattering). In this regard the toy model had to be extended to a spherically symmetric model for two main reasons. First, the determination of the Thomson emissivity requires knowledge of the mean intensity J. Second, we intended to see the effect on the angle-integrated quantities.
Figures 4−7 show a selection of situations we have simulated using this extended version. All low-resolution models use a uniformly spaced radial grid with 41 grid points and 5 core rays. The high-resolution grid is set up by dividing each interval into 14 subintervals and uses 20 core rays. The source function of the line was again set to Sline = 2 and the incident intensity at the core to I+ = 4. The opacity of the line was determined such that a given radial optical depth τline was reached. In all figures, the upper panel shows the derived mean intensity J without correction and the lower panel shows the respective models with the correction applied. All values of J have been obtained by iterating the ray-by-ray solution with the solution of the moment equation. (The final J from the different methods agreed on the level of a few percent, depending on the model.)
Figure 4 shows the setup with an optically thick line (τline = 50) and a low constant background source function and opacity (Sbg = 0.1, χbg = 0.1). In the presence of opacity on other grid points, the uncorrected solution outside the line couples more strongly to the local source function, since the coupling to the line is too small.
In Fig. 5 we show the same situation but include Thomson scattering instead as background opacity, whereas in Fig. 6 the background consists of both true and Thomson opacity. In both these cases the solution of the corrected method in the low-resolution case is very close to the high-resolution result, with only a fraction of the depth points needed. Finally in Fig. 7, we show the case of an optically thin line (τline = 0.5). In this case the new, corrected and the old, uncorrected method, as expected, give very similar results.
 |
Fig. 8 Emergent flux in the Lyman-α line of a Type II supernova model containing H and He. For better comparison, both models shown have been computed neglecting the contribution of H and He lines to the line blocking in all iterations except the last one. Thus, both models have very similar occupation numbers and temperature structures. The two lines indicated with “sampling” refer to the emergent flux in the last iteration using the opacity sampling technique. The other two lines represent the flux after the first iteration that uses the exact solution. The dotted line and the dash-dotted line belong to the model that uses the standard procedure in the solution of the Feautrier scheme; the dashed line and the solid line refer to the model that had the correction applied. |
Figure 8 shows the application of the non-LTE radiative transfer code to a test model of a Type II supernova containing only H and He. It compares the emergent flux in the Lyman-α line after the last iteration using the sampling method to that from the first iteration using the detailed radiative transfer, for both a model using the old, uncorrected method in the sampling iterations and one using the new, corrected method. For better comparison, both models were computed neglecting the contribution of H and He lines to the line blocking in all iterations except the last one. Thus, both models have very similar occupation numbers and temperature structures. One can see that the sampling iteration without the correction produces significantly less flux, which also affects the occupation numbers of the corresponding level. This also leads to spurious results in the detailed solution. With the correction included, the flux agrees much more closely with the detailed solution of method II. (Exact agreement is not possible since our sampling method considers the Doppler shifts of the central ray as being representative for the other rays as well, cf. Pauldrach et al. 2001.)
 |
Fig. 9 Synthetic SN Ia spectra of consistent ALImI-models (SN Ia models based on an accelerated lambda iteration procedure for the mutual interaction of strong spectral lines, cf. Pauldrach et al. 2014) using the original (red curve) and the new treatment (green curve) of the Feautrier method in the first iteration cycle (shown is the flux after the first iteration that uses the detailed solution). Although the two models are not strictly comparable since the occupation numbers, the ionization, and the temperature structure adjust differently because of the differences of the Feautrier schemes applied, it is readily seen that the behavior of the flux is different particularly for those wavelengths that are dominated by strong lines. For comparison, an equivalent blackbody spectrum (black curve) corresponding to the effective temperature of the atmosphere (Teff = 12 540 K) and the spectrum resulting from a formal solution without lines (blue curve) are also shown, demonstrating the very different slopes these two curves exhibit even in the wavelength range redward of 4000 Å where the supernova ejecta are much less dominated by spectral lines. (Blueward of 3000 Å the flux is of course blocked and strongly attenuated by spectral lines; flux conservation results in enhanced emission redward of 3000 Å compared to a black body.) |
Although the error introduced is less obvious for weaker lines that are blended with other lines, a multitude of extremely strong lines (like the Lyman-α line in this SN II model) are to be found in SN Ia, and the standard procedure systematically underestimates the radiation field outside of these lines. We note, however, that the total influence on a model is not as easy to predict as in the test cases where we held the occupation numbers fixed, since owing to the changed radiation field, the ionization and excitation rates may change, leading to different occupation numbers and thus different opacities and source functions of the lines.
5. Application to synthetic SN Ia spectra
Figure 9 shows the application of our current non-LTE radiative transfer procedure to a SN Ia model at an epoch of 25 days (~5 days after maximum). Besides the high expansion velocities, that the atmospheres of SN Ia have no appreciable true continuum over a significant spectral range and that the pseudo-continuum is actually formed by thousands of overlapping lines that influence each other required not only a modified Feautrier scheme, but also a solution of one of the biggest challenges we have found in modeling the radiative transfer in SN Ia: the transfer of the radiative energy from the UV into the optical regime via only spectral lines.
That radiation has to be transferred from the UV into the optical regime becomes evident from comparing the curves in Fig. 9. The blue curve has its maximum in the UV spectral range and shows the shape of the continuous radiation resulting from the true continuum plus Thomson-scattering opacities and emissivities of the innermost regions, whereas the green curve shows the true emergent spectrum of the model and has most of the flux in the optical range.
In most stellar objects it is the true continuous absorption and emission processes that cause this shifting of the spectral distribution from higher to lower energies, but this mechanism cannot work in SN Ia envelopes. Because of the low absolute densities (compared to stars) and a composition that is dominated by low ionization stages of intermediate-mass and iron-group elements, the free-free and bound-free continuum in the UV and optical regime is very weak in the outer parts of the atmospheres of these objects. In fact, electron scattering is the dominant source of opacity at wavelengths redward of about 5000 Å, even for deeper layers of the atmospheres. Blueward of about 4000 Å, however, the total continuous opacity is completely irrelevant when compared to the line opacities (cf. Pauldrach et al. 2014). This behavior illustrates the formation of the pseudo-continuum in the envelopes of SN Ia, which results solely from the overlap of several ten thousands of spectral lines and which is entirely responsible for the transfer of the radiative energy from the UV into the optical regime8.
As the conversion of radiation through the overlap of strong lines of different ionization stages and elements does not happen when using the standard single-line accelerated lambda iteration procedure9, we had to develop an improved treatment (“ALImI”; cf. Pauldrach et al. 2014) for these lines that mutually interact with each other in the pseudo-continuum. Thus, hydrodynamic explosion models and realistic model atmospheres that take the strong deviation from local thermodynamic equilibrium into account are not the only ingredients necessary for the spectral synthesis and analysis of SN Ia spectra, but also improved iteration schemes and radiative transfer methods.
Figure 9 further shows that the excess flux in the red and infrared wavelength regions, which most of the synthetic spectra for SN Ia at early epochs calculated up to now (cf. Pauldrach et al. 1996; Nugent et al. 1997; Sauer et al. 2006; Stehle et al. 2005) had shown compared to observations, does not appear in our model. This is because our new iteration scheme allows us to calculate much deeper into the “photosphere” while still permitting the iteration to converge despite the very high optical depths encountered in the UV.
Thus the observed steep slope in the continuum in between 4000 Å and 8000 Å can be understood to be the result of a much bluer, non-Planckian radiation field in the inner regions of the ejecta, which is mostly unobservable due to the strong line blocking in the UV, but which can be inferred from the red part of the spectrum where the opacities are low. Radiative transfer models which assume a customary diffusion approximation as inner boundary farther out in the ejecta will instead show much shallower slopes in this range comparable to that of a black body corresponding to the effective temperatures of SN Ia atmospheres.
6. Summary and conclusions
Our investigations have led to an improved understanding of how the emergent spectra of type Ia supernovae are being shaped within the ejecta, and how this relates to the particular physical properties of their envelopes and the resulting peculiarities in their radiative transfer compared to the much better studied atmospheres of stars. Because these spectra are assembled in a complex way by numerous mostly unobservable spectral features, this knowledge provides important insight into the process of extracting information from the observed SN Ia spectra.
In this paper we pointed out and investigated a necessary step for quantitative analysis of SN Ia spectra based on an elaborate approach to expanding atmospheres, characterized by (a) a sophisticated treatment of the strong spectral lines that mutually interact with each other via a “pseudo-continuum” entirely formed by these Doppler-shifted spectral lines themselves; and (b) by the treatment of a consistent solution of the full non-LTE rate equations along with a detailed solution of the radiative transfer.
In particular we showed that the Feautrier method of solving the radiative transfer equation can be extended to cases – strongly varying opacities and source functions from grid point to grid point – that by their very nature would argue against the Feautrier scheme as a solution method of choice. Indeed, the standard formulation of the Feautrier method as a finite-difference method attempting to approximate the differential equation of radiative transfer fails badly in these cases. However, knowing the nature of the physical conditions underlying these cases has allowed us to construct correction factors that mimic the true behavior of the radiation field without changing the structure of the algorithm, thus allowing for a direct plug-in replacement in the solver. Although some differences remain between the corrected Feautrier solution and the exact solution, that our corrected method yields much better results than the standard formulation is useful for applying this widespread method. In our model atmosphere code, it allows us to save computer time in the “pre-iteration” step since it provides a better starting point for the final iterations using the computationally much more expensive detailed radiative transfer solver, and as an observer’s-frame method, it principally also allows future application to situations where the velocity field is not monotonic and for which a comoving-frame treatment is not practicable. The results presented indicate that our presently applied method is now on a level where it may be considered for use in quantitative analyses.
Involving different levels of complexity, models have been developed by Branch et al. (1985), Mazzali et al. (1993), Mazzali & Lucy (1993), Eastman & Pinto (1993), Höflich et al. (1995), Nugent et al. (1995), Pauldrach et al. (1996), Nugent et al. (1997), Lentz et al. (2001), Höflich (2005), Stehle et al. (2005), Sauer et al. (2006), Baron et al. (2006), Kasen et al. (2006). With regard to the purpose of the specific codes various simplifications have been applied, since not all approaches are intended to provide a comprehensive description of the time-dependent spectra, including the detailed statistical equilibrium of all relevant elements.
The effect of line blocking refers to an attenuation of the radiative flux in the EUV and UV due to the combined opacity of a huge number of metal lines present in SN Ia in these frequency ranges. It drastically influences ionization and excitation rates owing to its impact on the radiation field through radiative absorption and scattering processes.
As a consequence of line blocking, only a small fraction of the radiation is re-emitted and scattered in the outward direction. Most of the energy is radiated back to deeper layers of the SN Ia, leading there to an increase in the temperature (“backwarming”). Due to this increase, more radiation is emitted at lower energies, an effect known as line blanketing.
We note, however, that a comoving-frame treatment is only practicable for monotonic velocity laws. Newer models for expanding stellar envelopes have begun to investigate the effects of non-monotonicity of the velocity field in connection with turbulence, and for these situations an observer’s frame solution of the radiative transfer remains the primary choice. This is why we consider a detailed understanding of the behavior of the numerical algorithms in such cases to be important.
We note that Feautrier presented his method in the form of Eq. (14), which does not suffer from this first problem. It is the description using the mixed “τ” (such as given by Auer 1971 or Mihalas 1978) that leads to these errors.
Because of the large velocity gradients, which – in a state of homologous expansion with velocities reaching up to 20 000 km s-1 – bring photons emitted at the photosphere and redshifted on their way outwards through the envelope into resonance with redder and redder lines, the UV part of the spectrum is effectively blocked by the superposition of strong metal absorption lines The number of such lines is very large and in the UV, where the metal lines crowd very densely, this line overlap in practice becomes a continuous source of opacity (cf. Fig. 10 of Pauldrach et al. 2014). A UV photon can thus only escape if, during its random walk being scattered and re-scattered in the optically thick atmosphere, it manages to connect to the thermal pool, is reborn as a redder photon, and finds a low-opacity window in the spectrum (cf. Pauldrach et al. 1996).
The classical accelerated lambda iteration (ALI) simply fails because it is based on the premise that only the one dominant process that has “frozen” the iteration must be canceled to let the system converge at each frequency, but in SN Ia at any frequency and depth point, the radiation field is actually influenced by several tens of strong lines.
Acknowledgments
We thank the anonymous referee for helpful comments that improved the paper. This work was supported by the Deutsche Forschungsgemeinschaft under Grant Pa 477/7-1.
References
- Auer, L. H. 1967, ApJ, 150, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, L. H. 1971, J. Quant. Spectr. Rad. Transf., 11, 573 [Google Scholar]
- Baron, E., Hauschildt, P. H., Nugent, P., & Branch, D. 1996, MNRAS, 283, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Baron, E., Bongard, S., Branch, D., & Hauschildt, P. H. 2006, ApJ, 645, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Doggett, J. B., Nomoto, K., & Thielemann, F. 1985, ApJ, 294, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, C. J. 1970, Proc. Astron. Soc. Austr., 1, 386 [NASA ADS] [Google Scholar]
- Eastman, R. G., & Pinto, P. A. 1993, ApJ, 412, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Feautrier, P. 1964, Comptes Rendus Acad. Sci. Paris, 258, 3189 [Google Scholar]
- Hoffmann, T. L., Lieb, S., Pauldrach, A. W. A., et al. 2012, A&A, 544, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Höflich, P. 2005, Ap&SS, 298, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., Khokhlov, A. M., & Wheeler, J. C. 1995, ApJ, 444, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Kalkofen, W., & Wehrse, R. 1982, A&A, 110, 18 [NASA ADS] [Google Scholar]
- Kaschinski, C. B., Pauldrach, A. W. A., & Hoffmann, T. L. 2012, A&A, 542, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaschinski, C. B., Pauldrach, A. W. A., & Hoffmann, T. L. 2013, A&A, submitted [arXiv:1307.2948] [Google Scholar]
- Kasen, D., Thomas, R. C., & Nugent, P. 2006, ApJ, 651, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Lentz, E. J., Baron, E., Branch, D., & Hauschildt, P. H. 2001, ApJ, 557, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., & Lucy, L. B. 1993, A&A, 279, 447 [NASA ADS] [Google Scholar]
- Mazzali, P. A., Lucy, L. B., Danziger, I. J., et al. 1993, A&A, 269, 423 [NASA ADS] [Google Scholar]
- Mihalas, D. 1978, Stellar atmospheres, 2nd edn. (San Francisco: W. H. Freeman and Co.) [Google Scholar]
- Mihalas, D., & Kunasz, P. B. 1986, J. Comput. Phys., 64, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, P., Baron, E., Hauschildt, P. H., & Branch, D. 1995, ApJ, 441, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, P., Baron, E., Branch, D., Fisher, A., & Hauschildt, P. H. 1997, ApJ, 485, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Pauldrach, A. 1987, A&A, 183, 295 [NASA ADS] [Google Scholar]
- Pauldrach, A. W. A. 2003, in Rev. Mod. Astron., ed. R. E. Schielicke (New York: Wiley), 133 [Google Scholar]
- Pauldrach, A. W. A., Kudritzki, R.-P., Puls, J., & Butler, K. 1990, A&A, 228, 125 [NASA ADS] [Google Scholar]
- Pauldrach, A. W. A., Kudritzki, R.-P., Puls, J., Butler, K., & Hunsinger, J. 1994, A&A, 283, 525 [Google Scholar]
- Pauldrach, A. W. A., Duschinger, M., Mazzali, P. A., et al. 1996, A&A, 312, 525 [NASA ADS] [Google Scholar]
- Pauldrach, A. W. A., Lennon, M., Hoffmann, T. L., et al. 1998, in Properties of Hot Luminous Stars, ed. I. Howarth, ASP Conf. Ser. 131, 258 [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Méndez, R. H. 2004, A&A, 419, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pauldrach, A. W. A., Vanbeveren, D., & Hoffmann, T. L. 2012, A&A, 538, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Hultzsch, P. J. N. 2014, A&A, accepted, DOI: 10.1051/0004-6361/201322253 [Google Scholar]
- Rybicki, G. B. 1971, J. Quant. Spectr. Rad. Transf., 11, 589 [Google Scholar]
- Sauer, D. N., Hoffmann, T. L., & Pauldrach, A. W. A. 2006, A&A, 459, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stehle, M., Mazzali, P. A., Benetti, S., & Hillebrandt, W. 2005, MNRAS, 360, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, J. A., Pauldrach, A. W. A., Knogl, J. S., & Hoffmann, T. L. 2013, A&A, 555, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Sketch of the p-z coordinate system that is used for the solution of the radiative transfer. In this geometry, at any given radius r, each p-ray corresponds to a different direction μ. |
| In the text | |
 |
Fig. 2 Toy model to illustrate the problem of self-absorption in the standard Feautrier scheme for a single p-ray (see text). The lower panel shows the opacity distribution for this model. The opacities of the models are chosen such that the same total optical depth over the entire radial interaction zone is reached. The upper panel shows the u function derived from the standard Feautrier solution using an incident intensity I+ = 4 from the left side and I− = 0 on the right side. The black lines denote the run of the source function Sline. |
| In the text | |
 |
Fig. 3 Single-ray models corresponding to Fig. 2 with the ξ-correction applied. While the high-resolution model remains unaffected, the model on the coarse grid now reproduces the analytically expected result much better. |
| In the text | |
 |
Fig. 4 Spherically symmetric test models for the corrected Feautrier coefficients. In all models the incident intensity at the core was set to I+ = 4, while at the outer boundary no incoming radiation was assumed. The upper panel shows the uncorrected model, and the lower panel shows the same setup with the correction applied. In this model we assumed an optically thick line (τline = 50), and a low background true opacity and source function. |
| In the text | |
 |
Fig. 5 Same setup as in Fig. 4, but instead with Thomson opacity and emissivity. |
| In the text | |
 |
Fig. 6 Same setup as in Fig. 4, but including both true opacity and source function, as well as Thomson opacity and emissivity as background. |
| In the text | |
 |
Fig. 7 Same situation as in Fig. 6, but for an optically much thinner line (τline = 0.5). Here the old and new methods, as expected, produce very similar results. |
| In the text | |
 |
Fig. 8 Emergent flux in the Lyman-α line of a Type II supernova model containing H and He. For better comparison, both models shown have been computed neglecting the contribution of H and He lines to the line blocking in all iterations except the last one. Thus, both models have very similar occupation numbers and temperature structures. The two lines indicated with “sampling” refer to the emergent flux in the last iteration using the opacity sampling technique. The other two lines represent the flux after the first iteration that uses the exact solution. The dotted line and the dash-dotted line belong to the model that uses the standard procedure in the solution of the Feautrier scheme; the dashed line and the solid line refer to the model that had the correction applied. |
| In the text | |
 |
Fig. 9 Synthetic SN Ia spectra of consistent ALImI-models (SN Ia models based on an accelerated lambda iteration procedure for the mutual interaction of strong spectral lines, cf. Pauldrach et al. 2014) using the original (red curve) and the new treatment (green curve) of the Feautrier method in the first iteration cycle (shown is the flux after the first iteration that uses the detailed solution). Although the two models are not strictly comparable since the occupation numbers, the ionization, and the temperature structure adjust differently because of the differences of the Feautrier schemes applied, it is readily seen that the behavior of the flux is different particularly for those wavelengths that are dominated by strong lines. For comparison, an equivalent blackbody spectrum (black curve) corresponding to the effective temperature of the atmosphere (Teff = 12 540 K) and the spectrum resulting from a formal solution without lines (blue curve) are also shown, demonstrating the very different slopes these two curves exhibit even in the wavelength range redward of 4000 Å where the supernova ejecta are much less dominated by spectral lines. (Blueward of 3000 Å the flux is of course blocked and strongly attenuated by spectral lines; flux conservation results in enhanced emission redward of 3000 Å compared to a black body.) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


