| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 22 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201424139 | |
| Published online | 04 September 2014 | |
Metallicity of M dwarfs
IV. A high-precision [Fe/H] and Teff technique from high-resolution optical spectra for M dwarfs ⋆,⋆⋆,⋆⋆⋆
1 Departamento de Física, Universidade Federal do Rio Grande do Norte, 59072-970 Natal, RN, Brazil
e-mail: vasco.neves@dfte.ufrn.br
2 Centro de Astrofísica and Faculdade de Ciências, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
3 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
4 CNRS, IPAG, 38000 Grenoble, France
5 Centre de Recherche Astrophysique de Lyon, UMR 5574: CNRS, Université de Lyon, École Normale Supérieure de Lyon, 46 allée d’Italie, 69364 Lyon Cedex 07, France
6 Observatoire de Genève, Université de Genève, 51 chemin des Maillettes, 1290 Sauverny, Switzerland
Received: 6 May 2014
Accepted: 23 June 2014
Aims. In this work we develop a technique to obtain high precision determinations of both metallicity and effective temperature of M dwarfs in the optical.
Methods. A new method is presented that makes use of the information of 4104 lines in the 530–690 nm spectral region. It consists in the measurement of pseudo equivalent widths and their correlation with established scales of [Fe/H] and Teff.
Results. Our technique achieves a rms of 0.08 ± 0.01 for [Fe/H], 91 ± 13 K for Teff, and is valid in the (−0.85,0.26 dex), (2800, 4100 K), and (M0.0, M5.0) intervals for [Fe/H], Teff and spectral type respectively. We also calculated the RMSEV which estimates uncertainties of the order of 0.12 dex for the metallicity and of 293 K for the effective temperature. The technique has an activity limit and should only be used for stars with log LHα/Lbol< − 4.0.
Key words: stars: atmospheres / stars: fundamental parameters / stars: late-type / stars: low-mass / methods: data analysis
Based on observations made with the HARPS instrument on the ESO 3.6 m telescope at La Silla Observatory under programme ID 072.C-0488(E)
Our method is available online at http://www.astro.up.pt/resources/mcal
Tables 1, 2, 4, 8 are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The precise derivation of M dwarf atmospheric parameters is still very challenging today. Cool and intrinsically faint, M dwarfs are not easy to study. As the M subtype increases more molecules form in their atmosphere, making the spectral continuum very hard or impossible to identify, at least in the visible region of the spectrum. Therefore, methods such as atomic line analysis that are dependent on the knowledge of the continuum are suited only for the metal poor and earliest types of M dwarfs (e.g. Woolf & Wallerstein 2005, 2006). On the other hand, spectral synthesis techniques do not reach yet a high precision comparable to FGK dwarf methods, due to the fundamental lack of knowledge of billions of molecular line strengths and transitions, and most studies have reached modest results (e.g. Valenti et al. 1998; Bean et al. 2006). Despite that, some important progress have been made using spectral synthesis fitting to high-resolution spectra in the infrared (Önehag et al. 2012), where the depression of the continuum in some regions is less intense than in the visible region of the spectrum (e.g. Rajpurohit et al. 2013b). However, only a few stars have been measured this way, and the technique lacks external confirmation. An alternative method, based on high-resolution template spectra, to calculate metallicity, distance, stellar mass, and radius, was presented by Pineda et al. (2013). This new technique, with similarities with our own method (Neves et al. 2013), is very promising but its [Fe/H] precision is still limited to 0.15 dex.
In this context, most parameter determinations, especially metallicity and effective temperature are instead based on calibrations using colours (e.g. Bonfils et al. 2005; Johnson & Apps 2009; Schlaufman & Laughlin 2010; Johnson et al. 2012; Neves et al. 2012) or spectroscopic indices (e.g. Rojas-Ayala et al. 2010, 2012; Mann et al. 2013a,b; Newton 2013).
Regarding metallicity, some progress has been made in the last few years. A steady improvement was achieved, bringing the typical uncertainties of ±0.20 dex of the photometric calibrations, below ~0.10 dex in the most recent low-resolution spectroscopic scales in the infrared (e.g. Rojas-Ayala et al. 2012; Mann et al. 2013a; Newton 2013), following the pioneering work of Rojas-Ayala et al. (2010). However a true high-precision determination with a rms of the order of 0.05 dex, on par with the ones obtained for FGK dwarfs (e.g. Santos et al. 2004; Sousa et al. 2007) has not yet been reached (see Neves et al. 2012 introduction).
For temperature, on the other hand, important uncertainties and systematics still persist today. Although internal precisions are reported to be lower than 100 K (e.g. Casagrande et al. 2008; Rojas-Ayala et al. 2012; Boyajian et al. 2012), their suffer from systematics ranging from 150 to 300 K making the determination of accurate temperature for M dwarfs a priority. In this context Boyajian et al. (2012) presented several calibrations of Teff, based on the largest sample to date of high precision interferometric measurements of K and M dwarf radii and bolometric fluxes, that in principle allow a very precise measurement of the effective temperature (a technique pioneered by Ségransan et al. 2003, for M dwarfs). However, some doubts still arise regarding the accuracy of the determination of the total flux of the stars, based on templates from Pickles (1998), as recently pointed out by Mann et al. (2013b). They have, in turn, also recently presented their own effective temperature method that is very similar to the one of Boyajian et al. (2012) but rely on a combination of their low resolution spectra with BT-SETTL synthetic spectra from Allard et al. (2011, 2013) to calculate the bolometric flux. From these high-precision effective temperatures they established four visual and infrared spectroscopic indices, with precisions (but not accuracies) between 62 and 100 K. A similar effort regarding Teff determination of M dwarfs using synthetic spectra came from Rajpurohit et al. (2013a), where they compare synthetic spectra from the latest BT-SETTL models (Allard et al. 2012) to low-resolution optical spectra. They obtain a better agreement between synthetic and observed spectra when compared with previous models, estimating uncertainties of Teff of the order of 100 K.
In this work we present a new method to try to overcome the aforementioned hurdles and improve on the precision of both metallicity and effective temperature of M dwarfs. An early version of this new technique was briefly presented in the Appendix of Neves et al. (2013) and used to investigate the planet-metallicity relation of the HARPS GTO M dwarf sample (Bonfils et al. 2013). In Sect. 2 we describe in detail our method, as well as the sample selection, uncertainty estimation and a test of the technique as a function of resolution and signal-to-noise ratio (S/N). Afterwards, in Sect. 3, we compare our results with other determinations from the literature. Finally, in Sect. 4 we discuss our results. The instructions to use our method are described in the Appendix.
2. The method
Our new method is based on the measurement of pseudo equivalent widths (EWs) of most lines/features in the 530–690 nm region of the spectra from a 102 star sample from the HARPS GTO M dwarf program, described in detail in Sect. 2 of Bonfils et al. (2013). It is a volume-limited sample (11 pc), and contains stars with δ< + 20°, V< 14 mag and includes only targets with vsin i ≤ 6.5 km s-1. Spectroscopic binaries as well as visual pairs with separations lower than 5″ were removed a priori.
The features are defined as regions of the spectra that are formed by more than one line. The EWs are then correlated with the reference photometric [Fe/H] and Teff scales from Neves et al. (2012) and Casagrande et al. (2008) respectively. The two scales are in turn based on [Fe/H] determinations from FGK primaries with a M dwarf secondary and on an adaptation of the IRFM technique (Blackwell & Shallis 1977) respectively.
This method achieves an increase in precision of both parameters whereas its accuracy is tied to the original calibrations. The methodology is detailed in Sect. 2.1.
The reference [Fe/H] was calculated using stellar parallaxes, V, and KS magnitudes following the procedure described in Neves et al. (2012). The reference Teff is the average value of the V − J, V − H, and V − K photometric scales taken from Casagrande et al. (2008). Table 1 lists the quantities used to calculate these parameters. Column 1 shows the star name, Cols. 2 and 3 the right ascension and declination respectively, Col. 4 the parallax of each star and its associated error, and Col. 5 the source of the parallax measurement. Column 6 depicts the stellar type of the star taken from Simbad1 (Wenger et al. 2000), except in the case of Gl438, where it was obtained from Hawley et al. (1997). The photometric stellar type presented in Col. 7 was calculated with the colour relation of Lépine et al. (2013), and Cols. 8 to 11 display the V, J, H, and KS photometry. Lastly, Col. 12 details the source of the photometry.
From the 110 stars of our sample we first selected 69 stars with spectra having a signal to noise higher than 100. The final spectrum of each star was constructed from median normalised individual observations. The S/N of the individual spectra were added in quadrature. Our final sample is determined by an activity cut, as detailed in Sect. 2.2.
 |
Fig. 1 Small region of the Gl 205 spectra illustrating pseudo equivalent width line measurement. The red dotted line represents the “peak-to-peak” flux. |
2.1. Method
From our final sample we measured pseudo EWs of lines and features (blended lines) from the spectra in the region between 530 and 690 nm, but excluded the features from the regions between 588–590.5, 656.1–656.4, and 686–690 nm due to the location of the activity sensitive Na doublet and Hα lines, and the heavy presence of telluric lines respectively. We define the pseudo EWs as 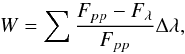 (1)where Fpp is the value of the flux between the peaks of the line/feature at each integration step and Fλ the flux of the line/feature. The measurements of the EWs are illustrated in Fig. 1, where the “peak-to-peak” flux corresponds to the red dotted lines and the flux of the star is shown as a black line.
(1)where Fpp is the value of the flux between the peaks of the line/feature at each integration step and Fλ the flux of the line/feature. The measurements of the EWs are illustrated in Fig. 1, where the “peak-to-peak” flux corresponds to the red dotted lines and the flux of the star is shown as a black line.
The very high S/N spectrum of the star Gl205 was used as a reference to establish the line/feature regions that were going to be measured in all spectra. We rejected all lines/features with a EW lower than 8 mÅ to ensure that all lines in stars with lower [Fe/H] or/and Teff can be properly measured. Lines with steep slopes are usually joined with adjacent lines, and measured as one feature. At the end of the line selection we obtained 4104 lines/features. An automatic search of the maximum values around ± 0.02 Å at the extremes of each line/feature is made to make sure that the “peak-to-peak” regions of all lines/features of the spectra are effectively covered.
The next step consisted in the investigation of the correlation between the measured EWs and the reference values for [Fe/H] and Teff. Figure 2 shows the histograms of the partial correlation coefficient values of the EWs with the value of the metallicity and effective temperature (solid blue and dashed green lines respectively). The partial correlation coefficient is defined as the correlation coefficient of one parameter keeping the other fixed. We observe, in Fig. 2 that a significant amount of lines have good correlation values with the parameters.
 |
Fig. 2 Histograms of the partial correlations of [Fe/H] (solid blue histogram) and Teff (dashed green histogram). |
Then we did a least squares linear fit of the EWs with the metallicity and effective temperature. The reference values were calculated with the calibration of Neves et al. (2012), for [Fe/H], and with the three (V − J, V − H, and V − KS) photometric calibrations of Casagrande et al. (2008), for Teff, where we took the average value. From each line/feature i of every star m we calculate a EW value. Then we have ![\begin{equation} W_{i,m} = \alpha_{i}[{\rm Fe/H}]_{m}^{\rm T} + \beta_{i}T_{{\rm eff},m}^{\rm T} + \gamma_{i}, \label{eq:fit} \end{equation}](/articles/aa/full_html/2014/08/aa24139-14/aa24139-14-eq29.png) (2)where W is the matrix containing the EWs, and both [Fe/H]T, and
(2)where W is the matrix containing the EWs, and both [Fe/H]T, and 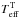 are the transpose vectors of the parameter values. The α and the β are the coefficients related to metallicity and effective temperature, respectively, while γ is an independent coefficient. The error associated to each parameter p is calculated as
are the transpose vectors of the parameter values. The α and the β are the coefficients related to metallicity and effective temperature, respectively, while γ is an independent coefficient. The error associated to each parameter p is calculated as 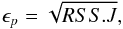 (3)where RSS is the residual sum of squares, expressed as
(3)where RSS is the residual sum of squares, expressed as 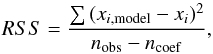 (4)and J is the diagonal of the estimate of the jacobian matrix around the solution. The xi,model, xi, nobs, and ncoef from Eq. (3) are, respectively, the predicted value of the data, xi, by the regression model, the data values, the number of data points, and the number of coefficients. We assume that both metallicity and effective temperature are independent and do not correlate with each other. This assumption was tested by perturbing each parameter in turn by introducing an positive or negative offset and then calculating both parameters. There was no difference in the obtained values of the unperturbed parameter. We also tried to use the full covariance matrix to calculate the uncertainties but in the end we got a worse result for the dispersion. Therefore, we decided to use only the diagonal values of the covariance matrix. The total error of the coefficients associated to each line i can then be written as
(4)and J is the diagonal of the estimate of the jacobian matrix around the solution. The xi,model, xi, nobs, and ncoef from Eq. (3) are, respectively, the predicted value of the data, xi, by the regression model, the data values, the number of data points, and the number of coefficients. We assume that both metallicity and effective temperature are independent and do not correlate with each other. This assumption was tested by perturbing each parameter in turn by introducing an positive or negative offset and then calculating both parameters. There was no difference in the obtained values of the unperturbed parameter. We also tried to use the full covariance matrix to calculate the uncertainties but in the end we got a worse result for the dispersion. Therefore, we decided to use only the diagonal values of the covariance matrix. The total error of the coefficients associated to each line i can then be written as 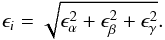 (5)The aim of our technique is to increase the precision of both [Fe/H] and Teff determinations. To do that we need to obtain the values of the metallicity and effective temperature via a weighted least squares refit, that is obtained after a left multiplication of (CTC)-1CT on both terms of Eq. (2), where C is the calibration matrix or the coefficient matrix, that can be written as
(5)The aim of our technique is to increase the precision of both [Fe/H] and Teff determinations. To do that we need to obtain the values of the metallicity and effective temperature via a weighted least squares refit, that is obtained after a left multiplication of (CTC)-1CT on both terms of Eq. (2), where C is the calibration matrix or the coefficient matrix, that can be written as ![\begin{eqnarray} \label{eq:matrix} C = \left[\begin{array}{ccc} \alpha_{1,1} & \beta_{1,2} & \gamma_{1,3} \\ \alpha_{2,1} & \beta_{2,2} & \gamma_{2,3} \\... & ... & ...\\ \alpha_{I,1} & \beta_{I,2} & \gamma_{I,3} \end{array}\right], \end{eqnarray}](/articles/aa/full_html/2014/08/aa24139-14/aa24139-14-eq45.png) (6)and CT is the transpose of C. The refit is then expressed, for each star m, as
(6)and CT is the transpose of C. The refit is then expressed, for each star m, as ![\begin{equation} \label{eq:refit} \left[\begin{array}{c} [{\rm Fe/H}] \\T_{\rm eff} \\ \Gamma \end{array}\right] = (C^{\rm T}C)^{-1}C^{\rm T}W, \end{equation}](/articles/aa/full_html/2014/08/aa24139-14/aa24139-14-eq47.png) (7)where Γ is the parameter related to the independent γ coefficients.
(7)where Γ is the parameter related to the independent γ coefficients.
In order to correct the offset of our method we added an extra parameter, while adding a corresponding dimension in Eq. (6), that corresponds to an array of ones. The updated matrix C has now dimension I × 4 instead of I × 3, where I has the value of the number of lines.
Finally we introduce a weight to Eq. (7), using a Levenberg-Marquardt (Press et al. 1992) algorithm. We can write the elements of the normalised weight E as 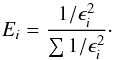 (8)Other methods were tested, such as choosing lines/features with the best correlations or partial correlations with the parameters. However, the weighted least squares approach performed best at minimising the uncertainties of both metallicity and temperature.
(8)Other methods were tested, such as choosing lines/features with the best correlations or partial correlations with the parameters. However, the weighted least squares approach performed best at minimising the uncertainties of both metallicity and temperature.
2.2. A posteriori sample selection
At this stage we observed that some stars appeared as outliers in the plots of the pseudo EWs versus the reference [Fe/H] and Teff for many lines. We suspected that this behaviour was due to activity or rotation and did a a posteriori study of the impact of the activity with our technique. To this end, we used the normalised Hα luminosity, log LHα/Lbol, from Reiners et al. (2012), for the stars in common with our full sample, as well as the median of individual measurements of the Hα index defined by Gomes da Silva et al. (2011), kindly provided by the author. Table 4 lists both activity indicators, in Cols. 5 and 6, for the stars in common with our sample. Figure 3 depicts the relation between both indices, where we observe the inactive stars, in the bottom left corner of the diagram, a linear trend between the indices for increasingly active stars, and a very active star, Gl285, in the top right corner of diagram, where the log LHα/Lbol indicator seems to have saturated. The dashed black lines show the limits above which the stars were excluded from the final sample, as described in the following paragraph.
 |
Fig. 3 Normalised Hα luminosity, taken from Reiners et al. (2012) versus the Hα index of Gomes da Silva et al. (2011) for the stars in common with our sample.The black dashed lines depict the limits that we have established for the sample selection. |
Figure 4 displays the normalised Hα luminosity and the Hα index defined by Gomes da Silva et al. (2011) as a function of the difference between the parameters obtained with our method and the initial parameters. The legend in panels c) and d) depict the stellar spectra with S/N ≥ 100 (blue dots), S/N between 30 and 100 (black crosses), S/N between 30 and 25 (red circles), and S/N lower than 25 (green stars). We observe no clear correlation of the activity indices or S/N with [Fe/H]. Regarding Teff however, we can see that there is a clear trend towards lower temperatures with both activity indices. To take this trend into account we decided to perform an activity cut, excluding all stars with log LHα/Lbol ≥ − 4.0 and Hα ≥ 0.25 from our final sample. We also note a trend of Hα with Teff towards higher temperatures for stars with S/N< 25 (see bottom right corner of Fig. 4 d). The trends of our method with S/N are studied in detail in Sect. 2.4.
 |
Fig. 4 a) Normalised Hα luminosity taken from Reiners et al. (2012) as a function of Δ[Fe/H]; b) normalised Hα luminosity taken from Reiners et al. (2012) as a function of ΔTeff; c) Hα index defined by Gomes da Silva et al. (2011) versus Δ[Fe/H]; d) Hα index defined by Gomes da Silva et al. (2011) versus ΔTeff. The stars in common were taken from our full sample. The red dashed lines mark the limits above which the stars were excluded from the final sample. |
In the end, with a final sample of 65 stars, we obtain a dispersion of 0.08 dex for the metallicity and 91 K for the effective temperature, as shown in Fig. 5. The technique is valid between −0.85 to 0.26 dex for [Fe/H], 2800 to 4100 K for Teff, and between M0.0 to M5.0. The dispersion around the calibration is quantified by the root mean square error (RMSE), and defined as 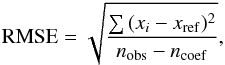 (9)where xi is the estimated quantity, xref the reference value for the same quantity, nobs the number of calibrators and ncoef the number of parameters used in the method (four in this case).
(9)where xi is the estimated quantity, xref the reference value for the same quantity, nobs the number of calibrators and ncoef the number of parameters used in the method (four in this case).
The calculated parameters as well as the reference determinations for [Fe/H] and Teff are listed in Table 2. Columns 1 and 3 contain the values for the reference calibrations, while Cols. 2 and 4 show the values obtained with our technique. We emphasise here that we only get an improvement on the precision. The accuracy of the method as well as its systematics are tied to the original determinations of the parameters.
2.3. Estimation of the uncertainties
To validate our method and have a better understanding of the uncertainties of our measurements we performed a bootstrap resampling and calculated the root mean square error of validation (RMSEV).
The bootstrap method we implemented tests how the rms of the method changes when using slightly different “bootstrapped” samples. To have a statistical significative number we first created 10 000 virtual samples by randomly drawing with repetition, for each virtual sample, a number of stars equal to the size of our sample. The random drawing followed a random uniform distribution. Then we calculated the rms for each trial and measured the 1σ gaussian equivalent interval between 15.9% and 84.1% from the resulting distribution, following the procedure of e.g. Burgasser et al. (2003); Neves et al. (2013). The distributions of the rms for both parameters are depicted in Fig. 6. The final result shows a variation of the rms of the [Fe/H] and Teff by ± 0.01 dex and ± 13 K respectively.
The calculation of the RMSEV is a predicted residual sum of squares (PRESS) procedure (Weisberg 2005) and follows the description in the Appendix of Rojas-Ayala et al. (2012). In short, we try to obtain the original value of the metallicity and temperature of each star i of the technique leaving that star out when calculating the parameters. Then, we calculate the residuals, or the difference between the original and obtained value for each star and add them up in quadrature. The PRESS statistic is then defined as 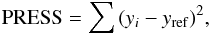 (10)where yi is the estimated value of the parameter and yref is the reference value of the measured quantity. From here we can calculate the root mean squared error of validation,
(10)where yi is the estimated value of the parameter and yref is the reference value of the measured quantity. From here we can calculate the root mean squared error of validation, 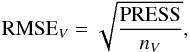 (11)where nV is the number of calibrators. The RMSEV value can then be used to obtain confidence intervals. We obtain a RMSEV value of 0.12 dex and ~293 K for the [Fe/H] and Teff respectively and will use these values as 1σ confidence intervals, assuming a normal cumulative distribution function. Table 3 summarises our results.
(11)where nV is the number of calibrators. The RMSEV value can then be used to obtain confidence intervals. We obtain a RMSEV value of 0.12 dex and ~293 K for the [Fe/H] and Teff respectively and will use these values as 1σ confidence intervals, assuming a normal cumulative distribution function. Table 3 summarises our results.
 |
Fig. 5 a) [Fe/H] comparison between this work and the photometric calibration of Neves et al. (2012); b) Teff comparison between this work and the photometric calibration of Casagrande et al. (2008). |
 |
Fig. 6 Dispersion given by bootstrap for [Fe/H] a) and Teffb). The N is the number of trials. |
Uncertainty estimators for [Fe/H] and Teff.
We observe that the uncertainties calculated with the different techniques are consistent with each other. The uncertainty for Teff is large but is in line with the expected uncertainties. We also perturbed our sample by introducing an offset in [Fe/H] or Teff, as explained in Sect. 2.1 but found that it does not affect the measurement of the parameters. In the end we assume our final uncertainty to be the maximum uncertainty of the RMSE given by the bootstrap, that translates into 0.09 dex for [Fe/H] and 110 K for Teff.
2.4. Testing our technique as a function of resolution and S/N
 |
Fig. 7 [Fe/H] of our procedure versus the [Fe/H] obtained with S/N = 50. The identity line is depicted in dashed black. The solid red line shows the linear fit. |
To further test our method, we calculated the dispersion of the parameters as a function of the resolution and S/N. The first step consisted in the study of the behaviour of the procedure as a function of S/N only. We injected random Gaussian noise in the spectra of the sample to obtain spectra with S/N @ 5500 Å between 100 and 10. Then, we calculated linear fits between the [Fe/H] and Teff obtained with the lower S/N spectra and the values of our method, for the full S/N range, as shown in Fig. 7 for [Fe/H] and S/N = 50. The dashed black line marks the identity line while the red line represents a linear fit to the data.
Figure 8 depicts the slope and offset of the linear fits for [Fe/H] and Teff, as a function of S/N. We observe a deviation from the identity line as the S/N decreases as expected, except in d), where the offset of Teff is reasonably constant, on average, with S/N. From here we investigated the cause of this trend and found that the measured EWs, roughly quantified as the median of all EWs, follow similar trends with S/N, as shown in Fig. 9 the for the star Gl479 ([Fe/H] = 0.01 dex, Teff = 3218 K) as example. The observed trends are similar in other stars, with different metallicities and effective temperatures.
Using this information, we corrected the values of both parameters for all stars of our sample with S/N< 100, where [Fe/H] (Corrected) = a[Fe/H] (Degraded) + b, and Teff (Corrected) = aTeff (Degraded) + b. The a is the slope and b is the offset. The uncertainties associated with each correction were estimated by calculating the dispersion of the residuals. However, we observed that these uncertainties are very small compared to the final uncertainty of our method, as shown in Sect. 2.3. Therefore, we assumed the uncertainty of our method for all stars, except for the active ones, according to the two estimated activity thresholds calculated in Sect. 2.2. In this case, we used the initial values of the parameters, calculated with the calibrations of Neves et al. (2012) and Casagrande et al. (2008). At this point, we also decided not to use our new values for stars with S/N ≤ 25, because the correction was not good enough to obtain a reasonable value for the objects depicted as green stars in Fig. 4. Moreover, we note that the stars LHS 1513 and Gl 803 give an estimated [Fe/H] value of −1.51 and 0.46 dex respectively, calculated with the calibration of Neves et al. (2012), our reference scale. Both values are outside the range of this method and will not be used. Table 4 shows the corrected results, along with the previous values of [Fe/H] from Neves et al. (2013). Column 1 describes the star designation and Cols. 2 and 3, the right ascension and declination of the star, respectively. Column 4 depicts the S/N, Col. 5 the normalised Hα index taken from Reiners et al. (2012), and Col. 6 the Hα index described by Gomes da Silva et al. (2011). Column 7 shows the metallicity calculated with the coefficient matrix used in our previous work, Neves et al. (2013), Col. 8 the [Fe/H] obtained in our work, along with its associated error in Col. 9. The Teff values of our stars, and its uncertainties are described in Cols. 10 and 11.
 |
Fig. 8 Slope and offset of [Fe/H] and Teff of our work as a function of S/N for star Gl479. |
 |
Fig. 9 Median of the pseudo EWs and [Fe/H] a) or Teffb) as a function of S/N for star Gl479. |
In the second step of this test we modified both resolution and S/N of our sample spectra. The resolution of the HARPS spectra was degraded by convolving the spectra with a normalised Gaussian curve, simulating the instrumental profile, with FWHM = λ/R, where λ is the wavelength and R the resolution we intend to obtain. From here, the standard deviation of the Gaussian is calculated with the well known formula 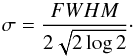 (12)The σ was adjusted to the HARPS resolution (R ~ 115.000) and to the original S/N @ 5500 Å of each spectrum. The final value for σ is then
(12)The σ was adjusted to the HARPS resolution (R ~ 115.000) and to the original S/N @ 5500 Å of each spectrum. The final value for σ is then 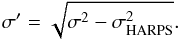 (13)Figures 10 and 11 show the difference of our parameters against the degraded values, as a function of resolution (while the S/N is kept constant at 100) and as a function of S/N (while the resolution is kept constant at 100.000) for [Fe/H] and Teff respectively. The red dotted line depicts the offset of the residuals.
(13)Figures 10 and 11 show the difference of our parameters against the degraded values, as a function of resolution (while the S/N is kept constant at 100) and as a function of S/N (while the resolution is kept constant at 100.000) for [Fe/H] and Teff respectively. The red dotted line depicts the offset of the residuals.
 |
Fig. 10 Difference of the [Fe/H] for this work and the [Fe/H] calculated with different resolution/signal-to-noise combinations as a function of the resolution and S/N. |
 |
Fig. 11 Difference of the Teff for this work and the Teff calculated with different resolution/signal-to-noise combinations as a function of the resolution and S/N. |
From the two figures we observe the existence of linear trends for different resolutions and S/N. To correct these trends we performed a linear fit for each Resolution/signal-to-noise combination with the functional form [Fe/H] (This work) = a[Fe/H] (Degraded) + b for metallicity, and Teff (This work) = aTeff (Degraded) + b for effective temperature. The values for each combination are shown in Table 5.
Linear fit coefficients a and b from the relation between the values of our parameters and the values calculated for different combinations of resolution and S/N.
Dispersion of the residuals of the parameters as a function of the resolution and S/N.
From here we calculated the dispersion of the difference between the corrected parameter values and the ones obtained from our original determinations, and added this dispersion with the one from our method in quadrature. Table 6 shows the results. The horizontal header of both tables correspond to the S/N of the spectra, between 100 and 10, while the vertical header depicts their resolution, from 100 000 to 10 000. The row with the resolution number is the value of the dispersion of our technique using the corresponding resolution/signal-to-noise combination. This table should be used as a guideline for the uncertainties of the parameters when using spectra other than HARPS.
From Table 6 and Figs. 10 and 11 we observe that, as the resolution degrades, the dispersion and offset of the residuals increase. In the case of [Fe/H], the dispersion value holds well for a resolution higher and equal to 40 000 respectively. From 35 000 and lower resolutions we observe that the uncertainties of the residuals are similar or greater than the original dispersion (0.17 dex), meaning that the method is not useful any more, providing we have precise parallaxes and visual magnitudes. Regarding Teff, we consider that the method is valid for the same resolution and S/N intervals as in [Fe/H]. We also limit the use of the technique for spectra with S/N greater than 25, as we cannot properly correct the parameters, as we have previously seen in this section. From here we investigated the nature of these correlations by plotting the median of all EWs with the parameters, as a function of resolution (with S/N = 100), for a metal-poor star Gl191 ([Fe/H] = −0.85 dex, Teff = 3510 K) and a metal-rich star, GJ 317 ([Fe/H] = 0.22 dex, Teff = 3106 K), as it was previously done for S/N, and shown in Fig. 9. Figure 12 pictures the results. The blue dots depict the median of the pseudo EWs while the red crosses show the metallicity or the effective temperature.
We observe that the EW and the parameters follow similar trends as the resolution degrades, as expected (except in Fig. 12a) where metallicity has an opposite trend to the EW. We do not know the cause of the different trend.
The increasing dispersions and offsets with the resolution observed in Figs. 10 and 11 should originate from the nature of our “peak-to-peak” technique because it does not consider the continuum. As the resolution gets worse, more and more flux from the “peak-to-peak” region is lost to the line wings. However, as the resolution decreases there is an increase of line blending that makes the measurement of the correct flux of the each line/feature increasingly difficult. Moreover, we also observe from Fig. 2 that we have similar numbers of correlation and anti-correlations of the lines with [Fe/H], and the overall effect of the weighted lines may change as the resolution degrades. The mix of any of these effects may be the reason behind we get different trends for [Fe/H] from Gl191 (Fig. 12a) and GJ436 (Fig. 12c).
In order to validate our estimation of the uncertainties we used a sample of spectra of stars in common taken from the SOPHIE spectrograph (Bouchy & The Sophie Team 2006) archive2. We downloaded individual observations taken with the “HR” (R ~ 75 000) and “HE” (R ~ 40 000) modes, with the reference fiber exposed to the sky rather than to the thorium–argon calibration lamp, to avoid potential contamination. The “HR” sample is comprised of 12 stars in common while the “HE” sample contains only 5 stars.
First, we summed the individual spectra of each star, after correcting the radial velocity of each spectrum, and calculated their pseudo EWs. The S/N of the summed spectra for each star in common range from 34 to more than 600. Then, we calculated the metallicity and effective temperature and applied the appropriate corrections shown in Table 5, following the resolution and S/N of each spectra. The final values of the parameters are displayed in Table 7. Column 2 lists the resolution, Col. 3 the S/N, and Cols. 4 to 7 the parameters of our method and the ones obtained with the SOPHIE spectra, respectively.
We obtain a rms for the [Fe/H] of 0.088 and 0.123 dex for the “HR” and the “HE” samples respectively. Both dispersions are very close the expected dispersions for R = 75 000 and R = 40 000, as depicted in Table 6. For Teff, we obtain a dispersion of 104 and 172 K for the “HR” and “HE” samples respectively. Both values are above the expected values, but in the case of the “HR” sample, the difference is only a few Kelvin. Regarding the “HE” sample, this difference is larger (~75 K), but the dispersion value is close to the one considered for the photometric calibration (~150 K). Moreover, we note that the sample size is very small (N = 5). These results give us confidence and validate our uncertainty estimation method.
3. Comparison with the literature
A comparison with other studies in the literature was performed. This comparison allow us to evaluate the accuracy of our method and the possible systematics that it may suffer. Table 8 shows our spectroscopic results compared to the ones found in the literature, for the stars in common. Column 1 depicts the star designations and Col. 2 informs if the star belongs or not to the selected sample that we used to calibrate our method. Columns 3 to 13 and Cols. 14 to 21 describe our [Fe/H] and Teff against the metallicity found in the literature, respectively. We note here that we only used the spectroscopic derived values for comparison. All active stars were excluded from this exercise.
We show in Table 9 the results of the comparison for the sample used in our technique and the full sample. The results for [Fe/H] are separated by photometric and spectroscopic techniques. The first column depicts the name of the method along with its reference. Column two and three describe the dispersion and offset. The last column reports the number of stars in common with our sample. We do not display the calibration of Mann et al. (2013a) in Table 9 because we only have two stars in common with them. However, we include the 4 measurements from the V- and K-band calibrations in the row “All [Fe/H] values”. We note here that we only compared stars in common for which we could calculate precise values of [Fe/H] and Teff with our methodology.
The photometric [Fe/H] was calculated with the relations of Bonfils et al. (2005), Schlaufman & Laughlin (2010) and Johnson et al. (2012), while the spectroscopic [Fe/H] was taken directly from the works of Woolf & Wallerstein (2005), Rojas-Ayala et al. (2012), Önehag et al. (2012), Terrien et al. (2012), Newton (2013), and Mann et al. (2013b), except in the case of Mann et al. (2013a), where the values of the visible (their Eq. (8)) and K-band (their Eq. (16)) calibrations were provided directly by the author. We note that we used the average of the H- and K-band spectroscopic relations of Terrien et al. (2012). Also, we restricted the calculation of the photometric calibrations to the stars from the sample selection, for which we have precise photometries and parallaxes, to insure the best possible results in the comparison exercise.
Figure 13 portrays two [Fe/H]-[Fe/H] plots, with data taken from the selected sample. The left plot (a) shows the comparison of our sample with the works based on photometric scales. The blue dots, red crosses and black plus signs indicate the results of Bonfils et al. (2005), Schlaufman & Laughlin (2010), and Johnson et al. (2012) respectively. The right plot (b) depicts the comparison of our selected sample with other spectroscopic methods. The purple triangles, red crosses, red circles, green plus signs, black stars, black diamonds, black plus signs, and blue dots correspond to the measurements of Woolf & Wallerstein (2005), Rojas-Ayala et al. (2012), Önehag et al. (2012), Terrien et al. (2012), Mann et al. (2013a,b), and Newton (2013) respectively. The (V) and (K) in Mann et al. (2013a) correspond to measurements performed with a V- and K-band calibration respectively. The solid black line in the upper panel of both plots defines an identity line. The lower panels show the residuals. The dashed black line marks the zero-point of the calibration.
 |
Fig. 12 Measured median of the pseudo EWs, [Fe/H] and Teff as a function of resolution for the stars Gl191 a) and b) and GJ317 c) and d). The blue dots depict the median of the pseudo EWs while the red crosses show the metallicity or the effective temperature. |
 |
Fig. 13 Upper panel: [Fe/H]-[Fe/H] plots comparing the values of this work, from the selected sample, against others in the literature. The solid black line of both a) and b) depict the identity line; lower panel: comparison plot residuals. The dashed black line marks the zero point of our technique. The plot a) shows the results of our work versus three photometric calibrations taken from the literature, while plot b) depicts the comparison between our results against other spectroscopic measurements. |
[Fe/H] and Teff calculated from a sample in common with SOPHIE observations.
Dispersion and offset of [Fe/H] and Teff from the residuals of the sample of the method and full sample against other studies.
For metallicity we observe a general agreement between our results and the ones from the literature. We note here that the calibration of Schlaufman & Laughlin (2010) is very similar to our reference calibration, from Neves et al. (2012), and this is the reason why we obtain a value of dispersion smaller than the one of the original calibration (0.11 vs. 0.17 dex). The dispersion of the oldest photometric calibration (Bonfils et al. 2005) is surprisingly low (0.11 dex), considering that the original dispersion for this calibration is 0.20 dex. However, the Bonfils et al. (2005) is also similar to Schlaufman & Laughlin (2010) and Neves et al. (2012) which may explain part of the low dispersion. Regarding the Johnson et al. (2012) calibration, we obtain a rms of 0.19 dex, higher that their reported value of 0.15 dex. The dispersion of the spectroscopic determinations are within the expected values (~0.11 dex), considering the uncertainties of each method, except in the case of Mann et al. (2013b), where we obtain a dispersion of 0.16 dex, and in two stars in common with Woolf & Wallerstein (2005), where the [Fe/H] difference for Gl191 and Gl526 is higher that the uncertainties reported here and in their work (0.14 and −0.12 dex, respectively). The offset of each calibration is smaller than the dispersion value of our calibration, aside from Mann et al. (2013b; 0.11 dex). We should note, however, that we only have seven stars in common with Mann et al. (2013b) and one of these stars, Gl205, has a [Fe/H] difference of 0.30 dex. When we consider the full sample we detect a slight increase of dispersion for Rojas-Ayala et al. (2012), and a considerable increase in both dispersion and offset for Newton (2013). This increase in the Newton (2013) dispersion is due to the addition of several stars in common with high [Fe/H], where the two calibrations show most disagreement.
Regarding the effective temperature, the photometric temperature scale of Boyajian et al. (2012) was calculated using the average value of the three colour-metallicity Teff relations (V − J, V − H, and V − KS) from their Table 9, and imposing a cutoff of V − K< 4.5 for the three scales, according to their limits. The Teff values of Woolf & Wallerstein (2005), Rojas-Ayala et al. (2012), Önehag et al. (2012), Mann et al. (2013a), and Rajpurohit et al. (2013a) were taken directly from their works. Figure 14 describes the comparison between our Teff results and those of the other authors. The purple (pointing up) triangles, red crosses, green circles, blue dots, and black (pointing down) triangles correspond to the measurements of Woolf & Wallerstein (2005), Rojas-Ayala et al. (2012), Önehag et al. (2012), Mann et al. (2013a), and Rajpurohit et al. (2013a) respectively. The solid black line in the upper panel defines an identity line. The lower panels show the residuals. The photometric [Fe/H] measurements as well as the Teff determinations using the calibration of Boyajian et al. (2012) were calculated with the data from Table 1.
 |
Fig. 14 Upper panel: Teff-Teff plot comparing the values of this work, taken from the selected sample, against others in the literature. The solid black line depicts the identity line; lower panel: comparison plot residuals. The dashed black line marks the zero point of our calibration. |
From Figure 14 and Table 9 we observe a good agreement with the results from Woolf & Wallerstein (2005) where we obtain a low dispersion and offset. However, we only have 5 stars in common with them, and they occupy a very narrow region of the Teff range, around 3500 K. Our results also match well the BT-SETTL based work of Rajpurohit et al. (2013a). However, when we look at the results of the full sample we observe a significant increase in the rms of Rajpurohit et al. (2013a), and we also witness a considerable dispersion with Rojas-Ayala et al. (2012) in both samples. The Önehag et al. (2012) and Boyajian et al. (2012) determinations tend to converge with ours as the Teff increases. We also note a systematic underestimation of our values of temperature in general that increases below 3200 K. The Önehag et al. (2012) determinations have the smallest offset, but this result is expected since they use the same reference Teff calibration as we do. When we consider the full sample we observe that the rms and offset do not change considerably, except in the case of Rajpurohit et al. (2013a). Finally, we calculated linear fits for the different Teff methods, where Teff (This work) = aTeff (Others) + b. The only exception concerns Woolf & Wallerstein (2005), because the 5 stars we have in common only cover a very narrow range in the effective temperature region. The coefficients a, b and respective uncertainties are reported in Table 10.
Linear fit coefficients for each Teff method
4. Discussion
In this paper we present a new high-precision technique to calculate metallicities and effective temperatures for M dwarfs. Within the activity and S/N limits of our method, we achieve a rms of 0.08 dex for metallicity and 91 K for effective temperature. Alternatively we obtain a RMSEV value of 0.12 dex for [Fe/H] and 293 K for Teff. A bootstrap resampling was also conducted, showing a variation of the rms of [Fe/H] and Teff of the order of ±0.01 dex and ±13 K respectively. Our technique is available for download3. The procedure to use our method is detailed in this webpage as well as in the Annexe. A test of the behaviour of the technique as a function of the resolution and S/N was also performed. We estimate that our method behaves properly down to R = 40 000 and S/N = 25, after correcting the observed trends. We also validated our results against a sample of stars in common with SOPHIE high resolution spectra.
To have a measure of the accuracy of our method, we tested it against several studies from the literature. Most studies agree well with our [Fe/H] determinations, and the offset is almost always below the precision of the method. For Teff however, the same agreement could not be met. Despite reaching a good agreement with the results of Woolf & Wallerstein (2005), and Rajpurohit et al. (2013a), that use synthetic spectra from the latest BT-SETTL models, the dispersion as well as the systematics between our determinations and the other works is considerable and beyond the calibration errors. Further studies are needed to investigate the nature of these systematics.
Online material
List containing our sample and the quantities used to calculate the reference [Fe/H] and Teff (sorted by right ascension).
Our sample table with the reference and calibrated metallicity and effective temperature (sorted by right ascension).
Full HARPS M dwarf GTO sample (sorted by right ascension).
Comparison of our parameters with other results from the literature for the stars in common (sorted by right ascension).
Acknowledgments
We would like to thank Barbara Rojas-Ayala for useful discussions. We would also like to thank Andrew Mann and João Gomes da Silva for kindly providing several metallicity values and the Hα determinations, respectively. We acknowledge the support by the European Research Council/European Community under the FP7 through Starting Grant agreement number 239953. The financial support from the “Programme National de Planétologie” (PNP) of CNRS/INSU, France, is also gratefully acknowledged. V.N. acknowledges the support from Fundação para a Ciência e a Tecnologia (FCT) of the fellowship SFRH/BD/60688/2009. N.C.S. also acknowledges the support in the form of a Investigador FCT contract funded by Fundação para a Ciência e a Tecnologia (FCT)/MCTES (Portugal) and POPH/FSE (EC). X.B., T.F. and X.D. would like to acknowledge the support of the French Agence Nationale de la Recherche (ANR), under program ANR-12-BS05-0012 Exo-Atmos. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.
References
- Allard, F., Homeier, D., & Freytag, B. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 91 [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 2765 [Google Scholar]
- Allard, F., Homeier, D., Freytag, B., et al. 2013, Mem. Soc. Astron. It. Suppl., 24, 128 [Google Scholar]
- Anglada-Escudé, G., Boss, A. P., Weinberger, A. J., et al. 2012, ApJ, 746, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Rojas-Ayala, B., Boss, A. P., Weinberger, A. J., & Lloyd, J. P. 2013, A&A, 551, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bean, J. L., Sneden, C., Hauschildt, P. H., Johns-Krull, C. M., & Benedict, G. F. 2006, ApJ, 652, 1604 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., & Shallis, M. J. 1977, MNRAS, 180, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2005, A&A, 442, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., & The Sophie Team. 2006, in Tenth Anniversary of 51 Peg-b: Status of and prospects for hot Jupiter studies, Colloquium held at Observatoire de Haute Provence, France, eds. L. Arnold, F. Bouchy, & C. Moutou, 319 [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Burgasser, A. J., Kirkpatrick, J. D., Reid, I. N., et al. 2003, ApJ, 586, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Flynn, C., & Bessell, M. 2008, MNRAS, 389, 585 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dawson, P. C., & Forbes, D. 1992, AJ, 103, 2063 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricius, C., Høg, E., Makarov, V. V., et al. 2002, A&A, 384, 180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2011, A&A, 534, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hawley, S. L., Gizis, J. E., & Reid, N. I. 1997, AJ, 113, 1458 [NASA ADS] [CrossRef] [Google Scholar]
- Henden, A. A., Welch, D. L., Terrell, D., & Levine, S. E. 2009, in AAS Meeting Abstracts, 214, 40702 [Google Scholar]
- Henden, A. A., Levine, S. E., Terrell, D., Smith, T. C., & Welch, D. 2012, J. Amer. Association Variable Star Observers (JAAVSO), 40, 430 [Google Scholar]
- Henry, T. J., Jao, W.-C., Subasavage, J. P., et al. 2006, AJ, 132, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., & Apps, K. 2009, ApJ, 699, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Gazak, J. Z., Apps, K., et al. 2012, AJ, 143, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., Kilkenny, D., van Wyk, F., & Marang, F. 2010, MNRAS, 403, 1949 [Google Scholar]
- Laing, J. D. 1989, South African Astronomical Observatory Circular, 13, 29 [Google Scholar]
- Leggett, S. K. 1992, ApJS, 82, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., Hilton, E. J., Mann, A. W., et al. 2013, AJ, 145, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, A. W., Brewer, J. M., Gaidos, E., Lépine, S., & Hilton, E. J. 2013a, AJ, 145, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, A. W., Gaidos, E., & Ansdell, M. 2013b, ApJ, 779, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N. C., et al. 2012, A&A, 538, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N. C., et al. 2013, A&A, 551, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newton, E. 2013, in Protostars and Planets VI, Heidelberg, July 15–20, Poster #1K093, 93 [Google Scholar]
- Önehag, A., Heiter, U., Gustafsson, B., et al. 2012, A&A, 542, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Pickles, A. J. 1998, PASP, 110, 863 [CrossRef] [Google Scholar]
- Pineda, J. S., Bottom, M., & Johnson, J. A. 2013, ApJ, 767, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing (Cambridge University Press) [Google Scholar]
- Rajpurohit, A. S., Reylé, C., Allard, F., et al. 2013a, A&A, 556, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rajpurohit, A. S., Reylé, C., Schultheis, M., & Allard, F. 2013b, in SF2A-2013: Proc. of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. L. Cambresy, F. Martins, E. Nuss, & A. Palacios, 259 [Google Scholar]
- Reiners, A., Joshi, N., & Goldman, B. 2012, AJ, 143, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Riedel, A. R., Subasavage, J. P., Finch, C. T., et al. 2010, AJ, 140, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2010, ApJ, 720, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas-Ayala, B., Covey, K. R., Muirhead, P. S., & Lloyd, J. P. 2012, ApJ, 748, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlaufman, K. C., & Laughlin, G. 2010, A&A, 519, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ségransan, D., Kervella, P., Forveille, T., & Queloz, D. 2003, A&A, 397, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terrien, R. C., Mahadevan, S., Bender, C. F., et al. 2012, ApJ, 747, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., Piskunov, N., & Johns-Krull, C. M. 1998, ApJ, 498, 851 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weis, E. W. 1993, AJ, 105, 1962 [NASA ADS] [CrossRef] [Google Scholar]
- Weisberg, S. 2005, Applied Linear Regression, Wiley Series in Probability and Statistics (Wiley) [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woolf, V. M., & Wallerstein, G. 2005, MNRAS, 356, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Woolf, V. M., & Wallerstein, G. 2006, PASP, 118, 218 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Using the method
The code of our technique is written in python 2.7 and can be downloaded at http://www.astro.up.pt/resources/mcal. The program is very simple to use. The first step is to write the filenames of your spectra into stars.txt, replacing the two demonstration filenames, Gl105B_S1D.fits and Gl849_S1D.fits. Then, one just needs to change the startup options, described in the startup section of the file runallv1.py. Depending on the resolution and S/N of the spectra, one should use the values of Table 6 as the reference of precision of [Fe/H] and Teff.
The compressed zip file calibrationv3.zip contains all the necessary files needed to run the program, as described in the following list:
-
runallv1.py – script to run all the other programs. In the startupsection one can choose to use fast Fourier transform (FFT) to filterhigh frequency noise, the file type of the input spectra (FITS or textfile), and the name of the file with the full path of the spectra.
-
fft_filterv1.py – function that performs the FFT filtering of the spectra. The default setting of the filter in runallv1.py is “off”.
-
int_calc_stars.py – function to calculate the pseudo EWs of the relevant lines. It uses lines.rdb as input. An output file, ew_out.npz, is also created. The function also estimates the Hα index described by Gomes da Silva et al. (2011) and warns if the star is too active. It takes 3–5 min per star to calculate the EWs.
-
mcalv1.npz – function that calculates the [Fe/H] and Teff of each star using the calibration matrix file coef_cal.npz. The output will be displayed on the screen and can also be optionally saved to a file (check the startup section of runallv1.py for details).
-
stars.txt – text file with the full path of the spectra. This file should have all the spectra files for analysis.
-
Gl105B_S1D.fits and Gl849_S1D.fits are two HARPS spectra that can be used to demonstrate how the program works. Their full file names appear in the file stars.txt. One should remove them from stars.txt before calibrating new stars.
All Tables
Linear fit coefficients a and b from the relation between the values of our parameters and the values calculated for different combinations of resolution and S/N.
Dispersion of the residuals of the parameters as a function of the resolution and S/N.
Dispersion and offset of [Fe/H] and Teff from the residuals of the sample of the method and full sample against other studies.
List containing our sample and the quantities used to calculate the reference [Fe/H] and Teff (sorted by right ascension).
Our sample table with the reference and calibrated metallicity and effective temperature (sorted by right ascension).
Comparison of our parameters with other results from the literature for the stars in common (sorted by right ascension).
All Figures
 |
Fig. 1 Small region of the Gl 205 spectra illustrating pseudo equivalent width line measurement. The red dotted line represents the “peak-to-peak” flux. |
| In the text | |
 |
Fig. 2 Histograms of the partial correlations of [Fe/H] (solid blue histogram) and Teff (dashed green histogram). |
| In the text | |
 |
Fig. 3 Normalised Hα luminosity, taken from Reiners et al. (2012) versus the Hα index of Gomes da Silva et al. (2011) for the stars in common with our sample.The black dashed lines depict the limits that we have established for the sample selection. |
| In the text | |
 |
Fig. 4 a) Normalised Hα luminosity taken from Reiners et al. (2012) as a function of Δ[Fe/H]; b) normalised Hα luminosity taken from Reiners et al. (2012) as a function of ΔTeff; c) Hα index defined by Gomes da Silva et al. (2011) versus Δ[Fe/H]; d) Hα index defined by Gomes da Silva et al. (2011) versus ΔTeff. The stars in common were taken from our full sample. The red dashed lines mark the limits above which the stars were excluded from the final sample. |
| In the text | |
 |
Fig. 5 a) [Fe/H] comparison between this work and the photometric calibration of Neves et al. (2012); b) Teff comparison between this work and the photometric calibration of Casagrande et al. (2008). |
| In the text | |
 |
Fig. 6 Dispersion given by bootstrap for [Fe/H] a) and Teffb). The N is the number of trials. |
| In the text | |
 |
Fig. 7 [Fe/H] of our procedure versus the [Fe/H] obtained with S/N = 50. The identity line is depicted in dashed black. The solid red line shows the linear fit. |
| In the text | |
 |
Fig. 8 Slope and offset of [Fe/H] and Teff of our work as a function of S/N for star Gl479. |
| In the text | |
 |
Fig. 9 Median of the pseudo EWs and [Fe/H] a) or Teffb) as a function of S/N for star Gl479. |
| In the text | |
 |
Fig. 10 Difference of the [Fe/H] for this work and the [Fe/H] calculated with different resolution/signal-to-noise combinations as a function of the resolution and S/N. |
| In the text | |
 |
Fig. 11 Difference of the Teff for this work and the Teff calculated with different resolution/signal-to-noise combinations as a function of the resolution and S/N. |
| In the text | |
 |
Fig. 12 Measured median of the pseudo EWs, [Fe/H] and Teff as a function of resolution for the stars Gl191 a) and b) and GJ317 c) and d). The blue dots depict the median of the pseudo EWs while the red crosses show the metallicity or the effective temperature. |
| In the text | |
 |
Fig. 13 Upper panel: [Fe/H]-[Fe/H] plots comparing the values of this work, from the selected sample, against others in the literature. The solid black line of both a) and b) depict the identity line; lower panel: comparison plot residuals. The dashed black line marks the zero point of our technique. The plot a) shows the results of our work versus three photometric calibrations taken from the literature, while plot b) depicts the comparison between our results against other spectroscopic measurements. |
| In the text | |
 |
Fig. 14 Upper panel: Teff-Teff plot comparing the values of this work, taken from the selected sample, against others in the literature. The solid black line depicts the identity line; lower panel: comparison plot residuals. The dashed black line marks the zero point of our calibration. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


