| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201423857 | |
| Published online | 08 August 2014 | |
Rotation of cometary meteoroids
Astronomical Institute of the Academy of Sciences, Fričova 298, 251 65 Ondřejov, Czech Republic
e-mail: capek@asu.cas.cz
Received: 20 March 2014
Accepted: 20 June 2014
Aims. The rotation of meteoroids caused by gas drag during the ejection from a cometary nucleus has not been studied yet. The aim of this study is to estimate the rotational characteristics of meteoroids after their release from a comet during normal activity.
Methods. The basic dependence of spin rate on ejection velocity and meteoroid size is determined analytically. A sophisticated numerical model is then applied to meteoroids ejected from the 2P/Encke comet. The meteoroid shapes are approximated by polyhedrons, which have been determined by a 3D laser scanning method of 36 terrestrial rock samples. These samples come from three distinct sets with different origins and characteristics, such as surface roughness or angularity. Two types of gas-meteoroid interactions and three gas ejection models are assumed. The rotational characteristics of ejected meteoroid population are obtained by numerical integration of equations of motion with random initial conditions and random shape selection.
Results. It is proved that the results do not depend on a specific set of shape models and that they are applicable to the (unknown) shapes of real meteoroids. A simple relationship between the median of meteoroid spin frequencies 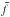 (Hz), ejection velocities vej (m s-1), and sizes D (m) is determined. For diffuse reflection of gas molecules from meteoroid’s surface it reads as
(Hz), ejection velocities vej (m s-1), and sizes D (m) is determined. For diffuse reflection of gas molecules from meteoroid’s surface it reads as 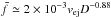 , and for specular reflection of gas molecules from meteoroid’s surface it is
, and for specular reflection of gas molecules from meteoroid’s surface it is 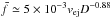 . The distribution of spin frequencies is roughly normal on log scale, and it is relatively wide: a 2σ-interval can be described as
. The distribution of spin frequencies is roughly normal on log scale, and it is relatively wide: a 2σ-interval can be described as 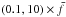 . Most of the meteoroids are non-principal axis rotators. The median angle between angular momentum vector and spin vector is 12°. About 60% of meteoroids rotate in long-axis mode. The distribution of angular momentum vectors is not random. They are concentrated in the perpendicular direction with respect to the gas flow direction. These results have been determined for the 2P/Encke comet, but their validity is general.
. Most of the meteoroids are non-principal axis rotators. The median angle between angular momentum vector and spin vector is 12°. About 60% of meteoroids rotate in long-axis mode. The distribution of angular momentum vectors is not random. They are concentrated in the perpendicular direction with respect to the gas flow direction. These results have been determined for the 2P/Encke comet, but their validity is general.
Key words: meteorites, meteors, meteoroids
© ESO, 2014
1. Introduction
From observations of meteors and bolides, there are several phenomena that suggest that meteoroids rotate. (i) The light curves of some bright meteors show quasi-periodic brightness variations (Spurný et al. 2007). This phenomenon, which is called flickering, is sometimes interpreted as the result of rotation of an asymmetric meteoroid (e.g., Beech & Brown 2000; Beech 2001; Spurný & Borovička 2001; Beech et al. 2003). The rotational origin of flickering has, however, been doubted, and other explanations, such as an autofluctuating mechanism or triboelectric effects, have been suggested (e.g., Babadzhanov & Konovalova 2004; Borovička 2006; Spurný & Ceplecha 2008; Spurný et al. 2012). (ii) Periodic variations in velocity of the Lost City bolide were also interpreted as the result of a changing cross-section due to rotation (Ceplecha 1996; Ceplecha & Revelle 2005). (iii) The initial radius of meteor trains (Hawkes & Jones 1978); and (iv) non-linear meteor trails (Beech 1988) can also be a result of meteoroid rotation, as can the meteoroid bursting in the atmosphere (e.g., Stokan & Campbell-Brown 2014). Unfortunately, precise and reliable determination of preatmospheric rotation from observations of meteors and bolides represents a significant problem so far.
The preatmospheric rotation of meteoroids (and more generally, the evolution of rotation in interplanetary space) can be studied theoretically. For such studies, it is necessary to describe the action of the processes that may affect the rotation. It was shown that the radiative effects more efficiently affect the rotation of meteoroids in space than collisions with dust (Olsson-Steel 1987). The asymmetry parameter determined by Paddack (1969), together with the time spent in interplanetary space has been used for estimates of the spin rate of meteoroids, but a detailed study that would describe complete physics of meteoroid rotation in space self-consistently is still missing.
For further modeling of the subsequent spin evolution in interplanetary space, knowledge of initial rotation, just after the meteoroid birth, is also necessary. For asteroidal meteoroids, which originate as debris from collisions in the Main Belt, the initial rotation can be estimated from results of hypervelocity fragmentation experiments (e.g., Fujiwara et al. 1989; Martelli et al. 1994; Giblin & Farinella 1997; Giblin et al. 1998).
The majority of shower meteoroids are released from parent cometary nucleus during the normal activity of the comet by gas drag (Whipple 1950, 1951). The gas drag mechanism is connected with sublimation of ice on the surface of the nucleus and acceleration of embedded dust grains and pebbles by gas flow away from the comet. If the meteoroid has an irregular shape with some degree of windmill asymmetry, the gas may also accelerate its rotation - similarly to the simple experiment of Paddack (1969). Although many authors have dealt with the ejection process (e.g., Crifo 1995; Jones 1995; Crifo & Rodionov 1997; Fulle 1997; Ma et al. 2002; Molina et al. 2008), the rotation of meteoroids caused by gas drag during the ejection has not been studied yet.
The aim of the present study is to fill this gap in our understanding of the meteoroids’ rotation and to estimate the rotation characteristics of the meteoroids after the ejection from the parent cometary nucleus. It is the first in the assumed series of articles devoted to rotation of meteoroids. In Sect. 2 a simple analytical theory is described, and Sect. 3 is devoted to the description of a sophisticated numerical model. The results from the numerical model can be found in Sect. 4
2. Simple analytical model
The meteoroid motion and related acceleration of rotation during ejection can be described by the following simple analytical model. We assume that the cometary nucleus is spherical with radius Rc and mass Mc. Sublimation of the cometary material by solar heating causes a gas flow in the radial direction from the nucleus along coordinate z (z = 0 in the center of the nucleus). The meteoroid has mass m and size D. We assume two forces acting on the meteoroid. The first one is the gravitational force of the nucleus, which can be expressed as 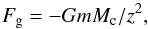 (1)where G = 6.67 × 10-11 N m2 kg-2 is the gravitational constant. Molecules of the gas interact with meteoroid surface and cause drag force, which can be expressed in a simplified form as
(1)where G = 6.67 × 10-11 N m2 kg-2 is the gravitational constant. Molecules of the gas interact with meteoroid surface and cause drag force, which can be expressed in a simplified form as 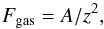 (2)where A is a positive constant (e.g., review of Ryabova 2013). The equation of motion is
(2)where A is a positive constant (e.g., review of Ryabova 2013). The equation of motion is 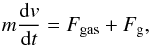 (3)where v is the velocity in the z-direction. Using the identity dv/ dt = v dv/ dz and initial conditions v = 0 and z = Rc (meteoroid is lying on the surface of the nucleus), the dependence of the meteoroid velocity on distance z can be found:
(3)where v is the velocity in the z-direction. Using the identity dv/ dt = v dv/ dz and initial conditions v = 0 and z = Rc (meteoroid is lying on the surface of the nucleus), the dependence of the meteoroid velocity on distance z can be found: 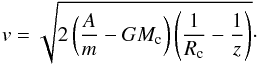 (4)If the body has an amount of windmill asymmetry, the gas produces not only force Fgas, but also torque Mgas. We then assume that the torque is related to the drag force through the effective moment arm ref (Paddack 1969) as
(4)If the body has an amount of windmill asymmetry, the gas produces not only force Fgas, but also torque Mgas. We then assume that the torque is related to the drag force through the effective moment arm ref (Paddack 1969) as 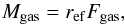 (5)or, with the help of a dimensionless asymmetry parameter ξ = ref/D (Paddack & Rhee 1975), as
(5)or, with the help of a dimensionless asymmetry parameter ξ = ref/D (Paddack & Rhee 1975), as 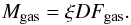 (6)The equation of motion for rotation is
(6)The equation of motion for rotation is  (7)where C is moment of inertia and ω is angular velocity. After substitution it has the form:
(7)where C is moment of inertia and ω is angular velocity. After substitution it has the form: 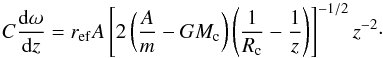 (8)Then, the relationship between spin frequency and velocity of the spherical meteoroid (i.e. C = mD2/ 10) can be derived as
(8)Then, the relationship between spin frequency and velocity of the spherical meteoroid (i.e. C = mD2/ 10) can be derived as 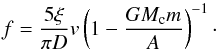 (9)We can see that the spin frequency of the meteoroid is directly proportional to the velocity and inversely proportional to the body size. There is no explicit dependence on meteoroid density, but it is included in the velocity v and also in the term in parentheses. The term in parentheses on the right-hand side corresponds to the ratio of gravitational and drag force. If the gravitational force weaker than the drag force, this term approaches zero. This is the case of small meteoroids1. The term grows with the increasing importance of the gravitational force (i.e., with increasing mass, size, or density of meteoroid). It is infinity when these two forces are equal. The explanation follows. The gravitational force does not affect the meteoroid rotation itself, but it reduces the meteoroid speed. The gas flow therefore has more time to accelerate the rotation.
(9)We can see that the spin frequency of the meteoroid is directly proportional to the velocity and inversely proportional to the body size. There is no explicit dependence on meteoroid density, but it is included in the velocity v and also in the term in parentheses. The term in parentheses on the right-hand side corresponds to the ratio of gravitational and drag force. If the gravitational force weaker than the drag force, this term approaches zero. This is the case of small meteoroids1. The term grows with the increasing importance of the gravitational force (i.e., with increasing mass, size, or density of meteoroid). It is infinity when these two forces are equal. The explanation follows. The gravitational force does not affect the meteoroid rotation itself, but it reduces the meteoroid speed. The gas flow therefore has more time to accelerate the rotation.
Equation (9) was derived with an assumption that the rotation is continuously accelerated. In real situations the steady acceleration (or deceleration!) begins after a phase of chaotic evolution of rotation (see Sect. 4.1). Due to this fact, it is more useful to write Eq. (9) without the term in parentheses. In this case ξ has the meaning of effective asymmetry parameter, which may slightly depend on size.
3. Numerical model
The analytical formula (9) for spin frequency was derived with crude simplifications and assumptions concerning the meteoroid shape, force and torque expression, and the motion. Moreover, the analytical model is neither able to predict the value of asymmetry parameter ξ nor to describe the distribution of spin frequencies, directions of the spin axes, degree of tumbling, etc.
In the following text, a more precise numerical model that is not limited by these simplifications is described. It uses meteoroid shapes approximated by polyhedrons that were obtained by 3D laser scanning of terrestrial rock samples. The force and torque of the gas flow is computed for each surface facet and then integrated over the whole meteoroid surface. The rotational motion is computed by numerical integration of Euler’s equations.
3.1. Meteoroid shapes
 |
Fig. 1 Example of the polyhedral models for meteoroid shapes. They were obtained by 3D laser scanning of 36 samples of various terrestrial rocks. Upper row: clay; middle row: trachybasalt fragments; lower row: gravel. The plots are not to scale. |
The shape of a body represents one of the most important quantities because it controls the ability of the object to be spun up. There is no torque on symmetrical bodies such as spheres, cubes, three-axial ellipsoids, or blocks. The meteoroid must have a certain amount of windmill asymmetry, which means the gas flow will be able to spin up the body.
What do the shapes of cometary meteoroids look like? This represents one of the main difficulties in this modeling. I decided to digitize the terrestrial samples differ in their origin, shape characteristics, and strength, and test how the results depend on the sample origin. For this purpose I chose three different sets of samples. Each set consists of 12 shapes that were selected randomly from larger groups of samples to avoid preferential selection of “nice” shapes by a collector.
The first set is composed of fragments from a volcanic rock (trachybasalt), which was broken apart by a hammer. These shapes are usually planar and sharp, and I call them “fragments”. The second set consists of pieces of gravel (a metamorphic rock). These samples are more rounded than fragments and are referred to as “gravel”. The third set contains pieces of broken block of dry clay. They have very bumpy surface, sometimes with holes and open cracks. They are called “clay”.
All shapes were digitized by 3D laser scanning method by SolidVision s.r.o. company. The precision of determining the shape is better than 0.5 mm, and the resulting shapes are represented by polyhedrons with several thousand triangular facets (Fig. 1). The volume of samples ranges from 0.51 to 17.29 cm3. The number of surface elements depends on the surface area and ranges from 3548 to 35 242 facets.
The polyhedral description allows a simple determination of volume, mass, tensor of inertia of the body, and the surface normal, area, and radius vector to the center of each surface facet. These quantities can be used for determining the forces and the torques acting on the meteoroid.
3.2. Gas ejection
The ejection of meteoroids during normal cometary activity is caused by the gas flow, which escapes from the cometary nucleus owing to sublimation of its material. The gas density ρgas and velocity vgas represent important quantities that determine the magnitude of the force. These quantities have been studied by many authors who deal with theoretical estimates of ejection velocity. It is obvious that different models give different results for ejection velocities (e.g., review of Ryabova 2013). Therefore, three distinct models were chosen for comparison.
The model J1995-100 is based on Jones (1995). Assuming spherical symmetric ejection, the gas density was determined from Eqs. (10)–(12) in Jones (1995). The gas velocity was computed from Eqs. (3), (4), (8), and those for gas density in Jones (1995). In this model, the adiabatic expansion of the gas is assumed, which causes the gas velocity to increase with distance z from the nucleus, and the gas density has a more complicated dependence than z-2.
The next two models are based on Ma et al. (2002). In this case the gas velocity vgas is constant and equal to velocity of water molecules at sublimation temperature, which is 580 m s-2. The gas density can be expressed from Eqs. (4) and (24) in Ma et al. (2002) as
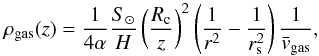 (10)where α is the fraction of the nucleus surface area that is active, S⊙ the solar constant, H sublimation heat, r heliocentric distance, and rs heliocentric distance at the beginning of cometary material sublimation. Model M2002-050 assumes ejection from the sunlit hemisphere (i.e., α = 0.5), and M2002-002 assumes that only 2% of the surface is active.
(10)where α is the fraction of the nucleus surface area that is active, S⊙ the solar constant, H sublimation heat, r heliocentric distance, and rs heliocentric distance at the beginning of cometary material sublimation. Model M2002-050 assumes ejection from the sunlit hemisphere (i.e., α = 0.5), and M2002-002 assumes that only 2% of the surface is active.
The three gas ejection models thus result in wide range of the strength of the gas’s action. Model J1995-100 corresponds to weak gas flow, since the ejection from whole cometary nucleus surface (including night side) is assumed. The other extreme is model M2002-002, which assumes that the whole mass is ejected in a very narrow jet, the result of which is a very strong gas flow. Model M2002-050 represents a conservative case.
3.3. Force, torque, and meteoroid motion
Gas molecules interact with the surface of the meteoroid and cause drag force and torque. The present model assumes free-molecular flow regime. It means that the size of meteoroids is smaller than the mean free path of molecules, and the interaction of gas flow with meteoroid can be described as impacts of solitary molecules. (This assumption is, however, not fully met for larger meteoroids, small heliocentric distances and proximity to the surface of the nucleus.) Two possible types meteoroid-gas interaction are assumed: (i) specular reflection that corresponds to the ideally elastic collisions; and (ii) diffuse reflection, which means temporary capture and emission of gas molecules in a random direction. In the case of the specular reflection, the force acting on ith small surface facet is 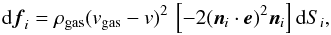 (11)where ni is the unit outer normal to the surface, e the unit vector in the direction of the gas flow, and dSi the area of the surface facet. This formula can be expressed simply for a polyhedral description of meteoroid shapes. For the diffuse reflection,
(11)where ni is the unit outer normal to the surface, e the unit vector in the direction of the gas flow, and dSi the area of the surface facet. This formula can be expressed simply for a polyhedral description of meteoroid shapes. For the diffuse reflection, 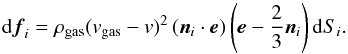 (12)The total force caused by gas is given by a sum over the whole surface:
(12)The total force caused by gas is given by a sum over the whole surface: 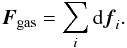 (13)The gravitational force also affects the meteoroid’s motion and it is given by Eq. (1). The centrifugal force is neglected in the model. The total torque reads
(13)The gravitational force also affects the meteoroid’s motion and it is given by Eq. (1). The centrifugal force is neglected in the model. The total torque reads 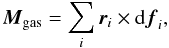 (14)where ri is radius vector to the center of the ith surface facet. The torque is only caused by gas flow, because gravitational torques are negligible for such small bodies.
(14)where ri is radius vector to the center of the ith surface facet. The torque is only caused by gas flow, because gravitational torques are negligible for such small bodies.
The translational and rotational motions were computed simultaneously, since the total force and torque depends on both the orientation and the distance from the nucleus (and also on the velocity). The motion of meteoroid can be described by radius vector r, velocity v, three Euler’s angles ϕ, ϑ, ψ, and three components of the angular velocity ω. For the numerical integrations of the Euler’s equations are, however, more suitable Euler’s parameters q0,q1,q2,q3, because they do not have singularities in the poles (e.g., Fukushima 2008)2. The system of equations of motion for translation and rotation was solved numerically by fourth-order Runge-Kutta method with variable timestep. The suitability of the numerical method was proved by conservation of energy and angular momentum tests.
3.4. Model parameters and computation details
The numerical model was applied to 2P/Encke comet, which belongs to the Taurid complex. The nucleus of this comet has a mean effective radius Rc = 3950 ± 60 m (Lowry & Weissman 2007) and mass Mc = 9.2 ± 5.8 × 1013 kg (Sosa & Fernández 2009). The perihelion distance is 0.33 AU, and the semimajor axis is 2.2178 AU. The meteoroid bulk densities are assumed to be the same as for Taurid meteoroids ρ = 1.6 g cm-3(Babadzhanov & Kokhirova 2009; Madiedo et al. 2014). Three sizes of meteoroids, corresponding to equivalent spheres of diameters 1 mm, 1 cm, and 10 cm were studied. The computational scheme was following:
-
Sizes of all meteoroid shapes were rescaled so that they have thesame volume as the sphere of assumed size(1 mm, 1 cm or10 cm).
-
Position on the orbit was randomly selected and appropriate amount of meteoroids was released. The amount was proportional to the mass loss rate (i.e. ∝ρgasvgas).
-
In the beginning of the integration, the shape and the initial orientation of each meteoroid was selected randomly. The integration started from the surface of the nucleus with zero velocity.
-
The equations of rotational and translational motion were integrated. If the meteoroid fell back to the surface, it was rejected. (This case was more frequent for large meteoroids at the larger heliocentric distances.) Otherwise, the integration stopped when it reached the distance of 25 × Rc.
-
The values of ejection velocity, spin frequency, direction of the moment of inertia, degree of tumbling, etc. were saved.
In total, ~800 000 integrations were done, which took ~700 CPU days.
4. Results
4.1. Rotation of individual meteoroids
The main aim of this study is to estimate the rotational properties of meteoroids far from the nucleus. It is, however, useful to briefly describe the evolution of rotation for individual meteoroids. The rotation during the ejection process can be divided into two stages:
I. Chaotic rotation.
After the release from the surface, the meteoroid usually rotates chaotically. It wobbles and tumbles, the spin axis orientation and direction of angular momentum changes in a random way, and the rotation speed is alternately accelerated and decelerated (Fig. 2).
II. Regular rotation.
After some time, the meteoroid rotation begins to evolve more regularly. The direction of angular momentum slowly drifts to a final stage, the spin axis moves about it, and the rotation speed is monotonically accelerated or decelerated (Fig. 2). With increasing distance from the nucleus, the gas density decreases as does the gas forces and torques acting on the body. Far from the nucleus, the meteoroid has a constant velocity, constant angular momentum vector and kinetic energy.
The transition between both stages is not sharp and it is difficult to estimate the time necessary for the transition from the Stage I to Stage II. The transition is usually reached at the distance from the nucleus, where the gas density is still sufficiently high. The steady evolution of rotation therefore begins not at surface but at this distance, whereas the velocity is accelerated from the surface. Moreover, the spin rate at the beginning of the Stage II is not zero, and it can be both accelerated and decelerated. This results in a deviation of frequency-velocity dependence from Eq. (9). Owing to higher inertia and the reduced velocity of larger meteoroids caused by a gravitational force, the stage of regular rotation begins at lower heights than for smaller meteoroids. Although the larger bodies rotate more slowly than the smaller ones, they finally have a higher ratio of the rotational to translational part of the kinetic energy.
The ejection from the surface to the distance of 25 × Rc lasted roughly from ten minutes for 1 mm bodies to three hours for 10 cm meteoroids in perihelion.
 |
Fig. 2 Example of evolution of rotation of 1 cm meteoroid. Upper plot: evolution of angular momentum direction with respect to the inertial frame. The numbers denote the distance from the surface in terms of nucleus radii Rc. Lower plot: evolution of the rotational part of the kinetic energy. Stage I of chaotic rotation and Stage II of regular rotation can be clearly distinguished in both plots. In this case the transition between them occurs at about 0.3 × Rc above the surface. |
4.2. Spin frequency
The spin frequencies of meteoroids far from the nucleus were computed for three gas ejection models, two types of gas-meteoroid interactions, and three sizes. Thus, 18 different distributions of spin frequencies were obtained. An example of the distribution of f for three meteoroid sizes can be seen in Fig. 3. In this case, the gas ejection model M2002-050 and diffuse reflection of gas molecules from the surface of meteoroids were considered. The meteoroid shapes of all three shape sets were used. The distribution is approximately normal on log scale and its width can be expressed by boundary values of 2σ intervals. Approximately 95% of values lie inside of this interval. For 1 mm meteoroids, the median value of spin frequency is 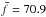 Hz with a 2σ interval (6.7–963) Hz. In case of 1 cm bodies, the median value
Hz with a 2σ interval (6.7–963) Hz. In case of 1 cm bodies, the median value 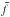 is 2.9 Hz with a 2σ interval (0.3−31.8) Hz, and the largest, 10 cm, bodies have median
is 2.9 Hz with a 2σ interval (0.3−31.8) Hz, and the largest, 10 cm, bodies have median 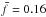 Hz and 2σ interval (0.02−1.2) Hz. It can be seen that the spin frequencies of meteoroids with particular size lie inside relatively wide interval ranging across about one order of magnitude. The median frequency decreases with increasing size as D-1.31 in this size range. Median frequencies determined separately for each shape set are almost the same. The difference between the highest and lowest values is less than 30%. It is negligible with respect to the width of 2σ intervals.
Hz and 2σ interval (0.02−1.2) Hz. It can be seen that the spin frequencies of meteoroids with particular size lie inside relatively wide interval ranging across about one order of magnitude. The median frequency decreases with increasing size as D-1.31 in this size range. Median frequencies determined separately for each shape set are almost the same. The difference between the highest and lowest values is less than 30%. It is negligible with respect to the width of 2σ intervals.
The resulting medians of spin frequencies, 2σ intervals, median ejection velocities, and other quantities for various gas ejection models and meteoroid sizes can be seen in Table 1. The median spin frequency depends on (i) meteoroid size; (ii) type of gas-meteoroid interaction; and (iii) also the gas ejection model. The dependence (iii) is caused by different ejection velocities corresponding to these models. The dependence of 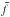 on the gas ejection model can be removed if asymmetry parameter ξ and median ejection velocity vej are taken into account. The rotation of meteoroid evolves in a more complicated way than assumed in Sect. 2, as was described in previous section. After a stage of chaotic acceleration and deceleration of rotation and chaotic movement of the angular momentum direction, the meteoroid reaches quasi-stable rotation, which evolves uniformly. This means that it is useful to determine the asymmetry parameter ξ as
on the gas ejection model can be removed if asymmetry parameter ξ and median ejection velocity vej are taken into account. The rotation of meteoroid evolves in a more complicated way than assumed in Sect. 2, as was described in previous section. After a stage of chaotic acceleration and deceleration of rotation and chaotic movement of the angular momentum direction, the meteoroid reaches quasi-stable rotation, which evolves uniformly. This means that it is useful to determine the asymmetry parameter ξ as
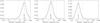 |
Fig. 3 Distribution of spin frequencies after ejection from 2P/Encke comet for 1 mm (left), 1 cm (middle), and 10 cm (right) meteoroids. Gas ejection is according to Ma et al. (2002), active fraction of the surface is 50%. The solid vertical line represents median value and dotted vertical lines bound 2σ interval. Small arrows with letters g, c, f denote median values for gravel, clay, and fragments shapes. |
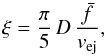 (15)where vej is the median of ejection velocity. The resulting values of ξ can be seen in Table 1 and also in Fig. 4. The asymmetry parameter ξ is almost independent of the gas ejection model. It still depends on the type of gas-meteoroid interaction and the size. Gas molecules specularly reflected from the meteoroid’s surface are able to spin up the meteoroid more quickly than molecules that are reflected diffusively. The ratio is about 2.5 ×. The dependency on size is caused by a more complicated evolution of rotation during meteoroid ejection. It is related to the height of transition between Stage I and Stage II which depends on meteoroid size (Sect. 4.1). The asymmetry parameter can be approximated as
(15)where vej is the median of ejection velocity. The resulting values of ξ can be seen in Table 1 and also in Fig. 4. The asymmetry parameter ξ is almost independent of the gas ejection model. It still depends on the type of gas-meteoroid interaction and the size. Gas molecules specularly reflected from the meteoroid’s surface are able to spin up the meteoroid more quickly than molecules that are reflected diffusively. The ratio is about 2.5 ×. The dependency on size is caused by a more complicated evolution of rotation during meteoroid ejection. It is related to the height of transition between Stage I and Stage II which depends on meteoroid size (Sect. 4.1). The asymmetry parameter can be approximated as
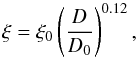 (16)where D0 = 0.001 m, and ξ0 = 4.5 × 10-4 for diffuse reflection and ξ0 = 11 × 10-4 for the specular reflection of gas molecules from the meteoroid’s surface (Fig. 4). Obviously, a better approximation can be found, e.g., rational function ξ = 1.55 (log D − 6.73)/(log D − 0.39) for the diffuse reflection and ξ = 8.28 (log D − 1.56)/(log D − 0.11) for specular reflection of gas molecules from meteoroid (dashed line in Fig. 4). The differences between numerically determined medians ξ and those from Eq. (16) are, however, lower than ~13%, which is substantially smaller than the typical width of the distribution, so this relationship is precise enough. The resulting relation for the median spin frequency can be determined from Eqs. (15) and (16):
(16)where D0 = 0.001 m, and ξ0 = 4.5 × 10-4 for diffuse reflection and ξ0 = 11 × 10-4 for the specular reflection of gas molecules from the meteoroid’s surface (Fig. 4). Obviously, a better approximation can be found, e.g., rational function ξ = 1.55 (log D − 6.73)/(log D − 0.39) for the diffuse reflection and ξ = 8.28 (log D − 1.56)/(log D − 0.11) for specular reflection of gas molecules from meteoroid (dashed line in Fig. 4). The differences between numerically determined medians ξ and those from Eq. (16) are, however, lower than ~13%, which is substantially smaller than the typical width of the distribution, so this relationship is precise enough. The resulting relation for the median spin frequency can be determined from Eqs. (15) and (16):
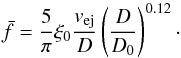 (17)This equation enables us to estimate the median of spin frequency of meteoroids ejected from comet 2P/Encke according to the size and ejection velocity. The meteoroid density is not explicitly present, but it determines the ejection velocity. The ejection velocity may be determined with a more appropriate gas ejection model, active nucleus surface ratio, or bulk density of meteoroids, or it may be determined from observations.
(17)This equation enables us to estimate the median of spin frequency of meteoroids ejected from comet 2P/Encke according to the size and ejection velocity. The meteoroid density is not explicitly present, but it determines the ejection velocity. The ejection velocity may be determined with a more appropriate gas ejection model, active nucleus surface ratio, or bulk density of meteoroids, or it may be determined from observations.
4.2.1. Width of the distribution
As can be seen in Fig. 3, the spin frequency distribution is relatively wide. The width is a result of (i) the different abilities of meteoroid shapes to be spun up; (ii) random initial orientation of meteoroid shapes; and (iii) different heliocentric distances of the ejection. The lower and upper boundaries of 2σ intervals were determined for all distributions. The lower boundary varies between 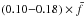 and the upper boundary between
and the upper boundary between 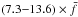 . These limits may be roughly estimated as
. These limits may be roughly estimated as 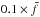 and
and 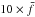 .
.
Resulting rotational characteristics of meteoroids ejected from the 2P/Encke comet for meteoroid sizes D 1 mm, 1 cm, and 10 cm, three ejection models (see Sect. 3.2), and two types of gas-meteoroid interactions (D means diffuse and S specular reflection of gas molecules from the meteoroid’s surface).
4.2.2. Rotational bursting
The rotation of smaller meteoroids can be accelerated up to several hundred or even several thousand of Hertz. Is it possible that these bodies can be destroyed by centrifugal forces? The tensile stress due to centrifugal force inside a rotating meteoroid can be estimated from a formula for the stress in the center of rotating sphere (e.g., Kadish et al. 2005):
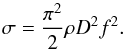 (18)After substitution from Table 1, the stress increases with decreasing meteoroid size. Assuming gas ejection model M2002-050 and specular reflection of gas molecules, the stress for the median spin frequency is ~200 kPa for 1 mm meteoroids, ~35 Pa for 1 cm meteoroids, and ~8 Pa for 10 cm meteoroids. The wide distribution of the spin frequencies means some meteoroids can reach much higher stresses. For example, if the spin frequency of 1 mm meteoroids is f ≃ 2000 Hz, the tensile stress due to centrifugal force is ~32 kPa, which is comparable to the apparent strength of Taurid meteoroids (Trigo-Rodríguez & Llorca 2006). The rotational bursting during ejection process can therefore be expected only for a small part of the fast, small meteoroids.
(18)After substitution from Table 1, the stress increases with decreasing meteoroid size. Assuming gas ejection model M2002-050 and specular reflection of gas molecules, the stress for the median spin frequency is ~200 kPa for 1 mm meteoroids, ~35 Pa for 1 cm meteoroids, and ~8 Pa for 10 cm meteoroids. The wide distribution of the spin frequencies means some meteoroids can reach much higher stresses. For example, if the spin frequency of 1 mm meteoroids is f ≃ 2000 Hz, the tensile stress due to centrifugal force is ~32 kPa, which is comparable to the apparent strength of Taurid meteoroids (Trigo-Rodríguez & Llorca 2006). The rotational bursting during ejection process can therefore be expected only for a small part of the fast, small meteoroids.
4.2.3. Differences between shape sets
 |
Fig. 4 Dependency of asymmetry parameter ξ on meteoroid size for three gas ejection models (see Sect. 3.2) and two types of gas-meteoroid interaction. The diamonds correspond to numerical results for diffuse reflection and the triangles the specular reflection of gas molecules from the meteoroid’s surface. The solid and dashed lines represent interpolation of the size dependency (see the text). |
The shape of a body is a very important characteristic, because it determines the final spin state. Since there is no possibility for obtaining the shapes of real cometary meteoroids, 36 shapes derived from terrestrial rock samples were used throughout the numerical modeling. But how good is the approximation of real shapes by them? The shapes belong to three sets according to their origin (clay, fragment, gravel − see Sect. 3.1). The bodies of these sets differ in surface character (bumpy or smooth) and in overall shape (rounded or sharp). A simple test is how the results change for each shape set. It is expressed by a column denoted as Δfcfg in Table 1, which means 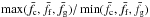 , where
, where 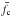 ,
, 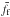 ,
, 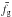 are medians of spin frequencies for clay, fragments and gravel shapes. It can be seen that the results differ by less than 30% for the diffusive reflection of gas molecules and by less than 11% for specular reflection of gas molecules from the meteoroid surface. This is a very good match. It indicates that the difference between results obtained by using shapes based on terrestrial rock samples and the results for potential real meteoroid shapes can be expected to be the same – say, within a factor of 2.
are medians of spin frequencies for clay, fragments and gravel shapes. It can be seen that the results differ by less than 30% for the diffusive reflection of gas molecules and by less than 11% for specular reflection of gas molecules from the meteoroid surface. This is a very good match. It indicates that the difference between results obtained by using shapes based on terrestrial rock samples and the results for potential real meteoroid shapes can be expected to be the same – say, within a factor of 2.
4.3. Degree of tumbling
Another important piece of information concerning the rotation of cometary meteoroids is whether they are principal axis rotators or non-principal axis rotators. Far from the cometary nucleus, where the torque due to escaping gas flow is negligible, the vector of angular momentum is constant. The spin axis of non-principal axis rotators rotates about the angular momentum vector along an unclosed trajectory. The mean angle between angular momentum vector and spin axis can be used as a degree of tumbling. (Another possibility is to use an angle between angular momentum vector and the shortest axis of inertia tensor, as in Pravec et al. 2014.) If it is zero, the body rotates about the principal axis of the inertia tensor. The non-principal axis rotation can take place in small-axis or long-axis mode. In the first case, the spin axis moves about the body axis which corresponds to the largest moment of inertia, I3. In the second case, the spin axis moves about the body axis which corresponds to the smallest moment of inertia, I1 (e.g., Pravec et al. 2005). The distribution of mean angle between angular momentum vector and spin axis can be seen in Fig. 5. This distribution does not depend on the meteoroid ejection model. The median is ~12°. Interestingly, in ~60% of the cases, the rotation is in long-axis mode. This is partially a result of the meteoroid shape models, which are more elongated than flattened.
 |
Fig. 5 Distribution of mean angle between angular momentum vector and spin axis. The solid vertical line represents median, which is 12.3°. |
4.4. Angular momentum direction
The last quantity that was investigated is direction of the angular momentum vector. It was found that its distribution is not random. The angular momentum vectors are concentrated toward the perpendicular direction with respect to the gas flow direction (see Fig. 6). If it is real, it may help explain some features of polarimetric observations of comets (e.g., review of Kolokolova et al. 2004).
 |
Fig. 6 Distribution of deviation of the angular momentum vector from the direction of the gas flow direction. The solid vertical line represents the median, which is 90.5°. The dotted curve corresponds to a random distribution of angular momentum vector directions. |
4.5. General validity of the results
The relationship for median spin frequency (17) should be valid in general and it should be applicable also to bodies with different parameters from those in Sect. 3.4. To check this assumption, the median spin rates were numerically determined for another radius and mass3 of 2P/Encke comet, Rc = 2400 m (Fernández et al. 2000), Mc = 5.8 × 1013 kg, Taurid meteoroid density 2.5 g cm-3 and compared with (17). Assuming gas ejection model M2002-050 and diffusive reflection, the numerical model leads to median spin frequency and ejection velocity of 46.54 Hz and 61.24 m s-1 for 1 mm meteoroids, 2.11 Hz and 22.36 m s-1 for 1 cm meteoroids, and 0.12 Hz and 7.39 m s-1 for 10 cm meteoroids. These values differ by 15% from the results determined by Eq. (17).
Similar computations were also performed for Perseid meteoroids. A gas ejection model M2002-050, mass 1.2 × 1013 kg, and radius 1800 m of parent comet 55P/Tempel-Tuttle (Jewitt 2004) and density 0.4 g cm-3 of meteoroids were assumed. The resulting median frequencies from numerical modeling differ from those determined by Eq. (17) by less than 15%. The results of the numerical modeling of Taurid meteoroids rotation can thus be cautiously applied to other meteoroid streams, which are the result of normal cometary activity. Some deviations from the results may occur when gravitation of cometary nucleus plays more important role than in the studied case. The rotation of meteoroids of various meteoroid streams will be studied in detail in a later paper.
5. Discussion
The present model is not able to determine the specific value of meteoroid spin frequency after ejection from the 2P/Encke comet owing to the lack of reliable ejection velocity data. The dependence of median spin frequency on ejection velocity and meteoroid size (17) is, however, common for all three gas ejection models, despite very different ejection velocities. The reliable estimate of the spin frequency therefore depends on a reliable value of ejection velocity. Equation (17) can be rewritten into more simple form as
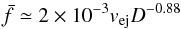 (19)for diffuse reflection of gas molecules from meteoroid’s surface, and
(19)for diffuse reflection of gas molecules from meteoroid’s surface, and 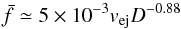 (20)for specular reflection of gas molecules from meteoroid’s surface (
(20)for specular reflection of gas molecules from meteoroid’s surface (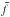 in Hz, vej in m s-1, and D in m). But the direct use of Eq. (17) for estimates of the preatmospheric spin rate of meteoroids is doubtful. During the time, that a meteoroid spent in the interplanetary space, the rotation is affected by several phenomena. In the studied size range, the most important are radiative effects (Olsson-Steel 1987), i.e. windmill effect and YORP. The timescale of YORP evolution can be estimated by rescaling of mean doubling time td = 14 Myr, which was determined by Čapek & Vokrouhlický (2004) for 2 km Gaussian random spheres with spin period of six hours on circular orbit with semimajor axis 2.5 AU, assuming principal axis rotation in asymptotic states. Corresponding values are about four years for 1 mm (50 Hz) and 70 years for 10 cm (0.1 Hz) Taurid meteoroids. The actual timescales will, however, be longer owing to (i) heat diffusion through the volume of such small bodies (Breiter et al. 2010), (ii) evolution of the spin axis direction by YORP effect and (iii) non-principal axis rotation of the most of meteoroids. In any case, the preatmospheric rotation may correspond to the initial rotational state only for the short time spent in the interplanetary space, but this subject is beyond the scope of this article and will be studied in the future.
in Hz, vej in m s-1, and D in m). But the direct use of Eq. (17) for estimates of the preatmospheric spin rate of meteoroids is doubtful. During the time, that a meteoroid spent in the interplanetary space, the rotation is affected by several phenomena. In the studied size range, the most important are radiative effects (Olsson-Steel 1987), i.e. windmill effect and YORP. The timescale of YORP evolution can be estimated by rescaling of mean doubling time td = 14 Myr, which was determined by Čapek & Vokrouhlický (2004) for 2 km Gaussian random spheres with spin period of six hours on circular orbit with semimajor axis 2.5 AU, assuming principal axis rotation in asymptotic states. Corresponding values are about four years for 1 mm (50 Hz) and 70 years for 10 cm (0.1 Hz) Taurid meteoroids. The actual timescales will, however, be longer owing to (i) heat diffusion through the volume of such small bodies (Breiter et al. 2010), (ii) evolution of the spin axis direction by YORP effect and (iii) non-principal axis rotation of the most of meteoroids. In any case, the preatmospheric rotation may correspond to the initial rotational state only for the short time spent in the interplanetary space, but this subject is beyond the scope of this article and will be studied in the future.
6. Summary
Simple relationships (19) and (20) were derived for medians of spin frequencies 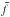 of meteoroids after ejection from a comet as a function of meteoroid size D and ejection velocity vej. These formulae were determined for 2P/Encke, but they are generally valid, and with caution they can be used for other comets. The dependence of the median of spin frequencies on meteoroid density and on the physical properties of cometary nucleus is hidden in the value of vej.
of meteoroids after ejection from a comet as a function of meteoroid size D and ejection velocity vej. These formulae were determined for 2P/Encke, but they are generally valid, and with caution they can be used for other comets. The dependence of the median of spin frequencies on meteoroid density and on the physical properties of cometary nucleus is hidden in the value of vej.
The distribution of spin frequencies is roughly normal on the log scale. It is relatively wide with more than 95% of values inside the interval 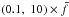 . Most of meteoroids are non-principal axis rotators. The median of mean angle between angular momentum vector and spin axes is ~12°. Angular momentum vectors are not distributed randomly in space, but are concentrated it the perpendicular directions with respect to the gas flow.
. Most of meteoroids are non-principal axis rotators. The median of mean angle between angular momentum vector and spin axes is ~12°. Angular momentum vectors are not distributed randomly in space, but are concentrated it the perpendicular directions with respect to the gas flow.
Meteoroid shapes were approximated by shape models derived from three distinct sets of different terrestrial rock samples. The results for these sets differ by less than 30% despite the different origin and shape characteristics of these sets. Therefore, the results are probably applicable to unknown shapes of real cometary meteoroids.
I point out the typographical error in Eq. A.31 of Fukushima (2008), where a factor of 2 is missing in the expression of the θ angle.
Acknowledgments
I thank Petr Pravec and Pavel Spurný for helpful discussions and suggestions. I am also grateful to Jan Starý for linguistic corrections. The 3D laser scanning was performed with the financial support of the Praemium Academicae of Academy of Sciences of the Czech Republic.
References
- Babadzhanov, P. B., & Kokhirova, G. I. 2009, A&A, 495, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babadzhanov, P. B., & Konovalova, N. A. 2004, A&A, 428, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beech, M. 1988, Earth Moon Planets, 42, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Beech, M. 2001, MNRAS, 326, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Beech, M., & Brown, P. 2000, Planet. Space Sci., 48, 925 [NASA ADS] [CrossRef] [Google Scholar]
- Beech, M., Illingworth, A., & Murray, I. S. 2003, Meteoritics, 38, 1045 [Google Scholar]
- Borovička, J. 2006, in Asteroids, Comets, Meteors, eds. L. Daniela, M. Sylvio Ferraz, & F. J. Angel, IAU Symp., 229, 249 [Google Scholar]
- Breiter, S., Vokrouhlický, D., & Nesvorný, D. 2010, MNRAS, 401, 1933 [NASA ADS] [CrossRef] [Google Scholar]
- Čapek, D., & Vokrouhlický, D. 2004, Icarus, 172, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Ceplecha, Z. 1996, A&A, 311, 329 [NASA ADS] [Google Scholar]
- Ceplecha, Z., & Revelle, D. O. 2005, Meteoritics, 40, 35 [Google Scholar]
- Crifo, J. F. 1995, ApJ, 445, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Crifo, J. F., & Rodionov, A. V. 1997, Icarus, 127, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, Y. R., Lisse, C. M., Ulrich Käufl, H., et al. 2000, Icarus, 147, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Fujiwara, A., Cerroni, P., Davis, D., Ryan, E., & di Martino, M. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews, 240 [Google Scholar]
- Fukushima, T. 2008, AJ, 135, 2298 [NASA ADS] [CrossRef] [Google Scholar]
- Fulle, M. 1997, A&A, 325, 1237 [NASA ADS] [Google Scholar]
- Giblin, I., & Farinella, P. 1997, Icarus, 127, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Giblin, I., Martelli, G., Farinella, P., et al. 1998, Icarus, 134, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Hawkes, R. L., & Jones, J. 1978, MNRAS, 185, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C. 2004, From cradle to grave: the rise and demise of the comets, eds. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson: University of Arizona Press), 659 [Google Scholar]
- Jones, J. 1995, MNRAS, 275, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Kadish, J., Barber, J., & Washabaugh, P. 2005, Int. J. Solids Struct., 42, 5322 [CrossRef] [Google Scholar]
- Kolokolova, L., Hanner, M. S., Levasseur-Regourd, A.-C., & Gustafson, B. Å. S. 2004, Physical properties of cometary dust from light scattering and thermal emission, eds. G. W. Kronk (Tucson: University of Arizona Press), 577 [Google Scholar]
- Lowry, S. C., & Weissman, P. R. 2007, Icarus, 188, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, Y., Williams, I. P., & Chen, W. 2002, MNRAS, 337, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Madiedo, J. M., Ortiz, J. L., Trigo-Rodríguez, J. M., et al. 2014, Icarus, 231, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Martelli, G., Ryan, E. V., Nakamura, A. M., & Giblin, I. 1994, Planet. Space Sci., 42, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Molina, A., Moreno, F., & Jiménez-Fernández, F. J. 2008, Earth Moon Planets, 102, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Olsson-Steel, D. 1987, MNRAS, 226, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Paddack, S. J. 1969, J. Geophys. Res., 74, 4379 [NASA ADS] [CrossRef] [Google Scholar]
- Paddack, S. J., & Rhee, J. W. 1975, Geophys. Res. Lett., 2, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Harris, A., Scheirich, P., et al. 2005, Icarus, 173, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Pravec, P., Scheirich, P., Ďurech, J., et al. 2014, Icarus, 233, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Ryabova, G. O. 2013, Sol. Syst. Res., 47, 219 [Google Scholar]
- Sosa, A., & Fernández, J. A. 2009, MNRAS, 393, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Spurný, P., & Borovička, J. 2001, in Meteoroids 2001 Conf., eds. B. Warmbein, ESA SP, 495, 519 [NASA ADS] [Google Scholar]
- Spurný, P., & Ceplecha, Z. 2008, A&A, 489, 449 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spurný, P., Borovička, J., & Shrbený, L. 2007, in IAU Symp., 236, eds. G. B. Valsecchi, D. Vokrouhlický, & A. Milani, 121 [Google Scholar]
- Spurný, P., Bland, P. A., Shrbený, L., et al. 2012, Meteoritics, 47, 163 [CrossRef] [Google Scholar]
- Stokan, E., & Campbell-Brown, M. 2014, Icarus, 232, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Trigo-Rodríguez, J. M., & Llorca, J. 2006, MNRAS, 372, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. L. 1950, ApJ, 111, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. L. 1951, ApJ, 113, 464 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Resulting rotational characteristics of meteoroids ejected from the 2P/Encke comet for meteoroid sizes D 1 mm, 1 cm, and 10 cm, three ejection models (see Sect. 3.2), and two types of gas-meteoroid interactions (D means diffuse and S specular reflection of gas molecules from the meteoroid’s surface).
All Figures
 |
Fig. 1 Example of the polyhedral models for meteoroid shapes. They were obtained by 3D laser scanning of 36 samples of various terrestrial rocks. Upper row: clay; middle row: trachybasalt fragments; lower row: gravel. The plots are not to scale. |
| In the text | |
 |
Fig. 2 Example of evolution of rotation of 1 cm meteoroid. Upper plot: evolution of angular momentum direction with respect to the inertial frame. The numbers denote the distance from the surface in terms of nucleus radii Rc. Lower plot: evolution of the rotational part of the kinetic energy. Stage I of chaotic rotation and Stage II of regular rotation can be clearly distinguished in both plots. In this case the transition between them occurs at about 0.3 × Rc above the surface. |
| In the text | |
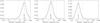 |
Fig. 3 Distribution of spin frequencies after ejection from 2P/Encke comet for 1 mm (left), 1 cm (middle), and 10 cm (right) meteoroids. Gas ejection is according to Ma et al. (2002), active fraction of the surface is 50%. The solid vertical line represents median value and dotted vertical lines bound 2σ interval. Small arrows with letters g, c, f denote median values for gravel, clay, and fragments shapes. |
| In the text | |
 |
Fig. 4 Dependency of asymmetry parameter ξ on meteoroid size for three gas ejection models (see Sect. 3.2) and two types of gas-meteoroid interaction. The diamonds correspond to numerical results for diffuse reflection and the triangles the specular reflection of gas molecules from the meteoroid’s surface. The solid and dashed lines represent interpolation of the size dependency (see the text). |
| In the text | |
 |
Fig. 5 Distribution of mean angle between angular momentum vector and spin axis. The solid vertical line represents median, which is 12.3°. |
| In the text | |
 |
Fig. 6 Distribution of deviation of the angular momentum vector from the direction of the gas flow direction. The solid vertical line represents the median, which is 90.5°. The dotted curve corresponds to a random distribution of angular momentum vector directions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


