| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201423934 | |
| Published online | 29 July 2014 | |
Spectral and temporal properties of RX J0520.5-6932 (LXP 8.04) during a type-I outburst⋆
1
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstraße,
85748
Garching,
Germany
e-mail:
gevas@mpe.mpg.de
2
Warsaw University Observatory, Al. Ujazdowskie 4, 00-478
Warszawa,
Poland
Received: 2 April 2014
Accepted: 26 May 2014
Aims. We observed RX J0520.5-6932 in the X-rays and studied the optical light curve of its counterpart to verify it as a Be/X-ray binary.
Methods. We performed an XMM-Newton anticipated target-of-opportunity observation in January 2013 during an X-ray outburst of the source in order to search for pulsations and derive its spectral properties. We monitored the source with Swift to follow the evolution of the outburst and to look for further outbursts to verify the regular pattern seen in the optical light curve with a period of ~24.4 d.
Results. The XMM-Newton EPIC light curves show coherent X-ray pulsations with a period of 8.035331(15) s (1σ). The X-ray spectrum can be modelled by an absorbed power law with photon index of ~0.8, an additional black-body component with temperature of ~0.25 keV, and an Fe K line. Phase-resolved X-ray spectroscopy reveals that the spectrum varies with pulse phase. We confirm the identification of the optical counterpart within the error circle of XMM-Newton at an angular distance of ~0.8′′, which is an O9Ve star with known Hα emission. By analysing the combined data from three OGLE phases we derived an optical period of 24.43 d.
Conclusions. The X-ray pulsations and long-term variability, as well as the properties of the optical counterpart, confirm that RX J0520.5-6932 is a Be/X-ray binary pulsar in the Large Magellanic Cloud. Based on the X-ray monitoring of the source, we conclude that the event in January 2013 was a moderately bright type-I X-ray outburst, with a peak luminosity of 1.79 × 1036 erg s-1.
Key words: Magellanic Clouds / X-rays: binaries / stars: emission-line, Be / stars: neutron / pulsars: individual: RX J0520.5-6932
© ESO, 2014
1. Introduction
Be/X-ray binaries (BeXRBs) are a major subclass of high-mass X-ray binaries (HMXBs, for a review see Reig 2011). These binaries consist of a compact object, typically a neutron star (NS), that accretes matter from a Be star. Be stars are rapidly rotating main-sequence, sub-giant, or giant stars typically having spectral classes between O5 and B9 (Coe et al. 2005). These early-type stars are surrounded by a circumstellar (decretion) disk formed by viscous diffusion of matter ejected from the star. The disk can be truncated by the tidal/resonant interaction with the NS (e.g., Okazaki & Negueruela 2001). BeXRBs often have wide and eccentric orbits (Townsend et al. 2011), although a population of low-eccentricity systems also exists and might indicate a distinct formation channel (Pfahl et al. 2002).
Generally in BeXRB systems, mass accretion strongly varies with orbital phase. Because of its eccentric orbit, a probable result of the supernova kick during the NS formation, or/and the possible misalignment between the inclination of the NS orbit and the orientation of the decretion disk, the NS can capture gas from the Be disk only for a short span of time during the close encounter with the Be disk. This brief interaction makes BeXRBs transient X-ray systems, mainly showing periodic (type I) outbursts (Lx ~ 1036−37 erg s-1) correlated with their orbital period. There are, however, known persistent systems as well (Lx ≲ 1034 erg s-1). These are believed to be low-eccentricity systems where the mass accretion is relatively constant. Sporadically, all BeXRBs might exhibit giant (type II) outbursts (Lx ≥ 1037 erg s-1) that could be associated with warping episodes of the Be disk (Okazaki et al. 2013). For some cases a temporary accretion disk can be formed around the NS, as indicated by the strong spin-up seen during bright outbursts.
BeXRBs may also show modulation of their X-ray flux with periods in the range of ~1−1000 s. These X-ray pulsations are due to the misalignment of the NSs rotation axis and its magnetic axis, and they provide one of the strongest pieces of evidence that the compact object is an NS. The strong magnetic field of the NS funnels mass accretion onto the magnetic poles and leads to the formation of an accretion column. Within these columns, shocks heat the gas, which then emits X-rays (for a detailed review of the emission mechanisms see Hickox et al. 2004; Frank et al. 2002). The pulse profiles can be single-peaked, double-peaked, or even more complex depending on the accretion geometry and viewing angle (Annala & Poutanen 2010).
Temporal variation in brightness can also be observed from the optical counterpart of BeXRBs. It is the equatorial disk of circumstellar material around the Be star that determines its observational properties (emission lines, infrared excess, variability). The long-term optical variability of the system can be attributed to the orbital period, disruption of the disk while the NS passes through the periastron, or other disk instabilities, such as truncation or precession of the disk. In addition, some Be stars show intrinsic, short-period variations of low amplitude that are probably associated with non-radial pulsations (NRP) of the primary star, with periods between 0.2 and 1.7 days (Schmidtke et al. 2008). Schmidtke et al. (2013) studied the optical light curves of BeXRBs in the Small Magellanic Cloud (SMC). They show that 44% of the systems exhibit signatures consistent with orbital periods, while 58% of them exhibit NRP.
The study of BeXRBs in nearby galaxies can provide more complete and homogeneous samples of BeXRB populations with the advantage of low foreground absorption and well known distances compared to sources in our Galaxy. The Magellanic Clouds (MCs) offer a unique possibility to study the population of high-energy sources of a complete galaxy. With a moderate and well known distance of 50 kpc for the Large Magellanic Cloud (LMC) and 60 kpc for the SMC, faint sources down to a few 1033 erg s-1 can be observed with XMM-Newton in relatively short exposures. Owing to recent episodes of star formation, ~40 Myr ago for the SMC and ~(15−50) Myr for the LMC (Antoniou et al. 2010, 2011), the MCs harbour a large population of HMXBs. Approximately 60 confirmed pulsars have been found in the SMC so far (Haberl & Pietsch 2004; Coe et al. 2005, 2010), and 45 candidates have been identified during the recent XMM-Newton survey of the SMC (Sturm et al. 2013; Haberl et al. 2012). On the other hand the LMC, which is 10 times more massive than the SMC, has only about 20 confirmed HMXB (see Liu et al. 2005; Maggi et al. 2013; Vasilopoulos et al. 2013a, and references within), of which 14 are HMXB pulsars. Still, since the X-ray coverage of the LMC is not nearly as complete as that of the SMC, early interpretations of the connection between star-formation rate and its BeXRB population would be dubious. Additionally, their transient behaviour complicates the investigation of BeXRBs, so new systems are often discovered by chance. For constructing a more complete sample of their population, it is crucial to continuously monitor candidate systems or regions with an increased probability to find these systems (e.g. where recent star formation occurred) and perform deeper observations during outbursts (e.g. Vasilopoulos et al. 2013a; Maggi et al. 2013; Sturm et al. 2012).
In this work we report on a newly confirmed BeXRB in the LMC, RX J0520.5-6932 (Vasilopoulos et al. 2013b). The source was discovered in X-rays by Schmidtke et al. (1994) with the ROSAT HRI. Subsequent ROSAT PSPC observations showed the source to be variable (Haberl & Pietsch 1999). Schmidtke et al. (1994) proposed an O8e star found within the ROSAT 90% error circle as the optical counterpart. Coe et al. (2001) performed optical spectroscopy of the star and determined a spectral type of O9Ve (with one spectral subtype uncertainty). In the same paper, an analysis of the Optical Gravitational Lensing Experiment (OGLE) data revealed a 24.45 d optical periodic modulation of about 0.03 mag. Edge et al. (2004) confirms this proposed optical period, based on the analysis of archival data from the Massive Compact Halo Objects (MACHO) project, while also reporting on the presence of an outburst lasting 200 d (~0.1 mag) around March 1995. From the same work, spectroscopic observations of the optical counterpart revealed a variable Hα emission line, with an equivalent width of 5.2±0.2 Å in 2001 November and 2.0±0.6 Å in 2002 December.
The source was later detected by XMM-Newton (2XMM J052029.7-693155) in an observation performed on 2004 January 17 (obsid: 0204770101), and in a recent observation performed on 2012 December 5 (obsid: 0690750901), as part of the XMM-Newton survey of the LMC (PI: F. Haberl). From the above it is clear that while many of the optical properties of the system have been reported, its X-ray behaviour is still poorly studied, and RX J0520.5-6932 was mainly described as a weak X-ray source, until 2013 January when the source was detected by Swift during the Swift UV survey of the LMC (PI: S. Immler), while undergoing a moderately bright X-ray outburst (Vasilopoulos et al. 2013b).
Following the first Swift detection, we further monitored the source and triggered an anticipated XMM-Newton target-of-opportunity (ToO) observation (obsid: 0701990101, PI: R. Sturm) during the observed X-ray maximum flux. In the following paragraphs, we discuss the results of the spectral and timing analysis of the XMM-Newton ToO observation, which resulted in the detection of coherent pulsations and a refined X-ray position. In Sect. 2, we describe the X-ray data reduction and present the results of the spectral and temporal X-ray analysis. From the Swift monitoring we had indications that the system experienced several minor X-ray outbursts (possibly type I) that seem to repeat with the optical period of the system. In Sect. 3, we present the updated optical light curve of the counterpart of RX J0520.5-6932. A timing analysis using the combined optical light curve from phases II, III, and IV of the OGLE survey resulted in a refined optical period. In Sect. 4, we discuss the results of the X-ray spectroscopy and summarise the main points that resulted from our analysis.
2. X-ray observations and data reduction
2.1. X-ray observations
A Swift observation performed on 2013 January 13 as part of the LMC UV survey detected the HMXB candidate RX J0520.5-6932 in a moderately bright X-ray outburst at a flux of 1.6±1.5 × 10-12 erg cm-2 s-1 (0.3−10 keV). This is significantly brighter than the XMM-Newton detection on 2012 December 5, which was at a flux level of 9.5±1.5 × 10-14 erg cm-2 s-1 (EPIC-pn: 0.3−10 keV). Following the Swift detection, we started to monitor RX J0520.5-6932 with Swift to study the ongoing event that revealed a high X-ray variability of the source. After the proceeding rise in the source luminosity, we triggered an XMM-Newton ToO observation that was performed on 2013 January 22. We continued the Swift monitoring after the decline of the outburst, to study its long-term X-ray variability and to search for a possible correlation between the X-ray and optical light curve. In total we acquired 22 Swift/XRT pointings with a typical exposure of 2000 s (flux limit at ~5 × 10-13 erg cm-2 s-1) within 130 days. Apart from the data collected from our monitoring, an additional six Swift/XRT fields from other surveys that covered the position of RX J0520.5-6932 were used in our analysis. The complete log of the Swift and XMM-Newton observations obtained and analysed for the current work is summarised in Table A.1.
Regarding the Swift/XRT data reduction, we downloaded the data from the Swift Data Center1. We estimated the source count rates by using the HEASoft2 task ximage, correcting for the vignetting and background effects, while we used the uplimit task to estimate upper limits for the non-detections. For the brightest detections (>100 counts), we created X-ray spectra. For the spectral extraction, we used the HEASoft task xselect and circular regions with radius 35′′ for the source and 300′′ for the background.
In the XMM-Newton ToO observation, the source was located on CCD4 of the EPIC-pn (Strüder et al. 2001) and on CCD1 of both the EPIC-MOS (Turner et al. 2001) detectors. XMM-Newton SAS 13.0.13 was used for data processing. The background stayed at a low level for almost all the observing time, and we excluded less than 2 ks of exposure due to a moderate flare seen in the EPIC-pn detector. We used background thresholds of 8 and 2.5 counts ks-1 arcmin-2 for the EPIC-pn and EPIC-MOS detectors, respectively. This resulted in net exposure times of 16.8/20.3/20.3 ks for EPIC-pn/MOS1/MOS2 after flare removal. The event extraction was performed using a circle around the source, while the background events were extracted from a point-source-free area on the same CCD but on different pixel columns for EPIC-pn. We optimised the size of the source extraction area using the SAS task eregionanalyse. For the EPIC-pn spectra and light curves, we selected single-pixel and double-pixel events (PATTERN ≤4), while in the case of EPIC-MOS, we used single to quadruple events (PATTERN ≤12). The quality flag FLAG = 0 was used throughout. The SAS task especget was used to create the spectra and response files for the spectral analysis. The spectra were binned to achieve a minimum signal-to-noise ratio of five for each bin.
2.2. X-ray position
The position of RX J0520.5-6932 was determined from the XMM-Newton ToO observation that provided the best statistics. X-ray images were created from all the EPIC cameras using the XMM-Newton standard energy sub-bands (Watson et al. 2009). Source detection was performed simultaneously on all the images using the SAS task edetect_chain. Boresight correction was performed on the images based on the position of five identified background X-ray sources in the field. The positional correction based on these sources was found to be ~1′′. The final source position was determined to RA = 05h20m29 99 and Dec = –69°31′55.̋3 (J2000), with a 1σ statistical uncertainty of 0.05′′. The total 1σ positional error, however, was determined by the remaining systematic uncertainty assumed to be 0.5′′ (see Sect. 4.3 of Sturm et al. 2013).
99 and Dec = –69°31′55.̋3 (J2000), with a 1σ statistical uncertainty of 0.05′′. The total 1σ positional error, however, was determined by the remaining systematic uncertainty assumed to be 0.5′′ (see Sect. 4.3 of Sturm et al. 2013).
2.3. Timing analysis
We used the SAS task barycen to correct the XMM-Newton EPIC event arrival times to the solar-system barycentre. To increase the signal-to-noise ratio we created time series from the merged event list of EPIC-pn and EPIC-MOS for the common good-time intervals. We used the HEASoft task powspec to search the X-ray light curve (0.2–10 keV) for periodicities. In Fig. 1, we present the inferred power density spectrum with a strong peak at the main period and its first harmonic. To improve the result of our initial estimation, we followed Haberl et al. (2008). By using a Bayesian periodic signal detection method (Gregory & Loredo 1996), we determined the pulse period with a 1σ uncertainty to 8.035331(15) s. Following the nomenclature introduced by Coe et al. (2005) for the BeXRB pulsars in the SMC, we suggest the alternative name of LXP 8.04 for the system in the LMC.
By using the five standard energy bands (0.2−0.5, 0.5−1.0, 1.0−2.0, 2.0−4.5, 4.5−10 keV), we can define four hardness ratios as HRi = (Ri + 1 − Ri) / (Ri + 1 + Ri), with Ri denoting the background-subtracted count rate in energy band i. The period-folded pulse profiles in the EPIC standard energy bands, together with the hardness ratios derived from the pulse profiles in two adjacent energy bands, are plotted in Fig. 2. To achieve better statistics, the first two energy bands were combined in the top left-hand panel, and the bottom panel shows all five energy bands combined.
From the HR diagrams, it seems that the pulse behaves differently in the soft and hard X-ray bands. The source first becomes harder (see HR3, HR4 at phase ~0.3−0.6) in the hard X-ray bands, and after the pulse maximum, it becomes harder in the soft X-rays (see HR2). To investigate this behaviour further, we created X-ray spectra for different phase intervals.
 |
Fig. 1 Power density spectrum created from the merged EPIC-pn and EPIC-MOS data in the 0.2−10.0 keV energy band. The time binning of the input light curve was 0.01 s. The best-fit frequency ω ~ 0.12445 Hz and its first harmonic are easily distinguished in the plot. |
 |
Fig. 2 Left: pulse profiles obtained from the merged EPIC data in different energy bands (P = 8.035331 s). All the profiles are background-subtracted and normalized to the average count rate (0.276, 0.454, 0.438, 0.311, 1.48 cts s-1, from top to bottom). Right: hardness ratios as a function of pulse phase derived from the pulse profiles in two neighbouring standard energy bands. |
Spectral fit results.
2.4. Spectral analysis
The spectral analysis was performed with xspec (Arnaud 1996) version 12.8.0. The high number of counts enabled us to use χ2 statistics in the fitting procedure. The XMM-Newton/EPIC spectra were fitted simultaneously using the same model parameters with an additional scaling factor to account for instrumental differences. For the EPIC-pn we fixed the scaling factor at 1, while for both EPIC-MOS, we obtained values of CMOS1 = 1.03 ± 0.03 and CMOS2 = 1.00 ± 0.03, which is consistent with the expected values, as EPIC-MOS is known to provide ~5% higher fluxes than EPIC-pn (see Stuhlinger et al. 2006, or the latest version of the XMM-Newton calibration manual4). The photo-electric absorption was modelled as a combination of Galactic foreground absorption and an additional column density accounting for both the interstellar medium of the LMC and the intrinsic absorption by the source. The Galactic photo-electric absorption was set to a column density of NH,GAL = 6.44 × 1020 cm-2 (Dickey & Lockman 1990) with abundances according to Wilms et al. (2000). The LMC-intrinsic column density NH,LMC was left as a free parameter with abundances of 0.49 for elements heavier than helium (Rolleston et al. 2002). All the uncertainties were calculated based on a Δχ2 statistic of 2.706, equivalent to a 90% confidence level for one parameter of interest.
The pulse-phase averaged spectra were first fitted with an absorbed power law, resulting in a reduced 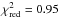 . We further tested models typically applied to the spectra of BeXRBs. In particular from the residuals of the fitted power-law model, there is evidence that adding a soft energy component (~1 keV) would improve the fit. The overall fit quality was marginally improved by the use of the mekal (thermal component based on emission from optically thin plasma), bbody, or diskbb (emission from an accretion disk consisting of multiple black-body components) models available in xspec. The tested models with their best-fit parameters are summarised in Table 1. However, all the thermal models improved the residuals at energies around 1 keV. The combination of a power-law and a black-body component provided two different solutions with similar residuals. The first solution described a black body that mainly attributed the softer X-rays, while the second solution (hereafter BBrad2) provided a black body of higher temperature (kT ~ 2.8 keV) that contributed most of the flux at higher energies. The photon index of the power law for all the tested models was between 0.8 and 0.9 (apart from model BBrad2), which falls within the typical range of 0.6 to 1.4 as reported by Haberl et al. (2008). The EPIC-pn data provide an indication of an emission line close to 6.4 keV. The line was fitted with a Gaussian profile (E = 6.4 ± 0.1 keV, σ ~ 0) with equivalent width of 50 ± 30 eV. The best-fit power-law model with the contribution of the low-temperature black body and the Fe line is shown in Fig. 3.
. We further tested models typically applied to the spectra of BeXRBs. In particular from the residuals of the fitted power-law model, there is evidence that adding a soft energy component (~1 keV) would improve the fit. The overall fit quality was marginally improved by the use of the mekal (thermal component based on emission from optically thin plasma), bbody, or diskbb (emission from an accretion disk consisting of multiple black-body components) models available in xspec. The tested models with their best-fit parameters are summarised in Table 1. However, all the thermal models improved the residuals at energies around 1 keV. The combination of a power-law and a black-body component provided two different solutions with similar residuals. The first solution described a black body that mainly attributed the softer X-rays, while the second solution (hereafter BBrad2) provided a black body of higher temperature (kT ~ 2.8 keV) that contributed most of the flux at higher energies. The photon index of the power law for all the tested models was between 0.8 and 0.9 (apart from model BBrad2), which falls within the typical range of 0.6 to 1.4 as reported by Haberl et al. (2008). The EPIC-pn data provide an indication of an emission line close to 6.4 keV. The line was fitted with a Gaussian profile (E = 6.4 ± 0.1 keV, σ ~ 0) with equivalent width of 50 ± 30 eV. The best-fit power-law model with the contribution of the low-temperature black body and the Fe line is shown in Fig. 3.
Given the variations in the HR diagrams (see Fig. 2), we continued performing phase-resolved spectroscopy using five phase bins. This was achieved with the use of the SAS task phasecalc, with zero phase defined as the date of the observation (MJD: 56 314.0), the same as used in Fig. 2. For the phase-resolved analysis we used only the EPIC-pn data, because the frame time of the EPIC-MOS cameras is longer than the duration of each phase bin. The phased-resolved spectra were again fitted with a single power law and power law plus thermal component models.
 |
Fig. 3 Pulse-phase averaged EPIC spectra of RX J0520.5-6932. The top panel shows the EPIC-pn (black), EPIC-MOS1 (red) and EPIC-MOS2 (green) spectra, together with the best-fit model (solid lines) composed of an absorbed power law with photon index of 0.83, a black body with kT = 0.24 keV (dotted lines), and a Gaussian line at 6.4 keV. The residuals for this model are plotted in the bottom panel. |
It should be noted that the addition of the thermal component did not always improve the fit without producing unphysical parameters (e.g. black-body temperature of >100 keV). Given this behaviour, we used a model with the same absorption for the five phases, linked the temperature of the thermal component and the power-law photon index, and let their normalisations vary. In Fig. 4 we plot the normalisation, therefore the strength, of each component versus the spin phase. The black-body component significantly contributes to the total flux during the first two phase bins (consistent with the worse fit quality found for the single power-law fit). The variation in the black-body intensity appears to be anti-correlated with that of the power-law component, although formally also a constant black-body flux cannot be excluded. When additionally allowing the absorption to vary with phase, we note similar behaviour by the normalisations. Again, there is some indication of a changing column density, but one more free fit parameter increases the errors on the individual parameters, not allowing any firm conclusion about which parameters are principally variable.
Following the detection of an emission line near 6.4 keV in the phase-averaged spectrum, we searched the phased spectra for similar features (see Table 1). Because of the lower statistics in the phased spectra, we tested the significance of the line by fitting the model with a Gaussian line with zero width, stepping the line energy between 2 and 9 keV (100 steps), for all the phased spectra. The derived equivalent widths of the fitted lines were always less than 60 eV, except close to 6.4 keV. At centroid energies near 6.4 keV, the equivalent width of the line exceeded 60 eV in two spectra (phase 0.2−0.4 and 0.6−0.8), suggesting a variation in the line intensity with pulse phase.
 |
Fig. 4 Best-fit values of the normalization parameters derived from phase-resolved spectroscopy. The absorption values were assumed to be constant. Error bars indicate the 90% confidence level. |
2.5. X-ray long-term variability
From the spectral analysis of the XMM-Newton ToO observation of RX J0520.5-6932, we calculated a flux of 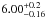 × 10-12 erg cm-2 s-1 in the 0.3–10.0 keV band. This translates into an absorption-corrected luminosity of 1.79 × 1036 erg s-1 for a distance to the LMC of 49 kpc (Inno et al. 2013). During the XMM-Newton observation performed on 2004 January 17, the source was located over a gap of the EPIC-pn camera and near bad columns of the EPIC-MOS cameras and was marginally detected at a flux level of 2.15 × 10-14 erg cm-2 s-1. Based on the XMM-Newton observations, we estimate a long-term X-ray variability factor of at least 280 for RX J0520.5-6932. Both the lowest and highest fluxes have been measured from XMM-Newton observations, while the Swift flux was always between these two values. The ROSAT measured flux was near the XMM-Newton ToO value; however, it does not provide any additional constraints, given that the two observatories cover different energy bands and that the photo-electric absorption will have a strong effect on the soft ROSAT energy band, which may introduce large systematic uncertainties.
× 10-12 erg cm-2 s-1 in the 0.3–10.0 keV band. This translates into an absorption-corrected luminosity of 1.79 × 1036 erg s-1 for a distance to the LMC of 49 kpc (Inno et al. 2013). During the XMM-Newton observation performed on 2004 January 17, the source was located over a gap of the EPIC-pn camera and near bad columns of the EPIC-MOS cameras and was marginally detected at a flux level of 2.15 × 10-14 erg cm-2 s-1. Based on the XMM-Newton observations, we estimate a long-term X-ray variability factor of at least 280 for RX J0520.5-6932. Both the lowest and highest fluxes have been measured from XMM-Newton observations, while the Swift flux was always between these two values. The ROSAT measured flux was near the XMM-Newton ToO value; however, it does not provide any additional constraints, given that the two observatories cover different energy bands and that the photo-electric absorption will have a strong effect on the soft ROSAT energy band, which may introduce large systematic uncertainties.
3. Analysis and results of optical data
3.1. Optical counterpart
The most accurate X-ray position of RX J0520.5-6932 was derived from XMM-Newton ToO data (Sect. 2.1). Within the 3σ error circle we found a V = 14.12 mag star as the only likely counterpart at a distance of ~0.8′′ to the X-ray position. This star is included in the 2MASS catalogue (2MASS J0520299-6931559). This confirms the previously suggested counterpart by Schmidtke et al. (1994), as the real companion of RX J0520.5-6932.
3.2. OGLE light curve
The Optical Gravitational Lensing Experiment (OGLE) started its initial observations in 1992 (Udalski et al. 1992) and continues observing today, with its most recent data release (OGLE III) in 2008 (Udalski et al. 2008). Observations were made with the 1.3 m Warsaw telescope at Las Campanas Observatory. Images were taken in the V and I filter pass-bands, while the data reduction is described in Udalski et al. (2008).
In the present work, we used the OGLE I and V band magnitudes for the counterpart of RX J0520.5-6932 that were taken before MJD = 56 600 (see Table 2). The latest I band light curve is seen in Fig. 6, where the different OGLE phases have been normalised to the same mean value to account for calibration offsets. The data can be downloaded from the OGLE-IV real time monitoring of X-ray sources web page5.
OGLE data for the optical counterpart of RX J0520.5-6932.
From the different OGLE data sets of the I band magnitudes, we computed periodograms by using the Lomb-Scargle (LS) algorithm (Scargle 1982; Horne & Baliunas 1986). We searched for periodicities that were up to half of the total OGLE observing period, which at the time of the analysis was ~5851 d. Since the LS algorithm does not determine the period error, we used the bootstrap method to estimate the period uncertainties. A random sampling was drawn from the light curve (one epoch can be drawn multiple times) and the period for that sampling was determined with the LS algorithm. This procedure was performed 1000 times for each light curve (OGLE phase), so that the 1σ uncertainty can be determined from the resulting distribution.
Based on the combined OGLE data, we derived a new improved period of 24.4302 ± 0.0026 d for the optical counterpart, while the average luminosity level was nearly constant for the past 15 years (variability less than 0.1 mag). By analysing the available V band data we found a similar period (24.22 d). We also analysed the I band data from the three different OGLE phases separately, to search for possible differences between them. This resulted in the detection of slightly different periods for the three OGLE phases. We also detected short periodicities with values 1.04 d, 0.958 d, 0.509 d, and 0.49 d, which can be associated to the 0.5 and 1 day aliases of the 24.43 d period (1 / (0.5-1 ± 24.43-1) and 1 / (1-1 ± 24.43-1)) and are not associated with the NRP phenomenon. When analysing the complete I band light curve from the three available OGLE phases, we found an indication of a long period of ~706.9 d.
Such super-orbital periods have been reported from other BeXRB systems in the MCs, and they might be related to the formation and depletion of the circumstellar disk around the Be star (Rajoelimanana et al. 2011). The results of our temporal analysis are listed in Table 2. For the period where both I and V band measurements are available, we are able to follow the evolution of the colour of the counterpart of RX J0520.5-6932. To calculate the I − V colour, we used only the measurements that are less than one day apart. In Fig. 7 we present the folded light curve for the OGLE I and V band magnitudes and the V − I colour of the optical counterpart of RX J0520.5-6932. In Fig. 8 we present the colour-magnitude diagram for the period between 55 260 and 56 600 (MJD).
 |
Fig. 5 Finding chart of RX J0520.5-6932. The image is a product of the OGLE project. The 3σ X-ray positional uncertainty is marked with a green circle. In the upper left part of the image, we find the star cluster NGC 1926, at a distance of ~0.64′. |
 |
Fig. 6 OGLE I band light curve of RX J0520.5-6932. Data from different OGLE phases are separated with vertical lines. |
 |
Fig. 7 OGLE I band, V band, and V − I light-curve profiles, folded for periods of 24.43 d and 706.9 d. The I band curve consists of data from phases II, III, and IV, while the V band we only had data from phase IV. All the data are folded using the first available OGLE data point (MJD: ~50 455.67) as a zero phase. |
 |
Fig. 8 Colour–magnitude diagram of RX J0520.5-6932. The OGLE data are divided into two groups according to the phase derived from the 24.43 d period. |
 |
Fig. 9 Optical and X-ray light curve of RX J0520.5-6932. Top panel: Swift/XRT count rates (0.3–10 keV band), 2σ upper limits are plotted with arrows. The vertical black dotted lines represent the 24.43 d optical period phased on the detected X-ray maximum, while the red dashed lines are spaced based on the 23.93 d orbital solution of Kuehnel et al. (2014; phased at the mean T90 time). Bottom panel: OGLE-IV I band optical light curve. |
4. Discussion
Analysing the EPIC data of our XMM-Newton ToO observation of RX J0520.5-6932, performed on 2013 January 22 during the maximum of a type I outburst, we detected coherent X-ray pulsations with a period of 8.035331(15) s (1σ). During the outburst, the X-ray spectrum is fitted best by an absorbed power law (Γ = 0.83) plus a low-temperature black-body (kT ~ 0.24 keV) model. From phase-resolved spectroscopy, we found that the spectral shape changes with spin phase. This modulation can be successfully modelled by the same model as is used for the phase-averaged spectrum, but with normalisations for the different components that vary with phase.
It has been suggested that the presence of a soft spectral component is a common feature intrinsic to X-ray pulsars, which is related to the total luminosity of the source (Hickox et al. 2004). For sources with higher luminosity (LX>1038 erg s-1), it could be a result of reprocessed hard X-rays from the NS by optically thick accreting material. While in less luminous sources (LX<1036 erg s-1), a soft excess could be due to emission by photo-ionised or collisionally heated gas or thermal emission from the surface of the NS. Either or both of these types of emission can be present for sources with intermediate luminosity.
In the past decade, a thermal soft excess has been detected in a number of BeXRB pulsars. In several persistent systems, with luminosities between 1034 erg s-1 and 1036 erg s-1, the X-ray spectra can be fitted by a power law and a black body with temperature values between 1.1 and 1.8 keV (e.g. La Palombara et al. 2013; Bartlett et al. 2013). Some other systems, commonly observed during outburst, also show evidence of thermal emission but with much lower temperatures around 0.3 keV (e.g. Haberl & Pietsch 2008; Sturm et al. 2011). In the case of RX J0520.5-6932, we note that the system was observed during an outburst, therefore we tried to test thermal models with a wider range in temperature. We find that although a black-body component of ~2.8 keV yields an acceptable fit quality (see PL+BBrad2 in Table 1), it also produces some questionable properties for the system. In the case of the higher temperature black-body model, the power-law component accounts for the softer X-rays, and the black-body component contributes the majority of the flux at high energies, which is difficult to explain by heating or reprocessing effects.
The change in the normalisations of the power-law and black-body components with spin phase might be explained by a simple picture. First, the maximum radius (~20 km) of the black-body emission region argues against a hot spot on the NS surface. More likely it could be a region in the inner part of an accretion disk. If we imagine that the accretion column originating in the disk and terminating on the NS surface, depending of the geometry of the system with respect to the observer, it might be possible for the accretion column to partially obscure the NS and/or the inner part of the accretion disk. However, in order to study this behaviour more deeply, observations with better quality statistics are required.
A total X-ray long-term variability factor of ~280 was derived from the available XMM-Newton observations of RX J0520.5-6932. In Fig. 9, we present the X-ray light curve from our Swift monitoring, together with the optical I-band light curve from the same period. The Swift/XRT fluxes (detections and upper limits) are all within the range found from the XMM-Newton observations. There is evidence of three additional outbursts after the first one, and these events seem to follow the periodic behaviour of the optical counterpart and the ~24.4 d period. Unfortunately, the available X-ray coverage does not allow making this case stronger.
In Fig. 7, we show that periodic behaviour is seen in both the I and V band light curves, as well as in the V − I colour. The colour periodicity is also translated as a greater variability in the I than in the V band magnitude. In Fig. 8 we show the evolution of the colour of the optical counterpart of RX J0520.5-6932 during an approximately three-year period. From the relative positions of the data points from different phases, it can be seen that the colour of the system correlates well with its luminosity, since it is redder when brighter. In similar studies concerning the optical properties of Be stars, a colour–magnitude variability pattern that follows an anticlockwise path in the colour–magnitude diagram (same axes as Fig. 8) has been reported (e.g. de Wit et al. 2006; Coe et al. 2012). Rajoelimanana et al. (2011) studied the colour–magnitude diagrams of 31 BeXRB systems, finding that only four or five of them become bluer when brighter. They propose that this is related to the orientation by which we observe the system, concluding that in systems with a bluer-brighter relation, the decretion disk obscures the Be star, while the redder-brighter relation describes a system where the disk is observed face-on.
In almost all these studies the systems showed a much higher variability in their magnitudes and exhibit some kind of sharp outburst rather than the case of a flat light curve of RX J0520.5-6932. In systems like XMMUJ010743.1-715953 (Coe et al. 2012), the colour-magnitude evolution pattern presumably reflects the growth of the disk as a large cooler component of the Be star. In the case of RX J0520.5-6932, we clearly see that this colour-magnitude relation does not reflect the complete loss and build up of the disk, since we only see a periodic variability of the magnitude with small amplitude. This behaviour indicates that a similar, although less intense, disk evolution happens within the orbital period of the system and is most likely related to the NS motion. The NS orbiting the Be star is perturbing the decretion disk, most likely via tidal truncation (Okazaki & Negueruela 2001), resulting in an increased emission from the redder component of the system (e.g. cooler disk).
Kuehnel et al. (2014) have recently analysed the pulse-period evolution provided by the Fermi Gamma-ray Burst Monitor (GBM) pulsar project to derive the orbital parameters of the binary system by modelling the Doppler shift due to the orbital motion. Including a luminosity-dependent intrinsic spin-period derivative, they found an orbital solution with a period of 23.93 ± 0.07 d, a projected semi-major axis of asini = 107.6 ls, and an eccentricity e = 0.0286, and the time at which the delay in the arrival of the pulse is maximized at T90 = 2 456 666.91(JD). This period is significantly shorter than the period derived from the OGLE photometry, but should be considered as the most accurate solution for the orbital motion of the binary. By using Kepler’s third law (neglecting the small eccentricity) and typical values for the masses of the system (1.4 and 23 M⊙, Vacca et al. 1996), we estimate the actual orbit of the system to be ~2.3 times larger than the projected semi-major axis. That suggests that the orbital plane of the NS has an inclination of about 26° (where 0° indicates a face-on system).
It is not uncommon for BeXRB systems to exhibit small differences in the periods derived from the optical and from pulse timing. Townsend et al. (2011) report that for two SMC pulsars, SXP2.37 and SXP6.85, their orbital periods derived from pulse timing are shorter than the optical (by 0.22 d and 3.9 d, respectively). A likely explanation for this difference is that the variability in the optical data is a combined product of two motions, the Keplerian orbit of the NS around its massive companion and the rotation of the circumstellar disk. In Table 2 we see that the periodicity values derived from OGLE phases II and IV are statistically different (3.5σ). This might be a result of small changes in the rotation speed or matter distribution of the decretion disk.
The observed outbursts in the optical might be a combined result of the co-rotation of the Be disk in the same direction as the NS orbit and inhomogeneities in the disk. Inhomogeneities are known from cyclic variations observed in emission line profiles of other systems. Okazaki (1991), explained these variations as a result of one-armed oscillations in the equatorial disks of the Be stars. Rajoelimanana et al. (2011) confirm that the long-term variation in the optical light curves of BeXRB systems is related to the behaviour of the Be circumstellar disk. From the OGLE light curve of the optical counterpart of RX J0520.5-6932, there is evidence for a super-orbital period. Both the amplitudes of this long-term periodicity and the total variability of the source are even smaller than the variability within the orbital period. This suggests a Be disk observed nearly face on, consistent with what we derived above.
Knowing that the BeXRB population correlates with star-formation regions with young ages, it is likely that the system originated in a nearby cluster. RX J0520.5-6932 is located near the star cluster NGC 1926 at a projected angular distance of 0.65′ (see Fig. 5). NGC 1926 has an age of 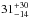 Myr (Popescu et al. 2012). For the case of BeXRBs in the SMC, a convincing link between the spatial position of the binary systems and near young star clusters has been reported by Coe (2005). Their analysis leads to an average space velocity of ~30 km s-1 for the binary systems, which is proposed to arise from a supernova kick. Assuming a value of 5 Myr for the most likely maximum lifetime of the Be star after the NS has been formed (Savonije & van den Heuvel 1977), we can estimate a lower limit for the runaway velocity imposed on the system by the supernova kick. In our case this leads to a velocity of 1.8 km s-1. Knowing that the system’s true motion has a random direction to our line of sight, the true velocity could be higher. On a statistical basis, this value is lower than the average velocity reported for BeXRB systems in the SMC or in our galaxy (e.g. 19 ± 8 km s-1, van den Heuvel et al. 2000). An independent argument in favour of the small kick velocity is the low eccentricity of the binary system.
Myr (Popescu et al. 2012). For the case of BeXRBs in the SMC, a convincing link between the spatial position of the binary systems and near young star clusters has been reported by Coe (2005). Their analysis leads to an average space velocity of ~30 km s-1 for the binary systems, which is proposed to arise from a supernova kick. Assuming a value of 5 Myr for the most likely maximum lifetime of the Be star after the NS has been formed (Savonije & van den Heuvel 1977), we can estimate a lower limit for the runaway velocity imposed on the system by the supernova kick. In our case this leads to a velocity of 1.8 km s-1. Knowing that the system’s true motion has a random direction to our line of sight, the true velocity could be higher. On a statistical basis, this value is lower than the average velocity reported for BeXRB systems in the SMC or in our galaxy (e.g. 19 ± 8 km s-1, van den Heuvel et al. 2000). An independent argument in favour of the small kick velocity is the low eccentricity of the binary system.
RX J0520.5-6932 adds to the important sample of BeXRBs with known spin period, orbital period, and eccentricity. The spin and orbital periods are consistent with the Corbet relation (Corbet 1984) and the low eccentricity of the system is expected for systems with short spin periods (Knigge et al. 2011). According to their interpretation, BeXRBs could stem from two different types of supernova progenitors, with electron-capture supernovae preferentially producing systems with short spin period, short orbital periods, and low eccentricity like RX J0520.5-6932.
We finally note that in 2014 January, RX J0520.5-6932 started a major outburst reaching a luminosity of 1.9 × 1038 erg s-1 (Vasilopoulos et al. 2014). This is almost 100 times brighter than the outburst of 2013 January. The outburst still continues at the time of writing and will be the subject of a subsequent paper.
5. Conclusion
The analysis of our XMM-Newton ToO observation of RX J0520.5-6932 revealed X-ray pulsations with a period of 8.035331(15) s. The X-ray spectrum is best fitted by an absorbed power law with a spectral index of ~0.83 plus a low-temperature black-body component with temperature of ~0.24 keV. The detailed pulse-phase-resolved analysis of its spectral properties reveals a significant change in its spectral shape. When assuming the same spectral model, the changes with pulse phase can be described by variations in the black-body and power-law intensities. A possible anti-correlation of black-body and power-law flux (possibly due to geometrical effects) requires confirmation with data of higher statistical quality. Our analysis of the OGLE light curve of the optical counterpart confirmed an optical period of 24.43 d. Our results confirm RX J0520.5-6932 as a BeXRB with a NS primary, making it the fifteenth known HMXB pulsar in the LMC.
Science Analysis Software (SAS), http://xmm.esac.esa.int/sas/
Acknowledgments
We would like to thank the referee, Prof. M. J. Coe, for his suggestions that helped improve the manuscript. The XMM-Newton project is supported by the Bundesministerium für Wirtschaft und Technologie/Deutsches Zentrum für Luft- und Raumfahrt (BMWi/DLR, FKZ 50 OX 0001) and the Max-Planck Society. The OGLE project has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007−2013)/ERC grant agreement no. 246678 to A. U. We thank the Swift team for accepting and carefully scheduling the target-of-opportunity observations, and we acknowledge the use of public data from the Swift data archive. G.V., P.M., and R.S. acknowledge support from the BMWi/DLR grants FKZ 50 OR 1208, 1201, and 0907, respectively.
References
- Annala, M., & Poutanen, J. 2010, A&A, 520, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antoniou, V., Zezas, A., Hatzidimitriou, D., & Kalogera, V. 2010, ApJ, 716, L140 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniou, V., Zezas, A., & Kalogera, V. 2011, in Am. Astron. Soc. Meet. Abstr., 218, 22829 [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bartlett, E. S., Coe, M. J., & Ho, W. C. G. 2013, MNRAS, 436, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, M. J. 2005, MNRAS, 358, 1379 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, M. J., Negueruela, I., Buckley, D. A. H., Haigh, N. J., & Laycock, S. G. T. 2001, MNRAS, 324, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, M. J., Edge, W. R. T., Galache, J. L., & McBride, V. A. 2005, MNRAS, 356, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Coe, M., Corbet, R. H. D., McGowan, K. E., & McBride, V. A. 2010, in High Energy Phenomena in Massive Stars, eds. J. Martí, P. L. Luque-Escamilla, & J. A. Combi, ASP Conf. Ser., 422, 224 [Google Scholar]
- Coe, M. J., Haberl, F., Sturm, R., et al. 2012, MNRAS, 424, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Corbet, R. H. D. 1984, A&A, 141, 91 [NASA ADS] [Google Scholar]
- de Wit, W. J., Lamers, H. J. G. L. M., Marquette, J. B., & Beaulieu, J. P. 2006, A&A, 456, 1027 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Edge, W. R. T., Coe, M. J., Galache, J. L., & Hill, A. B. 2004, MNRAS, 349, 1361 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics, 3rd edn. (Cambridge: Cambridge University Press) [Google Scholar]
- Gregory, P. C., & Loredo, T. J. 1996, ApJ, 473, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Haberl, F., & Pietsch, W. 1999, A&A, 344, 521 [NASA ADS] [Google Scholar]
- Haberl, F., & Pietsch, W. 2004, A&A, 414, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haberl, F., & Pietsch, W. 2008, A&A, 484, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haberl, F., Eger, P., & Pietsch, W. 2008, A&A, 489, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haberl, F., Sturm, R., Ballet, J., et al. 2012, A&A, 545, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hickox, R. C., Narayan, R., & Kallman, T. R. 2004, ApJ, 614, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Horne, J. H., & Baliunas, S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Inno, L., Matsunaga, N., Bono, G., et al. 2013, ApJ, 764, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C., Coe, M. J., & Podsiadlowski, P. 2011, Nature, 479, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Kuehnel, M., Finger, M. H., Fuerst, F., et al. 2014, ATel, 5856, 1 [NASA ADS] [Google Scholar]
- LaPalombara, N., Mereghetti, S., Sidoli, L., Tiengo, A., & Esposito, P. 2013, Central European Astrophysical Bulletin, 37, 277 [NASA ADS] [Google Scholar]
- Liu, Q. Z., van Paradijs, J., & van den Heuvel, E. P. J. 2005, A&A, 442, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maggi, P., Haberl, F., Sturm, R., et al. 2013, A&A, 554, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okazaki, A. T. 1991, PASJ, 43, 75 [NASA ADS] [Google Scholar]
- Okazaki, A. T., & Negueruela, I. 2001, A&A, 377, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okazaki, A. T., Hayasaki, K., & Moritani, Y. 2013, PASJ, 65, 41 [NASA ADS] [Google Scholar]
- Pfahl, E., Rappaport, S., Podsiadlowski, P., & Spruit, H. 2002, ApJ, 574, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Popescu, B., Hanson, M. M., & Elmegreen, B. G. 2012, ApJ, 751, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Rajoelimanana, A. F., Charles, P. A., & Udalski, A. 2011, MNRAS, 413, 1600 [NASA ADS] [CrossRef] [Google Scholar]
- Reig, P. 2011, Ap&SS, 332, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rolleston, W. R. J., Trundle, C., & Dufton, P. L. 2002, A&A, 396, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savonije, G. J., & van den Heuvel, E. P. J. 1977, ApJ, 214, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidtke, P. C., Cowley, A. P., Frattare, L. M., et al. 1994, PASP, 106, 843 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidtke, P. C., Chobanian, J. B., & Cowley, A. P. 2008, AJ, 135, 1350 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidtke, P. C., Cowley, A. P., & Udalski, A. 2013, MNRAS, 431, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stuhlinger, M., Altieri, B., Esquej, M. P., et al. 2006, in The X-ray Universe 2005, ed. A. Wilson, ESA SP, 604, 937 [NASA ADS] [Google Scholar]
- Sturm, R., Haberl, F., Coe, M. J., et al. 2011, A&A, 527, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sturm, R., Haberl, F., Rau, A., et al. 2012, A&A, 542, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sturm, R., Haberl, F., Pietsch, W., et al. 2013, A&A, 558, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Townsend, L. J., Coe, M. J., Corbet, R. H. D., & Hill, A. B. 2011, MNRAS, 416, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udalski, A., Szymanski, M., Kaluzny, J., Kubiak, M., & Mateo, M. 1992, Acta Astron., 42, 253 [NASA ADS] [Google Scholar]
- Udalski, A., Szymanski, M. K., Soszynski, I., & Poleski, R. 2008, Acta Astron., 58, 69 [NASA ADS] [Google Scholar]
- Vacca, W. D., Garmany, C. D., & Shull, J. M. 1996, ApJ, 460, 914 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J., Portegies Zwart, S. F., Bhattacharya, D., & Kaper, L. 2000, A&A, 364, 563 [NASA ADS] [Google Scholar]
- Vasilopoulos, G., Maggi, P., Haberl, F., et al. 2013a, A&A, 558, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasilopoulos, G., Maggi, P., Sturm, R., et al. 2013b, The ATel, 4748, 1 [Google Scholar]
- Vasilopoulos, G., Sturm, R., Maggi, P., & Haberl, F. 2014, The ATel, 5760, 1 [Google Scholar]
- Watson, M. G., Schröder, A. C., Fyfe, D., et al. 2009, A&A, 493, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: X-ray observation logs
X-ray observations of RX J0520.5-6932.
All Tables
All Figures
 |
Fig. 1 Power density spectrum created from the merged EPIC-pn and EPIC-MOS data in the 0.2−10.0 keV energy band. The time binning of the input light curve was 0.01 s. The best-fit frequency ω ~ 0.12445 Hz and its first harmonic are easily distinguished in the plot. |
| In the text | |
 |
Fig. 2 Left: pulse profiles obtained from the merged EPIC data in different energy bands (P = 8.035331 s). All the profiles are background-subtracted and normalized to the average count rate (0.276, 0.454, 0.438, 0.311, 1.48 cts s-1, from top to bottom). Right: hardness ratios as a function of pulse phase derived from the pulse profiles in two neighbouring standard energy bands. |
| In the text | |
 |
Fig. 3 Pulse-phase averaged EPIC spectra of RX J0520.5-6932. The top panel shows the EPIC-pn (black), EPIC-MOS1 (red) and EPIC-MOS2 (green) spectra, together with the best-fit model (solid lines) composed of an absorbed power law with photon index of 0.83, a black body with kT = 0.24 keV (dotted lines), and a Gaussian line at 6.4 keV. The residuals for this model are plotted in the bottom panel. |
| In the text | |
 |
Fig. 4 Best-fit values of the normalization parameters derived from phase-resolved spectroscopy. The absorption values were assumed to be constant. Error bars indicate the 90% confidence level. |
| In the text | |
 |
Fig. 5 Finding chart of RX J0520.5-6932. The image is a product of the OGLE project. The 3σ X-ray positional uncertainty is marked with a green circle. In the upper left part of the image, we find the star cluster NGC 1926, at a distance of ~0.64′. |
| In the text | |
 |
Fig. 6 OGLE I band light curve of RX J0520.5-6932. Data from different OGLE phases are separated with vertical lines. |
| In the text | |
 |
Fig. 7 OGLE I band, V band, and V − I light-curve profiles, folded for periods of 24.43 d and 706.9 d. The I band curve consists of data from phases II, III, and IV, while the V band we only had data from phase IV. All the data are folded using the first available OGLE data point (MJD: ~50 455.67) as a zero phase. |
| In the text | |
 |
Fig. 8 Colour–magnitude diagram of RX J0520.5-6932. The OGLE data are divided into two groups according to the phase derived from the 24.43 d period. |
| In the text | |
 |
Fig. 9 Optical and X-ray light curve of RX J0520.5-6932. Top panel: Swift/XRT count rates (0.3–10 keV band), 2σ upper limits are plotted with arrows. The vertical black dotted lines represent the 24.43 d optical period phased on the detected X-ray maximum, while the red dashed lines are spaced based on the 23.93 d orbital solution of Kuehnel et al. (2014; phased at the mean T90 time). Bottom panel: OGLE-IV I band optical light curve. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


