| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 4 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201423766 | |
| Published online | 04 July 2014 | |
Research Note
Population of the Galactic X-ray binaries and eRosita
Institut für Astronomie und Astrophysik,
Sand 1,
72076
Tübingen,
Germany
e-mail:
doroshv@astro.uni-tuebingen.de
Received: 6 March 2014
Accepted: 12 April 2014
The population of the Galactic X-ray binaries has been mostly probed with moderately sensitive hard X-ray surveys so far. The eRosita mission will provide for the first time a sensitive all-sky X-ray survey in the 2−10 keV energy range, where the X-ray binaries emit most of the flux and discover the still unobserved low-luminosity population of these objects. In this paper, we briefly review the current constraints for the X-ray luminosity functions of high- and low-mass X-ray binaries and present our own analysis based the INTEGRAL 9-year Galactic survey, which yields improved constraints. Based on these results, we estimate the number of new XRBs to be detected in the eRosita all-sky survey.
Key words: X-rays: binaries / Galaxy: structure / stars: luminosity function, mass function / surveys
© ESO, 2014
1. Introduction
The evolution of astrophysical objects usually occurs on timescales that are inaccessible to direct observations (≥106 yr), and population studies are the only way to tackle it. From an observational point of view, the distribution of sources with luminosity or the luminosity function (LF) is often used to characterise a given population. Since the X-ray binaries (XRB) emit most of the energy in X-rays, the X-ray luminosity function (XLF) is usually considered. It has been shown that the XLF of both low and high mass X-ray binaries (LMXB, HMXB) is a broken power law flattening below ~1036−1037 erg s-1 (Grimm et al. 2002; Voss & Ajello 2010; Mineo et al. 2011; Lutovinov et al. 2013, and references therein). Taking the power-law nature of the XLF into account, most of the sources are expected to have low luminosities, so observing them is essential for constraining the basic properties of XRB population. With current instrumentation, this can only be done for the Galactic XRBs based on the data from all-sky X-ray surveys (Grimm et al. 2002).
Highly non-uniform spatial distribution of XRBs within the Milky Way, however, makes it non-trivial to reconstruct the XLF from the observed fluxes and assess the completeness of a given survey. The non-uniform X-ray absorption further complicates the situation, especially for soft X-ray surveys like ROSAT, so currently hard X-ray surveys by Swift (Ajello et al. 2008) and INTEGRAL (Krivonos et al. 2012) observatories provide the best constraints on the XLF parameters. However, both surveys are limited in sensitivity to ~10-11 erg s-1 cm-2. Therefore, probing the XLF below 1035 erg s-1 is still challenging.
The Swift BAT survey is being carried out in the 15−55 keV energy range, and the majority of the sources detected so far are X-ray binaries. For sources with known distances, Voss & Ajello (2010) derived the observed XLF and corrected it for being incomplete by following the approach suggested by Grimm et al. (2002). For the LMXBs, the authors confirm the previously reported (Grimm et al. 2002; Revnivtsev et al. 2008) break in the XLF at ~3 × 1036 erg s-1 with slopes of ~0.9 and ~2.4 below and above the break, respectively. For the first time, they found that the XLF of HMXBs also likely has a break at Lbr ~ 2.5 × 1037 erg s-1 with slopes of ~1.3 and ≥2 below and above the break, respectively.
Lutovinov et al. (2013) investigated the XLF of HMXBs detected in the INTEGRAL 9-year survey in the 17−60 keV energy range considering only the persistent sources. To assess the completeness of the sample, Lutovinov et al. (2013) divided it into a set of flux-limited samples within concentric annuli around the Galactic centre based on known distances. The surface density of HXMBs was assumed constant within each annulus, while the XLF shape was assumed to be the same throughout the Galaxy. The corrected XLF was found to have a break at 2.5 × 1036 erg s-1 and slopes of ~1.4 and ≥2.2 for the dim and bright parts respectively, which is consistent with the values reported by Voss & Ajello (2010).
The reported uncertanties for XLF parameters are, however, rather large in both cases, which makes it difficult to extrapolate results to lower luminosities and to estimate the total number of yet undetected XRBs in the Milky Way. The uncertanties are mainly driven by the limited size of the source sample, particularly at low luminosities. Indeed, limited sensitivity of INTEGRAL and Swift BAT surveys implies that weaker sources may only be detected if they are close to Earth, and these are not many.
The upcoming eRosita all-sky X-ray survey (Merloni et al. 2012) will bring a significant improvement in sensitivity over the existing surveys and is likely to detect a number of new low-luminosity XRBs thus improving the constraints on the XLF parameters. The main objective of the present paper is to assess the anticipated impact of eRosita survey in this context.
To get a more robust forecast, we start by analysing the XLF of the Galactic XRBs using available data, namely the INTEGRAL 9-year Galactic plane survey (Krivonos et al. 2012). It is the most sensitive survey available for low Galactic latitudes, where most XRBs are located, and the resulting source catalogue contains about twice as many identified XRBs as the Swift BAT survey used by Voss & Ajello (2010). To further increase the size of the source sample, we propose a novel method for XLF reconstruction, which does not require the knowledge of the distances to individual sources but rather relies on modeling the observed flux distribution of a given survey based on the input model XLF and the spatial distribution of the sources in the sample. The results are consistent with the values reported by Voss & Ajello (2010) and Lutovinov et al. (2013), although we do find a flatter low-luminosity slope and a lower break luminosity (and, therefore, fewer objects) for the HMXBs. Using these results, we then conclude optimistically that the eRosita survey might be expected to double the number of the observed XRBs in Galaxy and improve the constraints on the XLF parameters if sufficient identification completeness is achieved.
2. XLF reconstruction
The standard method to characterise the luminosity distribution of a population is to calculate it directly from the observed fluxes for a sub-sample of objects with known distances. The observed XLF must then be corrected for effects of incompleteness that are related, for instance, to the inhomogeneous survey sensitivity or spatial distribution of the population members. For instance, the LMXBs roughly trace the stellar mass distribution, and the sources located in the Galactic bulge represent substantial fraction of entire population. However, only relatively luminous bulge LMXBs can be detected in shallow surveys, so a substantial fraction of all low-luminosity LMXBs in Galaxy are not detected and, therefore, the observed XLF are biased towards high-luminosity sources. The observed XLF can be corrected for this effect by estimating (for each luminosity) the fraction of sources expected to be detected in a survey, providing that the source spatial distribution is known or can be modeled (Grimm et al. 2002).
The corrected luminosity distribution depends, however, on not only flux and distance estimates for the observed sources but also on the overall distribution of distances to sources in population. We suggest, however, that the expected flux distribution for any assumed intrinsic luminosity distribution in population can be calculated with no additional assumptions in this case. The parameters of the assumed XLF might then be tuned so that the model and observed flux distributions match, and therefore, the intrinsic XLF of the population may be recovered. The reconstructed XLF obviously depends on the assumed spatial distribution of sources in population, but this is also the case for the directly derived XLF due to incompleteness effects. Modeling of the observed flux rather than luminosity distribution has, however, an important advantage that even the sources lacking distance estimates might be included in the analysis thus reducing statistical uncertanties. We note that the observed flux or luminosity distribution is still affected by identification completeness effects which must be considered separately in XLF reconstruction.
A very similar approach has been used by Pretorius et al. (2007) to assess the influence of selection effects on the observed population of cataclysmic variables (CVs) in the optical domain. These authors also modeled the flux distribution of the observed CV population by assuming certain intrinsic luminosity distribution, spatial distribution of the CVs, their spectral properties, and outburst activity. We note that other effects such as dependence of the identification completeness in a survey on flux might also be accounted. The latter is likely to be important for the upcoming eRosita survey. However, it is not trivial to assess how complete identification is before the actual survey is finished. Now, we are more interested in calculating the total number of XRBs likely to be detected by eRosita. To assess the expected improvement in constraints on XLF parameters, we optimistically assume that most sources will be eventually identified.
To make a more realistic forecast for eRosita and improve the constraints on XLF parameters using available data, we first reconstruct the XLF using the INTEGRAL 9-year Galactic survey catalogue (Krivonos et al. 2012). This provides survey averaged fluxes in the 17−60 keV energy range for 108 LMXBs and 82 HMXBs. This dataset has very high identification completeness and is not sensitive to interstellar absorption, which makes it ideal for population studies. Therefore, it can be safely assumed that the observed flux distribution is only defined by the intrinsic XLF, spatial distribution of the sources, and the sensitivity of the survey. Moreover, this dataset has not been used for detailed analysis of the XLF of X-ray binaries so far.
Only a fraction of the total flux is emitted in 17−60 keV, so the simulated bolometric flux needs to be multiplied by some factor to derive the flux detected by a particular instrument. To estimate the X-ray contribution detected by INTEGRAL, we calculate F17−60/F1−200 ratios explicitly using the spectral parameters reported for some of the known XRBs in the INTEGRAL reference catalogue (Ebisawa et al. 2003) and randomly pick the conversion factor from the resulting empirical distribution for the simulated sources. This is particularly important for LMXBs, which exhibit well-defined hard/soft spectral states and are hard to describe by just stacking spectra of all sources to derive the hard X-ray contribution, as done by Voss & Ajello (2010).
The sensitivity of a survey in a given direction is assumed to depend only on exposure as Flim ~ 1.1 × 10-8/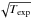 erg s-1 cm-2 (Krivonos et al. 2012) and can be calculated from the survey exposure maps for each simulated source to determine whether it would be detected in the survey.
erg s-1 cm-2 (Krivonos et al. 2012) and can be calculated from the survey exposure maps for each simulated source to determine whether it would be detected in the survey.
 |
Fig. 1 Simulation results for the LMXB (left) and the HMXB (right) populations. Black contours and points show a 68% probability that the simulated population will have the same flux distribution as observed in INTEGRAL 9-year Galactic survey and the best-fit results. The red countours show the forecast for the eRosita 4-year survey assuming the best-fit XLF found from INTEGRAL data. The black and red dotted contours represent results for the synthetic HMXB populations 1) by assuming the XLF parameters reported by Lutovinov et al. (2013) and observed with INTEGRAL and 2) by assuming the best-fit XLF parameters with α1 = 1.1 fixed at the highest value allowed and observed with eRosita, which is an optimistic forecast. The XLF parameters as reported by Voss & Ajello (2010) and Lutovinov et al. (2013) are also shown for reference. |
 |
Fig. 2 Cumulative luminosity functions for LMXBs (left) and HMXBs (right) as derived in this work using the INTEGRAL data (hatched area). Best-fit estimates by Grimm et al. (2002), Voss & Ajello (2010), and Lutovinov et al. (2013) are also plotted for reference. |
To model the populations of HMXBs and LMXBs we use the spatial distributions of XRBs obtained by Bahcall & Soneira (1980) and Grimm et al. (2002), and for the spiral arm shape, we use the parameters reported by Cordes & Lazio (2002). The XLF is parametrised with a broken power-law dN/ dL ∝ (L/Lbr)− α1,2with three free parameters: the break luminosity Lbr and the slopes α1 and α2 below and above the break luminosity respectively. To obtain the observable flux distribution, we simulate a population of objects with a given spatial and intrinsic luminosity distributions, converting the luminosity to observed flux. This is done for a set of input XLF parameters and then compared with the observed flux distribution using the non-parametric two-sample Kolmogorov-Smirnov test (Conover 1971). This test gives the probability PKS that both the observed and simulated flux samples originate from the same distribution, that is, the model XLF is able to reproduce the observed fluxes. Setting a threshold on PKS allows, therefore, the restriction of the XLF parameters.
Note that the normalisation of the XLF only affects the total number of observed sources but does not affect the shape of the distribution and PKS value. Therefore, it is not considered a free parameter, and we calculate it later by comparing the number of sources predicted for a given XLF with the total number of observed sources. Our method to derive the XLF can be, therefore, summarised as follows:
-
Based on the spatial distribution model, we generate coordinates for a large (~104) population of sources.
-
We assume a broken power law XLF parametrized with Lbr,α1,α2, and pick a random luminosity for each source from this model distribution.
-
using the sampled coordinates and luminosity, we then calculate the expected bolometric flux from each source, and convert it to instrumental flux using the spectral information available from the INTEGRAL reference catalogue.
-
For each simulated source we determine whether it would be detected by INTEGRAL by comparing its flux with the survey sensitivity in a given direction and obtain the final model flux distribution.
-
We calculate the normalisation of the model XLF by comparing the number of sources detected in simulation with number of sources detected in the INTEGRAL survey.
-
Finally, we compare the model and the observed flux distributions at each point on a grid of input XLF parameters Lbr,α1,α2 using the two-sample Kolmogorov-Smirnov test to calculate the probability PKS(Lbr,α1,α2) that two samples come from the same distribution. Setting a threshold on PKS allows the acceptable values for XLF parameters to be restricted.
To smooth out the variations due to the random nature of simulation, we repeat the steps above about ten times for each combination of XLF parameters until the resulting sample of PKS values become normally distributed and then calculate the mean value.
3. Results and discussion
Taking the previous estimates of the XLF parameters into account, we considered the parameter ranges of 0.1 ≤ α1 ≤ 1.8, 0.9 ≤ α1 ≤ α2 ≤ 3.5, and 1035 ≤ Lbr ≤ 1038. The results are presented in Table 1 and Fig. 1. Here, the contours mark regions where the maximum value of PKS for a given α1,2 and any Lbr exceeds the selected threshold of PKS ≥ 68%. Earlier reported estimates of XLF parameters by Voss & Ajello (2010); Lutovinov et al. (2013) are also shown for reference. The respective cumulative luminosity functions are shown in Fig. 2.
Estimated XLF parameters for high- and low- mass X-ray binaries from INTEGRAL 9-year survey, and expected number and fraction of sources to be detected by INTEGRAL and eRosita.
Our results for both the HMXBs and LMXBs are consistent within uncertanties with previous reports. We find, however, a somewhat flatter slope at low luminosities and a lower break luminosity than both Voss & Ajello (2010) and Lutovinov et al. (2013). However, being based on a different (extended) source sample and a different XLF reconstruction method, our analysis is completely independent, hence, some differences are expected. To verify the robustness of our method, we repeated the analysis using a synthetic HMXB distribution, which is derived by assuming the XLF parameters reported by Lutovinov et al. (2013) as an observational reference. We were able to reliably reconstruct the input parameters (see Fig. 1). We conclude, therefore, that the slope of HMXBs XLF found in previously mentioned works was likely overestimated. On the other hand, our estimate might be also biased. Indeed, the simple estimate of INTEGRAL sensitivity, which we use might be too optimistic at lower fluxes, particularly if weak sources are observed within the same field of view with brighter ones (Fenimore & Cannon 1978). Some of the dim sources, which we assume are detectable by INTEGRAL are, therefore, likely not detected. On the other hand, the eRosita survey will be free from such complications.
To get a forecast for the eRosita survey, we use the same approach described above. We simulate the expected XRB flux distributions using the expected survey sensitivity and flux conversion factors calculated in a same way as for INTEGRAL. Although the eRosita is most sensitive to soft X-rays below ~2 keV, the X-ray spectra of XRBs are known to be intrinsically hard and often strongly absorbed, so we restrict our analysis to the hard 2−10 keV energy range where the absorption is less important.
For the input XLF parameters and normalisations, we take our results from the analysis of the INTEGRAL data. The limiting flux for eRosita in 2−10 keV energy range is assumed to be 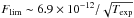 erg s-1 cm-2 where the exposure maps are taken from Merloni et al. (2012). The results are presented in Fig. 1 and Table 1.
erg s-1 cm-2 where the exposure maps are taken from Merloni et al. (2012). The results are presented in Fig. 1 and Table 1.
The INTEGRAL survey is already sensitive enough to detect most if not all sources with high luminosities, so the uncertainty in the XLF slope above the break for both HMXBs and LMXBs is mainly driven by the limited number of such sources in Galaxy.
At low luminosities, eRosita will detect a number of new sources, potentially doubling the numbers of known XRBs. This does not, however, directly imply that the constraints on the XLF parameters is significantly improved (see Fig. 1). For the LMXBs, the uncertanties for Lbr and α1 might be reduced by factor of two if all detected LMXBs are identified. However, this is unlikely to be the case, as the source identification is a major challenge for low-luminosity LMXBs, which are easily confused with cataclysmic variables (Jonker et al. 2011; Torres et al. 2014).
For HMXBs, the source identification is less complicated, as their luminous optical counterparts are detectable throughout the Galaxy (Reed 2003). Therefore, eRosita is likely to put a stronger limit on α1 (see Fig. 1).
4. Conclusions
We presented a detailed analysis of the X-ray luminosity function of the Galactic X-ray binaries. Our analysis is based on the most sensitive hard X-ray survey available, the INTEGRAL 9-yr Galactic Survey. Previously, this dataset had only been used to constrain the XLF of persistent HMXBs, whereas we consider the entire populations of both LMXBs and HMXBs.
We also suggested a method for XLF reconstruction, which allowed us to further increase the source sample size by the inclusion of sources with no distance estimates. We model the observed flux rather than luminosity distribution and considering the spectral properties of individual objects and the variable survey sensitivity accross the sky. Our results generally agree with the previous reports, although we find a flatter slope for HMXBs at low luminosities, which implies that there are fewer HMXBs in the Milky Way. Based on the reconstructed XLF parameters and using a similar simulation procedure, we conclude that eRosita shall detect up to 160 new LMXBs and 140 HMXBs and significantly improve the constraints on the low luminosity part of the XLF of the Galactic X-ray binaries. We note, however, that such analysis requires survey identification to be reasonably complete, which will be particularly challenging for the LMXBs.
Acknowledgments
The authors thank the Deutsches Zentrums für Luft- und Raumfahrt (DLR) and Deutsche Forschungsgemeinschaft (DFG) for financial support (grants DLR 50 OR 0702, FKZ 50 OG 1301, SA2131/1-1).
References
- Ajello, M., Greiner, J., Kanbach, G., et al. 2008, ApJ, 678, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Soneira, R. M. 1980, ApJS, 44, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Conover, W. J. 1971, Practical nonparametric statistics (New York: Wiley) [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002 [arXiv:astro-ph/0207156] [Google Scholar]
- Ebisawa, K., Bourban, G., Bodaghee, A., Mowlavi, N., & Courvoisier, T. J.-L. 2003, A&A, 411, L59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fenimore, E. E., & Cannon, T. M. 1978, Appl. Opt., 17, 337 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Grimm, H. J., Gilfanov, M., & Sunyaev, R. 2002, MNRAS, 391, 923 [Google Scholar]
- Jonker, P. G., Bassa, C. G., Nelemans, G., et al. 2011, ApJS, 194, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Krivonos, R., Tsygankov, S., Lutovinov, A., et al. 2012, A&A, 545, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutovinov, A. A., Revnivtsev, M. G., Tsygankov, S. S., & Krivonos, R. A. 2013, MNRAS, 431, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Predehl, P., Becker, W., et al. 2012 [arXiv:1209.3114] [Google Scholar]
- Mineo, S., Gilfanov, M., & Sunyaev, R. 2011, Astron. Nachr., 332, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Pretorius, M. L., Knigge, C., & Kolb, U. 2007, MNRAS, 374, 1495 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, B. C. 2003, AJ, 125, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Revnivtsev, M., Lutovinov, A., Churazov, E., et al. 2008, MNRAS, 491, 209 [Google Scholar]
- Torres, M. A. P., Jonker, P. G., Britt, C. T., et al. 2014, MNRAS, 440, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Voss, R., & Ajello, M. 2010, ApJ, 721, 1843 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Estimated XLF parameters for high- and low- mass X-ray binaries from INTEGRAL 9-year survey, and expected number and fraction of sources to be detected by INTEGRAL and eRosita.
All Figures
 |
Fig. 1 Simulation results for the LMXB (left) and the HMXB (right) populations. Black contours and points show a 68% probability that the simulated population will have the same flux distribution as observed in INTEGRAL 9-year Galactic survey and the best-fit results. The red countours show the forecast for the eRosita 4-year survey assuming the best-fit XLF found from INTEGRAL data. The black and red dotted contours represent results for the synthetic HMXB populations 1) by assuming the XLF parameters reported by Lutovinov et al. (2013) and observed with INTEGRAL and 2) by assuming the best-fit XLF parameters with α1 = 1.1 fixed at the highest value allowed and observed with eRosita, which is an optimistic forecast. The XLF parameters as reported by Voss & Ajello (2010) and Lutovinov et al. (2013) are also shown for reference. |
| In the text | |
 |
Fig. 2 Cumulative luminosity functions for LMXBs (left) and HMXBs (right) as derived in this work using the INTEGRAL data (hatched area). Best-fit estimates by Grimm et al. (2002), Voss & Ajello (2010), and Lutovinov et al. (2013) are also plotted for reference. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


