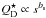EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 567 (July 2014) A&A, 567 (2014) A127 Full HTML
Free Access
Issue
A&A
Volume 567, July 2014
Article Number A127
Number of page(s) 11
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201423523
Published online 28 July 2014

© ESO, 2014

1. Introduction

HIP 17439 (HD 23484) is a nearby solar-type star with an estimated age of 0.8–3.7 Gyr (Mamajek & Hillenbrand 2008; Garcés et al. 2010; Fernandes et al. 2011). The first clear evidence for a circumstellar dust disc around HIP 17439 was found by Koerner et al. (2010), who detected a far-IR excess in Spitzer/MIPS data. Recently, the HIP 17439 system was observed as part of the Herschel1 (Pilbratt et al. 2010) open time key programme DUst around NEarby Stars (DUNES, Eiroa et al. 2010, 2013). The disc appeared spatially resolved in the far-IR images of the PACS (Poglitsch et al. 2010) and SPIRE instruments (Griffin et al. 2010; Swinyard et al. 2010). Together with the discs around HD 202628 (Krist et al. 2012), HD 207129 (Krist et al. 2010; Marshall et al. 2011; Löhne et al. 2012), and HD 107146 (Ertel et al. 2011), HIP 17439’s disc is amongst the most extended around the Sun-like stars identified to date.

Theory predicts that the lifetime of the dust in such a disc is shorter than the lifetime of the star, owing to the mutual collisions and radiative forces. Therefore, the dust is thought to be continually replenished through collisional grinding of km-sized asteroidal bodies (planetesimals) that are remnants of the planet formation process (Backman & Paresce 1993; Wyatt 2008; Krivov 2010). In the DUNES programme, those debris discs have been detected with a rate of at least 20% around solar-type main-sequence stars (Eiroa et al. 2013). Their presence may or may not be correlated in one way or another with the presence of planets (Moro-Martín et al. 2007; Kóspál et al. 2009; Bryden et al. 2009; Maldonado et al. 2012; Wyatt et al. 2012; Matthews et al. 2014; Marshall et al. 2014).

Modelling the spectral energy distribution (SED) of a debris disc is in general a degenerate problem. For example, the observed flux can be reproduced by the thermal emission of large dust grains close to the star or small ones located far away. A spatially resolved debris disc where the location of the dust is directly measurable offers the best opportunity to break those degeneracies. Modelling resolved systems places meaningful constraints on the discs’ radial and temperature structures, as well as on the grain sizes and compositions (e.g., Matthews et al. 2010; Ertel et al. 2011; Eiroa et al. 2011; Lestrade et al. 2012; Booth et al. 2013).

Simultaneous modelling of the SED and the radial surface brightness profiles extracted from the PACS images of the HIP 17439 system was done by Ertel et al. (2014) for the first time. There, a dust surface number density n ∝ sγrα was assumed, i.e., a combination of two independent power laws for the size distribution (exponent γ) and the radial distribution (exponent α) of the grains, fitted to the observational data by a multi-wavelength χ2 minimisation. This way, one can readily explore a huge parameter space, thereby finding the most appropriate disc configurations. Ertel et al. showed that the SED and the radial profiles can be reproduced well by either a one- or a two-component scenario (Table 1).

Table 1

Best-fit results with 3σ uncertainties of the power-law models from Ertel et al. (2014).

The best-fit one-component model found is a broad dust disc with a radial extension of several hundreds of au where the number density is nearly constant (α = − 0.1). Two possible morphologies of such a disc are conceivable. The first one is a narrow planetesimal belt near the outer disc edge. Through transport processes such as Poynting-Robertson (P-R) drag dust particles move inwards, filling the inner disc region and ensuring a broad distribution of dust. The second possibility is a broad planetesimal ring. This implies that dust is produced everywhere in the whole disc, which – under certain assumptions – may result in a constant dust surface density as well. The two-component model consists of two rings with inner edges around 29 and 91 au. Due to the high negative α values, most of the dust is located near the inner disc edges of the two components, and the rings are spatially separated by a wide gap.

Continuing the study by Ertel et al. (2014), this paper presents an in-depth collisional modelling of the HIP 17439 system. To this end, we start with an initial distribution of planetesimals, which we also refer to as parent bodies, and consider their subsequent collisional evolution. As a result, the bodies are ground down to dust where the smallest particles end up with typical sizes in the order of 1 μm or smaller. The collisional outcomes depend on the size of the impactors, the material properties, and the relative velocities in the disc. Our modelling also includes dust transport mechanisms in the form of stellar wind and P-R drag, which depend on grain size, material properties, and stellar distance. As a result, the dust radial and size distributions are intrinsically coupled. Their slopes can no longer be controlled directly, but instead are determined by the evolution of the planetesimal disc. This way, we model the actual physical processes operating in a debris disc. However, the numerical complexity of this method means that we can only explore a limited number of parameter combinations. As a starting point, we use the one- and two-belt models from Ertel et al. (2014) and check whether these are physically plausible.

In Sect. 2, we describe the data used and the technique of our modelling. Sections 3 and 4 present simulations with one narrow parent belt and two such belts, respectively. Section 5 discusses the possibility of a single extended planetesimal disc. Some prospects for future observations are given in Sect. 6. Section 7 contains conclusions and a discussion of our results.

2. Model setup

2.1. Stellar properties

HIP 17439 is a K2 V star (Torres et al. 2006; Gray et al. 2006) at a distance of 16 pc (van Leeuwen 2007). We assumed a mass of 0.82 M⊙ (Fernandes et al. 2011), a bolometric luminosity of 0.40 L⊙ (Eiroa et al. 2013), and an effective temperature of 5166 K (Eiroa et al. 2013). We used a synthetic atmosphere model for the stellar spectrum from the PHOENIX/Gaia grid (Brott & Hauschildt 2005), scaled to WISE and near-IR fluxes (see Ertel et al. 2014).

2.2. Observational data for the debris disc

We took the photometric data listed in Table 3 of Ertel et al. (2014). The SED is densely sampled between 12 and 500 μm by measurements of IRAS, Spitzer, and Herschel. The PACS images show an increasing disc extension from 131 au at 70 μm to 253 au at 160 μm along the major axis. Throughout this paper, we use the radial profiles derived by Ertel et al. from the PACS images at 70, 100, and 160 μm, but not from the SPIRE images, since the disc appears only marginally resolved at SPIRE wavelengths, and the source brightness profile is sparsely sampled, which causes larger uncertainties in the radial profiles.

2.3. Collisional modelling

We carried out the modelling with our parallelised C++ code ACE that determines the distributions of solids in a rotationally symmetric debris disc. The code follows a statistical approach to solve the kinetic equation which includes the combined effects of gravity, direct radiation pressure, drag forces, and non-elastic collisions (for details see Krivov et al. 2005, 2006; Löhne et al. 2008, 2012). We used the latest version of ACE that works on a three-dimensional grid with logarithmic bins for object mass, pericentre, and eccentricity, as described in Krivov et al. (2013).

All solids, from dust grains to planetesimals, were assumed to have a spherical shape. Their sizes are characterised by the radius s. The outcome of each collision depends on the material strength and relative velocity of the colliders. The inclination distribution of bodies in the disc was assumed to be uniform within a constant semi-opening angle, which was set to half the planetesimal’s maximum eccentricity emax (energy equipartition relation, e.g., Greenberg et al. 1991). The eccentricity distribution was also taken to be uniform within a minimum value close to zero and emax. The dust distribution generated by ACE at a certain time instant served as input for our tools SEDUCE and SUBITO that compute the thermal emission and the radial profiles, respectively (Müller et al. 2010).

We characterise the material strength by the critical specific energy for disruption and dispersal 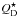QD⋆\hbox{$Q_\text{D}^\star$}, which is the projectile energy per target mass needed to disperse half the target mass: 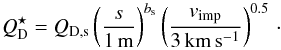QD⋆=QD,s(s1 m)bs(vimp3 km s-1)0.5 · \begin{eqnarray} Q_\text{D}^\star = Q_{\text{D,s}} \left(\frac{s}{1\,\metre}\right)^{b_\text{s}} \left(\frac{v_\text{imp}}{3\,\kilo\metre \, \second^{-1}}\right)^{0.5}\cdot \label{equ:QD} \end{eqnarray}(1)Equation (1) follows the formulation of Benz & Asphaug (1999) for the strength regime, which we have modified by a power-law dependence on the impact speed vimp (Stewart & Leinhardt2009; see also Löhne et al.2012). In all our simulations, the largest bodies considered in the disc were 10 m in radius. Therefore, 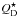QD⋆\hbox{$Q_\text{D}^\star$} is determined solely by the material strength and we neglected the gravitational binding energy that is usually included in the description of 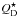QD⋆\hbox{$Q_\text{D}^\star$}. We set QD,s = 107erg g-1 and bs = − 0.37, which are close to the values used by different authors (Housen & Holsapple 1990; Holsapple 1994; Benz & Asphaug 1999; Stewart & Leinhardt 2009).

2.4. Grain properties

After collisions the orbits of the newly born fragments are affected by radiation pressure, which has the net result of increasing the semi-major axes and eccentricities of the fragments compared to those of the parent bodies. This is determined by β, the ratio between radiation pressure and gravitational attraction. For parent bodies in nearly circular orbits, the eccentricities of fragments are >1 for β> 0.5, and they leave the system on unbound orbits (e.g., Burns et al. 1979).

Figure 1 compares β as a function of the dust grain radius s for different materials. For all compositions assumed here, β = 0.5 is not reached in the HIP 17439 system and the blowout limit does not exist. For the modelling in this paper, we chose the 50:50 mixture of astrosilicate and water ice with a density of 2.35 g cm-3. The optical constants of this mixture were determined via effective medium theory and the Bruggeman mixing rule (Ossenkopf 1991). The absorption and radiation pressure efficiencies are calculated by means of Mie theory (Bohren & Huffman 1983). These techniques have been used for modelling other discs in the Herschel/DUNES (e.g., Löhne et al. 2012), GASPS2 (e.g., Lebreton et al. 2012), and DEBRIS3 (e.g., Churcher et al. 2011) programmes.

thumbnail Fig. 1

β ratio for several grain materials. The values are calculated with the stellar parameters of HIP 17439. Refractive indices are taken from Draine (2003, astrosilicate), Li & Greenberg (1998, water ice), and Zubko et al. (1996, amorphous carbon).

3. One parent belt

At first we analysed the scenario where dust is produced in a single narrow planetesimal ring far away from the host star. Owing to transport processes through P-R drag and stellar wind drag, the dust grains move inwards and fill the inner disc region. A similar scenario was considered for ε Eri by Reidemeister et al. (2011), who show that warm dust close to the star could stem from an outer Kuiper belt analogue between 55 and 90 au.

3.1. Model description

We performed several ACE runs with input parameters listed in Table 2. The parameter space was sampled by 35 bins in mass from 5 × 10-18 g to 1 × 1010 g (i.e., 0.01 μm to 10 m in size) and 21 bins in pericentric distance from 9 to 250 au. The eccentricity grid covered values from 0.001 to 2.5 with 25 bins.

After a certain timestep, the simulations reach an equilibrium state in which the amounts of particles with different sizes on different orbits stay constant relative to each other. Once the equilibrium state is reached, the dust mass in the systems decreases continually with time. We stopped the simulations as soon as the dust’s thermal emission had reduced to the observed excess strength, given by the photometric data. Because the simulation times tsim depend strongly on the choice of the initial conditions, tsim do not necessarily correspond to the system’s physical age tphys, which means that tsim can possibly exceed tphys. For instance, if we start with a massive planetesimal belt, much dust is produced and it takes time to reach a rather low excess level. For all runs in Table 2, the initial planetesimal populations were uniformly distributed between rp,1 and rp,2 with size distribution index γ = − 3.5 and initial masses of ≈1 M⊕. The corresponding tsim turned out to be ≲2 Gyr, so longer than the relaxation times (≲500 Myr) needed to reach the equilibrium state.

Table 2

ACE input parameters for one-belt models.

3.2. First-guess modelling

We started with a first-guess (FG) run where we assumed a location of the planetesimal belt between 120 and 150 au, which is at the lower boundary of the 3σ confidence level for the outer radius of the one-component model of Ertel et al. (2014; Table 1). The dust particles are transported by P-R drag from their birth places towards the star. Figure 2 shows the resulting SED and radial profiles.

thumbnail Fig. 2

Observed SED and radial profiles plotted along with the simulated data from the FG, SW1, and SW2 models in Table 2. For a detailed description of the observational data see Ertel et al. (2014). Note that data points with a signal-to-noise ratio <3 are excluded from the available Spitzer/IRS spectrum. In the radial profile plots, the gray-shaded areas depict the observed data with 1σ uncertainties at PACS wavelengths (from top to bottom: 70, 100, and 160μm). Cuts along the long and short axes are given in the left and right column, respectively.

The SED reproduces the observations quite well, except that the mid-IR flux probed by Spitzer/IRS is underestimated. Although the radial profiles are almost within the 1σ uncertainties of the observational data at 160 μm, they are distinctly too shallow for r< 7′′ at 70 and 100 μm. This clearly illustrates a deficit of particles in the inner part of our modelled disc. We expect that a conceivable relocation of the initial planetesimal belt would not lead to significant improvements. If the belt is shifted inwards, the averaged collisional velocities will increase (vimp ∝ r-0.5), thus lowering the collisional lifetime of larger grains. The amount of larger particles would be reduced, and as a result, the submillimetre emission is depressed. That would have a detrimental effect because the FG model is already well fitted to the submillimetre emission. Conversely, shifting the belt outwards would hamper the collisional depletion of larger particles, hence the production of smaller ones. As a result, even fewer small particles would be transported into the inner region. On the basis of a narrow parent belt, an increase in the inner disc emission without changing the submillimetre flux substantially can only be possible by strengthening the inward transport of dust and not by shifting the belt.

3.3. Adding stellar winds

Stellar winds cause dust grains to lose angular momentum due to collisions with the wind particles, thereby enhancing the P-R drag. Accordingly, the P-R timescale for the inward transport is shortened by a factor of [1 + (βSW/β) (c/vSW)]-1 (Mukai & Yamamoto 1982), where c is the speed of light and vSW the speed of the stellar wind particles. Here, βSW denotes the ratio between stellar wind pressure and gravity, which is proportional to the stellar mass loss rate Ṁ (Minato et al. 2006).

Many cool, late-type stars on the main sequence are known to possess strong stellar winds (Wood et al. 2002, 2005) that can have significant impact on the dynamics of dust around those stars (e.g., Plavchan et al. 2009). For moderately rotating K main sequence stars with radius R⋆, Wood et al. (2005) found a correlation between the stellar X-ray flux FX and the mass loss rate by 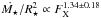M⋆˙/R⋆2∝FX1.34±0.18\hbox{$\dot{M_\star}/R_\star^2 \propto F_\text{X}^{1.34\pm0.18}$}, as long as FX ≲ 8 × 105 erg s-1cm-2. For the HIP 17439 X-ray luminosity of log LX/L⋆ = − 4.9 (ROSAT all-sky survey bright source catalogue, Voges et al. 1999) and R⋆ = 0.8 R⊙, this yields 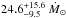24.6-9.5+15.6Ṁ⊙\hbox{$24.6^{+15.6}_{-9.5}~\dot{M}_\odot$}. On the other hand, the theoretical prediction of Ṁ⋆ by Cranmer & Saar (2011) for the HIP 17439 mean rotation period of 11 days is significantly lower, about 5 Ṁ⊙ (see Fig. 13 in Cranmer & Saar 2011). Furthermore, there are no clear observational indicators that HIP 17439 is active enough to have strong stellar winds (Sanz-Forcada, priv. comm.). Therefore, a strong stellar wind assumption should be seen as critical. Nevertheless, we ran simulations with stellar winds to probe their effects on the dust distribution and to test whether the model can be improved this way.

We started two stellar wind runs, SW1 and SW2, where we assumed 15 and 30 Ṁ⊙, respectively. The SW1 mass loss rate corresponds to the lower limit of the Wood et al. criterion mentioned above. The SW2 rate is equal to what has been proposed for ε Eri (Wood et al. 2002), a star that is similar to HIP 17439 in mass, radius, and X-ray luminosity (Benedict et al. 2006; di Folco et al. 2007; Schmitt et al. 1995). Although there is still a lack of observations, cool K-dwarfs are expected to have hot coronae and stellar winds that are driven by gas pressure similar to solar winds (e.g., Lamers & Cassinelli 1999; Wood 2004). Therefore, we assume vSW = 400 km s-1 equal to the averaged solar wind speed in SW1 and SW2.

Figure 2 demonstrates that the SEDs of the stellar wind runs predict more emission between 20 and 70 μm compared to FG. The radial profiles become steeper with increasing stellar wind strength and match the observational data considerably better. This is especially the case for SW1, whereas the bigger deviations from the data in model SW2 show that the winds are already too strong there. The reasons for the SED and radial profile modifications through stellar winds can be understood better by comparing the size distributions of the different models. For this purpose, Figs. 3a, b show the normal optical thickness per size decade τ⊥(s) ∝ n(s) · s3 for FG and SW1.

thumbnail Fig. 3

Size and radial distributions of particles in disc models FG (left column) and SW1 (right column). Top: normal optical thickness per size decade τ⊥ as a function of grain size s. The curves depict the contributions at several distances from the star. For comparison, the straight line in panel a) shows the theoretically predicted slope for an infinite collisional cascade assuming QD⋆∝sbs\hbox{$Q_\text{D}^\star \propto s^{b_\text{s}}$} with bs = − 0.37, which is n(s) ∝ s-3.7 (O’Brien & Greenberg 2003). Bottom: radial profiles of the total optical thickness (integrated over all grain sizes).

thumbnail Fig. 4

Ratio of the collision and transport timescales of the FG and SW1 run inside (10 au), within (130 au) and outside (200 au) the planetesimal ring. Only particles with eccentricities e< 0.02 are included.

The amount of particles with s> 1 μm is clearly increased inside the planetesimal belt in run SW1 (curves for r< 130 au in Fig. 3b are more extended towards bigger sizes compared to those of the FG model). Furthermore, the presence of stellar winds causes τ⊥ to go down sharply for s< 0.02 μm because β + βSW> 0.5 and the grains are blown away. In the FG model there is a deep minimum of τ⊥ around s = 0.3 μm for r ≲ 130 au (see Fig. 3a). Since β is highest around s = 0.3 μm (Fig. 1), these particles are pushed on eccentric orbits after their collisional production and contribute little to the dust density in the inner disc region. In the SW1 model, this minimum is markedly shallower because small particles move quickly towards the star and are thus less efficiently destroyed by collisions.

To confirm the last statement, we also checked the role of transport by evaluating the collisional and transport lifetimes (Fig. 4). We define the collisional timescale as Tcol = Ni/Ṅi. Here, Ni denotes the number of particles per mass, pericentre, and eccentricity bin i (where i is a three-dimensional multi-index), and Ṅi is the particle loss rate due to disruptive and cratering collisions in bin i, determined by ACE4. We calculated Tcol only for particles in the lowest eccentricity bin whose pericentres are roughly equal to their mean orbital distances. Using the change rate of orbital elements under the influence of a drag force given in Wyatt & Whipple (1950), we estimate the transport time for particles on low-eccentricity orbits as Ttrans=400(r au)2(M⊙M⋆)1β[1+750 (βSWβ)]-1yr.\begin{eqnarray} T_\text{trans}= 400 \left(\frac{r}{\au}\right)^2 \left(\frac{M_\odot}{M_\star}\right) \frac{1}{\beta} \left[1+ 750 \, \left( \frac{\beta_\text{SW}}{\beta}\right) \right]^{-1} \text{yr} . \label{equ:T_trans} \end{eqnarray}(2)Equation (2) describes the time it takes for a particle to spiral inwards from a certain distance r onto the star (r = 0). If Tcol ≫ Ttrans, the particles are most affected by transport, for Tcol ≪ Ttrans by collisions.

Comparing Figs. 4a and b shows now that small particles in the SW1 run are more affected by transport than collisions. Accordingly, the number of collisionally produced fragments on eccentric orbits reduces and τ⊥ tends to flatten from s = 10 μm down to the smallest grains. The inner region of the planetesimal ring is filled more strongly by dust and has a nearly uniform density profile proportional to r0 (Fig. 3d). Consequently, the excess emission for λ< 70 μm increases and the radial profiles steepen.

3.4. Shifting the planetesimal belt

The previous section illustrated that adding stellar winds with a moderate strength of 15 times the solar value can improve the model significantly. However, the long-axis radial profiles at 100/160μm are below the observed emission outside the planetesimal ring (r> 10′′), whereas they tend to overestimate it for r< 5′′. There are at least two modelling options for reducing the surface flux close to the star and simultaneously enhancing it farther out: 1. lowering the stellar wind strength (compare SW1 and SW2 in Sect. 3.3) or 2. shifting the planetesimal ring outwards (see discussion in Sect. 3.2). We explicitly tested the second possibility in a model with outwardly shifted planetesimals (OSP). As expected, the 100/160μm profiles flatten and match the observational data better than do those of the SW1 model (Fig. 5). We found a fractional luminosity of 9.5 × 10-5 and a dust mass (particles with radii below 1 mm) of 9.5 × 10-3M⊕ for the OSP run.

At this point, we refrain from further refinements of the one-disc model. It would certainly be possible to find a still better fit to the data than the one shown, but owing to the time-consuming collisional modelling (e.g., run OSP took about 72 CPU days), we have to restrict our analysis to a few test runs. We deem the results presented here to be sufficient for illustrating the feasibility of the one-belt scenario.

thumbnail Fig. 5

Same as Fig. 2, but for FG and OSP (Table 2).

4. Two parent belts

As shown by Ertel et al. (2014), the one-component model in Table 1 fits the data in general with reasonably low χ2, but the 100 μm major axis profile is not extended enough, leading to the biggest deviations between the observational data and this model (see Fig. 3 in Ertel et al. 2014). All modifications that cause a broader emission at 100 μm would also result in a substantially broader emission at 70 μm that is not observed. This problem motivated a two-component model where the emissions at 70 and 100 μm can be adjusted independently if the inner disc mostly contributes to 70 μm but marginally to 100 μm, and vice versa for the outer disc.

We now attempt to find an appropriate two-component disc by collisional modelling. Similar to the results of Ertel et al., we are searching for an outer disc that dominates the flux at 160 μm, but at the same time has less influence at shorter wavelengths. Consequently, the typical grain size of the dust has to be increased, otherwise the thermal emission would be too warm. This can be achieved if the dynamical excitation of the planetesimals in a disc is low. Owing to the low collisional velocities between the largest bodies, the production of small dust grains is inhibited. On the other hand, the destruction rate of small particles is high because they have large eccentricities induced by radiation pressure. This imbalance would clean out the disc of small particles (Thébault & Wu 2008).

4.1. Model description

We placed two narrow, well-separated planetesimal belts and modelled the evolutions of the produced dust independently. To this end, we started ACE twice – once only for the inner and once only for the outer belt – and combined the final simulation results. We manually determined the time steps tsim in the evolution of inner and outer components where the sums of their SEDs and radial profiles match the observational data the best. Because the evolution of both discs are not coupled in any way, we chose tsim independently for the inner and outer components.

We tested two different combinations of an inner and an outer disc (Models I and II), listed in Table 3. In all models the particles were transported by P-R drag alone. We used the same mass and eccentricity resolution as described in Sect. 3.1. The pericentre grid was set from 1 to 100 au for the inner discs and from 10 to 200 au for the outer discs, each with 21 bins. Under the same initial conditions as given in Sect. 3.1 we found tsim ≲ 1 Gyr and tsim ≲ 8 Gyr for the inner and outer discs, respectively. The simulation times merely reflect the initial conditions of the ACE models. If they are chosen inappropriately, tsim can exceed the physical age of the HIP 17439 system (see Sect. 3.1).

Table 3

ACE input parameters for two-belt models.

4.2. Results

Although the parent rings of the inner and outer discs are separated by ≳100 au, there is some overlap of the local dust densities, because of both the particles transported inwards from the outer disc and the halo grains of the inner one. However, judging by the simulations in Models I and II, the outer disc optical thickness is more than one order of magnitude lower at the location of the inner planetesimal belt, and the inner disc optical thickness is several orders of magnitude lower at the position of the outer planetesimal belt (Fig. 6). Thus, inner and outer discs can be seen as collisionally decoupled, and their independent treatment is justified.

thumbnail Fig. 6

Radial profile of the optical thickness in Model II. The shaded regions mark the extent of the inner and outer parent belts.

thumbnail Fig. 7

SEDs and radial profiles for Model I (left column) and Model II (right column) in Table 3. Profiles for inner and outer discs are star-subtracted.

In Model I, we set the planetesimal belts close to the locations of the inner edges of the Ertel et al. two-component model. Our first guess for emax of the outer disc was 0.001, which is quite a low value inspired by the modelling in Krivov et al. (2013) for the Herschel cold disc candidates, and distinctly lower than emax for the inner disc (0.04). The results are presented in Fig. 7. The SEDs of both components are rather separated; i.e., the outer disc SED peaks beyond 160 μm and has a minor contribution to 70 and 100 μm compared to the inner one. The overall SED clearly shows emission that is too low at 100 and 160 μm, whereas it tends to overestimate the SPIRE photometry by ≈1σ. Putting more weight on the outer disc SED by taking the dust mass from an earlier time step, consequently improves the agreement with the 100 and 160 μm points but has the opposite effect at longer wavelengths. The radial profiles have a steep fall-off that contradicts the observations. This is because they are mostly affected by the inner component, which is only marginally resolved.

A significant improvement in the model requires the radial profiles at 100 and 160 μm to be broadened without simultaneously increasing the flux at SPIRE wavelengths, equivalent to a higher contribution of the outer, colder component. To this end, we departed from the Ertel et al. setup, since it is difficult to translate their findings directly into a consistent collisional model. Both components of their best-fit model have large minimum grain sizes and size distributions with exponents γ< − 4 (Table 1). These steep size distributions cannot be explained by modelling with standard collisional prescriptions. The resulting size distributions from statistical codes such as ACE are typically broader, leading to broader SEDs as well. The entanglement in terms of resolvable emission from the two components in our Model I is thus greater than in Ertel et al. (2014), reducing the ability to adjust the radial profiles at 70 μm and 100 / 160 μm independently.

In our Model II, we therefore shifted the outer planetesimal belt farther away from the star and additionally increased emax up to 0.04 for this component. Compared to Model I, the outer disc SED peaks at about 160 μm and is markedly more extended towards shorter wavelengths (Fig. 7). The proportion changes therefore, which means that the outer disc is more weighted and largely determines the overall SED at λ> 100 μm. Model II fits the PACS photometric points well, but still shows the trend of overestimating the SPIRE photometry. Thanks to the stronger contribution of the outer disc, all profiles are sufficiently broadened. For this inner/outer discs combination we found dust masses of Md,inner = 4.4 × 10-4M⊕ and Md,outer = 8.7 × 10-3M⊕.

Here again, we stress that from numerous parameters, such as the position and extent of the parent belts as well as their maximum orbital eccentricities, we explicitly tested only a few ones. The already good fitting result of Model II, which can surely be improved by further parameter variations, demonstrates that a two-belt model is capable of explaining the data.

5. One extended parent belt

Alternatively to the one narrow belt and the two-belt model, Ertel et al. (2014) also suggested that the data may be compatible with one extended parent belt. Such a disc with planetesimals distributed over a range from a few au to a few hundred au cannot be treated with ACE because it would need a prohibitively long computation time. However, the results from our two-ring model give us a clue to the structure of an extended belt model. If we added a third ring between the two existing ones, the resulting system would serve as a proxy for an extended planetesimal belt configuration. Surely, an intermediate ring would lead to the effect that the belts are no longer collisionally decoupled. Thébault & Augereau (2007) consider a comparable situation where they divided an extended debris disc into several annuli and studied their collisional evolution. Inter-annuli interactions were taken into account by the transport of small grains due to radiation pressure. Therefore, particles within a certain annulus can collide with high-β grains produced in another annulus closer in. Because the impact velocities in such events are higher than the ones between locally produced objects of the same size, the number of destructive collisions increases. We expect the same effect in ACE simulations for a setup of adjacent planetesimal rings in the HIP 17439 system. Thus, the number of particles on eccentric orbits, which have high β’s but always <0.5, increases compared to the case of non-interacting rings. Consequently, the overall size distribution in the inner disc regions would have a more pronounced minimum at s ≈ 0.3 μm where β is greatest for our chosen dust material. Thus, a simplified assumption of several non-collisionally interacting rings, instead of a real extended disc, will lead to some shortcomings that mainly become apparent in the excess strength at short wavelengths, but are rather unimportant for a qualitative discussion of this model.

Figure 6 shows that the peak values of the optical thickness of inner and outer rings are roughly the same, about 1.4 × 10-3. A conceivable additional planetesimal ring between the two existing would increase the dust density at r ≈ 70 au, flattening the overall optical thickness. For such a “quasi-extended” planetesimal ring, we predict a size distribution index of ≈− 3.7 for s ≳ 10 μm according to the slope within the narrow parent belt of the FG model (Sect. 3). This would be close to − 4.0 that Ertel et al. (2014) found for the extended one-component model.

An extended planetesimal belt scenario could naturally be expected, for instance, if the planetesimals succeeded to form at a wide range of distances from the star but, for some reasons, have not grown further to gas giants. Such a belt would undergo a long-term collisional erosion. This erosion is faster closer to the star, leading to a radial mass surface density profile Σ(r) of the planetesimal disc rising outwards with a slope of about 7 / 3 (e.g., Kennedy & Wyatt 2010; Wyatt et al. 2012), although the exact value can be different under different assumptions for the initial radial profile of solids in the disc by the time of gas dispersal, critical fragmentation energy of planetesimals, and other parameters. We have checked the radial slope αΣ of the mass surface density by evaluating 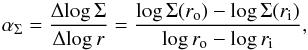αΣ=ΔlogΣΔlogr=logΣ(ro)−logΣ(ri)logro−logri,\begin{eqnarray} \alpha_\Sigma = \frac{\Delta \!\log \Sigma}{\Delta\! \log r} = \frac{\log \Sigma(r_\text{o})-\log \Sigma(r_\text{i})}{\log r_\text{o}-\log r_\text{i}}, \end{eqnarray}(3)where ri and ro are the mean distance of the inner and outer planetesimal belt, respectively. We found αΣ ≈ 1.1 for Model I and αΣ ≈ 0.7 for Model II, which are close to one and clearly confirm a solid density profile rising from the inside out. Also, that emax in the outer component is lower than in the inner one for Model I is consistent with this collisional erosion scenario, because the biggest stirrers in the disc are smaller farther out from the star, and their formation takes longer there (e.g., Kenyon & Bromley 2008). We conclude that our Models I and II are consistent, at least qualitatively, with a long-term inside-out collisional erosion of an extended planetesimal disc.

6. Prospects for observations

In the previous sections we presented several scenarios that can reproduce SED and radial profiles in the HIP 17439 system. We now test the capability of present-day observational facilities to reveal the actual debris disc structure.

In a first test, we intended to predict how our best one- and two-belt model would be seen by a single-dish telescope. The 50-m Large Millimetre Telescope (LMT) atop Sierra Negra is the most powerful telescope with respect to high resolution imaging of HIP 17439’s disc at millimetre wavelengths, although it is located in the northern hemisphere (latitude ≈+ 19°), and HIP 17439 (declination ≈− 38°) is difficult to observe from this latitude. Inspired by the resolution of the LMT/AzTEC camera, we convolved images of OSP and Model II at λ = 1.1 mm with a Gaussian profile with FWHM = 6′′. We assumed a signal-to-noise ratio (S/N) of 6 and estimated the standard deviation σ of the background fluctuation as the given S/N divided by the peak flux in the simulated observations. In Fig. 8 the synthetic AzTEC image of Model II shows an inner emission above the 5σ level and gives direct evidence for the presence of an inner planetesimal belt. However, the comparison between OSP and Model II shows that the difference in the inner disc emission is small, ≈1σ and is not enough to clearly distinguish between them. To reach a significant detection of the inner belt, its emission should differ by at least 3σ compared to the inner surface brightness dip of the one-belt scenario. This requires an S/N that is three times higher than assumed. Unfortunately, the LMT/AzTEC Photometry Mode Calculator5 predicts an observing time of six days (including all overheads) to reach S/N = 6. Thus, a significant detection of an inner disc emission is impossible with LMT in a reasonable time.

In a second attempt, we simulated interferometric observations with the Atacama Large Millitmetre/submillimetre Array (ALMA). We used CASA 4.1.06 (procedure simalma) to generate synthetic ALMA images. We assumed observations in Band 7 under good weather conditions (precipitable water vapour =0.1 mm) and found that the inner ring in the two-belt model is barely detectable, although a long integration time of 15 h was applied (Fig. 8). Thus, it would be difficult, but not impossible, to distinguish between the one-belt and two-belt models considered. We stress that other two-belt configurations that reproduce SED and radial profiles data to a similar quality as the ones found may mitigate the challenge of this work. For instance, if the inner planetesimal belt lies slightly farther away from the star as in our Model II, the produced dust will become colder and brighter at long wavelengths, favouring its detectability with ALMA.

Furthermore, measurements of the radial surface brightness profiles in submillimetre/millimetre images will reveal the extension of the planetesimal belts. In this way, the hypothesis of a broad planetesimal disc as described in Sect. 5 can be tested.

thumbnail Fig. 8

Discs with one (OSP, Table 2) and two (Model II, Table 3) components as seen by different telescopes. Top panels: unconvolved discs at 870 μm and 1.1 mm (left- and right-hand side of each splitted image). Units are Jy/pixel, where 1 pixel = 0.2′′ × 0.2′′. Middle panels; simulated LMT/AzTEC images that were generated by convolving the models at 1.1 mm with a Gaussian (FWHM = 6′′). The white circle in the lower right of the left image illustrates the beam size. The contours in each image represent 2σ, 3σ, 4σ, and 5σ levels. Bottom panels: synthetic ALMA images in Band 7 (central wavelength 870 μm), using antenna configuration alma.out01 and a water vapour overburden of 0.1 mm. The beam size is 1.1′′ × 0.9′′. With an on-source integration time of 15 h a sensitivity of ≈10μJy/beam was achieved.

7. Conclusions and discussion

Our collisional modelling of the HIP 17439’s debris disc does not allow us to draw any strict conclusions as to the underlying architecture of the system. The data can be fitted well with a single disc or two separated discs, with the radial distribution of the planetesimals being narrow in both cases. Furthermore, we argue that an extended planetesimal belt, approximated by a multicomponent disc, would reproduce the data as well. Below we discuss the astrophysical plausibility of all three models.

  • 1.

    One parent belt. Provided that a planetesimal belt is located at adistance >120 au from the star, suggested by the one-component model of Ertel et al. (2014), dust material has to be transported efficiently from the planetesimal location to the inner region of the system, otherwise the inner disc’s surface brightness is too shallow and contradicts the observed radial profiles. Since Poynting-Robertson drag alone is not enough, we found a need for strong stellar winds. We identified a wind strength of 15 times the solar value as the upper limit to prevent the radial profiles from being steepened too much if the inner edge of the planetesimal belt lies closer than 150 au to the star. The question remains whether HIP 17439 does possess winds of that strength. In our best run the planetesimals reside between 150 and 180 au; that is to say, they are much closer to the star than in the one-component scenario of Ertel et al. (2014). There, the outer ring edge was found at about 400 au, but could also be located much further inside due to large uncertainties. In general, planetesimals and dust production at very large stellar distances seem to be unlikely because of the increasingly long growth and stirring timescales of planetesimals (e.g., Kenyon & Bromley 2008). The moderate radial range of planetesimals in the one-belt model presented in this study therefore fits better in the debris disc formation theory.

  • 2.

    Two parent belts. Without stellar winds of sufficient strength, the data are consistent with a two-ring disc, with a warm inner and a cold outer component. Many systems are believed to have a two-belt configuration since their SEDs can be well fitted by using two blackbody curves (e.g., Matthews et al. 2010; Donaldson et al. 2013; Broekhoven-Fiene et al. 2013; Su et al. 2013). Surveys of two-component discs around stars of different spectral types highlight that inner and outer components have median temperature values of ≈190 K and ≈60 K, respectively (e.g., Morales et al. 2011; Ballering et al. 2013). This yields a distance ratio of router/rinner = (190 / 60)2 ≈ 10, indicating a distinct gap between both components. One possible explanation of this result considers planets that have formed within the discs and split them up (e.g., Ertel et al. 2012). In our best-fit two-belt model (Model II) the mean planetesimal distances for the inner and outer discs have a ratio of ≈5, which is close to what was found for many other systems. By testing different maximum eccentricities emax of the inner and outer planetesimal belt, we discovered that both components must have similar dynamical excitation of emax ≈ 0.04 to be in good agreement with the radial profile data. One problem is that this level, especially in the inner belt, is lower than what is expected for the stirring by a planet (e.g., Mustill & Wyatt 2009), suggesting that the gap between the two belts may not be populated by planets. In that case, however, it would be difficult to explain what else, if not planets, has cleared up the wide gap between the two belts. Nevertheless, the problem can be mitigated by the assumption that possible planets in the gap are in nearly circular orbits and/or have low masses.

  • 3.

    One extended parent belt. We discuss this possible disc architecture by using more than two belts adjacent to each other as a proxy. In principle, this could be the best model consistent with planet(esimal) formation theories. The optical thickness profile would be nearly constant over a wide radial range, starting to decrease beyond ≈200 au. The radial surface density profile of the underlying planetesimal disc is rising outwards, consistent with a long-term inside-out collisional erosion of such a disc. Therefore, from the point of view of collisional modelling we can also confirm the extended planetesimal belt hypothesis already proposed in Ertel et al. (2014).

More observations are required to distinguish between the competing scenarios discussed in this paper. LMT and ALMA are the most promising facilities for shedding light on the actual structure of HIP 17439’s debris disc. We simulated LMT and ALMA images of our best one- and two-belt models at millimetre/submillimetre wavelengths. These tests highlight that present-day telescopes are possibly capable of distinguishing between a one- or a two-belt model but only with strong observational effort.

1

Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.

2

GAS in Protoplanetary Systems (Dent et al. 2013).

3

Disc Emission via Bias-free Reconnaissance in the Infrared/ Submillimetre (Phillips et al.2010; Matthews et al., in prep.).

4

Ṅi describes the middle term with the loss function Lij of Eq. (8) in Löhne et al. (2012).

Acknowledgments

We thank the reviewer for a speedy and constructive report that helped to improve the manuscript. C.S., T.L., and A.V.K. acknowledge support by the Deutsche Forschungsgemeinschaft (DFG) through projects Kr 2164/10-1 and Lo 1715/1-1. S.E. thanks the French National Research Agency (ANR, contract ANR-2010 BLAN-0505-01, EXOZODI) and PNP-CNES for financial support. J.P.M. and C.E. are partly supported by Spanish grant AYA 2011-26202.

References

  1. Backman, D. E., & Paresce, F. 1993, in Protostars and Planets III, eds. E. H. Levy, & J. I. Lunine, 1253 [Google Scholar]
  2. Ballering, N. P., Rieke, G. H., Su, K. Y. L., & Montiel, E. 2013, ApJ, 775, 55 [NASA ADS] [CrossRef] [Google Scholar]
  3. Benedict, G. F., McArthur, B. E., Gatewood, G., et al. 2006, AJ, 132, 2206 [NASA ADS] [CrossRef] [Google Scholar]
  4. Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bohren, C. F., & Huffman, D. R. 1983, Absorption and scattering of light by small particles (New York: Wiley) [Google Scholar]
  6. Booth, M., Kennedy, G., Sibthorpe, B., et al. 2013, MNRAS, 428, 1263 [NASA ADS] [CrossRef] [Google Scholar]
  7. Broekhoven-Fiene, H., Matthews, B. C., Kennedy, G. M., et al. 2013, ApJ, 762, 52 [NASA ADS] [CrossRef] [Google Scholar]
  8. Brott, I., & Hauschildt, P. H. 2005, in The Three-Dimensional Universe with Gaia, eds. C. Turon, K. S. O’Flaherty, & M. A. C. Perryman, ESA SP, 576, 565 [Google Scholar]
  9. Bryden, G., Beichman, C. A., Carpenter, J. M., et al. 2009, ApJ, 705, 1226 [NASA ADS] [CrossRef] [Google Scholar]
  10. Burns, J. A., Lamy, P. L., & Soter, S. 1979, Icarus, 40, 1 [NASA ADS] [CrossRef] [Google Scholar]
  11. Churcher, L. J., Wyatt, M. C., Duchêne, G., et al. 2011, MNRAS, 417, 1715 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cranmer, S. R., & Saar, S. H. 2011, ApJ, 741, 54 [NASA ADS] [CrossRef] [Google Scholar]
  13. Dent, W. R. F., Thi, W. F., Kamp, I., et al. 2013, PASP, 125, 477 [NASA ADS] [CrossRef] [Google Scholar]
  14. di Folco, E., Absil, O., Augereau, J.-C., et al. 2007, A&A, 475, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Donaldson, J. K., Lebreton, J., Roberge, A., Augereau, J.-C., & Krivov, A. V. 2013, ApJ, 772, 17 [NASA ADS] [CrossRef] [Google Scholar]
  16. Draine, B. T. 2003, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
  17. Eiroa, C., Fedele, D., Maldonado, J., et al. 2010, A&A, 518, L131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Eiroa, C., Marshall, J. P., Mora, A., et al. 2011, A&A, 536, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Eiroa, C., Marshall, J. P., Mora, A., et al. 2013, A&A, 555, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Ertel, S., Wolf, S., Metchev, S., et al. 2011, A&A, 533, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Ertel, S., Wolf, S., & Rodmann, J. 2012, A&A, 544, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Ertel, S., Marshall, J. P., Augereau, J.-C., et al. 2014, A&A, 561, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Fernandes, J. M., Vaz, A. I. F., & Vicente, L. N. 2011, A&A, 532, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Garcés, A., Ribas, I., & Catalán, S. 2010, in Pathways Towards Habitable Planets, eds. V. Coudé du Foresto, D. M. Gelino, & I. Ribas, ASP Conf. Ser., 430, 437 [Google Scholar]
  25. Gray, R. O., Corbally, C. J., Garrison, R. F., et al. 2006, AJ, 132, 161 [NASA ADS] [CrossRef] [Google Scholar]
  26. Greenberg, R., Bottke, W. F., Carusi, A., & Valsecchi, G. B. 1991, Icarus, 94, 98 [NASA ADS] [CrossRef] [Google Scholar]
  27. Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
  28. Holsapple, K. A. 1994, Planet. Space Sci., 42, 1067 [NASA ADS] [CrossRef] [Google Scholar]
  29. Housen, K. R., & Holsapple, K. A. 1990, Icarus, 84, 226 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kennedy, G. M., & Wyatt, M. C. 2010, MNRAS, 405, 1253 [NASA ADS] [Google Scholar]
  31. Kenyon, S. J., & Bromley, B. C. 2008, ApJS, 179, 451 [NASA ADS] [CrossRef] [Google Scholar]
  32. Koerner, D. W., Kim, S., Trilling, D. E., et al. 2010, ApJ, 710, L26 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kóspál, Á., Ardila, D. R., Moór, A., & Ábrahám, P. 2009, ApJ, 700, L73 [NASA ADS] [CrossRef] [Google Scholar]
  34. Krist, J. E., Stapelfeldt, K. R., Bryden, G., et al. 2010, AJ, 140, 1051 [NASA ADS] [CrossRef] [Google Scholar]
  35. Krist, J. E., Stapelfeldt, K. R., Bryden, G., & Plavchan, P. 2012, AJ, 144, 45 [NASA ADS] [CrossRef] [Google Scholar]
  36. Krivov, A. V. 2010, RA&A, 10, 383 [Google Scholar]
  37. Krivov, A. V., Sremčević, M., & Spahn, F. 2005, Icarus, 174, 105 [NASA ADS] [CrossRef] [Google Scholar]
  38. Krivov, A. V., Löhne, T., & Sremčević, M. 2006, A&A, 455, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Krivov, A. V., Eiroa, C., Löhne, T., et al. 2013, ApJ, 772, 32 [NASA ADS] [CrossRef] [Google Scholar]
  40. Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to Stellar Winds [Google Scholar]
  41. Lebreton, J., Augereau, J.-C., Thi, W.-F., et al. 2012, A&A, 539, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Lestrade, J.-F., Matthews, B. C., Sibthorpe, B., et al. 2012, A&A, 548, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Li, A., & Greenberg, J. M. 1998, A&A, 331, 291 [NASA ADS] [Google Scholar]
  44. Löhne, T., Krivov, A. V., & Rodmann, J. 2008, ApJ, 673, 1123 [NASA ADS] [CrossRef] [Google Scholar]
  45. Löhne, T., Augereau, J.-C., Ertel, S., et al. 2012, A&A, 537, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Maldonado, J., Eiroa, C., Villaver, E., Montesinos, B., & Mora, A. 2012, A&A, 541, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
  48. Matthews, B. C., Sibthorpe, B., Kennedy, G., et al. 2010, A&A, 518, L135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Marshall, J. P., Löhne, T., Montesinos, B., et al. 2011, A&A, 529, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Marshall, J. P., Moro-Martín, A., Eiroa, C., et al. 2014, A&A, 565, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Matthews, B. C., Krivov, A. V., Wyatt, M. C., Bryden, G., & Eiroa, C. 2014, in Protostars and Planets VI, eds. H. Beuther, R. Klessen, C. Dullemond, & T. Henning (Univ. of Arizona Press), in press [arXiv:1401.0743] [Google Scholar]
  52. Minato, T., Köhler, M., Kimura, H., Mann, I., & Yamamoto, T. 2006, A&A, 452, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Morales, F. Y., Rieke, G. H., Werner, M. W., et al. 2011, ApJ, 730, L29 [NASA ADS] [CrossRef] [Google Scholar]
  54. Moro-Martín, A., Carpenter, J. M., Meyer, M. R., et al. 2007, ApJ, 658, 1312 [NASA ADS] [CrossRef] [Google Scholar]
  55. Mukai, T., & Yamamoto, T. 1982, A&A, 107, 97 [NASA ADS] [Google Scholar]
  56. Müller, S., Löhne, T., & Krivov, A. V. 2010, ApJ, 708, 1728 [NASA ADS] [CrossRef] [Google Scholar]
  57. Mustill, A. J., & Wyatt, M. C. 2009, MNRAS, 399, 1403 [NASA ADS] [CrossRef] [Google Scholar]
  58. O’Brien, D. P., & Greenberg, R. 2003, Icarus, 164, 334 [CrossRef] [Google Scholar]
  59. Ossenkopf, V. 1991, A&A, 251, 210 [NASA ADS] [Google Scholar]
  60. Phillips, N. M., Greaves, J. S., Dent, W. R. F., et al. 2010, MNRAS, 403, 1089 [NASA ADS] [CrossRef] [Google Scholar]
  61. Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  62. Plavchan, P., Werner, M. W., Chen, C. H., et al. 2009, ApJ, 698, 1068 [NASA ADS] [CrossRef] [Google Scholar]
  63. Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Reidemeister, M., Krivov, A. V., Stark, C. C., et al. 2011, A&A, 527, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Schmitt, J. H. M. M., Fleming, T. A., & Giampapa, M. S. 1995, ApJ, 450, 392 [NASA ADS] [CrossRef] [Google Scholar]
  66. Stewart, S. T., & Leinhardt, Z. M. 2009, ApJ, 691, L133 [NASA ADS] [CrossRef] [Google Scholar]
  67. Su, K. Y. L., Rieke, G. H., Malhotra, R., et al. 2013, ApJ, 763, 118 [NASA ADS] [CrossRef] [Google Scholar]
  68. Swinyard, B. M., Ade, P., Baluteau, J.-P., et al. 2010, A&A, 518, L4 [Google Scholar]
  69. Thébault, P., & Augereau, J.-C. 2007, A&A, 472, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Thébault, P., & Wu, Y. 2008, A&A, 481, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Torres, C. A. O., Quast, G. R., da Silva, L., et al. 2006, A&A, 460, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
  74. Wood, B. E. 2004, Liv. Rev. Sol. Phys., 1, 2 [Google Scholar]
  75. Wood, B. E., Müller, H.-R., Zank, G. P., & Linsky, J. L. 2002, ApJ, 574, 412 [NASA ADS] [CrossRef] [Google Scholar]
  76. Wood, B. E., Müller, H.-R., Zank, G. P., Linsky, J. L., & Redfield, S. 2005, ApJ, 628, L143 [Google Scholar]
  77. Wyatt, M. C. 2008, ARA&A, 46, 339 [NASA ADS] [CrossRef] [Google Scholar]
  78. Wyatt, S. P., & Whipple, F. L. 1950, ApJ, 111, 134 [NASA ADS] [CrossRef] [Google Scholar]
  79. Wyatt, M. C., Kennedy, G., Sibthorpe, B., et al. 2012, MNRAS, 424, 1206 [NASA ADS] [CrossRef] [Google Scholar]
  80. Zubko, V. G., Mennella, V., Colangeli, L., & Bussoletti, E. 1996, MNRAS, 282, 1321 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Best-fit results with 3σ uncertainties of the power-law models from Ertel et al. (2014).

In the text
Table 2

ACE input parameters for one-belt models.

In the text
Table 3

ACE input parameters for two-belt models.

In the text

All Figures

thumbnail Fig. 1

β ratio for several grain materials. The values are calculated with the stellar parameters of HIP 17439. Refractive indices are taken from Draine (2003, astrosilicate), Li & Greenberg (1998, water ice), and Zubko et al. (1996, amorphous carbon).
In the text
thumbnail Fig. 2

Observed SED and radial profiles plotted along with the simulated data from the FG, SW1, and SW2 models in Table 2. For a detailed description of the observational data see Ertel et al. (2014). Note that data points with a signal-to-noise ratio <3 are excluded from the available Spitzer/IRS spectrum. In the radial profile plots, the gray-shaded areas depict the observed data with 1σ uncertainties at PACS wavelengths (from top to bottom: 70, 100, and 160μm). Cuts along the long and short axes are given in the left and right column, respectively.

In the text
thumbnail Fig. 3

Size and radial distributions of particles in disc models FG (left column) and SW1 (right column). Top: normal optical thickness per size decade τ⊥ as a function of grain size s. The curves depict the contributions at several distances from the star. For comparison, the straight line in panel a) shows the theoretically predicted slope for an infinite collisional cascade assuming QD⋆∝sbs\hbox{$Q_\text{D}^\star \propto s^{b_\text{s}}$} with bs = − 0.37, which is n(s) ∝ s-3.7 (O’Brien & Greenberg 2003). Bottom: radial profiles of the total optical thickness (integrated over all grain sizes).

In the text
thumbnail Fig. 4

Ratio of the collision and transport timescales of the FG and SW1 run inside (10 au), within (130 au) and outside (200 au) the planetesimal ring. Only particles with eccentricities e< 0.02 are included.

In the text
thumbnail Fig. 5

Same as Fig. 2, but for FG and OSP (Table 2).
In the text
thumbnail Fig. 6

Radial profile of the optical thickness in Model II. The shaded regions mark the extent of the inner and outer parent belts.

In the text
thumbnail Fig. 7

SEDs and radial profiles for Model I (left column) and Model II (right column) in Table 3. Profiles for inner and outer discs are star-subtracted.
In the text
thumbnail Fig. 8

Discs with one (OSP, Table 2) and two (Model II, Table 3) components as seen by different telescopes. Top panels: unconvolved discs at 870 μm and 1.1 mm (left- and right-hand side of each splitted image). Units are Jy/pixel, where 1 pixel = 0.2′′ × 0.2′′. Middle panels; simulated LMT/AzTEC images that were generated by convolving the models at 1.1 mm with a Gaussian (FWHM = 6′′). The white circle in the lower right of the left image illustrates the beam size. The contours in each image represent 2σ, 3σ, 4σ, and 5σ levels. Bottom panels: synthetic ALMA images in Band 7 (central wavelength 870 μm), using antenna configuration alma.out01 and a water vapour overburden of 0.1 mm. The beam size is 1.1′′ × 0.9′′. With an on-source integration time of 15 h a sensitivity of ≈10μJy/beam was achieved.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.