| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201322171 | |
| Published online | 04 July 2014 | |
Numerical simulations of stellar jets and comparison between synthetic and observed maps: clues to the launch mechanism⋆
1
Dipartimento di Fisica e Astronomia, Università di
Firenze, via G. Sansone 1, 50019
Sesto F. no, Firenze, Italy
2
INFN – Sezione di Firenze, via G. Sansone 1, 50019 Sesto F. no,
Firenze,
Italy
3
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5,
50125
Firenze,
Italy
Received:
28
June
2013
Accepted:
14
April
2014
High angular resolution spectra obtained with the Hubble Space Telescope Imaging Spectrograph (HST/STIS) provide rich morphological and kinematical information about the stellar jet phenomenon, which allows us to test theoretical models efficiently. In this work, numerical simulations of stellar jets in the propagation region are executed with the PLUTO code, by adopting inflow conditions that arise from former numerical simulations of magnetized outflows, accelerated by the disk-wind mechanism in the launching region. By matching the two regions, information about the magneto-centrifugal accelerating mechanism underlying a given astrophysical object can be extrapolated by comparing synthetic and observed position-velocity diagrams. We show that quite different jets, like those from the young T Tauri stars DG-Tau and RW-Aur, may originate from the same disk-wind model for different configurations of the magnetic field at the disk surface. This result supports the idea that all the observed jets may be generated by the same mechanism.
Key words: stars: variables: T Tauri, Herbig Ae/Be / accretion, accretion disks / shock waves / methods: numerical / Herbig-Haro objects
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
The jet phenomenon appears to be very robust and ubiquitous in nature, as collimated outflows are seen on a large variety of spatial scales and masses of the central source, from active galactic nuclei to compact objects, and to forming stars. Since the jet properties scale with the depth of the gravitational potential well of the central object, it is widely viewed that jet formation may rely on an universal mechanism. Observations can only provide the elements necessary to test the validity of the proposed theories for stellar jets, however, because of the proximity of star formation regions and the abundance of emitted spectral lines.
Stellar jets are found in association with accretion disks, and are observed at all stages of the formation process, from the protostar phase to the dissipation of the disk itself. Jets are associated with all kinds of stellar masses and are believed to play a fundamental role in the formation process, as they may regulate the extraction of the excess angular momentum from the star-disk system, allowing the accretion of matter onto the central source. For this reason, in recent years, jets from young stellar objects have been the target of many observational campaigns at different wavelengths (Bally et al. 2007). In particular, high angular resolution images and spectra taken with the Hubble Space Telescope (HST) at optical wavelengths have provided unprecedented information on the morphology and kinematics of these systems, with data resolved spectrally and spatially both along and across the flow (see, e.g., Bacciotti et al. 2000; Bacciotti 2002; Hartigan & Morse 2007; Coffey et al. 2007). One of the most interesting results of these observations is the radial velocity shift between two sides of a jet with respect to the axis (Bacciotti et al. 2002; Woitas et al. 2005; Coffey et al. 2008). If interpreted as jet rotation, this result would confirm the idea that jets carry away angular momentum from the accretion disk in line with the magneto-hydrodynamic (MHD) models, and the jet generation process would be due to the combination of magnetic and centrifugal forces (Blandford & Payne 1982; Pudritz 1992; Ferreira 1997).
According to the magneto-centrifugal theory, the wind material is launched along the magnetic surfaces attached to the rotating star and disk. The winds are then collimated magnetically just a few AUs above the star/disk by the action of a self-generated strong toroidal magnetic field. In the process, the excess angular momentum is extracted from the system and carried away with the jet, and the matter is allowed to accrete onto the star, whose rotation is also slowed down. The theory is elegant and very general, and within its framework various models have been proposed that differ for the region from which the disk is accelerated: stellar winds from the star surface (Sauty et al. 1999), the X-wind, originating from the inner edge of the accretion disk (Shu et al. 2000), or the disk-wind, where particles are launched from an extended region of the magnetized, Keplerian disk (Pudritz et al. 2007).
Unfortunately, observations cannot directly test the magneto-centrifugal launch mechanism yet because of the small scale involved (a few AUs at most). In fact, neither the optics of HST nor the ground telescopes equipped with adaptive optics can reach an angular resolution higher than 0.1′′, equivalent to ~12−14 AUs for the nearest star formation regions. In addition, the dusty formation cloud can hide the launching region in younger systems, which favors the observations of jets from more evolved, cleared T-Tauri stars. Finally, in both cases the interpretation of the jet spectra is made difficult by projection effects along the line of sight. Nevertheless, valuable observational studies at high resolution and in different wavelengths have successfully investigated the properties of the jets in the acceleration region immediately downstream from the collimation zone, between ~10 and 100 AU from the star, and have provided important constraints to the launch process (e.g., Bacciotti et al. 2000; Woitas et al. 2002; Melnikov et al. 2009; Coffey et al. 2008; Takami et al. 2004; Pyo et al. 2003, 2006; Hartigan & Morse 2007; Agra-Amboage et al. 2011). The only way to connect the observed region to the launch zone, however, is to create a logical link via numerical studies.
Numerical simulations are a very powerful tool to go beyond the limits encountered by observations, and to probe theoretical models or interpret observational data. Nevertheless, running simulations that include both the launching region, a few AU wide, and the propagation region, extending up to hundreds or thousands AU from the star-disk system, is still a goal beyond the present possibilities. In fact, the values of the physical quantities differ by many orders of magnitude in the two zones, and this introduces severe numerical difficulties. For this reason the two regions are, usually, investigated separately. So, the jet launching is investigated with numerical simulations based on magneto-centrifugal models (e.g., Pudritz et al. 2006; Zanni et al. 2007; Meliani et al. 2006; Romanova et al. 2009; Tzeferacos et al. 2013), while the jet propagation is studied by running simulations of a supersonic collimated jet flowing beyond an ideal nozzle placed at some distance from the disk (e.g., Rubini et al. 2007; Bonito et al. 2010).
In this paper, the problem has been overcome with a procedure that operates a matching of the values of the quantities derived from the simulations in the two zones. This is done by imposing that the supersonic jet evolves in the propagation region from a formerly accelerated outflow arising from the launching and collimation region. The general acceleration-propagation matching procedure developed by the authors, (hereafter APM procedure, see Sect. 3) goes through the following three steps:
 |
Fig. 1 Continuum-subtracted HST/STIS position-velocity diagrams of the flow from DG Tau, in the [S ii] λ6731 line and in slit positions from S1 to S7 (from southeast to northwest), offset by 0.07 arcsec across the jet width. The colored contours are from 1.1 × 10-15 erg s-1 arcsec-2 cm-2 Å-1 (equivalent to 3σ), with a ratio of 22/5. The vertical line marks zero velocity with respect to the star. The horizontal lines mark the position of the star and of previously identified knots. Adapted from MA14. |
-
1.
The determination of the quantities in the launching-collimation region bounded by the rotating disk has been addressed by referring to numerical works already in the literature, and in particular the study of Pudritz et al. (2006, hereafter P06). This paper provides axisymmetric numerical solutions of outflows accelerated magneto-centrifugally by an underlying accretion disk. The nondimensional solutions described there have been specialized to the cases of interest to us by introducing proper scale factors (stellar mass, width of the launching region, gas parameters, etc...) derived from observational studies of the real cases considered.
-
2.
We use the solutions derived in this way to provide the inflow conditions for numerical simulations of propagating jets flowing from a nozzle, ideally placed at the border of the accelerating region. The propagation is then followed by axisymmetric simulations in (r,z) cylindrical coordinates, which evolve the outflow up to distances of the order of hundreds of AUs, i.e., the regions observed at high angular resolution. In this model, the point (z = 0,r = 0) represents the star position, and the nozzle is placed at the distance znozzle from the disk, representing the border of the launching region simulated in P06. The final result of this step is a set of maps of the physical quantities in the jet meridional plane produced at the end of the run.
-
3.
The gas parameters calculated in the propagation region are entered as input values in a code developed by us (Optical Telescope Simulator, OTS) to generate images and synthetic position-velocity diagrams (PVDs) of the line emission as they would be produced by a given instrument working at optical wavelengths. The synthetic maps are produced by calculating the emissivity in each cell on the basis of the physical quantities obtained in step 2, and then integrating through the body of the jet and along the line of sight. The aim of this step is to compare the emission produced by the numerical jet to the emission observed in reality to get feedback on the validity of the assumptions made for the launch mechanism in the first step.
In this paper, we focus on the initial section of jets from cleared T-Tauri stars, and in particular on the bright 5 arcseconds of the outflows from DG-Tau (Bacciotti et al. 2000, 2002; Bacciotti 2002; Coffey et al. 2008), and from RW-Aur (Woitas et al. 2002, 2005; Melnikov et al. 2009), for which a big wealth of data obtained at 0.1′′ with HST is available. In the third step, therefore, we mimic the properties of the Space Telescope Imaging Spectrograph (STIS) onboard HST, using in the OTS code the same spatial and spectral resolution and slit setting of the real instrument. As we show in the following, this procedure demonstrates to be a powerful tool to set useful constraints on the launch process, and to proceed toward a complete understanding of the role of collimated outflows in the formation of a stellar system.
The paper is organized as follows. The indications on kinematic and morphological properties of DG-Tau and RW-Aur jets provided by observations are summarized in Sect. 2. Section 3 describes the general setup procedure, including the choice of the physical parameters (Sect. 3.3) and details about the profiles of the quantities at the inlet (Sect. 3.3.3). In particular, Sect. 3.4 contains a short description of the post-processing OTS code designed to return synthetic PVDs. Our results are described in Sect. 4, and a discussion is offered in Sect. 5, together with our main conclusions. In the Appendix, we discuss the validity of our results with an additional test case simulation.
2. Observations of the DG-Tau and RW-Aur jets
The jet associated with DG-Tau, named HH 158, was one of the first Harbig-Haro objects discovered (Mundt & Fried 1983; Solf & Boehm 1993), and the jet-like nature was definitely confirmed by Lavalley et al. (1997). Its inclination with respect to the line of sight is about 38° (Eislöffel & Mundt 1998), and in its first arcseconds the jet appears as a series of luminous opening bubbles, as suggested first in the images formed in bright optical forbidden lines in Lavalley et al. (1997); Lavalley-Fouquet et al. (2000); Dougados et al. (2002). Further downstream, the object HH-702 at ~11′′ away from the source may be part of the same outflow (McGroarty et al. 2007), indicating that the bright microjet close to the star flows in the wake of a previous emission episode. The observations in the [Fe ii] λ1.644 μm line discussed in Pyo et al. (2003) reveal two distinct radial velocity components in the blue-shifted lobe, and detect the redshifted counterflow whose emission features suggest the presence of an optically thick circumstellar disk of ~140 AU in radius. A warm molecular wind component thermalized at 2000 K has also been detected (Takami et al. 2004).
The jet has been widely studied at high resolution with HST/STIS, as described in Bacciotti et al. (2000); Bacciotti (2002); Coffey et al. (2007, 2008). Recently, (Maurri et al. 2014, hereafter MA14), provided a complete set of PVDs of the surface brightness in this jet, and maps of physical quantities derived with spectral diagnostic techniques. Finally, multiepoch observations in the X-ray domain (Güdel et al. 2008) show a rich phenomenology. In particular, luminous moving outer knots appear to fade compatibly with cooling models, while closer to the star there is a component showing a steady source of soft X-Rays. These observations provide a huge amount of information that must be taken into account in the set-up of the numerics. In particular, the PVD maps in MA14 constitute the testbed of our simulations for this jet.
The seven long-slit spectra analyzed in MA14 were taken on January 14 1999, keeping the slit parallel to the outflow axis and stepping it by 0.7′′ across the jet width. In this way it was possible to obtain a three-dimensional data cube of the optical outflow, with two spatial dimensions and one in radial velocity. The spectra included several strong forbidden lines, as [S ii] λλ6731, [N ii] λλ6583, [O i] λλ6363, and have spectral and spatial resolution of 0.554 Å and ~0.1′′, respectively. To ease the comparison with synthetic PVDs (see Sect. 4), we report in Fig. 1 the seven observational PVDs for the [S ii] λ6731 line.
The PVDs of the jet show two distinct regions of high brightness, the first one between the source and 1.4′′, called hereafter the first blob, and the second one between ~3′′ and ~4.5′′, defined hereafter as the second blob. The plasma has a wide range of velocities (up to ~−300 km s-1) close to the source, confirming that most of the accelerating process is confined in the very first AUs; in the outer slit positions, however, lower and lower velocities are seen, supporting an onion-like kinematic structure (Bacciotti et al. 2000). For all the forbidden lines, and for all the slit positions, the surface brightness peaks at low velocities at the beginning of the jet. Further away, the first blob appears to have at least two different velocity components, one at constant low velocity, and one of progressively higher speed moving away from the star. This could be due to either a persisting acceleration or to the fact that progressively slower material is emitted from the source as time passes. The region of low emission between 1.4′′ and ~3.1′′ from the star turns out to be occupied by tenuous plasma at high ionization and temperature (Dougados et al. 2000). The second blobshines between ~3′′ and ~4.5′′ in all the emission lines, and the emission properties suggest that the gas is reheated by shocks (MA14). This is also probably the nature of a faint third blob observed at 7′′ in the HST spectra, arising from a previous emission episode and not analyzed in MA14.
Similar data are available for the bipolar jet from the T-Tauri star RW-Aur, located in the same star forming region as DG-Tau (at a distance of 140 parsecs). The spectra, taken by HST/STIS with the same slit setting and processed with the same technique used in MA14 to generate the PVDs of the jet from DG-Tau, are discussed in Woitas et al. (2002, 2005); Melnikov et al. (2009). In particular, Melnikov et al. (2009, Fig. 1) provide a set of seven parallel PVDs for the [S ii] λ6731 lines, extending over 4′′ on both sides of the source.
The PVDs show that the jet is highly collimated, and presents a chain of emitting knots, over the whole jet length, that has been widely investigated in the last decade. There is a general agreement about the existence of pulsating mechanisms at work at the base of the jet, though some uncertainty holds about the temporal gap between knots. Moving knots in the [SII] lines, down to 56 AU from the source, have been observed by Dougados et al. (2000). These knots might be due to temporal fluctuations with period ranging from ~5 to ~10 yr, (Melnikov et al. 2009). Lopez-Martin et al. (2003) have suggested that the inner knot spacing might originate by superposition of short timescale random perturbations (with period of order 3−10 years), and more regular fluctuations on longer timescales of ≈20 yr. Finally, the correlation between time variability outflows in T-Tauri stars, and the driving source of unsteady mass accretion has more recently been investigated by Chou et al. (2013).
The jet is highly asymmetric in brightness, velocity, and physical properties. The radial velocity peaks at −180 km s-1 in the blue lobe and at +100 km s-1 in the red lobe, and there is not a spread in velocity as wide as in DG-Tau. In general, the properties of the RW-Aur jet appear to be very different from those in the DG-Tau jet, and we have thus chosen to consider this dataset as a useful test of the predictive properties of our numerical procedure.
3. Numerical simulations setup
3.1. Equations and algorithms
We perform numerical simulations of a magnetized, rotating jet in cylindrical coordinates r and z, under the assumption of axisymmetry (∂/∂φ ≡ 0).
With the exception of the test case described in Apprndix A, in all our simulations the jet propagates into a computational domain of 300 × 1200 AU in r − z, described by a grid of 420 × 1500 cells clustered in the nozzle area, with grid density that decreases for increasing z and r.
The adopted code is PLUTO (Mignone 2009). PLUTO
provides a multiphysics, multialgorithm modular environment, especially tailored for
simulations of time-dependent, shocked flows in Newtonian or relativistic regime. The code
exploits a general framework designed to integrate a system of fluid equations written in
conservative form, and based on Godunov-like, shock-capturing schemes. The equations can
be written as 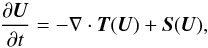 (1)where U denotes the
state vector of conservative variables, T(U)
is a tensor whose rows are the fluxes of each component of U, and
S(U)
is the source terms vector. When using the ideal MHD module, the former system reads
(1)where U denotes the
state vector of conservative variables, T(U)
is a tensor whose rows are the fluxes of each component of U, and
S(U)
is the source terms vector. When using the ideal MHD module, the former system reads
![\begin{equation} \vec{U} = \left[ \begin{array}{c} \rho\\ \vec{m}\\ \vec{B}\\ E \end{array} \right], \qquad \vec{T} = \left[ \begin{array}{c} \vec{m}\\ \vec{mv}-\vec{BB}+p_{\rm t}\vec{I}\\ \vec{vB}-\vec{Bv}\\ (E+p_{\rm t})\vec{v}-(\vec{v}\cdot\vec{B})\vec{B} \end{array} \right], \end{equation}](/articles/aa/full_html/2014/07/aa22171-13/aa22171-13-eq38.png) (2)where ρ is the mass density,
v the fluid velocity, B the magnetic
field, m =
ρv the momentum
density, B the unit tensor, E = ρ |
v | 2/2 +
p/ (γ − 1) + |
B | 2/2
the total energy density (assuming an ideal gas law with adiabatic index γ), and p and pt = p + |
B | 2/ 2
are the thermal and total pressures, respectively. The source just contains the
geometrical terms appropriate to cylindrical coordinates: since the jet nozzle is placed
at a distance from the star where gravity effects are negligible, gravity and other body
forces have been neglected.
(2)where ρ is the mass density,
v the fluid velocity, B the magnetic
field, m =
ρv the momentum
density, B the unit tensor, E = ρ |
v | 2/2 +
p/ (γ − 1) + |
B | 2/2
the total energy density (assuming an ideal gas law with adiabatic index γ), and p and pt = p + |
B | 2/ 2
are the thermal and total pressures, respectively. The source just contains the
geometrical terms appropriate to cylindrical coordinates: since the jet nozzle is placed
at a distance from the star where gravity effects are negligible, gravity and other body
forces have been neglected.
The transport equation for the electron density
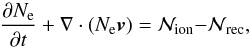 (3)is also included
in the conservative system, allowing us to evolve the ionization fraction for the atomic
hydrogen specie. The terms
(3)is also included
in the conservative system, allowing us to evolve the ionization fraction for the atomic
hydrogen specie. The terms 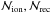 represent the ionization and recombination source terms. The radiative cooling processes
are described by the one-ion nonequilibrium model (option “SNeq” into the
PLUTO code), which introduces a simplified radiative cooling source term in the energy
equation. Such a choice relies on the assumption that emissivity, in the region of
interest, arises from weakly shocked gas, whose temperature should not exceed 75 000 K,
the maximum value allowed in this model. The reliability of former assumptions has been
checked in the test cases TESTDG3 and TESTDG4 (see Appendix A).
represent the ionization and recombination source terms. The radiative cooling processes
are described by the one-ion nonequilibrium model (option “SNeq” into the
PLUTO code), which introduces a simplified radiative cooling source term in the energy
equation. Such a choice relies on the assumption that emissivity, in the region of
interest, arises from weakly shocked gas, whose temperature should not exceed 75 000 K,
the maximum value allowed in this model. The reliability of former assumptions has been
checked in the test cases TESTDG3 and TESTDG4 (see Appendix A).
The system of equations should be closed by the solenoidal condition of the magnetic field, ∇·B = 0. However, in our simulations Br = Bz = 0 will be always zero, so that, thanks to the axisymmetric assumption, the solenoidal condition is automatically satisfied everywhere and anytime.
The adopted Riemann solver is a simple but robust two-wave solver (HLL); we used a linear upwind method for reconstruction of primitive variables (namely ρ, v, B, p, and nH) at cell interfaces, and we adopted the second order accurate Runge-Kutta scheme to update the discretized equations in time.
As far as boundary conditions are concerned, the jet and the outflow as arising from the extrapolation of the P06 model are injected in our simulations from the lefthand side (z = 0) boundary at all times, as will be specified further on in Sects. 3.3.3 and 3.3.4. Along the z-axis (r = 0) we assume standard conditions for axisymmetry, whereas zeroth-order outflow conditions are imposed at the outer boundaries in both r and z directions.
3.2. Summary of disk-wind theory and P06 results
Numerous theoretical and numerical works demonstrate that magneto-centrifugal winds can
efficiently extract gravitational energy and angular momentum from the accreting disk
(see, e.g., Blandford & Payne 1982; Ferreira 1997; Shu
et al. 2000; Romanova et al. 2002; Pudritz et al. 2007). Observations suggest the
existence of jets with different degree of collimation (Dougados et al. 2002, 2004), in agreement
with MHD models that predict the collimation of jets depends on the initial magnetic
configurations. According to the most popular models, magnetic field lines either
originate on the star surface and connect with the disk (e.g., Goodson et al. 1997), or they only thread the disk (Ouyed & Pudritz 1997). In the latter case, a
variety of radial magnetic configurations are possible, according to the power law
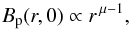 (4)which describes the
behavior of the poloidal magnetic field at the surface of the rotating disk. Both magnetic
configurations strongly peaked in the inner part of the disk, similar to the X-wind
configuration by Shu et al. (2000), and almost flat
magnetic profiles (Ouyed & Pudritz 1997)
can be generated by changing the value of μ; the “classical” self-similar disk-wind magnetic
geometry of Blandford & Payne (1982) is the
intermediate case for μ = −0.25, which yields Bp ∝ r−5/4.
(4)which describes the
behavior of the poloidal magnetic field at the surface of the rotating disk. Both magnetic
configurations strongly peaked in the inner part of the disk, similar to the X-wind
configuration by Shu et al. (2000), and almost flat
magnetic profiles (Ouyed & Pudritz 1997)
can be generated by changing the value of μ; the “classical” self-similar disk-wind magnetic
geometry of Blandford & Payne (1982) is the
intermediate case for μ = −0.25, which yields Bp ∝ r−5/4.
In P06, Pudritz and collaborators investigate four values of μ, the parameter that
drives both the jet mass load and the opening angle, or the collimation degree. The four
cases (0.0, −0.25, −0.50, −0.75) correspond to
poloidal magnetic fields more and more steeply declining with r. In particular, the
author shows that magnetic configurations corresponding to μ = 0.0 and −0.25 lead to highly collimated jets,
whereas μ = −0.5, −0.75
generate wide-angle outflows. Using the gas parameters at the surface of the rotating
accretion disk as boundary conditions, the authors let the outflow self-generate, and
provide the axisymmetric solution vector 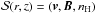 at the distance z = 72
ri from the central object,
ri being the simulation length scale,
defined as the inner disk radius threaded by the magnetic field lines.
at the distance z = 72
ri from the central object,
ri being the simulation length scale,
defined as the inner disk radius threaded by the magnetic field lines.
3.3. Initial and boundary conditions
The boundary inflow conditions at the inlet left side of the computational box, and the initial conditions representing the unperturbed ISM at time t = 0 must be initialized prior to running numerical simulations of propagating jets. While the ISM parameters can be chosen in a given range of “reasonable” values (and have weak influence on the results, see Sect. 4), the inflow conditions at the nozzle play a crucial role, and are derived from P06 solutions according to the afore mentioned APM procedure. In particular, the radial profiles of the hydrogen numerical density nH, velocities components (vz,vr,vφ), toroidal magnetic field Bφ, temperature T and ionization fraction xe must be assigned at the position z = znozzle.
In P06 the radial profiles of the solution 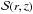 are given in nondimensional units, as functions of length, density, and velocity scales,
ri,
are given in nondimensional units, as functions of length, density, and velocity scales,
ri,
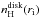 and
and
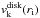 , defined, respectively, as
the disk radius threaded by the inner magnetic field lines on the disk surface, and the
corresponding gas density and Keplerian velocity. Therefore, once we chose the value of
the model parameter μ, and the corresponding numerical solution
, defined, respectively, as
the disk radius threaded by the inner magnetic field lines on the disk surface, and the
corresponding gas density and Keplerian velocity. Therefore, once we chose the value of
the model parameter μ, and the corresponding numerical solution
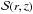 ,
the scale factors must be computed, taking both the physical properties of the observed
stellar jet and the prescriptions given in (Ouyed
& Pudritz 1997) into account.
,
the scale factors must be computed, taking both the physical properties of the observed
stellar jet and the prescriptions given in (Ouyed
& Pudritz 1997) into account.
3.3.1. The parameter μ
The simulations in P06 are driven by the choice of μ, which yields the radial profile of the poloidal magnetic field Bp(r) on the disk surface, and the outflow collimation degree. In particular, μ = 0.0 (i.e., Bp ∝ r-1) and μ = −0.25 (i.e., Bp ∝ r−5/4) generate profiles that smoothly decrease with r, and enforce the collimation effects (small angle jets) with respect to cases μ = −0.5 (i.e., Bp ∝ r−3/2) and μ = −0.75 (i.e., Bp ∝ r−7/4), where Bp(r) is peaked in the inner disk region and rapidly vanishes when moving outward (wide-angle jets). Our simulations have considered the four values of μ. Nevertheless, since parameters μ = 0.0 and μ = −0.25 provided quite similar solutions, only results for the case μ = −0.25 have been shown.
3.3.2. The scale factors
The scale factors depend on the properties of the jet under investigation, and drive
the choice of the simulation parameters. Namely, the length scale ri directly
affects the nozzle position with respect to the star, znozzle. In
P06 the solution 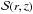 is provided at a distance ẑ
= 72 ri, beyond which we assume that the
gross features of the accelerated flow stay unchanged. Since the estimated length scale
ri is 0.07 AU for both DG-Tau and
RW-Aur, we have ẑ =
5.04 AU. As a consequence, the nozzle is supposed to be at
znozzle ≥
5.04 AU from the star.
is provided at a distance ẑ
= 72 ri, beyond which we assume that the
gross features of the accelerated flow stay unchanged. Since the estimated length scale
ri is 0.07 AU for both DG-Tau and
RW-Aur, we have ẑ =
5.04 AU. As a consequence, the nozzle is supposed to be at
znozzle ≥
5.04 AU from the star.
The choice of znozzle affects the value of some main inflow parameters, such as temperature, density, and ionization fraction. Their mean value can be computed by using the so-called BE technique, which allows us to estimate ionization fraction, electron density and, hence, total hydrogen density, from the ratios of some optical forbidden emission lines (see Bacciotti & Eislöffel 1999; Podio et al. 2006). In the recent past, the BE technique has been widely used to obtain physical parameters of observed jets (see, e.g., Bacciotti 2002; Hartigan & Morse 2007; Coffey et al. 2008; Melnikov et al. 2009). In Bacciotti (2002), the authors find a temperature of DG Tau jet, in the high-velocity channel and at z = 0.3 arcsec from the star, of ≈104 K, with positive gradient toward the source. In this frame we have decided to assume a value of 1.5 × 104 K at the nozzle position, for z = 0.2 arcsec. Moreover, Figs. 12 and 13 (Sect. 4) of MA14 provide the longitudinal profiles of the mean electron fraction and hydrogen density in the high-velocity channel. According to these figures, at z = 0.2 arcsec we have xe ≈ 0.3, and the hydrogen density is ≈8 × 105 cm-3 (Melnikov et al. 2009 provides a value of ≈3.2 × 104 cm-3 for RW-Aur).
The temperature and ionization fraction might be due to the presence of a photoionizing X-ray source, (Teşileanu et al. 2012). The assumption that a photoionizing X-ray flux is at work is also supported by recent observations of DG-Tau microjet, which shows a rich X-ray phenomenology with a hard component centered on the central object (Güdel et al. 2011). The values mentioned earlier in this paper are averaged through the body of the jet, and are typical of the high-velocity component. We can use them as local values if we assume that, at the nozzle, the flow is dominated by the high-velocity component. These physical parameters are needed to compute velocity, density, and magnetic scales, and to move from the nondimensional plots of P06 to dimensional plots, as explained here in the following.
Concerning the velocity scale, since the mass and the length scales are the same for
DG-Tau and RW-Aur jets, (M⋆ = 1
M⊙, ri = 0.07 AU),
the velocity scale defined as the Keplerian velocity on the disk surface at radius
ri for both jets is
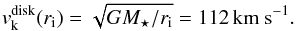 (5)The density scale
(5)The density scale
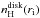 used in P06 cannot be
provided by direct observations of the disk surface, instead, it can be inferred by
matching some reference point in the nondimensional radial density profiles from P06
with real data. So, if we make reference to the density bulk close to the axis
(≈0.0013 for all values of
μ, see
P06, Fig. 2b), the scale factors are obtained by dividing the above cited values by
0.0013, leading to
used in P06 cannot be
provided by direct observations of the disk surface, instead, it can be inferred by
matching some reference point in the nondimensional radial density profiles from P06
with real data. So, if we make reference to the density bulk close to the axis
(≈0.0013 for all values of
μ, see
P06, Fig. 2b), the scale factors are obtained by dividing the above cited values by
0.0013, leading to 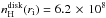 cm-3 for DG-Tau, and
cm-3 for DG-Tau, and
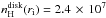 cm-3 for RW-Aur. It stands to
reason that these numbers suffer from some uncertainty, though results from numerical
simulations have shown to be robust with respect to small changes in their values.
cm-3 for RW-Aur. It stands to
reason that these numbers suffer from some uncertainty, though results from numerical
simulations have shown to be robust with respect to small changes in their values.
Once 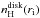 and
and
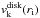 are computed, the
magnetic field scale, defined as the magnetic field strength on the disk surface at
radius ri, can finally be evaluated as
are computed, the
magnetic field scale, defined as the magnetic field strength on the disk surface at
radius ri, can finally be evaluated as
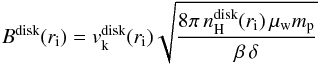 (6)where
μw, the mean molecular weight, depends
on the relative metal abundance in the accreting disk (μw = 1.4 for
solar-like abundances), mp is the proton mass, β is the gas to magnetic
pressure ratio, and δ is the Keplerian kinematic to thermal energy
density ratio, taken at the distance ri from the central object on the disk
surface. Assuming β = 1
/ 3 and δ = 300, as in P06, we find
(6)where
μw, the mean molecular weight, depends
on the relative metal abundance in the accreting disk (μw = 1.4 for
solar-like abundances), mp is the proton mass, β is the gas to magnetic
pressure ratio, and δ is the Keplerian kinematic to thermal energy
density ratio, taken at the distance ri from the central object on the disk
surface. Assuming β = 1
/ 3 and δ = 300, as in P06, we find
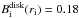 G for DG-Tau and 0.04
G for RW-Aur.
G for DG-Tau and 0.04
G for RW-Aur.
The set up parameters and the normalization factors are listed in Table 1.
Initialization parameters and scale factors.
 |
Fig. 2 Dimensional radial profiles at the nozzle from P06, for each value of the parameter μ. |
3.3.3. The inflow radial profiles
After computing the scale factors, the solution vector arising from the P06 model
 ,
is retrieved, and the dimensional radial profiles of nH(r,znozzle),
vz(r,znozzle),
vφ(r,znozzle)
and Bφ(r,znozzle)
can be injected into the simulation box. In all our simulations, we set vr(r,znozzle),
Bz(r,znozzle),
and Br(r,znozzle)
equal to zero. In fact, the nozzle is far enough from the source to assume that a purely
toroidal magnetic field is generated from the poloidal configuration on the disk (see,
e.g., Pudritz et al. 2006; Zanni et al. 2007), and that the flow is aligned with the axis.
Figure 2 shows the dimensional inflow profiles of
the solution vector
,
is retrieved, and the dimensional radial profiles of nH(r,znozzle),
vz(r,znozzle),
vφ(r,znozzle)
and Bφ(r,znozzle)
can be injected into the simulation box. In all our simulations, we set vr(r,znozzle),
Bz(r,znozzle),
and Br(r,znozzle)
equal to zero. In fact, the nozzle is far enough from the source to assume that a purely
toroidal magnetic field is generated from the poloidal configuration on the disk (see,
e.g., Pudritz et al. 2006; Zanni et al. 2007), and that the flow is aligned with the axis.
Figure 2 shows the dimensional inflow profiles of
the solution vector  in the inner region described in P06, up 1.4 AU from the axis.
in the inner region described in P06, up 1.4 AU from the axis.
We used the same shape for both the temperature T(r,znozzle) and the ionization fraction xe(r,znozzle) profiles, with constant values within the first 2 AU from the axis (15 000 K and 0.4, respectively) and linear extrapolation up to r ≈ 67 AU, where the gas parameters match the values of the ISM and stay unchanged up the border of the numerical box, which is located 300 AU far from the axis (see the discussion in Sect. 3.3.4).
3.3.4. The “tails”
As shown in Fig. 2, the inflow profiles do not go beyond the point r = 20ri (1.4 AU for both DG-Tau and RW-Aur), while the numerical box is 300 AU large. Therefore, one more degree of freedom arises from the choice of the function used to match inner and outer regions (from here on, the “tail”). Tails are meant to represent the wind lifted from the disk. Coaxial low velocity, wider winds seen in [H 2] lines are observed in many stellar outflows in the IR spectral range (see, e.g., Takami et al. 2004; Agra-Amboage et al. 2011). As an example, Takami et al. (2004) reports a molecular outflow from DG-Tau thermalized at 2000 K that extends up to ~50 AU from the jet axis in the transverse direction. A detailed study of low-velocity winds, together with their effects on the emission properties, is beyond the aim of this work. Here, we only show that tails play a crucial role to reproduce the observed jet features.
We use two different kinds of tails for our simulations:
-
Linear tail: profiles in the inner region decrease linearly from1.4 AU up to 67 AU(1 code unit), where they match the ISM values.Beyond this point they stay constant up to the numerical boxdomain, 300 AU far from the axis.
-
Exponential tail: same as linear tails, with exponential decrease from 1.4 to 67 AU.
3.4. The post-processing code OTS
The PLUTO code provides, cell-by-cell, the physical parameters in the 2D numerical domain. The post-processing code OTS inputs the values of the physical parameters in the gas and computes the emission producing synthetic PVDs of forbidden emission lines.
This goal is achieved in two steps. In the first step, we calculate the luminosity cell by cell in three selected forbidden lines commonly observed in these objects, that is [S ii]λ6731, [N ii]λ6583, and [O i]λ6363. To this aim, we follow the procedure described in Bacciotti & Eislöffel (1999). Briefly, the ionization state of oxygen and nitrogen is calculated by a dedicated routine that considers charge-exchange with hydrogen, collisional ionization and radiative and dielectronic recombination. Charge-exchange is the dominant mechanism for oxygen, while for nitrogen the contribution of the different processes is comparable. For both ions, the ionization fraction turns out to be a function of Te and xe. Because of its low ionization potential, sulphur can be considered totally ionized once in the regions of interest. The emissivities in the selected lines are calculated determining the electronic level population through the statistical equilibrium equations applied to a five-levels atom model. Elemental abundances are taken from Osterbrock (1989).
In the second step, after rotating the map of the emissivity in the (r,z) plane around the z-axis, to generate the azimuthal dimension φ, emissivities are summed up along the line of sight, and synthetic PVDs are created. In the present case, to simulate HST/STIS, cell-by-cell integration occurs inside “coring tubes” whose section mimics the HST angular resolution, 0.1′′ × 0.1′′ (14 AU × 14 AU at the distance of DG-Tau and RW-Aur), is inclined in the cylinder with the proper angle for the line of sight (38° w.r.t. the jet axis for DG-Tau, 46° for RW-Aur), and intercepts the (r,z) plane, perpendicular to the slit “plane of sight”, at a distance zc from the origin.
The considered forbidden lines have low radiative transition probabilities and at the densities retrieved in our simulations (n < 109−10 cm-3) the medium can be considered optically thin for those lines. The OTS code, however, calculates the population of the levels in statistical equilibrium, also allowing for a correct determination of the emissivities above the critical density for collisional de-excitation. Therefore, once the numerical cells contained in each tube have been identified, the corresponding emissivities, multiplied by the cell volumes, are summed up and distributed into velocity channels. Such a procedure yields the emissivity/radial velocity histogram for a given value of zc, or for a given coring tube in the same slit position. Integrated emissivities (in erg s-1) must be divided by 4πr2 and by the HST pixel extension in arcsec to obtain the total surface brightness of the numerical jet in the proper units, erg s-1 arcsec-1 cm-2. Finally, moving zc along the axis, and stepping the parallel planes of view of 0.7′′, leads to the seven different PVDs, labeled from S1 to S7 as in MA14.
The z component in synthetic PVDs represents the tangential dimension, or the z component in the jet frame projected onto the plane of the sky. Velocities, as usual, must be interpreted as observed radial velocities, that is to say, the total velocity in the jet frame projected onto the line of sight. The velocity channels range from zero to the largest value measured in a given object. Their size depends on the spectral resolution of STIS spectra (0.554 Å corresponding to ~25 km s-1 for the [S ii]λ6731 line).
The structure of the OTS code allows us to compute parallel and perpendicular PVDs of different species, as well as 2D images of the surface brightness. Moreover, different objects and/or observational instruments can be simulated, since both the instrumental parameters (spatial and spectral resolution), and the observational features (distance, angle of sight) can be changed quite easily.
4. Results
4.1. Stationary and time-dependent simulations
As already pointed out, we have focused on the microjets of DG-Tau and RW-Aur in the bright region up to 4−5 arcsec from the source (~500 AU at the distance of 140 pc from Earth). For DG-Tau, observed PVDs reveal the existence of a first almost stationary emission blob within the first 2 arcsec from the star. The second moving blob observed at ~4 arcsec downward the flow, however, might be due to temporary fluctuations of the ejection mechanism. The jet from RW-Aur shows a pattern of moving knots too, that probably reflects fluctuations with a period of a few years. In this frame we have first performed stationary simulations, to reproduce the “wiping-out” effects that long-period “macrojets” may have on the ISM, and the consequent formation of steady structures. Eventually, we superimposed time-dependent simulations to generate the nonstationary observed features.
List of parameters used in the various runs.
Numerical simulations are listed in Table 2 with labels that refer to the jets under investigation, DG for DG-Tau and RW for RW-Aur. The parameter μ, the kind of tail, the maximum velocity and magnetic field at the nozzle are reported with a flag, in the last column, indicating the type of inflow conditions imposed (steady or time-dependent). The simulation parameters are summarized in Table 1, whereas the inflow conditions are shown in Fig. 2. In most cases, only the “paradigmatic” [S ii]λ6731 forbidden line emission has been shown. Forbidden lines for the [O i]λ6300 are reported in the most representative cases only.
Simulations from DG1 to DG4 are performed by using the physical parameters that are typical of the jet from DG-Tau, whereas those from RW1 to RW4 refer to RW-Aur data. Taking M⋆ = M⊙ and ri = 0.07 AU, for both stellar jets, makes the velocity scale, and Vnozzle, to depend on μ only. In particular, velocity up to to 250 km s-1 arises from wide-angle accelerating models, (μ = −0.5), whereas collimated outflows (μ close to 0) show lower speed.
4.2. Simulations of the DG-Tau case: collimated jets
The case DG1 is representative of four different simulations, where the models μ = 0.0 and μ = −0.25 are explored with both exponential and linear tails. These cases provided quite similar results, therefore we gather them using the same label.
 |
Fig. 3 2D emissivity in the μ = 0 for the exponential tail case. Dotted lines show the integration path along the line of sight, whose angle with the jet axis is 38°. The lines marked with a triangle and a square correspond to positions z = 0 and ~3.4 arcsec in the PVD. |
Figure 3 represents the emissivity (or, the numerical emission power density) for [S ii] λ6731 in the r–z plane for a stationary jet, ~400 years old. Most of the optical emission within the first ~250 AU from the source comes from the red-colored, internal beam surrounding the axis (hereafter, the beam), and from the cone-like expansion region close to the nozzle, fueled by the injected hot gas (the cone). The light-blue region close to the left boundary, generated by the pressure and density boundary values, is too weak to affect the synthetic PVD.
Downward from the nozzle, at z > 250 AU, internal oblique shocks, typical of collimated jets, drive the formation of a pattern of emitting knots (in the picture, visible in red) slowly moving with the flow, (Rubini et al. 2007), while the surrounding green-colored cocoon is filled with weakly emitting gas. The outer dark-blue colored, not-emitting part of the domain, represents the empty and cold region where the ISM has been stripped off by the bow-shock.
However, synthetic PVDs look quite different with respect to 2D emissivity maps because of the integration along the line of sight (represented with dotted lines) and the splitting into the velocity channels. The surface brightness contour levels, too, are those used in Fig. 1.
 |
Fig. 4 Synthetic PVDs obtained for the μ = 0.0 case with exponential tail added to profiles in P06. Contour levels and reference lines are as in Fig. 1, as well as the spatial and spectral resolution. |
Results for DG1 case, shown in Fig. 4, can be summarized as follows:
-
Propagating jets for μ = 0.0,−0.25 keep a high degree of collimation. Internal oblique shocks form, which are not visible in lateral slit positions;
-
The emitting zones are too weak and small to generate surface brightness comparable with observations, except for the central slit position, where a faint chain of internal-shocks-driven knots is seen, there is almost no emission;
-
The [S ii]λ6731 surface brightness is concentrated in the low velocity channel only.
In conclusion, the four cases labeled as DG1 do not match the observational features and, independent of the type of tail, models μ = 0.0 and μ = −0.25 do not reproduce the properties of the jet from DG-Tau.
4.3. Simulations of the DG-TAU case: wide-angle jets
The model μ = −0.5 corresponds to “wide-angle” outflows (according to the definition given in P06), and is a better candidate to reproduce the real jets with respect to the μ = 0 case, since it is suitable to generate faster jets, with velocity in the range of DG-Tau, see Table 2 and Fig. 2. Figures 5 and 6 show the 2D emissivity for cases DG2 and DG3, corresponding to exponential and linear tails, respectively.
 |
Fig. 5 2D emissivity map in the μ = −0.5 case. Inflow conditions correspond to exponential tails. Dotted lines show the integration path along the line of sight, whose angle with the jet axis is 38°. Lines marked with a triangle and a square correspond to positions z = 0 and ~3.4 arcsec in the PVD. |
As in the case of DG1, the surface brightness still originates from cone, beam, and
cocoon, but in the case of μ =
−0.5 no internal shock is present, and the less collimated outflow
unwraps downward from the nozzle. This different behavior is measured by the function that
we have called collimation function Fc(r), defined as
follows: given the cylinder aligned with the axis z, of radius
r, and
length Δz
(the longitudinal cell size), Fc(r) is the radial
flux of the radial momentum across the cylindrical surface of area 2πrΔz,
divided by the longitudinal flux of the longitudinal momentum across the circle of area
πr2. We thus write
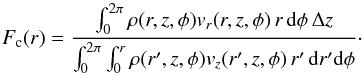 (7)Figure 7 shows Fc(r) computed at a
distance z =
16 AU from the nozzle. The model μ = 0 is, substantially, in
radial equilibrium, whereas in the μ = −0.5 case the gas is pushed outward, the
outflow unfolds downward from the nozzle and generates the empty cavity surrounding the
beam, which is visible in Fig. 5 and Fig. 6.
(7)Figure 7 shows Fc(r) computed at a
distance z =
16 AU from the nozzle. The model μ = 0 is, substantially, in
radial equilibrium, whereas in the μ = −0.5 case the gas is pushed outward, the
outflow unfolds downward from the nozzle and generates the empty cavity surrounding the
beam, which is visible in Fig. 5 and Fig. 6.
 |
Fig. 7 Collimation function vs. r in μ = 0.0 and −0.5 cases. The solid line shows that in wide-angle jets (μ = −0.5) the gas is pushed outward by the total pressure gradient. |
In wide-angle jets, a crucial role is played by tails. In the case of DG3 (Fig. 6), wider emitting cones are created by faster, linear tail-driven winds, which are able to push the hot gas much farther than the exponential tail-driven winds of the case of DG2 (Fig. 5). In both cases, the bifurcation of the red-emitting cone indicates the flow opening. The case of DG2 still shows an almost empty synthetic PVD, with a faint surface brightness, close to the nozzle, whose pattern is quite similar to that shown in Fig. 4. A richer kinematic structure appears in DG3, Fig. 8, where the surface brightness and the velocity spread are comparable with the observed velocity spread in all slit positions.
 |
Fig. 8 Synthetic PVDs obtained for the μ = −0.5 case, with linear tails added to the profiles in P06. Contour levels and reference lines are as in Fig. 1. |
The emitting blob extends up to ~1.5′′ from the nozzle, and in the central slit position radial velocities (with respect to the observer) of order 200 km s-1 are observed. Lateral slit positions show lower velocities that increase when moving away from the source, in agreement with the features of the stationary first blob of DG-Tau (see Sect. 2). Nevertheless, it is apparent that other mechanisms should be included to reproduce all the properties of DG-Tau microjet. Namely, the second moving, emitting blob at 3−4′′, shown in Fig. 1 is probably due to temporal variations of the ejection properties. In order to reproduce it, in the next case a time-dependent component has been added to the steady component of the flow.
Finally, in observational PVDs the first blob shows a velocity gradient that might be due to either local (i.e., in time) particle deceleration at the nozzle position, or spatial particle acceleration across the blob region. This latter kind of gradient cannot be reproduced in our simulations, since spatial acceleration mechanisms are not at work in our model. On the other hand, local temporal fluctuations at the nozzle can be reproduced by setting unsteady inflow conditions, as in the case of DG4.
4.4. Simulations of the DG-Tau case: the time-dependent model
To reproduce the second moving blob in images of the DG-Tau jet, in this experiment (DG4) we added a time-dependent component to the stationary flow used for DG3 (μ = −0.50), regardless of the physical mechanism responsible for such a component. Including temporal fluctuations introduces many new parameters: perturbation shape and strength, period (defined as the single event life-time) and periodicity (gap between two episodes). Exploring the full range of these parameters is far beyond the scope of this experiment, whose sole aim is to add a variation in the ejection process capable to justify the moving, fainter knots at 3−4′′. At this scope, we adopted a saw-tooth velocity profile, where the velocity perturbation linearly grows from 0 to ~v(r,znozzle) × 0.9 in one period of time, and then abruptly drops to 0. Period and periodicity are set equal to 4 yr and 8 yr.
 |
Fig. 9 Emissivity map for the unsteady DG4 (μ = −0.5) case. The dotted line marked with a triangle indicates the integration path along the line of sight, whose angle with the jet axis is 38°. The lines marked with a square, at ~4 arcsec from the source, shows the position of the head of the second blob. |
 |
Fig. 10 PVDs for the nonsteady μ = −0.5 case (see also MA14). |
Figure 9 shows the 2D emissivity map in [S ii]λ6731, whereas synthetic PVDs in sulphur and oxygen are shown in Figs. 10 and 11, These figures reveal similarities and discrepancies with observations. The blobs position is correct, in the range between 3−4′′ from the source, and the oxygen emissivity is weaker than sulphur emissivity as expected (see MA14). On the other hand, the spatial extension and the velocity spread are still too small. In particular, the second blob brightness is too strong, and positions from S2 to S6 show a red-emitting zone (in the figure colors palette) that is not present in observational images.
Discrepancies probably depend on the choice of the perturbation parameters. In particular, the saw-teeth fluctuation profile tends to steepen when propagating with the flow, the same way the solution of the nonlinear Burgers equation does, forming strong shocks near the nozzle. We are confident that a more exhaustive exploration of unsteady inflow conditions will lead to more realistic emitting patterns. The main result, however, is the robust link between synthetic PVDs and μ values. In fact, when the temporal fluctuations used in DG4 case are applied to models μ = 0.0 and −0.25 (case DG1), or to the μ = −0.5 model with exponential tail of case DG2, quite different solutions are obtained, which are not at all comparable with observations.
4.5. The RW-Aur jet
Cases RW1, RW2, and RW3 try to reproduce the features of the microjet from RW-Aur. At this scope, we used the values of the physical parameters of RW-Aur cited in Table 1, in particular, nH(ri) = 2.4 × 107 cm-3 and B(ri) = 0.04 G, which are different with respect to DG-Tau values. We run models for μ = −0.5, −0.25 and 0.0, respectively, by using linear tails to extrapolate the inflow radial profiles. In order to reproduce the moving chain of observed emission knots, time-varying inflow conditions are used, defined by a positive sinusoidal temporal profile
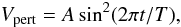 where the
amplitude A
is 255, 190, 155 km s-1 for μ = −0.50, −0.25 and 0.0, respectively, and T = 5 yr, which yields the
perturbation growth timescale to be Tg = 2.5 yr, a value that is close to
the high-frequency perturbation period cited by Lopez-Martin et al. (2003). Amplitudes, in turn, have been assumed to be equal
to the velocity peak values computed from the P06 models, see Fig. 2.
where the
amplitude A
is 255, 190, 155 km s-1 for μ = −0.50, −0.25 and 0.0, respectively, and T = 5 yr, which yields the
perturbation growth timescale to be Tg = 2.5 yr, a value that is close to
the high-frequency perturbation period cited by Lopez-Martin et al. (2003). Amplitudes, in turn, have been assumed to be equal
to the velocity peak values computed from the P06 models, see Fig. 2.
Results for the three models have been collected in Fig. 12, where synthetic PVDs for the central slit position S4 are shown. The figure reveals that models μ = −0.5 and −0.25 are far from the morphological features of the microjet from RW-Aur Melnikov et al. (2009), Fig. 1, whereas μ = 0.0 provides better results. In particular, a chain of emitting knots appears in the first 5 arcsec, though the velocity spread is still smaller than the observed spread.
These results suggest that the jet from RW-Aur might originate from outflows with collimation degrees even higher than that of μ = 0. In this frame, we run the case of RW4, listed in Table 2 as a super collimated (SC) outflow.
 |
Fig. 12 Synthetic PVDs for S4, central slit position, and for three different models, μ = −0.5, −0.25, 0.0 (from left to right). |
 |
Fig. 13 Emissivity map for case RW3 (μ = 0.0). Dotted lines show the integration path along the line of sight, whose angle with the jet axis is 46°. The lines marked with a triangle and a square correspond to positions z = 0 and ~3.4′′ in the PVD. |
We highlight that the inflow profiles of case RW4 do not correspond to any model from P06. Instead, by following the gross behavior of the profiles of Fig. 2 when moving from larger to smaller (negative) values of μ, or from less collimated to more collimated outflows, we calculate the profiles by doubling the intensity of the magnetic field and halving the longitudinal velocity with respect to the μ = 0 case.
Results for this case are shown in Figs. 13 and 14. Figure 14 can be directly compared with the observed PVDs of Fig. 1 (Melnikov et al. 2009), since velocity interval and scale are the same.
Synthetic PVDs reveal a chain of emitting knots, which are also visible in the 2D emissivity map of Fig. 13, whose morphology and kinematical features are in good agreement with the observed PVDs . Results of pulsating simulations, for both DG4 and RW4 cases, strictly rely on the perturbation shape and growth timescale, (4 and 2.5 yr, respectively). Changing these parameters yields quite different solutions. We stress that investigating the pulsating inflow conditions parameters is beyond the scope of this paper. Temporal fluctuations parameters of cases DG4 and RW4 were chosen according to the following criteria:
-
1.
We chose the fluctuation growth timescale, Tg, in the range of the values reported in Sect. 2. In particular, we adopted a small timescale perturbation, with Tg = 2.5 yr for the case of RW4 (Lopez-Martin et al. 2003), and Tg = 4 yr for the case of DG4 (Pyo et al. 2003).
-
2.
For both DG4 and RW4, we avoided sharp discontinuities to suppress strong post bow-shock emission lines, in favor of smooth saw-tooth or sinusoidal temporal profiles.
The aforementioned choices have proved to achieve better results in terms of comparison between synthetic and observed PVDs.
 |
Fig. 14 Results for the RW4 case, corresponding to the SC run, see for comparison Melnikov et al. (2009, Fig. 1). |
5. Discussion and conclusions
We performed numerical simulations of axisymmetric magneto-hydrodynamic jets with the PLUTO code. First, a supersonic outflow, injected from a nozzle placed on the left boundary, sweeps the numerical domain, until the heading bow-shock leaves the right boundary. Then, the simulation continues with a jet flowing in the domain. Initial and boundary conditions were retrieved by using a mix of observational constraints and theoretical models.
In particular, the nondimensional radial profiles of the main physical quantities at the
nozzle position are taken from Pudritz et al. (2006).
In this paper, self-collimating outflows have been generated via numerical simulations at
the distance of ~5 AU from the
disk. Each solution corresponds to a different value of the parameter μ in the relation that rules
the behavior of the poloidal magnetic field on the disk surface: 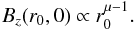 (8)In particular, we
consider four different values of this parameter: μ = 0.0, −0.25, −0.5, −0.75. The nondimensional profiles are converted
into dimensional profiles, with proper scale factors. Since the inflow profiles from P06
extend for a few AUs from the jet axis, linear or exponential extrapolations (the tails) are
used to match the inflow conditions and the ISM. Finally, the inflow temperature and
ionization fraction profiles are chosen according to observational criteria. The numerical
solutions obtained by the PLUTO code are finally used by the Optical Telescope Simulator
post-processing code, and synthetic PVDs of optical forbidden emission lines are obtained.
The comparison between synthetic and observational PVDs allows us to check the reliability
of the inflow conditions at the nozzle and, in turn, provides feedback on the
magneto-centrifugal launch models used to generate the conditions themselves. In this
preliminary work, simulations and synthetic PVDs extend over the first 5′′, since we focus on the
microjets from DG-Tau and RW-Aur, that have bright emission over that distance from the
star.
(8)In particular, we
consider four different values of this parameter: μ = 0.0, −0.25, −0.5, −0.75. The nondimensional profiles are converted
into dimensional profiles, with proper scale factors. Since the inflow profiles from P06
extend for a few AUs from the jet axis, linear or exponential extrapolations (the tails) are
used to match the inflow conditions and the ISM. Finally, the inflow temperature and
ionization fraction profiles are chosen according to observational criteria. The numerical
solutions obtained by the PLUTO code are finally used by the Optical Telescope Simulator
post-processing code, and synthetic PVDs of optical forbidden emission lines are obtained.
The comparison between synthetic and observational PVDs allows us to check the reliability
of the inflow conditions at the nozzle and, in turn, provides feedback on the
magneto-centrifugal launch models used to generate the conditions themselves. In this
preliminary work, simulations and synthetic PVDs extend over the first 5′′, since we focus on the
microjets from DG-Tau and RW-Aur, that have bright emission over that distance from the
star.
Our main results are listed below:
-
The setup procedure shown in Sect. 3 enables us to match numerical simulations in the launching and propagation region. Under the prescriptions given in the acceleration-propagation matching (APM) procedure, magnetized fluids that are numerical solutions of magneto-centrifugal models inside the accelerating region, are allowed to flow into the (observable) propagation region. Synthetic PVDs of optical forbidden lines are returned by the OTS code, and the surface brightness in various velocity channels are reconstructed with the same resolution used by the HST/STIS spectrograph.
-
Results from P06 show that different radial profiles of the magnetic field at the disk surface, characterized by different values of the parameter μ, lead to accelerated outflows with different degrees of collimation. In particular, cases μ = 0.0, −0.25 yield collimated outflows, while μ = −0.50, −0.75 lead to wide-angle jets, with a hollow cylinder in the central region. We show that such behavior is maintained in the propagation region.
-
The synthetic PVDs of the jet from DG-Tau show that inflow conditions corresponding to collimated outflows in the acceleration region (μ = 0.0, −0.25) are not consistent with observations. In fact, high-velocity components are not present in lateral slit positions, and the surface brightness is dominated by the oblique shocks surrounding the jet axis. The 2D emissivity maps of the case μ = −0.50, however, reveal a lack of internal shocks and a weaker beam component. When linear tails are used to extrapolate the radial profiles at the nozzle, the obtained synthetic PVDs are in good agreement with the observed profiles. Linear tails, in fact, increase the surface brightness in lateral slit positions, and reproduce the observed low-velocity lateral winds, close to the star.
-
The jet from RW-Aur can be better reproduced at a quality level by inflow conditions corresponding to collimated outflows. The profiles derived by the case μ = 0, in fact, produces synthetic PVDs that show the gross features of the observed profiles: namely, the knotty structure and the narrow velocity spread, centered around the value 100 km s-1, as in Fig. 1 (Melnikov et al. 2009). Even better results are obtained with inflow profiles not available in P06 (i.e., our SC, Super Collimated, case). The model μ = −0.50 yields wide-angle jets in the propagating region, where the flow unfolds downward from the nozzle, and the emissivity features do not match observations.
-
Finally, to reproduce the features in observed PVDs of both jets, it is necessary to add temporal perturbations to the steady solutions computed by the theoretical acceleration models. In particular, a saw-tooth time-dependent velocity component was added in DG-Tau simulations, whereas sinusoidal perturbations of the velocity field were used for RW-Aur. In both cases, the perturbation amplitude is of the order of the steady velocity field, and the period is of a few years. This kind of perturbation reproduces the gross features of the observed emitting blobs, though discrepancies are still present. Time-dependent simulations, however, yield a wide range of free numerical parameters to be set, and the exhaustive exploration of this parameter space is far beyond the aim of this work.
In conclusion, we have shown that the disk-wind model can lead to completely different kinds of jets, suggesting that the mechanism could be at the base of all observed stellar jets, possessing quite different properties. In particular, the jet from DG-Tau is better reproduced by inflow conditions derived from wide-angle disk-wind simulations, (μ = −0.50), surrounded by low-velocity winds, whereas the model for collimated outflows (μ = 0.0) reproduces the features of the jet from RW-Aur much better. In both cases, steady simulations are not able to reproduce all the observed features, and supplementary time-dependent components of the inflow conditions must be included.
Online material
Appendix A: The test case
The simulations discussed in Sect. 4 were run in two steps. In the first, stationary phase, the bow-shock sweeps out the ISM that fills the numerical box, up to 300 AU and 1200 AU in radial and longitudinal direction, respectively. Once it has left the numerical domain from the right side of the box, and the solution inside the domain has achieved a quasi-stationary configuration, the next pulsated phase is switched on, and the emissivity properties of the inner region, close to the source, are investigated.
In the present Appendix, the effects of the adopted numerical domain size and cooling model are discussed in some detail. For what concerns the cooling model, in particular, the nonequilibrium SNeq cooling model was used, which takes hydrogen ionization-recombination effects and the corresponding cooling losses into account, under the prescription that temperature does not exceed 75 000 K.
 |
Fig. A.1 Selected outputs from a large-scale simulation (TestDG3). Solid lines in the nozzle region represent the area investigated in all simulations listed in Table 2. |
 |
Fig. A.2 Density (top) and temperature (bottom) fields: the DG3 case patterns (left) vs. the stationary test case ones (right). |
 |
Fig. A.3 Two-dimensional emissivity patterns: the DG4 case (left) vs. the test case (right). The figures show both the stationary configuration (top) and the pulsated one (bottom). |
 |
Fig. A.4 Left: synthetic PVDs for the stationary μ = −0.5 test case, that is simulation TestDG3, to be compared with Fig. 8 of case DG3. Right: same for the unsteady simulation of case TestDG4, to be compared with Fig. 10. |
Two questions arise:
-
1.
It is well known that bow-shocks (namely, the triple-point Mach-disk region behind them) are suitable to generate recirculating flows of matter that can move in reverse, and that they affect the region close to the nozzle. If so, how can we be sure that expelling the bow-shock from the simulation box at only 1300 AU from the source does not alter dynamical and emitting properties of the region under investigation, the emitting region, extending from the nozzle up to the first ~5 arcsec?
-
2.
Though in the emitting region weak shocks are at work, with temperatures of order a few thousands degrees, well below the cooling model limit, it is well known that in the post bow-shock region temperature may achieve values of order 106 K. If so, how can we be sure that miscalculating the cooling losses in the post-bow shock region does not affect the global jet dynamics and the properties of the emitting region as a consequence?
In order to be confident with the results presented in the paper, we run a three-step test-case. In the first step, a stationary jet propagates into a wider, large-scale domain that extends over 870 × 6700 AU in r and z respectively, (1340 × 8060 grid points). Figure A.1 shows density and temperature fields (top and bottom, respectively) in the domain used in this large-scale simulation (to make a comparison, the small-scale domain of the runs of Table 2 is highlighted in the figure with solid lines).
The adopted, simplified tabulated cooling model, in which cooling losses are a function of temperature and assigned (solar) abundances only, allows us to skip the temperature limit of the Sneq model. Thanks to both the larger domain size and the cooling model, the quasistationary solution obtained in this first step, once the bow-shock has left the domain, guarantees a better description of the jet global dynamics, with respect to the simulations of Table 2.
In the second step (simulation TestDG3), the internal portion of the stationary solution of the first step, marked in blue in Fig. A.1, is used to restart a stationary, small-scale simulation in which the precise Sneq cooling model is recovered to properly calculate the emissivity pattern and synthetic PVds. Finally, in the third step (TestDG4) pulsating inflow conditions like those of case DG4 are imposed. Also, for this case, the emissivity field and synthetic PVDs are calculated. The test case results are reported in Figs. A.2–A.4.
Figure A.2 shows density and temperature fields (top and bottom, respectively) for the test case (right column) vs. the DG4 case (left column). The patterns are basically the same. Actually, filaments of recirculating matter in the cocoon region, which are still visible in the DG4 case, have disappeared in TestDG3, because of the “older” age of the jet. The panel of Fig. A.3 shows the emissivity patterns in the r − z plane for the DG4 case (on the left), and for the test case (on the right), for both the stationary (top) and pulsated (bottom) phase. The already mentioned filaments in the cocoon region do not provide relevant contribution to the jet emissivity, and play no role in PVDs formation, as shown by comparing Fig. A.4 with Figs. 8 and 10.
As a conclusion, the test case confirms that the adopted domain size and cooling model do not affect the bow-shock feedback in the emitting region and the reliabilty of the results.
Acknowledgments
The authors wish to thank Claudio Zanni (Osservatorio Astronomico di Torino, Italy), Silvano Massaglia, and Andrea Mignone (Università di Torino, Italy) for very useful and friendly discussions, and the referee for helping us to improve the paper with pertinent comments. We acknowledge the CINECA Award IsC04_INJECTS, 2011 for the availability of high-performance computing resources and support.
References
- Agra-Amboage, V., Dougados, C., Cabrit, S., & Reunanen, J. 2011, A&A, 532, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacciotti, F. 2002, in Rev. Mex. Astron. Astrofis. Conf. Ser. 13, eds. W. J. Henney, W. Steffen, L. Binette, & A. Raga, 8 [Google Scholar]
- Bacciotti, F., & Eislöffel, J. 1999, A&A, 342, 717 [NASA ADS] [Google Scholar]
- Bacciotti, F., Mundt, R., Ray, T. P., et al. 2000, ApJ, 537, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Bacciotti, F., Ray, T. P., Mundt, R., Eislöffel, J., & Solf, J. 2002, ApJ, 576, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J., Reipurth, B., & Davis, C. J. 2007, Protostars and Planets V (Tucson: University of Arizona Press), 215 [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Bonito, R., Orlando, S., Peres, G., et al. 2010, A&A, 511, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chou, M. Y., Takami, M., Manset, N., et al. 2013, AJ, 145, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Coffey, D., Bacciotti, F., Ray, T. P., Eislöffel, J., & Woitas, J. 2007, ApJ, 663, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Coffey, D., Bacciotti, F., & Podio, L. 2008, ApJ, 689, 1112 [NASA ADS] [CrossRef] [Google Scholar]
- Dougados, C., Cabrit, S., Lavalley, C., & Ménard, F. 2000, A&A, 357, L61 [NASA ADS] [Google Scholar]
- Dougados, C., Cabrit, S., & Lavalley-Fouquet, C. 2002, in Rev. Mex. Astron. Astrofis. Conf. Ser. 13, eds. W. J. Henney, W. Steffen, L. Binette, & A. Raga, 43 [Google Scholar]
- Dougados, C., Cabrit, S., Ferreira, J., et al. 2004, Ap&SS, 293, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Eislöffel, J., & Mundt, R. 1998, AJ, 115, 1554 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreira, J. 1997, A&A, 319, 340 [NASA ADS] [Google Scholar]
- Goodson, A. P., Winglee, R. M., & Boehm, K.-H. 1997, ApJ, 489, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Güdel, M., Skinner, S. L., Audard, M., Briggs, K. R., & Cabrit, S. 2008, A&A, 478, 797 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., Audard, M., Bacciotti, F., et al. 2011, in ASP Conf. Ser. 448, eds. C. Johns-Krull, M. K. Browning, & A. A. West, 617 [Google Scholar]
- Hartigan, P., & Morse, J. 2007, ApJ, 660, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Lavalley, C., Cabrit, S., Dougados, C., Ferruit, P., & Bacon, R. 1997, A&A, 327, 671 [NASA ADS] [Google Scholar]
- Lavalley-Fouquet, C., Cabrit, S., & Dougados, C. 2000, A&A, 356, L41 [NASA ADS] [Google Scholar]
- Lopez-Martin, L., Cabrit, S., & Dougados, C. 2003, A&A, 405, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maurri, L., Bacciotti, F., Podio, L., et al. 2014, A&A, 565, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGroarty, F., Ray, T. P., & Froebrich, D. 2007, A&A, 467, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meliani, Z., Casse, F., & Sauty, C. 2006, A&A, 460, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melnikov, S. Y., Eislöffel, J., Bacciotti, F., Woitas, J., & Ray, T. P. 2009, A&A, 506, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignone, A. 2009, Mem. Soc. Astron. It. Suppl., 13, 67 [Google Scholar]
- Mundt, R., & Fried, J. W. 1983, ApJ, 274, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, Sky and Telescope, 78, 491 [Google Scholar]
- Ouyed, R., & Pudritz, R. E. 1997, ApJ, 482, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Podio, L., Bacciotti, F., Nisini, B., et al. 2006, A&A, 456, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pudritz, R. E. 1992, in Physics of Active Galactic Nuclei, eds. W. J. Duschl, & S. J. Wagner, 459 [Google Scholar]
- Pudritz, R. E., Rogers, C. S., & Ouyed, R. 2006, MNRAS, 365, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Pudritz, R. E., Ouyed, R., Fendt, C., & Brandenburg, A. 2007, Protostars and Planets V (Tucson: University of Arizona Press), 277 [Google Scholar]
- Pyo, T.-S., Kobayashi, N., Hayashi, M., et al. 2003, ApJ, 590, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Pyo, T.-S., Hayashi, M., Kobayashi, N., et al. 2006, ApJ, 649, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2002, ApJ, 578, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2009, MNRAS, 399, 1802 [NASA ADS] [CrossRef] [Google Scholar]
- Rubini, F., Lorusso, S., Del Zanna, L., & Bacciotti, F. 2007, A&A, 472, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sauty, C., Tsinganos, K., & Trussoni, E. 1999, A&A, 348, 327 [NASA ADS] [Google Scholar]
- Shu, F. H., Najita, J. R., Shang, H., & Li, Z.-Y. 2000, Protostars and Planets IV (Tucson: University of Arizona Press), 789 [Google Scholar]
- Solf, J., & Boehm, K. H. 1993, ApJ, 410, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Takami, M., Chrysostomou, A., Ray, T. P., et al. 2004, A&A, 416, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teşileanu, O., Mignone, A., Massaglia, S., & Bacciotti, F. 2012, ApJ, 746, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Tzeferacos, P., Ferrari, A., Mignone, A. i., et al. 2013, MNRAS, 428, 3151 [NASA ADS] [CrossRef] [Google Scholar]
- Woitas, J., Ray, T. P., Bacciotti, F., Davis, C. J., & Eislöffel, J. 2002, ApJ, 580, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Woitas, J., Bacciotti, F., Ray, T. P., et al. 2005, A&A, 432, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zanni, C., Ferrari, A., Rosner, R., Bodo, G., & Massaglia, S. 2007, A&A, 469, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Continuum-subtracted HST/STIS position-velocity diagrams of the flow from DG Tau, in the [S ii] λ6731 line and in slit positions from S1 to S7 (from southeast to northwest), offset by 0.07 arcsec across the jet width. The colored contours are from 1.1 × 10-15 erg s-1 arcsec-2 cm-2 Å-1 (equivalent to 3σ), with a ratio of 22/5. The vertical line marks zero velocity with respect to the star. The horizontal lines mark the position of the star and of previously identified knots. Adapted from MA14. |
| In the text | |
 |
Fig. 2 Dimensional radial profiles at the nozzle from P06, for each value of the parameter μ. |
| In the text | |
 |
Fig. 3 2D emissivity in the μ = 0 for the exponential tail case. Dotted lines show the integration path along the line of sight, whose angle with the jet axis is 38°. The lines marked with a triangle and a square correspond to positions z = 0 and ~3.4 arcsec in the PVD. |
| In the text | |
 |
Fig. 4 Synthetic PVDs obtained for the μ = 0.0 case with exponential tail added to profiles in P06. Contour levels and reference lines are as in Fig. 1, as well as the spatial and spectral resolution. |
| In the text | |
 |
Fig. 5 2D emissivity map in the μ = −0.5 case. Inflow conditions correspond to exponential tails. Dotted lines show the integration path along the line of sight, whose angle with the jet axis is 38°. Lines marked with a triangle and a square correspond to positions z = 0 and ~3.4 arcsec in the PVD. |
| In the text | |
 |
Fig. 6 Same as Fig. 5, with linear tails added to the P06 inflow profiles. |
| In the text | |
 |
Fig. 7 Collimation function vs. r in μ = 0.0 and −0.5 cases. The solid line shows that in wide-angle jets (μ = −0.5) the gas is pushed outward by the total pressure gradient. |
| In the text | |
 |
Fig. 8 Synthetic PVDs obtained for the μ = −0.5 case, with linear tails added to the profiles in P06. Contour levels and reference lines are as in Fig. 1. |
| In the text | |
 |
Fig. 9 Emissivity map for the unsteady DG4 (μ = −0.5) case. The dotted line marked with a triangle indicates the integration path along the line of sight, whose angle with the jet axis is 38°. The lines marked with a square, at ~4 arcsec from the source, shows the position of the head of the second blob. |
| In the text | |
 |
Fig. 10 PVDs for the nonsteady μ = −0.5 case (see also MA14). |
| In the text | |
 |
Fig. 11 Same as Fig. 10 for a different emission line. |
| In the text | |
 |
Fig. 12 Synthetic PVDs for S4, central slit position, and for three different models, μ = −0.5, −0.25, 0.0 (from left to right). |
| In the text | |
 |
Fig. 13 Emissivity map for case RW3 (μ = 0.0). Dotted lines show the integration path along the line of sight, whose angle with the jet axis is 46°. The lines marked with a triangle and a square correspond to positions z = 0 and ~3.4′′ in the PVD. |
| In the text | |
 |
Fig. 14 Results for the RW4 case, corresponding to the SC run, see for comparison Melnikov et al. (2009, Fig. 1). |
| In the text | |
 |
Fig. A.1 Selected outputs from a large-scale simulation (TestDG3). Solid lines in the nozzle region represent the area investigated in all simulations listed in Table 2. |
| In the text | |
 |
Fig. A.2 Density (top) and temperature (bottom) fields: the DG3 case patterns (left) vs. the stationary test case ones (right). |
| In the text | |
 |
Fig. A.3 Two-dimensional emissivity patterns: the DG4 case (left) vs. the test case (right). The figures show both the stationary configuration (top) and the pulsated one (bottom). |
| In the text | |
 |
Fig. A.4 Left: synthetic PVDs for the stationary μ = −0.5 test case, that is simulation TestDG3, to be compared with Fig. 8 of case DG3. Right: same for the unsteady simulation of case TestDG4, to be compared with Fig. 10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


