| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | L2 | |
| Number of page(s) | 5 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201423862 | |
| Published online | 05 June 2014 | |
A dearth of small particles in debris disks⋆
An energy-constrained smallest fragment size
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden,
The Netherlands
e-mail:
krijt@strw.leidenuniv.nl
Received:
21
March
2014
Accepted:
22
May
2014
Context. A prescription for the fragment size distribution resulting from dust grain collisions is essential when modelling a range of astrophysical systems, such as debris disks and planetary rings.
Aims. While the slope of the fragment size distribution and the size of the largest fragment are well known, the behaviour of the distribution at the small size end is theoretically and experimentally poorly understood. This leads debris disk codes to generally assume a limit equal to, or below, the radiation blow-out size.
Methods. We use energy conservation to analytically derive a lower boundary of the fragment size distribution for a range of collider mass ratios. Focusing on collisions between equal-sized bodies, we apply the method to debris disks.
Results. For a given collider mass, the size of the smallest fragments is found to depend on collision velocity, material parameters, and the size of the largest fragment. We provide a physically motivated recipe for the calculation of the smallest fragment, which can be easily implemented in codes for modelling collisional systems. For plausible parameters, our results are consistent with the observed predominance of grains much larger than the blow-out size in Fomalhaut’s main belt and in the Herschel cold debris disks.
Key words: planets and satellites: rings / interplanetary medium / minor planets, asteroids: general / solid state: refractory
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Fragmenting collisions are important in a range of astrophysical systems. While the slope of the fragment size distribution and the size of the largest fragment are well characterized and can be used confidently in models, the smallest fragment size is less well understood and is usually assumed to be constant for all collisions. We provide a framework for self-consistently calculating the smallest fragment size as a function of material and collision parameters (Sect. 2), and discuss its implications for modelling debris disks (Sect. 3).
Numerous experimental studies have looked at the fragment size distribution of destructive collisions, focussing on the slope of the power law(s), and on the size of the largest fragment (Davis & Ryan 1990; Ryan et al. 1991; Nakamura & Fujiwara 1991; Ryan 2000). The smaller end of the size distribution has received considerably less attention; the smallest fragments are hard to count experimentally, and require a very high resolution to be captured in numerical simulations. Fragment distributions are therefore incomplete below sizes of 100 μm, or masses below 10-3 gr (Fujiwara et al. 1977; Takagi et al. 1984). Molecular dynamics (e.g. Dominik & Tielens 1997) or smooth particle hydrodynamics (Geretshauser et al. 2010) simulations have limited resolution and tend to focus on the fragmentation threshold velocity rather than the smallest fragments.
2. Minimum fragment size in a single collision
We consider collisions below the hypervelocity regime, i.e. the relative velocity of the
colliders is much smaller than their internal sound speed, generally implying
vrel ≲ 1
km s-1. Based on experiments, we adopt the standard fragment size
distribution 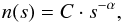 (1)with 3
<α< 4,
and C a
coefficient we express below. While the mass is dominated by the largest particles, the
surface area and thus the surface energy is dominated by the smallest fragments. As the
creation of infinitely small fragments would require an infinite amount of energy, while the
amount of kinetic energy available in a collision is finite, the power law must stop or
flatten at some small fragment size. To the best of our knowledge, however, the regime of
fragment sizes relevant for the analysis below has not yet been probed by available
experimental data nor described theoretically in an astrophysical context.
(1)with 3
<α< 4,
and C a
coefficient we express below. While the mass is dominated by the largest particles, the
surface area and thus the surface energy is dominated by the smallest fragments. As the
creation of infinitely small fragments would require an infinite amount of energy, while the
amount of kinetic energy available in a collision is finite, the power law must stop or
flatten at some small fragment size. To the best of our knowledge, however, the regime of
fragment sizes relevant for the analysis below has not yet been probed by available
experimental data nor described theoretically in an astrophysical context.
Assuming spherical fragments with sizes between smin and smax(
≫smin), the total fragment mass and surface
area are 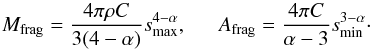 (2)For a collision
between two bodies of size s0 and mass
(2)For a collision
between two bodies of size s0 and mass
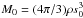 , mass conservation
implies Mfrag =
2M0, and thus
, mass conservation
implies Mfrag =
2M0, and thus 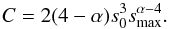 (3)The pre-collision kinetic
energy is simply
(3)The pre-collision kinetic
energy is simply 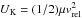 , where
μ =
M0/2 denotes the reduced
mass. The difference in surface energy before and after the collision equals
, where
μ =
M0/2 denotes the reduced
mass. The difference in surface energy before and after the collision equals
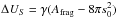 , where γ equals the surface energy
per unit surface of the material. Assuming that only a fraction η of the kinetic energy is
used for creating new surface, we can combine Eqs. (2) and (3) to obtain a lower limit
for the smallest fragment size. For the specific case of α = 3.5, this reduces to
, where γ equals the surface energy
per unit surface of the material. Assuming that only a fraction η of the kinetic energy is
used for creating new surface, we can combine Eqs. (2) and (3) to obtain a lower limit
for the smallest fragment size. For the specific case of α = 3.5, this reduces to
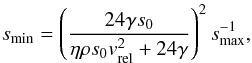 (4)and gives the size
of the smallest fragments created in a collision at vrel, assuming
α = 3.5 and
smax ≫
smin.
(4)and gives the size
of the smallest fragments created in a collision at vrel, assuming
α = 3.5 and
smax ≫
smin.
Instead of forming a fragment distribution, we imagine the limiting case in which the
kinetic energy just suffices to split both colliders in half1, i.e. 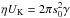 . Solving for s0, we obtain
. Solving for s0, we obtain
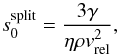 (5)which is the smallest
particle that can be split in half. The smallest fragment is slightly smaller, but does not
have a rigorously defined radius because we assume spherical particles. Equation (5) is similar to the result of Biermann & Harwit (1980) if η = 1.
(5)which is the smallest
particle that can be split in half. The smallest fragment is slightly smaller, but does not
have a rigorously defined radius because we assume spherical particles. Equation (5) is similar to the result of Biermann & Harwit (1980) if η = 1.
The same limit can be explored using Eq. (4), by forcing smin ~ smax ~ 2−1
/3s0. This
results in 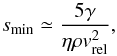 (6)which is very similar to
Eq. (5). To summarise, in an energetic
collision in which many fragments are created, the size of the smallest fragment is given by
Eq. (4). When the relative velocity is
decreased, the fragment distribution becomes more and more discrete, until we reach the
limit described by Eq. (6), in which
particles can only just be split into two.
(6)which is very similar to
Eq. (5). To summarise, in an energetic
collision in which many fragments are created, the size of the smallest fragment is given by
Eq. (4). When the relative velocity is
decreased, the fragment distribution becomes more and more discrete, until we reach the
limit described by Eq. (6), in which
particles can only just be split into two.
 |
Fig. 1 Top: minimum fragment size smin in a 20 m/s collision (Eq. (4)) for three materials, as a function of collider size s0. We have assumed η = 10-2 and smax = 2−1 / 3s0. The grey shaded areas are excluded because of mass conservation (left), and self-gravity (right). The dotted lines indicate the limit of Eq. (6). Bottom: critical energies versus size for equal-sized collisions. The energy needed to split a particle (e.g. Eq. (6)) is shown for η = 10-3 (dotted) and η = 1 (dashed). The solid curves correspond to catastrophic fragmentation of aggregates (Beitz et al. 2011), and ice and basalt (Benz & Asphaug 1999), showing both the strength-dominated (small sizes) and self-gravity dominated regimes (large sizes). |
Figure 1 shows the minimum size from Eq. (4) as a function of collider size, assuming vrel = 20 m/s, η = 10-2, and a maximum fragment that carries half of the initial collider mass. Gravity is important for bodies larger than 100 m (see below). Smaller bodies are weaker, and can produce fragments down to the smin indicated by the solid curve. For example, SiO2 fragments smaller than a micron can, at this velocity, only be formed by collisions of bodies larger than a few centimetres. The shaded region, top left, is forbidden, as there Mfrag> 2M0 and mass is not conserved. Close to smin ~ s0, the solid curves are non-linear as the pre- and post-collision surface areas become comparable.
It is interesting to compare Eq. (6) with
the traditional form of the catastrophic fragmentation threshold velocity in equal-sized
collisions: 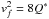 . The critical energy,
Q∗, has units of erg/g, and varies with
particle mass. For small bodies, the strength is dominated by cohesion, and for large ones
by gravity (Benz & Asphaug 1999). For solid
bodies, this transition occurs around 100 m in size. Values of Q∗ ~ 107 erg/g are often taken as typical for asteroids, and
experimentally obtained values for small grains (mm to cm sizes) can be several orders of
magnitude smaller (Blum & Münch 1993; Beitz et al. 2011). Figure 1 shows the critical energy for splitting predicted by Eq. (6) as a function of size for the materials in
Table 1 assuming η = 10-3 and
η = 1. The
solid lines indicate critical fragmentation energies for basalt and ice (Benz & Asphaug 1999) and silicate aggregates
(Beitz et al. 2011). The critical fragmentation
energies exceed the splitting energy, indicating that substantially more energy is required
to destroy – rather than split – colliders. The values plotted for ice and basalt were
obtained at collision velocities of 3 km s-1, substantially higher than the velocities considered
here, and Q∗ is known to depend on velocity (Leinhardt & Stewart 2012). While such a velocity
dependence appears absent in the splitting energy, it might be implicitly included in
η. In fact,
η is expected
to vary with material and impact energy. We adopt a constant value of η = 10-2.
. The critical energy,
Q∗, has units of erg/g, and varies with
particle mass. For small bodies, the strength is dominated by cohesion, and for large ones
by gravity (Benz & Asphaug 1999). For solid
bodies, this transition occurs around 100 m in size. Values of Q∗ ~ 107 erg/g are often taken as typical for asteroids, and
experimentally obtained values for small grains (mm to cm sizes) can be several orders of
magnitude smaller (Blum & Münch 1993; Beitz et al. 2011). Figure 1 shows the critical energy for splitting predicted by Eq. (6) as a function of size for the materials in
Table 1 assuming η = 10-3 and
η = 1. The
solid lines indicate critical fragmentation energies for basalt and ice (Benz & Asphaug 1999) and silicate aggregates
(Beitz et al. 2011). The critical fragmentation
energies exceed the splitting energy, indicating that substantially more energy is required
to destroy – rather than split – colliders. The values plotted for ice and basalt were
obtained at collision velocities of 3 km s-1, substantially higher than the velocities considered
here, and Q∗ is known to depend on velocity (Leinhardt & Stewart 2012). While such a velocity
dependence appears absent in the splitting energy, it might be implicitly included in
η. In fact,
η is expected
to vary with material and impact energy. We adopt a constant value of η = 10-2.
Appendix B investigates similar limits for colliders with different mass ratios, and shows that collisions with a mass ratio close to unity are the most effective at creating small fragments.
Material properties for silicate and ice used in this work.
3. Application to debris disks
Debris disks are leftovers of planet formation, and are usually described by a birth-ring of km-sized asteroid-like particles orbiting their parent star, together with a population of smaller bodies formed in a collisional cascade (for a recent review, see Matthews et al. 2014). A steady-state and scale-independent population of bodies will follow a size distribution given by a power law with α = 3.5 (Dohnanyi 1969). Some variation in α has been found in different simulations. Pan & Schlichting (2012) find up to α = 4 for cohesion-dominated collisional particles, and up to α = 3.26 for gravity-dominated ones.
Models of debris disks most often assume a smallest fragment size equal to the blow-out size, sblow (Wyatt & Dent 2002; Wyatt et al. 2010), or some constant, but arbitrary, smin<sblow for all collisions (Thébault et al. 2003; Krivov et al. 2008). The blow-out size corresponds to particles with β = 1/2, where β = 1.15Qpr(L⋆/L⊙)(M⋆/M⊙)-1(ρ/ g cm-3)-1(s/μm)-1 is the ratio of the radiation and gravitational force. Particles with β > 1/2 are removed from the system by radiation pressure. Alternatively, Gáspár et al. (2012) calculate a collision-dependent smin from mass conservation, but do not study the surface energy.
If, however, for any relevant collision Eq. (4) predicts smin>sblow, extrapolating the fragment size distribution down to these sizes is not justified. For example, starting from Eq. (2) of Krivov et al. (2008), cm-sized bodies have Q∗ ≃ 5 × 106 erg/g. In the Krivov et al. framework, a collision between two such bodies at 70 m/s will then result in fragmentation, as the kinetic energy (≃12 J, assuming ρ = 2.35 g/cm3) slightly exceeds the critical energy (=2mQ∗ ≃ 10 J), and fragments will be created from a size comparable to the impactor (Eq. (21) of Krivov et al. 2006) down to the blow-out size. For this particular collision, Eq. (4) yields smin ≪ sblow for η = 0.1 and γ = 0.1 J / m2, but smin ≃ 6 μm for η = 10-3. Thus, the difference between our results and the fragment sizes of Krivov et al. may be substantial, depending on the true value of η. We stress that our theory is valid for 3 > α > 4, and does not apply to models that use shallower power laws, for example Sect. 4.2 of Krivov et al. (2013).
The importance of the limit given by Eq. (4) depends on the parameters, and can vary per individual collision, depending on the collision velocity and choice for smax. In the rest of this section, we explore in which cases this limit is most relevant.
In a debris disk, a particle of size s0 is most likely formed in a collision between only slightly larger particles. In addition, we focus on collisions between equal-sized particles, as these are most efficient at forming small fragments (Appendix B). Therefore, we use Eq. (6) as an indication for the lower limit of the particle size distribution. Quantitative comparisons require relative collision velocities, which for the largest bodies are often written in terms of the Keplerian orbital velocity at the corresponding distance from the central object. For bodies on orbits with identical semi-major axes, the relative velocity can then be written in terms of orbital eccentricity and inclination as f ≡ vrel/vK = (1.25e2 + i2)1 /2, with vK = (GM⋆/a)1 /2 the Keplerian orbital velocity (Wyatt & Dent 2002). In a debris disk, a range of eccentricities and inclinations will be present. For a rough comparison, we use average quantities ⟨ e ⟩ and ⟨ i ⟩ to obtain typical collision velocities. In reality, ⟨ e ⟩ and ⟨ i ⟩ are poorly constrained. Estimates range from ⟨ e ⟩ ~ ⟨ i ⟩ ~ 10-3−10-1, depending on the level of stirring (Matthews et al. 2014).
 |
Fig. 2 Predicted smin/sblow in debris disks, as a function of disk radius. Arrows indicate how the ratio changes with stellar luminosity, surface energy, f, and η. Coloured regions indicate observational constraints on smin/sblow for various systems (see text), and the diagonal solid lines give our calculations for each system. We fix γ = 0.1 J m-2, f = 10-2, and η = 10-2 for this comparison. |
The ratio between the smallest grain size from Eq. (6) and the blow-out size then becomes 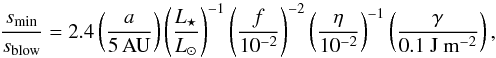 (7)where both the stellar mass
and the material density drop out, and we assumed Qpr = 1. Figure 2 compares this ratio with observations of debris disks at large radii,
where we predict the most pronounced effect. We have used a fixed γ = 0.1 J m-2,
f =
10-2, and η = 10-2, and the arrows indicate the
dependence of smin/sblow
on various parameters. For the main dust belt around Fomalhaut, Min et al. (2010) found the
scattering properties to be consistent with predominantly ~100 μm silicate grains
(sblow = 13
μm Acke et al.
2012). The relative velocities in Fomalhaut are typically taken a factor of 10
higher (Wyatt & Dent 2002). For HD 105, Donaldson et al.
(2012) derived smin = 8.9 μm
(sblow =
0.5 μm) at orbital distances above ~50 AU. Notably, very large grain sizes of
~100 μm (sblow ≲
1 μm) are inferred for the recently discovered
“Herschel cold debris disks” (Krivov et
al. 2013), which are seen around F, G, and K type stars. Krivov et al. were not able to model these systems with a collisional
cascade reaching down to smin = 3 μm, and proposed
that the large grains in these systems are primordial, unstirred material. Our calculations
suggest that they can also be explained as the outcome of a collisional cascade. However,
the model is highly degenerate, as material properties (η and γ) and belt properties
(f) are
usually poorly known, and all have a large impact on smin.
(7)where both the stellar mass
and the material density drop out, and we assumed Qpr = 1. Figure 2 compares this ratio with observations of debris disks at large radii,
where we predict the most pronounced effect. We have used a fixed γ = 0.1 J m-2,
f =
10-2, and η = 10-2, and the arrows indicate the
dependence of smin/sblow
on various parameters. For the main dust belt around Fomalhaut, Min et al. (2010) found the
scattering properties to be consistent with predominantly ~100 μm silicate grains
(sblow = 13
μm Acke et al.
2012). The relative velocities in Fomalhaut are typically taken a factor of 10
higher (Wyatt & Dent 2002). For HD 105, Donaldson et al.
(2012) derived smin = 8.9 μm
(sblow =
0.5 μm) at orbital distances above ~50 AU. Notably, very large grain sizes of
~100 μm (sblow ≲
1 μm) are inferred for the recently discovered
“Herschel cold debris disks” (Krivov et
al. 2013), which are seen around F, G, and K type stars. Krivov et al. were not able to model these systems with a collisional
cascade reaching down to smin = 3 μm, and proposed
that the large grains in these systems are primordial, unstirred material. Our calculations
suggest that they can also be explained as the outcome of a collisional cascade. However,
the model is highly degenerate, as material properties (η and γ) and belt properties
(f) are
usually poorly known, and all have a large impact on smin.
In Fig. 2, we assume constant and equal relative
velocities for all particles. In reality, radiation pressure will also increase the
eccentricities of small particles with β ≲ 0.5. The enhanced eccentricity can be written as
eβ
= β/(1−β). The
relative velocity of such a radiation-influenced particle scales with its size as
vrel ∝
β ∝ s-1, while Eq. (6) predicts the fragmentation velocity scales as
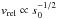 .
Hence, the relative velocity between the smallest particles increases faster
than the velocity needed for fragmentation. As a result, particles can reach
arbitrarily small sizes in this regime. Particles smaller than sblow are then
removed on a short timescale. For a more detailed estimation, β should be evaluated for
each particular case, considering the optical properties of the material and the shape of
the stellar spectrum.
.
Hence, the relative velocity between the smallest particles increases faster
than the velocity needed for fragmentation. As a result, particles can reach
arbitrarily small sizes in this regime. Particles smaller than sblow are then
removed on a short timescale. For a more detailed estimation, β should be evaluated for
each particular case, considering the optical properties of the material and the shape of
the stellar spectrum.
A dearth of small grains in weakly stirred disks is also predicted by Thébault & Wu (2008), but the cause is not a limit on smin. In their scenario, smin is fixed and the production rate of the smallest grains decreases with weaker stirring, while the destruction rate is determined by radiation forces and is unaffected by stirring. While the smallest grains present are always of blow-out size, their abundance is set by the balance between their creation and destruction (their Fig. 7).
While the theory developed in this work predicts that the smallest particles that can fragment further can be quite large and sizes just below this will be depleted, some smaller particles will still be created as a result of erosive collisions, collisions between larger bodies, and collisions that occur above the average collision velocity. Detailed debris disk models implementing the surface energy constraint are needed to determine the resulting size distribution.
4. Discussion
Of the fundamental parameters in our model, the largest uncertainty affects η, the fraction of kinetic energy used for the creation of new surface. While information may be available about the kinetic and surface energy of the largest fragments, it is hard to quantify whether the remainder of the available energy went into surface creation, heat generation, or kinetic energy of the smallest fragments. Experimentally, studying η is challenging, since it requires sensitive and complete measurements down to very small sizes. Once the functional form of η is quantified by laboratory and numerical experiments, observations of smin in a system of interest may constrain f and thus the local relative velocities.
During the preparation of this manuscript, we discovered that a similarly defined smin to the one we present has been explored in a more abstract framework, and without elaborating on applications, by Bashkirov & Vityazev (1996). We note that the lack of data on the size distribution of small collision fragments, as well as the fraction of kinetic and internal energy in the fragments already noted by Bashkirov & Vityazev, still prevails and we encourage further experiments to quantify these important parameters.
Thus far, we have focussed on equal-sized collisions. While collisions with a larger mass
ratio might not lead to catastrophic fragmentation, cratering and erosion may still be
important, and might be able to form small particles (Appendix B). Assuming a fixed relative velocity, we focus on a particle of size
s1. We define a mass loss rate ṁ(s) for the
larger particle, dependent on collider size s. Assuming a collision with a particle of size
s<s1
erodes a mass ∝s3, and noting the
collision timescale is proportional to the particle density and collision cross-section, we
obtain for the total mass loss rate Ṁ = ṁ(s)
ds ∝
s-3.5s3(s +
s1)2 ds. If the
collisional cross-section is dominated by s1, we find
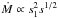 , and
thus the mass loss is dominated by the larger bodies. When s ~
s1, we obtain Ṁ ∝ s5
/2.
, and
thus the mass loss is dominated by the larger bodies. When s ~
s1, we obtain Ṁ ∝ s5
/2.
We have adopted a constant value of 50% of the collider mass for the largest fragment.
However, experiments show smax can be substantially smaller as a
function of material and impact velocity (e.g. Davis
& Ryan 1990; Ryan et al. 1991). Such
results can easily be implemented in Eq. (4)
(and Eqs. B.2 and B.3) as necessary. Since
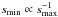 ,
smaller sizes for the largest remnant will make the production of small particles even more
difficult.
,
smaller sizes for the largest remnant will make the production of small particles even more
difficult.
Other collisional systems where the proposed fragment size limit operates include planetary rings. Our calculations are consistent with the observed dominant grain sizes in the rings of Saturn, Jupiter, and Uranus. Because of additional relevant physics, such as tidal and electromagnetic effects, consistency does not directly imply the dominant grain size in all these rings is fragmentation-dominated.
The full implications of an energy-limited smin on systems such as debris disks and planetary rings can only be assessed with models tracking the full particle population with all relevant processes included. For example, if small particles cannot be destroyed in collisions, Poynting-Robertson (PR) drag will influence their orbits, and cause particles to drift towards the star on timescales of Gyr in the outer parts of disks (Wyatt 2005; van Lieshout et al. 2014). Such modelling is outside the scope of the present paper.
5. Conclusions
We investigated the energetic constraints on the lower size limit in a distribution of collision fragments. A quantification of the lower limit of such size distributions is relevant for the modelling
of debris disks and other astrophysical systems where collisional fragmentation is important.
-
1.
Based on surface energy constraints, we derive a parameterised recipe for the smallest fragment size in individual grain-grain collisions.
-
2.
The smallest size in a distribution of fragments from a two-particle collision, constrained by the collision energy, is given by Eq. (4), and illustrated in Fig. 1. For example, at 20 m/s, submicron silicate particles can only be effectively produced by centimeter-sized colliders.
-
3.
In the limit where the colliding bodies are split in half, the fragmentation threshold velocity is given by Eq. (6).
-
4.
While dedicated models are needed to reveal the full implications of the fragment size limit, Fig. 2 offers an indication of where the size distribution is expected to be influenced.
-
5.
In systems where the collision velocities are low, our theory may offer a natural explanation for a paucity of small grains in debris at large orbital distances, such as observed in Fomalhaut and the Herschel cold debris disks (Fig. 2).
Online material
Appendix A: Applicability to aggregates
For porous aggregates, the basic principles explored here are expected to hold, but some material properties have to be altered. First, aggregates have an internal filling factor φ = ρagg/ρ that is <1, and might be as low as 10-4 in some extreme cases (Okuzumi et al. 2012; Kataoka et al. 2013). Second, the ’effective’ surface energy γagg will be smaller, since there is only limited contact between the aggregate’s constituents to begin with. Assuming the parent bodies are built up of spherical monomers, the effective surface energy can be estimated as γagg ~ (a/R)2φ2/3γ, where a and R denote the radius of the contact area shared by monomers, and the radius of the monomers themselves. The fraction (a/R) depends on the size of the monomers and the material properties, but for 0.1-micron-sized monomers, (a/R) ~ 0.1 is reasonable.
For aggregates, N-body simulations have been performed with particles containing up to 106 monomers, and values of η range from close to unity (Dominik & Tielens 1997; Wada et al. 2009), to several orders of magnitude less (Ringl et al. 2012), and depend on the employed contact model (Seizinger et al. 2013).
Appendix B: Collisions with different mass ratios
Here we extend the theory to collisions between “targets” and “projectiles” of
arbitrary sizes st>sp.
Assuming the fragment distribution can be described as before, we can still use Eq.
(2), while the pre-collision kinetic
energy now equals 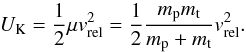 (B.1)For a given collision
velocity, we might then think of two cases, complete fragmentation when sp ~
st, and erosion/cratering when
st ≫
sp.
(B.1)For a given collision
velocity, we might then think of two cases, complete fragmentation when sp ~
st, and erosion/cratering when
st ≫
sp.
Appendix B.1: Catastrophic fragmentation
Since both particles are destroyed completely we may set Mfrag =
mp + mt.
For simplicity we will assume in this section that the change in surface energy is
dominated by the fragments ΔUS =
γAfrag. Using the
same definition for η as before and focussing on the α = 3.5 case, we obtain
![\appendix \setcounter{section}{2} \begin{equation} \label{eq:s_min_uneq} s_{\rm min} = \left[ \frac{ 6 \gamma (s_{\rm p}^3+s_{\rm t}^3)^2}{\eta \rho v_{\rm rel}^2 (s_{\rm p}s_{\rm t})^3}\right]^2 s_{\rm max}^{-1}. \end{equation}](/articles/aa/full_html/2014/06/aa23862-14/aa23862-14-eq116.png) (B.2)
(B.2)
Appendix B.2: Erosion
When the mass ratio becomes very large, it is no longer realistic to assume the
target is completely disrupted. Rather, such collisions result in erosion, and the
eroded mass is typically of the order of the mass of the projectile (Schräpler & Blum 2011). Thus, we write
Mfrag =
κmp, with
κ of
the order of unity. For large mass ratios μ → mp.
Furthermore, assuming that the change in surface energy is dominated by the new
fragments, ΔUS =
γAfrag, we obtain
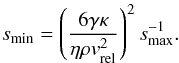 (B.3)Consider now
a particle with a size s0 close to the smaller end of the
size distribution, colliding with particle of sizes sx, ranging from
slightly smaller to much larger than s0. Figure B.1 shows the minimum size of the fragments produced as a function
of collider size sx. The
y-axis
is normalized to the value obtained in equal-sized collisions (i.e. between two
s0 particles). For mass ratios below
unity, s0 acts as the target, and the mass of
the largest fragment is assumed to equal m0/2. For large
mass ratios, s0 acts as a projectile instead, and
the largest fragment mass is set to mx/
2. Collisions at mass ratios above 102 are assumed to be erosive
(Seizinger et al. 2013), with the largest
fragment equalling m0/2. Since both
the excavated mass, and the largest fragment mass, depend on the projectile, the
curves in the erosive regime do not depend on the mass ratio directly. However, the
size of the target does set an upper limit on κ.
(B.3)Consider now
a particle with a size s0 close to the smaller end of the
size distribution, colliding with particle of sizes sx, ranging from
slightly smaller to much larger than s0. Figure B.1 shows the minimum size of the fragments produced as a function
of collider size sx. The
y-axis
is normalized to the value obtained in equal-sized collisions (i.e. between two
s0 particles). For mass ratios below
unity, s0 acts as the target, and the mass of
the largest fragment is assumed to equal m0/2. For large
mass ratios, s0 acts as a projectile instead, and
the largest fragment mass is set to mx/
2. Collisions at mass ratios above 102 are assumed to be erosive
(Seizinger et al. 2013), with the largest
fragment equalling m0/2. Since both
the excavated mass, and the largest fragment mass, depend on the projectile, the
curves in the erosive regime do not depend on the mass ratio directly. However, the
size of the target does set an upper limit on κ.
 |
Fig. B.1 Minimum fragment size resulting from destructive unequal collisions, assuming smin ≪ smax, and relating the largest fragment size to the heavier collider. The y-axis has been normalized with the value for smin in equal-mass collisions. |
One could imagine splitting only one of the colliders, or indeed chipping off only small parts of one of the collider bodies. Since less surface area is created, this would still be allowed at very low velocities. However, in that case the largest fragment is of the same size as s0. We refrain from identifying this as fragmentation, and use the size derived in Eq. (5) as the size below which fragmentation becomes inefficient.
Acknowledgments
The authors wish to thank Carsten Dominik and Xander Tielens for comments and discussions. Dust studies at Leiden Observatory are supported through the Spinoza Premie of the Dutch science agency, NWO. Astrochemistry in Leiden is supported by NOVA, KNAW and EU A-ERC grant 291141 CHEMPLAN.
References
- Acke, B., Min, M., Dominik, C., et al. 2012, A&A, 540, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bashkirov, A. G., & Vityazev, A. V. 1996, Planet. Space Sci., 44, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Beitz, E., Güttler, C., Blum, J., et al. 2011, ApJ, 736, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Biermann, P., & Harwit, M. 1980, ApJ, 241, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, J., & Münch, M. 1993, Icarus, 106, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, D. R., & Ryan, E. V. 1990, Icarus, 83, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Dohnanyi, J. S. 1969, J. Geophys. Res., 74, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, C., & Tielens, A. G. G. M. 1997, ApJ, 480, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Donaldson, J. K., Roberge, A., Chen, C. H., et al. 2012, ApJ, 753, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Fujiwara, A., Kamimoto, G., & Tsukamoto, A. 1977, Icarus, 31, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Gáspár, A., Psaltis, D., Özel, F., Rieke, G. H., & Cooney, A. 2012, ApJ, 749, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Geretshauser, R. J., Speith, R., Güttler, C., Krause, M., & Blum, J. 2010, A&A, 513, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kataoka, A., Tanaka, H., Okuzumi, S., & Wada, K. 2013, A&A, 557, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivov, A. V., Löhne, T., & Sremčević, M. 2006, A&A, 455, 509 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krivov, A. V., Müller, S., Löhne, T., & Mutschke, H. 2008, ApJ, 687, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Krivov, A. V., Eiroa, C., Löhne, T., et al. 2013, ApJ, 772, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Leinhardt, Z. M., & Stewart, S. T. 2012, ApJ, 745, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, B. C., Krivov, A. V., Wyatt, M. C., Bryden, G., & Eiroa, C. 2014, Protostars & Planets VI, in press [arXiv:1401.0743] [Google Scholar]
- Min, M., Kama, M., Dominik, C., & Waters, L. B. F. M. 2010, A&A, 509, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakamura, A., & Fujiwara, A. 1991, Icarus, 92, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Okuzumi, S., Tanaka, H., Kobayashi, H., & Wada, K. 2012, ApJ, 752, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, M., & Schlichting, H. E. 2012, ApJ, 747, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Ringl, C., Bringa, E. M., Bertoldi, D. S., & Urbassek, H. M. 2012, ApJ, 752, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, E. V. 2000, Ann. Rev. Earth Planet. Sci., 28, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Ryan, E. V., Hartmann, W. K., & Davis, D. R. 1991, Icarus, 94, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Schräpler, R., & Blum, J. 2011, ApJ, 734, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Seizinger, A., Krijt, S., & Kley, W. 2013, A&A, 560, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takagi, Y., Mizutani, H., & Kawakami, S.-I. 1984, Icarus, 59, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P., & Wu, Y. 2008, A&A, 481, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thébault, P., Augereau, J. C., & Beust, H. 2003, A&A, 408, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Lieshout, R., Dominik, C., Kama, M., & Min, M. 2014, A&A, in press [arXiv:1404.3271] [Google Scholar]
- Wada, K., Tanaka, H., Suyama, T., Kimura, H., & Yamamoto, T. 2009, ApJ, 702, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C. 2005, A&A, 433, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyatt, M. C., & Dent, W. R. F. 2002, MNRAS, 334, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Wyatt, M. C., Booth, M., Payne, M. J., & Churcher, L. J. 2010, MNRAS, 402, 657 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top: minimum fragment size smin in a 20 m/s collision (Eq. (4)) for three materials, as a function of collider size s0. We have assumed η = 10-2 and smax = 2−1 / 3s0. The grey shaded areas are excluded because of mass conservation (left), and self-gravity (right). The dotted lines indicate the limit of Eq. (6). Bottom: critical energies versus size for equal-sized collisions. The energy needed to split a particle (e.g. Eq. (6)) is shown for η = 10-3 (dotted) and η = 1 (dashed). The solid curves correspond to catastrophic fragmentation of aggregates (Beitz et al. 2011), and ice and basalt (Benz & Asphaug 1999), showing both the strength-dominated (small sizes) and self-gravity dominated regimes (large sizes). |
| In the text | |
 |
Fig. 2 Predicted smin/sblow in debris disks, as a function of disk radius. Arrows indicate how the ratio changes with stellar luminosity, surface energy, f, and η. Coloured regions indicate observational constraints on smin/sblow for various systems (see text), and the diagonal solid lines give our calculations for each system. We fix γ = 0.1 J m-2, f = 10-2, and η = 10-2 for this comparison. |
| In the text | |
 |
Fig. B.1 Minimum fragment size resulting from destructive unequal collisions, assuming smin ≪ smax, and relating the largest fragment size to the heavier collider. The y-axis has been normalized with the value for smin in equal-mass collisions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


